② 中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 湖南长沙 410083;
③ 东方地球物理公司综合物化探处, 河北涿州 072751
② Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring of Ministry of Education, Central South University, Changsha, Hunan 410083, China;
③ GME & Geochemical Surveys, BGP, CNPC, Zhuozhou, Hebei 072751, China
在电磁场地球物理方法中,均匀层状介质电磁场解析表达式含有汉克尔积分[1-2],其核函数为0阶和1阶Bessel函数。随着其宗量的增大,Bessel函数呈现快速振荡和慢衰减的特征,造成汉克尔积分难以实现高效、高精度的计算,特别是高频和大收发距情况下难度更大。为了解决这个问题,学者们提出了许多方法,主要分为两大类:第一类为数字滤波方法;第二类为直接积分法(Direct integration method,DIM)。Ghosh[3]首先将数字滤波法引入地球物理数值计算;针对电磁法,Johansen等[4]提出了汉克尔数字滤波系数的解析计算方法。之后,很多研究者给出了不同优化滤波系数[5-6]。蔡盛[7]对比了5组高精度快速汉克尔长滤波系数的计算精度,研究结果表明在一定的收发距和频率范围内,计算精度较高,但耗时太大,随着滤波系数的增大而增长。总体来说,数字滤波法适用于中、低频和适中的收发距情况,在高频和大收发距的情况下计算精度很低。考虑到数字滤波法的局限性,众多学者利用多项式精确拟合核函数的思想,达到求解解析解的目的,提出了直接积分类方法。代表性方法包括高斯积分法[8]、基于快速正弦余弦算法的汉克尔变换算法[9]、直接法[10]、离散复镜像法[11-12]、谱域法[13]、基于高阶窗函数的结合非线性变换的算法[14]、外推积分方法(QWE)[15]、三次样条插值法[16]等。其中最后一种方法采用三次样条函数对核函数进行插值,得到一系列核函数为多项式的简单Sommerfeld积分,再利用Bessel函数的递推公式和Lommel公式的渐进展开求解。这些方法虽能较好地应用于低频和适中收发距的均匀层状介质电磁场的计算,但随着频率和收发距的增大,这些方法的计算精度逐渐降低,甚至失效。针对高频电磁场的计算,郑圣谈等[17]提出了高密度采样数字滤波法,但当介质导电率变小、介电常数变大、收发距变大、频率增加时,该方法计算精度会大幅度降低,不具普适性。
针对电磁场汉克尔积分核函数复杂的特点,本文提出一种高效、高精度直接积分方法,用于频率和收发距广普适用的电磁场高效、高精度的数值计算。其基本思想是Bessel函数可以在两个区间分别用不同的多项式展开,每一区间的汉克尔积分可离散为多个单元积分之和,每个单元被积函数采用三次样条插值函数表示,由此可求得积分的解析解,并通过求和获得汉克尔积分的数值解。在此基础上,利用均匀全空间电偶极子电磁场的解析解,正确选取积分范围,并合理剖分积分单元。数值解与解析解对比表明,本文算法正确、可靠。与数字滤波类算法的比较表明,本文算法广泛适用于不同频率和不同收发距电磁场的计算,具有较强的普适性。
1 方法原理均匀层状介质电磁场的解析解可用汉克尔积分表示
| $ F = \int_0^\infty g (m){J_n}(mr){\rm{d}}m $ | (1) |
式中:g(m)为大地响应函数,m表示积分参数;r为发射源到接收点的水平距离,mr为宗量;Jn(·)为n阶Bessel函数。
式(1)中,Bessel函数为0阶和1阶,根据特殊函数手册[18],可以分别在两个区间用不同的多项式展开。第一区间为0≤mr≤4,Bessel函数可展开为简单的代数多项式,每个积分单元内代数多项式与响应函数的乘积可用三次样条插值函数表示。第二区间为4 < mr < ∞,Bessel函数可展开为含有正余弦函数的多项式,每个积分单元内正余弦函数之前的系数多项式与响应函数的乘积可用三次样条插值函数表示。下面以0阶Bessel函数汉克尔积分的计算为例,给出解析表达式。1阶Bessel函数汉克尔积分的解析表达式详见附录A。
令
在第一个区间(0≤mr≤4)有
| $ \begin{array}{*{20}{l}} {{J_0}(mr) = - 0.0005014415{t^7} + 0.0076771853{t^6} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.0709253492{t^5} + 0.4443584263{t^4} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 1.7777560599{t^3} + 3.9999973021{t^2} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 3.9999998721t + 1.0 + {e_0}(mr)} \end{array} $ | (2) |
式中截断误差e0≤1×10-8。
在第二个区间(4 < mr < ∞)有
| $ {J_0}(mr) = \sqrt {\frac{2}{{\pi mr}}} ({P_0}(mr)\cos {\theta _0} - {Q_0}\sin {\theta _0}) $ | (3) |
式中
| $ \left\{ \begin{array}{l} {\theta _0} = mr - \frac{\pi }{4}\\ \begin{array}{*{20}{l}} {{P_0}(mr) = - 0.000009285{t^{ - 5}} + 0.000043506{t^{ - 4}} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.000122226{t^{ - 3}} + 0.000434725{t^{ - 2}} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.004394275{t^{ - 1}} + 0.999999997 + {e_1}(mr)} \end{array}\\ \begin{array}{*{20}{l}} {{Q_0}(mr) = \frac{4}{{mr}}(0.000008099{t^{ - 5}} - 0.000035614{t^{ - 4}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.000085844{t^{ - 3}} - 0.000218024{t^{ - 2}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.001144106{t^{ - 1}}) - 0.031249995 + {e_2}(mr)} \end{array} \end{array} \right. $ | (4) |
其中截断误差e1、e2≤1×10-8。
对第一区间0≤mr≤4,将积分范围均匀剖分为N个单元。由式(2)可知,Bessel函数的展开式为简单的代数多项式,因此设f(m)=g(m)J0(mr),这个区间的积分F1可表示为
| $ {F_1} = \sum\limits_{i = 1}^N {\int_{{m_i}}^{{m_{i + 1}}} {{f_i}} } (m){\rm{d}}m $ | (5) |
式中mi(i=1, 2, …, N, N+1)为离散采样点。每个单元内被积函数fi用三次样条插值函数[18-19]表示为
| $ \begin{array}{l} {f_i} = {d_i}{(m - {m_i})^3} + {c_i}{(m - {m_i})^2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {b_i}(m - {m_i}) + {a_i} \end{array} $ | (6) |
式中ai、bi、ci、di为单元i的三次样条插值函数的系数。设Li=mi+1-mi为单元i的长度,单元i的积分解析表达式为
| $ I_{\rm{e}}^i = \frac{1}{4}{d_i}L_i^4 + \frac{1}{3}{c_i}L_i^3 + \frac{1}{2}{b_i}L_i^2 + {a_i}{L_i} $ | (7) |
因此,第一区间各单元积分累加的结果为
| $ {F_1} = \sum\limits_{i = 1}^N {I_{\rm{e}}^i} $ | (8) |
对于第二区间4 < mr < ∞,可剖分为M个单元,mi(i=1, 2, …, M, M+1)为离散采样点,网格长度为dmi,这个区间的积分可表示为
| $ \begin{array}{*{20}{l}} {{F_2} = \sum\limits_{i = 1}^M {\int_{{m_i}}^{{m_{i + 1}}} {\left\{ {g({m_i})\sqrt {\frac{1}{{\pi {m_i}r}}} {P_0}[\cos ({m_i}r) + \sin ({m_i}r)] - } \right.} } }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {g({m_i})\sqrt {\frac{1}{{\pi {m_i}r}}} {Q_0}[\sin ({m_i}r) - \cos ({m_i}r)]} \right\}{\rm{d}}{m_i}} \end{array} $ | (9) |
设
| $ \left\{ {\begin{array}{*{20}{l}} {F_i^{\rm{p}} = g({m_i})\sqrt {\frac{1}{{\pi {m_i}r}}} {P_0}}\\ {F_i^{\rm{q}} = g({m_i})\sqrt {\frac{1}{{\pi {m_i}r}}} {Q_0}} \end{array}} \right. $ | (10) |
在每个单元内,Fip、Fiq变化规律简单,可采用三次样条插值函数近似表示为
| $ \left\{ {\begin{array}{*{20}{l}} {F_i^{\rm{p}} = d_i^{\rm{p}}{{(m - {m_i})}^3} + c_i^{\rm{p}}{{(m - {m_i})}^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} b_i^{\rm{p}}(m - {m_i}) + a_i^{\rm{p}}}\\ {F_i^{\rm{q}} = d_i^{\rm{q}}{{(m - {m_i})}^3} + c_i^{\rm{q}}{{(m - {m_i})}^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} b_i^{\rm{q}}(m - {m_i}) + a_i^{\rm{q}}} \end{array}} \right. $ | (11) |
式中app、aqq、bpp、bqq、cpp、cqq、dpp、dqq表示插值系数,可利用三次样条插值方法求得。将式(11)代入式(9),求得该区间单元积分Tei的解析表达式为
| $ \begin{array}{*{20}{l}} {T_{\rm{e}}^i = (d_i^{\rm{p}} + d_i^{\rm{q}})T_1^i + (d_i^{\rm{p}} - d_i^{\rm{q}})T_2^i + (c_i^{\rm{p}} + c_i^{\rm{q}})T_3^i + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (c_i^{\rm{p}} - c_i^{\rm{q}})T_4^i + (b_i^{\rm{p}} + b_i^{\rm{q}})T_5^i + (b_i^{\rm{p}} - b_i^{\rm{q}})T_6^i + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (a_i^{\rm{p}} + a_i^{\rm{q}})T_7^i + (a_i^{\rm{p}} - a_i^{\rm{q}})T_8^i} \end{array} $ | (12) |
式中
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {T_1^i = \frac{{3( - 2 + {r^2}{t^2})\cos ({m_{i + 1}}r) + rt( - 6 + {r^2}{t^2})\sin ({m_{i + 1}}r) + 6\cos ({m_i}r)}}{{{r^4}}}}\\ {T_2^i = \frac{{3( - 2 + {r^2}{t^2})\sin ({m_{i + 1}}r) - rt( - 6 + {r^2}{t^2})\cos ({m_{i + 1}}r) + 6\sin ({m_i}r)}}{{{r^4}}}}\\ {T_3^i = \frac{{2rt\cos ({m_{i + 1}}r) + ( - 2 + {r^2}{t^2})\sin ({m_{i + 1}}r) + 2\sin ({m_i}r)}}{{{r^3}}}} \end{array}\\ \begin{array}{*{20}{l}} {T_4^i = \frac{{2rt\sin ({m_{i + 1}}r) - ( - 2 + {r^2}{t^2})\cos ({m_{i + 1}}r)}}{{{r^3}}}}\\ {T_5^i = \frac{{\cos ({m_{i + 1}}r) + rt\sin ({m_{i + 1}}r) - \cos ({m_i}r)}}{{{r^2}}}}\\ {T_6^i = \frac{{\sin ({m_{i + 1}}r) - rt\cos ({m_{i + 1}}r) - \sin ({m_i}r)}}{{{r^2}}}}\\ {T_7^i = \frac{{\sin ({m_{i + 1}}r) - \sin ({m_i}r)}}{r}}\\ {T_8^i = \frac{{\cos ({m_{i + 1}}r) - \cos ({m_i}r)}}{r}} \end{array} \end{array} \right. $ | (13) |
因此,第二区间各单元积分累加求和结果为
| $ {{F_2} = \sum\limits_{i = 1}^M {T_{\rm{e}}^i} } $ | (14) |
最终汉克尔积分为
| $ {F = {F_1} + {F_2}} $ | (15) |
为了提高计算精度和效率,需合理选取积分范围,恰当地进行单元剖分,而这些参数的选取依赖于响应函数的特征和变化规律[19-20]。本文以均匀全空间电偶极子源电磁场为例,通过研究不同响应函数的变化规律,确定积分范围,并选定单元剖分方案。
在均匀全空间中,将x方向上电偶极子源产生的电、磁场用汉克尔积分表示,其解析解的汉克尔积分表达式分别为
| $ \left\{ \begin{array}{l} {E_x} = \frac{{I{\rm{d}}l}}{{4\pi }}\frac{1}{{\hat y}}\frac{{{{\rm{e}}^{ - {\rm{i}}kR}}}}{{{R^3}}}\left[ {\frac{{{{\left( {x - {x_{\rm{s}}}} \right)}^2}}}{{{R^2}}}\left( { - {k^2}{R^2} + 3{\rm{i}}kR + 3} \right) + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\left( {{k^2}{R^2} - {\rm{i}}kR - 1} \right)} \right]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{I{\rm{d}}l}}{{4\pi }} - \hat z\int_0^\infty {\frac{m}{{{m_1}}}} {{\rm{e}}^{ - {m_1}\left| {z - {z_{\rm{s}}}} \right|}}{J_0}(mr){\rm{d}}m + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{I{\rm{d}}l}}{{4\pi }}\frac{1}{{\hat y}}\frac{{2{{\left( {x - {x_{\rm{s}}}} \right)}^2} - {r^2}}}{{{r^3}}}\int_0^\infty {\frac{{{m^2}}}{{{m_1}}}} {{\rm{e}}^{ - {m_1}\left| {z - {z_{\rm{s}}}} \right|}}{J_1}(mr){\rm{d}}m - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{I{\rm{d}}l}}{{4\pi }}\frac{1}{{\hat y}}\frac{{{{\left( {x - {x_{\rm{s}}}} \right)}^2}}}{{{r^2}}}\int_0^\infty {\frac{{{m^3}}}{{{m_1}}}} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\rm{e}}^{ - {m_1}\left| {z - {z_{\rm{s}}}} \right|}}{J_0}(mr){\rm{d}}m \end{array} \right. $ | (16a) |
| $ \left\{ \begin{array}{l} {E_y} = \frac{{I{\rm{d}}l}}{{4\pi }}\frac{1}{{\hat y}}\frac{{{{\rm{e}}^{ - {\rm{i}}kR}}}}{{{R^3}}}\frac{{\left( {x - {x_{\rm{s}}}} \right)\left( {y - {y_{\rm{s}}}} \right)}}{{{R^2}}} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( { - {k^2}{R^2} + 3{\rm{i}}kR + 3} \right)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = - \frac{{I{\rm{d}}l}}{{4\pi }}\frac{1}{{\hat y}}\frac{{\left( {x - {x_{\rm{s}}}} \right)\left( {y - {y_{\rm{s}}}} \right)}}{{{r^2}}} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_0^\infty {\frac{{{m^3}}}{{{m_1}}}} {{\rm{e}}^{ - {m_1}\left| {z - {z_{\rm{s}}}} \right|}}{J_0}(mr){\rm{d}}m + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{I{\rm{d}}l}}{{4\pi }}\frac{1}{{\hat y}}\frac{{2\left( {x - {x_{\rm{s}}}} \right)\left( {y - {y_{\rm{s}}}} \right)}}{{{r^3}}} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_0^\infty {\frac{{{m^2}}}{{{m_1}}}} {{\rm{e}}^{ - {m_1}\left| {z - {z_{\rm{s}}}} \right|}}{J_1}(mr){\rm{d}}m\\ {E_z} = \frac{{I{\rm{d}}l}}{{4\pi }}\frac{1}{{\hat y}}\frac{{{{\rm{e}}^{ - {\rm{i}}kR}}}}{{{R^3}}}\frac{{\left( {x - {x_{\rm{s}}}} \right)\left( {z - {z_{\rm{s}}}} \right)}}{{{R^2}}} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( { - {k^2}{R^2} + 3{\rm{i}}kR + 3} \right)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{I{\rm{d}}l}}{{4\pi }}\frac{1}{{\hat y}}\frac{{x - {x_{\rm{s}}}}}{r}{\mathop{\rm sign}\nolimits} \left( {z - {z_{\rm{s}}}} \right) \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_0^\infty {{m^2}} {{\rm{e}}^{ - {m_1}\left| {z - {z_{\rm{s}}}} \right|}}{J_1}(mr){\rm{d}}m \end{array} \right. $ | (16b) |
| $ \left\{ {\begin{array}{*{20}{l}} {{H_x} = 0}\\ {{H_y} = - \frac{{I{\rm{d}}l}}{{4\pi }}\frac{{{{\rm{e}}^{ - {\rm{i}}kR}}}}{{{R^2}}}({\rm{i}}kR + 1)\frac{{z - {z_{\rm{s}}}}}{R}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = - \frac{{I{\rm{d}}l}}{{4\pi }} {\rm{sign}} (z - {z_{\rm{s}}})\int_0^\infty m {{\rm{e}}^{ - {m_1}|z - {z_{\rm{s}}}|}}{J_0}(mr){\rm{d}}m}\\ {{H_z} = \frac{{I{\rm{d}}l}}{{4\pi }}\frac{{{{\rm{e}}^{ - {\rm{i}}kR}}}}{{{R^2}}}({\rm{i}}kR + 1)\frac{{y - {y_{\rm{s}}}}}{R}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{I{\rm{d}}l}}{{4\pi }}\frac{{y - {y_{\rm{s}}}}}{r}\int_0^\infty {\frac{{{m^2}}}{{{m_1}}}} {{\rm{e}}^{ - {m_1}|z - {z_{\rm{s}}}|}}{J_1}(mr){\rm{d}}m} \end{array}} \right. $ | (17) |
式中:E、H分别代表电场和磁场;R表示发射源到接收点的水平距离;
| $ \left\{ {\begin{array}{*{20}{l}} {{g_1} = \frac{m}{{{m_1}}}{{\rm{e}}^{ - {m_1}|z - {z_{\rm{s}}}|}}}\\ {{g_2} = \frac{{{m^2}}}{{{m_1}}}{{\rm{e}}^{ - {m_1}|z - {z_{\rm{s}}}|}}}\\ {{g_3} = \frac{{{m^3}}}{{{m_1}}}{{\rm{e}}^{ - {m_1}|z - {z_{\rm{s}}}|}}} \end{array}} \right. $ | (18) |
取电导率σ=0.0001S/m,相对介电常数ε=1,电偶极子源中心坐标为(0, 0, 0),偶极矩为1C·m,频率v=1×108Hz,积分变量m在[1×10-12, 1×108]区间按对数等间距均匀采样,每一个对数单位内采样点为5000个。计算上述三种响应函数的值,结果如图 1所示。

|
图 1 三种响应函数随m的变化曲线 |
由图 1可以看出,m从1×10-6增大到1×10-1时,三种响应函数的对数值呈线性增大;当m为1×10-1~1×101时,三种响应函数值随m变化较快,尤其在1×100附近出现尖脉冲;m>102时三种响应函数随着m的增大按照对数以近似线性规律迅速衰减;在m接近1×103时,三种函数的值均衰减至低于10-20。根据上述分析结果,m的积分范围可选取为[0, 1×104],并整体上按照对数等间距规律进行单元剖分。特别地,在m为1×10-1~1×102时,因响应函数值变化较快,单元剖分可适当加密,尤其在m接近1×100时,响应函数变化剧烈,单元剖分需格外加密。
根据以上原则,对均匀全空间电偶极子源产生电磁场用汉克尔积分表达式进行数值计算,并与解析解进行比较,以验证算法的正确性。下文分别计算均匀全空间中1×104、1×108Hz的电场响应。
对v=1×104Hz,计算zr=40m所在平面的电磁场,计算范围:x方向为-500~500m,y方向为-500~500m,m的采样区间为0~1×104。在区间1×10-3~1×101加密积分单元,总采样点数为373。图 2为电场分量的数值解、解析解及相对误差平面图。由图可见,数值解与解析解曲线形态基本一致,相对误差都很小,最大为8×10-6(Ex分量),即便在源附近,其误差也不大于1%,表明本文算法的正确性和可靠性,且精度较高。
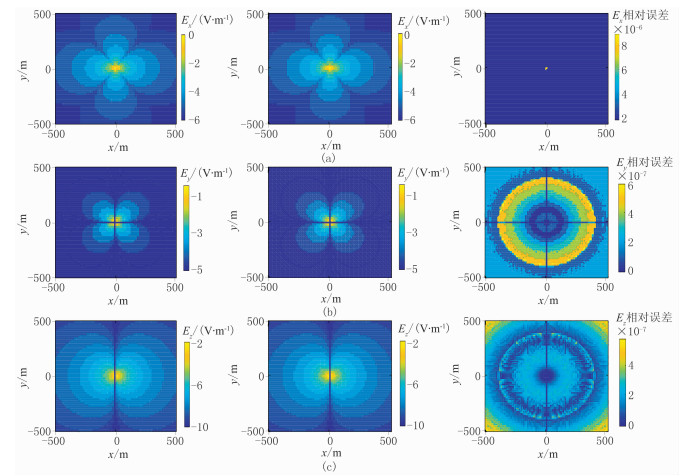
|
图 2 v=1×104Hz时电场分量Ex(a)、Ey(b)、Ez(c)的解析解(左)、数值解(中)及其相对误差(右) |
对v=1×108Hz,计算zr=10m所在平面的电场。计算的平面范围x方向为-15~15m,y方向为-15~15m,m的采样区间为0~1×105,在区间1×10-2~1×100加密采样点,总采样点数为811。图 3为该模型的电场分量数值解、解析解及相对误差平面图。从图 3可看出,数值解与解析解曲线形态基本一致,相对误差很小,其中Ey分量的误差最大,最大为4×10-6,即便如此,在源附近的误差也都不大于1%,这表明算法在高频时计算的场值是正确、可靠的,且精度较高。
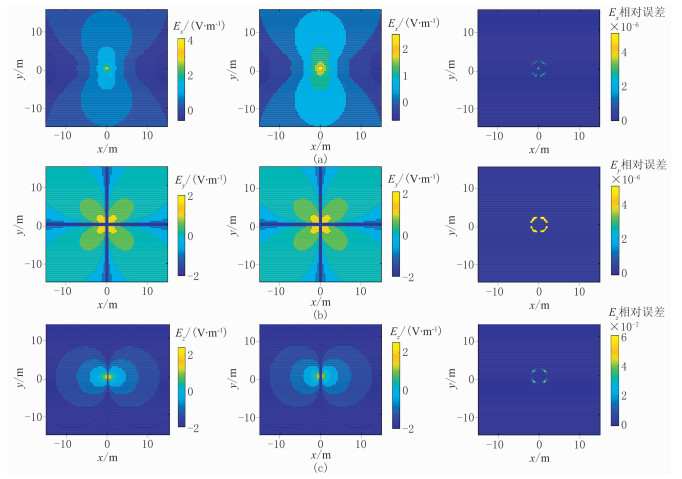
|
图 3 v=1×108Hz时电场分量Ex(a)、Ey(b)、Ez(c)的解析解(左)、数值解(中)及其相对误差(右) |
上述两个频率的计算结果证明了本文算法正确、可靠,且能适应高频电磁场的计算。
3 模型算例设计均匀全空间模型和均匀层状介质模型,分别使用本文DIM算法和常用的数字滤波类算法模拟电磁场,以验证本文算法对不同频率、不同收发距电磁场模拟计算的广普适用性。
3.1 均匀全空间模型首先验证本文算法对于频率的广普适用性。在均匀全空间中,设发射源到接收点的水平距离R=100m,计算频率范围为1×10-2~1×1010Hz,电导率σ=0.0001S/m,相对介电常数ε=1,电偶极子源中心坐标为(0, 0, 0),偶极矩为1C·m。分别使用本文算法与四种经典的数字滤波算法计算该模型的数值解与解析解的相对误差,其中四种数字滤波算法的滤波系数选取见表 1。数字滤波方法①和②参见文献[21],方法③和方法④分别参见文献[22]和文献[23]。这四种方法及本文提出的直接积分法计算结果如图 4所示,其中黑色直线表示相对误差为1%。从图 4可看出,在频率v < 1×106Hz的情况下,这四种数字滤波类算法的计算误差均小于1%;随着频率的升高,四种滤波系数类算法的误差越来越大,而本文直接积分法的计算误差小于1%。表明本文提出的直接积分法计算精度高,在广泛的频率范围内适用。
|
|
表 1 四种常用的数字滤波算法的滤波系数长度取值 |
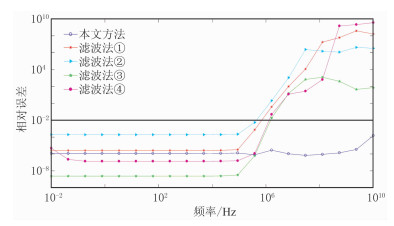
|
图 4 均匀全空间模型不同频率下直接积分法与四种常用数字滤波类法Ex分量计算误差对比 |
为验证该方法对收发距的广普适用性,在均匀全空间中,取频率v=1×107Hz,发射源到接收点的水平距离r范围为1×10-3~1×103m,其他参数不变。使用本文算法与四种经典的数字滤波算法分别计算不同收发距时的数值解与解析解的相对误差,其中四种数字滤波算法的滤波系数选取同上(表 1)。计算结果见图 5。可以看出,在收发距r < 2m时,直接积分法和四种数字滤波类算法的计算误差均小于1%;但随着收发距的增大,四种滤波系数类算法的误差越来越大,而直接积分法在任意r时,计算误差均不大于1%。表明本文提出的直接积分法计算精度高,在广泛的收发距范围内适用。

|
图 5 均匀全空间模型不同收发距下直接积分法与四种常用数字滤波类法Ex分量计算误差对比 |
设计一个三层层状介质模型,模型参数见图 6。电偶极子源中心坐标为(0, 0, 0),偶极矩为1C·m。计算频率v=1×108Hz、z=10m所在平面的电场分量,计算平面范围x方向和y方向均为-15~15m。

|
图 6 三层层状模型断面示意图 |
图 7和图 8分别为表 1中第④种数字滤波法与本文直接积分法计算的Ex、Ey、Ez实部与虚部平面等值线图。由图可见,数字滤波法计算的Ex、Ey、Ez等值线圆滑度较低,表明计算结果有一定误差,而直接积分算法计算的电场等值线圆滑度较高,表明计算结果更准确、精度更高。

|
图 7 三层层状介质模型直接积分法(上)与数字滤波法(下)计算的电场分量Ex(a)、Ey(b)和Ez(c)实部平面等值线图 |
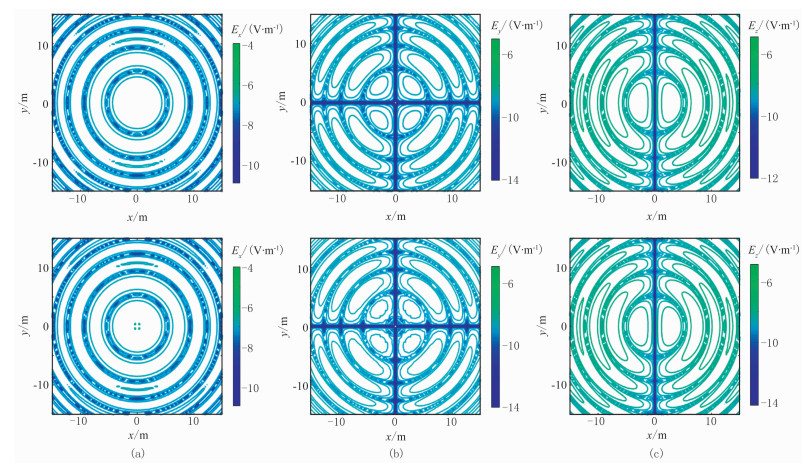
|
图 8 三层层状介质模型直接积分法(上)与数字滤波法(下)计算的电场分量Ex(a)、Ey(b)和Ez(c)虚部平面等值线图 |
本文提出一种高效、高精度的直接积分方法,适用于不同频率和不同收发距的电磁场模拟计算,尤其适合高频电磁场的计算,具体取得以下结论。
(1) 利用Bessel函数可以在两个积分区间分别用不同的多项式展开。将每一区间的汉克尔积分离散成多个单元积分之和,每个单元被积函数采用三次样条插值函数表示,由此可求得积分的解析解。通过叠加,求得汉克尔积分的数值解。
(2) 响应函数的特征和变化规律是积分参数选取的关键因素。为此,以均匀全空间电偶极子源电磁场为例,研究了三种典型的响应函数随积分变量的变化规律。计算结果表明,三种响应函数随积分变量呈对数规律变化,据此按对数规律确定积分范围和单元剖分:在响应函数值变化快的地方,单元剖分可适当加密,尤其在尖脉冲附近,单元剖分需格外加密;在响应函数值变化慢的地方,单元剖分可适当稀疏。这样合理剖分积分单元可提高直接积分法的计算精度和效率。均匀全空间电偶极子源电磁场数值解与解析解对比表明本文算法更正确、可靠。
(3) 分别设计均匀全空间模型和层状介质模型,对本文提出的直接积分法与数字滤波方法电磁场数值计算结果进行对比,结果表明本文积分法对频率和收发距具有广普适用性,尤其对高频电磁场,其优势更加突出,为高频电磁场的计算提供了重要的方法基础。
附录A 1阶Bessel函数汉克尔积分的解析表达式推导过程根据特殊函数手册[18],对J1(mr)函数分两个区间进行展开。
在第一个区间(0≤mr≤4)
| $ \begin{array}{*{20}{l}} {{J_1}(mr) = \sqrt t ( - 0.0001289769{t^7} + 0.002206915{t^6} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.0236616773{t^5} + 0.1777582922{t^4} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.8888839648{t^3} + 2.6666660544{t^2} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 3.9999999710t + 1.9999999998) + {e_0}(mr)} \end{array} $ | (A-1) |
其中截断误差e0≤1×10-8。
在第二个区间(4 < mr < ∞)
| $ {J_1}(mr) = \sqrt {\frac{2}{{\pi mr}}} ({P_1}\cos {\theta _1} - {Q_1}\sin {\theta _1}) $ | (A-2) |
式中
| $ \left\{ {\begin{array}{*{20}{l}} {{\theta _1} = mr - \frac{\pi }{4}}\\ {{P_1}(mr) = 0.000010632{t^{ - 5}} - 0.000050363{t^{ - 4}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.000145575{t^{ - 3}} - 0.000559487{t^{ - 2}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.007323931{t^{ - 1}} + 1.000000004 + {e_1}(mr)} \end{array}} \right. $ | (A-3) |
| $ \begin{array}{*{20}{l}} {{Q_1}(mr) = \frac{4}{{mr}}( - 0.000009173{t^{ - 5}} + 0.000040658{t^{ - 4}} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.000999941{t^{ - 3}} + 0.000266891{t^{ - 2}} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 0.001601836{t^{ - 1}} + 0.093749994) + {e_2}(mr)} \end{array} $ | (A-4) |
其中截断误差e1、e2≤1×10-8。
对于第一区间(0≤mr≤4),将其剖分为N个单元,由式(A-2)可知,Bessel函数的展开式为简单的代数多项式,因此设f(m)=g(m)J1(mr),这部分的积分为
| $ {F_1} = \int_0^{\frac{4}{r}} f (m){\rm{d}}m $ | (A-5) |
设mi (i=1, 2, …, N, N+1)为离散采样点,每个单元内被积函数fi可采用三次样条插值函数表示为
| $ \begin{array}{l} {f_i} = {d_i}{(m - {m_i})^3} + {c_i}{(m - {m_i})^2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {b_i}(m - {m_i}) + {a_i} \end{array} $ | (A-6) |
设Li=mi+1-mi为每个单元的长度,单元积分Iei的解析表达式为
| $ I_{\rm{e}}^i = \frac{1}{4}{d_i}L_i^4 + \frac{1}{3}{c_i}L_i^3 + \frac{1}{2}{b_i}L_i^2 + {a_i}{L_i} $ | (A-7) |
第一区间各单元积分累加表达式为
| $ {F_1} = \sum\limits_{i = 1}^N {I_{\rm{e}}^i} $ | (A-8) |
对第二区间(4 < mr < ∞),将其剖分为M个单元,mi (i=1, 2, …, M, M+1)为离散采样点,这个区间的积分可表示为
| $ \begin{array}{l} {F_2} = \sum\limits_{i = 1}^M {\int_{{m_i}}^{{m_{i + 1}}} {\left\{ {g\left( {{m_i}} \right)\sqrt {\frac{1}{{\pi {m_i}r}}} {P_1}\left[ {\cos \left( {{m_i}r} \right) + \sin \left( {{m_i}r} \right)} \right] - } \right.} } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {g\left( {{m_i}} \right)\sqrt {\frac{1}{{\pi {m_i}r}}} {Q_1}\left[ {\sin \left( {{m_i}r} \right) - \cos \left( {{m_i}r} \right)} \right]} \right\}{\rm{d}}m \end{array} $ | (A-9) |
设
| $ \left\{ {\begin{array}{*{20}{l}} {{F^{\rm{p}}} = g(m)\sqrt {\frac{1}{{\pi mr}}} {P_1}}\\ {{F^{\rm{q}}} = g(m)\sqrt {\frac{1}{{\pi mr}}} {Q_1}} \end{array}} \right. $ | (A-10) |
在每个单元内,Fp、Fq变化规律简单,可采用三次样条插值函数近似表示为
| $ \left\{ {\begin{array}{*{20}{l}} {F_i^{\rm{p}} = d_i^{\rm{p}}{{(m - {m_i})}^3} + c_i^{\rm{p}}{{(m - {m_i})}^2} + b_i^{\rm{p}}(m - {m_i}) + a_i^{\rm{p}}}\\ {F_i^{\rm{q}} = d_i^{\rm{q}}{{(m - {m_i})}^3} + c_i^{\rm{q}}{{(m - {m_i})}^2} + b_i^{\rm{q}}(m - {m_i}) + a_i^{\rm{q}}} \end{array}} \right. $ | (A-1) |
利用三次样条插值方法理论,可求出上式中的未知量aip、aiq、bip、biq、cip、ciq。将式(A-11)代入式(A-9)中,求得这个分段区间的单元积分Tei的解析表达式为
| $ \begin{array}{*{20}{l}} {T_{\rm{e}}^i = (d_i^{\rm{p}} + d_i^{\rm{q}})T_1^i + (d_i^{\rm{p}} - d_i^{\rm{q}})T_2^i + (c_i^{\rm{p}} + c_i^{\rm{q}})T_3^i + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (c_i^{\rm{p}} - c_i^{\rm{q}})T_4^i + (b_i^{\rm{p}} + b_i^{\rm{q}})T_5^i + (b_i^{\rm{p}} - b_i^{\rm{q}})T_6^i + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (a_i^{\rm{p}} + a_i^{\rm{q}})T_7^i + (a_i^{\rm{p}} - a_i^{\rm{q}})T_8^i} \end{array} $ | (A-12) |
式中
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {T_1^i = [3( - 2 + {r^2}{t^2})\cos ({m_{i + 1}}r) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} rt( - 6 + {r^2}{t^2})\sin ({m_{i + 1}}r) + 6\cos ({m_i}r)]{r^{ - 4}}}\\ {T_2^i = [3( - 2 + {r^2}{t^2})\sin ({m_{i + 1}}r) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} rt( - 6 + {r^2}{t^2})\cos ({m_{i + 1}}r) + 6\sin ({m_i}r)]{r^{ - 4}}}\\ {T_3^i = [2rt\cos ({m_{i + 1}}r) + ( - 2 + {r^2}{t^2})\sin ({m_{i + 1}}r) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2\sin ({m_i}r)]{r^{ - 3}}} \end{array}\\ \begin{array}{*{20}{l}} {T_4^i = [2rt\sin ({m_{i + 1}}r) - ( - 2 + {r^2}{t^2})\cos ({m_{i + 1}}r)]{r^{ - 3}}}\\ {T_5^i = [\cos ({m_{i + 1}}r) + rt\sin ({m_{i + 1}}r) - \cos ({m_i}r)]{r^{ - 2}}}\\ {T_6^i = [\sin ({m_{i + 1}}r) - rt\cos ({m_{i + 1}}r) - \sin ({m_i}r)]{r^{ - 2}}}\\ {T_7^i = [\sin ({m_{i + 1}}r) - \sin ({m_i}r)]{r^{ - 1}}}\\ {T_8^i = - [\cos ({m_{i + 1}}r) - \cos ({m_i}r)]{r^{ - 1}}} \end{array} \end{array} \right. $ | (A-13) |
可求得第二区间各单元的积分为
| $ {{F_2} = \sum\limits_{i = 1}^M {T_{\rm{e}}^i} } $ | (A-14) |
据此,汉克尔积分为
| $ {F = {F_1} + {F_2}} $ | (A-15) |
| [1] |
欧阳芳, 戴世坤, 张钱江, 等. 层状单轴各向异性介质中长导线源电磁响应的快速计算[J]. 石油地球物理勘探, 2016, 51(5): 1012-1020. OUYANG Fang, DAI Shikun, ZHANG Qianjiang, et al. A fast calculation method for electromagnetic fields generated by finite-length wire sources in stratified uniaxial anisotropic medium[J]. Oil Geophysical Prospecting, 2016, 51(5): 1012-1020. |
| [2] |
徐建华, 朱德怀, 胡文宝, 等. 多层介质中偶极子场的系数递推关系[J]. 石油地球物理勘探, 1994, 29(1): 69-74, 126. XU Jianhua, ZHU Dehuai, HU Wenbao, et al. Coefficient recursion relation for dipole fields in multilayer medium[J]. Oil Geophysical Prospecting, 1994, 29(1): 69-74, 126. |
| [3] |
Ghosh D P. The application of linear filter theory to the direct interpretation of geoelectrical resistivity sounding measurements[J]. Geophysical Prospecting, 1971, 19(2): 192-217. DOI:10.1111/j.1365-2478.1971.tb00593.x |
| [4] |
Johansen H K, Sorensen K. Fast Hankel transforms[J]. Geophysical Prospecting, 1979, 27(4): 876-901. DOI:10.1111/j.1365-2478.1979.tb01005.x |
| [5] |
Chave A D. Numerical integration of related Hankel transforms by quadrature and continued fraction expansion[J]. Geophysics, 1983, 48(12): 1671-1686. DOI:10.1190/1.1441448 |
| [6] |
Michalski K A. Extrapolation methods for Sommerfeld integral tails[J]. IEEE Transactions on Antennas and Propagation, 1998, 46(10): 1405-1418. DOI:10.1109/8.725271 |
| [7] |
蔡盛. 快速汉克尔变换及其在正演计算中的应用[J]. 地球物理学进展, 2014, 29(3): 1384-1390. CAI Sheng. The fast Hankel transformation and its applications in forward calculations[J]. Progress in Geophysics, 2014, 29(3): 1384-1390. |
| [8] |
Anderson W L. A hybrid fast Hankel transform algorithm for electromagnetic modeling[J]. Geophysics, 1989, 54(2): 263-266. |
| [9] |
Knockaert L. Fast Hankel transform by fast sine and cosine transforms:the Mellin connection[J]. IEEE Transactions on Signal Processing, 2000, 48(6): 1695-1701. DOI:10.1109/78.845927 |
| [10] |
Kong F N. Hankel transform filters for dipole antenna radiation in a conductive medium[J]. Geophysical Prospecting, 2007, 55(1): 83-89. DOI:10.1111/j.1365-2478.2006.00585.x |
| [11] |
Fang D G, Yang J J, Delisle G Y. Discrete image theory for horizontal electric dipoles in a multilayered medium[J]. Microwaves Antennas & Propagation IEEE Proceedings, 1988, 135(5): 297-303. |
| [12] |
邵长金, 李相方. 离散复镜像法求取层状介质的格林函数[J]. 中国石油大学学报(自然科学版), 2006, 30(1): 150-153. SHAO Changjin, LI Xiangfang. Calculation of spatial-domain Creen's functions for multi-layered media by discrete complex image method[J]. Journal of the China University of Petroleum(Edition of Natural Science), 2006, 30(1): 150-153. |
| [13] |
徐利明, 聂在平, 胡俊. 半空间环境中任意位置三维导体目标的电磁建模[J]. 电波科学学报, 2005, 20(3): 330-335, 346. XU Liming, NIE Zaiping, HU Jun. Electromagnetic modeling of three dimension perfectly conducting object located arbitrarily in half space environment[J]. Journal of Radio Science, 2005, 20(3): 330-335, 346. |
| [14] |
陈桂波, 汪宏年, 姚敬金, 等. 水平层状各向异性介质中电磁场并矢Green函数的一种高效算法[J]. 物理学报, 2009, 58(3): 1608-1618. CHNE Guibo, WANG Hongnian, YAO Jingjin, et al. An efficient algorithm of the electromagnetic dyadic green's function in a horizontal-layered anisotropic medium[J]. Acta Physica Sinica, 2009, 58(3): 1608-1618. |
| [15] |
Key K. Is the fast Hankel transform faster than qua-drature?[J]. Geophysics, 2012, 77(3). |
| [16] |
周建美.各向异性地层中可控源电磁法一维全参数反演及三维有限体积正演算法研究[D].吉林长春: 吉林大学, 2014.
|
| [17] |
郑圣谈, 曾昭发, 张代国, 等. 层状介质高频电磁场计算方法及结果分析[J]. 地球物理学进展, 2007, 20(6): 1772-1776. ZHENG Shengtan, ZENG Zhaofa, ZHANG Daiguo, et al. Calculation about high-frequency electromagnetic response and cases analyzing[J]. Progress in Geophysics, 2007, 20(6): 1772-1776. |
| [18] |
拜尔W H. 标准数学手册(第26版)[M]. 北京: 化学工业出版社, 1988.
|
| [19] |
王彦国, 罗潇, 邓居智, 等. 基于改进tilt梯度的三维磁异常解释技术[J]. 石油地球物理勘探, 2019, 54(3): 685-691. WANG Yanguo, LUO Xiao, DENG Juzhi, et al. 3D magnetic data interpretation based on improved tilt angle[J]. Oil Geophysical Prospecting, 2019, 54(3): 685-691. |
| [20] |
周印明, 戴世坤, 李昆, 等. 基于样条插值的FFT及其在重磁场正演中的应用[J]. 石油地球物理勘探, 2020, 55(4): 915-922, 930. ZHOU Yinming, DAI Shikun, LI Kun, et al. Cubic-spline-interpolation-based FFT and its application in forward modeling of gravity and magnetic fields[J]. Oil Geophysical Prospecting, 2020, 55(4): 915-922, 930. |
| [21] |
Guptasarma D, Singh B. New digital linear filters for Hankel J0 and J1 transforms[J]. Geophysical Prospecting, 1997, 45(5): 745-762. DOI:10.1046/j.1365-2478.1997.500292.x |
| [22] |
Anderson W L. Numerical integration of related Hankel transforms of orders 0 and 1 by adaptive digital filtering[J]. Geophysics, 1979, 47(7): 1287-1305. |
| [23] |
Fong G L, Martin O B, Stephen G Y. Prelamin A and Lamin A appear to be dispensable in the nuclear lamina Loren Young[J]. The Journal of Clinical Investigation, 2006, 116(3): 743-752. DOI:10.1172/JCI27125 |



 曾铃, 湖南省长沙市岳麓区麓山南路932号中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 410083。Email:
曾铃, 湖南省长沙市岳麓区麓山南路932号中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 410083。Email: