2 青岛海洋科学与技术国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266100;
3 南方科技大学地球与空间科学系, 广东深圳 518000
2 Laboratory of Marine Mineral Resources Evaluation and Detection, Qingdao, Shandong 266100, China;
3 Department of Earth and Space Science, South University of Science and Technology, Shenzhen, Guangdong 518000, China
近年来,全波形反演(FWI)方法在理论和实际应用方面均取得了较大进展[1-5]。但是,FWI的庞大计算量和过低的计算效率是限制该方法进入三维地震勘探领域的瓶颈之一。目前,业界提高反演效率的思路主要有两种:一是提高收敛速度;二是提升正演(反演需要不断进行多次正演)计算速度。前者通过改进反演算法减少迭代次数,降低计算量[6-10];后者采用高性能的计算机硬件提高计算效率或采用降维思路降低计算量[11-26]。
本文主要讨论第二种思路。FWI大部分运算量集中在正演计算过程中(FWI的每次迭代至少需要三次正演),因此业界普遍认为高效的正演计算是解决FWI反演效率问题的有效途径,采用降维思路减少运算量是提高正演效率的有效方法。降维技术的本质是采用某种压缩方式减少参与反演的炮数,主要方法包括震源编码法[16-20]、炮采样法[21-23]和主成分分析法[24-28]等。
Romero等[16]在地震资料的逆时偏移处理中提出了相位编码技术,将多炮数据压缩为几个超级炮进行计算,但编码算法会在偏移结果中产生串扰噪声。Krebs等[17]将相位编码技术引入FWI领域,利用随机的极性编码函数压制反演中的串扰噪声,将所有炮转换成一个超级炮集记录并进行反演,提升了运算效率。此外,学者们还提出了平面波编码[18]、频域随机相位编码[19]、频率组编码[20]、频域分割编码[27]等方法,完善并丰富了编码方案。
炮采样法也是一种高效的加速策略。Díaz等[21]提出了一种随机抽取炮集进行反演的方法,每次迭代时仅使用部分炮,在保证效果的同时能够减少运算。Ha等[22]提出了在Laplace域循环炮采样,不同于随机炮采样,该方法循环使用炮集中的所有炮,使反演中每一炮的使用次数较均衡。Shi等[23]将炮采样技术应用到频率多尺度FWI中,在每个频率段均随机抽取炮集参与反演,该方法不仅能加速运算,而且不会引入额外的串扰噪声。
主成分分析法也是一种经典的降维方法,Liu等[24]将主成分分析法应用于FWI,减少了炮集的数量,提高了计算效率。段超然等[25]在高频部分使用主成分分析法,使FWI在缺少低频成分时也能高效收敛。
震源编码技术实现简单、效果明显,是目前应用最广泛的加速方法,但同时也存在一些缺陷,主要表现在传统震源编码技术严重依赖于观测系统。震源编码技术应用的前提是采用检波点固定的方式观测,因而在模拟同时激发震源时,无法对单炮获取特定炮检距的地震记录。对于滚动排列观测系统,震源编码会造成模拟与观测资料的不匹配。鉴于此,Choi等[29]提出了基于归一化互相关目标函数的波形反演,提升了震源编码对海上拖缆资料的反演精度。夏冬明等[30]在此基础上发展了基于归一化局部互相关目标函数的反演方法,进一步改善了对拖缆数据的反演效果。Huang等[31]提出了基于分频编码的最小二乘偏移方法,能够真正实现拖缆资料中多炮数据的完全分离。Zhang等[32]将分频编码应用于声波FWI,并且讨论了其在计算效率、内存消耗、抗噪性方面的优点。
在前人研究的基础上,本文主要解决目前编码方法只适用于特殊观测系统的缺陷,提出了一种基于震源分频编码的混合域弹性波FWI方法。首先为同时进行正向延拓的每一炮赋以不同的频率,并利用该频率对应的谐波代替原时间域子波进行正演,通过相位灵敏度检测(Phase Sensitivity Detection,PSD)提取单频波场,从而实现各炮频率域波场的完全分离;然后实现多炮编码反演。这样既能压制炮间串扰噪声,又能对每一炮波场和记录实现灵活处理,可以适应排列滚动的观测系统。
1 震源编码技术混合域弹性波FWI的运算量和炮集数成正比,运用震源编码技术将多炮数据进行组合、正演,可有效减少计算量。震源编码技术借助于编码函数,将炮集叠加、组合得到超级炮记录,利用常规方法对该超级炮记录进行反演。
在频率域,超级炮记录可表示为
| $ \mathit{\boldsymbol{\tilde d}} = \sum\limits_{n = 1}^{{N_{\rm{S}}}} {{\gamma _n}} {\mathit{\boldsymbol{d}}_n} $ | (1) |
式中:上标“~”表示超级炮;dn是第n炮得到的观测地震记录;γn表示第n炮的编码函数序列;NS为总炮数。
相对应的超级炮震源可表示为
| $ \mathit{\boldsymbol{\tilde s}} = \sum\limits_{n = 1}^{{N_{\rm{S}}}} {{\gamma _n}} {\mathit{\boldsymbol{s}}_n} $ | (2) |
式中sn是第n炮的震源子波。波动方程是关于震源项的线性方程组,可知超级炮对应的正传波场
| $ {\mathit{\boldsymbol{\widetilde P}} = \sum\limits_{n = 1}^{{N_{\rm{S}}}} {{\gamma _n}} {\mathit{\boldsymbol{P}}_n}} $ | (3) |
| $ {\mathit{\boldsymbol{\widetilde B}} = \sum\limits_{n = 1}^{{N_{\rm{S}}}} {{\gamma _n}} {\mathit{\boldsymbol{B}}_n}} $ | (4) |
式中:Pn是第n炮的正传波场;Bn是第n炮的残差波场。
推导得出超级炮对应的梯度
| $ \begin{array}{*{20}{l}} {\frac{{\partial E(\mathit{\boldsymbol{m}})}}{{\partial \mathit{\boldsymbol{m}}}} = - \mathscr{R}\left( {\frac{{\partial \mathit{\boldsymbol{A}}}}{{\partial \mathit{\boldsymbol{m}}}}\sum\limits_{n = 1}^{{N_{\rm{S}}}} {{\gamma _n}} \gamma _n^*\mathit{\boldsymbol{P}}_n^{\rm{T}}\mathit{\boldsymbol{B}}_n^* + } \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\frac{{\partial \mathit{\boldsymbol{A}}}}{{\partial \mathit{\boldsymbol{m}}}}\sum\limits_{n = 1}^{{N_{\rm{S}}}} {\sum\limits_{l = 1,l \ne n}^{{N_{\rm{S}}}} {{\gamma _n}} } \gamma _l^*\mathit{\boldsymbol{P}}_n^{\rm{T}}\mathit{\boldsymbol{B}}_l^*} \right)} \end{array} $ | (5) |
式中:E(m)为目标函数,m为待反演参数,本文指速度;
式(5)说明由震源编码技术计算得到的梯度包含两部分,第一部分由系数γnγn*加权,γnγn*的值通常为固定常数,因此这一部分相当于对常规方法中各炮独立计算出的梯度求和,也即常规方法计算得到的梯度;第二部分是不同炮的震源波场和残差波场的互相关,是由参与震源编码的多炮数据相互影响而产生的串扰噪声,不是真正的梯度项,因此这一部分干扰需要消除。常用的方法是对γn随机赋值,使每次迭代时产生的串扰噪声互不相关,经过多次迭代后,能够有效压制由γnγl*加权的串扰项。
2 分频编码技术 2.1 分频编码策略本文把分频编码技术引入弹性波波形反演中。其核心思想是:在正演过程中,同时对多个炮记录进行正向延拓,给每一炮赋以不同频率的谐波震源,使同时正向延拓的各炮波场在频谱上互不重合。同时,在炮点波场正传和残差反传过程中,采用相位灵敏度检测技术提取每炮的单频波场,实现各炮波场的完全分离,避免炮间串扰。
利用式(5)可以很好地解释编码技术压制串扰噪声的原理:由于各炮频带不重合,所以在计算特定频率ω的梯度时,不同炮的
分频编码技术的核心在于给每炮赋以不同频带的震源函数,避免多炮同时延拓中的炮间串扰。震源的频带一般由震源函数的中心频率控制,不同炮可以选择不同主频的震源函数。但由于不同主频的震源函数往往具有一定的频带宽度,当炮数较多时,难以完全分离多炮频谱,利用谐波作为震源可以避免这一缺陷。
利用谐波震源进行正演,首先需要提取正确的波场信息。本文引入PSD正演方法实现频率域波场的准确提取。Nihei等[26]提出的基于PSD的正演方法用谐波作为震源,在正演过程中可以很方便地提取出不同频率的单频波场,实现多震源的同步模拟且互不干扰。
PSD方法是利用一个参考信号和参考信号的90°相移信号计算原谐波信号的频谱。对于含有两个频率的信号,原信号εsig用振幅Esig和相位θsig表示为
| $ {\varepsilon _{{\rm{sig}}}} = {E_{{\rm{sig1}}}}\cos ({\omega _1}t + {\theta _{{\rm{sig1}}}}) + {E_{{\rm{sig2}}}}\cos ({\omega _2}t + {\theta _{{\rm{sig2}}}}) $ | (6) |
式中下标“1”和“2”分别对应这两个频率。
选取两个不同的频率ω1和ω2,令它们满足以下关系
| $ \left\{ {\begin{array}{*{20}{l}} {\Delta \omega = {\omega _2} - {\omega _1}}\\ {{\omega _1} = k\Delta \omega } \end{array}} \right. $ | (7) |
式中k为正整数。
以ω1为例,设计如下参考信号和相移信号
| $ \left\{ {\begin{array}{*{20}{l}} {{\varepsilon _{{\rm{ref1}}({0^\circ })}} = {E_{{\rm{ref1}}}}\cos ({\omega _1}t + {\theta _{{\rm{ref1}}}})}\\ {{\varepsilon _{{\rm{ref1}}({{90}^\circ })}} = {E_{{\rm{ref1}}}}\cos ({\omega _1}t + {\theta _{{\rm{ref1}}}} + {{90}^\circ })} \end{array}} \right. $ | (8) |
式中ref1表示参考信号。
ω1对应的单频信号的振幅和相位[26]可以表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{E_{{\rm{sig1}}}} = \frac{{2\sqrt {{X^2} + {Y^2}} }}{{{E_{{\rm{ref1}}}}}}}\\ {{\theta _{{\rm{sig1}}}} = {{\tan }^{ - 1}}\frac{Y}{X} + {\theta _{{\rm{ref1}}}}} \end{array}} \right. $ | (9) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {X = \frac{1}{T}\int_0^T {{\varepsilon _{{\rm{sig}}}}} {\varepsilon _{{\rm{ref1}}\left( {{0^\circ }} \right)}}{\rm{d}}t}\\ {Y = \frac{1}{T}\int_0^T {{\varepsilon _{{\rm{sig}}}}} {\varepsilon _{{\rm{ref1}}\left( {{{90}^\circ }} \right)}}{\rm{d}}t}\\ {T = \frac{{2\pi }}{{\Delta \omega }}} \end{array}} \right. $ | (10) |
Nihei等[26]证明:在包含两个频率的信号中,只要积分时长和频率满足一定条件,PSD能够分别求出其频率响应。这一结论可推广到包含多个频率的信号中,条件是各个频率都为某一个基频Δω的整数倍,积分的时间长度满足T=
Nihei等[26]证明PSD算法与傅里叶变换的功能是相同的,但是前者更适用于对谐波信号进行处理。对只包含几个等间隔频率的信号,PSD算法仅需要选择很小长度的信号进行运算就能够得到其频率响应,效率更高。
在时间域正演过程中,通常使用Ricker子波作为震源,但PSD算法需要以谐波震源作为输入。为了得到与常规正演方法等价的结果,需要建立Ri-cker子波和谐波震源之间的数学联系。实际上,谐波震源能够视为Ricker子波的某一个或几个频率成分,所以仅需要将Ricker子波做离散傅里叶变换后,提取出某几个频率的响应,再做傅里叶反变换,就能得到谐波震源。处理实际资料时,对真实的子波做类似操作即可。当然,这样做的前提是能够获取较为准确的震源子波,否则使用不正确的子波将会导致错误的反演结果。子波的提取是波形反演需要解决的一个重要问题,但是本文的研究目标是加快反演速度,暂不考虑如何提取子波的问题。另外,本文方法可以与当前的不依赖于子波的反演方法相结合[33-35],即使利用错误的震源子波进行反演也能得到正确的反演结果。
本文基于PSD的弹性波正演方法流程如图 1所示。
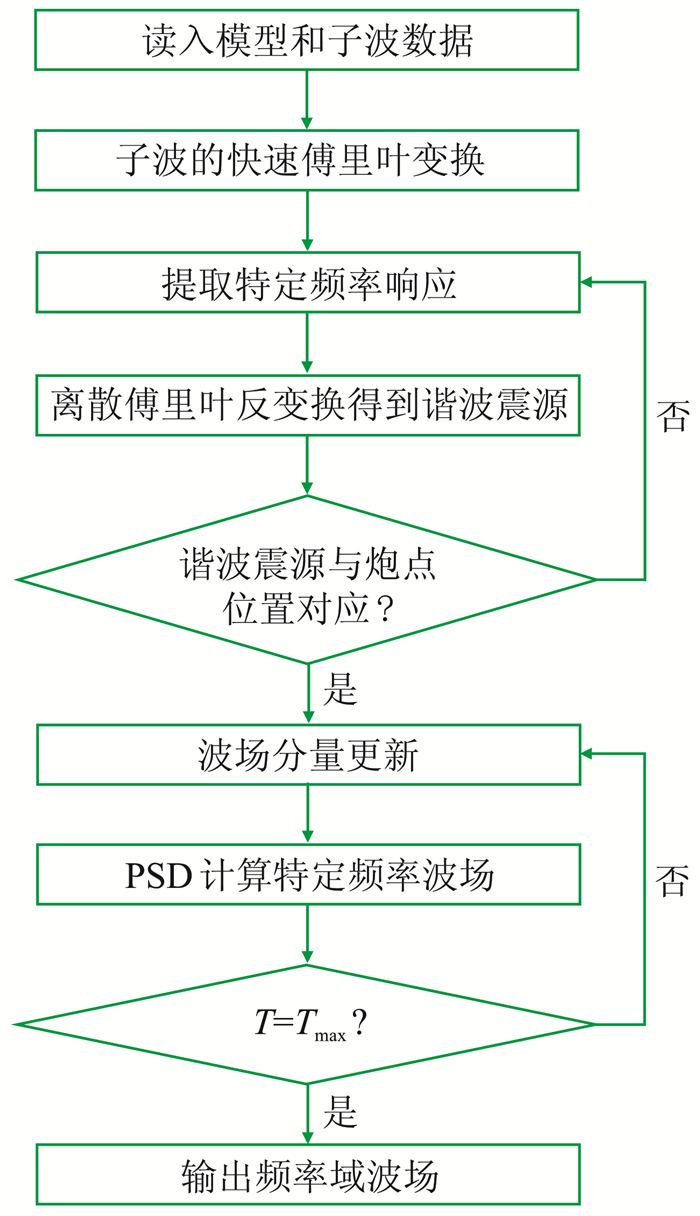
|
图 1 基于PSD的弹性波分频编码正演流程 |
利用PSD算法实现分频多炮正演实验可以验证PSD算法的有效性。以简单的均匀介质为例,网格数设为150×200,网格间距为10m,纵、横波速度分别为2500、1500m/s。设有4个炮点,炮点深度为20m,炮点等间隔分布,横向坐标分别为400、800、1200和1600m,原始子波是主频8Hz的Ricker子波,时间长度设为4s,四个炮点分别同时正演2、3、4、5Hz的单频波场。
利用PSD方法进行正演所得到的各炮点频率响应如图 2所示,其中几乎见不到多炮的串扰。
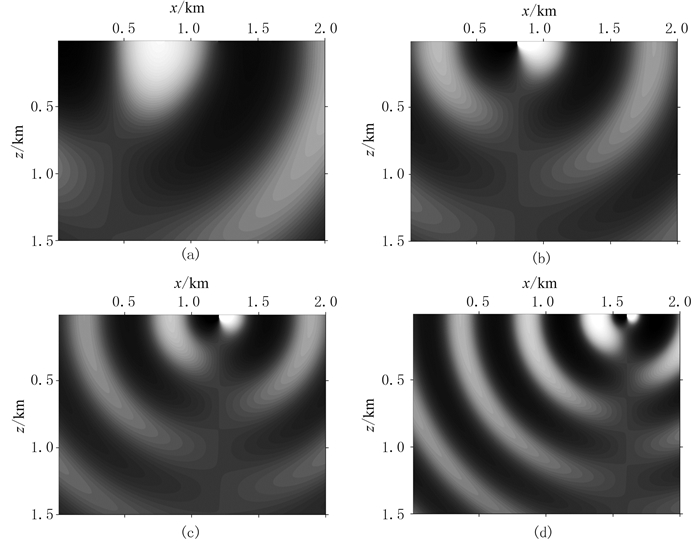
|
图 2 分频编码单次正演的各炮频率响应(实部) (a)2Hz;(b)3Hz;(c)4Hz;(d)5Hz |
为精确验证PSD算法能够有效避免炮间串扰,做了如下对照实验:每次只设置一个震源一个频率,其他参数与图 2保持一致,得到不含炮间串扰的波场。将两次实验结果中横坐标1km处不同深度的波场值绘制成图 3。对比可知,两次实验得到的波场几乎一致,这也说明PSD算法具有足够的精度,可以在分频率的多炮正演中得到准确的频率域波场值。
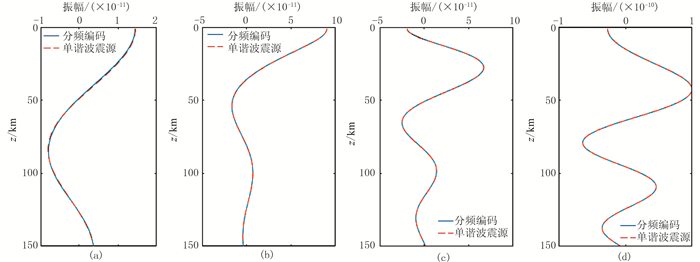
|
图 3 分频编码与单谐波震源波场值对比 (a)2Hz;(b)3Hz;(c)4Hz;(d)5Hz |
从理论上讲,分频编码技术不会引入额外噪声[31]。本文应用分频编码方法以实现混合域的弹性波反演。与Huang等[31]实现的最小二乘偏移方法不同,混合域FWI一般采用多尺度反演策略,在每一个尺度下,可供使用的频段是受限的,所以频率的选择在分频编码混合域反演中非常重要。
每一尺度下反演频率的选择需要满足两个条件:一是PSD算法本身的要求,即PSD计算时长和频率间隔满足特定关系(在包含多个频率的信号中,每个频率都必须是基频Δω的整数倍,积分时间长度
通常而言,随多尺度反演的递进,可供选择的频段逐渐拓宽。如果对每一尺度反演都设置相同的频率数目,结合上述两个限制条件,就不难得出如下结论:小尺度反演时,频率间隔大,Δω较大而PSD计算时长小;大尺度反演时,频率选择较密集,Δω较小而PSD计算时长大。反之,若Δω固定不变,则在大尺度反演时,可供选择的频率更少,进一步造成能同时正演的炮数变少,正演次数就会明显增加。本文选择用较多的频率个数完成多炮同时正演。具体到反演过程中,首先确定反演使用的频率个数M,把每M炮数据组合成为一个超级炮(组合方法可以有多种,本文选择把空间上邻近的M炮数据进行组合);然后每次迭代前把M个频率的数据随机分配给组合中的M炮,让迭代过程中各炮使用的频率不断变化,这样可以使原始数据得到充分利用。
3 模型算例 3.1 分频编码对FWI的加速效果为证明本文方法的加速效果,用部分Overthrust模型的正演记录进行测试。图 4为部分Overthrust纵、横波速度模型,该模型网格数为500×160,网格间隔为25m×25m。正演记录的炮点均匀分布于地表,第一炮位于0m处,炮间距为125m,共得到100炮合成地震记录,全排列接收,道间距为25m。反演所用的初始模型(图 5)是将图 4进行高斯平滑得到的。
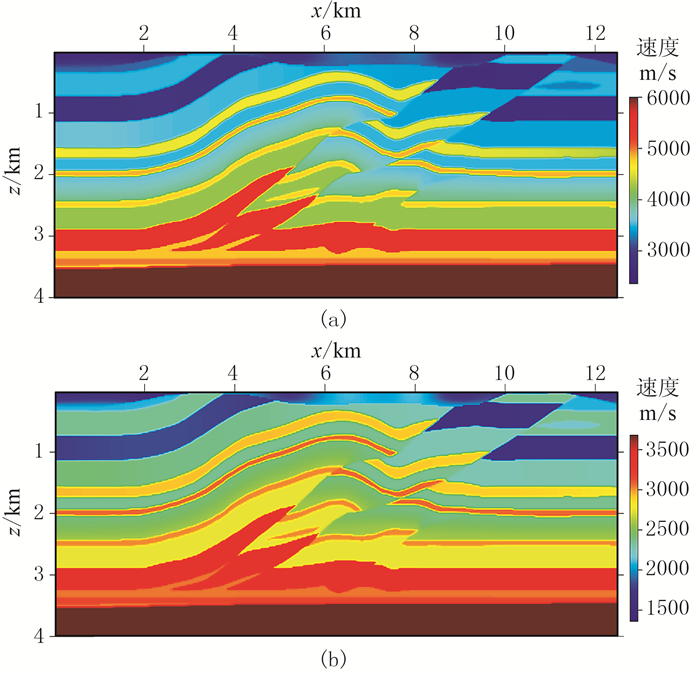
|
图 4 部分Overthrust速度模型 (a)纵波;(b)横波 |

|
图 5 反演使用的初始速度模型 (a)纵波;(b)横波 |
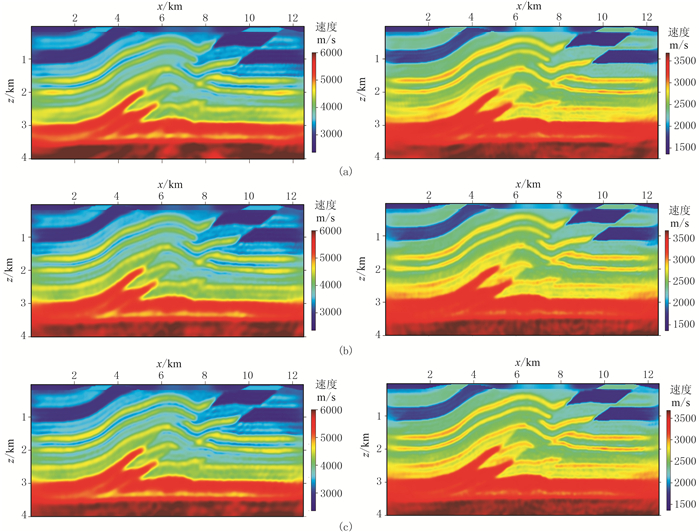
采用多尺度反演策略,每个频率组包含10个频率(表 1),反演分5个频段,每个频段迭代15次。分别采用常规全部炮反演、传统震源编码(极性编码)反演和分频编码反演,并将三者反演结果(图 6)进行对比。
|
|
表 1 分频编码反演的频率组信息 |
|
图 6 全排列接收时不同方法纵波速度(左)、横波速度(右)反演结果 (a)常规全部炮反演;(b)分频编码反演;(c)传统震源编码(极性编码) |

|
图 7 误差分析对比 (a)纵波速度;(b)横波速度 |
| $ {\rm{err}} = \frac{{{{\left\| {{\mathit{\boldsymbol{m}}_{{\rm{FWI}}}} - {\mathit{\boldsymbol{m}}_{{\rm{TRUE}}}}} \right\|}_2}}}{{{{\left\| {{\mathit{\boldsymbol{m}}_{{\rm{TRUE}}}}} \right\|}_2}}} $ | (11) |
式中:mFWI和mTRUE分别为反演结果和真实模型的弹性参数;‖·‖2表示L2范数。
从图 6、图 7可以看出,分频编码方法和极性编码方法的反演精度与常规方法相近。但就计算量而言,由于每次迭代需要4次正演(梯度计算需要两次,步长估计需要两次),因此常规全部炮反演需要计算30000(100×5×15×4)次正演,而本文方法与极性编码一样,将10炮数据组合为1炮进行反演,因此正演次数仅为常规方法的十分之一。
当然,计算效率的提升与组合的炮数有关。通常反演中能够进行组合的炮数受频带宽度的影响,不能把任意多的炮集进行组合。此算例中,每个超级炮都由固定的10炮数据组成。而在一般的多尺度反演中,大尺度反演时给定的频带宽度往往较小,能够选择的频率点(亦即能够进行组合的炮数)也比较少;随着尺度变小,频带可以更宽,从而可以用更多的炮进行组合。但是由于混合域算法中需要存储每个频率的波场,更多的频率点意味着存储量的增加,同时也意味着需更多的计算完成PSD的频率分离,因此最终选择多少个频率需视情况而定。
3.2 滚动排列观测系统反演测试应用传统震源编码方法反演时,每炮的接收排列必须相同且覆盖整个工区,但是排列滚动的数据只在炮点附近一定范围内接收,远炮点并没有数据,所以面对滚动排列观测系统传统编码方法反演效果很差。
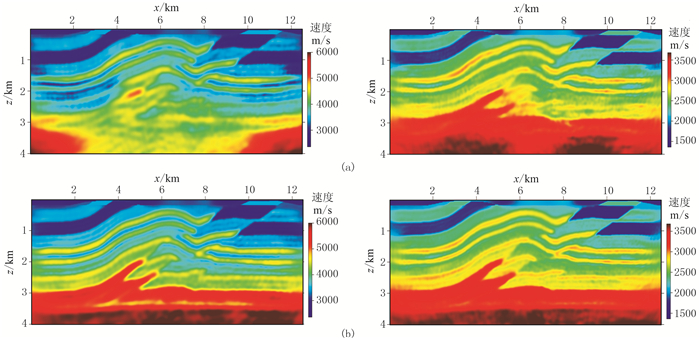
仍以图 4所示的部分Overthrust模型为例,采用中间放炮的方式进行观测,炮点均匀分布于地表,第一炮位于0m处,炮间距为125m,每炮300道接收,道间距为25m,在模型两边排列固定不动,炮点滚动,共得到100炮两分量记录。首先采用传统震源编码反演方法(极性编码)对合成记录进行反演,反演结果如图 8a所示。显然,常规震源编码方法反演得到的结果与真实模型相差很大。由图 8a可以看出,横波的反演结果优于纵波,这与本文的实验条件有关。传统震源编码方法应用于排列滚动的地震数据时,误差主要源于排列范围之外(远炮检距)的数据缺失。具体到本文的实验,采用爆炸震源激发,横波分量均来自于波的类型转换,因此占比较少。远炮检距存在很强的纵波分量,尤其是直达纵波,这一部分数据的缺失会对纵波反演产生极大的不利影响。结合图 6给出的反演结果,可以看出,传统编码方法在全排列接收时可以给出正确的反演结果,但是在滚动排列情况下会受到严重的干扰。
|
图 8 流动排列接收时不同方法纵波(左)、横波(右)速度反演结果 (a)传统编码方法;(b)分频编码反演 |
利用本文的分频编码方法对排列滚动的数据进行反演,结果如图 8b所示。由图可见本文方法的反演结果结构清晰,与真实模型基本一致,远远优于图 8a的反演结果。计算效率方面,本文基于GPU集群环境利用MPI+CUDA实现多炮并行反演,采用16张Tesla K80运算。反演共进行75次迭代,分频编码方法完成反演用时70min,极性编码方法用时66min,分频编码方法耗时略高。分频编码方法首先需要对记录做分频处理;其次,本文在实施相位灵敏度检测时需要适当延长正演时间,因此产生了一些额外计算量。但是这些额外的计算量相比于波场正演和反传而言影响较小,所以整体上两种编码方法计算效率相近。
4 结束语分频编码方法在不明显降低反演精度的基础上,能够将运算效率提升数倍,有效减少正演次数,减小全波形反演的计算量。本文的分频编码方法首先利用谐波震源实现分频的多炮同步正演,再利用基于相位灵敏度检测的波场分离方法,实现不同炮波场的完全分离,从而能够在梯度计算中避免引入多炮串扰噪声。另外,本文使用的这种分离方法仅依靠频率信息,与震源、接收点的排列布置无关,能够适用于滚动排列观测系统,弥补了传统震源编码方法在观测系统适应性上存在的不足。
| [1] |
Tarantola A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [2] |
Bunks C, Saleck F M, Zaleski S, et al. Multiscale seismic waveform inversion[J]. Geophysics, 1995, 60(5): 1457-1473. DOI:10.1190/1.1443880 |
| [3] |
Pratt R G. Seismic waveform inversion in the frequency domain, Part1:Theory and verification in a physical scale model[J]. Geophysics, 1999, 64(3): 888-901. DOI:10.1190/1.1444597 |
| [4] |
Sirgue L, Pratt R G. Efficient waveform inversion and imaging:A strategy for selecting temporal frequencies[J]. Geophysics, 2004, 69(1): 231-248. |
| [5] |
胡光辉, 李熙盛, 郭丽, 等. 构造约束全波形反演及其海上资料应用[J]. 石油物探, 2018, 57(4): 592-596. HU Guanghui, LI Xisheng, GUO Li, et al. Structure-constrained full waveform inversion and its application in marine seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(4): 592-596. |
| [6] |
Pratt R G, Shin C, Hicks. Gauss-Newton and full Newton methods in frequency-space seismic waveform inversion[J]. Geophysical Journal International, 1998, 133(2): 341-362. DOI:10.1046/j.1365-246X.1998.00498.x |
| [7] |
Sheen D H, Tuncay K, Baag C E, et al. Time domain Gaussâ-Newton seismic waveform inversion in elastic media[J]. Geophysical Jornal of the Royal Astronomical Society, 2006, 167(3): 1373-1384. DOI:10.1111/j.1365-246X.2006.03162.x |
| [8] |
Epanomeritakis I, Akcelik V, Ghattas O, et al. A Newton-CG method for large-scale three-dimensional elastic full-waveform seismic inversion[J]. Inverse Problems, 2008, 24(3): 034015. DOI:10.1088/0266-5611/24/3/034015 |
| [9] |
Ma Y, Hale D. Quasi-Newton full-waveform inversion with a projected Hessian matrix[J]. Geophysics, 2012, 77(5): R207-R216. |
| [10] |
刘璐, 刘洪, 张衡, 等. 基于修正拟牛顿公式的全波形反演[J]. 地球物理学报, 2013, 56(7): 2447-2451. LIU Lu, LIU Hong, ZHANG Heng, et al. Full waveform inversion based on modified quasi-Newton equation[J]. Chinese Journal of Geophysics, 2013, 56(7): 2447-2451. |
| [11] |
韩璇颖, 印兴耀, 曹丹平, 等. 基于分段快速模拟退火的零偏VSP全波形反演[J]. 石油物探, 2019, 58(1): 103-111. HAN Xuanying, YIN Xingyao, CAO Danping, et al. Zero-offset VSP velocity inversion with FWI using segmented fast simulated annealing[J]. Geophysical Prospecting for Petroleum, 2019, 58(1): 103-111. |
| [12] |
Mao J, Wu R S, Wang B L.Multiscale full waveform inversion using GPU[C].SEG Technical Program Expanded Abstracts, 2012, 31: 1-7.
|
| [13] |
Shin J, Ha W, Jun H, et al. 3D Laplace-domain full waveform inversion using a single GPU card[J]. Computers & Geosciences, 2014, 67(6): 1-13. |
| [14] |
王拓.基于GPU加速的混合域全波形反演技术研究[D].北京: 中国石油大学(北京), 2016. WANG Tuo.Method Studty of Hybrid Time-frequency Domain FWI Based GPU Acceleration[D].China University of Petroleum (Beijing), Beijing, 2016. |
| [15] |
张光超.基于GPU并行计算的时间域弹性波全波形反演方法研究[D].北京: 中国石油大学(北京), 2016. ZHANG Guangchao.Time-domain Elastic Full Waveform Inversion with GPU Parallel Computing[D].China University of Petroleum (Beijing), Beijing, 2016. |
| [16] |
Romero L A, Ghiglia D C, Ober C C, et al. Phase encoding of shot records in prestack migration[J]. Geophysics, 2000, 65(2): 426-436. |
| [17] |
Krebs J R, Anderson J E, Hinkley D, et al. Fast full-wave field seismic inversion using encoded sources[J]. Geophysics, 2009, 74(6): WCC177-WCC188. DOI:10.1190/1.3230502 |
| [18] |
Tao Y, Sen M K. Frequency-domain full waveform inversion with plane-wave data[J]. Geophysics, 2013, 78(1): R13-R23. |
| [19] |
Ben-Hadj-Ali H, Operto S, Virieux J. An efficient frequency-domain full waveform inversion method using simultaneous encoded sources[J]. Geophysics, 2011, 76(4): R109-R124. |
| [20] |
Han M, Han L G, Liu C C, et al. Frequency-domain auto-adapting full waveform inversion with blended source and frequency-group encoding[J]. Applied Geophysics, 2013, 10(1): 41-52. |
| [21] |
Díaz E, Guitton A.Fast full waveform inversion with random shot decimation[C].SEG Technical Program Expanded Abstracts, 2011, 30: 2804-2808.
|
| [22] |
Ha W, Shin C. Efficient Laplace-domain full waveform inversion using a cyclic shot subsampling method[J]. Geophysics, 2013, 78(2): R37-R46. |
| [23] |
Shi C W, He B S. Multiscale full-waveform inversion based on shot subsampling[J]. Applied Geophysics, 2018, 15(2): 261-270. DOI:10.1007/s11770-018-0669-6 |
| [24] |
Liu C C, Han M, Han L G, et al.Application of principal component analysis for frequency-domain full waveform inversion[C].SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [25] |
段超然, 韩立国. 主成分分析波场重构反演与全波形反演联合速度重构[J]. 石油地球物理勘探, 2016, 51(6): 1134-1140. DUAN Chaoran, HAN Liguo. A joint velocity reconstruction method:principal component analysis based wavefield-reconstruction inversion conbined with full waveform inversion[J]. Oil Geophysical Prospecting, 2016, 51(6): 1134-1140. |
| [26] |
Nihei K T, Li X. Frequency response modelling of seismic waves using finite difference time domain with phase sensitive detection (TD-PSD)[J]. Geophysical Journal of the Royal Astronomical Society, 2007, 169(3): 1069-1078. DOI:10.1111/j.1365-246X.2006.03262.x |
| [27] |
Huang Y S, Schuster G T. Full waveform inversion with multisource frequency selection of marine streamer data[J]. Geophysical Prospecting, 2018, 66(7): 1243-1257. DOI:10.1111/1365-2478.12588 |
| [28] |
史才旺, 何兵寿. 基于主成分分析和梯度重构的全波形反演[J]. 石油地球物理勘探, 2018, 53(1): 95-104. SHI Caiwang, HE Bingshou. Full waveform inversion based on principal component analysis and gradient reconstruction[J]. Oil Geophysical Prospecting, 2018, 53(1): 95-104. |
| [29] |
Choi Y, Alkhalifah T. Application of multi-source waveform inversion to marine streamer data using the global correlation norm[J]. Geophysical Prospecting, 2012, 60(4): 748-758. DOI:10.1111/j.1365-2478.2012.01079.x |
| [30] |
夏冬明, 宋鹏, 谭军, 等. 基于归一化局部互相关算法的相位编码全波形反演[J]. 中国海洋大学学报(自然科学版), 2017, 47(7): 105-111. XIA Dongming, SONG Peng, TAN Jun, et al. The phase-encoded full waveform inversion based on normalized local cross-correlation algorithm[J]. Periodical of Ocean University of China, 2017, 47(7): 105-111. |
| [31] |
Huang Y S, Schuster G T. Multisource least-squares migration of marine streamer and land data with frequency-division encoding[J]. Geophysical Prospecting, 2012, 60(4): 663-680. DOI:10.1111/j.1365-2478.2012.01086.x |
| [32] |
Zhang Q C, Mao W J, Zhou H. Hybrid-domain simultaneous-source full waveform inversion without crosstalk noise[J]. Geophysical Journal International, 2018, 215(3): 1659-1681. DOI:10.1093/gji/ggy366 |
| [33] |
Choi Y, Alkhalifah T. Source-independent time-domain waveform inversion using convolved wavefields:App-lication to the encoded multisource waveform inversion[J]. Geophysics, 2011, 76(5): R125-R134. DOI:10.1190/geo2010-0210.1 |
| [34] |
杨涛, 张会星, 史才旺. 不依赖子波的弹性波混合域全波形反演[J]. 石油地球物理勘探, 2019, 54(2): 348-355. YANG Tao, ZHANG Huixing, SHI Caiwang. Wavelet-independent elastic wave full waveform inversion in hybrid domain[J]. Oil Geophysical Prospecting, 2019, 54(2): 348-355. |
| [35] |
辛天亮, 黄建平, 解飞, 等. 基于数据相似性的不依赖子波的频率域全波形反演[J]. 石油地球物理勘探, 2020, 55(2): 341-350. XIN Tianliang, HUANG Jianping, XIE Fei, et al. Source-independent frequency-domain full wavefrom inversion based on data similarity[J]. Oil Geophysical Prospecting, 2020, 55(2): 341-350. |



 何兵寿, 山东省青岛市松岭路238号中国海洋大学海底科学与探测技术教育部重点实验室, 266100。Email:
何兵寿, 山东省青岛市松岭路238号中国海洋大学海底科学与探测技术教育部重点实验室, 266100。Email: