由于地层吸收造成强烈的能量衰减及起伏地表的复杂结构对地震正演、偏移造成不利影响,降低了地震成像分辨率。为补偿衰减,通常使用时变反褶积[1-2]、谱白化[3]和反Q滤波[4-5]等成像方法。这些方法基于一维Q模型,可提高叠后地震记录的分辨率[6]。实际上,振幅衰减和相位畸变都发生在波传播过程中,因此在叠前深度偏移中消除不利影响更符合物理原理[7-8]。叠前深度偏移方法分为射线偏移、单程波偏移和逆时偏移(RTM)[9-11],其中RTM是基于双程波的偏移,不需要波场解耦,因此偏移精度更高。黏声RTM(Q-RTM)是指在偏移时,波场正向和反向延拓过程均进行Q补偿。与常规RTM相比,Q-RTM能够补偿能量衰减和校正相位畸变,进而可获得高质量的成像结果[12-13]。
Q-RTM主要包括波场正向延拓、波场反向延拓和互相关成像三个步骤。波场模拟精度决定最终的成像质量。与时间域模拟相比,在频率域更容易补偿衰减[14],因此在频率域进行Q-RTM更具优势。Lysmer等[15]首先提出了频率域正演模拟,并用有限元方法实现了地震波数值模拟。Marfurt[16]指出,在频率域可以有效地模拟波在各向异性介质中的传播和衰减效应,适用于多炮并行模拟。Pratt等[17]利用5点有限差分格式离散声波方程,推导了声波方程和弹性波方程的频率域差分格式,构造了阻抗矩阵,为频率域地震模拟奠定了基础。Jo等[18]首先引入旋转坐标算子,将传统网格所需的5个网格点扩展到9个网格点,实现了频率域黏声模拟,并很好地抑制了频散;随后,Shin等[19]将9点差分格式扩展到25点,提高了模拟精度。Chu等[20]展示了数值模拟在频率域的优势。随着计算机并行及全波形反演技术的发展,频率域模拟技术得到进一步发展[21-26]。
除偏移方法外,剖分网格也是影响Q-RTM结果的重要因素。对于起伏浅表层,常规矩形网格无法精确剖分速度模型,甚至会因剖分不精确而产生干扰波。为此,贴体网格被引入起伏地表地震波偏移。1971年,首次出现贴体网格的概念[27],随后Thomas等[28]将其成功用于流体力学问题。Tessmer等[29]在映射法的基础上,将贴体网格用于处理起伏地表的地球物理问题并获得较好效果。由于贴体坐标生成技术的快速发展,贴体网格得到广泛应用。针对地球物理的不规则边界问题,人们研究了光滑体拟合网格的自动生成方法,并用于起伏地表等地球物理模型剖分[30-33]。近年来,贴体网格广泛用于起伏地表黏弹介质正演模拟和RTM[34-35]。
本文基于前人认识,研究了起伏浅表层频率域Q-RTM方法。通过对频率域波动方程增加一个稳定项,推导了稳定的频率域Q-RTM波动方程,解决了Q-RTM的不稳定问题。通过计算空间和物理空间的转换,成功地实现了起伏浅表层稳定的频率域Q-RTM。通过对振幅的稳定补偿,消除了浅表层衰减效应,获得了高质量的成像结果。
1 稳定的频率域Q-RTM 1.1 频率域黏声模拟频率域声波和黏声波方程分别为
| $ \begin{array}{*{20}{l}} {\frac{{{\partial ^2}U(x,z,\omega )}}{{\partial {x^2}}} + \frac{{{\partial ^2}U(x,z,\omega )}}{{\partial {z^2}}} + \frac{\omega }{{{v^2}}}U(x,z,\omega )}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = - F(x,z,\omega )} \end{array} $ | (1) |
| $ \begin{array}{l} \frac{{{\partial ^2}U(x,z,\omega )}}{{\partial {x^2}}} + \frac{{{\partial ^2}U(x,z,\omega )}}{{\partial {z^2}}} + \frac{\omega }{{{V^2}}}U(x,z,\omega )\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = - F(x,z,\omega ) \end{array} $ | (2) |
式中:U(x, z, ω)为频率域波场,(x, z)为空间坐标,ω为角频率;F(x, z, ω)为震源项;v为介质速度;V为复速度,且有
| $ \frac{1}{V} = \frac{{1 \pm {\rm{i}}/(2Q)}}{v} $ | (3) |
式中:Q为品质因子;“+”表示补偿效应;“-”表示衰减效应。
由式(1)和式(2)可见,二者具有相似的形式,差别仅在于式(2)在计算时使用复速度,因此在频率域进行Q补偿更容易。本文采用优化的9点差分网格(图 1)求解式(2)。拉普拉斯项由常规坐标(x, z)及其逆时针旋转45°的坐标(x′, z′)的加权值表示

|
图 1 优化9点差分网格 m、n分别为x、z方向的网格序号 |
| $ {\nabla ^2}U = a\nabla _{({0^\circ })}^2U + (1 - a)\nabla _{({{45}^\circ })}^2U $ | (4) |
式中a为权系数。U(x, z, ω)则由网格内9个点的加权值表示为
| $ \begin{array}{*{20}{l}} {{U_{m,n}} = c{U_{m,n}} + d({U_{m - 1,n}} + {U_{m + 1,n}} + {U_{m,n - 1}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {U_{m,n + 1}}) + e({U_{m - 1,n - 1}} + {U_{m + 1,n - 1}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {U_{m - 1,n + 1}} + {U_{m + 1,n + 1}})} \end{array} $ | (5) |
其中
| $ c + 4d + 4e = 1 $ | (6) |
式中c、d、e为权系数。则式(2)的有限差分格式为
| $ \begin{array}{l} {\alpha _z}{U_{m - 1,n - 1}} + {\beta _z}{U_{m,n - 1}} + {\alpha _x}{U_{m + 1,n - 1}} + {\beta _x}{U_{m - 1,n}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \gamma {U_{m,n}} + {\beta _x}{U_{m + 1,n}} + {\alpha _x}{U_{m - 1,n + 1}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\beta _z}{U_{m,n + 1}} + {\alpha _z}{U_{m + 1,n + 1}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = - F(x,z,\omega )\delta (x - {x_{\rm{s}}})\delta (z - {z_{\rm{s}}}) \end{array} $ | (7) |
其中
| $ {{\alpha _x} = \frac{{1 - a}}{{{{(\Delta x)}^2} + {{(\Delta z)}^2}}} + \frac{{1 - c - 4d}}{4}\frac{{{\omega ^2}}}{{{V^2}}}} $ | (8) |
| $ {{\alpha _z} = \frac{{1 - a}}{{{{(\Delta x)}^2} + {{(\Delta z)}^2}}} + \frac{{1 - c - 4d}}{4}\frac{{{\omega ^2}}}{{{V^2}}}} $ | (9) |
| $ {{\beta _x} = \frac{a}{{{{(\Delta x)}^2}}} + d\frac{{{\omega ^2}}}{{{V^2}}}} $ | (10) |
| $ {{\beta _z} = \frac{a}{{{{(\Delta z)}^2}}} + d\frac{{{\omega ^2}}}{{{V^2}}}} $ | (11) |
| $ \gamma = \frac{{2a}}{{{{(\Delta x)}^2}}} + \frac{{2a}}{{{{(\Delta z)}^2}}} + \frac{{2(1 - a)}}{{{{(\Delta x)}^2} + {{(\Delta z)}^2}}} - c\frac{{{\omega ^2}}}{{{V^2}}} $ | (12) |
式(4)~式(12)中:Δx、Δz分别为x、z方向的网格间距;a=0.5461、c=0.6248、d=0.09381均为最优化差分系数。
经离散,式(2)可表示为一组线性方程组
| $ \mathit{\boldsymbol{A}}(x,z,\omega )\mathit{\boldsymbol{U}}(x,z,\omega ) = - \mathit{\boldsymbol{F}}(x,z,\omega ) $ | (13) |
式(13)左端的系数矩阵A(x, z, ω)为一大型稀疏矩阵,称为阻抗矩阵,其结构与差分网格有关。不同格式的差分网格对应A(x, z, ω)的带宽和非零元素不同。U(x, z, ω)、F(x, z, ω)分别为U(x, z, ω)、F(x, z, ω)的矩阵形式。
1.2 常规Q-RTM的不稳定问题及改进由式(7)~式(12)求解式(2)得到频率域波场,在此基础上,由傅里叶反变换得到时间域波场进行RTM。波动理论指出,地震波在地下传播时,其能量呈指数衰减。常规Q-RTM的模拟过程是要补偿这种衰减,其解析解随频率呈指数增长,即
| $ u = {u_0}{\rm{ex}}{{\rm{p}}^{\frac{{\omega t}}{{2Q}}}} $ | (14) |
式中:u0为初始波场;u为补偿后波场;t为传播时间。这种解会造成频率域波场补偿的不稳定现象,甚至使有效波场被高频噪声覆盖,导致模拟失败。为解决Q-RTM的不稳定问题,本文从波动方程的解出发,反推稳定补偿波场的差分表达式。首先,在式(14)添加一个稳定项
| $ u = {u_0}{\rm{ex}}{{\rm{p}}^{\frac{{\omega (1 - \varepsilon \omega )t}}{{2Q}}}} $ | (15) |
式中ε为稳定因子。则频率域黏声波场为
| $ \begin{array}{l} \frac{{{\partial ^2}U(x,z,\omega )}}{{\partial {x^2}}} + \frac{{{\partial ^2}U(x,z,\omega )}}{{\partial {z^2}}} + \frac{\omega }{{V_c^2}}U(x,z,\omega )\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = - F(x,z,\omega ) \end{array} $ | (16) |
相应地,黏声复速度Vc可表示为
| $ \frac{1}{{{V_{\rm{c}}}}} = \frac{{1 + \frac{{{\rm{i}}(1 - \varepsilon \omega )}}{{2Q}}}}{v} $ | (17) |
式(15)中指数项的分子关于ω的二次函数为
| $ {{f_{\rm{q}}} = \omega - \varepsilon {\omega ^2}} $ | (18) |
其对称轴为
| $ {{\omega _{\rm{s}}} = \frac{1}{{2\varepsilon }}} $ | (19) |
即
| $ {\varepsilon = \frac{1}{{2{\omega _{\rm{s}}}}}} $ | (20) |
则式(17)变为
| $ \frac{1}{{{V_{\rm{c}}}}} = \frac{{1 + {\rm{i}}\left( {1 - \frac{\omega }{{2{\omega _{\rm{s}}}}}} \right)/(2Q)}}{v} $ | (21) |
图 2为不同ε的增益函数。由图可见:ε可调节增益函数的对称轴位置ωs,进而控制高频分量的增长程度;当ω < 2ωs,对模拟过程补偿,ω>2ωs,对模拟过程衰减,即在有效频带内补偿,在有效频带外衰减。因此,ωs应近似等于或略高于震源子波的主频,才能实现适当补偿,既能改善不稳定现象也不会抑制有效高频。此外,ε只改变有效频带外高频的计算符号,不增加额外的计算量,由此实现了不牺牲计算效率的稳定Q-RTM。
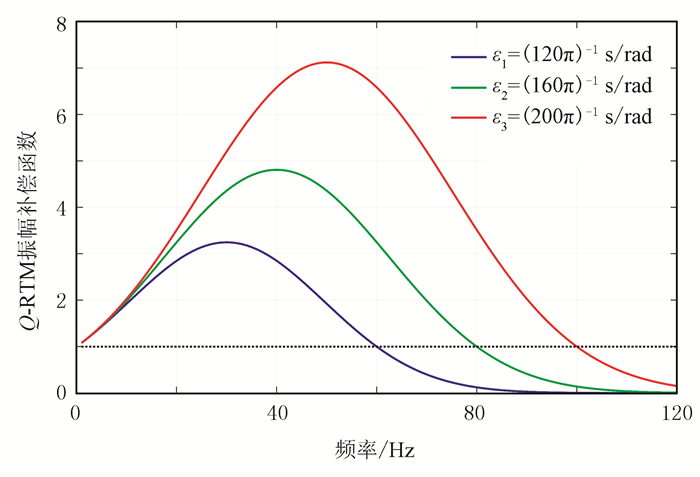
|
图 2 不同ε的增益函数 |
精确地震正演的前提是在几何上能够由剖分网格精确地描述模型形状。常规的矩形或三角形网格无法准确剖分起伏地表模型,并由此产生干扰波。为此,本文采用贴体网格代替常规网格。
贴体网格作为一种“边界拟合网格”,其本质是进行坐标变换,即通过映射关系建立不规则物理空间(图 3a)与规则计算空间(图 3b)的对应关系。利用规则网格划分计算空间,再进行坐标变换,得到适合物理空间不规则地形的曲面网格。本文采用改进的网格生成算法[36]。
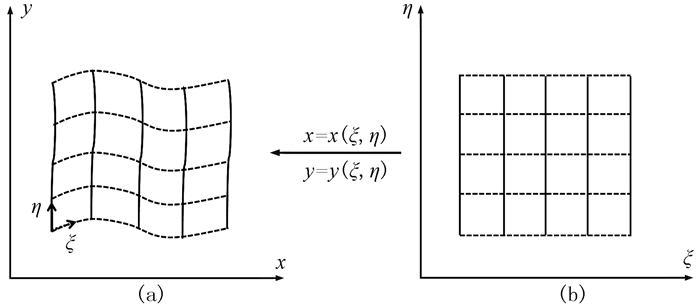
|
图 3 贴体网格与坐标变换 (a)不规则物理空间;(b)规则计算空间 笛卡尔坐标系(x, y)和曲线坐标系(ξ, η)的网格点建立了一一对应关系,从而可求得两个坐标系间的映射关系(即雅克比矩阵)ξx,ξy,ηx,ηy,其中符号 |
起伏地表频率域稳定Q-RTM流程(图 4)如下。
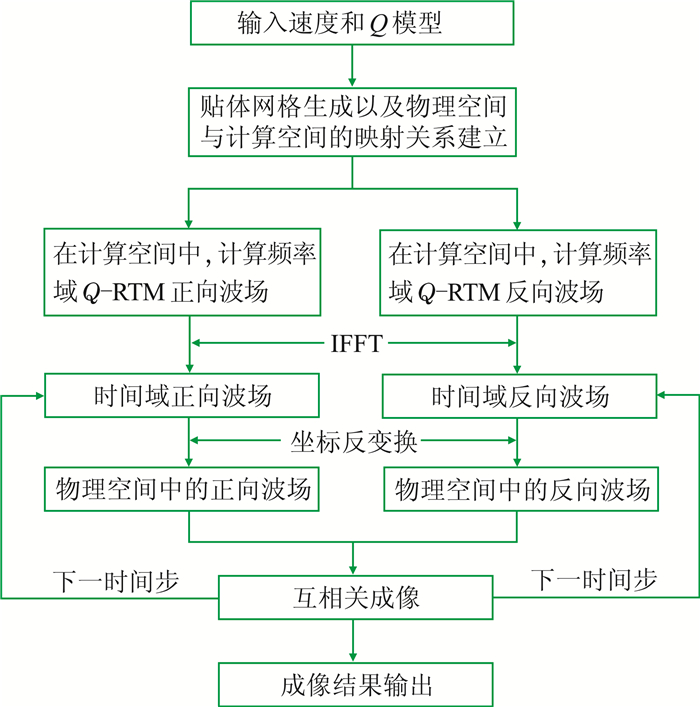
|
图 4 起伏地表频率域稳定Q-RTM流程 |
(1) 生成贴体网格以及建立物理空间与计算空间的映射关系;
(2) 在计算空间计算频率域Q-RTM正向传播波场,利用反傅里叶变换(IFFT)得到相应的时间域波场;
(3) 在计算空间计算频率域Q-RTM反向传播波场,利用IFFT得到相应的时间域波场;
(4) 利用建立的映射关系的逆映射得到物理空间正、反向传播波场;
(5) 利用互相关成像条件对上述时间域波场成像,并输出成像结果。
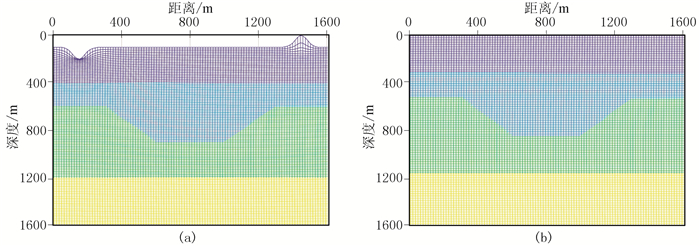
2 偏移效果分析 2.1 凹陷模型为验证起伏浅表层频率域稳定的Q-RTM的效果,首先设计一个起伏地表凹陷模型(图 5),基于贴体网格将速度场和Q场在计算空间中均匀剖分(图 6b),并使用主频为30Hz的雷克子波作为震源进行模拟。

|
图 5 起伏地表凹陷模型速度场(a)和Q场(b) |
|
图 6 起伏地表凹陷模型物理空间(a)和计算空间(b)剖分网格 计算空间的网格数为310×310(含30个PML边界网格),Δx=Δz=5m |
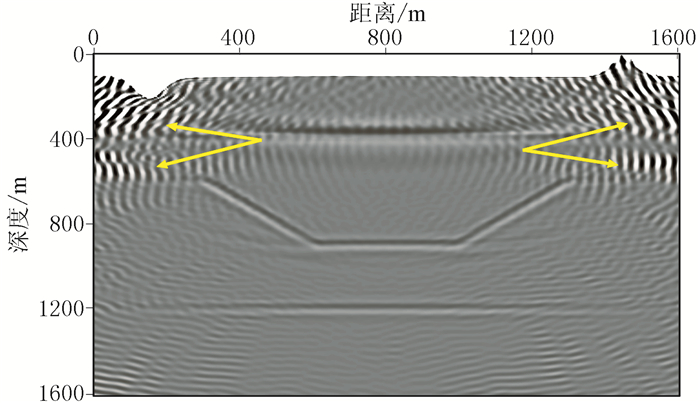
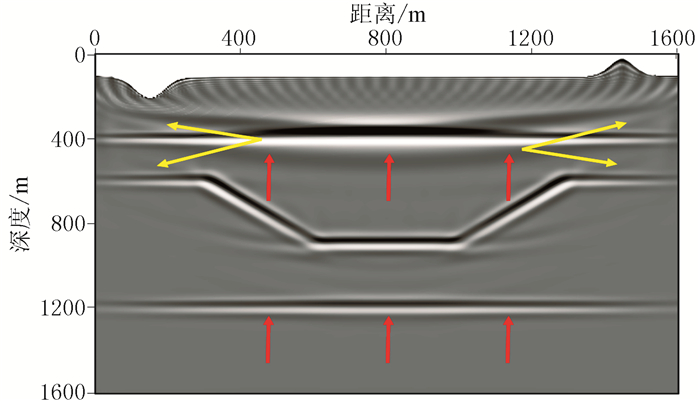
为对比不同方法的效果,同时进行声波RTM(图 7)、RTM(图 8)、常规Q-RTM(图 9)和起伏浅表层频率域稳定的Q-RTM(即本文方法,图 10)。声波RTM使用声波数据,另外三种偏移方法均使用黏声数据(下文同)。可见:①与声波RTM剖面(图 7)相比,RTM剖面(图 8)能量损失严重,同相轴变粗,分辨率明显降低,不利于地震解释和储层识别。②常规Q-RTM剖面(图 9)出现明显的不稳定现象,且浅层尤其严重(黄色箭头处);随着补偿量的增加,高频噪声覆盖整个剖面。③本文方法所得剖面(图 10)显著提升了能量和分辨率(对比图 8、图 10的红色箭头处),有助于对浅表层精确成像。

|
图 7 凹陷模型声波RTM剖面 |

|
图 8 凹陷模型RTM剖面 |
|
图 9 凹陷模型常规Q-RTM剖面 |
|
图 10 凹陷模型起伏浅表层频率域稳定的Q-RTM剖面 ε=(2×2π×40)-1s/rad,即补偿函数的对称轴位于40Hz处 |
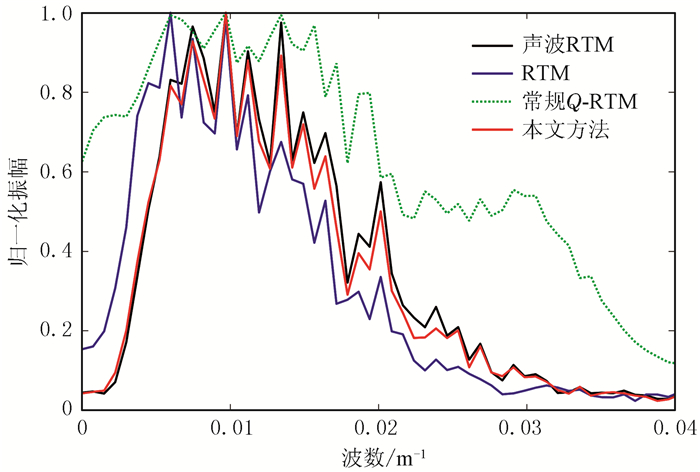
对比以上几种偏移结果的平均波数谱(图 11)可知:RTM能量峰值向低波数方向(对应低频方向)移动,高波数(高频)成分的能量被吸收,且带宽比声波RTM窄;常规Q-RTM的高波数(高频)能量非常强,这是由于不稳定问题放大的高频噪声所致;本文方法与声波RTM的波数谱曲线非常接近,说明本文方法可以稳定地补偿振幅与提高分辨率,利于浅表层精确成像。
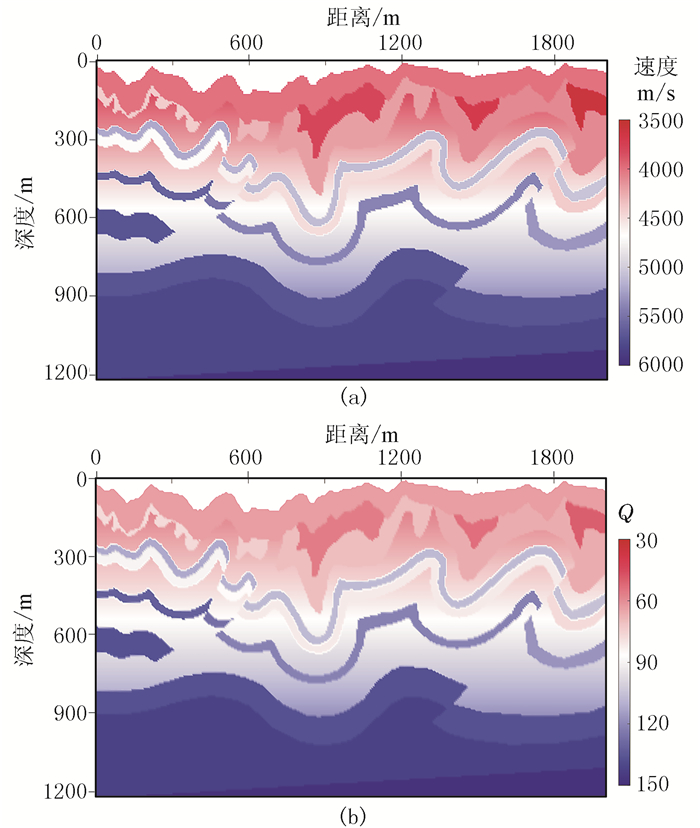
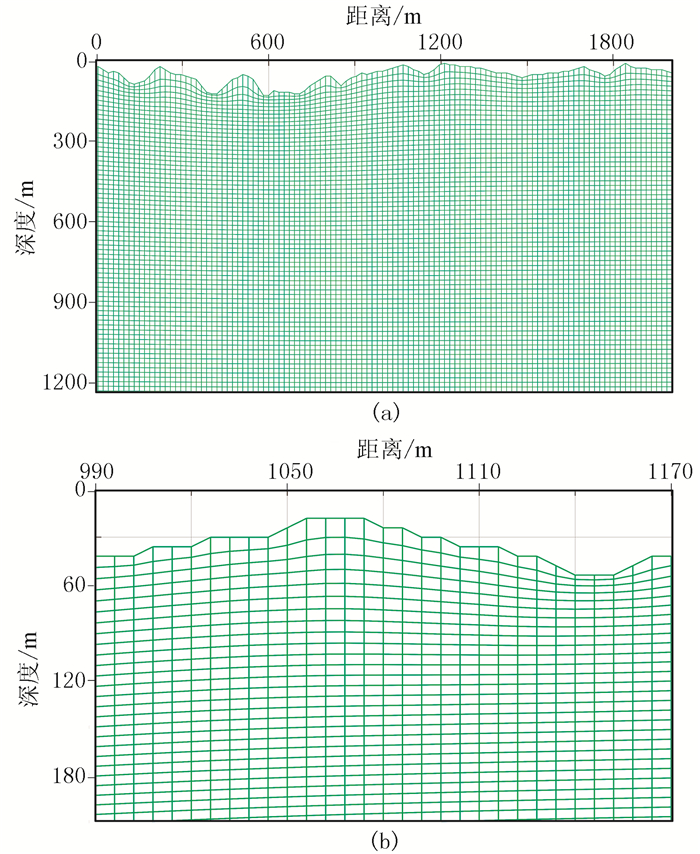
2.2 复杂模型加拿大落基山模型(图 12)为加拿大落基山脉的一个横截面[37],浅表层结构复杂,介质横向变化剧烈,基于贴体网格将速度场和Q场在计算空间中均匀剖分(图 13)。使用30Hz雷克子波作为震源,同样进行声波RTM(图 14)、RTM(图 15)、常规Q-RTM(图 16)和起伏浅表层频率域稳定的Q-RTM(图 17)。
|
图 12 加拿大落基山模型速度场(a)和Q场(b) |
|
图 13 加拿大落基山模型贴体网格(a)及其局部放大(b) |
|
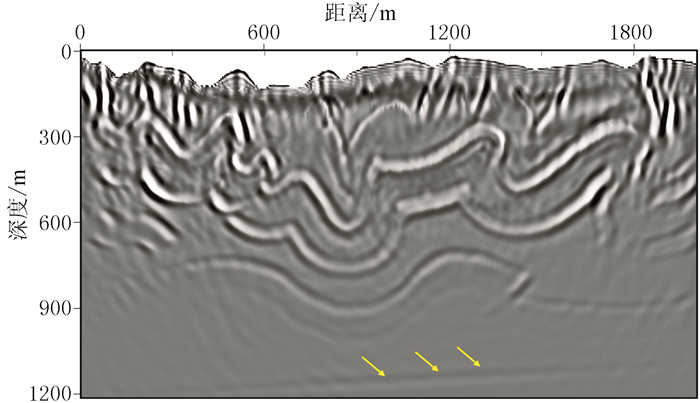
图 14 加拿大落基山模型声波RTM剖面 |
|
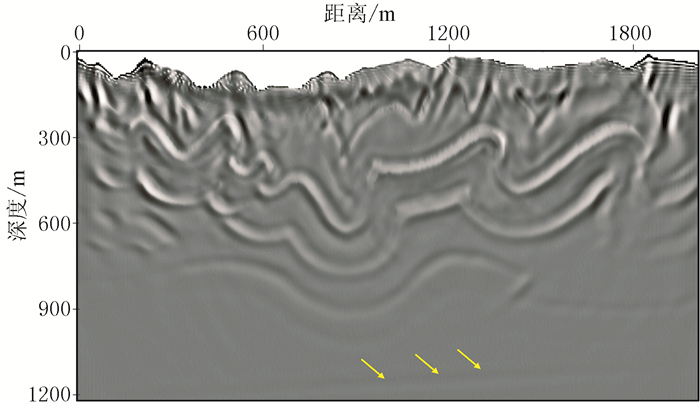
图 15 加拿大落基山模型RTM剖面 |
|
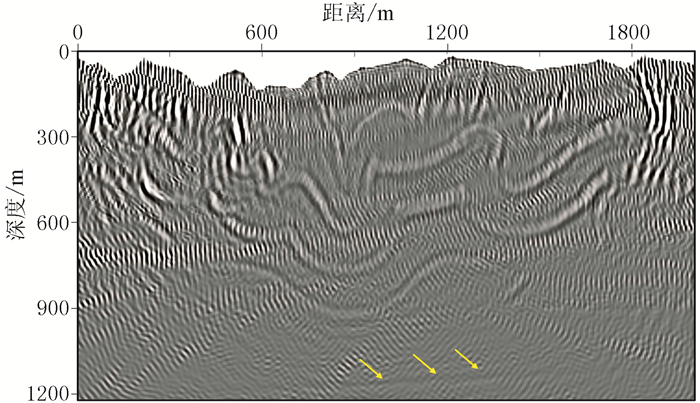
图 16 加拿大落基山模型常规Q-RTM剖面 |

|
图 17 加拿大落基山模型起伏浅表层频率域稳定的Q-RTM剖面 考虑到模型较复杂,波场信息较丰富,取ε=(2×2π×45)-1s/rad, 即补偿函数的对称轴位于45Hz处 |
对比不同方法的偏移结果可见:①由于浅层的Q值较小,导致地震波能量迅速衰减,RTM、常规Q-RTM难以对深层构造有效成像(图 15、图 16的黄色箭头处的倾斜层);高频噪声基本覆盖了常规Q-RTM剖面(图 16),从而影响构造识别,降低了成像品质。②本文方法在不放大噪声的情况下有效补偿了能量,较深的倾斜层也能很好地成像(图 17),剖面整体能量和分辨率基本可以恢复到声波RTM(图 14)的效果。
图 18为x=1098m处的单道记录和沿深度方向的波数谱。由图可见:①衰减导致地震信号能量变弱及相位变化,波峰和波谷变“平缓”(图 18a椭圆和箭头处),降低了信号的分辨能力;常规Q-RTM由于存在不稳定问题,导致虚假高频成分骤然增加,淹没了原始有效信息;本文方法恢复了信号能量,明显提高了分辨率,基本可以恢复到声波RTM的水平(图 18a)。②本文方法波数谱的主频和带宽接近声波RTM,较好地恢复了高频成分;RTM受高频噪声影响严重,导致波数谱形状发生较大变化(图 18b)。对比RTM与本文方法剖面(图 19)可见,后者补偿了能量及有效高频成分,提高了偏移结果的分辨率。
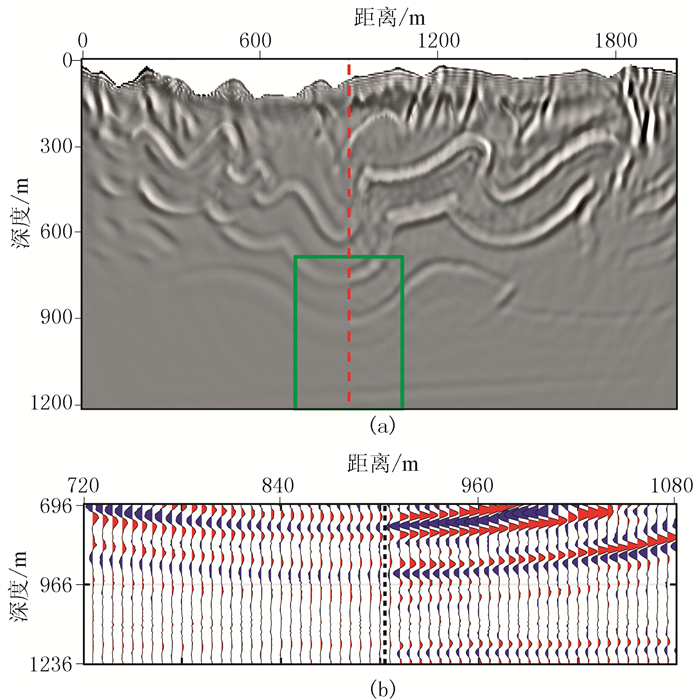
|
图 19 RTM(左)与本文方法(右)剖面拼接(a)及其局部放大(b) |
模型测试结果表明,即使在浅表层复杂条件下,本文方法仍能稳定而有效地补偿能量和高频成分,是一种可靠的偏移方法。
2.3 实际应用经模型测试后,将本文方法用于C区实际资料(图 20),并使用主频为30Hz的雷克子波作为震源进行模拟。
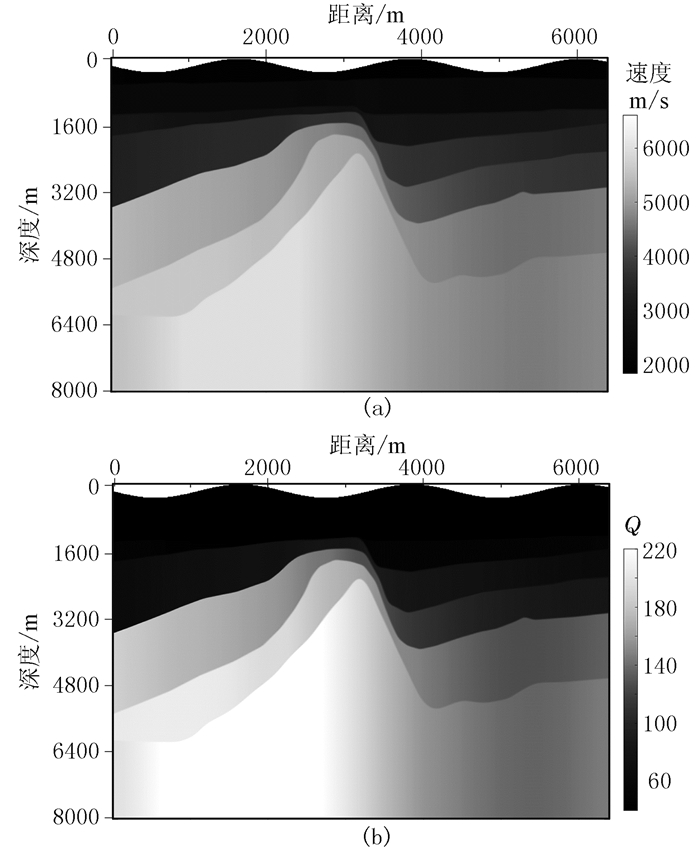
|
图 20 C区速度场(a)及其换算的Q场(b) |
对比、分析RTM与本文方法的结果可见,后者对构造的刻画更精细,且能量分布较均衡(图 21b)。由RTM与本文方法结果的平均波数谱(图 22)可见,后者的主频虽未明显提高,但带宽显著拓展,即提高了剖面分辨率,利于资料解释与储层预测。
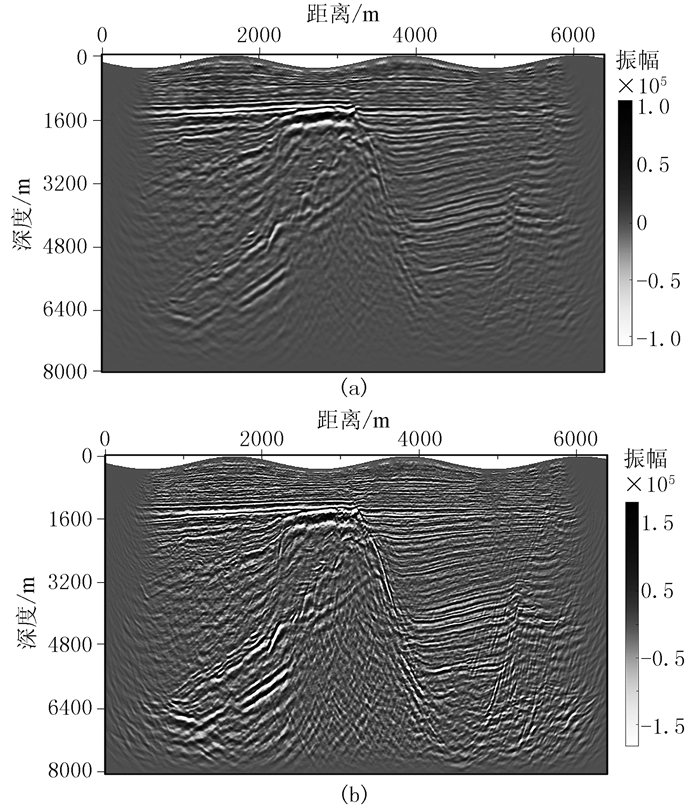
|
图 21 RTM (a)与本文方法(b)剖面 网格数为1600×1278,网格间距为5m, 共264炮,每炮240道接收,道间距为5m。ε=(2×2π×40)-1s/rad,即补偿函数的对称轴位于40Hz处 |
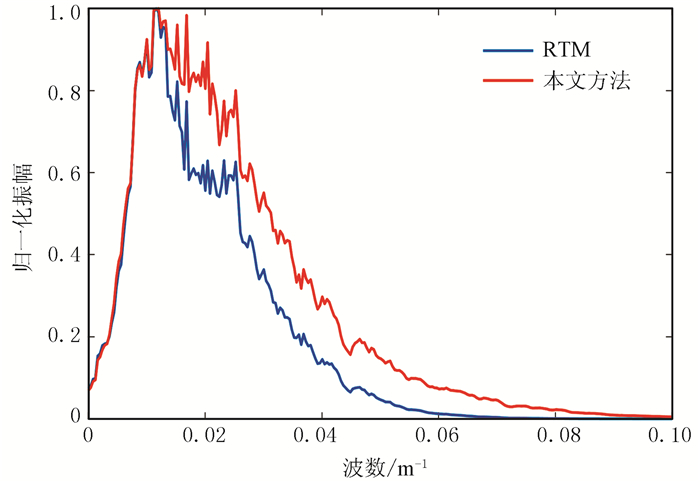
|
图 22 RTM和本文方法沿深度方向的平均波数谱计算波数谱时,深度范围为1~8km(图 21) |
在偏移中,浅表层能量衰减和起伏是影响偏移结果的两个重要因素。与时间域相比,频率域正演、偏移更利于模拟衰减和补偿效应。本文给出了起伏浅表层稳定的频率域Q-RTM完整流程。为了解决常规Q-RTM的不稳定性问题,在频率域波动方程中加入一个稳定项,推导了压制高频噪声的稳定的频率域波动方程。当稳定因子为0、Q为无穷大时,可以退化为声波方程。针对起伏地表问题,本文采用贴体网格将物理空间转换到计算空间,从而消除了常规网格剖分带来的干扰波。
模型测试和实际资料应用表明,本文提出的起伏浅表层稳定的频率域Q-RTM方法能补偿由衰减引起的振幅和高频成分损失,从而显著提高地震资料的分辨率,改善浅表层的成像品质,是一种稳定而有效的Q-RTM方法。
| [1] |
Clarke C G K. Time-varying deconvolution filters[J]. Geophysics, 1968, 33(6): 936-944. |
| [2] |
Margrave G F, Lamoureux M P, Henley D C. Gabor deconvolution:Estimating reflectivity by nonstationary deconvolution of seismic data[J]. Geophysics, 2011, 76(3): W15-W30. |
| [3] |
Yilmaz O.Seismic Data Analysis[M].Society of Ex-ploration Geophysicists, 2001.
|
| [4] |
WANG Y H. A stable and efficient approach of inverse Q filtering[J]. Geophysics, 2002, 67(2): 657-663. |
| [5] |
WANGYH. Inverse Q-filter for seismic resolutionenhancement[J]. Geophysics, 2006, 71(3): V51-V60. |
| [6] |
Wang Y F, Zhou H, Chen H M, et al. Adaptive stabilization for Q-compensated reverse time migration[J]. Geophysics, 2018, 83(1): S15-S32. |
| [7] |
Zhang Y, Zhang P, and Zhang H Z.Compensating for visco-acoustic effects in reverse-time migration[C].SEG Technical Program Expanded Abstracts, 2010, 29: 3160-3164.
|
| [8] |
Zhu T Y. Time-reverse modelling of acoustic wave propagation in attenuating media[J]. Geophysical Journal International, 2014, 197(1): 483-494. DOI:10.1093/gji/ggt519 |
| [9] |
Dai N and West G F.Inverse Q migration[C].SEG Technical Program Expanded Abstracts, 1994, 13: 1418-1421.
|
| [10] |
Zhang J F and Wapenaar K. Wavefield extrapolation and prestack depth migration in anelastic inhomogeneous media[J]. Geophysical Prospecting, 2002, 50(6): 629-643. DOI:10.1046/j.1365-2478.2002.00342.x |
| [11] |
Deng F and Mcmechan G A. True-amplitude prestack depth migration[J]. Geophysics, 2007, 72(3): S155-S166. |
| [12] |
Qu Y M, LI J L, Guan Z, et al. Viscoacoustic reverse time migration of joint primaries and different-order multiples[J]. Geophysics, 2020, 85(2): S71-S87. |
| [13] |
Qu Y M, Guan Z, LI J L, et al. Fluid-solid coupled full-waveform inversion in the curvilinear coordinates for ocean-bottom cable data[J]. Geophysics, 2020, 85(3): R113-R133. |
| [14] |
梁昊.二维频率域声波方程正演模拟及其全波形反演研究[D].北京: 中国地质大学(北京), 2016. LIANG Hao.2-D Frequency Acoustic Wave Equation Modeling and Full Wave Inversion[D].China University of Geosciences (Beijing), Beijing, 2016. |
| [15] |
Lysmer J and Drake L A. A finite element method for seismology[J]. Methods in Computational Physics:Advances in Research and Applications, 1972, 11: 181-216. |
| [16] |
Marfurt K J. Accuracy of finite-difference and finite-element modeling of the scalar and elastic wave equations[J]. Geophysics, 1984, 49(5): 533-549. DOI:10.1190/1.1441689 |
| [17] |
Pratt R G and Worthington M H. Inverse theory applied to multi-source cross-hole tomography.Part 1:acoustic wave-equation method[J]. Geophysical Prospecting, 1990, 38(3): 287-310. DOI:10.1111/j.1365-2478.1990.tb01846.x |
| [18] |
Jo C H, Shu J J, Shin C S. An optimal 9-point, finite-difference, frequency-space, 2-D scalar wave extrapolator[J]. Geophysics, 1996, 61(2): 529-537. |
| [19] |
Shin C S, Yoon K, Marfurt K J, et al. Efficient calculation of a partial-derivative wavefield using reciprocity for seismic imaging and inversion[J]. Geophysics, 2001, 66(6): 1856-1863. DOI:10.1190/1.1487129 |
| [20] |
Chu C L, Phillips C, and Stoffa P L.Frequency domain modeling using implicit spatial finite difference operators[C].SEG Technical Program Expanded Abstracts, 2010, 29: 3076-3080.
|
| [21] |
刘璐, 刘洪, 刘红伟. 优化15点频率-空间域有限差分正演模拟[J]. 地球物理学报, 2013, 56(2): 644-652. LIU Lu, LIU Hong, LIU Hongwei. Optimal 15-point finite difference forward modeling in frequency-space domain[J]. Chinese Journal of Geophysics, 2013, 56(2): 644-652. |
| [22] |
Zhao Z Y and Sen M K. Frequency-domain double-plane-wave least-squares reverse time migration[J]. Geophysical Prospecting, 2019, 67(8): 2061-2084. DOI:10.1111/1365-2478.12803 |
| [23] |
董士琦, 韩立国, 胡勇, 等. 基于MCPML边界条件的频率域声波方程高精度模拟[J]. 石油地球物理勘探, 2018, 53(1): 47-54. DONG Shiqi, HAN Liguo, HU Yong, et al. Acoustic equation high-accuracy modeling in the frequency domain based on MCPML absorbing boundary[J]. Oil Geophysical Prospecting, 2018, 53(1): 47-54. |
| [24] |
韩如冰, 郎超. 频率域八阶NAD有限差分模拟及全波形反演[J]. 石油地球物理勘探, 2019, 54(6): 1254-1266. HAN Rubing, LANG Chao. The eighth-order frequency-domain NAD method and full-waveform inversion[J]. Oil Geophysical Prospecting, 2019, 54(6): 1254-1266. |
| [25] |
邹强, 黄建平, 李庆洋, 等. 伪深度域弹性波有限差分数值模拟及逆时偏移[J]. 石油地球物理勘探, 2020, 55(2): 321-330. ZOU Qiang, HUANG Jianping, LI Qingyang, et al. Elastic-wave numerical simulation and reverse time migration in pseudo-depth domain[J]. Oil Geophysical Prospecting, 2020, 55(2): 321-330. |
| [26] |
吴吉忠, 左虎. 叠前衰减补偿时间偏移及GPU实现[J]. 石油地球物理勘探, 2019, 54(1): 84-92. WU Jizhong, ZUO Hu. Attenuation compensation in prestack time migration and its GPU implementation[J]. Oil Geophysical Prospecting, 2019, 54(1): 84-92. |
| [27] |
Chu W H. Development of a general finite difference approximation for a general domain, part Ⅰ:Machine transformation[J]. Journal of Computational Physics, 1971, 8(3): 392-408. |
| [28] |
Thomas P D and Middlecoff J F. Direct control of the grid point distribution in meshes generated by elliptic equations[J]. AIAA Journal, 1980, 18(6): 652-656. DOI:10.2514/3.50801 |
| [29] |
Tessmer E, Kosloff D, Behle A. Elastic wave propagation simulation in the presence of surface topography[J]. Geophysical Journal International, 1992, 108(2): 621-632. DOI:10.1111/j.1365-246X.1992.tb04641.x |
| [30] |
Hilgenstock A.A fast method for the elliptic generation of three-dimensional grids with full boundary control[C].Numerical Grid Generation in Computational Fluid Mechanics, 1988, 137-146.
|
| [31] |
蒋丽丽, 孙建国. 基于Poisson方程的曲网格生成技术[J]. 世界地质, 2008, 27(3): 298-305. JIANG Lili, SUN Jianguo. Source terms of elliptic system in grid generation[J]. Global Geology, 2008, 27(3): 298-305. |
| [32] |
丘磊.正交曲线坐标系下的地震波数值模拟技术研究[D].浙江杭州: 浙江大学, 2012. QIU Lei.Study on Seismic Wave Simulations on Orthogonally Curvilinear Coordinate System[D].Zhejiang University, Hangzhou, Zhejiang, 2012. |
| [33] |
杨宇.基于贴体网格的黏弹性介质起伏地表正演模拟研究[D].山东青岛: 中国石油大学(华东), 2016. YANG Yu.Study on Forward Modeling for Irregular Free-Surface in Viscoelastic Media Based on Body-Fitted Grid[D].China University of Petroleum (East China), Qingdao, Shandong, 2016. |
| [34] |
Qu Y M, Li J L. Q-compensated reverse time migration in viscoacoustic media including surface topography[J]. Geophysics, 2019, 84(4): S201-S217. |
| [35] |
李庆洋. T分布起伏地表最小二乘逆时偏移[J]. 石油地球物理勘探, 2019, 54(5): 1075-1083. LI Qingyang. Least-squares reverse time migration on undulated surface based on T-distribution[J]. Oil Geophysical Prospecting, 2019, 54(5): 1075-1083. |
| [36] |
魏文礼, 王德意, 刘玉玲. 正交曲线网格生成技术的一点改进[J]. 武汉水利电力大学学报, 2000, 33(2): 40-42. WEI Wenli, WANG Deyi, LIU Yuling. Some improvement on technique of orthogonal curvilinear grid generation[J]. Engineering Journal of Wuhan University, 2000, 33(2): 40-42. |
| [37] |
Gray S H and Marfurt K J. Migration from topography:Improving the near-surface image[J]. Canadian Journal of Exploration Geophysics, 1995, 31(4): 18-24. |



 李振春, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
李振春, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: