2 南方科技大学地球与空间科学系, 广东深圳 518055;
3 南方科技大学深圳市深远海油气勘探技术重点实验室, 广东深圳 518055
2 Department of Earth and Space Sciences, Sou-thern University of Science and Technology, Shen-zhen, Guangdong 518055, China;
3 Shenzhen Key Laboratory of Deep offshore Oil and Gas Exploration Technology, Southern University of Science and Technology, Shenzhen, Guangdong 518055, China
完全匹配层(Perfectly matched layer,PML)被广泛应用于波动传播的数值模拟,以解决数值模型的边界吸收问题。其初期应用是Bérenger[1]在计算电磁学领域提出的一种有效吸收的边界条件。由于PML具有吸收效果好、适用范围广的特点,Chew等[2]将其引入地震波数值模拟。此后,PML在地震波模拟中被广泛应用[3-7]。
后续研究发现PML对掠射到吸收层的虚假反射的吸收效果欠佳。在计算电磁学领域,为了增强对掠射波和非均匀波的吸收效果,Kuzuoglu等[8]提出将PML在复数域的坐标拉伸方程的极点移到非零区域。在计算地震学领域,Festa等[5]将基于复频移的PML应用于地震波数值模拟,证实这样可提高掠射波的吸收。Roden等[9]将这种PML的改进形式命名为复频移完全匹配层(Complex frequency-shifted PML,CFS-PML)。
在此基础上,近年也有不少学者对已提出的PML方法进行对比和改进[10-12]。李佩笑等[10]对比分析了非分裂与分裂两种实现方法;廉西猛等[11]研讨了多种吸收方式的异同;Liu等[12]剖析了影响衰减的各因子。为了在地震波数值模拟程序中应用CFS-PML,人们研发了多种具体实现形式,包括卷积法PML(C-PML)[9, 13]、积分法[14]、Z变化法[15]和辅助微分方程法(ADE CFS-PML)[16-17]等。其中ADE CFS-PML将CFS-PML转换成偏微分方程,可使用与内部相同的数值格式求解,具有实现简单、非分裂形式、不依赖于时间积分格式等优点,获得广泛应用[16-17]。
实际应用CFS-PML需合理设置三个参数:衰减参数d、频移参数α和坐标实拉伸参数β。d是地震波在PML传播中最主要的衰减因子,表征地震波在PML内传播时的振幅和能量衰减。α使PML的衰减变成与频率相关,即低频(频率小于α)是衰减弱→不衰减,高频(频率大于α)是正常衰减。该参数使CFS-PML对地震波传播的作用类似于低通滤波器。α的引入尽管破坏了标准PML对所有频段都相同吸收的优异性能,但实际模拟中发现该参数可降低掠射波入射到PML界面时产生的非均匀波[9, 13]。补偿该参数对低频吸收的破坏的一种方案是采用双极点CFS-PML[18-19]。β使垂向空间长度拉伸β倍,等效于长度不拉伸、但介质变成垂向VTI,使掠射波在PML中波前面向界面法线方向弯曲,增大方程中的角度项,增强掠射波吸收效果[19]。
CFS-PML的参数设置包括两个方面:一是参数沿PML的变化形式,即空间分布;二是参数在最内或最外层的最大值。前人对d提出过多种空间分布(函数)形式,如幂函数[3, 13, 16, 20-21]、对称函数[22]、正余弦函数[23-24]、复合函数[25-26]等形式。α、β的空间分布以幂函数形式为主[13, 16]。
衰减参数最大值d0的取值本质上取决于预期最小反射系数R,通常采用Collino等[3]给出的经验设置。Festa等[5]给出频移参数最大值取值公式α0=πfc,其中fc是震源子波中心频率。Zhang等[16]指出β0可允许坐标拉伸后中心波长对应的每波长网格数降为色散误差允许的每波长网格数的一半。
以上各参数的最大值都是基于均匀速度模型设置的。复杂速度模型存在横向和纵向速度变化,对衰减起关键作用的参数d0与吸收层内速度值相关;在复杂速度模型情况下,是按每个点速度值估算参数最大值,还是在整个吸收层按统一参考速度设置衰减参数最大值,尚难觅相关文献报道及对此的系统评估。本文充分调研了复杂速度模型CFS-PML参数设置方法,通过对多种复杂速度模型做数值测试,总结出复杂速度模型CFS-PML优化取值方案,为CFS-PML的实际应用提供参考。
1 CFS-PML公式形式和参数取值 1.1 ADE CFS-PML实现形式从CFS-PML的各种实现方式看,ADE CFS-PML具有适用于各种时间积分法的优势,本文以ADE CFS-PML为例介绍CFS-PML的实现[16]。
ADE CFS-PML主要思想是在吸收边界内对弹性波动方程进行复坐标的拉伸变换,通过引入辅助变量对吸收层内的弹性波动方程做修正从而达到吸收的目的。下面仅以+x方向为例进行说明。将实坐标
| $ \tilde x = \int_0^x {{s_x}} (\eta ){\rm{d}}\eta $ | (1) |
式中:sx(η)表示拉伸方程;η表示x方向积分变量。
不同的拉伸方程对应不同类型的PML。对式(1)等号两边分别求导可得复坐标下的空间导数与实坐标下的空间导数的关系
| $ \frac{\partial }{{\partial \tilde x}} = \frac{1}{{{s_x}}}\frac{\partial }{{\partial x}} $ | (2) |
以二维P-SV波波动方程为例,方程如下
| $ {\rho {v_{x,t}} = {\tau _{xx,x}} + {\tau _{xz,z}}} $ | (3) |
| $ {\rho {v_{z,t}} = {\tau _{zx,x}} + {\tau _{zz,z}}} $ | (4) |
| $ {{\tau _{xx}} = (\lambda + 2\mu ){v_{x,x}} + \lambda {v_{z,z}}} $ | (5) |
| $ {{\tau _{zz}} = \lambda {v_{x,x}} + (\lambda + 2\mu ){v_{z,z}}} $ | (6) |
| $ {{\tau _{xz}} = \mu ({v_{x,z}} + {v_{z,x}})} $ | (7) |
式中:ρ是密度;λ、μ是拉梅常数;vx、vz为时间域速度分量;τxx、τzz、τxz为时间域应力分量,下标中逗号后的t、x、z表示对t、x、z的导数。以式(3)为例,将拉伸方程代入得到
| $ {\rm{i}}\omega \rho {\hat v_x} = \frac{1}{{{s_x}}}\frac{\partial }{{\partial x}}{\hat \tau _{xx}} + \frac{\partial }{{\partial z}}{\hat \tau _{xz}} $ | (8) |
式中:ω是角频率;
| $ {s_n} = {\beta _n} + \frac{{{d_n}}}{{{\alpha _n} + {\rm{i}}\omega }} = {\beta _n}\left[ {1 + \frac{{\frac{{{d_n}}}{{{\beta _n}}}}}{{{\alpha _n} + {\rm{i}}\omega }}} \right] $ | (9) |
| $ \frac{1}{{{s_n}}} = \frac{1}{{{\beta _n}}}\frac{1}{{1 + \frac{{\frac{{{d_n}}}{{{\beta _n}}}}}{{{\alpha _n} + {\rm{i}}\omega }}}} = \frac{1}{{{\beta _n}}}\left[ {1 - \frac{{\frac{{{d_n}}}{{{\beta _n}}}}}{{{\alpha _n} + {\rm{i}}\omega + \frac{{{d_n}}}{{{\beta _n}}}}}} \right] $ | (10) |
式中n表示x、y和z中的一个方向,则dn、αn、βn分别是对应方向上的衰减参数、频移参数和坐标实拉伸参数。以下简述ADE方法实现方式。
式(8)等号右侧代入拉伸方程后的微分项为
| $ \frac{1}{{{s_x}}}{\hat \tau _{xx,x}} = \frac{1}{{{\beta _x}}}{\hat \tau _{xx,x}} - \frac{1}{{{\beta _x}}}\psi _x^{{{\hat \tau }_{xx}}} $ | (11) |
其中辅助变量
| $ \frac{{{d_x}}}{{{\beta _x}}}{\hat \tau _{xx,x}} = {\rm{i}}\omega \psi _x^{{{\hat \tau }_{xx}}} + \left( {{\alpha _x} + \frac{{{d_x}}}{{{\beta _x}}}} \right)\psi _x^{{{\hat \tau }_{xx}}} $ | (12) |
将式(12)代入式(8),可得
| $ {\rm{i}}\omega \rho {\hat v_x} = \frac{1}{{{\beta _x}}}{\partial _x}{\hat \tau _{xx}} + {\partial _z}{\hat \tau _{xz}} - \frac{1}{{{\beta _x}}}\psi _x^{{{\hat \tau }_{xx}}} $ | (13) |
将式(11)和式(12)从频率域转换到时间域,就得到了辅助方程CFS-PML方程
| $ {\rho {v_{x,t}} = {\tau _{xx,x}} + {\tau _{xz,z}} - \left( {\frac{1}{{{\beta _x}}} - 1} \right)\psi _x^{{\tau _{xx}}}} $ | (14) |
| $ {\psi _x^{{\tau _{xx,t}}} + \left( {{\alpha _x} + \frac{{{d_x}}}{{{\beta _x}}}} \right)\psi _x^{{\tau _{xx}}} = \frac{{{d_x}}}{{{\beta _x}}}{\tau _{xx,x}}} $ | (15) |
将以上方法用于整个一阶速度—应力方程组就是ADE CFS-PML的实现方式。
1.2 CFS-PML性质分析以沿+x方向传播的行波(traveling wave)、非均匀波(evanescent wave)两类平面地震波为例,通过二维平面(x,z)波动方程的传播具体分析地震波在PML中的传播和衰减特性。行波可表示为
| $ {u^{\rm{t}}} = u_0^{\rm{t}}{\rm{exp}}[{\rm{i}}\omega t - {\rm{i}}k(\hat x{\rm{cos}}\theta + z{\rm{sin}}\theta )] $ | (16) |
式中:θ表示行波入射角;u0t为行波初始时刻振幅,上标t表示行波。
平行于介质—PML下界面传播,沿界面法线方向衰减的非均匀波可表示为
| $ {u^{\rm{e}}} = u_0^{\rm{e}}{\rm{exp}}( - \omega \xi \tilde x){\rm{exp}}({\rm{i}}\omega t - {\rm{i}}kz) $ | (17) |
式中:ξ是依赖于介质的参数;u0e为非均匀波初始时刻振幅,上标e表示非均匀波。基于式(1)做变换,其实部和虚部分别表示为
| $ \tilde x = \int_0^x {{s_x}} (\eta ){\rm{d}}\eta = {\tilde x_{\rm{R}}} + {\rm{i}}{\tilde x_{\rm{I}}} $ | (18) |
将式(18)代入式(16),则可转化为
| $ {u^{\rm{t}}} = u_0^{\rm{t}}{\rm{exp}}(k{\tilde x_{\rm{I}}}\cos \theta )\exp [{\rm{i}}\omega t - {\rm{i}}k({\tilde x_{\rm{R}}}\cos {\theta _{\rm{R}}} + z\sin \theta )] $ | (19) |
再将式(18)代入式(17),可转化为
| $ {u^{\rm{e}}} = u_0^{\rm{e}}{\rm{exp}}( - \omega \xi {\tilde x_{\rm{R}}}){\rm{exp}}({\rm{i}}\omega t - {\rm{i}}\omega \xi {\tilde x_{\rm{I}}} - {\rm{i}}kz) $ | (20) |
从式(19)、式(20)可知,复坐标拉伸的虚部
CFS-PML复拉伸方程对应的实部和虚部分别是
| $ {{{\tilde x}_{\rm{R}}} = \int_0^x {\left( {\beta + \frac{{\alpha d}}{{{\alpha ^2} + {\omega ^2}}}} \right)} {\rm{d}}\eta } $ | (21) |
| $ {{{\tilde x}_{\rm{I}}} = - \int_0^x {\frac{{\omega d}}{{{\alpha ^2} + {\omega ^2}}}} {\rm{d}}\eta } $ | (22) |
行波和非均匀波在CFS-PML中的方程分别是
| $ \begin{array}{*{20}{l}} {{u^{\rm{t}}} = u_0^{\rm{t}}{\rm{exp}}\left( { - \frac{{\cos \theta }}{v}\int_0^x {\frac{{{\omega ^2}d}}{{{\alpha ^2} + {\omega ^2}}}} {\rm{d}}\eta } \right) \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}\left[ {{\rm{i}}\omega t - {\rm{i}}k\cos \theta \int_0^x {\left( {\beta + \frac{{\alpha d}}{{{\alpha ^2} + {\omega ^2}}}} \right)} {\rm{d}}\eta - {\rm{i}}kz\sin \theta } \right]} \end{array} $ | (23) |
| $ \begin{array}{*{20}{l}} {{u^{\rm{e}}} = u_0^{\rm{e}}{\rm{exp}}( - \omega \xi x) \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}\left( {{\rm{i}}\omega t + {\rm{i}}\xi \int_0^x {\frac{{{\omega ^2}d}}{{{\alpha ^2} + {\omega ^2}}}} {\rm{d}}\eta - {\rm{i}}kz} \right) \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}\left[ { - \omega \xi \int_0^x {(\beta - 1 + \frac{{\alpha d}}{{{\alpha ^2} + {\omega ^2}}})} {\rm{d}}\eta } \right]} \end{array} $ | (24) |
从式(23)、式(24)易知,CFS-PML存在相应的虚部对行波衰减、相应的实部对非均匀波衰减,吸收效果大大提升。
1.3 均匀速度模型CFS-PML参数取值由于参数的空间分布形式对结果影响不大,这里采用最常用的幂函数形式[16, 20]
| $ {d = {d_0}{{\left( {\frac{D}{L}} \right)}^{{p_d}}}} $ | (25) |
| $ {\alpha = {\alpha _0}\left[ {1 - {{\left( {\frac{D}{L}} \right)}^{{p_\alpha }}}} \right]} $ | (26) |
| $ {\beta = 1 + ({\beta _0} - 1){{\left( {\frac{D}{L}} \right)}^{{p_\beta }}}} $ | (27) |
式中:指数pd通常取2、3、4,现有研究尚未发现这三个不同取值对结果具有本质影响;指数pα通常取1、pβ通常取2;d0、α0、β0分别是衰减、频移、坐标实拉伸参数最大值;D是波传播到吸收层内的距离;L是吸收层的厚度。
上述三种参数最大值中,d0是控制地震波在PML中衰减程度的参数,即是决定吸收效果的一个重要因子。d0值通常依据对于垂直入射的平面波经过PML后的预期反射系数R确定:理论上,越小的预期反射系数越符合实际需求;但预期反射系数太小,会导致d在PML内的空间分布变化过快,有可能由于过快的空间分布变化导致反射波。因此对不同的PML层数通常设置不同的预期反射系数。不同层数对应的最优R值大多是按经验设定的,并往往通过数值测试进行测定。Collino等[3]经验性地给出5层R=10-2,10层R=10-3,20层R=10-4。为了能对任意PML层数设置R值,Marcinkovich等[21]对Collino等[3]的离散值进行了拟合。Zhang等[16]通过分析离散值之间的关系,得到如下更具一般性的层数与R值的经验关系式
| $ {\rm{lg}}R = - \frac{{{\rm{lg}}N - 1}}{{{\rm{lg}}2}} - 3 $ | (28) |
式中N为设定的吸收层层数。给定预期反射系数R后,根据垂直入射的平面波,按d的空间函数分布穿过PML再反射回物理区间的衰减预取反射系数R,给出最大值d0。沿x传播的平面波经坐标拉伸后表示为
| $ u = {u_0}{\kern 1pt} {\rm{exp}}({\rm{i}}k\tilde x) $ | (29) |
式中u0为初始时刻振幅。
结合式(1)、式(21)、式(22)可得地震波在垂直入射时标准PML传播方程
| $ u = {u_0}{\rm{exp}}\left( { - \frac{{\rm{i}}}{v}\int_0^x \omega {\rm{d}}\eta } \right){\rm{exp}}\left( { - \frac{1}{v}\int_0^x d {\rm{d}}\eta } \right) $ | (30) |
该式第二个指数项是衰减项。考虑双程衰减,R可用衰减项表示为
| $ R = {\rm{exp}}\left( { - \frac{2}{v}\int_0^x d {\rm{d}}\eta } \right) $ | (31) |
针对式(25)中不同的pd形式,利用垂直入射测试模型进行数值测试,发现Collino等[3]给出的预期反射系数不是最优结果,相同层数下的预期反射系数可更低。按照原始公式进行设置:N=5时R=10-2,N=10时R=10-3,N=20时R=10-4;不同吸收层数对应的误差量级分别为:N=5时为10-2,N=10时为10-3,N=20时为10-4。而实际上按照N=5时R=10-3、N=10时R=10-4、N=20时R=10-5设置,误差在原有基础上减小一个量级,即N=5时为10-3、N=10时为10-4、N=20时为10-5,显然其吸收效果更优。
通过对不同层数对应的最优R值的测试结果进行拟合,得到如下的层数与预期反射系数关系
| $ {\rm{lg}}R = - \frac{{{\rm{lg}}N - 1}}{{{\rm{lg}}2}} - 4 $ | (32) |
将相应的衰减参数d的取值公式代入式(31),通过积分变换就可得到用R表示的d0取值公式[3]
| $ {d_0} = - {\rm{ln}}R\frac{{({p_d} + 1){V_{{\rm{Pr}}}}}}{{2L}} $ | (33) |
式中VPr是吸收层内设置的参考P波速度。
α0是CFS-PML作为低通滤波器时的拐角角频率[4],取值太低时CFS-PML对地震波传播等效于常规PML,不能发挥抑制非均匀波的作用;取值太高则导致大部分频率不吸收,没有起到PML的作用。通常设置为震源中心角频率fc的一半[5],即
| $ {\alpha _0} = 2\pi \times \frac{{{f_{\rm{c}}}}}{2} = \pi {f_{\rm{c}}} $ | (34) |
β0是垂直坐标的最大拉伸程度,拉伸程度越大就越有利于将波前向界面法线方向弯曲;但过大的β0会导致等效网格的尺度过大,超过数值格式分辨能力,进而导致强反射。可以预期,网格的空间步长越小(相比于色散误差要求的网格大小),β0越大。通过数值实验,Zhang等[16]指出最大β0可允许坐标拉伸后中心波长对应的每波长网格数降为色散误差允许的每波长网格数的一半。冯海珂[19]进一步将该准则明确表示为如下形式
| $ {\beta _0} = 2\frac{{P_{{f_{\rm{c}}}}^{\rm{s}}}}{{{P_{{\rm{FD}}}}}} $ | (35) |
式中:PFD是数值方法允许的每波长网格数(如四阶交错网格有限差分时PFD为5~6);Pfcs=
式(25)~式(27)和式(32)~式(35)构成CFS-PML参数的最优取值方案。从上述公式易知,这些取值都只是针对均匀速度模型。
1.4 复杂速度模型CFS-PML参数取值从上述针对CFS-PML各参数的取值公式及最大值设置的讨论得知:预期反射系数R和频移参数α0不依赖于速度模型,反射系数取值(式(32))仅与吸收层数相关,频移参数取值(式(34))仅与震源中心频率相关;但衰减参数d0和坐标实拉伸参数β0除了与固定的震源性质和网格性质相关外,还同吸收层内速度值和波长相关,即依赖于速度模型,其中d0与P波速度相关而β0与S波速度相关,d0的设置对吸收效果最为重要。从式(33)可看出,复杂速度模型下关键是如何设置参考速度VPr。所谓PML层内参考速度,即按该速度垂直传播进入边界的波,正好可实现预计的反射系数R的吸收。理论上若实际传播速度小于该速度,则在吸收层内经历过多衰减;若实际传播速度大于该速度,则在吸收层内吸收不足,在边界处产生较大反射。
根据实际情况,本文归纳出三种实用的复杂模型参考速度取值方法:①PML层内逐点设置不同的值,每点取所处物理区间P波速度;②针对复杂速度模型取一个等效速度值作为参考速度值,可以是最大值(即相应PML层内所有速度的最大值)或中间值(即PML层内所有速度的平均值);③对物理区间真实垂向速度值分布进行光滑,每点取光滑后逐点对应的不同的速度值。
2 模型实测结果分析与对比采用上述各方法针对多种速度模型进行实测和分析,以对比和遴选针对复杂模型的参考速度取值方案。
2.1 双层速度模型首先考察存在速度剧烈变化的双层模型,本次测试所用双层模型的速度设定为:上层VP1=0.5km/s、VS1=0.3km/s,下层VP2=10.0km/s、VS2=6.0km/s,速度变化幅度达20倍(图 1)。各衰减参数空间分布参照式(25)~式(27)进行选取,与VP相关的d0和β0通过选取VP而确定;反射系数R按式(32)选取为10-5;频移参数按式(34)选取为α0=πfc≈4.71。

|
图 1 高波速比双层模型 模型尺寸为5.7km×3.0km,网格单元为10m×10m,吸收层数N=20;震源是中心频率为1.5Hz雷克子波,位于(0.4km,-1.0km),与边界距离为0.2km;三个检波点由上至下编号为1~3,所处位置横坐标均为0.3km,纵坐标为-0.5~-2.5km,深度间隔为1.0km |
采取以下四种方式(图 2)设置参考速度:①逐点取边界介质速度对应值;②统一取边界介质速度中间值(5km/s);③统一取边界介质速度最大值;④计算一维垂向分布的每层平均速度,光滑后作为该层参考速度。

|
图 2 双层模型不同参考速度设置方式下垂直速度分布 |
测试的参考解通过在原模型上保持震源、检波点相对位置不变,扩大计算区间(7km×7km)设计而成。扩大后形成的参考模型保证在观测时窗内、最外层边界产生的误差不会被检波器接收到,从而使检波器在固定时窗内接收到的波形等效为在该时间范围内“无限大理想模型”接收到的地震波。
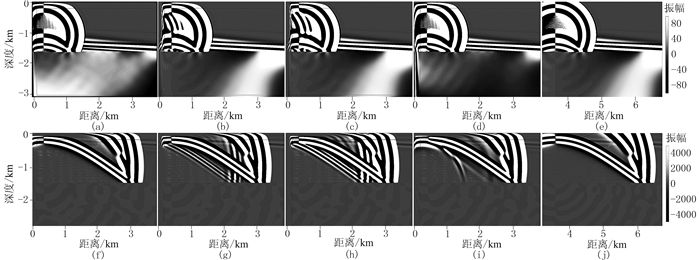
在t=2.4s时通过各取值方式与参考模型(图 3e)波场快照的对比可明显看出,设置为对应值(图 3a)或垂向速度值(图 3d)在左侧下半部边界处吸收不干净并有一定程度的反射,取统一值(图 3b、图 3c)吸收效果更好。而t=6.0s时,对于上部低速层,取对应值(图 3f)时反射较弱,吸收效果较好,其余方式(图 3g~图 3j)均有不同程度的反射。因上、下层速度差异很大,界面反射程度高,上层的波场振幅和能量更大。为了更清楚地显示下层波动,所以波场快照范围较小,显示的反射波对主波的影响无法定量估量。为定量地考察上、下层吸收效果,通过波形图和误差图进行进一步分析、讨论。
|
图 3 吸收层参考速度不同取值方式下双层模型的波场快照 (a)、(f)对应值;(b)、(g)中间值;(c)、(h)最大值;(d)、(i)垂向平滑值;(e)、(j)参考模型;上部t=2.4s;下部t=6.0s |
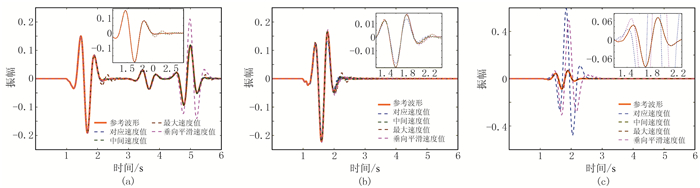
从位于不同深度检波器接收的波形对比图(图 4)不难看出,参考速度设置为对应值和垂向平滑值时在下部高速层(图 4c)呈现与参考波形的大幅度差异,但在两层界面处(图 4b)参考速度设置为对应值和垂向平滑值在主波幅值上与其余两种方法差异较小,只是吸收效果仍不理想,且设置为垂向平滑值在上部低速层(图 4a)主波后也出现较明显差异。统一设置为中间值或最大值时则与参考波形更契合,但在上部低速层(图 4a)和两层界面处(图 4b)主波后也出现小幅度反射现象。
|
图 4 双层模型四种参数设置方法记录波形与参考波形对比 (a)、(b)、(c)对应1~3号检波点;每个子图的局部放大图为其各自主波附近的波形 |
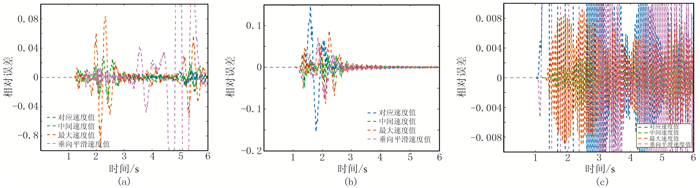
图 5用具象化误差对比展示四种方法吸收效果的差异。以参考模型为标准,参考波形最大值为归一化值对参考模型归一化。测试模型波形除以该值与参考模型归一化的差,即两者间的相对误差。不同参数设置方法的误差不同,从误差值的差异评估不同方法的吸收效果。统一设置为中间值或最大值在波形上都较为契合,但从误差的数值分布可见设置为中间值或最大值的误差远小于另两种方法(图 5c),那两种方法的误差远超出图示范围。而相较于统一设置为最大值,统一设置为中间值时在各深度处(检波器)的吸收效果都更好(图 5a~图 5c),吸收误差(范围约为10-3~10-2)相对更小、更平稳。
|
图 5 双层模型四种参数设置方法的测试波形与参考波形的相对误差对比 (a)、(b)、(c)对应1~3号检波点;相对误差为绝对误差除以参考波形后的归一化值 |
双层模型中设定了一个极端的上下速度比为20的例子说明统一设置参考速度吸收效果的优越性,在实际应用中很少出现类似情况,因此又设计了多层且速度逐渐变化的模型,以更契合地模拟实际复杂地形情况下的吸收效果。

|
图 6 多层速度模型 各层速度和对应界面深度由浅至深分别为1.0、2.5、4.0、5.5、7.0km/s,-0.7、-1.2、-1.8、-2.3km;震源是中心频率为5Hz的雷克子波,其位置及距边界的距离、三个检波点所处位置、深度间隔及编号等同图 1 |
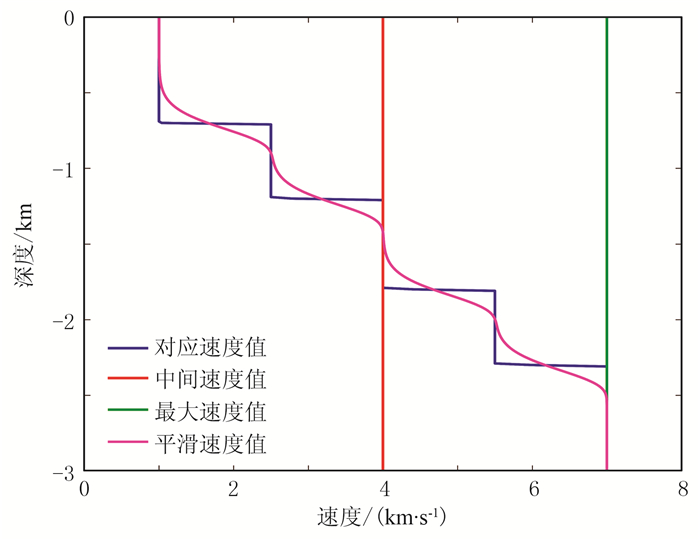
参考速度设置(图 7)采取与双层模型相同的四种方式,只是第二种取边界介质速度中间值时改用4.0km/s作为该层参考速度值。
|
图 7 多层模型参考速度不同设置方式下垂直速度分布 |
t=0.84s时刻不同设置方式波场快照与参考模型(图 8e)对比可显示四种方法差异,设置为对应值(图 8a)和垂向速度值(图 8d)在红圈区域产生较明显反射波,而统一设置(图 8b、图 8c)则吸收得较干净。

|
图 8 吸收层参考速度不同取值方式下多层模型t=0.84s时刻波场快照 (a)对应值;(b)中间值;(c)最大值;(d)垂向光滑值;(e)参考模型 |
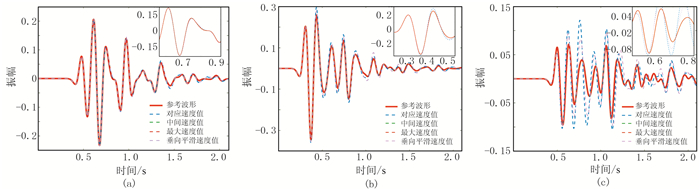
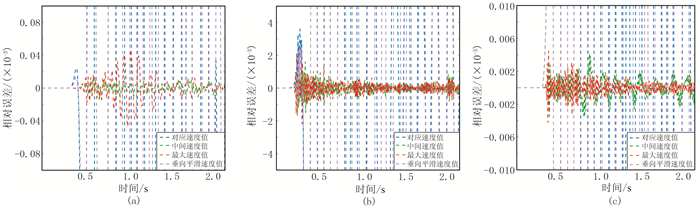
类似于双层模型,参考速度设置为对应值和垂向速度值在上部低速层(图 9a)与参考波形较吻合,而随着深度(速度)增加波形的不匹配性逐渐显著(图 9b),到下部高速层(图 9c)出现远高于主波的反射。统一设置为中间值和最大值,在3个检波点与参考波形的对比中都展现出高度匹配性,两者几乎重合。统一设置为中间值和最大值的相对误差低至10-4~10-3,而其余两种方法的误差为统一设置速度值的102~103倍,因此在误差对比图中远超出图幅范围。统一设置为中间值和最大值两者吸收差异在中部较高速层(图 10b、图 10c)相对较小,但在上部低速层(图 10a)统一设置为最大值时则呈现较大误差值。虽然统一设置为中间值在高速层(图 10c)的误差略高于设定为最大值,但从整体吸收效果看,参考速度统一设置为中间值吸收效果更优异。
|
图 9 多层模型四种参数设置方法记录波形与参考波形对比 (a)、(b)、(c)对应1~3号检波点;每个子图的局部放大图为其各自主波附近的波形 |
|
图 10 多层模型四种参数设置方法的测试波形与参考波形的相对误差对比 (a)、(b)、(c)对应1~3号检波点;相对误差为绝对误差除以参考波形后的归一化值 |
为了验证上述结果的普适性,针对不同方向(z)、不同吸收层数(N=10、15)也进行了相同测试,所得结果基本一致。通过对双层、多层模型不同设置方法的波场快照、波形和误差的对比及综合分析可知,对于复杂速度模型而言,参考速度统一设置为中间速度值对衰减参数进行取值的吸收效果更优越。
2.3 Marmousi模型与上述模型相比,Marmousi模型除了存在多层变化速度外,还存在局部速度陡增(如断层)等情况。震源参数除子波中心频率为10Hz外,其余与上述相同。
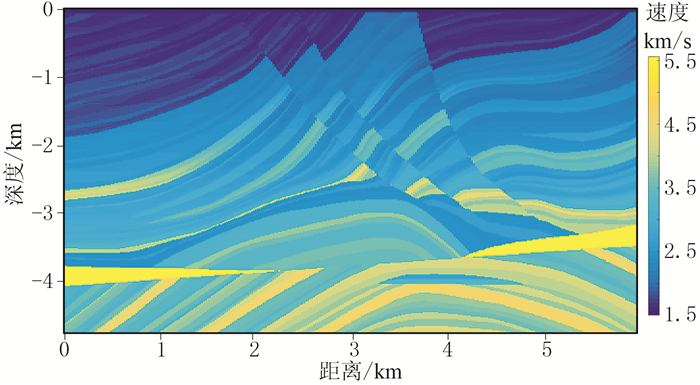
由于Marmousi模型无完全参考解,所以测试模型仅选取图 11的中间部分,吸收层数为20。而参考解则是略微扩大模型将吸收层数增至100。
|
图 11 Marmousi模型示意图 |
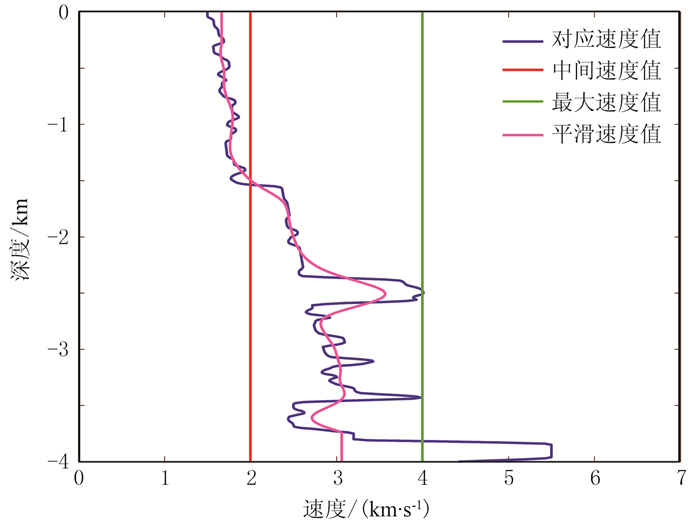
参考速度设置(图 12)仍采用与上述模型相同的四种方式,只是第二种取边界介质速度中间值时改用2.0km/s,且第三种取边界介质速度最大值是4.0 km/s,作为对应层位的参考速度值。
|
图 12 Marmousi模型不同参考速度设置方式下垂直速度分布 |
对比参考速度四种选取方法波场快照(图 13a),发现这四者基本一致;再与参考模型(图 13b)相比,波场快照也基本一致。说明这四种方法在吸收过程中波场残留较弱,均未出现明显的非均匀转换波和强不稳定杂波而大范围、大幅度地影响正常的波传播。

|
图 13a Marmousi测试模型取边界介质速度中间值在不同时刻(t=0.30、0.66、1.14、1.50s)的波场快照 |

|
图 13b Marmousi参考模型(速度场Vx)在不同时刻(t=0.30、0.66、1.14、1.50s)的波场快照 |
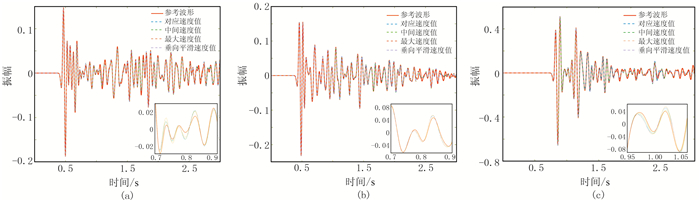
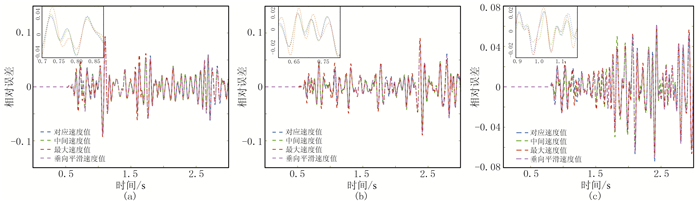
对于Marmousi模型,无论是波场快照(图 13),还是波形图(图 14),四种方法的吸收效果基本一致,误差也基本在一个量级(10-2)。因为Marmousi模型虽较复杂,但其层间速度变化和整体速度变化相对较小,因此四种方法的吸收效果也很接近。尽管四种方法在1号(图 15a)、2号(图 15b)检波点的误差基本一致,但在3号检波点(图 15c)中t=0.8~ 1.5s时段统一设置为中间值的误差比其他方法略小(误差范围约为±3×10-2)。综合考虑速度差异大和速度差异小的情况,建议统一设置为中间取值方式。
|
图 14 Marmousi模型四种参数设置方法记录波形与参考波形对比 (a)、(b)、(c)对应1~3号检波点;每个子图的局部放大图为其各自主波附近的波形 |
|
图 15 Marmousi模型四种参数设置方法的测试波形与参考波形的相对误差对比图 (a)、(b)、(c)对应1~3号检波点;相对误差为绝对误差除以参考波形后的归一化值 |
在数值模拟中,CFS-PML对虚假反射的吸收效果尤为突出。本文对各参数设置和作用进行了深入讨论,归纳出各参数的取值方式并进行了优化,对反射系数R提出了新的取值公式;针对复杂速度模型,其参数设置方式(取值公式)的关键在参考速度的选取,与参考速度无关的衰减参数(反射系数、频移参数)可按模型相关参数代入取值公式进行设置,与参考速度相关的衰减参数(衰减参数d0、坐标实拉伸参数)则采取先选定参考速度值再做设置。
通过双层高速度比模型、多层渐变速模型、Marmousi模型,对参考速度的几种设置方法进行测试,对比分析了各方法所得波场快照、波形图和误差图,发现“统一设置参考速度值为边界介质速度中间值”的方法简捷、吸收效果稳定,可为实际复杂速度模型的地震波数值模拟提供参考和借鉴。
| [1] |
Berenger J P. A perfectly matched layer for the absorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200. |
| [2] |
Chew W C, Liu Q H. Perfectly matched layers for elastodynamics:A new absorbing boundary condition[J]. Journal of Computational Acoustics, 1996, 4(4): 341-359. DOI:10.1142/S0218396X96000118 |
| [3] |
Collino F, Tsogka C. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J]. Geophysics, 2001, 66(1): 294-307. |
| [4] |
Komatitsch D, Tromp J. A perfectly matched layer absorbing boundary condition for the second-order seismic wave equation[J]. Geophysical Journal International, 2003, 154(1): 146-153. DOI:10.1046/j.1365-246X.2003.01950.x |
| [5] |
Festa G, Vilotte J P. The Newmark scheme as velocity-stress time-staggering:an efficient PML implementation for spectral element simulations of elastodyna-mics[J]. Geophysical Journal International, 2005, 161(3): 789-812. DOI:10.1111/j.1365-246X.2005.02601.x |
| [6] |
郭念民, 吴国忱. 基于PML边界的变网格高阶有限差分声波方程逆时偏移[J]. 石油地球物理勘探, 2012, 47(2): 256-265. GUO Nianmin, WU Guochen. High-order finite difference method in reverse-time migration with variable grids based on PML boundary condition[J]. Oil Geophysical Prospecting, 2012, 47(2): 256-265. |
| [7] |
高正辉, 孙建国, 孙章庆, 等. 基于完全匹配层构建新方法的2.5维声波近似方程数值模拟[J]. 石油地球物理勘探, 2016, 51(6): 1128-1133. GAO Zhenghui, SUN Jianguo, SUN Zhangqing, et al. 2.5D acoustic approximate equation numerical simulation with a new construction method of the perfectly matched layer[J]. Oil Geophysical Prospecting, 2016, 51(6): 1128-1133. |
| [8] |
Kuzuoglu M, Mittra R. Frequency dependence of the constitutive parameters of causal perfectly matched anisotropic absorbers[J]. IEEE Microwave and Guided Wave Letters, 1996, 6(12): 447-449. DOI:10.1109/75.544545 |
| [9] |
Roden J A, Gedney S D. Convolution PML (CPML):An efficient FDTD implementation of the CFS-PML for arbitrary media[J]. Microwave and Optical Technology Letters, 2000, 27(5): 334-339. DOI:10.1002/1098-2760(20001205)27:5<334::AID-MOP14>3.0.CO;2-A |
| [10] |
李佩笑, 林伟军, 张秀梅, 等. 常规分裂和非分裂完全匹配层吸收边界比较研究[J]. 声学学报, 2015, 40(1): 44-53. LI Peixiao, LIN Weijun, ZHANG Xiumei, et al. Comparisons for regular splitting and non-splitting perfectly matched layer absorbing boundary conditions[J]. Acta Acustica, 2015, 40(1): 44-53. |
| [11] |
廉西猛, 单联瑜, 隋志强. 地震正演数值模拟完全匹配层吸收边界条件研究综述[J]. 地球物理学进展, 2015, 30(4): 1725-1733. LIAN Ximeng, SHAN Lianyu, SUI Zhiqiang. An overview of research on perfectly matched layers absorbing boundary condition of seismic forward nume-rical simulation[J]. Progress in Geophysics, 2015, 30(4): 1725-1733. |
| [12] |
刘瑞合, 印兴耀, 浦义涛. 波动方程模拟PML吸收影响因素分析[J]. 物探与化探, 2016, 40(4): 757-762. LIU Ruihe, YIN Xingyao, PU Yitao. Analyzing PML absorbing impact factors with wave equation simulation[J]. Geophysical & Geochemical Exploration, 2016, 40(4): 757-762. |
| [13] |
Komatitsch D, Martin R. An unsplit convolutional perfectly matched layer improved at grazing incidence for the seismic wave equation[J]. Geophysics, 2007, 72(5): SM155-SM167. DOI:10.1190/1.2757586 |
| [14] |
Drossaert F H, Giannopoulos A. A nonsplit complex frequency-shifted PML based on recursive integration for FDTD modeling of elastic waves[J]. Geophysics, 2007, 72(2): T9-T17. |
| [15] |
Li J, Dai J. Z-transform implementations of the CFS-PML[J]. IEEE Antennas and Wireless Propagation Letters, 2006, 5(1): 410-413. |
| [16] |
Zhang W, Shen Y. Unsplit complex frequency-shifted PML implementation using auxiliary differential equations for seismic wave modeling[J]. Geophysics, 2010, 75(4): T141-T154. |
| [17] |
熊章强, 毛承英. 声波数值模拟中改进的非分裂式PML边界条件[J]. 石油地球物理勘探, 2011, 46(1): 35-39. XIONG Zhangqiang, MAO Chengying. Improved unsplit PML boundary conditions in acoustic wave numerical simulation[J]. Oil Geophysical Prospecting, 2011, 46(1): 35-39. |
| [18] |
Correia D, Jin J M. On the development of a higher-order PML[J]. IEEE Transactions on Antennas and Propagation, 2005, 53(12): 4157-4163. DOI:10.1109/TAP.2005.859901 |
| [19] |
冯海珂.复频移及双极点复频移完全匹配层在地震波高效数值模拟中的应用研究[D].安徽合肥: 中国科学技术大学, 2017. FENG Haike.Applications of the CFS-PML and Double-pole CFS-PML for Efficient Seismic Wave Numerical Simulation[D].University of Science and Technology of China, Hefei, Anhui, 2017. |
| [20] |
Gedney S D. The perfectly matched layer absorbing medium[J]. Advances in Computational Electrodynamic, 1998, 263-344. |
| [21] |
Marcinkovich C, Olsen K. On the implementation of perfectly matched layers in a three-dimensional fourth-order velocity-stress finite difference scheme[J]. Journal of Geophysical Research, 2003, 108(B5): 2276-2292. |
| [22] |
Appelo D, Kreiss G. A new absorbing layer for elastic waves[J]. Journal of Computatioal Physics, 2006, 215(2): 642-660. |
| [23] |
陈可洋. 声波完全匹配层吸收边界条件的改进算法[J]. 石油物探, 2009, 48(1): 76-79. CHEN Keyang. Improved algorithm for absorbing boundary condition of acoustic perfectly matched layer[J]. Geophysical Prospecting for Petroleum, 2009, 48(1): 76-79. |
| [24] |
陈可洋. 完全匹配层吸收边界条件研究[J]. 石油物探, 2010, 49(5): 472-477. CHEN Keyang. Study on perfectly matched layer absorbing boundary condition[J]. Geophysical Prospecting for Petroleum, 2010, 49(5): 472-477. |
| [25] |
罗玉钦, 刘财. 多轴复频移近似完全匹配层弹性波模拟[J]. 石油地球物理勘探, 2019, 54(5): 1024-1033. LUO Yuqin, LIU Cai. Multi-axial complex-frequency shifting nearly perfectly matched layer for seismic forward modeling in elastic media[J]. Oil Geophysical Prospecting, 2019, 54(5): 1024-1033. |
| [26] |
罗玉钦, 刘财. 近似完全匹配层边界条件吸收效果分析及衰减函数的改进[J]. 石油地球物理勘探, 2018, 53(5): 903-913. LUO Yuqin, LIU Cai. Absorption effects in nearly perfectly matched layers and damping factor improvement[J]. Oil Geophysical Prospecting, 2018, 53(5): 903-913. |
| [27] |
Bérenger J P. Numerical reflection from FDTD-PMLs:a comparison of the split PML with the unsplit and CFS PMLs[J]. IEEE Transactions on Antennas and Pro-pagation, 2002, 50(3): 258-265. DOI:10.1109/8.999615 |
| [28] |
Bérenger J P. Application of the CFS PML to the absorption of evanescent waves in waveguides[J]. IEEE Microwave and Wireless Components Letters, 2002, 12(6): 218-220. DOI:10.1109/LMWC.2002.1010000 |
| [29] |
Festa G, Delavaud E, Vilotte J P. Interaction between surface waves and absorbing boundaries for wave propagation in geological basins:2D numerical simulations[J]. Geophysical Research Letters, 2005, 32(20): L20306. DOI:10.1029/2005GL024091 |



 张伟, 广东省深圳市南山区学苑大道1088号南方科技大学地球与空间科学系, 518055。Email:
张伟, 广东省深圳市南山区学苑大道1088号南方科技大学地球与空间科学系, 518055。Email: