2 电子科技大学信息与通信工程学院, 四川成都 611731;
3 国家电网重庆市电力公司电力科学研究院, 重庆 404100
2 School of Information and Communication Engineering, University of Electronic Science and Technology of China, Chengdu, Sichuan 611731, China;
3 State Grid Chongqing Electric Power Research Institute, Chongqing, 404100, China
随着油气勘探的不断深入,地震勘探也面临越来越大的挑战,勘探目标逐渐从简单构造转向更复杂的地质构造。在构造复杂的低信噪比地区,其发育的噪声干扰往往会弱化或掩盖有效波信息,导致地震资料无法准确反映地下真实地质状况[1-2]。地震资料中的噪声主要是面波、多次波及随机噪声,其中多次波的存在不仅严重干扰一次波的成像质量,降低成像结果信噪比,且在地震剖面上易产生构造假象,掩盖中深部有利构造,影响地震资料的精细解释,所以在偏移前需压制和去除多次波[2-3]。抛物线Radon变换[4]是现今压制多次波的常用方法。
Radon变换[5]由奥地利数学家拉东(Radon)率先提出,后被广泛地应用于医学、地球物理、核磁共振、天文和分子生物等领域。1971年,Claerbout等[6]将其引入地震数据处理中,奠定了Radon变换在该领域的应用基础。Thorson等[7]将Radon建模为一个稀疏逆问题,在Radon域实现了高分辨率数据处理。随后Scales等[8]利用迭代加权最小二乘算法求解了稀疏逆问题。Sacchi等[9]提出的频域稀疏Radon变换方法被广泛地应用于地震信号处理。Trad等[10]通过混合Radon变换成功地压制了噪声。刘喜武等[11]基于最小二乘反演法并导出稀疏约束条件下的共轭梯度算法,实现了高分辨率Radon变换。Schonewille等[12]证明了Radon变换在时域的稀疏性高于频域,故认为Radon变换在时域具有更高分辨率。Lu[13]提出一种基于迭代收缩的快速稀疏Radon变换方法,提高了Radon模型的稀疏性。
在实际地震数据处理中,Radon变换存在分辨率低和计算效率不高两大缺陷[14]。Radon模型分辨率的提高可减少空间假频和假象的产生而取得更佳处理效果,但伴随更大计算量。况且,地震勘探数据量的日益庞大,使抛物线Radon变换在地震数据处理上耗费更长时间。
随着GPU-CPU异构结构的出现,高性能计算技术取得快速且巨大的发展,并逐渐应用于地震勘探领域。张军华等[15]全面调研了地球物理勘探领域对高性能计算的需求和应用现状。近年来,更有众多学者将CPU-GPU异构并行方法应用于叠前数据处理[16-20]。本文基于CPU-GPU异构平台,对抛物线Radon变换算法做并行化分析和实现。
1 算法原理及串行流程 1.1 算法原理多次波的压制通常是在做动校正后进行的。经合适的动校正后,一次波同相轴水平;而校正不足时多次波同相轴沿抛物线轨迹分布,则可沿抛物线做Radon变换,并在Radon域压制多次波。本文采用Lu[13]提出的抛物线Radon变换法。混合域抛物线Radon变换的数学模型表示为
| $\boldsymbol{d}^{\prime}=\mathrm{F}^{-1}[\boldsymbol{L} \mathrm{F}(\boldsymbol{m})] $ | (1) |
式中:m为Radon域数据;d′为地震数据;L为频域Radon算子;F(·)为傅里叶变换;F-1(·)为傅里叶逆变换。为了使Radon域数据尽量稀疏且Radon反变换后的数据d′与地震数据的误差尽量小,所以最小化如下目标方程
| $\min\limits_{m} \lambda\|\boldsymbol{m}\|_{1}+\left\|\boldsymbol{d}-\boldsymbol{d}^{\prime}\right\|_{2}^{2} $ | (2) |
式中λ为正则化系数。
结合迭代收缩阈值算法[21],对目标方程最优解的求解变为迭代计算mk,即有
| $\boldsymbol{m}_{k}=T_{\alpha}\left\{\boldsymbol{m}_{k-1}+2 t \mathrm{~F}^{-1}\left[\boldsymbol{A}\left(\mathrm{F}(\boldsymbol{d})-\boldsymbol{L} \mathrm{F}\left(\boldsymbol{m}_{k-1}\right)\right)\right]\right\} $ | (3) |
式中:k表示迭代次数;mk表示迭代第k次的Radon域数据;t为迭代步长;A=(LTL)-1LT为算子L的广义逆。
迭代收缩阈值算法是在每一步迭代过程中采用
| $T_{a}\left\{\boldsymbol{m}_{k}\right\}_{i j}=\left(\left|m_{i j}\right|-\alpha_{\mathrm{r}} \frac{K-k}{K} \hat{m}_{i j}\right)_{+} \operatorname{sgn}\left(m_{i j}\right) $ | (4) |
对Radon域数据做收缩阈值操作。式中:αr为标量系数,满足0<αr<1;K为最大迭代次数;mij、
| $\hat{\boldsymbol{m}}=\operatorname{ave}(|\boldsymbol{m}|) \frac{\max (|\boldsymbol{m}|)}{\max [\operatorname{ave}(\boldsymbol{m})]} $ | (5) |
式中:ave表示二维均值滤波;max表示取最大值;|m|表示对向量m每个元素取绝对值。且有
| $\left\{\begin{array}{l}(\alpha)_{+}=\left\{\begin{array}{ll}\alpha & \alpha \geqslant 0 \\ 0 & \alpha<0\end{array}\right. \\ \operatorname{sgn}(\alpha)=\left\{\begin{array}{ll}1 & \alpha>0 \\ 0 & \alpha=0 \\ -1 & \alpha<0\end{array}\right.\end{array}\right. $ | (6) |
式中α为标量。
1.2 串行算法流程根据Lu[13]提出的一种基于迭代收缩的快速稀疏Radon变换方法的算法原理,算法实现流程如图 1所示,核心计算部分分为如下四步。
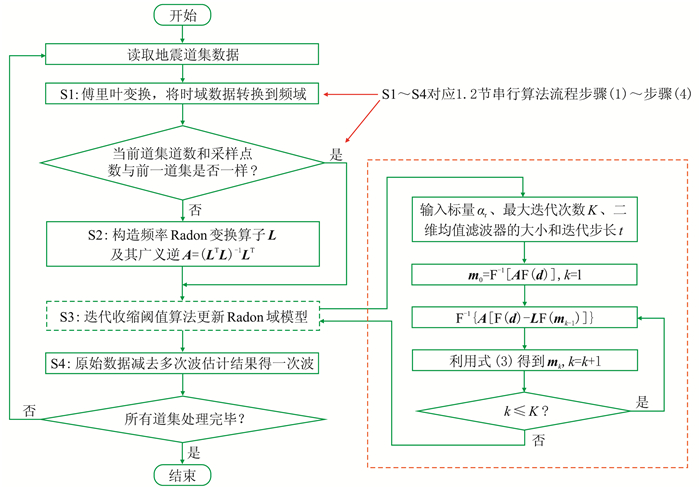
|
图 1 抛物线Radon变换串行算法流程 |
(1) 首先从硬盘读取一个地震道集数据到内存,通过傅里叶变换将地震数据从时域转换到频域;然后计算频域Radon算子L。由于此时L的计算只与地震道集的道数和采样点数有关,所以当前道集与前一道集的道数和采样点数相同时,不需再计算L,能直接用前一道集的计算结果,即可转到步骤(3);不相同时需重新计算L,顺接到步骤(2)。
(2) 在频域内构造Radon变换算子L,并计算其广义逆A=(LTL)-1LT。
(3) 基于迭代收缩阈值算法更新Radon域模型,根据步骤(2)计算结果,得到初始Radon域模型m0=F-1[AF(d)],且k=k+1,利用式(3)得到第k次迭代的Radon域模型mk。当k≤K时,不断更新mk。该步骤为本算法的计算热点。
(4) 设定一个曲率q,将曲率大于q的Radon域数据作为多次波估计结果,用原始地震数据减去多次波估计结果,就得到一次波。所有道集处理完毕则结束,否则转到步骤(1)。
2 并行抛物线Radon变换算法 2.1 GPU的并行实现首先在单个GPU上实现抛物线Radon变换算法的并行化,其流程如图 2所示。

|
图 2 抛物线Radon变换GPU并行算法流程 |
由于CPU与GPU不能相互访问各自存储器,所以通过PCIE总线用拷贝方式实现数据在内存与显存间的传输。首先在CPU上从硬盘读取地震数据到内存,然后将地震数据和所需参数拷贝到GPU,在GPU端实施抛物线Radon变换,最后将计算结果拷贝到CPU,由CPU将结果从内存写回硬盘。在GPU上实施抛物线Radon变换分为四个步骤。
(1) 由于算法在频域内实现,首先要将时域地震数据转换到频域,本文采用CUDA提供的快速傅里叶变换(cuFFT)实现。在后述步骤中,地震数据和Radon域数据在计算过程中仍需在频域与时域间进行傅里叶正、逆变换,一律使用CUDA提供的cuFFT库进行处理。cuFFT库的使用一方面能给算法带来性能提升,另一方面可降低程序设计复杂度,提高开发效率。值得注意的是,GPU上利用cuFFT库计算傅里叶变换的结果与CPU上的计算结果存在一定差异,但这种差异是由于两种不同的处理器架构在机器指令上的差异导致的,该差异与真值的比值在10-6以下,通常可忽略。
(2) 首先构造频率域算子L,再计算矩阵LTL和(LTL)-1,最后计算A=(LTL)-1LT。通过调用CUDA提供的cuBLAS库、cuSOLVER库做线性代数运算。
(3) 基于迭代收缩阈值算法更新Radon域模型。首先使用cuFFT库和线性代数库计算Radon初始估计模型m0=F-1[AF(d)];再通过式(3)进行收缩阈值操作,这时需对Radon域数据(nq×np,nq为曲率个数,np为采样点数)进行均值滤波处理,均值滤波模板尺寸为n×m。在做均值滤波前,需先扩充Radon域数据矩阵,扩充后大小为(nq+2n)×(np+2m)。矩阵扩充后进行均值滤波,分别用两个核函数实现,一个核函数按模板m在列方向上累加求平均值,另一个核函数按模板n在行方向上累加求平均值,最终得到均值滤波结果;在迭代更新Radon域模型时计算A[F(d)-LF(mk-1)],使用cuFFT库计算傅里叶变换,使用线性代数库计算矩阵乘法;抛物线Radon变换算法中Radon域模型更新为迭代过程,在迭代开始前将所需数据从CPU一次拷贝到GPU,避免了迭代时CPU与GPU之间数据的传输,使得迭代过程可全速进行。
(4) 对步骤(3)所得Radon域数据m中曲率大于q的数据作为多次波估计结果F-1[LF(m)],通过cuFFT库和CUDA提供的线性代数库进行计算。最后通过d-F-1[LF(m)]得到有效波。
2.2 CPU-GPU异构平台的协同并行实现对于上述GPU的并行算法,在执行过程中需要主机的一个线程完成GPU核函数的调用,主机的其他线程都处于空闲状态,势必造成计算资源的浪费。为了充分利用多核CPU和多GPU异构计算平台的计算资源,本文进一步提出一种协同计算方案,实现抛物线Radon变换算法。
该方案中,对于支持m个CPU线程和n个GPU的异构计算平台,有具体的并行优化流程(图 3)。

|
图 3 CPU-GPU异构协同并行流程 |
(1) 主机端主线程获取CPU支持的线程数m,并对N个地震道集进行任务的划分,创建一个有N个地震道集的任务队列。
(2) 每个子线程从任务队列取一个任务执行,即每个子线程负责一个地震道集的抛物线Radon变换的计算,m个子线程并行执行m个任务。
(3) 每个子线程领取一个地震道集任务后,要将该地震道集数据从硬盘读取到内存;然后申请CPU计算资源,若子线程成功获取CPU计算资源,则对抛物线Radon变换算法进行预处理;否则,子线程被阻塞,直到计算机操作系统将其调度。
(4) 子线程申请GPU计算资源,若成功获取GPU计算资源,就可调用GPU核函数完成并行抛物线Radon变换算法;否则,调用CPU计算资源完成串行抛物线Radon变换算法。
(5) 每个子线程在计算结束后将地震数据从内存写回硬盘。最后判断任务队列是否为空,当任务队列为空,则任务结束;否则,每个线程继续获取任务,重复上面的操作。
本实验中使用的CPU-GPU异构平台由12个CPU核心和两个GPU组成。该平台支持CPU超线程技术,每个核心支持双线程,所以该异构计算平台支持24个CPU线程。在该实验异构平台上任务分配与执行情况如图 4所示:输入N个地震道集,主线程创建23个子线程,然后进行任务分配并参与计算,从而实现24个线程并行执行不同道集任务。由于该实验平台有两块GPU(GPU0和GPU1),则由两个CPU线程分别调用GPU0和GPU1对地震道集进行计算。因为GPU计算速度比CPU快,所以在一个CPU线程执行周期,GPU计算了多个地震道集。最终,在CPU-GPU异构计算平台上,计算结果分别由CPU和GPU的计算结果构成。
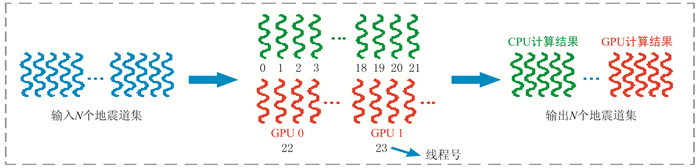
|
图 4 异构平台任务分配与执行 |
本文使用SeismicLab工具包中合成的CMP多次波模拟数据。该动校正后的CMP数据(图 5a)包括49道,每道有1001个采样点。对比SeismicLab工具包中抛物线Radon变换压制多次波的结果(图 5b)与本文方法的去噪结果(图 5c),可见后者对多次波有更好压制效果。

|
图 5 动校正后CMP道集(a)及SeismicLab抛物线Radon变换法(b)与本文算法(c)压制多次波效果对比 |
针对CPU-GPU异构平台抛物线Radon变换算法并行优化的性能进行测试。所有测试均在表 1的软硬件环境下进行,所使用的实验平台有两个CPU处理器12个核心(支持24线程)和两块NVIDIA Tesla K20c。
|
|
表 1 软硬件测试环境 |
实测数据取自珠江口盆地白云深水区。该区地形崎岖,地层倾角较大,横向岩性变化剧烈,地质构造复杂多变,多次波极为发育,是影响该区地震资料成像效果的主要原因[22]。实际测线范围是:Inline2200~2300,Xline1500~1700,且每个地震道集有51道,采样点数为376,采样间隔为4ms。
先测试并考察算法精度,通过比较CPU串行算法与单GPU并行算法对多次波的压制结果,验证GPU并行结果的正确性。由于CPU-GPU并行结果是由CPU结果和GPU结果组成的,所以只需验证GPU结果即验证了CPU-GPU结果的正确性。选取该区某一地震道集,从其动校正后的原始道集数据(图 6a)中可看到明显存在的多次波,在经CPU串行算法(图 6b)、单GPU并行算法(图 6c)的处理结果中,多次波已被压制。由于乘加运算在GPU上由一条指令完成,而CPU需多条指令,从而导致计算结果有微小差异,但这种差异在高性能计算领域属正常现象,可忽略不计[23]。
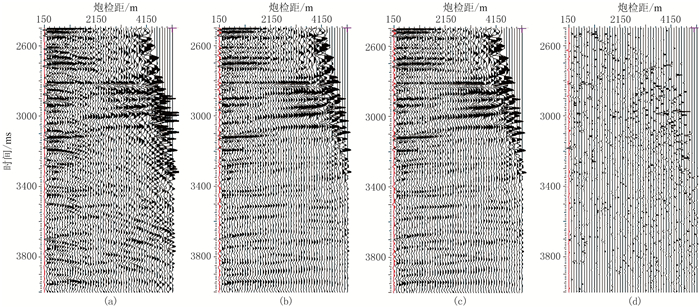
|
图 6 CPU与GPU平台上多次波去除效果 (a)多次波去除前;(b)CPU运行去除多次波后;(c)GPU运行去除多次波后;(d)CPU与GPU运行结果差异 |
以CPU处理结果为参照,将CPU运行结果减去GPU运行结果得到两者的计算差异(图 6d),其范围在10-8量级,显然该差异可忽略不计。对比多次波压制前(图 7a)与在CPU-GPU异构平台上多次波压制后(图 7b)的叠加剖面,可见后者的多次波被衰减(红色箭头),层次变得清晰,使得一次波同相轴更突出。

|
图 7 CPU-GPU异构计算平台多次波去除前(a)、后(b)叠加剖面 |
在保证结果正确的前提下,再对CPU-GPU异构平台并行加速的效果进行测试。不计数据从硬盘读写的时间,分别测得CPU串行、单核CPU-单GPU、12核CPU和12核CPU-双GPU的计算耗时,其结果如表 2所示。并根据本文加速比公式
|
|
表 2 不同平台上的计算耗时 |
| $r=\frac{T_{\mathrm{R}}}{T_{\mathrm{C}}}$ | (7) |
分别计算不同平台加速比。式中TR和TC对应异构平台运行时间、串行运行时间。
图 8为三种异构平台的加速比。分析表 2和图 8可知:当地震数据范围是Inline2200~2205、Xline1500~1510(即地震道集数为6×11)时,硬件资源未充分利用,加速比不稳定;当地震数据范围是Inline2200~2300、Xline1500~1700(地震道集数为101×201)时,硬件资源得到充分利用,且在密集计算时CPU利用率达到100%,GPU利用率最高达88%,加速比趋于稳定。此时单核CPU—单GPU异构平台的加速比达到13以上;12核CPU的平台实际加速比达到12以上;12核CPU—双GPU的加速比也超过30。由于Windows操作系统不是实时的,会受到其他程序影响,加速比会小幅波动。
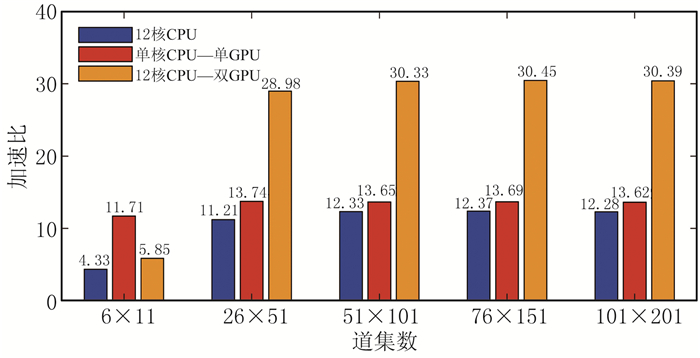
|
图 8 不同异构计算平台加速比 |
抛物线Radon变换算法可压制和去除多次波,提高地震资料的信噪比。但对于数据规模巨大的地震道集,进行抛物线Radon变换需较长运行时间。为此,本文基于CPU-GPU异构平台对抛物线Radon变换算法做并行化分析,通过CUDA优化技术在GPU平台实施并行化,且利用多核CPU多线程技术,提出一种通用的CPU-GPU异构并行方案,充分地利用了CPU和GPU的计算资源,在保证道集质量的前提下,大幅度提高了该算法的计算效率,加速比达30。
成都晶石石油软件有限公司在课题研究中提供了GEOSCOPE地质放大镜软件,在此深表感谢!
| [1] |
李志娜.多次波分离与成像方法研究[D].山东青岛: 中国石油大学(华东), 2015. LI Zhina.Study on Methods of Multiple Separation and Multiple Imaging[D].China University of Petroleum (East China), Qingdao, Shandong, 2015. |
| [2] |
胡浩.Radon变换及其在地震资料去噪中的应用研究[D].四川成都: 成都理工大学, 2014. HU Hao.Research on Radon Transform and Its Application in Seismic Data Noise Elimination[D].Chengdu University of Technology, Chengdu, Sichuan, 2014. |
| [3] |
侯维丽, 刘洪林, 刘云鑫, 等. 多次波压制方法及优化组合压制技术研究[J]. 内陆地震, 2015, 29(2): 122-128. HOU Weili, LIU Honglin, LIU Yunxin, et al. Study on multiple suppression methods and optimum combination suppression technique[J]. Inland Earthquake, 2015, 29(2): 122-128. |
| [4] |
张振波, 轩义华. 高分辨率抛物线拉冬变换多次波压制技术[J]. 物探与化探, 2014, 38(5): 981-988. ZHANG Zhenbo, XUAN Yihua. High resolution para-bolic radon transform multiple wave suppression technique[J]. Geophysical and Geochemical Exploration, 2014, 38(5): 981-988. |
| [5] |
Deans S R. The Radon Transform and Some of Its Applications[M]. New York: John Wiley and Sons Inc, 1983.
|
| [6] |
Claerbout J F, Johnson A G. Extrapolation of time-dependent waveforms along their path of propagation[J]. Geophysical Journal International, 1971, 26(1): 285-293. |
| [7] |
Thorson R, Claerbout J. Velocity stack and slant stack-stochastic inversion[J]. Geophysics, 1985, 50(12): 2727-2741. DOI:10.1190/1.1441893 |
| [8] |
Scales J, Gersztenkorn A and Treitel S. Fast lp solution of large, sparse, linear systems:Application to seismic travel time tomography[J]. Journal of Computational Physics, 1988, 75(2): 314-333. DOI:10.1016/0021-9991(88)90115-5 |
| [9] |
Sacchi M, Ulrych T. High-resolution velocity gathers and offset space reconstruction[J]. Geophysics, 1995, 60(4): 1169-1177. DOI:10.1190/1.1443845 |
| [10] |
Trad D, Ulrych T and Sacchi M. Latest views of the sparse Radon transform[J]. Geophysics, 2003, 68(1): 386-399. DOI:10.1190/1.1543224 |
| [11] |
刘喜武, 刘洪, 李幼铭, 等. 高分辨率Radon变换方法及其在地震信号处理中的应用[J]. 地球物理学进展, 2004, 19(1): 8-15. LIU Xiwu, LIU Hong, LI Youming, et al. High resolution radon transform and its application in seismic signal processing[J]. Progress in Geophysics, 2004, 19(1): 8-15. |
| [12] |
Schonewille M A and Aaron P A.Applications of time-domain high-resolution Radon demultiple[C].SEG Technical Program Expanded Abstracts, 2007, 26: 2565-2569.
|
| [13] |
Lu W K. An accelerated sparse time-invariant Radon transform in the mixed frequency-time domain based on iterative 2D model shrinkage[J]. Geophysics, 2013, 78(4): V147-V155. DOI:10.1190/geo2012-0439.1 |
| [14] |
熊登, 赵伟, 张剑锋. 混合域高分辨率抛物Radon变换及在衰减多次波中的应用[J]. 地球物理学报, 2009, 52(4): 1068-1077. XIONG Deng, ZHAO Wei, ZHANG Jianfeng. Hybrid-domain high-resolution parabolic Radon transform and its application to demultiple[J]. Chinese Journal of Geophysics, 2009, 52(4): 1068-1077. |
| [15] |
张军华, 臧胜涛, 单联瑜, 等. 高性能计算的发展现状及趋势[J]. 石油地球物理勘探, 2010, 45(6): 918-925. ZHANG Junhua, ZANG Shengtao, SHAN Lianyu, et al. Development status and trends for high perfor-mance computing[J]. Oil Geophysical Prospecting, 2010, 45(6): 918-925. |
| [16] |
吴吉忠, 左虎. 叠前衰减补偿时间偏移及GPU实现[J]. 石油地球物理勘探, 2019, 54(1): 84-92. WU Jizhong, ZUO Hu. Attenuation compensation in prestack time migration and its GPU implementation[J]. Oil Geophysical Prospecting, 2019, 54(1): 84-92. |
| [17] |
刘帅, 季晓慧, 芦俊, 等. CPU与GPU协同并行的多分量地震数据各向异性叠前时间偏移[J]. 石油地球物理勘探, 2019, 54(1): 65-72. LIU Shuai, JI Xiaohui, LU Jun, et al. Multi-component anisotropy prestack time migration based on collaborative parallel computing with CPU and GPU[J]. Oil Geophysical Prospecting, 2019, 54(1): 65-72. |
| [18] |
赵虎, 武泗海, 尹成, 等. 基于OpenACC编程模型的逆时偏移多级并行的设计与优化[J]. 石油地球物理勘探, 2018, 53(6): 1307-1313, 1325. ZHAO Hu, WU Sihai, YIN Cheng, et al. Multi-level parallel design and optimization for reverse time migration based on OpenACC programming model[J]. Oil Geophysical Prospecting, 2018, 53(6): 1307-1313, 1325. |
| [19] |
王一达, 赵长海, 李超, 等. 异构计算环境下的三维Kirchhoff叠前深度偏移混合域并行算法[J]. 石油地球物理勘探, 2018, 53(3): 478-486. WANG Yida, ZHAO Changhai, LI Chao, et al. Hybrid domain parallel algorithm for 3D Kirchhoff prestack depth migration in the heterogeneous environment[J]. Oil Geophysical Prospecting, 2018, 53(3): 478-486. |
| [20] |
张全, 林柏栎, 彭博, 等. 基于CUDA的地震相干体并行算法[J]. 地质与勘探, 2020, 56(1): 147-153. ZHANG Quan, LIN Baiyue, PENG Bo, et al. Seismic coherence parallel algorithm based on CUDA[J]. Geology and Exploration, 2020, 56(1): 147-153. |
| [21] |
Beck A, Teboulle M. A fast iterative shrinkage-thresholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(1): 183-202. DOI:10.1137/080716542 |
| [22] |
贾连凯.南海深水区多次波压制技术研究[D].山东青岛: 中国科学院研究生院(海洋研究所), 2014. JIA Liankai.Study of Multiple Elimination Techniques in the Deepwater Area of South China Sea[D].Graduate University of the Chinese Academy of Sciences (The Institute of Oceanology), Qingdao, Shandong, 2014. |
| [23] |
Whitehead N, Fit-Florea A. Precision & performance:Floating point and IEEE 754 compliance for NVIDIA GPUs[J]. rn (A+B), 2011, 21(1): 18749-19424. |



 张全, 四川省成都市新都区新都大道8号西南石油大学计算机科学学院, 610500。Email:
张全, 四川省成都市新都区新都大道8号西南石油大学计算机科学学院, 610500。Email: