辽西M工区目的层位于潜山上方,有效地层圈闭发育在不整合面附近。潜山不整合面整体上地震反射较强、连续性较好,下伏地层削截明显,同向轴能量减弱,上覆地层同相轴具有上超的特征,地层圈闭识别困难。如何有效提高该地区的地震剖面分辨率、准确识别地层尖灭点,是描述和刻画该区地层圈闭的关键。为此,本文通过时频(S)域相位校正反褶积处理提高工区地震资料分辨率,以达到准确识别尖灭点的目的。
由于介质的吸收效应,随着传播距离增加,地震记录纵向分辨率降低。Wang[1-3]认为非弹性介质的衰减可以通过反Q滤波补偿,因此很多学者对反Q模型进行了研究,在叠加偏移之前或者在偏移的过程中对地震数据进行反Q滤波,以恢复地震波能量和校正地震记录相位。该处理方法是通过补偿信号高频段的能量,提高原始信号频带范围,从而提高地震资料的高分辨率。反Q滤波最大的困难在于如何准确估计地层品质因子Q,以及保证反Q过程中算法的稳定性。反Q滤波的不稳定性主要由振幅补偿时指数增益导致,但其相位校正过程是稳定的。Margrave等[4]基于Gabor变换提出了非平稳反褶积,通过在每个时间点的反褶积处理,避免了子波衰减问题。金明霞等[5]对Gabor反褶积进行了研究,并应用于深水数据处理。在Gabor反褶积算法中,由于Gabor变换时窗固定,影响了时频域反褶积的结果。Zhou等[6-7]、郭廷超等[8]在S域实现反褶积,避免了Gabor变换时窗固定的缺陷,但是没有解决非平稳地震记录的相位畸变导致信号从时频域转换到时间域中产生的误差。
M工区地震数据整体频带较宽,高频信号能量弱。常规S变换基函数固定,高频信号识别能力低,达不到精细时频分析的要求。为此,对S变换窗函数进行扩展,提出并推导了改进的广义S变换。调节改进广义S变换参数,可获取非平稳地震记录的精细时频谱,有效地提高时频聚焦度,达到对信号的高频成分进行精确分析的目的。
本文首先利用相位校正将地震记录零相位化;再使用改进的广义S变换对没有相位畸变的地震记录进行精细时频谱分析,从而在S域中精确提取子波,实现S域反褶积。与传统时间域反褶积相比,相位校正S域反褶积能得到更高分辨率的地震资料,可有效识别出M工区的地层尖灭点位置和薄互层,为地层圈闭刻画和储层综合研究提供了优质的资料基础。
1 方法原理 1.1 改进广义S变换Stockwell在短时傅里叶变换和小波变换的基础上提出了S变换,基于高斯窗能量归一以及其在时域和频域形态相同的优点[9],实现了无损的S正、反变换,提高了信号时频分析精度。信号x(t)的S变换为
| $ \begin{array}{*{20}{l}} {S(\tau ,f) = \int_{ - \infty }^\infty x (t)\left\{ {\frac{{|f|}}{{\sqrt {2\pi } }}\exp \left[ {\frac{{ - {f^2}{{(\tau - t)}^2}}}{2}} \right] \times } \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{\rm{exp}}( - {\rm{i}}2\pi ft)} \right\}{\rm{d}}t} \end{array} $ | (1) |
式中τ为变换域时间。S变换的基本小波函数定义为
| $ \begin{array}{*{20}{l}} {h(t) = \frac{{|f|}}{{\sqrt {2\pi } }}{\rm{exp}}\left( {\frac{{ - {t^2}{f^2}}}{2} - {\rm{i}}2\pi ft} \right)}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = g(t){\rm{exp}}( - {\rm{i}}2\pi ft)} \end{array} $ | (2) |
其中g(t)为高斯窗函数
| $ g(t) = \frac{{|f|}}{{\sqrt {2\pi } }}{\rm{exp}}\left( { - \frac{{{t^2}{f^2}}}{2}} \right) $ | (3) |
由上式可知,S变换将窗函数与信号的频率建立起直接联系,因此可根据信号频率变化调节窗函数的宽窄,提高时频分辨率。但S变换窗函数对信号频率变化不够敏感,在实际处理的过程中缺乏灵活性。为了适应海上宽频地震数据,对S变换的窗函数进行改进,以提高高斯窗函数对频率的敏感程度。
引入参数λ、r调节高斯函数的形状,即
| $ g(t) = \frac{{|f{|^r}}}{{\lambda \sqrt {2\pi } }}{\rm{exp}}\left( { - \frac{{{t^2}|f{|^{2r}}}}{{2{\lambda ^2}}}} \right) $ | (4) |
则信号x(t)的改进广义S变换为
| $ \begin{array}{*{20}{l}} {G(\tau ,f) = \int_{ - \infty }^{ + \infty } x (t)\frac{{|f{|^r}}}{{\lambda \sqrt {2\pi } }}{\rm{exp}}\left[ {\frac{{ - {{(\tau - t)}^2}|f{|^{2r}}}}{{2{\lambda ^2}}}} \right] \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}( - {\rm{i}}2\pi ft){\rm{d}}t} \end{array} $ | (5) |
Futterman[10]基于品质因子Q与频率无关的假设和一维波动方程,提出了描述地震波振幅衰减和速度频散的方程。基于Futterman模型的地震波吸收衰减方程为
| $ S(\tau + \Delta t,f) = S(\tau ,f){\rm{exp}}\left[ {{\rm{i}}\varphi (f) + \frac{{\varphi (f)}}{{2Q}}} \right] $ | (6) |
式中:S(τ,f)为S域τ时刻的地震波波场;φ(f)为频率域的衰减函数,即
| $ \varphi (f) = - {\left( {\frac{f}{{{f_{\rm{h}}}}}} \right)^{ - \gamma }}f\Delta t $ | (7) |
其中
由式(6)可以看出,Futterman的衰减模型表现为,随着传播时间的增加, 信号的振幅衰减和相位产生畸变。为了消除这种影响,一般对信号进行反Q滤波处理[11]实现相位校正和振幅补偿。针对反Q滤波特点,本文将稳定的相位校正算法与时频域反褶积算法进行结合。时频域反褶积的精度主要是取决于精细的时频谱分析以及时频域子波谱的准确提取。S域子波谱一般利用多项式平滑的方式进行提取[6-7],即
| $ |W(t,f)| = |f{|^k}{\rm{exp}}\left[ {\sum\limits_{n = 0}^N {{a_n}} (t){f^n}} \right] $ | (8) |
式中k、N为正整数,取值范围为1 < k < 3、2 < N < 7。利用式(7)提取子波谱均基于子波是零相位的假设,当子波不满足该假设时,时频域反褶积结果从S域转换到时间域会产生误差。
根据式(5),信号相位校正可表示为
| $ S(\tau + \Delta t,f) = S(\tau ,f){\rm{exp}}[ - {\rm{i}}\varphi (f)] $ | (9) |
对S(τ+Δt,f)进行逆Fourier变换,可得相位校正后的信号
| $ {x_{\rm{p}}} = {\rm{IFT}} [S(\tau + \Delta t)] $ | (10) |
对校正相位后的地震信号xp进行改进的广义S变换,在S域实现反褶积[4]。在S域,地震信号xp的时频振幅谱等于子波的时频振幅谱|Gw(f, τ)|与反射系数时频振幅谱|GR(f, τ)|的乘积,即
| $ |{G_{{x_{\rm{p}}}}}(f,\tau )| \approx |{G_w}(f,\tau )| \cdot |{G_R}(f,\tau )| $ | (11) |
假设反射系数满足白谱特性,地震记录振幅谱的锯齿波动是反射系数引起的,利用式(7)平滑每个时间点τ处的非平稳地震记录时频振幅谱值|Gxp(f, τ)|,可估计|Gw(f, τ)|,则在S域估计的反射系数时频振幅谱[12-13]为
| $ |{G_R}(f,\tau )| = \frac{{|{G_{{x_{\rm{p}}}}}(f,\tau )|}}{{|{G_w}(f,\tau )| + u(\tau )}} $ | (12) |
式中u(τ)为引入的调谐参数,以免分母出现零值。则最终的时间域反射系数为
| $ R(t) = \sum\limits_\tau {{\rm{ IS }}} [{G_R}(f,\tau )] $ | (13) |
式中IS(·)为逆S变换。
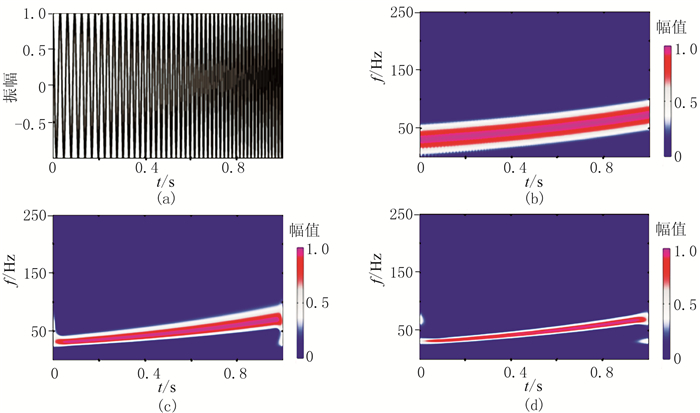
2 模型数据验证Chirp信号[14-15]如图 1a所示,在30~75Hz频率范围呈二次函数递增变化;图 1b~图 1d分别为Gabor变换、S变换[16-19]和改进的广义S变换(λ=1.5、r=0.8)的时频分析结果。可以看出:短时傅里叶变换存在整体频率分辨率低的问题;S变换改善了短时傅里叶变换的时频分辨率,但是随着频率的升高,其高频分辨能力明显降低;改进的广义S变换在信号处于低频和高频时,都体现出较高的时频分辨能力,且能量更聚焦,可为后续时频域反褶积奠定良好的基础。
|
图 1 复合信号时频分析对比 (a)Chirp信号;(b)Gabor变换;(c)S变换;(d)改进的广义S变换 |
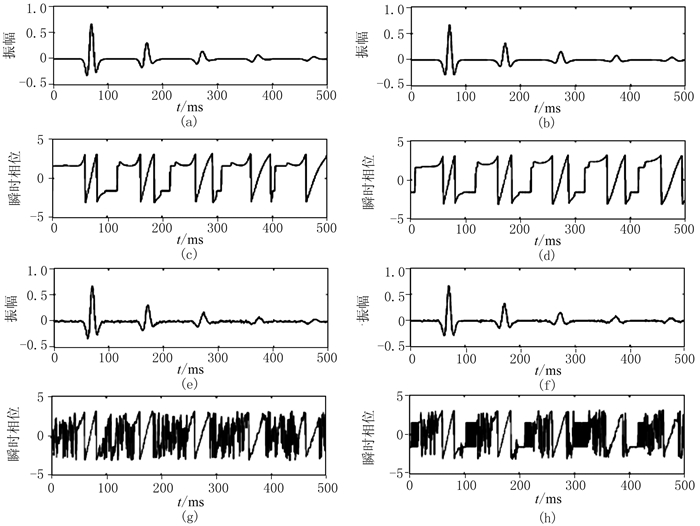
模拟单道衰减地震记录验证相位校正对地震波形的影响以及其抗噪性能。图 2a为Q=30用零相位Ricker子波合成的衰减地震记录,随着传播时间的增大,子波波形发生畸变。对图 2a记录应用式(8)进行相位校正,结果如图 2b所示。可见相位校正后,衰减地震记录子波已零相位化,基本消除波形畸变。图 2c和图 2d分别为图 2a、图 2b记录的瞬时相位谱,校正后相位谱得以归位,且更精确描述了地震信号随时间的突然相位变化关系。对图 2a记录加入信噪比为35dB的随机噪声,如图 2e所示,图 2f是其相位校正结果。图 2g和图 2h分别为图 2e和图 2f记录的瞬时相位谱。对比图 2e和图 2f可以看出,噪声对相位校正的过程影响不大,基本不影响相位校正的稳定性。对比图 2g和图 2h可以看出,该相位校正算法抗噪能力强,但噪声无法通过相位校正去除。
|
图 2 相位校正效果分析 (a)Q=30的衰减地震记录;(b)图a的相位校正结果;(c)图a的相位谱;(d)图b的相位谱;(e)图a的加噪结果;(f)图e的相位校正结果;(g)图e的相位谱;(h)图f的相位谱 |
建立简单模型说明本文相位校正方法可以有效改善反褶积效果。图 3a为反射系数序列,用主频为35Hz的Ricker子波与其合成的地震记录如图 3b所示[20],波形和相位不随时间变化。Q=40的衰减记录如图 3c所示,随着传播时间的增长,能量衰减、波形畸变[21-23]。图 3c的衰减地震记录的相位校正结果如图 3d所示。对比图 3c和图 3d可以看出,相位校正成功地消除了地震记录传播过程中的相位畸变。分别对相位校正前、后的地震记录进行S域反褶积,结果如图 3e、图 3f所示。在图 3e红框内,由于没有校正相位,反褶积结果出现两个不正确的尖脉冲,这是由于地震子波在传播过程中相位发生畸变,而S域反褶积算法无法准确提取子波的相位谱,导致信号从S域转换到时间域出现了误差。对相位校正后的地震记录进行S域反褶积,能够很好地压缩子波旁瓣、获取准确的反射系数,与真实的反射系数具有很好地对应关系(图 3f红框所示)。单道模型试算结果表明,将相位校正与S域反褶积相结合能够得到更加准确的反褶积结果,避免了子波相位谱提取不准的缺陷。

|
图 3 相位校正对反褶积的影响分析 (a)反射系数序列;(b)平稳地震记录;(c)Q=40的衰减地震记录;(d)图c的相位校正结果;(e)图c的直接S域反褶积结果;(f)图d的S域反褶积结果 |
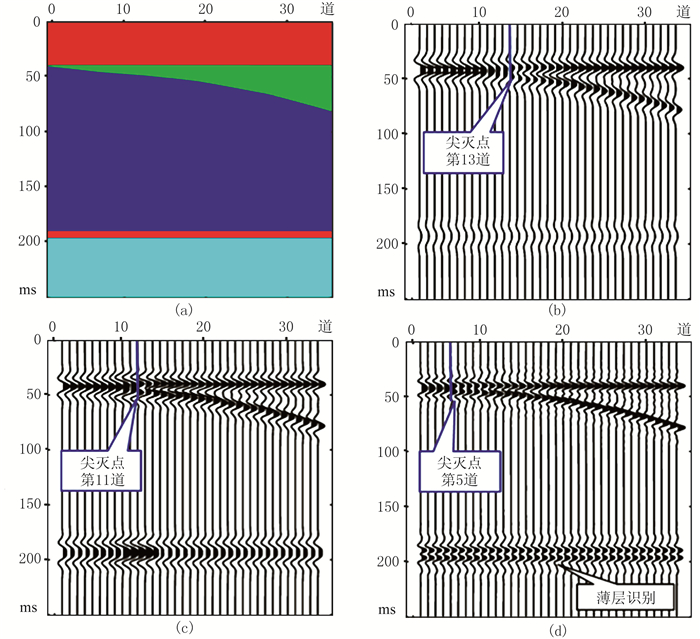
建立二维地震模型(图 4a)验证本文的相位校正S域反褶积的正确性。该模型在浅部存在一个较小的超覆体,深部存在一个薄层。对图 4a的速度模型进行正演获得衰减地震剖面(图 4b),其中Q值从上往下依次为30、35、50、60、80,随着传播时间的增大,地震记录的能量发生衰减,振幅减弱,薄层不清晰[24-25]。对图 4b的正演记录分别用传统反褶积方法和本文方法处理,结果如图 4c和图 4d所示。传统的反褶积有效地补偿了深层地震波能量,同时一定程度上提高了剖面的分辨率,但整体效果不明显。
|
图 4 二维模型两种反褶积方法对比 (a)时间域模型;(b)正演的衰减剖面;(c)传统反褶积剖面;(d)本文方法处理剖面 |
本文的相位校正S域反褶积算法可以有效地压缩地震记录旁瓣,获得分辨率更高的地震剖面。从正演剖面识别的超覆体尖灭点位于第14道;传统反褶积处理后,可在第11道识别出尖灭点位置(图 4c),但不能识别出深部的薄层;而经过相位校正S域反褶积处理后,在第4道就可以识别出尖灭点(箭头所示),与真实的尖灭点更接近,同时能识别出深部薄层的顶、底界(图 4d)。
3 实际资料处理选取渤海辽西M工区地震资料(图 5a)验证相位校正S域反褶积方法在实际资料处理中的适用性。该工区目的层位于潜山顶界上,砂岩超覆现象明显,多处砂岩受潜山隆起影响,出现了同相轴能量减弱、层位消失的现象,导致后期井位设计出现困难。

|
图 5 实际数据两种方法反褶积剖面对比 (a)原始数据;(b)传统反褶积;(c)本文方法 |
如何有效地识别该地区地层实际尖灭位置,刻画地层尖灭线是亟需解决的问题。因此,将本文的反褶积方法应用于该工区,旨在恢复该地区地震波能量,提高地震剖面分辨率,达到识别该地区地层尖灭点和薄互层的目的。分别对原始数据使用传统反褶积和相位校正S域反褶积处理,结果如图 5b和图 5c所示。传统反褶积处理后,整个剖面的能量更强,改善了同相轴连续性,潜山上覆地层的弱反射能量得到了一定的恢复(图 5b箭头所示),提高了原始地震剖面的分辨率。与传统反褶积方法处理结果(图 5b)相比,本文方法更好地恢复了潜山上覆地层反射波组的能量,且层间连续性要优于传统反褶积处理结果(图 5c箭头所示)。
为了凸显处理结果的细节部分,将图 5中的箭头处放大显示,如图 6所示。在图中红色虚线框处,原始剖面上为一套厚层,经传统反褶积处理后,压缩了该处的同相轴,但并没有识别出薄层,而本文方法处理后,有效地识别出该处的薄互层,地震剖面分辨率明显更高。在原始地震剖面上,储层弱反射在第130道消失,出现地层尖灭(红色虚线处箭头所示)。经过传统的反褶积处理后,有效将该地层尖灭点前推至第118道处,而经过本文方法处理后,在108道可见该地层反射,能更准确地识别出地层尖灭点。可见,本文的相位校正S域反褶积方法能有效提高地震资料纵、横向分辨率,为精确刻画岩性圈闭提供有力支撑。

|
图 6 图 5的放大显示 (a)原始剖面;(b)传统反褶积剖面;(c)本文方法处理剖面 |
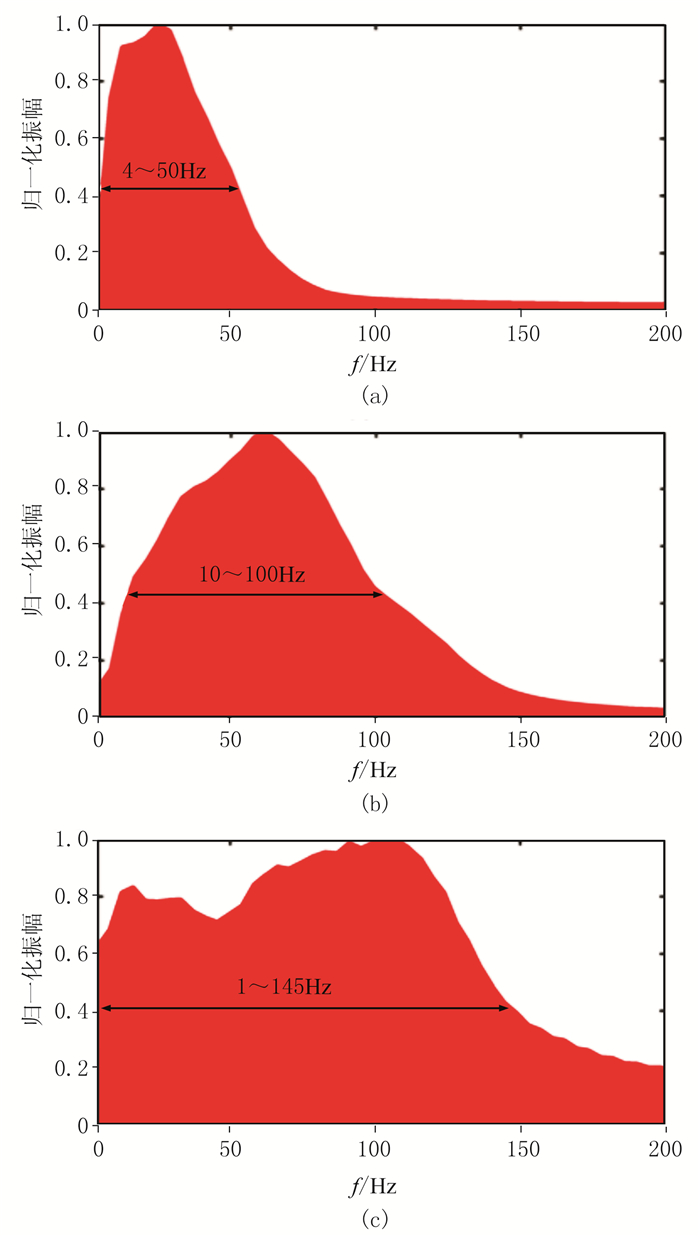
为了展示高分辨处理前、后时频能量变化,分别从图 6中抽取的第120道地震记录进行时频分析,结果如图 7所示。对比原始信号(图 7a)与两种反褶积方法处理结果时频谱(图 7b和图 7c)可见,本文方法处理效果好,在保持强信号能量的基础上恢复了弱信号的能量(红色箭头所示);主频(图中白线为主频随时间的变化)明显提升,大幅提高了地震记录分辨率。图 8为图 5剖面的振幅谱,原始数据、传统反褶积方法和本文方法处理结果的有效频带范围分别为4~50Hz(图 8a)、10~100Hz(图 8b)和1~140Hz(图 8c),可见本文方法处理后,在保留原始数据的低频信息基础上,有效拓宽了地震资料的频带宽度,结果更优。

|
图 7 两种方法反褶积前、后第120道时频谱对比 (a)原始数据;(c)传统反褶积方法;(c)本文方法 |
|
图 8 两种方法反褶积前、后振幅谱对比 (a)原始剖面;(b)传统反褶积方法;(c)本文方法 |
本文在相位校正基础上进行时频域反褶积处理,形成了一套适用性广的高分辨处理方法,并通过模型和实际资料处理取得了良好的应用效果,得到以下几点认识:
(1) 针对数据不同频率成分能量不同的特点,对S变换的窗函数进行扩展,可以提高其对信号不同频率成分的识别能力,达到灵活时频分析的目的。
(2) 在反褶积的处理过程中,本文结合了传统的反Q滤波中的相位校正方法,对地震数据进行相位校正后,可以更准确地将时频域反褶积结果转换到时间域中,使反褶积的效果更好,薄层识别能力更强。
(3) 经本文的相位校正S域反褶积处理后,能有效拓宽原始地震资料的频带、提高分辨率。
| [1] |
Wang Y H. Quantifying the effectiveness of stabilized inverse Q-filtering[J]. Geophysics, 2003, 68(1): 337-345. |
| [2] |
Wang Y H. Inverse Q-filter for seismic resolution enhancement[J]. Geophysics, 2006, 71(3): V51-V60. |
| [3] |
Wang Y H.Seismic Inverse Q Filtering[M].Blackwell Publishing, UK, 2008.
|
| [4] |
Margrave G F, Lamoureux M P, Henley D C, et al. Gabor deconvolution:Estimating reflectivity by nonstationary[J]. Geophysics, 2011, 76(3): W15-W30. DOI:10.1190/1.3560167 |
| [5] |
金明霞, 张冰, 易淑昌. 基于Gabor变换反褶积技术在渤海某工区的应用研究[J]. 地球物理学进展, 2017, 32(2): 856-861. JIN Mingxia, ZHANG Bing, YI Shuchang. Research on the application to seismic data in Bohai bay based on Gabor deconvolution[J]. Progress in Geophysics, 2017, 32(2): 856-861. |
| [6] |
Zhou H L, TianY M, Ye Y, et al. Dynamic deconvolution of seismic data based on generalized S-transform[J]. Journal of Applied Geophysics, 2014, 10(8): 1-11. |
| [7] |
Zhou H L, Wang C C, Marfurt K J, et al. Enhancing the resolution of non-stationary seismic data using improved time-frequency spectral modelling[J]. Geophysical Journal International, 2016, 20(5): 203-219. |
| [8] |
郭廷超, 曹文俊, 陶长江, 等. 时变谱模拟反褶积方法研究[J]. 石油物探, 2015, 54(1): 36-42. GUO Tingchao, CAO Wenjun, TAO Changjiang, et al. Research on time-varying spectral modeling deconvolution method[J]. Geophysical Prospecting for Petroleum, 2015, 54(1): 36-42. |
| [9] |
陈学华, 贺振华, 黄德济. 广义S变换及其时频滤波[J]. 信号处理, 2008, 24(1): 28-31. CHEN Xuehua, HE Zhenhua, HUANG Deji. Genera-lized S-transform and its time-frequency filtering[J]. Signal Processing, 2008, 24(1): 28-31. |
| [10] |
Futterman W I. Dispersive body waves[J]. Journal of Geophysical Research, 1962, 69(13): 5279-5291. |
| [11] |
李雪英, 沈加雪, 于生云, 等. 频域反Q滤波稳定性控制方法[J]. 地球物理学进展, 2016, 31(4): 1608-1613. LI Xueying, SHEN Jiaxue, YU Shengyun, et al. Stability control method of inverse Q filtering in frequency domain[J]. Progress in Geophysics, 2016, 31(4): 1608-1613. |
| [12] |
Rosa A L R. Processing via spectral modeling[J]. Geophysics, 1991, 56(8): 1244-1251. DOI:10.1190/1.1443144 |
| [13] |
Milton J P, Ursin B. Mixed-phase deconvolution[J]. Geophysics, 1998, 63(2): 637-647. |
| [14] |
邹锋, 薛雅娟. 基于同步挤压小波变换的煤层强振幅抑制[J]. 地球物理学进展, 2018, 33(3): 1198-1204. ZOU Feng, XUE Yajuan. Strong amplitude suppre-ssion of coal seam based on synchrosqueezed wavelet transform[J]. Progress in Geophysics, 2018, 33(3): 1198-1204. |
| [15] |
邓攻, 梁锋, 李晓婷, 等. S变换谱分解技术在深反射地震弱信号提取中的应用[J]. 地球物理学报, 2015, 58(12): 4594-4604. DENG Gong, LIANG Feng, LI Xiaoting, et al. S-transform spectrum decomposition technique in the application of the extraction of weak seismic signals[J]. Chinese Journal of Geophysics, 2015, 58(12): 4594-4604. |
| [16] |
张固澜, 熊晓军, 容娇君, 等. 基于改进的广义S变换的地层吸收衰减补偿[J]. 石油地球物理勘探, 2010, 45(4): 512-515. ZHANG Gulan, XIONG Xiaojun, RONG Jiaojun, et al. Stratum absorption and attenuation compensation based on improved generalized S transform[J]. Oil Geophysical Prospecting, 2010, 45(4): 512-515. |
| [17] |
Gholami A, Sacchi M D. A fast and automatic sparse deconvolution in the presence of outliers[J]. IEEE Transactions on Geosciences and Remote Sensing, 2012, 50(10): 4105-4116. DOI:10.1109/TGRS.2012.2189777 |
| [18] |
姜晓宇, 宋涛, 杜文辉, 等. 利用广义S变换频谱分解不连续性检测技术预测断溶体油藏[J]. 石油地球物理勘探, 2019, 54(6): 1324-1328. JIANG Xiaoyu, SONG Tao, DU Wenhui, et al. Fault-karst carbonate reservoir prediction with the spectral decomposition discontinuity detection based on gene-ralized S transform spectrum[J]. Oil Geophysical Prospecting, 2019, 54(6): 1324-1328. |
| [19] |
李雪英, 田亚军, 程云, 等. 基于仿射类平滑伪Wigner分布的厚度有序递变型薄互层时频特征分析[J]. 石油地球物理勘探, 2019, 54(5): 1094-1105. LI Xueying, TIAN Yajun, CHENG Yun, et al. Time-frequency characteristic analysis of orderly thickness-graded thin inter-beds based on affine smooth pseudo Wigner distribution[J]. Oil Geophysical Prospecting, 2019, 54(5): 1094-1105. |
| [20] |
潘树林, 闫柯, 李凌云, 等. 自适应步长FISTA算法稀疏脉冲反褶积[J]. 石油地球物理勘探, 2019, 54(4): 737-743. PAN Shulin, YAN Ke, LI Lingyun, et al. Sparse-spike deconvolution based on adaptive step FISTA algorithm[J]. Oil GeophysicalProspecting, 2019, 54(4): 737-743. |
| [21] |
曹鹏涛, 张敏, 李振春. 基于广义S变换及高斯平滑的自适应滤波去噪方法[J]. 石油地球物理勘探, 2018, 53(6): 1128-1136. CAO Pengtao, ZHANG Min, LI Zhenchun. An adaptive filtering denoising method based on generalized S-transform and Gaussian smoothing[J]. Oil Geophysical Prospecting, 2018, 53(6): 1128-1136. |
| [22] |
薛亚茹, 王敏, 陈小宏. 基于SL0的高分辨率Radon变换及数据重建[J]. 石油地球物理勘探, 2018, 53(1): 1-7. XUE Yaru, WANG Min, CHEN Xiaohong. High re-solution Radon transform based on SL0 and its application in data reconstruction[J]. Oil Geophysical Prospecting, 2018, 53(1): 1-7. |
| [23] |
姚振兴, 高星, 李维新. 用于深度域地震剖面衰减与频散补偿的反Q滤波方法[J]. 地球物理学报, 2003, 46(2): 229-233. YAO Zhenxing, GAO Xing, LI Weixin. The forward Q method for compensating attenuation and frequency dispersion used in the seismic profile of depth domain[J]. Chinese Journal of Geophysics, 2003, 46(2): 229-233. |
| [24] |
Zhang C, Ulrych T J. Seismic absorption compensation:A least-squares inverse scheme[J]. Geophysics, 2007, 72(6): R109-R115. DOI:10.1190/1.2766467 |
| [25] |
戴永寿, 王晓波, 丁进杰, 等. 自适应分段的时变子波估计方法[J]. 石油地球物理勘探, 2015, 50(4): 607-612. DAI Yongshou, WANG Xiaobo, DING Jinjie, et al. Time-variant wavelet estimation based on adaptive segmentation[J]. Oil Geophysical Prospecting, 2015, 50(4): 607-612. |



 谭辉煌, 天津市滨海新区海川路2121号中海石油(中国)有限公司天津分公司渤海石油研究院, 300452。Email:
谭辉煌, 天津市滨海新区海川路2121号中海石油(中国)有限公司天津分公司渤海石油研究院, 300452。Email: