② 成都理工大学地球勘探与信息技术教育部重点实验室, 四川成都 610059;
③ 中海油田服务公司物探事业部特普公司, 广东湛江 524057
② Key Laboratory of Earth Exploration and Information Technology of Ministry of Education, Chengdu University of Technology, Chengdu, Sichuan 610059, China;
③ Data Processing Company, Geophysical Branch, China Oilfield Services Limited, CNOOC, Zhanjiang, Guangdong 524057, China
相较于时间域地震资料,深度域地震资料在地质构造复杂的区域能提供更准确的构造信息[1-3]。直接利用深度域地震资料进行属性分析和反演有助于提高储层预测和含油气性检测精度[4-8],其中准确提取地震子波是关键,在很大程度上影响最终反演结果的可靠性。然而,深度域地震波场不满足“线性时不变”系统的条件,地震子波在不同速度的介质中传播时,除了受地下介质的衰减、频散影响,还受介质速度的影响,其波形和延续度均不断发生变化。因此,如何提取深度域地震子波非常重要。
何惺华[9]利用理论模型和实际资料说明地震子波、褶积和Fourier变换等概念同样适用于深度域数据。林伯香等[10]指出,深度域中的地震子波是介质速度的函数,其在地下介质的传播过程不满足“线性时不变”系统的条件,必须对深度域速度函数进行适当变换,使其满足由褶积方法计算合成地震记录的条件。Hu等[11]给出了速度变换的具体方法,为提取深度域地震子波提供了一种思路。所谓速度变换,就是给定一个标准速度,将深度域中各采样点的速度都调整到该速度,同时深度域中的采样间隔也要做相应的调整,即等间隔的采样厚度被相应地“挤压”或“拉伸”,以保证旅行时不变。速度变换后,将原深度域变为常速度深度域,其采样间隔不再相等,故还需对常速度深度域的数据进行等间隔的重采样。在常速度深度域,可以引入褶积模型[11]。因此,可用时间域地震子波提取方法提取常速度深度域地震子波。时间域地震子波提取方法主要有两类,一是利用地震数据本身的统计信息提取地震子波[12-17],二是利用测井信息和地震数据提取地震子波[18-23],本文主要涉及后者。
在时间域,提取地震子波的时窗长度通常约为子波长度的5~10倍[24]。然而,在常速度深度域,只有数百米深度范围的可用测井信息,相当于常速度深度域子波长度的2~5倍。因此,在常速度深度域中从“短数据”中提取可靠的地震子波难度较大。此外,还需要考虑数据的截断效应[16]以提高子波提取精度。为此,本文提出了一种基于子空间约束Huber范数的深度域地震子波提取方法。正演模型测试和实际数据应用结果表明,该方法从有限深度范围内的数据中提取的地震子波更可靠。
1 方法原理常速度深度域中的地震记录为地震子波与反射系数的褶积和噪声相加的结果,其矩阵形式为
| $ \mathit{\boldsymbol{s}} = \mathit{\boldsymbol{Rw}} + \mathit{\boldsymbol{n}} $ | (1) |
式中:s为包含N个采样点的地震记录向量;R为反射系数构建的N×N阶矩阵;w为地震子波向量;n为噪声向量。对于式(1),基于L2范数的求解w的最小二乘法目标函数为
| $ \mathop {\min }\limits_\mathit{\boldsymbol{w}} J\left( \mathit{\boldsymbol{w}} \right) = \mathop {\min }\limits_\mathit{\boldsymbol{w}} \parallel \mathit{\boldsymbol{s}} - \mathit{\boldsymbol{Rw}}\parallel _2^2 $ | (2) |
式(2)的解析解为
| $ \mathit{\boldsymbol{\hat w}} = {({\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{R}})^{ - 1}}{\mathit{\boldsymbol{R}}^{\rm{T}}}\mathit{\boldsymbol{s}} $ | (3) |
式中
| $ \mathop {\min }\limits_\mathit{\boldsymbol{w}} J\left( \mathit{\boldsymbol{w}} \right) = \mathop {\min }\limits_\mathit{\boldsymbol{w}} \parallel \mathit{\boldsymbol{s}} - \mathit{\boldsymbol{Rw}}\parallel _2^2\;\;\;{\rm{s}}{\rm{.t}}{\rm{.}}\;\;\;\mathit{\boldsymbol{Pw}} = \mathit{\boldsymbol{w}} $ | (4) |
式中P为N×N阶的投影对角矩阵,其结构为
| $ \mathit{\boldsymbol{P = }}{\rm{diag}}\left[ {\overbrace {\begin{array}{*{20}{c}} {\underbrace {\begin{array}{*{20}{c}} 1&1& \cdots &1 \end{array}}_M}&{\begin{array}{*{20}{c}} 0& \cdots &0 \end{array}} \end{array}}^N} \right] $ | (5) |
且P2=P,PT=P。式(4)的解析解为
| $ \mathit{\boldsymbol{\hat w}} = {\left[ {{{\left( {\mathit{\boldsymbol{RP}}} \right)}^{\rm{T}}}\left( {\mathit{\boldsymbol{RP}}} \right)} \right]^{ - 1}}{\left( {\mathit{\boldsymbol{RP}}} \right)^{\rm{T}}}\mathit{\boldsymbol{s}} $ | (6) |
实际上,RP的第M+1至第N列元素均为零。因此可用N×M阶矩阵Rp替换RP,则式(6)变为
| $ \mathit{\boldsymbol{\hat w}} = {(\mathit{\boldsymbol{R}}_p^{\rm{T}}{\mathit{\boldsymbol{R}}_p})^{ - 1}}\mathit{\boldsymbol{R}}_p^{\rm{T}}\mathit{\boldsymbol{s}} $ | (7) |
通过上述子空间约束,不但改善了过拟合现象,还提高了计算效率。然而,由于Rp不是方阵,在矩阵求逆时会出现不稳定现象,可以通过岭回归方法
| $ \mathit{\boldsymbol{\hat w}} = {(\mathit{\boldsymbol{R}}_p^{\rm{T}}{\mathit{\boldsymbol{R}}_p} + \lambda \mathit{\boldsymbol{I}})^{ - 1}}\mathit{\boldsymbol{R}}_p^{\rm{T}}{\mathit{\boldsymbol{R}}_p}\mathit{\boldsymbol{s}} $ | (8) |
改善。式中:λ>0为正则化参数,可以通过广义交叉验证(generalized cross-validation, GCV)函数确定λ;I为单位矩阵。
由于截断效应的影响,当计算目标函数时,在数据两端很容易出现异常值,上述方法易受异常值的影响[25]。此外,确定式(8)的λ也并非易事。一个更稳健的方案是采用基于L1范数的目标函数,但求得的解可能是稀疏的,不适合子波提取。对此,可以考虑结合L1和L2范数——Huber范数的方案[26]。子空间约束Huber范数的目标函数定义为
| $ J\left( \mathit{\boldsymbol{w}} \right) = \sum\limits_i^N {{\rho _{{\rm{Huber}}}}\left( {{\eta _i}} \right)} $ | (9) |
其中
| $ {\rho _{{\rm{Huber}}}}\left( {{\eta _i}} \right){\rm{ = }}\left\{ \begin{array}{l} \;\;\;\;\;\;\;\;\frac{{\eta _i^2}}{2}\;\;\;\;\;\;{\eta _i} \le \varepsilon \\ \varepsilon {\eta _i} - {\varepsilon ^2}/2\;\;\;{\eta _i} > \varepsilon \end{array} \right. $ | (10) |
式中:
| $ \mathit{\boldsymbol{\hat w}} = {(\mathit{\boldsymbol{R}}_p^{\rm{T}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{Huber}}}}{\mathit{\boldsymbol{R}}_p})^{ - 1}}\mathit{\boldsymbol{R}}_p^{\rm{T}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}_{{\rm{Huber}}}}\mathit{\boldsymbol{s}} $ | (11) |
式中ΦHuber为权重对角矩阵,其对角元素φi定义为
| $ {\varphi _i} = \left\{ \begin{array}{l} \;1\;\;\;\;\;{\eta _i} \le \varepsilon \\ \frac{\varepsilon }{{{\eta _i}}}\;\;\;\;{\eta _i} > \varepsilon \end{array} \right. $ | (12) |
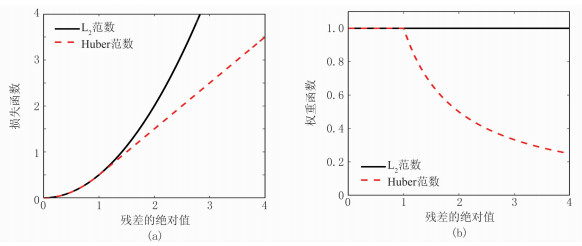
图 1为L2范数、Huber范数的损失函数和权重函数。由图可见:当残差的绝对值大于给定阈值(ε=1)时,Huber范数相当于L1范数;当残差的绝对值小于给定阈值时,Huber范数相当于L2范数。因此,Huber范数主要对大于阈值的异常值使用小权重处理,以得到更稳健的结果。
|
图 1 L2范数与Huber范数的损失函数(a)和权重函数(b) |
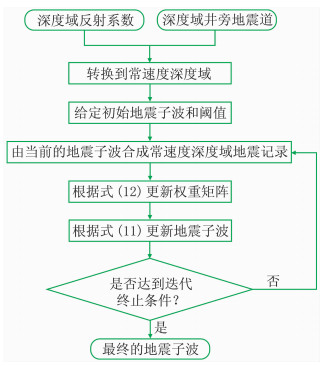
在使用IRLS求解子空间约束Huber范数的目标函数时,需要给定初始子波和阈值。实际上对初始子波的要求并不高,可以给定一组随机值或使用最小二乘法的结果。此外,阈值也容易给定,一般取0.0001或0.00001。求解子空间约束Huber范数的目标函数的IRLS算法流程如图 2所示。
|
图 2 求解子空间约束Huber范数的目标函数的IRLS算法流程 |
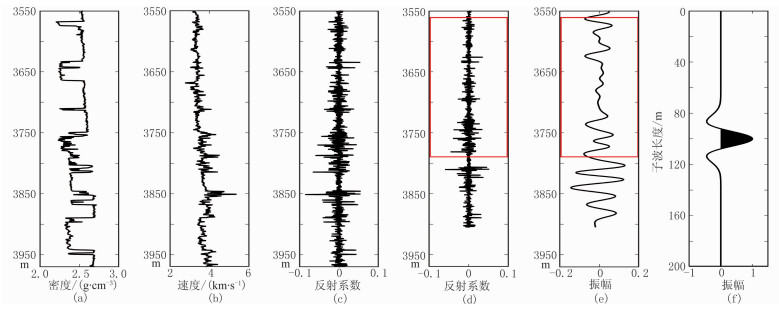
正演模型(图 3)由实际测井数据和给定的常速度深度域Ricker子波合成。可见:由于给定的常速度小于最大测井速度(图 3b),故对应常速度的深度小于真深度,因此相对于深度域反射系数(图 3c),常速度深度域数据(图 3d、图 3e)被“压缩”,同样的现象也出现在实际数据中;常速度深度域Ricker子波含有681个采样点,对应一个43Hz主频的时间域Ricker子波(图 3f)。
|
图 3 正演模型 (a)测井密度曲线;(b)测井速度曲线;(c)深度域反射系数;(d)常速度深度域反射系数;(e)常速度深度域合成地震记录;(f)常速度深度域Ricker子波 测井深度采样间隔为0.2m,用于速度转换的常速度为3000m/s;常速度深度域数据包含3176个采样点,采样间隔为0.1118m |
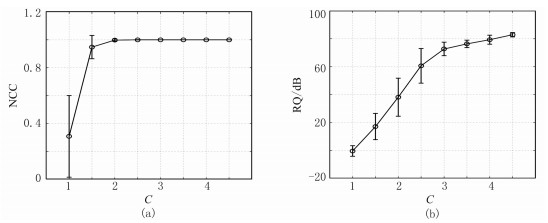
为了测试数据长度对子波提取的影响,分别对不同长度的数据使用本文方法提取地震子波。正演测试中,使用一组随机数据作为初始子波,设置阈值为0.00001。对不同长度的数据分别进行500次实验,每次实验随机在不同深度位置截取数据并提取子波,由归一化相关系数(normalized correlation coefficient)NCC和重构质量(reconstruction quality)RQ[29]评价子波提取结果(图 4)。可见,当截取的常速度深度域数据长度与子波长度的比值C≥3时,由本文方法得到的结果较可靠。鉴于此,随机截取C=3的数据(图 3d、图 3e红色矩形框中的数据),分别用最小二乘法(least-squares, LS)、子空间约束最小二乘法(subspace-constrained LS, SCLS)、子空间约束岭回归方法(subspace-constrained ridge regression, SCRR)和子空间约束Huber范数方法(subspace-constrained Huber norm, SCHN)从该段数据中提取地震子波(图 5),表 1为几种方法的计算时间和评价指标。此外,对每一种方法也分别进行500次随机实验,每次实验在不同深度位置截取C=3的数据提取子波并评价结果(图 6)。需要指出的是,使用子空间约束后,矩阵R的大小由3176×3176减小到2044×681。由图 5、图 6和表 1可见,本文方法从较短的数据中提取的地震子波更可靠。因此,若实际数据长度合适,利用该方法还可以提取深变地震子波。
|
图 4 不同数据长度对地震子波提取的影响 (a)NCC;(b)RQ |
|
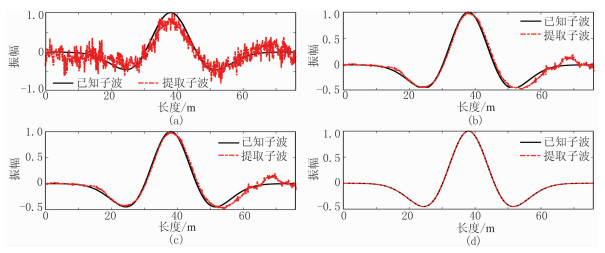
图 5 对同一段数据使用四种方法提取子波的结果 (a)LS;(b)SCLS;(c)SCRR;(d)SCHN |
|
|
表 1 几种方法的计算时间和评价指标 |
|
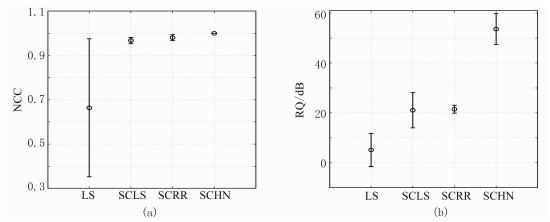
图 6 四种方法对同一数据段提取子波的随机试验评价结果 Figure 6 (a)NCC; (b)RQ |
利用W区的A井、B井的测井数据以及叠前深度偏移地震数据验证本文方法的有效性。利用不同常速度分别对A井、B井的数据进行速度变换,考虑到数据长度、信噪比、前期数据处理流程等因素,截取C=4的数据提取子波。通过SCLS确定了A井、B井的地震子波长度。将初始子波设定为一组随机数据,设置阈值为0.0001。图 7、图 8分别为A井、B井测井数据及地震子波提取结果。由图可见:由提取的地震子波(图 7e、图 8e)合成的深度域地震记录(图 7b、图 8b中的红色地震道)与A井、B井的井旁地震道(图 7b、图 8b中的蓝色地震道)的相关性很好。
|
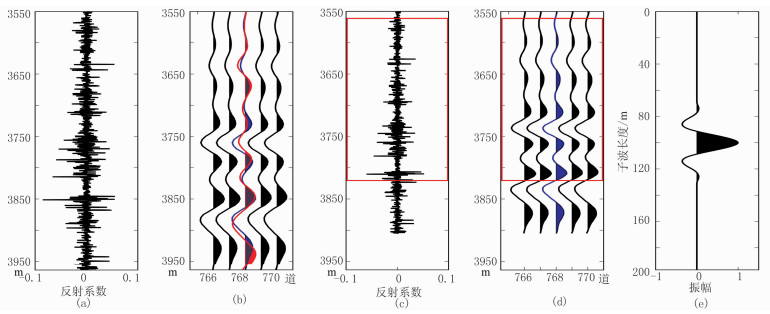
图 7 A井测井数据及地震子波提取结果 (a)测井反射系数;(b)地震道(蓝色为井旁地震道,红色为由图e合成的地震记录);(c)常速度深度域反射系数;(d)常速度深度域井旁地震道;(e)提取的常速度深度域地震子波(提取地震子波的数据为图c和图d中红色矩形框内的数据) 由常速度3000m/s对井数据速度变换,井数据包含3176个采样点,常速度深度采样间隔为0.1118m;由SCLS确定的地震子波长度为580个采样点;NCC=0.85,RQ=5.3dB |
|
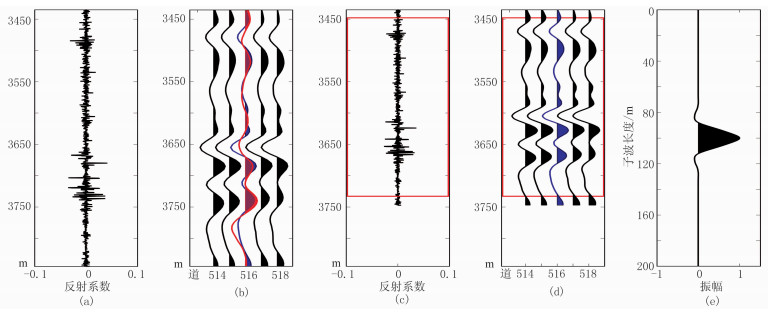
图 8 B井测井数据及地震子波提取结果 (a)测井反射系数;(b)地震道(蓝色为井旁地震道,红色为由图e合成的地震记录);(c)常速度深度域反射系数;(d)常速度深度域井旁地震道;(e)提取的常速度深度域地震子波(提取地震子波的数据为图c和图d中红色矩形框内的数据) 由常速度2536m/s对井数据速度变换,井数据包含2394个采样点,常速度深度采样间隔为0.1305m;由SCLS确定的地震子波长度为521个采样点;NCC=0.83,RQ=4.6dB |
本文提出了基于子空间约束Huber范数的深度域地震子波提取方法,该方法不涉及正则化参数,且容易给定初始地震子波和阈值。虽然该方法使用了迭代求解方案,但相较于其在精度和可靠性上的显著提升,计算量的少许增加是能够接受的。更为重要的是,与一些常规方法相比,本文方法从较短的深度域数据中提取的地震子波更可靠,这对于反映深度域地震子波随深度变化的特征,并根据需要提取深变地震子波具有重要意义。
| [1] |
李振春. 地震偏移成像技术研究现状与发展趋势[J]. 石油地球物理勘探, 2014, 49(1): 1-21. LI Zhenchun. Research status and development trends for seismic migration technology[J]. Oil Geophysical Prospecting, 2014, 49(1): 1-21. |
| [2] |
罗红梅, 王长江, 刘书会, 等. 深度域高精度井震动态匹配方法[J]. 石油地球物理勘探, 2018, 53(5): 997-1005. LUO Hongmei, WANG Changjiang, LIU Shuhui, et al. Well-to-seismic calibration in the depth domain using dynamic depth warping[J]. Oil Geophysical Prospecting, 2018, 53(5): 997-1005. |
| [3] |
Fletcher R P, Archer S, Nichols D, et al.Inversion after depth imaging[C].SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [4] |
周赏, 汪关妹, 张万福, 等. 深度域地震资料解释技术应用及效果[J]. 石油地球物理勘探, 2017, 52(增刊1): 92-98. ZHOU Shang, WANG Guanmei, ZHANG Wanfu, et al. Depth-domain seismic data interpretation[J]. Oil Geophysical Prospecting, 2017, 52(S1): 92-98. |
| [5] |
彭军, 周家雄, 王宇, 等. 基于褶积理论的深度域地震资料反演[J]. 科学技术与工程, 2014, 14(19): 40-45. PENG Jun, ZHOU Jiaxiong, WANG Yu, et al. Depth domain seismic inversion base on convolution theory[J]. Science Technology and Engineering, 2014, 14(19): 40-45. |
| [6] |
Letki L, Darke K, Borges Y.A comparison between time domain and depth domain inversion to acoustic impedance[C].SEG Technical Program Expanded Abstracts, 2015, 34: 3376-3380.
|
| [7] |
Singh Y. Deterministic inversion of seismic data in the depth domain[J]. The Leading Edge, 2012, 31(5): 538-545. DOI:10.1190/tle31050538.1 |
| [8] |
Sengupta M, Zhang H, Jervis M.Direct depth domain elastic inversion[C].SEG Technical Program Expanded Abstracts, 2018, 37: 506-510.
|
| [9] |
何惺华. 深度域地震资料若干问题初探[J]. 石油物探, 2004, 43(4): 353-358. HE Xinghua. Discussion on seismic data of depth domain[J]. Geophysical Prospecting for Petroleum, 2004, 43(4): 353-358. |
| [10] |
林伯香, 胡中平, 薛诗桂. 利用变换深度域速度函数制作深度域合成地震记录[J]. 石油地球物理勘探, 2006, 41(6): 640-643. LIN Boxiang, HU Zhongping, XUE Shigui. Using velocity function in transformed depth domain to make synthetic seismograph in depth domain[J]. Oil Geophysical Prospecting, 2006, 41(6): 640-643. |
| [11] |
Hu Z, Zhu H, Lin B, et al.Wavelet analysis and convolution in depth domain[C].SEG Technical Program Expanded Abstracts, 2007, 26: 2733-2737.
|
| [12] |
Lazear G. Mixed-phase wavelet estimation using fourth-order cumulants[J]. Geophysics, 1993, 58(7): 1042-1051. DOI:10.1190/1.1443480 |
| [13] |
Sacchi M D, Ulrych T J. Nonminimum-phase wavelet estimation using higher order statistics[J]. The Lea-ding Edge, 2000, 19(1): 80-83. DOI:10.1190/1.1438466 |
| [14] |
尹成, 唐斌, 谢桂生. 地震子波估计——高阶累积量矩阵方程法[J]. 信号处理, 2000, 16(增刊1): 83-87. YIN Cheng, TANG Bin, XIE Guisheng. Seismic wavelet estimation:matrix-equation method of high-order cumulants[J]. Signal Processing, 2000, 16(S1): 83-87. |
| [15] |
戴永寿, 郑德玲, 魏磊, 等. 高阶统计量地震子波估计建模[J]. 石油地球物理勘探, 2006, 41(5): 514-518, 540. DAI Yongshou, ZHENG Deling, WEI Lei, et al. Estimation of high-order statistic seismic wavelet[J]. Oil Geophysical Prospecting, 2006, 41(5): 514-518, 540. |
| [16] |
Mirko V D B, Pham D T. Robust wavelet estimation and blind deconvolution of noisy surface seismics[J]. Geophysics, 2008, 73(5): V37-V46. DOI:10.1190/1.2965028 |
| [17] |
Zhang R, Deng Z. A depth variant seismic wavelet extraction method for inversion of poststack depth-domain seismic data[J]. Geophysics, 2017, 82(6): R569-R579. |
| [18] |
Danielson V, Karlsson T V. Extraction of signatures from seismic and well data[J]. First Break, 1984, 2(4): 15-21. |
| [19] |
Lines L R, Treitel S. Wavelets, well logs and Wiener filters[J]. First Break, 1985, 3(8): 9-14. |
| [20] |
梁光河. 地震子波提取方法研究[J]. 石油物探, 1998, 37(1): 31-39. LIANG Guanghe. On the methods of seismic wavelet extraction[J]. Geophysical Prospecting for Petro-leum, 1998, 37(1): 31-39. |
| [21] |
Buland A, Omre H. Bayesian wavelet estimation from seismic and well data[J]. Geophysics, 2003, 68(6): 2000-2009. DOI:10.1190/1.1635053 |
| [22] |
Gunning J, Glinsky M E. Wavelet extractor:A Baye-sian well-tie and wavelet extraction program[J]. Computers and Geosciences, 2006, 32(5): 681-695. DOI:10.1016/j.cageo.2005.10.001 |
| [23] |
Bianco E. Tutorial:Wavelet estimation for well ties[J]. The Leading Edge, 2016, 35(6): 541-543. DOI:10.1190/tle35060541.1 |
| [24] |
Bunch A W H, White R E. Least-squares filters wi-thout transient errors:an examination of the errors in least-squares filter design[J]. Geophysical Prospecting, 1985, 33(5): 657-673. DOI:10.1111/j.1365-2478.1985.tb00771.x |
| [25] |
Ji J. Robust inversion using biweight norm and its application to seismic inversion[J]. Exploration Geophysics, 2012, 43(2): 70-76. DOI:10.1071/EG12014 |
| [26] |
Huber P J. Robust regression: Asymptotics, conjec-tures, and Monte Carlo[J]. The Annals of Statistics, 1973, 1(5): 799-821. DOI:10.1214/aos/1176342503 |
| [27] |
Scales J A, Gersztenkorn A. Robust methods in inverse theory[J]. Inverse Problems, 1988, 4(4): 1071-1091. DOI:10.1088/0266-5611/4/4/010 |
| [28] |
Daubchies I, DeVore R, Fornasier M, et al. Iteratively re-weighted least squares minimization for sparse recovery[J]. Communications on Pure and Applied Mathematics, 2010, 63(1): 1-38. |
| [29] |
Kazemi N, Sacchi M S. Sparse multichannel blind deconvolution[J]. Geophysics, 2014, 79(5): V143-V152. DOI:10.1190/geo2013-0465.1 |



 陈学华, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室, 610059。Email:
陈学华, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室, 610059。Email: