0 引言

提高地震资料的信噪比是地震数据处理的重要任务。随着勘探、开发的精度提高及面对的勘探目标越来越复杂，对地震数据去噪技术的要求也逐步提高^[1]。传统地震数据去噪方法通过寻找和识别地震数据中的冗余信息，利用地震数据自身的数据结构特点去噪^[2-3]。随着稀疏表示理论的发展，基于稀疏表示的去噪方法逐渐进入人们的视野。曹静杰等^[4]提出一种基于曲波变换的稀疏变换自适应去噪方法，只需设置初始阈值和迭代次数，便可通过迭代过程中解的稀疏性与拟合误差之间的内在关系确定合适的阈值，进而压制随机噪声。张华等^[5]将非均匀快速傅里叶变换引入多尺度、多方向二维曲波变换，应用二维非均匀曲波变换压制地震随机噪声，在将非均匀采样地震数据内插为均匀采样数据的同时，有效地压制了噪声。与传统方法相比，稀疏表示方法将去噪问题转化为优化问题，基于稀疏变换的方法使用专门设计的变换稀疏表示地震数据。为了提升字典表示的准确性，可以采用学习训练的方法构造表示字典，与其他传统的字典构造方法(如曲波变换以及Shearlet变换等)^[6-8]相比，可准确地稀疏表示地震数据。李勇等^[9]提出了一种数据驱动与模型驱动联合的模型约束下的在线字典学习去噪方法，先通过模型驱动方式获得一个较优质的学习样本以构建字典再进行去噪处理，能在高噪声背景下有效地提取地震数据中的弱信号。张良等^[10]等使用一种基于双稀疏字典和快速迭代收缩阈值算法(FISTA)的方法对地震数据去噪，能够自适应地稀疏表示地震数据，当地震数据较复杂时的信噪比更高，不仅去噪处理速度较快，而且克服了字典学习缺少先验约束的不足。近年来基于过完备字典信号稀疏表示(K-SVD)的一系列算法被广泛使用和扩展，为了获得良好的降噪效果，这些字典学习方法需要根据经验反复测试并微调参数^[11]。

随着计算机硬件技术的飞速发展，图形处理能力得到极大提升，深度学习网络自2010年以来成为热门话题，深度置信网络^[12]、堆叠式自动编码器^[13]和深度卷积神经网络(CNN)^[14]等大量的深度学习网络应运而生。传统去噪方法通过寻找和识别地震数据中的冗余信息，利用地震数据自身的数据结构特点去噪，主要集中在数据建模和优化。深度学习网络走了一条完全不同的道路，直接针对推理阶段，学习其参数以优化端到端性能。其中CNN已在解决不同领域的高度非线性计算机视觉问题方面取得了成功^[15]。Zhang等^[16]使用具有17个卷积层的去噪卷积神经网络(DnCNN，Denoising Convolutional Neural Networks)将噪声作为输出(即残差学习方法)对数据降噪，降噪效果较好且提高了训练速度。与具有单层分解的字典学习相比，具有更深层次的深度学习网络能够在具有不同抽象级别的地震数据训练集中获得更好的处理效果^[17-19]。由于单独使用稀疏字典和深度学习方法都存在局限性，因此人们探索将二者结合的去噪方法。将稀疏表示结构嵌入深度学习网络体系中，以使整个算法既有深度方法的灵活性，又有稀疏表示方法带来的信息。

Scetbon等^[20]提出了基于深度学习的过完备字典信号稀疏表示算法(Deep-KSVD)用于图像数据去噪，取得了理想的去噪效果。以往在地震数据去噪过程中使用的仅仅是K-SVD去噪算法。本文进一步研究了基于Deep-KSVD的地震数据随机噪声压制方法，将K-SVD去噪算法与深度学习网络相结合，综合考虑深度学习网络与稀疏表示方法的优点，使Deep-KSVD算法更有效。

1 算法原理 1.1 K-SVD算法

K-SVD算法由Aharon等^[21]、Elad等^[22]根据误差最小原则提出，利用基向量的线性组合表示输入信号的数据特征，通过数据训练不断更新字典基向量及其表示系数，将逼近误差调整到最小，完成对数据的充分表示。K-SVD算法包括稀疏编码和字典更新两个基本步骤。

1.1.1 稀疏编码

将地震数据x表示为一个大小为$\sqrt p \times \sqrt p $的小数据块，按字典顺序排序成长度为p的列向量(也称为原子)。根据稀疏表示模型，假设x是从预先指定的字典D∈R^p×m(m为字典中的原子数量)中获取的s≪p个列向量的线性组合，即x=Dα, 其中α∈R^m是一个包含s个非零元素的稀疏向量，用‖α‖₀=s表示。将x加入加性零均值高斯白噪声获得含噪结果y，其噪声标准差为σ。噪声估计值的稀疏编码${\mathit{\boldsymbol{\hat \alpha }}}$通过求解下式获得^[23-24]

$ \mathit{\boldsymbol{\hat \alpha }} = \arg {\rm{ }}\mathop {\min }\limits_{\boldsymbol{\alpha}} \left( {\lambda \parallel \mathit{\boldsymbol{\alpha }}{\parallel _0} + \frac{1}{2}\parallel \mathit{\boldsymbol{D\alpha }} - \mathit{\boldsymbol{y}}\parallel _2^2} \right) $

(1)

随后通过$\mathit{\boldsymbol{\hat x}} = \mathit{\boldsymbol{D\hat \alpha }}$得到去噪结果${\mathit{\boldsymbol{\hat x}}}$。式(1)中λ为正则化系数。

假设基础字典D已知，将上述稀疏编码操作应用于更大的数据及其含噪数据Y时会有两个未知信息：每个位置的稀疏表示和输出数据X。块坐标最小化算法首先将含噪数据Y作为X的初始值，然后寻找所有位置k的最优α_k。这个阶段类似对尺寸为$\sqrt p \times \sqrt p $的每个块做一个滑动窗口稀疏编码。

1.1.2 字典更新

假定所有块的稀疏表示为${\{ {{\mathit{\boldsymbol{\hat \alpha }}}_k}\} _k}$，为了更新X，需求解下式

$ \begin{array}{l} \mathit{\boldsymbol{\hat X}} = \arg {\rm{ }}\mathop {\min }\limits_\mathit{\boldsymbol{X}} (\frac{\mu }{2}\parallel \mathit{\boldsymbol{X}} - \mathit{\boldsymbol{Y}}\parallel _2^2 + \\ \;\;\;\;\;\;\frac{1}{2}\sum\limits_k {\parallel \mathit{\boldsymbol{D}}{{\mathit{\boldsymbol{\hat \alpha }}}_k} - {\mathit{\boldsymbol{R}}_k}\mathit{\boldsymbol{X}}\parallel _2^2} {\rm{ )}} \end{array} $

(2)

式中：μ为正则化参数；R_k∈R^p×N表示从数据中提取的第k块算子。可将D的计算嵌入贝叶斯公式中

$ \begin{array}{l} \mathop {\min }\limits_{{{\left\{ {{\alpha _k}} \right\}}_k}, X, D} \left[ {\frac{\mu }{2}\parallel \mathit{\boldsymbol{X}} - \mathit{\boldsymbol{Y}}\parallel _2^2 + \sum\limits_k {({\lambda _k}\parallel {\mathit{\boldsymbol{\alpha }}_k}{\parallel _0} + } } \right.\\ \left. {\;\;\;\;\;\;\;\;\frac{1}{2}\parallel \mathit{\boldsymbol{D}}{\mathit{\boldsymbol{\alpha }}_k} - {\mathit{\boldsymbol{R}}_k}\mathit{\boldsymbol{X}}\parallel _2^2)} \right] \end{array} $

(3)

在这种情况下，D使用所有现有的噪声数据块从Y本身学习。采用块坐标最小化将D初始化为过完备的离散余弦变换(DCT)矩阵，并设置X=Y，然后在数据块的正交匹配追踪(OMP)计算结果和K-SVD更新的D之间迭代。在循环之后，D能够适应被处理的数据。

在实际应用时，不断循环稀疏编码和字典更新这两个步骤，直至达到设定逼近误差标准或迭代次数。基于构造学习字典的稀疏表示方法通过学习训练算法从输入数据中提取数据特征，完成对字典基函数的不断更新和完善。因此，相较于传统方法，该方法具有更好的数据适应性，可提高对不同数据结构特点的表示精度，从而改善去噪效果。

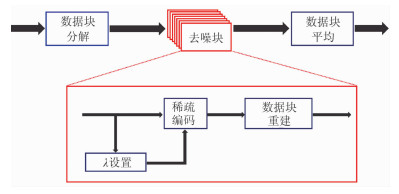
1.2 Deep-KSVD去噪原理

Deep-KSVD方法结合了K-SVD稀疏去噪算法和深度学习的思想^[20]，为了使该网络有能力学习参数，在追踪阶段用一个等价的可学习的替代方案代替OMP算法。计算过程包括将数据分解为重叠的数据块、通过适当的追踪对每个数据块去噪以及通过去噪后的数据块加权重建整个数据^[25-26]。图 1为Deep-KSVD网络结构，其去噪处理包括稀疏编码、λ估计以及数据块重建三个部分，分述如下。

1.2.1 稀疏编码

给定一个加入标准差为σ的高斯噪声的数据块$\mathit{\boldsymbol{y}} \in {\mathit{\boldsymbol{R}}^{\sqrt p \times \sqrt p }}$(保持长度为p的列向量)，目标是根据已知字典D∈R^p×m获得其稀疏编码^[27-28]。该问题的近似解为

$ \mathit{\boldsymbol{\hat \alpha }} = \arg {\rm{ }}\mathop {\min }\limits_\mathit{\boldsymbol{\alpha }} \left( {\frac{1}{2}\parallel \mathit{\boldsymbol{D\alpha }} - \mathit{\boldsymbol{y}}\parallel _2^2 + \lambda \parallel \mathit{\boldsymbol{\alpha }}{\parallel _1}} \right) $

(4)

通过迭代软阈值算法(ISTA)求解上式，能够保证收敛到全局最优

$ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\hat \alpha }}}_{t + 1}} = {\mathit{\boldsymbol{S}}_{\lambda /c}}\left[ {{{\mathit{\boldsymbol{\hat \alpha }}}_t} - \frac{1}{c}{\mathit{\boldsymbol{D}}^{\rm{T}}}\left( {\mathit{\boldsymbol{D}}{{\mathit{\boldsymbol{\hat \alpha }}}_t} - \mathit{\boldsymbol{y}}} \right)} \right]\\ {{\mathit{\boldsymbol{\hat \alpha }}}_0} = 0 \end{array} \right. $

(5)

式中：c为D的平方谱范数；S_λ/c为分量软阈值算子；${{{\mathit{\boldsymbol{\hat \alpha }}}_t}}$为第t次迭代时求得的稀疏编码。

在求解过程中采用梯度下降法迭代求取最优解，这样可以使稀疏编码阶段具有可学习性^[29-30]。

1.2.2 λ估计

正则化系数λ不仅依赖于σ，而且还依赖于数据块y本身。根据K-SVD去噪算法，需要为每个数据块y^k设置λ_k，以产生具有控制误差水平的稀疏表示$\parallel \mathit{\boldsymbol{D}}{{\mathit{\boldsymbol{\hat \alpha }}}_k} - {\mathit{\boldsymbol{y}}_k}\parallel _2^2 \le p{\sigma ^2}$。可从y^k出发回归相应的正则化参数λ_k，使用多层感知器(MLP)网络表示为λ=f_θ(y)，其中θ是MLP参数的向量。MLP由三个隐藏层组成，每层都由一个全连接的线性映射和一个激活函数(ReLU)(除了最后一层)组成。输入层由p个节点组成，p为矢量化数据块的维数，输出层由单个节点组成。

1.2.3 数据块重建

使用D和稀疏编码${\mathit{\boldsymbol{\hat \alpha }}}$重建数据块y对应的无噪组合${\mathit{\boldsymbol{\hat x }}}$。学习网络中，字典代表一组参数。Deep-KSVD首先将输入数据分割成完全重叠的数据块，然后通过上述的数据块去噪方案处理每个含噪数据块，最后通过加权平均这些数据块的去噪结果重建数据^[31-32]。最后一个阶段允许学习加权组合的数据块，用$\mathit{\boldsymbol{w}} \in {\mathit{\boldsymbol{R}}^{\sqrt p \times \sqrt p }}$表示该数据块权值矩阵，得到重建结果

$ \mathit{\boldsymbol{\hat X}} = \frac{{\sum\limits_k {\mathit{\boldsymbol{R}}_k^{\rm{T}}(\mathit{\boldsymbol{w}} \odot {{\mathit{\boldsymbol{\hat x}}}_k})} }}{{\sum\limits_k {\mathit{\boldsymbol{R}}_k^{\rm{T}}\mathit{\boldsymbol{w}}} }} $

(6)

式中⊙表示Schur乘积。Deep-KSVD网络F是θ、c、D和w的参数化函数。给定含噪数据Y，通过$\mathit{\boldsymbol{\hat X}} = F\left( \mathit{\boldsymbol{Y}} \right)$返回数据去噪结果。由上述所有参数训练F，将损失函数$L = \sum\nolimits_i {\parallel {\mathit{\boldsymbol{X}}_i} - F\left( {{\mathit{\boldsymbol{Y}}_i}} \right)\parallel } _2^2$最小化，集合{X_i}_i代表训练数据，{Y_i}_i为合成噪声形式，由Y_i=X_i+V_i获得，其中V_i为零均值高斯白噪声。

1.3 网络训练

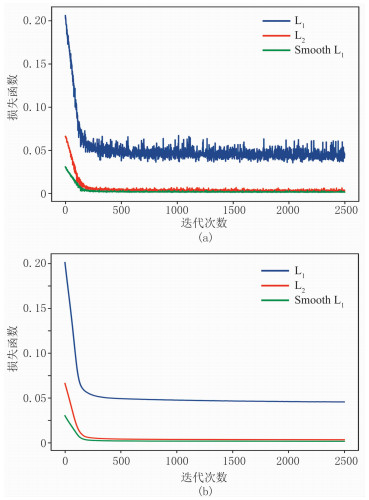
本文基于Pytorch构建网络模型，使用一台CPU为i7-7700、内存为20G、系统为Windows10专业版64位操作系统的台式电脑训练网络模型。利用2770个大小为128×128的地震数据建立数据集，其中2500个数据组成训练集，270个数据组成测试集，训练和测试集是严格不相交的，训练阶段随机抽取训练集中的数据，添加高斯白噪声。为了更合理地选择网络参数，为网络选取L₁、L₂和Smooth L₁等损失函数进行训练并测试(图 2)。可见，当选取Smooth L₁损失函数时，训练(图 2a)和测试(图 2b)的函数值收敛更好，即：迭代次数为0~300时函数值逐步降至约0.005；迭代次数为300~2500时损失函数值趋于稳定。初步说明网络模型得到有效训练。

2 模型数据测试

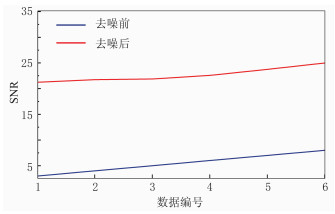
为了验证网络模型的训练效果，使用添加高斯随机噪声的不同信噪比(SNR)的含噪模型数据测试网络的去噪能力(图 3)，结果表明，不同信噪比模型数据经过Deep-KSVD算法去噪后显著提高了信噪比，进一步说明网络模型的训练效果很好。

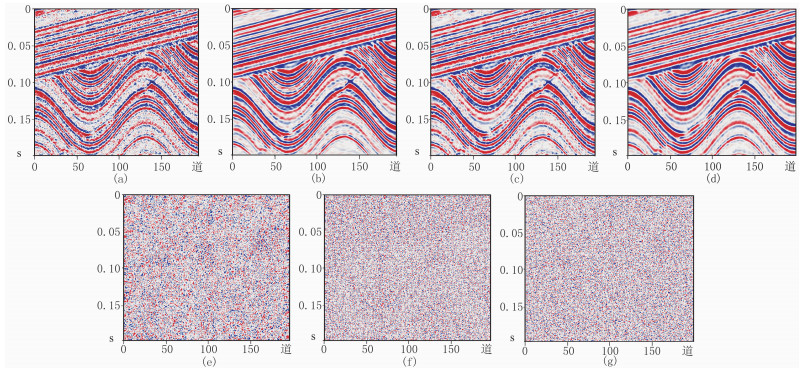
为了更形象地展示对模型数据的去噪效果，选取并展示SNR=8的含噪模型数据及其去噪结果(图 4)。可见：对原始含噪数据(图 4a)的曲波变换去噪结果(图 4b)残留噪声点，在残差剖面(图 4e)边缘存在有效信号；K-SVD去噪结果(图 4c)残留噪声，并存在轻微的伪影现象，部分地层信息较模糊，在残差剖面(图 4f)上存在有效信号；Deep-KSVD去噪结果(图 4d)及其残差剖面(图 4g)的断点及地层尖灭点处的同相轴没有畸变，弯曲程度较大的同相轴也无变形，说明Deep-KSVD方法可较好地保护断层和同相轴边缘等不连续性信息。

3 实际数据测试 3.1 测试数据1

为了进一步检验实际数据应用效果，对N区实际地震资料采用不同方法去噪并分析去噪效果(图 5)。可见：①叠后地震剖面中存在较严重的随机干扰，同相轴模糊且同相轴边界及断点不明显、地层接触关系不清，给处理、解释带来困难(图 5a)。②曲波变换去噪结果(图 5b)存在严重伪影现象，且存在多个噪声点。③与K-SVD去噪结果(图 5c)相比，Deep-KSVD去噪结果(图 5d)削弱了背景斑块的影响，由两者的残差剖面(图 5f、图 5g)可知，Deep-KSVD方法能够更好地保留有效信号，去噪效果更好。

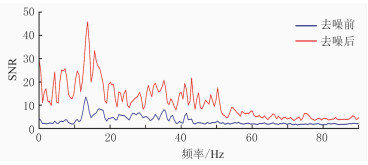
图 6为Deep-KSVD去噪前、后信噪比谱。由图可见，去噪后中、低频范围的信噪比显著提升，进一步量化说明了Deep-KSVD对实际含噪数据也具有较好的去噪效果。

基于Deep-KSVD的去噪方法可以有效地提高资料的信噪比，以稀疏表示为基础，目标明确，结构简洁，效果良好，主要特点为：①由于空间冗余信息存在于数据块，因此Deep-KSVD网络采用稀疏建模方法；②考虑了数据块的平均效应；③Deep-KSVD网络利用非局部自相似性作为额外的先验信息，因此可有效捕捉相隔很远的数据块之间的相关性，从而改进去噪效果。

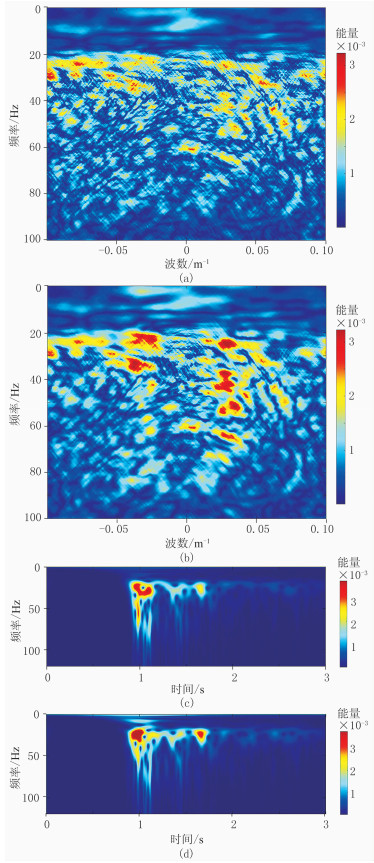
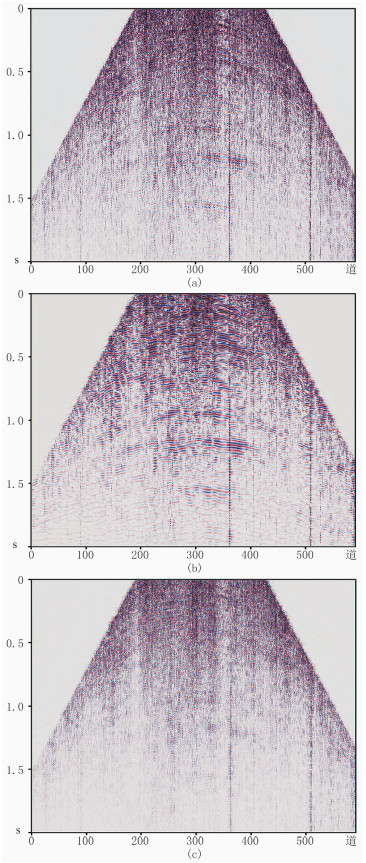
3.2 测试数据2

对叠前数据做切除直达波和面波处理，得到含噪数据(图 7a)，其中包含较强的随机噪声。采用Deep-KSVD方法压制随机噪声，有效衰减了随机噪声且有效信号未遭到过度破坏(图 7b)。因此Deep-KSVD方法可为解释、处理提供信噪比较高的地震数据。

图 8为图 7数据第200道的F-K谱与时频谱。由图可见：①原始数据中含有较强的随机噪声，导致F-K谱较杂乱(图 8a)；去噪后F-K谱得到改善(图 8b)。②由去噪前(图 8c)、后(图 8d)时频谱可见，后者的高频段能量减少，且充分保留了低频段能量，说明有效压制了随机噪声且没有破坏低频段有效信号。

4 结束语

曲波变换去噪处理使同相轴在断层等不连续区域发生畸变，对有效信号产生干扰。K-SVD算法需要人工反复调整参数才能改善去噪效果。本文将K-SVD去噪算法与深度学习网络相结合，综合考虑深度学习网络与稀疏表示方法的优点，研究了基于Deep-KSVD的地震数据随机噪声压制方法。模型数据和实际数据测试结果表明，当Deep-KSVD网络训练完成后，给定含噪数据，能够自适应地衰减地震噪声，并保护有效不连续性信息及数据结构特点，无需再进行参数调整。与K-SVD去噪方法相比，Deep-KSVD去噪方法的噪声压制效果更好，可提高全频带数据的信噪比。