② 中海油研究总院有限责任公司, 北京 100020;
③ 中国地质大学(北京)能源学院, 北京 100083
② CNOOC Research Institute Ltd., Beijing 100020, China;
③ School of Energy Resources, China University of Geosciences(Beijing), Beijing 100083, China
薄储层的预测和表征是油田勘探开发的重点,目前主要有三种策略:①基于谱分解技术的薄层预测[1-3],根据薄层顶、底反射界面干涉特点优选时窗,以振幅谱出现的两个频陷之间的距离作为薄层的时间厚度。②基于地震反演技术的薄层预测[4-6],如沈洪涛等[7]利用地震资料高横向分辨率与地质、测井资料高纵向分辨率的优势进行互补,应用地质统计学反演技术预测薄砂岩储层;高君等[8]通过波形指示反演技术将地震波形横向变化融入薄储层预测中。③基于多属性回归方法的薄层预测[9],有监督地学习输入地震属性与测井储层参数之间的模型表征,从而实现井间储层预测,如张显文等[10]预测碳酸盐岩储层孔隙因子参数刻画储层有利区;张晶玉等[11]对多属性预测三个关键环节进行优化与质控。相比于前两种策略,多属性回归方法能够避免时窗难确定、子波不准确、预测结果分辨率低与模型化严重等问题;同时,由于能够表征储层特征与输入属性之间的非线性关系,因此具有提高预测结果精度的潜能。然而,传统多属性回归方法非线性表征能力仍然较弱,训练模型泛化能力不足,常导致井间薄储层预测结果可靠性不足。
近年来,深度学习技术在分类[12-13]、目标检测[14-15]、分割图像处理[16-17]等方面取得了成功,在地球物理勘探领域也逐渐推广运用,如地震资料处理[18-20]与解释[21-23]、地震反演[24-26]等。深度学习技术训练的模型完全基于数据驱动,能够挖掘输入数据与期望输出之间的深层联系,常具有非线性、高分辨、去模型化等特点。
多层感知机(Multi-Layer Perceptron,MLP)是一种经典的深度学习网络模型,也是现阶段所有主流深度学习网络的基础。该网络包含输入层、输出层以及多个隐含层,以神经元为最小单位,将输入的多个节点信息非线性映射到单一输出上。
本文将多层感知机深度学习网络与多属性回归方法相结合,预测砂岩薄储层。通过基于数据驱动的新方法训练具有高泛化能力的模型,以进一步提升薄储层预测分辨率与井间预测结果合理性。同时,从三方面优化多属性回归方法:①属性输入方面,除原始地震数据外,将90°相移数据成果[27]用于储层结构近似估计,代替常规的反演阻抗体,并作为外部属性;同时将储层不连续界限地震属性[28]用于分析储层空间的展布。②目标预测方面,以对岩性最为敏感的自然伽马参数作为期望输出,同时保留自然伽马曲线高频成分进行模型学习,以提高薄储层预测分辨率。③样本规模与模型评价方面,选择多种类型、多口井组成训练集和验证集,保障模型泛化能力;同时避免预测结果过拟合。最后,通过在A油田的测试验证该方法的应用效果。
1 方法原理 1.1 多属性回归多属性回归方法的本质是有监督学习,是一种将地震资料及其属性体(如反演体、分频体等)转化为储层表征参数体(如阻抗体、自然伽马体等)的方法。该方法通过从井旁地震道中提取各类属性进行优选与组合,训练并获得优选属性与井点测量参数(如密度、自然伽马等)之间的模型表征,并外推应用于井间储层参数预测。其中有两个重要环节。
(1) 优选地震属性组合。常采用“专家法”(根据人工经验主观选择属性组合)与“步聪法”(通过误差最小准则,依次优选与储层参数相关度更高的属性进行组合)结合方式[9],通过“专家法”主观地初筛出被认为与储层参数具有高关联度的属性集合,通过“步聪法”逐个计算初筛属性与储层参数的关联程度,保留相关程度最高的属性,然后按照最小二乘误差准则依次确定后续属性,直至误差满足要求或达到预设最大属性个数。
(2) 模型表征。常利用多元线性回归或经典神经网络非线性回归方法表征模型,其中线性回归模型为
| $ \mathit{\boldsymbol{P}} = \sum\limits_{k = 1}^M {({\mathit{\boldsymbol{u}}_k}{\mathit{\boldsymbol{A}}_k} + {v_k})} $ | (1) |
式中:P为预测的井点储层参数向量;Ak为优选出的第k个地震属性(二维或三维矩阵);M为优选属性总个数;uk=[u1 u2 … uk]T和vk=[v1 v2 … vk]T分别为待求的Ak的权重系数和尺度常数组成的列向量。通过误差最小二乘准则建立凸优化目标泛函
| $ \mathop {{\rm{min}}}\limits_{{u_k}, {v_k}} (\parallel \mathit{\boldsymbol{d}} - \mathit{\boldsymbol{P}}\parallel _2^2) $ | (2) |
式中:‖·‖2代表L2范数;d为测井实测储层参数向量。通常应用梯度下降类算法(共轭梯度法、最速下降法)快速求解式(2)得到uk与vk,从而完成模型表征。
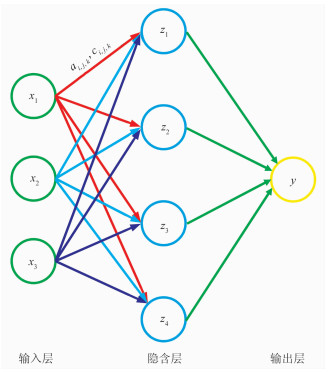
训练非线性模型表征属性组合与储层参数的关系,经典神经网络包含1个输入层、1个输出层及1个隐含层。输入层有3个节点、隐含层有4个节点的网络结构如图 1所示,各层之间以连接系数ai, j, k与偏置常数ci, j, k相连接。其中,下标(i, j, k)为第k-1层第i个元素与第k层第j个神经元之间的连接。与式(2)类似,通过最小化网络输出y与实测值的误差,获得ai, j, k和ci, j, k,建立非线性模型。经典神经网络的模型表征能力在线性回归基础上得到了较大提升,但常由于训练样本多样性的不足和网络泛化能力有限,导致井间薄储层预测结果出现同向轴破碎、连续性过差等问题。
|
图 1 经典神经网络结构 |
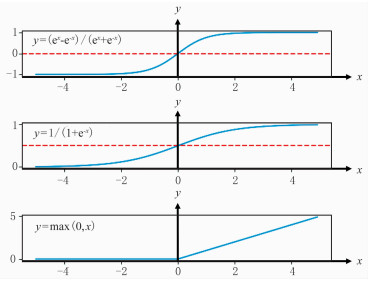
图 2示意了一种多层感知机网络结构,输入层为3分量,输出层为1分量,具有4层隐含层,每层包含4个神经元。f(x)代表激活函数,可以为Sigmoid、Tanh或者ReLu函数中的一种,其表达式及函数形态如图 3所示。激活函数的作用是向学习网络中引入非线性运算,使网络能够逼近任何非线性函数,大幅度提升模型泛化能力。目前使用最广泛的是ReLu激活函数,相比于Sigmoid、Tanh函数,避免了“梯度消失”缺陷,即x取值很大以后,y对x的增大不再敏感。

|
图 2 多层感知机深度学习网络结构示意图 |
|
图 3 Tanh(上)、Sigmoid(中)、ReLu(下)三种激活函数的解析表达式及其形态 |
以图 2所示网络结构为例,第1个隐含层的4个神经元与输入层3个分量(x1,x2,x3)的解析表达式为
| $ z_j^1 = f\left[ {\sum\limits_{i = 1}^{{N_x}} {({w_{i, j, 1}}{x_i} + {b_{i, j, 1}})} }\right] $ | (3) |
式中:zj1表示第1个隐含层上的第j个神经元,j=1、2、3、4;Nx为输入层维度,本例中Nx=3;xi为输入层第i个分量;wi, j, 1是输入层第i个分量与第1个隐含层上第j个神经元的连接权重。向后继续传播时,以zj1作为新的输入,对式(3)依次递归,可得各隐含层各个神经节点的计算结果
| $ z_j^k = f\left[ {\sum\limits_{i = 1}^{{N_z}} {({w_{i, j, k}}z_i^{k - 1} + {b_{i, j, k}})} } \right] $ | (4) |
式中:zjk代表第k(k>1)个隐含层上的第j个神经元;Nz代表第k-1个隐含层包含的神经元总数,本例中Nz=4;wi, j, k为第k-1个隐含层上第i个分量与第k个隐含层上第j个神经元的连接权重。由式(4)进一步得到输出层的解析表达式
| $ {y_j} = f\left[{\sum\limits_{i = 1}^{{N_z}} {({w_{i, j, M}}z_i^M + {b_{i, j, M}})} }\right] $ | (5) |
式中:yj代表输出层第j个分量;M为隐含层总层数。本例中j≡1、M=4。结合式(3)~式(5),可建立多层感知机网络结构的由输入x到输出y的正演模型。
MLP模型中待求解参数是连接权重wi,j,k和偏置常数bi,j,k。首先通过预测误差最小二乘准则及正则化约束条件建立MLP模型凸优化目标泛函
| $ \mathop {{\rm{min}}}\limits_{{w_{i, j, k}}, {b_{i, j, k}}} \left[ {\sum\limits_{i = 1}^{{N_z}} {{{({d_i} - {y_i})}^2}} + \mu ({\rm{ }}\sum {w_{i, j, k}^2} + \sum {b_{i, j, k}^2} )} \right] $ | (6) |
式中:di代表真实值;yi为预测值。该方程采用误差反向传播(Back Propagation,BP)策略进行求解(图 4)。多层感知机网络由于具有多隐含层、多神经节点以及激活函数等模块,非线性表征能力、模型泛化能力及预测精度较经典神经网络模型均有显著提升。

|
图 4 多层感知机深度学习网络求解算法流程 |
将多层感知机深度学习网络移植于地震多属性回归方法,可以预测砂岩薄储层。
1.3.1 输入属性传统多属性回归方法常以地震数据及反演的阻抗体作为输入,加入阻抗体的目的是提升预测结果与测井参数的吻合程度。然而,由于阻抗反演过程中子波提取、时深标定、模型插值、反演参数等环节引起的不确定性误差,容易造成多属性回归结果过于模型化,井间预测结果合理性不足。
地震90°相移技术已被证实在储层结构相对简单的条件下(泥包砂)能够较理想地描述λ/4~λ(波长)厚度的薄储层[27]。与地震反演技术相比,该技术高效、简单。更为重要的是,90°相移技术完全基于地震数据而不破坏地震信息的保幅和保真处理。基于此,本文提出以地震90°相移数据代替阻抗,作为提供储层结构近似信息的外部属性,加入到多属性回归方法中。
范廷恩[28]提出的储层不连续界限地震属性能够表征沉积作用、成岩改造及构造运动等因素形成的岩性尖灭、砂体叠置、物性变化及小断层等,本文将储层不连续界限属性作为多属性回归输入之一,分析储层空间展布。
1.3.2 预测目标传统多属性回归方法常需要对预测目标参数(如密度、自然伽马等)进行低通滤波以匹配井震频率,提高训练结果与测井实际资料的吻合程度,但这种做法降低了预测结果的分辨率,不利于薄储层预测。
由于测井资料采样率为0.125m,有效高截频至少在150Hz以上;以40Hz主频、0~60Hz有效频带地震资料为例,传统多属性回归方法预测结果难以包含测井资料携带的60~150Hz高频信息。很多油田砂岩薄储层厚度在10m以下,如果以渤海地区2.5km/s地层速度估算,分辨10m薄层需要地震视主频至少达到65Hz以上,这使传统多属性回归方法应用受限。
多层感知机深度学习网络具有高度非线性特征,一定程度上能够学习到由低频数据到高频信息之间的模型表征。本文以有效高截频(150Hz)以内的测井数据为预测目标,建立由有限带宽地震数据到高频测井数据的映射,以期改善预测结果纵向分辨率,提升薄储层刻画能力。
1.3.3 数据预处理深度学习网络对数据的分布规律相当敏感,一般要求输入数据与期望输出都服从(0,1)正态分布。本文采用以下步骤进行数据预处理:
(1) 测井数据标准化,保证训练集与验证集自然伽马曲线的泥岩基线基本一致;
(2) 输入数据与期望输出的归一化,采用u1=[u0-mean(u0)]/std(u0)(u0为原始数据,u1为归一化结果,mean、std分别为均值、方差函数)的归一化方式,依次实现对输入属性(地震数据、90°相移数据、储层不连续界限属性)与期望输出(训练集和验证集的自然伽马测井数据)的归一化处理,保证输入与输出服从(0,1)正态分布。
1.3.4 样本规模与模型评价训练样本的多样性直接影响深度学习算法中模型的泛化能力。以不同钻遇结果和钻遇靶点尽可能覆盖研究区为训练集组成原则,建立类型丰富的训练样本,样本规模达到10口井以上。
此外,将数据样本划分为训练集和测试集,基于前者训练模型,再利用后者的预测结果与实际数据的误差评估模型。
1.3.5 模型建立以叠前时间偏移数据及其90°相移数据、相移数据的储层不连续界限属性为输入,井点高频自然伽马数据为期望输出。10口井组成训练集,两口井组成验证集。通过试错法在小规模数据集上试验,确定具有7个隐含层,每层15个神经元的多层感知机深度学习网络具有最佳效果,同时采用ReLu激活函数搭建深度学习网络,预测井间自然伽马值。
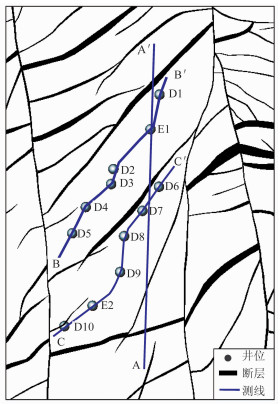
2 测试实例利用中国A油田实际资料测试该方法。A油田位于渤海海域,井网密集(图 5),馆陶组上段(L40~L80,图 6)砂泥岩薄互层发育,单砂体厚度不足5m。选取12口井,其中探井两口(E1井、E2井),定向开发井10口(D1井~D10井)(图 5)。
|
图 5 研究区井点分布及地震测线位置 |
|
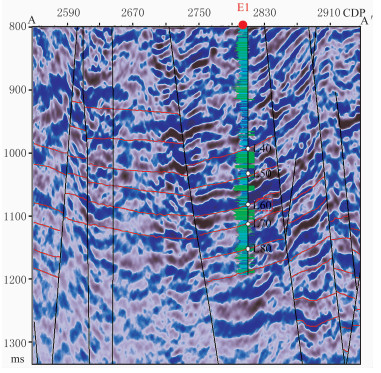
图 7 AA′线90°相移剖面 |
|
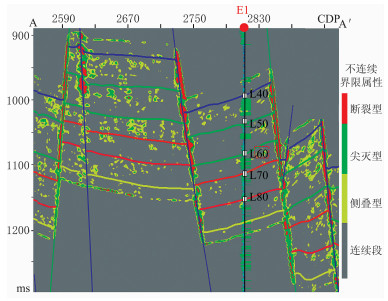
图 8 AA′线不连续界限属性剖面 |

|
图 11 BB′线90°相移剖面(a)与预测自然伽马剖面(b)对比 |
|
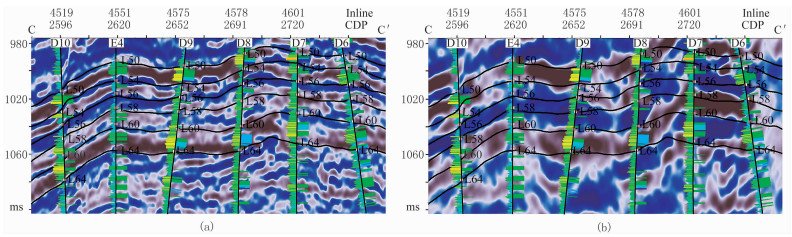
图 12 CC′线小层顶面解释结果 (a)自然伽马剖面;(b)90°相移剖面 |
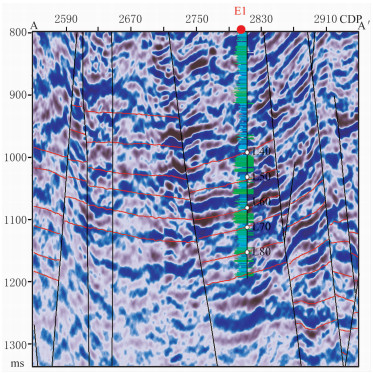
对比叠前地震时间偏移剖面(图 6)与其90°相移剖面(图 7),可见90°相移剖面与L50段相对较厚的储层对应关系较好,反射波谷能够代表砂岩响应。但对于L60、L80段薄互层,波谷对应整套复合砂体的响应,依靠相移剖面难以识别其中的单砂体。基于90°相移数据提取的不连续界限属性(图 8)能够刻画三类不连续界限,即断裂(红色)、尖灭型砂体接触关系(绿色)、叠置型或侧叠型砂体接触关系(黄色),以及图 8中灰色表示的连续层段。对比图 8与图 7方框区域可知,E1井测井解释结果表明L60层段多期砂体叠置,引起90°相移剖面上地震反射产状与振幅能量发生改变,而不连续界限属性表现为砂体尖灭型与侧叠型接触关系,与相移剖面信息吻合。
2.2 模型训练本文以1口探井(E1井)和9口开发井(D1~D5井、D7~D9井)作为训练集,1口探井(E2井)和1口开发井(D6井)作为验证集,利用多层感知机深度学习网络训练模型,预测L40~L80段自然伽马值。
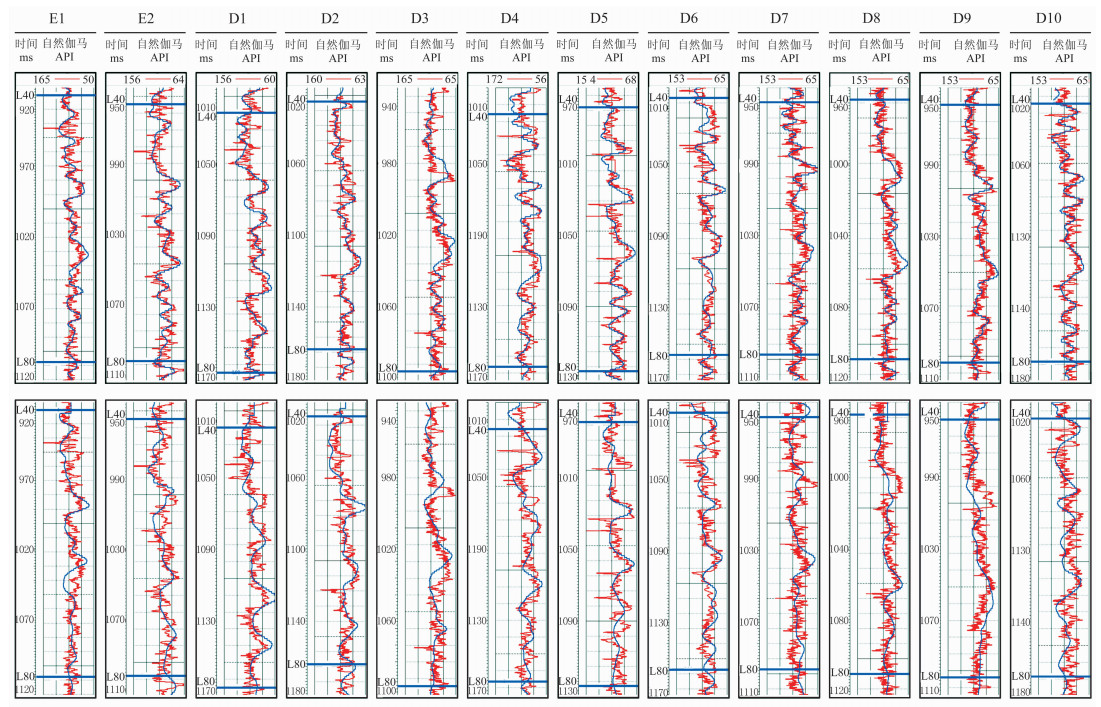
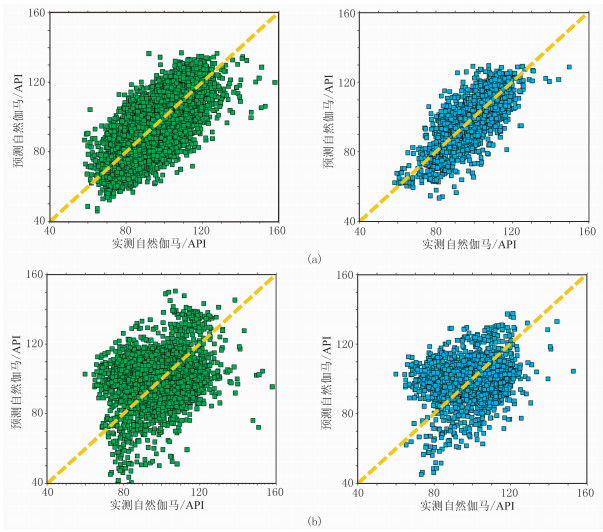
由图 9可知,深度学习模型训练集和验证集的预测结果与实测结果吻合较好,未出现过拟合(图 9上);采用传统多属性回归方法建立的模型在各井的预测结果与实测吻合程度不如前者(图 9下)。图 10进一步揭示了深度学习模型预测效果明显优于传统多属性回归方法,前者预测值与真实值平均相关系数达到86.4%(训练集)和85.5%(验证集),而传统多属性回归结果预测值与真实值平均相关系数仅为65.1%(训练集)和59.3%(验证集)。
|
图 9 多层感知机学习网络(上)与传统属性回归模型(下)的真实值(红线)与预测值(蓝线)对比 |
|
图 10 多层感知机网络(a)与传统多属性回归模型(b)训练集(左)、验证集(右)自然伽马预测值与实测值交会对比 黄色虚线代表y=x线,越靠近该线说明预测值越接近实测值 |
通过联井剖面可评估多层感知机模型井间自然伽马预测效果。由图 11可知,自然伽马剖面较90°相移剖面垂向分辨率有较大程度提升,并与实钻结果较吻合,同时反射同向轴横向连续性较好。图 11b剖面中红色虚线框标记的一套储层在90°相移剖面难以识别,而自然伽马剖面满足砂体解释精度要求,可以进一步精细刻画该砂体。
3 应用效果 3.1 小层解释应用自然伽马数据体对L50~L60储层段开展小层研究,精细解释L50、L54、L56、L58、L60、L64等6套小层顶面层位(图 12)。
从图 12可以看出,自然伽马剖面与钻井各小层岩性解释结果吻合度较高,基本可以预测薄储层;在90°相移剖面上,L50、L54、L56、L58、L60等5套小层顶面较难追踪解释。由于L60~L64小层储层厚度较大,在相移数据中能够追踪解释L64顶面,但自然伽马剖面反映的L60~L64储层视厚度与钻井岩性解释厚度视觉上更为吻合。
3.2 储层展布研究应用自然伽马数据体解释的小层顶面开展储层平面展布研究,本文展示L54~L56层储层预测成果。
分别提取基于自然伽马数据体与相移数据体的沿层敏感属性(总负振幅),与训练集和测试集12口井钻遇的累计砂岩厚度叠合(图 13)。由图可知,自然伽马数据体对于薄储层刻画能力明显优于90°相移数据体,在研究区中央断层以北区域尤为突出。D5、D4、D3、D2、E1、D1等井实钻累计砂岩厚度与自然伽马数据体总负振幅属性均有较好对应关系,而在90°相移数据中,上述6口井二者之间对应关系较差。中央断层以南,在D6、D7、D8、D9井东南侧,自然伽马数据体总负振幅属性可见河道外形。除D8井累计砂岩厚度与自然伽马数据体总负属性对应关系较差之外,断层以南其余5口井累计砂岩厚度与自然伽马数据体总负振幅属性均对应较好;90°相移数据体总负振幅属性与这6口井累积厚度对应关系普遍较差。D8井自然伽马与砂岩厚度对应较差的原因可能是在该井附近由于波峰消失导致了L54层位解释(追踪波峰)偏高(图 12a)。

|
图 13 L54~L56层总负振幅属性与井点砂岩厚度叠合 (a)自然伽马数据;(b)90°相移数据。井号下数值为小层砂岩厚度,单位为m |
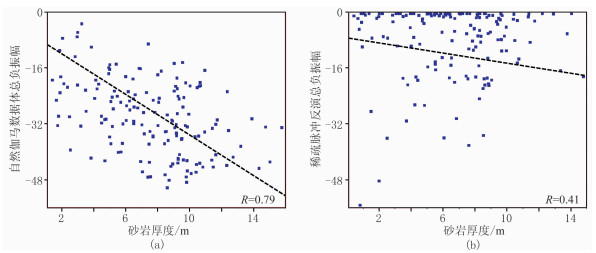
研究区其余共156口井在L54~L56小层钻遇砂岩厚度与总负振幅属性值的相关程度如图 14所示。由图可知,自然伽马数据体总负振幅属性与砂岩厚度相关程度更好,90°相移数据体总负振幅属性对砂岩厚度不敏感。自然伽马数据体总负振幅属性与砂岩厚度的相关系数比90°相移数据体的高约38%。考虑到本文训练只采用了10口井的训练样本,样本数量与类型对于预测全工区156口大斜度定向井而言仍然能力有限,还存在较大提升空间。
|
图 14 L54~L56小层156口井砂岩厚度与自然伽马数据体(a)、90°相移数据体(b)总负振幅属性交会图 R为相关系数 |
基于深度学习的多属性回归方法结果分辨率更高,模型泛化能力更强。运用该方法预测砂岩薄储层,在提升薄层刻画能力与保证井间储层连续性方面优势较为明显。基于多层感知机深度学习网络的薄储层预测方法效果较好,储层敏感属性与井点砂岩厚度相关性提升较为明显。由于文中只采用10口井的训练样本,在样本数量与多样性方面都还存在进一步升级优化的潜力。未来将尝试采用规模更大、类型更丰富的钻井样本,同时考虑利用叠前深度偏移资料直接在深度域学习,可进一步提升薄层预测表征精度。
| [1] |
王延光, 李皓, 李国发, 等. 一种用于薄层和薄互层砂体厚度估算的复合地震属性[J]. 石油地球物理勘探, 2020, 55(1): 153-160. WANG Yanguang, LI Hao, LI Guofa, et al. A composite seismic attribute used to estimate the sand thickness for thin bed and thin interbed[J]. Oil Geophysical Prospecting, 2020, 55(1): 153-160. |
| [2] |
徐丽英, 徐鸣洁, 陈振岩. 利用谱分解技术进行薄储层预测[J]. 石油地球物理勘探, 2006, 41(3): 299-302. XU Liying, XU Mingjie, CHEN Zhenyan. Using spectrum decomposition technique for prediction of thin reservoir[J]. Oil Geophysical Prospecting, 2006, 41(3): 299-302. |
| [3] |
孙学栋, 赵建儒, 白军, 等. 谱分解技术在营尔凹陷长沙岭地区薄储层预测中的应用[J]. 石油地球物理勘探, 2011, 46(增刊1): 72-75. SUN Xuedong, ZHAO Jianru, BAI Jun, et al. Spectrum decomposition application in thin-reservoir prediction in Changshaling belt, Yinger Depression[J]. Oil Geophysical Prospecting, 2011, 46(S1): 72-75. |
| [4] |
Du X, Li G, Zhang M, et al. Multichannel band-controlled deconvolution based on a data-driven structural regularization[J]. Geophysics, 2018, 83(5): R401-R411. DOI:10.1190/geo2017-0516.1 |
| [5] |
王香文, 刘红, 滕彬彬, 等. 地质统计学反演技术在薄储层预测中的应用[J]. 石油与天然气地质, 2012, 33(5): 730-735. WANG Xiangwen, LIU Hong, TENG Binbin, et al. Application of geostatistical in inversion to thin reservoir prediction[J]. Oil & Gas Geology, 2012, 33(5): 730-735. |
| [6] |
张义, 尹艳树, 秦志勇. 地质统计学反演在薄砂体储层预测中的应用[J]. 断块油气田, 2015, 22(5): 565-569. ZHANG Yi, YIN Yanshu, QIN Zhiyong. Application of geostatistical inversion in thin sandstone reservoir prediction[J]. Fault-Block Oil & Gas Field, 2015, 22(5): 565-569. |
| [7] |
沈洪涛, 郭乃川, 秦童, 等. 地质统计学反演技术在超薄储层预测中的应用[J]. 地球物理学进展, 2017, 32(1): 248-253. SHEN Hongtao, GUO Naichuan, QIN Tong, et al. Application of geostatistical inversion for super thin reservoir prediction[J]. Progress in Geophysics, 2017, 32(1): 248-253. |
| [8] |
高君, 毕建军, 赵海山, 等. 地震波形指示反演薄储层预测技术及其应用[J]. 地球物理学进展, 2017, 32(1): 142-145. GAO Jun, BI Jianjun, ZHAO Haishan, et al. Seismic waveform inversion technology and application of thinner reservoir prediction[J]. Progress in Geophy-sics, 2017, 32(1): 142-145. |
| [9] |
蔡冬梅, 赵弟江, 彭靖松, 等. 优质烃源岩识别及其多属性反演技术定量评价——以渤海海域辽东南洼陷为例[J]. 石油地球物理勘探, 2018, 53(2): 330-338. CAI Dongmei, ZHAO Dijiang, PENG Jinsong, et al. High-quality hydrocarbon source rock identification and quantitative evaluation with multi-attribute inversion:A case study of Liaodong south sub-sag, Bohai Bay Basin[J]. Oil Geophysical Prospecting, 2018, 53(2): 330-338. |
| [10] |
张显文, 曹树春, 聂妍, 等. 地震多属性孔隙因子参数反演及其在伊拉克M油田碳酸盐岩储层预测中的应用[J]. 石油物探, 2018, 57(5): 756-763. ZHANG Xianwen, CAO Shuchun, NIE Yan, et al. Seismic multi-attribute inversion for pore-sensitive factor and its application in carbonate reservoir prediction of M oilfield in Iraq[J]. Geophysical Prospecting for Petroleum, 2018, 57(5): 756-763. |
| [11] |
张晶玉, 范廷恩, 王宗俊, 等. 多属性储层参数反演方法在M油田中的应用[J]. 油气藏评价与开发, 2019, 9(1): 8-14. ZHANG Jingyu, FAN Ting'en, WANG Zongjun, et al. Application of reservoir parameters inversion method by using multi-attributes in M oilfield[J]. Reservoir Evaluation and Development, 2019, 9(1): 8-14. |
| [12] |
Krizhevsky A, Sutskever I, and Hinton G E. Imagenet classification with deep convolutional neural networks[J]. Advances in Neural Information Processing Systems, 2012, 25(2): 1097-1105. |
| [13] |
Zeiler M D and Fergus R.Visualizing and understanding convolutional networks[C].European Conference on Computer Vision, 2014, 818-833.
|
| [14] |
Girshick R, Donahue J, Darrell T, et al.Rich feature hie-rarchies for accurate object detection and semantic segmentation[C].Proceedings of the IEEE Confe-rence on Computer Vision and Pattern Recognition, 2014, 580-587.
|
| [15] |
Ren S, He K, Girshick R, et al. Faster R-CNN:to-wards real-time object detection with region proposal networks[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(6): 1137-1149. DOI:10.1109/TPAMI.2016.2577031 |
| [16] |
Ronneberger O, Fischer P, and Brox T.U-net: Con-volutional networks for biomedical image segmentation[C].International Conference on Medical Image Computing and Computer-Assisted Intervention, 2012, 234-241.
|
| [17] |
Badrinarayanan V, Kendall A, and Cipolla R. Segnet:A deep convolutional encoder-decoder architecture for image segmentation[J]. IEEE Transactions on Pattern Analysis and Machine Intelligence, 2017, 39(12): 2481-2495. DOI:10.1109/TPAMI.2016.2644615 |
| [18] |
Yuan S, Liu J, and Wang S X. Seismic waveform classification and first-break picking using convolution neural networks[J]. IEEE Geoscience & Remote Sensing Letters, 2018, 15(2): 272-276. |
| [19] |
韩卫雪, 周亚同, 池越. 基于深度学习卷积神经网络的地震数据随机噪声去除[J]. 石油物探, 2018, 57(6): 862-869. HAN Weixue, ZHOU Yatong, CHI Yue. Deep lear-ning convolutional neural networks for random noise attenuation in seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 862-869. |
| [20] |
Deng L, Yuan S Y, Wang S X. Sparse Bayesian lear-ning-based seismic denoise by using physical wavelet as basis functions[J]. IEEE Geoscience & Remote Sensing Letters, 2017, 14(11): 1993-1997. |
| [21] |
Wu X M, Shi Y Z, Fomel S, et al. Fault Net 3D:predicting fault probabilities, strikes, and dips with a single convolutional neural network[J]. IEEE Transactions on Geoscience Remote Sensing, 2019, 57(11): 9138-9155. DOI:10.1109/TGRS.2019.2925003 |
| [22] |
Shi Y Z, Wu X M, Fomel S. Saltseg:automatic 3D salt segmentation using a deep convolutional neural network[J]. Interpretation, 2019, 7(3): SE113-SE122. DOI:10.1190/INT-2018-0235.1 |
| [23] |
Yang F, Ma J. Deep-learning inversion:a next-gene-ration seismic velocity model building method[J]. Geophysics, 2019, 84(4): R583-R599. DOI:10.1190/geo2018-0249.1 |
| [24] |
Li S C, Liu B, Ren Y X, et al.Deep learning inversion of seismic data[DB/OL].arXiv: 1901.07733, 2019. doi: 10.1109/TGRS.201902953473.
|
| [25] |
刘力辉, 陆蓉, 杨文魁. 基于深度学习的地震岩相反演方法[J]. 石油物探, 2019, 58(1): 123-129. LIU Lihui, LU Rong, YANG Wenkui. Seismic lithofacies inversion based on deep learning[J]. Geophysical Prospecting for Petroleum, 2019, 58(1): 123-129. |
| [26] |
Zeng H, Backus M M. Interpretive advantages of 90°-phase wavelets, Part 1:Modeling[J]. Geophysics, 2005, 70(3): C5-C15. |
| [27] |
Zeng H, Backus M M. Interpretive advantages of 90°-phase wavelets, Part 2:Seismic applications[J]. Geophysics, 2005, 70(3): C17-C24. |
| [28] |
范廷恩.点坝砂体储层内部不连续界线类型及预测方法研究[D].四川成都: 西南石油大学, 2016. FAN Ting'en.The Discontinuous Boundary of Thin Fluvial Reservoir and Its Prediction[D].Southwest Petroleum University, Chengdu, Sichuan, 2016. |



 杜昕, 北京市朝阳区太阳宫南街6号院中海油研究总院有限责任公司, 100020。Email:
杜昕, 北京市朝阳区太阳宫南街6号院中海油研究总院有限责任公司, 100020。Email: