② 地球内部多尺度成像湖北省重点实验室, 湖北武汉 430074;
③ 中国石化胜利油田分公司勘探开发研究院, 山东东营 257015;
④ 中石化工程地球物理有限公司华北分公司, 河南郑州 450000
② Hubei Key Labrotary for Subsurface Multi-scale Imaging, China University of Geosciences, Wuhan, Hubei 430074, China;
③ Research Institute of Exploration & Development, Sinopec Shengli Oilfield Comopany, Dong-ying, Shandong 257015, China;
④ North China Branch, Sinopec Engineering Geophysics Co., Ltd., Zhengzhou, Henan 450000, China
地震相可以理解为沉积相在地震资料上反射特征的总和,为分析地质条件和预测油气藏提供了参考。早期的地震相分析通常需要解释人员根据专业知识与地区经验,以人的视觉为基础,通过地震波运动学几何特征参数进行地震相识别[1-2];或是根据客观的地震属性[3],按一定的程序对地震相单元进行识别和作图。这些传统的地震相识别方法通常需要大量的人工操作,并且结果不可避免地受到一些主观因素的影响。因此, 有必要研究一种快速有效的地震相分类方法, 减少地震资料解释人员的人工操作。
近年来,深度学习技术在计算机视觉等领域取得了重大进展,基于地震资料解释与计算机视觉间的相似性,许多学者使用能够自动提取有用特征的卷积神经网络(CNN)进行地震相的分类及预测。段玉顺等[4]运用人工神经网络分析技术对地震道波形及其反映的地质特征进行自动识别和分类;Jesper[5]使用VGG16网络模型识别地震相;Zhao[6]使用编码—解码模型对小块数据进行地震相分类;Lei等[7]使用了一种基于循环神经网络的地震波形分类方法,对地震相进行分类;Qi等[8]将地震属性与机器学习技术相结合,从而达到地震相预测的目的。这些用于地震相识别的CNN架构大多是在卷积层之后附加全连接层,只能进行图像级别的地震相分类及预测,或是选择局部窗口遍历地震图像上的每个像素以进行预测,精度有限且消耗大量的计算时间。因此,用于解决语义分割问题的全卷积神经网络(FCN)开始被应用于地震资料智能解释之中。
FCN模型全部采用卷积层结构。Wu等[9]、Shi等[10]首先将带有跳跃连接结构的U-Net模型分别应用于断层识别和盐丘识别,结果表明基于图像分割技术的U-Net模型对于叠后地震数据的目标检测具有良好的效果。之后,Alaudah等[11]提出用一种弱监督学习方法预测地震相,可以大幅度地减少人工制作标签数据的耗时,但其识别精度远低于主流的强监督学习。Mukhopadhyay等[12]使用了基于贝叶斯SegNet模型的深度学习方法,能够在识别地震相的同时评判预测结果的不确定性,但贝叶斯深度学习方法会消耗大量的计算时间,不适用于大型数据。Zhang等[13]使用了在图像分割领域较先进的DeepLab v3+模型,对F3工区进行地震相识别并取得了良好的效果,但该网络模型结构复杂,参数较多,更胜任具有大量训练数据的复杂图像分割任务,相较一些轻量级网络模型而言泛化性较差。
上述图像分割技术所用框架均基于FCN模型,在识别地震相时,虽然可以有效地提取地震相的边缘、纹理等绝对特征,但忽略了存在于图像中相邻像素之间的约束关系,无法有效地处理场景之间的关系和全局信息。不同于识别盐丘、断层这类在地震剖面上与背景围岩具有明显差异的二分类目标,图像分割技术在地震相识别中存在以下问题:①地震相识别需要分类的种类较多,且不同地震相之间可能会存在相似的地震波场特征,仅根据视觉纹理特征难以区分;②地震相分布遵循沉积规律,在纵向上具有一定的空间分布特征,判别地震相时,需要参考其所在空间位置,而上述网络模型缺乏这种获取空间先验信息的能力;③地震相的边界往往是不同沉积层的交界,也是岩石矿物质逐渐转变的过渡带,模型对地震相边界的识别结果具有较高的不确定性,这一方面会影响模型对边界识别的效果,另一方面,现有地震相识别技术缺乏一个关于预测结果不确定性的评价体系。基于以上问题,本文提出一套适用于地震相识别和预测评价的深度学习方法。
本文对U-Net模型进行了改进,在网络末端加入一种金字塔池化模块(Pyramid Pooling Module,PPM),该模块由多种不同尺度的卷积核组成,可以提取不同等级的特征信息,使模型能够并行考虑多个接收域下的目标特征,获取包含不同尺度、不同子区域间关系的分层信息,从而更综合地考虑地震剖面各个深度上的全局空间信息。同时,对目标函数进行了改进,在交叉熵函数(用于评价每个像素点分类准确性)基础上,添加了用于评价图像分割效果的Dice指数,该指数衡量预测样本与真实样本之间的重叠程度。将两部分函数通过加权组合在一起,一并更新梯度,既能保证地震相分类的正确性又能保证少数类地震相边界刻画的准确性。最后,针对现有深度学习技术缺乏对模型预测结果的不确定性分析的情形,本文提出用“预测信息熵”这一概念进行评估与可视化展现。
1 方法原理 1.1 模型构建地震相的空间分布存在一定的规律,所以地震剖面上空间分布的先验信息,对于地震相划分起着至关重要的作用。传统的卷积神经网络因其结构所限,信息流动局限在当前像素周围的局部区域中,对于获取空间位置这种大范围的上、下文信息和表达能力有限。为了弥补先验信息的不足,本文选择了一种适用于地震相分类识别的深度学习网络模型——U-Net模型,该模型特有的跳跃结构能够融合浅层与深层信息,在处理叠后地震数据目标识别问题时具有优秀的表现[9-10],且网络结构相对简单,参数较少,不易导致过拟合。因此,本次试验选择U-Net模型为基础模型,并在末端加入一种能融合多尺度特征的PPM模块[14],其具体结构如图 1所示。

|
图 1 用于地震相分类识别的全卷积神经网络模型 |
图 1中每个立方体展示了输入地震剖面在经过各层后输出的特征图的维度及尺寸。该网络模型以U-Net模型[5]为框架,分为编码和解码两部分。编码部分每层包含卷积核尺寸为3×3的两个卷积层以及池化核尺寸为2×2的一个最大池化层,输入地震剖面在经过编码部分每层的计算后,图像尺寸逐层减半,通道数逐层翻倍直至1024;解码部分每层包含核尺寸为3×3的两个卷积层及核尺寸为2×2的一个上采样层,可将特征图的尺寸还原到原始大小,并将通道数从1024依次压缩到64。在深度神经网络中,浅层网络输出的特征图分辨率高,保留有更多细节信息;深层网络学习输出的特征则更加抽象,保留了更多语义信息。U-Net模型在解码部分将网络中具有相同尺寸的特征图通过跳跃结构(蓝色箭头)进行连接,从而改善上采样过程中信息不足的问题。
输入地震剖面在经过U-Net模型的编码—解码过程后,提取出较为精确的地震相纹理特征。在深度神经网络中,接收域的大小可以在一定程度上体现模型使用的上、下文信息量[14]。但U-Net等大多数网络模型只能提取单一接收域大小的目标特征,这使网络结构无法充分获取重要的上、下文信息。因此,希望改进后的网络能并行考虑多个接收域的目标特征,获取包含不同尺度、不同子区域间关系的分层全局信息。
为了解决上述问题,本文在U-Net模型中添加了PPM模块,即将之前提取的特征图分别经过不同尺寸的平均池化层,输出尺寸为1×1、2×2、3×3、6×6四个等级的特征图,其中最粗糙的1×1平均池化是全局尺度的池化,其余层次的池化层会将特征图划分为不同子区域,并分别带有不同程度的语义信息和边缘精度信息,最终结合起来可展现较完整的空间信息。为了保证全局特征的权重,四个级别的特征图经由1×1的卷积核将通道数分别降为原来的1/4,再分别通过上采样获得未池化前的尺寸,与未经过PPM模块的特征图合并在一起。在经过最终的卷积层后,输出每一像素点上对应的地震相分类结果。
模型中所有的上采样过程均采用双线性插值。改进后的网络模型在保证U-Net模型分类精度的基础上,通过PPM模块提取不同等级的特征信息,聚合了不同区域的上、下文信息,提高了模型获取全局信息的能力。
1.2 混合损失函数在神经网络的训练中,能够评估网络性能的函数被称为目标函数或损失函数。本文深度学习模型所处理的问题可以被看成一个逐像素点的地震图像多分类任务。传统的多分类问题一般使用多元交叉熵损失函数[15],但该损失函数是逐像素计算,不考虑邻域的标签,对于在数据中占比较少的地震相分割效果较差。因此,本文所用的目标函数在传统多元交叉熵损失函数的基础上加入了Dice指数损失函数[16],分别用于评价模型对每一像素点的分类效果与整体图像分割效果。多元交叉熵(LCE)损失函数表达式为
| $ \left\{ \begin{array}{l} {L_{{\rm{CE}}}} = - \sum\limits_{c = 1}^C {\sum\limits_{n = 1}^N {{y_{c, n}}\lg \left( {{p_{c, n}}} \right)} } \\ {p_{c, n}} = \frac{{{{\rm{e}}^{{z_{c, n}}}}}}{{\sum\limits_{c = 1}^C {{{\rm{e}}^{{z_{c, n}}}}} }} \end{array} \right. $ | (1) |
式中:C为地震相的总类数;N为输入地震剖面上所包含的像素点总数;yc, n为标签数据,即实际地震剖面上第n个像素点是否为第c类地震相,若是则为1,不是则为0;zc, n为神经网络最终输出的结果,其物理意义可以理解为该点被预测为第c类地震相的可能性;pc, n是对zc, n进行softmax函数归一化后的结果,使其值分布于0到1之间,更加符合概率的意义。
由式(1)可见,交叉熵损失函数将每一个像素点都视作独立的存在,分别计算每个像素点的交叉熵并求和,这使该损失函数不能把握全局的信息,导致分割出来的地震相形状与真实值差异较大,边界分割效果较差。尤其被用于不均衡数据集的预测时,为了使交叉熵函数更容易达到最小值,模型会倾向于把最大的权重分给数量最多的类别,最终导致模型忽略占比较小的地震相特征。在实际地震剖面上,占比较小的地震相往往是盐丘等异常体,数量虽少但尤为重要。因此,本文引入可以评价整体分割效果的Dice损失函数解决上述问题。Dice指数是一种集合相似度度量函数,可以体现两个区域轮廓的相似程度,取值范围为[0, 1],表达式为
| $ {\rm{Dice}}\left( {\mathit{\boldsymbol{A}}, \mathit{\boldsymbol{B}}} \right) = 1 - 2\frac{{|\mathit{\boldsymbol{A}} \cap \mathit{\boldsymbol{B}}|}}{{|\mathit{\boldsymbol{A}}| + |\mathit{\boldsymbol{B}}|}} $ | (2) |
式中:A∩B为A和B之间的交集;|A|和|B|分别为A和B的元素的个数。用于地震相预测时,Dice损失函数可以写作如下形式
| $ {L_{{\rm{Dice}}}} = \sum\limits_{c = 1}^C {\frac{1}{N}} {\rm{ }}\left( 1 - 2{\frac{{\sum\limits_{n = 1}^N {{p_{c, n}}{y_{c, n}} + \varepsilon } }}{{{\rm{ }}\sum\limits_{n = 1}^N {{p_{c, n}}} + {\rm{ }}\sum\limits_{n = 1}^N {{y_{c, n}} + \varepsilon } }}} \right) $ | (3) |
式中ε为平滑值,本次研究取值为1,在防止分母为0的同时也可以防止模型的过拟合。
Dice损失函数通过计算分类概率图和真实分割图中所有像素点的误差,最大程度地衡量两者相似性,使预测结果与标签尽可能重合。一方面减小不均衡数据对模型训练的影响,另一方面有助于分割出来的地震相边界变得相对清晰,且形状与真实值相似,增强地震相边界的分割效果。最终的目标函数Lloss为式(1)与式(3)的线性加权组合,即
| $ {L_{{\rm{loss}}}} = {L_{{\rm{CE}}}} + e{L_{{\rm{Dice}}}} $ | (4) |
式中e为Dice损失函数的权重。
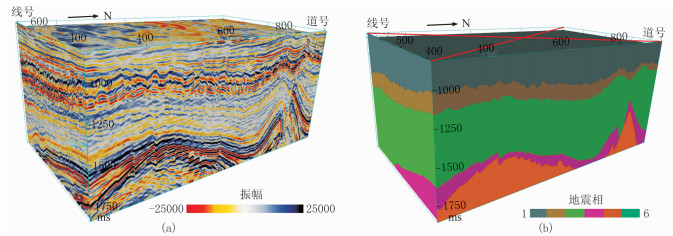
2 应用实例实验训练数据选用北海F3工区公开数据。该工区位于荷兰北部,发育大型河控三角洲体系。主测线从100到700,共600条剖面,701道。从地震剖面上可以识别一些地震反射结构:空白反射、杂乱反射、平行—亚平行反射、叠瓦状反射等。测井资料显示空白反射结构由岩性均一的砂岩或泥岩构成;杂乱反射结构表示滑塌沉积;斜坡沉积底部的叠瓦状反射结构显示为砂质浊积岩[17]。如图 2所示,参考F3工区测井资料对三维地震数据体进行人工地震相解释,以此作为训练数据的标签,主要根据岩性差异对地震相进行分类。将工区数据体中的300到700号剖面作为训练集;100到299号剖面作为测试集,用于评估模型的预测效果。
|
图 2 F3工区训练数据 (a)三维地震数据体;(b)地震相标签 |
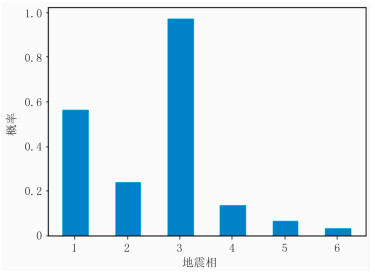
现有的深度学习方法会对训练数据进行翻转、镜像复制等数据增广操作,以增加样本的数量和多样性,但这种方法应用于地震相数据时会破坏地震相原有的形态与空间分布规律。一方面,随着地层深度的增加地震波会逐渐衰减,导致主频降低;另一方面,一些本该出现在深层的地震相在经翻转后会出现在浅层,从而违背地质沉积规律。因此,沿三维数据体的主测线、联络测线、SW-NE、NW-SE四个方向划分出二维地震剖面,再在每一条地震剖面上选取尺寸为256×256大小的窗口,通过选取不同的重叠步长滑动截取所需的训练数据,在保证遵循地震相空间分布规律的基础上增加样本的多样性。为了加快目标函数收敛,对训练数据中所有地震数据的振幅值进行标准化处理,使其值域在-1到1之间。本文在训练集中共截取了3005组数据,标签中共包含6类地震相,各类地震相出现概率归一化后的分布情况如图 3所示。
|
图 3 训练数据各地震相出现概率分布直方图 |
由于各个地震相标签的数值之间不存在连续性关系,所以在训练前需将标签数据转化为独热编码,以增强其稀疏性。对于地震剖面上第n个像素点,其独热编码标签yn可以用一个由0、1组成,大小为1×C的向量表示,即yn=[y1, n, …, yc, n, …, yC, n],若该点实际地震相为c,则对应yc, n的值为1,其余的值为0。各类地震相标签与对应的独热编码如表 1所示。
|
|
表 1 地震相标签与对应的独热编码 |
为了对比评价改进前、后网络模型与目标函数的效果,设计了一系列对比试验。首先设置一组常规U-Net模型作为对照,为了保证对照模型的网络层数与所含参数量级相同,常规U-Net网络仅将改进后网络的PPM部分替换为相同数量的卷积层。将训练集中的地震数据和对应的地震相标签分别成对输入至两组深度网络模型中,进行正向传播与反向传播,计算网络的损失函数值,更新网络的可调整参数,并通过迭代训练令损失函数值越来越小。当损失函数值降低到较小值并且基本不再变化时,说明该模型已经达到收敛。本次训练采用Adam优化算法[18],学习率设置为1×10-4。改进目标函数中需要人工调试的参数只有Dice项的权重e,这里分别取0(即目标函数中不含Dice指数项)、0.01、0.05、0.10,损失函数值随迭代次数的变化曲线对比如图 4所示。

|
图 4 损失函数值随迭代次数变化曲线 (a)U-Net模型;(b)U-Net+PPM模型 |
从图 4可以看出,当迭代达到1300次后,各组模型的损失函数值均已收敛。且Dice指数项权重e大于0.05时,损失函数曲线振荡越发剧烈,这是因为随着e值的增大,目标函数中的Dice项逐渐主导收敛过程。式(3)对正向传播的结果p的梯度可表示为2y2/(p+y)2,在某些情况下由于p过小或过大,计算得到的梯度值会产生剧烈波动,导致训练不稳定,从而使训练中的损失函数值产生震荡。
2.3 实验结果对于输入模型中进行地震相分类预测的地震剖面,深度神经网络会对每个像素点计算出一个概率分布pn=[p1, n, …, pc, n, …, pC, n],分别对应n点为某类地震相的概率,从中选择概率pc, n最大的那一类判断为该点的预测地震相c。将训练好的各组模型作用于测试集数据进行地震相预测,并将预测地震相分类结果与真实值比较,以评价模型效果。为了更加客观、全面地评价不同参数及结构的各组模型在测试集数据上的表现,采用了准确率(PA)、类准确率(CA)、平均交并比(mIOU)三项指标进行评价。PA表示整个测试数据集中被正确分类的像素点与总像素点比值,用于评估模型整体预测效果,表达式为
| $ {\rm{PA}} = \frac{{\sum\limits_{c = 1}^C {{\rm{|}}{\mathit{\boldsymbol{P}}_c} \cap {\mathit{\boldsymbol{Y}}_c}{\rm{|}}} }}{{\sum\limits_{c = 1}^C {{\rm{|}}{\mathit{\boldsymbol{Y}}_c}{\rm{|}}} }} \times 100\% $ | (5) |
式中:Yc表示在地震剖面上属于第c类地震相的像素点集合;Pc表示被网络模型预测为第c类地震相的像素点集合;运算符|·|表示集合中的元素总数。
CAc表示第c类地震相在整个数据集中的预测准确率,用于评估模型对每一类地震相的预测效果
| $ {\rm{C}}{{\rm{A}}_c} = \frac{{|{\mathit{\boldsymbol{P}}_c} \cap {\mathit{\boldsymbol{Y}}_c}|}}{{|{\mathit{\boldsymbol{Y}}_c}|}} \times 100\% $ | (6) |
准确率指标是基于单独的像素点计算分类的正确率,在评价图像分割问题时,无法判断全局的分割效果[12]。因此,本次研究通过计算mIOU指标来评估模型的表现。mIOU与Dice指数的作用相似,均用于衡量两个集合的重叠程度
| $ {\rm{mIOU}} = \frac{1}{C}\frac{{\sum\limits_{c = 1}^C {{\rm{|}}{\mathit{\boldsymbol{P}}_c} \cap {\mathit{\boldsymbol{Y}}_c}{\rm{|}}} }}{{\sum\limits_{c = 1}^C {|{\mathit{\boldsymbol{P}}_c} \cup {\mathit{\boldsymbol{Y}}_c}|} }} \times 100\% $ | (7) |
对于不同参数、结构的各组模型在测试集数据上的预测结果,分别用以上指标进行计算,其结果统计如表 2所示。
|
|
表 2 不同参数、结构网络模型对地震相预测结果统计表 |
表 2统计结果表明,加入PPM模块后,网络模型对于地震相预测准确率明显高于常规U-Net模型;且无论是在常规网络模型还是改进模型上,训练时采用带有Dice指数项的目标函数,预测效果均有一定提升,各项评价指标表明预测结果优于单一的交叉熵损失函数。在常规U-Net模型中,当目标函数中e取0.10时,模型对地震相分类预测的效果最好,准确率为91.61%,平均交并比为64.51%;在含有PPM模块的网络模型中,当目标函数中e取0.05时,模型的预测效果最好,准确率为94.74%,平均交并比为73.92%。另外,从统计结果可以看出,深度网络模型在预测第5、第6类地震相时效果较差,而对于第1、第3类地震相有着较高的预测精度。其原因在于该工区训练数据属于典型的不均衡分类[19],训练集中归属于第5、第6类地震相的像素点数量远远少于第1类和第3类(图 3)。在多元交叉熵损失函数的最优化过程中,网络模型会更倾向于学习这些样本数量较多的地震相特征。因此,网络模型对于样本数量较少的第5、第6类地震相的预测类准确率较低。而在目标函数中添加Dice指数项后,这些少数类地震相的预测准确率较之前有明显的提高,配合带有PPM模块的网络模型,其类准确率均达到了80%以上,且模型预测结果的平均交并比也有了一定提升。在测试集数据中选取Inline280剖面为例,改进前、后的模型及目标函数对该剖面预测结果如图 5所示。

|
图 5 Inline280剖面预测结果 (a)地震剖面;(b)真实地震相分类结果;(c)U-Net模型+交叉熵损失函数预测结果;(d)U-Net模型+改进目标函数最优预测结果;(e)改进后网络模型+交叉熵损失函数最优预测结果;(f)改进后网络模型+改进目标函数最优预测结果 |
常规U-Net模型对于地震相分类预测存在较多问题,如图 5c所示,剖面底部的地震相被错误划分为第3类、第4类等一些存在于其他深度的地震相。这一方面是由于训练集中这些地震相的样本数量较少,因数据不均衡而导致的学习效果较差,另一方面则是因为模型缺乏依据上、下文推断的能力,造成一些具有相似的弱振幅特征的地震相被错误地预测为第5类地震相。右下角的第6类地震相属于盐丘构造,数量较少但往往受到地震解释人员的关注,在被准确识别的同时也需要准确刻画其边界。但传统的交叉熵损失函数只能评估模型对于单个像素点的预测准确性,却无法衡量地震相的分割形状是否与实际接近,从而导致图 5c中盐丘边界刻画效果较差。在U-Net模型的目标函数中添加e=0.10的Dice指数项后,模型对于盐丘形状有了较为准确的预测(图 5d),虽然预测结果仍存在部分地震相的错误分类,但对于盐丘边界的预测效果提升显著。加入PPM模块后的U-Net模型对于该剖面的地震相分类表现出良好的效果(图 5e),由于PPM模块提升了模型获取全局信息的能力,预测结果中基本不存在地震相在深度上的错误分布,但对于盐丘边界的预测效果依然不理想。在使用含有Dice指数项的改进目标函数后(e=0.05),预测的盐丘形状已十分接近真实值(图 5f),说明改进后的网络模型与目标函数更适合于地震相的分类及预测。
2.4 不确定性评估不确定性评估对于人工神经网络这类可解释性较差的模型来说是十分重要的。对模型预测结果的不确定性分析有助于了解模型对于预测结果的“自信”程度。对于断层识别等二分类问题,可以直接输出一个二维的概率特征图,并通过选定阈值调整想要的预测结果[10]。而地震相分类预测属于多分类问题,网络模型输出结果是一个三维数组,对于每类地震相的预测概率难以可视化展现。另一方面,由于式(1)中softmax函数的性质,模型在训练中为了尽可能地最小化目标函数,会盲目增大或减小模型输出的结果zc, n,导致模型对于预测结果过于“自信”,使预测概率pc, n无法真实地展现模型对于预测结果的不确定性。
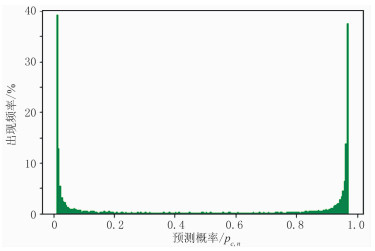
图 6为改进后模型对地震相预测结果分布。图中,80%以上的预测结果概率pc, n分布在0.01以下和0.98以上,也就是说模型认为剖面上各像素点被预测为某类地震相的概率几乎为100%。这样的结果显然过于“自信”,因而无法关注到那些在模型预测过程中模棱两可的像素点,也使解释人员无法对地震相分类预测模型结果的可靠性进行评估。为此,本文引入信息论中的信息熵[20]的概念,并提出运用预测信息熵对模型预测结果的不确定性进行评估。在信息论中, 信息熵用于度量信息中随机变量的确定性。在用于地震相预测模型中,地震剖面上第n个像素点处的预测信息熵En可表示为
| $ {E_n} = - \sum\limits_{c = 1}^C {{p_{c, n}}\lg {p_{c, n}}} $ | (8) |
|
图 6 改进后模型对地震相预测结果分布 |
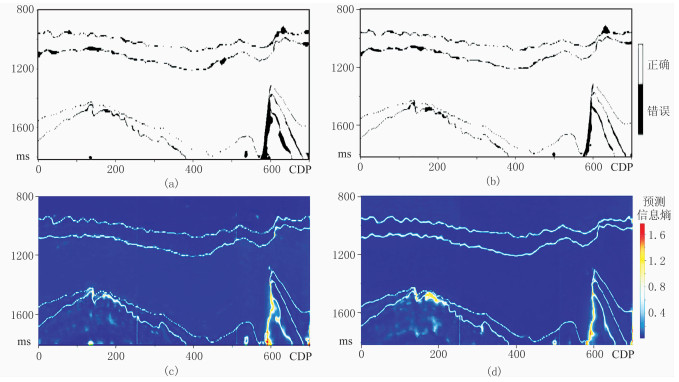
预测信息熵越高,表示预测结果pc, n的概率分布越混乱,不确定性越高;反之则表示预测结果不确定性越低,可靠性越高。根据信息熵这一评价标准,可以对地震相预测结果的不确定性进行可视化,方便地震解释人员对于模型不太确定的地方进行人工核实及修正。计算图 5e、图 5f两组模型预测结果的信息熵,并与预测误差进行对比,结果如图 7所示。
从图 7a、图 7b可以进一步看出改进后模型对地震相预测结果具有较高的精度,除不同地震相交界处以外,几乎不存在预测错误,且在使用含Dice指数项的目标函数后,模型对于剖面右下角盐丘边界处预测错误的像素点更少,结果更为准确。从图 7c、图 7d可以看出,地震相交界处预测信息熵较高,其值基本在0.7以上,且该处同样存在较多的预测误差。这是由于地震相的边界往往是地质沉积过程中沉积层交界的区域,边界附近的岩石岩性与物质成分是逐渐过渡变化的,因此,在地震相分类预测中,这些交界部分的预测准确率较低。将预测误差与预测信息熵进行对比,发现模型预测错误的像素点具有较高的信息熵,即该处模型预测结果的可靠性较低,如此便能较好地评估模型预测结果的不确定性。在使用改进网络模型对该剖面进行地震相分类预测的结果中,当某处En低于0.8时,表示模型对该处预测结果较为“自信”;当En高于0.8时,就可认为该处预测不准确,需要解释人员进行核实与修正。
3 结束语地震剖面上全局空间分布的先验信息对于地震相划分有着非常重要的作用,而现有基于深度学习方法的地震相识别模型缺乏获取空间先验信息的能力,且缺乏一个对于模型预测结果的不确定性进行评估的指标。针对这些问题,采用在U-Net模型中加入PPM模块,使模型能够获取多个接收域下的特征,从而学习到地震剖面上包含不同尺度、不同子区域间关系的分层全局信息。使用一种综合交叉熵与Dice指数的目标函数改善不均衡数据中少数类地震相边界刻画问题。提出用预测信息熵分析模型的不确定性。将该方法应用于F3工区海上地震数据地震相预测,实验结果表明:
(1) 加入PPM模块后,网络模型对该工区地震相识别准确率有了明显提高;使用融合了Dice指数的新目标函数后,对于少数类地震相预测结果有了一定提升,可使地震相边界刻画获得更为良好的效果。
(2) 预测信息熵这一指标能较好地评价地震相预测模型的不确定性,对预测结果的可靠性进行可视化展现。预测信息熵越低,模型对该处预测结果的不确定性越低,表明预测结果越可靠。在实际地震资料解释中,解释人员可以通过选定预测信息熵的阈值对模型预测结果进行修正。
本文的深度网络模型采用Facebook公司的Pytorch平台搭建,使用的所有训练数据与代码开源在https://github.com/yxycug/Seismic-Facies-clas-sification。
| [1] |
朱剑兵, 赵培坤. 国外地震相划分技术研究新进展[J]. 勘探地球物理进展, 2009, 32(3): 167-171. ZHU Jianbing, ZHAO Peikun. Advances in seismic facies classification technology abroad[J]. Progress in Exploration Geophysics, 2009, 32(3): 167-171. |
| [2] |
唐金炎, 杜品, 陈智雍. 地震几何属性参数在地震相识别中的应用[J]. 油气地球物理, 2011, 9(1): 34-35. TANG Jinyan, DU Pin, CHEN Zhiyong. Application of the seismic geometric attributes parameters in seismic facies identification[J]. Petroleum Geophysics, 2011, 9(1): 34-35. |
| [3] |
张林科, 覃丽君, 张国焘. 基于地震属性的地震相分析思路[J]. 工程地球物理学报, 2010, 7(6): 694-698. ZHANG Linke, QIN Lijun, ZHANG Guotao. On seismic facies analysis based on seismic attributes[J]. Chinese Journal of Engineering Geophysics, 2010, 7(6): 694-698. |
| [4] |
段玉顺, 李芳. 地震相的自动识别方法及应用[J]. 石油地球物理勘探, 2004, 39(2): 158-162. DUAN Yushun, LI Fang. Automatic identification of seismic facies and application[J]. Oil Geophysical Prospecting, 2004, 39(2): 158-162. |
| [5] |
Jesper S.Deep learning seismic facies on state-of-the-art CNN architectures transfer learning seismic facies[C].SEG Technical Program Expanded Abstracts, 2018, 37: 2036-2040.
|
| [6] |
Zhao T.Seismic facies classification using different deep convolutional neural networks[C].SEG Technical Program Expanded Abstracts, 2018, 37: 2046-2050.
|
| [7] |
Lei L, Yu L, Xiong Z, et al.Convolutional recurrent neural networks based waveform classification in seismic facies analysis[C].SEG Technical Program Expanded Abstracts, 2019, 38: 2599-2603.
|
| [8] |
Qi J, Ha T, Lyu B, et al.Seismic attribute selection for machine learning based facies analysis choosing the best seismic attributes[C].SEG Technical Program Expanded Abstracts, 2019, 38: 1853-1857.
|
| [9] |
Wu X, Shi Y, Fomel S, et al.Convolutional neural net-works for fault interpretation in seismic images[C].SEG Technical Program Expanded Abstracts, 2018, 37: 1946-1950.
|
| [10] |
Shi Y, Wu X, Fomel S.Automatic salt-body classification using deep-convolutional neural network[C].SEG Technical Program Expanded Abstracts, 2018, 37: 1971-1975.
|
| [11] |
Alaudah Y, Alfarraj M. Structure label prediction using similarity-based retrieval and weakly supervised label mapping[J]. Geophysics, 2019, 84(1): V67-V79. |
| [12] |
Mukhopadhyay P, Mallick S.Bayesian deep learning for seismic facies classification and its uncertainty estimation[C].SEG Technical Program Expanded Abstracts, 2019, 38: 2488-2492.
|
| [13] |
Zhang H, Liu Y, Zhang Y, et al.Automatic seismic facies interpretation based on an enhanced encoder-decoder structure[C].SEG Technical Program Expanded Abstracts, 2019, 38: 2408-2412.
|
| [14] |
Zhao H, Shi J, Qi X, et al.Pyramid scene parsing network[C].Proceedings IEEE Conference on Computer Vision and Pattern Recognition, 2017, 6230-6239.
|
| [15] |
Panchapagesan S, Sun M, Khare A, et al. Multi-task learning and weighted cross-entropy for DNN-based keyword spotting[M]. Interspeech, 2016: P760-P764.
|
| [16] |
Sudre C H, Li W, Vercauteren T, et al. Generalized Dice Overlap as a Deep Learning Loss Function for Highly Unbalanced Segmentations, Deep Learning in Medical Image Analysis and Multimodal Learning for Clinical Decision Support[M]. Cham: Springer, 2017: 240-248.
|
| [17] |
Alaudah Y, Michalowicz P, Alfarraj M, et al. A machine-learning benchmark for facies classification[J]. Interpretation, 2019, 7(3): SE175-SE187. DOI:10.1190/INT-2018-0249.1 |
| [18] |
Kingma D P, Ba J.Adam: A Method for Stochastic Optimization[C].The 3rd International Conference for Learning Representations, 2015, http://arxiv.org/abs/1412.6980.
|
| [19] |
闫星宇, 顾汉明, 肖逸飞, 等. XGBoost算法在致密砂岩气储层测井解释中的应用[J]. 石油地球物理勘探, 2019, 54(2): 447-455. YAN Xingyu, GU Hanming, XIAO Yifei, et al. XGBoost algorithm applied in the interpretation of tight-sand gas reservoir on well logging data[J]. Oil Geophysical Prospecting, 2019, 54(2): 447-455. |
| [20] |
Shannon, Claude E. A mathematical theory of communication[J]. Bell System Technical Journal, 1948, 27(3): 379-423. DOI:10.1002/j.1538-7305.1948.tb01338.x |



 顾汉明, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院, 430074。Email:
顾汉明, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院, 430074。Email: