2 油气藏地质及开发工程国家重点实验室(成都理工大学), 四川成都 610059
2 State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation(Chengdu University of Technology), Chengdu, Sichuan 610059, China
实际地震数据在空间方向往往存在不规则的缺失道[1-2],要想得到完整的地震数据,通常需要插值处理[3]。地震资料插值方法大致可以分为两类[4-5]:①利用线性空间预测滤波器插值[6-7];②借助数学变换(如傅里叶变换)插值[8-9],其中凸集投影(POCS)算法和迭代阈值(IST)算法是较为经典的算法[10],利用地震数据变换域的稀疏性对地震数据插值,由于原理直观、实现简单,并且具有稳定性,因此发展迅速。Menke[11]认为POCS算法具有普适性,并将其引入地球物理领域。近年来,各种基于传统POCS算法的改进方法被提出且被广泛应用。刘红喜等[12]提出了边缘保持的POCS超分辨率重建方法;王本锋等[13]引入了结合POCS和Curvelet的超分辨率重建算法重建三维数字内核;Abma等[9]将POCS算法引入地震插值领域,获得了很好的效果;王本锋等[14]提出了POCS插值重建地震数据的质量控制新准则,在保证插值精度的同时提高了计算效率。在POCS算法发展的同时,人们也对IST算法进行研究。Herrmann等[15]基于基追踪降噪模型,将IST算法用于非均匀记录地震道插值;由于现有IST算法收敛速度较慢,Beck等[16]从一般的数学背景出发,提出了快速迭代收缩阈值(FIST)算法;Gao等[17]使用指数递减阈值策略代替线性阈值策略。近年来,业界着重对IST和POCS算法迭代慢的不足进行优化,提高了算法的计算效率和精度。
为了提高插值效率以及选择最优的插值方案,本文基于IST算法和POCS算法的分析公式,发展了FIST算法和快速凸集投影(FPOCS)算法。基本思想是:将前一步的插值结果与前两步的插值结果通过线性算子进行线性组合,得到迭代收缩算子;通过插值算法进行插值。同时引入质量控制新准则[14],提高了计算效率和精度。通过理论模型筛选出最优的阈值策略以及最大迭代次数,实际资料处理结果表明,文中方法在较少迭代次数下的插值效果较好,验证了算法的高效性。
1 基本原理 1.1 地震资料插值原理将采集到的不规则的随机地震资料记为dobs,期望得到的完整数据记为d,则
| $ {\mathit{\boldsymbol{d}}_{{\rm{obs}}}} = \mathit{\boldsymbol{Md}} $ | (1) |
式中M为采样算子,是由元素0和1组成的对角矩阵。
为了方便插值,根据压缩感知原理[18-20],将地震数据投影到变换域,即
| $ {\mathit{\boldsymbol{d}}_{{\rm{obs}}}} = \mathit{\boldsymbol{Md}} = \mathit{\boldsymbol{MA\chi }} $ | (2) |
式中:A∈Rn×m为正交坐标系的合成算子,且是一个紧框架;χ为变换域的表示系数。
然而式(2)是一个欠定方程,具有多解性,因此需要添加一些限制性条件求解。由于稀疏性在变换域内始终适用[21],通常与χ相对应。因此,求解式(2)就转化为L0范数的最小化问题
| $ \mathop {{\rm{min}}}\limits_{\mathit{\boldsymbol{\chi }} \in {\mathit{\boldsymbol{R}}^n}} {\left\| {{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} - \mathit{\boldsymbol{K\chi }}} \right\|_0} $ | (3) |
式中K=MA。由于L0范数的最小化非凸复杂性[22],常常使用L1范数代替L0范数,并与L0范数的稀疏性相同[18]。因此,式(3)变为
| $ \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{\chi }} J(\mathit{\boldsymbol{\chi }}) = \frac{1}{2}\left\| {{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} - \mathit{\boldsymbol{K\chi }}} \right\|_2^2 + \tau {\left\| \mathit{\boldsymbol{\chi }} \right\|_1} $ | (4) |
式中τ为正则化参数。由于A为紧框架,根据A*A=I(I为单位矩阵)以及χ=A*Aχ=A*d(“上角*”表示伴随),则
| $ \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{d}} J(\mathit{\boldsymbol{d}}) = \frac{1}{2}\left\| {{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} - \mathit{\boldsymbol{K\chi }}} \right\|_2^2 + \tau {\left\| {{\mathit{\boldsymbol{A}}^*}\mathit{\boldsymbol{d}}} \right\|_1} $ | (5) |
式(5)为地震插值分析公式,因为该式直接将地震资料d作为未知数进行分析[23]。
1.2 IST算法有很多算法求解式(4)。Figueiredo等[24]和Daubechies等[25]提出了IST算法,一般表示为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{\chi }}^{(k + 1)}} = {T_\lambda }\{ {\mathit{\boldsymbol{\chi }}^{(k)}} + {\mathit{\boldsymbol{K}}^*}[{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} - \mathit{\boldsymbol{K}}{\mathit{\boldsymbol{\chi }}^{(k)}}]\} }\\ {k = 1,2, \cdots ,N} \end{array} $ | (6) |
式中:λ为正阈值参数;k为迭代次数,N为最大迭代次数;Tλ为阈值函数,与τ的取值有关,当λ=τ时,Tλ为软阈值函数,定义软阈值算子为
| $ {S_\lambda }(u) = \left\{ {\begin{array}{*{20}{c}} {u - \lambda \frac{u}{{|u|}}}&{|u| > \lambda }\\ 0&{|u| \le \lambda } \end{array}} \right. $ | (7) |
式中u为单道地震数据。与式(5)相同的思路,将式(6)两边左乘A,得到IST算法公式
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{d}}^{(k + 1)}} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{\chi }}^{(k + 1)}} = \mathit{\boldsymbol{A}}{T_\lambda }\{ {\mathit{\boldsymbol{\chi }}^{(k)}} + {\mathit{\boldsymbol{K}}^*}[{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} - \mathit{\boldsymbol{K}}{\mathit{\boldsymbol{\chi }}^{(k)}}]\} }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathit{\boldsymbol{A}}{\mathit{\boldsymbol{T}}_\lambda }\{ {\mathit{\boldsymbol{A}}^*}{\mathit{\boldsymbol{d}}^{(k)}} + {{(\mathit{\boldsymbol{MA}})}^*}[{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} - \mathit{\boldsymbol{MA}}{\mathit{\boldsymbol{\chi }}^{(k)}}]\} }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathit{\boldsymbol{A}}{T_\lambda }\{ {\mathit{\boldsymbol{A}}^*}[{\mathit{\boldsymbol{d}}^{(k)}} + {\mathit{\boldsymbol{M}}^*}({\mathit{\boldsymbol{d}}_{{\rm{obs}}}} - \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{d}}^{(k)}})]\} }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathit{\boldsymbol{A}}{T_\lambda }\{ {\mathit{\boldsymbol{A}}^*}[{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} + (\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{M}}){\mathit{\boldsymbol{d}}^{(k)}}]\} } \end{array} $ | (8) |
式中d(k)、χ(k)分别为第k次迭代时的d与χ的值。
1.3 POCS算法定义
| $ {\mathit{\boldsymbol{u}}^{(k)}} = {\mathit{\boldsymbol{d}}_{{\rm{obs}}}} + (\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{M}}){\mathit{\boldsymbol{d}}^{(k)}} $ | (9) |
式中u(k)为第k次迭代后原始地震道的插入数据。对于式(8),有
| $ {\mathit{\boldsymbol{d}}^{(k + 1)}} = \mathit{\boldsymbol{A}}{T_\lambda }[{\mathit{\boldsymbol{A}}^*}{\mathit{\boldsymbol{u}}^{(k)}}] $ |
在第k+1次迭代时,结合式(9),有
| $ {\mathit{\boldsymbol{u}}^{(k + 1)}} = {\mathit{\boldsymbol{d}}_{{\rm{obs}}}} + (\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{M}})\mathit{\boldsymbol{A}}{T_\lambda }[{\mathit{\boldsymbol{A}}^*}{\mathit{\boldsymbol{u}}^{(k)}}] $ | (10) |
需要注意的是,
| $ \mathop {{\rm{lim}}}\limits_{k \to \infty } {\mathit{\boldsymbol{u}}^{(k)}} = \mathop {{\rm{lim}}}\limits_{k \to \infty } [{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} + (\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{M}}){\mathit{\boldsymbol{d}}^{(k)}}] = \mathit{\boldsymbol{d}} $ | (11) |
由M(I-M)=0,得
| $ \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{u}}^{(k)}} = {\mathit{\boldsymbol{d}}_{{\rm{obs}}}} $ | (12) |
在式(10)中用d(k)取代u(k),得
| $ {\mathit{\boldsymbol{d}}^{(k + 1)}} = {\mathit{\boldsymbol{d}}_{{\rm{obs}}}} + (\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{M}})\mathit{\boldsymbol{A}}{T_\lambda }[{\mathit{\boldsymbol{A}}^*}{\mathit{\boldsymbol{d}}^{(k)}}] $ | (13) |
这样,便得到POCS算法,该算法已广泛用于许多领域,如图像重建和修复等。
1.4 两步插值: FIST和FPOCS由于IST算法的收敛速度很慢。Beck等[16]提出了快速迭代收缩阈值算法(FIST),可以表示为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\tilde x}}}^{(k)}} = {\mathit{\boldsymbol{x}}^{(k)}} + \frac{{{\mathit{\boldsymbol{t}}^{(k)}} - 1}}{{{\mathit{\boldsymbol{t}}^{(k + 1)}}}}[{\mathit{\boldsymbol{x}}^{(k)}} - {\mathit{\boldsymbol{t}}^{(k - 1)}}]}\\ {{\mathit{\boldsymbol{x}}^{(k + 1)}} = {T_\lambda }\{ {{\mathit{\boldsymbol{\tilde x}}}^{(k)}} + {\mathit{\boldsymbol{K}}^*}[{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} - \mathit{\boldsymbol{K}}{{\mathit{\boldsymbol{\tilde x}}}^{(k)}}]\} } \end{array}} \right. $ | (14) |
式中:
式(14)代表两步插值的过程:将前一步的插值结果x(k)与前两步的插值结果x(k-1)通过线性算子t进行线性组合,得到迭代收缩算子
与式(8)推导相同,式(14)两边左乘A得到FIST算法公式
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\tilde d}}}^{(k)}} = {\mathit{\boldsymbol{d}}^{(k)}} + \frac{{{\mathit{\boldsymbol{t}}^{(k)}} - 1}}{{{\mathit{\boldsymbol{t}}^{(k + 1)}}}}[{\mathit{\boldsymbol{d}}^{(k)}} - {\mathit{\boldsymbol{d}}^{(k - 1)}}]}\\ {{\mathit{\boldsymbol{d}}^{(k + 1)}} = \mathit{\boldsymbol{A}}{T_\lambda }\{ {\mathit{\boldsymbol{A}}^*}[{\mathit{\boldsymbol{d}}_{{\rm{obs}}}} + (\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{M}}){{\mathit{\boldsymbol{\tilde d}}}^{(k)}}]\} } \end{array}} \right. $ | (15) |
式中:(k)为地震数据插值的迭代收缩算子;d(k)为第k次迭代后的地震数据。
在式(15)的基础上,按照式(13)思路,可以推出FPOCS算法公式
| $ \left\{ {\begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\tilde d}}}^{(k)}} = {\mathit{\boldsymbol{d}}^{(k)}} + \frac{{{\mathit{\boldsymbol{t}}^{(k)}} - 1}}{{{\mathit{\boldsymbol{t}}^{(k + 1)}}}}[{\mathit{\boldsymbol{d}}^{(k)}} - {\mathit{\boldsymbol{d}}^{(k - 1)}}]}\\ {{\mathit{\boldsymbol{d}}^{(k + 1)}} = {\mathit{\boldsymbol{d}}_{{\rm{obs}}}} + (\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{M}})\mathit{\boldsymbol{A}}{T_\lambda }[{\mathit{\boldsymbol{A}}^*}{{\mathit{\boldsymbol{\tilde d}}}^{(k)}}]} \end{array}} \right. $ | (16) |
正则化参数τ具重要作用,并且与每次迭代的阈值λ密切相关。因此定义软阈值
| $ \lambda = \tau $ | (17) |
通过对比不同阈值策略的实际效果,筛选最佳的阈值策略。
(1) 恒阈值
| $ {\tau _k} = C\quad k = 1,2, \cdots ,N $ | (18) |
式中C为常数。
(2) 阈值线性递减
| $ {\tau _k} = {\tau _{{\rm{max}}}} - \frac{{k - 1}}{{N - 1}}({\tau _{{\rm{max}}}} - {\tau _{{\rm{min}}}})\quad k = 1,2, \cdots ,N $ | (19) |
(3) 阈值指数递减
| $ {\tau _k} = {\left( {\frac{{{\tau _{{\rm{max}}}}}}{{{\tau _{{\rm{min}}}}}}} \right)^{\frac{{k - 1}}{{N - 1}}}}{\tau _{{\rm{max}}}}\quad k = 1,2, \cdots ,N $ | (20) |
(4) 数据驱动阈值
| $ \left\{ {\begin{array}{*{20}{l}} {{\tau _1} = {v_1}}\\ {{\tau _k} = {v_j}}\\ {{\tau _N} = {v_N}}\\ {j = \left\lceil {(k - 1){N_v}/(N - 1)} \right\rceil } \end{array}} \right. $ | (21) |
且
| $ \left\{ {\begin{array}{*{20}{l}} {{\tau _{{\rm{max}}}} = {p_{{\rm{max}}}} \cdot {\rm{max}}\{ |{{({\mathit{\boldsymbol{A}}^*}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}})}_i}|\} }\\ {{\tau _{{\rm{min}}}} = {p_{{\rm{min}}}} \cdot {\rm{max}}\{ |{{({\mathit{\boldsymbol{A}}^*}{\mathit{\boldsymbol{d}}_{{\rm{obs}}}})}_i}|\} } \end{array}} \right. $ | (22) |
式中:τmax和τmin分别为所选的最大和最小正则化参数;pmax和pmin分别为所定义的最大和最小百分比;序列
以上介绍了两步插值算法的原理。由于地震资料在变换域具有稀疏性,根据压缩感知理论可知,将地震数据投影到变换域,选取阈值策略进行反复迭代,即可完成地震数据插值。
2 仿真实验和实际应用 2.1 两步插值法的终止准则文中介绍的IST、POCS、FIST和FPOCS等4种插值算法都属于迭代方法,这就意味着在达到所定义的最大迭代次数N之前,算法不会终止。因此,需要建立一个终止准则适时地结束迭代。Gao等[4-5]等给出了两种终止准则,王本锋等[14]在此基础上提出了灵活、适用性更好的质量控制新准则
| $ \frac{{\left\| {{\mathit{\boldsymbol{d}}^{(k)}} - {\mathit{\boldsymbol{u}}^{(k)}}} \right\|_2^2}}{{\left\| {{\mathit{\boldsymbol{d}}_{{\rm{obs}}}}} \right\|_2^2}} < \eta $ | (23) |
进一步提高了计算效率。式中η为公差,需要在程序运行前设置。
文中使用信噪比
| $ {\rm{SNR}} = 10{\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{lg}}\frac{{\left\| \mathit{\boldsymbol{d}} \right\|_2^2}}{{\left\| {\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{\hat d}}} \right\|_2^2}} $ | (24) |
评估插值质量。式中
综上所述,总结了地震资料插值流程(图 1)。

|
图 1 地震资料插值流程 |
使用IST、POCS、FIST和FPOCS等算法分别对由Seismic Lab建立的四层地震模型(图 2a)、Marmousi模型(图 2b)的不完整地震数据(图 2d、图 2e)进行插值,筛选出最佳的阈值策略,并最终由实际地震资料(图 2c、图 2f)进行验证。

|
图 2 实验算例 (a)由Seismic Lab建立的四层地震模型(35Hz雷克子波),共512道,每道512个样点,采样间隔为0.002s;(b)Marmousi地震模型,共201道,每道600个样点,采样间隔为0.003s;(c)实际地震资料,共430道,每道512个样点;(d)~(f)对应图a~图c缺失30%的数据 |
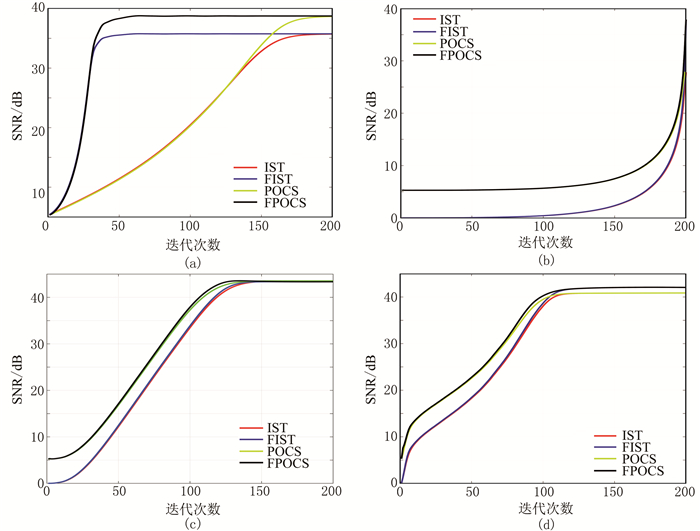
首先在由Seismic Lab建立的四层地震模型上使用不同的阈值策略插值,以此筛选最优的阈值策略。应用IST、POCS、FIST和FPOCS等算法对缺失数据(图 2d)插值,并绘制信噪比曲线(图 3)。可见:在恒阈值时的信噪比为38.5863 dB,两步插值法在50次迭代时便完成了图像重建,较一步插值法的图像重建速度更快(图 3a);在阈值线性递减时的信噪比为35.1875dB,在迭代次数较少时图像重建效果不明显,随着迭代次数增加,重构作用越来越大,但会引入噪声,导致信噪比降低(图 3b);在阈值指数递减时的信噪比为43.4571dB(图 3c);数据驱动阈值时的信噪比为41.1818dB(图 3d)。因此,阈值指数递减与数据驱动阈值的插值结果信噪比较高,数据重建效果较好。图 4为使用阈值指数递减策略对图 2d的插值结果及其与图 2a数据的差异。由图可见,经过插值后的地震数据恢复完好,且没有引入大量噪声。
|
图 3 应用不同阈值策略对图 2d插值的信噪比曲线 (a)恒阈值(τ=0.005,N=200);(b)阈值线性递减(N=200);(c)阈值指数递减(N=200);(d)数据驱动阈值(N=200) |
|
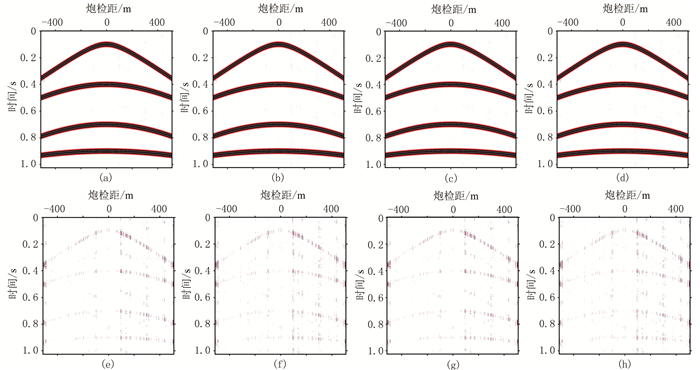
图 4 使用阈值指数递减策略对图 2d的插值结果及其与图 2a数据的差异 (a)IST软阈值插值(SNR=38.5863dB);(b)FIST软阈值插值(SNR=40.6514dB);(c)POCS软阈值插值(SNR= 38.5864dB;(d)FPOCS软阈值插值(SNR=40.6516dB);(e)~(h)对应图a~图d数据与图 2a数据的差值 |
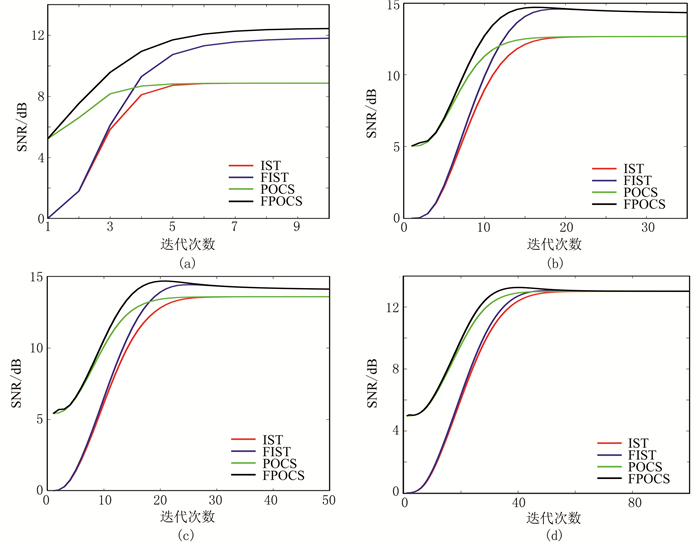
利用Marmousi模型验证两步插值方法的收敛性。图 5为应用阈值指数递减策略对图 2e插值的信噪比曲线。由图可见:在迭代次数较小时,重建效果较差,两步插值法的收敛速度略快于一步插值法,因此两步插值法可提高收敛速度;由于观测数据的复杂性,对Marmousi地震模型的重构精度不高;在50次迭代后得到了较好的收敛解(图 5c),再增加迭代次数对插值精度的改善很小(图 5d),通过多次测试发现,当N∈[35, 50]时可以取得满意的插值效果。图 6为使用阈值指数递减策略迭代50次对图 2e的插值结果及其与图 2b数据的差异。由图可见,四种算法具有相近的插值效果,在没有引入大量噪声的情况下,地震数据恢复完好。
|
图 5 应用阈值指数递减策略对图 2e插值的信噪比曲线 (a)N=10;(b)N=35;(c)N=50;(d)N=100 |

|
图 6 使用阈值指数递减策略迭代50次对图 2e的插值结果及其与图 2b数据的差异 (a)IST软阈值插值(SNR=13.7268dB);(b)FIST软阈值插值(SNR=14.312dB);(c)POCS软阈值插值(SNR= 13.7268dB);(d)FPOCS软阈值插值(SNR=14.3119dB);(e)~(h)对应图a~图d数据与图 2b数据的差值 |
此外,在迭代次数较少时POCS、FPOCS算法的信噪比始终高于IST、FIST算法,这是由于所有算法在初始化时将d(k)置0所致。由式(12)可知,在POCS、FPOCS算法中,有
| $ \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{d}}^{(k + 1)}} = {\mathit{\boldsymbol{d}}_{{\rm{obs}}}} = \mathit{\boldsymbol{Md}}\quad \forall k $ | (25) |
因此
| $ \left\| {{\mathit{\boldsymbol{d}}^{(k + 1)}} - \mathit{\boldsymbol{d}}} \right\| = {\left\| {(\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{M}})[{\mathit{\boldsymbol{d}}^{(k + 1)}} - \mathit{\boldsymbol{d}}]} \right\|_2} $ | (26) |
这是POCS、FPOCS算法的信噪比曲线的起点总是不为0的原因。由式(8)、式(21)可知,在IST、FIST算法中,开始设计了较大的阈值,几乎忽略了所有的傅里叶系数,导致d(k+1)中的值过多,使‖d‖22≈‖d-d(k+1)‖22、SNR≈0。
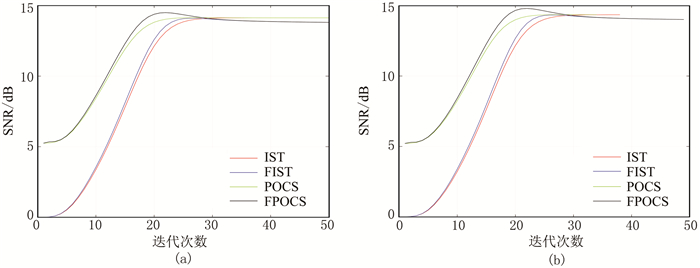
2.5 合理的终止准则以及实际地震数据插值效果通过对不完整的理论模型数据(图 2d、图 2e)进行插值,筛选出最优的阈值策略和最大迭代次数,在此基础上验证实际地震数据(图 2c、图 2f)的插值效果。图 7为使用阈值指数递减策略迭代50次对图 2f的插值结果及其与图 2c数据的差异,图 8为应用阈值指数递减策略对图 2f插值的信噪比曲线。由图可见:①四种算法插值结果的信噪比约为14dB,均能较好地重建缺失数据(图 7)。②两步插值算法相对于单步插值算法具有更快的收敛速度(图 8);与没有加入终止准则的结果(图 8a)相比,应用终止准则后,算法能更快地结束迭代,从而提高计算效率(图 8b),如分别在35、30次迭代时IST、FIST算法得到了收敛解。

|
图 7 使用阈值指数递减策略迭代50次对图 2f的插值结果及其与图 2c数据的差异 (a)IST软阈值插值(SNR=14.3489dB);(b)FIST软阈值插值(SNR=14.0115dB);(c)POCS软阈值插值(SNR=14.3519dB);(d)FPOCS软阈值插值(SNR=14.0115dB);(e)~(h)对应图a~图d数据与图 2c数据的差值 |
|
图 8 应用阈值指数递减策略对图 2f插值的信噪比曲线 (a)未应用终止准则;(b)应用终止准则 |
本文研究了加速迭代的快速凸集投影算法和快速迭代阈值算法,基本思想是:将前一步的插值结果与前两步的插值结果通过线性算子进行线性组合,得到迭代收缩算子;通过插值算法进行插值。同时引入质量控制新准则,提高了计算效率和精度。仿真实验和实际应用证明:阈值指数递减策略较恒阈值、阈值线性递减、数据驱动阈值等策略获得的插值结果的信噪比更高;结合终止准则,最大迭代次数为35~50时,可以获得较好的插值效果。
| [1] |
童思友, 高航, 刘锐, 等. 基于Shearlet变换的自适应地震资料随机噪声压制[J]. 石油地球物理勘探, 2019, 54(4): 744-750. TONG Siyou, GAO Hang, LIU Rui, et al. Seismic random noise adaptive suppression based on Shearlet transform[J]. Oil Geophysical Prospecting, 2019, 54(4): 744-750. |
| [2] |
Curry W.Interpolation with Prediction-Error Filters and Training Data[D]. Stanford University, 2008.
|
| [3] |
Trickett S, Burroughs L, Milton A, et al.Rank-reduction-based trace interpolation[C]. SEG Technical Program Expanded Abstracts, 2010, 29: 3829-3833.
|
| [4] |
Gao J J, Chen X H, Li J Y, et al. Irregular seismic data reconstruction based on exponential threshold model of POCS method[J]. Applied Geophysics, 2010, 7(3): 229-238. DOI:10.1007/s11770-010-0246-5 |
| [5] |
Gao J J, Sacchi M D, Chen X H.Convergence improvement and noise attenuation considerations for POCS reconstruction[C]. Extended Abstracts of 73rd EAGE Conference & Exhibition, 2011, 2214-4609.
|
| [6] |
Spitz S. Seismic trace interpolation in the F-X domain[J]. Geophysics, 1991, 56(6): 785-794. DOI:10.1190/1.1443096 |
| [7] |
Wang Y H. Seismic trace interpolation in the f-x-y domain[J]. Geophysics, 2002, 67(4): 1232-1239. |
| [8] |
Sacchi M D, Ulrych T J, Walker C J, et al. Interpolation and extrapolation using a high-resolution discrete Fourier transform[J]. IEEE Transactions on Signal Processing, 1998, 46(1): 31-38. |
| [9] |
Abma R, Kabir N. 3D interpolation of irregular data with a POCS algorithm[J]. Geophysics, 2006, 71(6): E91-E97. DOI:10.1190/1.2356088 |
| [10] |
温睿, 刘国昌, 冉扬. 压缩感知地震数据重建中的三个关键因素分析[J]. 石油地球物理勘探, 2018, 53(4): 682-693. WEN Rui, LIU Guochang, RAN Yang. Three key factors in seismic data reconstruction based on compressive sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 682-693. |
| [11] |
Menke W. Applications of the POCS inversion method to interpolating topography and other geophysical fields[J]. Geophysical Research Letters, 1991, 18(3): 435-438. DOI:10.1029/90GL00343 |
| [12] |
刘红喜, 孙凯, 孙宏彬, 等. 具有边缘保持特性的POCS超分辨率图像重建方法[J]. 吉林大学学报(信息科学版), 2015, 33(6): 620-624. LIU Hongxi, SUN Kai, SUN Hongbin, et al. Super-resolution image reconstruction of POCS with edge preserving[J]. Journal of Jilin University(Information Science Edition), 2015, 33(6): 620-624. |
| [13] |
王本锋, 李景叶, 陈小宏, 等. 基于Curvelet变换与POCS方法的三维数字岩心重建[J]. 地球物理学报, 2015, 58(6): 2069-2078. WANG Benfeng, LI Jingye, CHEN Xiaohong, et al. Curvelet-based 3D reconstruction of digital cores using the POCS method[J]. Chinese Journal of Geophysics, 2015, 58(6): 2069-2078. |
| [14] |
王本锋, 陈小宏, 耿建华. 地震数据POCS插值重建中的一种新型质量控制准则[J]. 石油物探, 2019, 58(1): 71-77. WANG Benfeng, CHEN Xiaohong, GENG Jianhua. A novel quality control criterion in the POCS interpolation of seismic data[J]. Geophysical Prospecting for Petroleum, 2019, 58(1): 71-77. |
| [15] |
Herrmann F J, Hennenfent G. Non-parametric seismic data recovery with Curvelet frames[J]. Geophysical Journal of the Royal Astronomical, 2008, 173(1): 233-248. DOI:10.1111/j.1365-246X.2007.03698.x |
| [16] |
Beck A, Teboulle M. A fast iterative shrinkage-thre-sholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(1): 183-202. DOI:10.1137/080716542 |
| [17] |
Gao J J, Stanton A, Naghizadeh M, et al. Convergence improvement and noise attenuation considerations for beyond alias projection onto convex sets reconstruction[J]. Geophysical Prospecting, 2013, 61(S1): 138-151. |
| [18] |
Donoho D. Compressed sensing[J]. IEEE Transac-tions on Information Theory, 2006, 52(4): 1289-1306. DOI:10.1109/TIT.2006.871582 |
| [19] |
陈祖斌, 王丽芝, 宋杨, 等. 基于压缩感知的小波域地震数据实时压缩与高精度重构[J]. 石油地球物理勘探, 2018, 53(4): 674-681, 693. CHEN Zubin, WANG Lizhi, SONG Yang, et al. Seismic data real-time compression and high-precision reconstruction in the wavelet domain based on the compressed sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 674-681, 693. |
| [20] |
Candes E.Compressive sampling[C]. Proceedings of the International Congress of Mathematicians, 2006, 1433-1452.
|
| [21] |
Candes E J, Tao T. Near-optimal signal recovery from random projections:universal encoding strategies[J]. IEEE Tansactions on Information Theory, 2006, 52(12): 5406-5425. DOI:10.1109/TIT.2006.885507 |
| [22] |
薛亚茹, 王敏, 陈小宏. 基于SL0的高分辨率Radon变换及数据重建[J]. 石油地球物理勘探, 2018, 53(1): 1-7. XUE Yaru, WANG Min, CHEN Xiaohong. High re-solution Radon transform based on SL0 and its application in data reconstruction[J]. Oil Geophysical Prospecting, 2018, 53(1): 1-7. |
| [23] |
Michael E, Peyman M, Ron R. Analysis versus syn-thesis in signal priors[J]. Inverse Problems, 2007, 23(3): 947-968. DOI:10.1088/0266-5611/23/3/007 |
| [24] |
Figueiredo M A T, Nowak R D. An EM algorithm for wavelet-based image restoration[J]. IEEE transactions on Image Processing, 2003, 12(8): 906-916. DOI:10.1109/TIP.2003.814255 |
| [25] |
Daubechies I, Defrise M, Christine D M. An iterative thresholding algorithm for linear inverse problems with a sparsity constraint[J]. Communications on Pure and Applied Mathematics, 2004, 57(11): 1413-1457. DOI:10.1002/cpa.20042 |



 李勇, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院, 610059。Email:
李勇, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院, 610059。Email: