2 吉林省勘查地球物理研究院, 吉林长春 130062
2 Geophysical Exploration Institute of Jilin Pro-vince, Changchun, Jilin 130062, China
在地震数据处理中,初至拾取的精度和效率是一个基本且重要的问题。初至拾取尤其在静校正、层析成像等地震数据处理过程中具有重要作用,进而直接影响后期综合地质解释。
早期人工地震初至拾取方法虽然精度高,但效率低下,限制了地震数据处理的速度;另外,因拾取精度受人为因素操控,稳定性难以保障[1]。针对现今海量的地震数据,选用自动初至拾取方法,则可大幅度减少人为因素干扰并提高工作效率。
早在20世纪70年代初,Peraldi等[2]就率先提出基于相邻地震道互相关获得初至到达与信号峰值之间的时差,但当相邻道波形相差很大或存在缺失道时,该方法难以奏效。
Coppens[3]于80年代创立的能量比值法已成为迄今应用最普遍的自动初至拾取方法。即通过计算地震信号的长短时窗特征函数的比值(STA/LTA),设置触发阈值,比值大于阈值的第一个时刻即为地震初至波到达时刻[4]。但该方法易受初至波到达前的随机干扰影响[5-7]。
Boschetti等[8]曾提出基于分形维方法的初至拾取方法,但因需做插值处理,导致计算速度慢,且其结果取决于插值的准确性[9]。
李辉峰等[10]提出基于边缘检测的初至拾取方法,通过把待处理的地震数据转变成灰二值化灰度图,再进行边缘检测。该方法虽能有效地拾取地震初至,但需大量训练数据以提高拾取的准确性,耗时长,效率低。在低信噪比情况下难以达到预期效果,需人工干预。
谭玉阳等[11]设计了一种SLPEA算法用于微地震自动初至拾取,利用地震信号与环境噪声之间的差异,根据信号信噪比构造不同检测函数拾取初至。该方法克服了传统方法抗噪性弱的缺点,但计算量大、耗时长,且时窗的选择依据不明确,依赖经验或反复调试[12]。
随着地震勘探的不断深入,上述方法已无法满足日益增长的庞大数据量要求,所以需要一种人工干预小的准确地震初至拾取方法,尤其是针对低信噪比的、海量的地震数据情形。
基于上述成果调研,本文提出一种基于超虚干涉(Super-virtual interferometry,SVI)约束的模糊C均值(Fuzzy C-means,FCM)聚类地震自动初至拾取方法。FCM聚类分析是一种非监督的机器学习方法,只使用数据本身对数据进行分类[13]。与严重依赖于输入训练数据的监督机器学习方法不同,聚类分析仅依赖于数据本身,因此更加灵活,更容易应用于实际的地震初至拾取。除此以外,由于球面扩散、衰减和环境噪声的影响,远炮检距初至波的信号弱,噪声强,信噪比低,特征值非常混乱,常常无法直接拾取。本文利用SVI法加强初至波的能量,提高地震数据的信噪比[14-16],在此基础上开展FCM聚类分析,并自动拾取低信噪比地震资料的初至。
1 方法原理 1.1 FCM聚类算法地震记录由有效信号和噪声两部分构成。有效信号部分的第一个时刻被视为地震的发生,即初至波的到达时刻。因此,在给定一组数据的情况下,初至拾取的本质就变成了分类问题。当一组训练数据与预定义的数据特征一起给出时,这种分类问题可被视为监督分类问题。若只使用数据本身的属性特征对地震记录进行分类,该问题就变成了典型的聚类分析问题,即非监督机器学习[17]。
模糊聚类分析是一种利用模糊数学语言对事物按照一定标准进行分类的数学方法[18],通过利用聚类对象的属性特征建立模糊矩阵,并在其之上按适当隶属度进行聚类分析。因此每个点可属于具有不同隶属度的两个或更多聚类,即不再像传统分类一样只属于某一类,而是可通过多个隶属度矩阵表示数据点属于不同分类的概率[19]。FCM是一种目标函数迭代优化基础上的非监督聚类分析方法。相比于监督机器学习方法,非监督学习方法只对数据本身进行模糊聚类分析且在实现过程中不需人为干预;另外,无需大量训练样本,相比于监督机器学习方法,其计算速度更快。
FCM方法的实现过程:首先是构建目标函数;然后不断迭代更新隶属度矩阵和聚类中心,让目标函数取到极小值;最终根据最小误差原则获取较好聚类分析结果。该聚类结果并非每个数据点属于哪个分类,而是每个数据点对聚类中心的隶属概率,它允许一个数据属于两个或多个聚类[20]。
FCM是基于以下目标函数的最小化[21]
| $ J = \sum\limits_{i = 1}^N {\sum\limits_{j = 1}^C {\mathit{\boldsymbol{u}}_{i,j}^m} } {\left\| {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{c}}_j}} \right\|^2}\quad 1 \le m \le \infty $ | (1) |
式中:m为模糊指标;xi表示nx维数据中的第i个数据点(nx是xi的维数);ui,j表示分类j中xi的隶属度;cj表示nc维的聚类中心;‖·‖表示任意数据点与聚类中心之间的相似性的某种范数(如L2);C表示聚类数目;N表示输入数据的个数。
xi和cj是相同维度向量,其维数由特征函数的数量决定,本文用均值M、能量E和长短时窗均值(STA、LTA)之比R作为初至拾取的三个特征函数,每个xi由对应采样点i处所有特征函数值组成。
三个特征函数定义如下
| $ {M(i) = \frac{1}{{{T_{\rm{w}}}}}\sum\limits_{i - N/2}^{i + N/2} d (i)} $ | (2) |
| $ {E(i) = \frac{1}{{{T_{\rm{w}}}}}\sum\limits_{i - N/2}^{i + N/2} {{d^2}} (i)} $ | (3) |
| $ \left\{ {\begin{array}{*{20}{l}} {R(i) = \frac{{ {\rm{STA}} (i)}}{{ {\rm{LTA}} (i)}}}\\ { {\rm{STA}}(i) = \frac{1}{{{N_{{\rm{STA}}}}}}\sum\limits_{j = i - {N_{{\rm{STA}}}}}^i d (j)}\\ { {\rm{LTA}}(i) = \frac{1}{{{N_{{\rm{LTA}}}}}}\sum\limits_{j = i - {N_{{\rm{LTA}}}}}^i d (j)} \end{array}} \right. $ | (4) |
式中:Tw为时窗长度;d(i)为地震记录;NLTA、NSTA表示长、短时窗长度。
通过式(1)的迭代优化进行模糊分类,其中隶属度ui, j和聚类中心cj的更新表达式分别为
| $ {{\mathit{\boldsymbol{u}}_{i,j}} = \frac{1}{{\sum\limits_{k = 1}^C {{{\left( {\frac{{\left\| {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{c}}_j}} \right\|}}{{\left\| {{\mathit{\boldsymbol{x}}_i} - {\mathit{\boldsymbol{c}}_k}} \right\|}}} \right)}^{\frac{2}{{m - 1}}}}} }}} $ | (5) |
| $ {{\mathit{\boldsymbol{c}}_j} = \frac{{\sum\limits_{i = 1}^N {\mathit{\boldsymbol{u}}_{i,j}^m} {\mathit{\boldsymbol{x}}_i}}}{{\sum\limits_{i = 1}^N {\mathit{\boldsymbol{u}}_{i,j}^m} }}} $ | (6) |
当
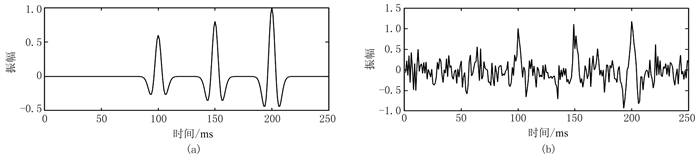
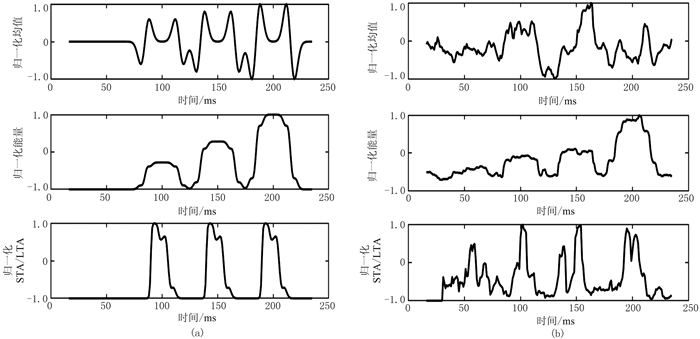
为了验证FCM方法的有效性,合成了简单的无噪声(图 1a)和含噪声(图 1b,信噪比为1dB)的单道数据,得到对应数据的三个特征函数(图 2)。
|
图 1 无噪(a)和含噪(b,1dB)简单合成数据 |
|
图 2 无噪(a)和含噪(b,1dB)数据聚类算法特征函数 |
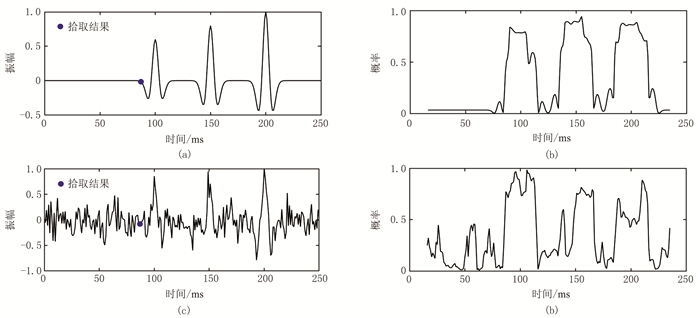
图 3为简单合成数据计算得到的拾取结果和隶属度,可见利用三个特征函数(图 3a、图 3b为无噪声,图 3c、图 3d为含噪声)同时进行聚类分析能得到较好结果,可拾取有效信号,拾取位置大致相同,即证明该方法能有效地拾取初至。利用三个特征函数对计算互相约束,可提高聚类分析的稳定性,增强方法的抗干扰能力。
|
图 3 聚类分析的计算结果 (a)无噪声拾取结果;(b)无噪声隶属度;(c)含噪声拾取结果;(d)含噪声隶属度 |
SVI是一种完全数据驱动的方法,不依赖地震数据的频率或视速度信息[22]。传统的SVI方法使用互相关和卷积叠加的方法,通过大幅提高信噪比增强初至信号[23]。但经过处理后,地震子波旁瓣数量增加,旁瓣能量也同时提升。Nakata等[24]提出了基于互相干代替互相关的地震数据干涉重构方法,很好地从本质上避免了SVI处理后初至波产生的虚假旁瓣。Place等[25]将该方法应用到浅层主动源地震数据中,并对比与互相关应用效果的差别。
首先,对检波点R1与R2处记录的信号做相互干(图 4a),得到虚拟记录,它表示由虚拟源R'1产生的信号(包括负旅行时间,图 4a中的虚线)在检波点R2处被接收。对位于检波点R1临界炮检距(初至波由直达波变为折射波所对应的炮检距)后的任何震源S重复该过程,可产生相同效果的虚拟记录。对这些记录叠加求和,增强由R′1产生的虚拟信号,并衰减非相干噪声,以提高数据信噪比。当源位于位置S时,将叠加的虚拟记录与检波点R1的原始记录进行卷积,产生SVI记录,就像由震源S产生在检波点R2接收的记录一样。对于S与R2之间超出临界距离的所有检波点R1,可获得相同效果的SVI记录,叠加求和进一步提高数据信噪比[26]。
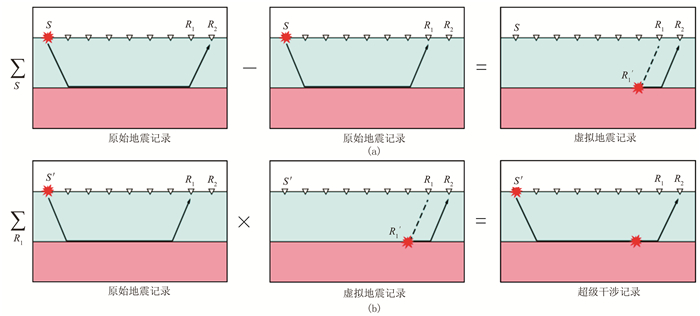
|
图 4 SVI方法原理示意图 |
将两个不同点R1和R2处记录的两条地震数据的互相关在傅里叶域中定义为
| $ {C_{{R_1}{R_2}}} = u({R_1},S){u^*}({R_2},S) $ | (7) |
式中:u(R1, S)表示震源S在检波点R1记录的地震波场;*表示复共轭。
互相干定义为频率归一化的互相关,表示为
| $ \begin{array}{*{20}{l}} {{R_2} = \frac{{{C_{{R_1},{R_2}}}}}{{|u({R_1},S)||u({R_2},S)|}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{u({R_1},S){u^*}({R_2},S)}}{{|u({R_1},S)||u({R_2},S)|}}} \end{array} $ | (8) |
式中|·|表示振幅谱。
互相干表达式(式(8))的分子与互相关表达式(式(7))相同,分母为波的振幅谱的乘积。与互相关相比,互相干忽略振幅信息的影响,只使用相位信息,有效地从提取的地震信号中去除震源的特征,即使在强噪声情况下也能得到稳定的结果,因此互相干比互相关更稳健。
忽略噪声的存在,可将从震源S处到R处记录的地震波场写为傅里叶域中的乘积
| $ u(R,S) = W(S)G(R,S) $ | (9) |
式中:W(S)是信号源在S处产生的信号;G(R,S)是R与S之间的格林函数。
恢复震源特征是SVI方法的重要步骤[25],将式(9)分别代入式(7)和式(8),可得
| $ {{C_{{R_1}{R_2}}} = |W(S){|^2}G({R_1},S){G^*}({R_2},S)} $ | (10) |
| $ {{H_{{R_1}{R_2}}} = \frac{{G({R_1},S){G^*}({R_2},S)}}{{|G({R_1},S)||{G^*}({R_2},S)|}}} $ | (11) |
虚拟记录与实际原始记录卷积形成SVI地震记录,重新恢复震源的特征(图 4b),表示为
| $ \begin{array}{*{20}{l}} {{u_{{\rm{SVI}}}}({R_2},{S^\prime }) = \sum\limits_{{R_1} = {R_{{\rm{1min}}}}}^{{R_{{\rm{1max}}}}} W ({S^\prime })G({R_1},{S^\prime }) \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{S = {S_{{\rm{min}}}}}^{{S_{{\rm{max}}}}} {\frac{{G({R_1},S){G^*}({R_2},S)}}{{|G({R_1},S)||{G^*}({R_2},S)|}}} } \end{array} $ | (12) |
式中uSVI表示SVI处理后的波场,第二个总和项表示叠加的互相干函数(图 4a)。
2 初至拾取流程基于SVI方法约束的FCM地震初至拾取流程如图 5所示,具体实现过程如下。

|
图 5 基于SVI方法约束的FCM地震初至拾取流程 |
(1) 加窗处理获取包含初至信号的地震资料——加窗可避免对全波场进行运算,降低计算量并减少虚假同相轴的产生;
(2) 选取某炮,将检波点R1与R2的波场做互相干处理,得到虚拟记录;
(3) 将每炮互相干处理结果做叠加求和,增强虚拟记录的能量,提高信噪比,得到检波点R1与R2之间的虚拟记录;
(4) 选取震源S,将检波点R1波场与检波点R1和R2之间虚拟记录做卷积处理,得到SVI记录;
(5) 对每道卷积结果叠加求和,增强SVI记录,再次提高信噪比,得到最终经SVI处理的信号;
(6) 将处理后的记录作为FCM算法的输入数据进行计算,给定算法参数,如聚类数目C、模糊指标m、迭代停止条件ε;
(7) 初始化隶属度矩阵U,U(0)=[ui, j];
(8) 利用U(k)根据式(6)计算聚类中心c(k)=[cj];
(9) 根据式(5)更新U(k),得到U(k+1);
(10) 如果‖U(k+1)-U(k)‖<ε,则停止迭代,输出拾取结果;否则k=k+1,返回第3步继续计算。
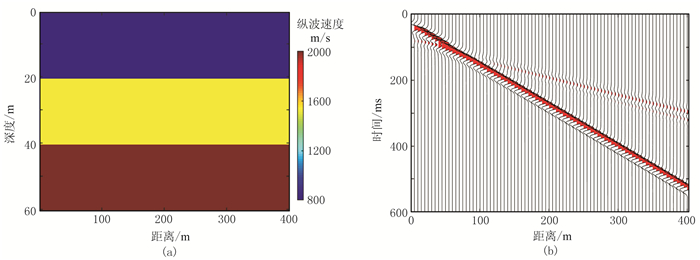
3 理论模型测试 3.1 水平层状模型为了验证本文方法的有效性和稳定性,建立了一个三层水平层状纵波速度模型(图 6a)并进行声波有限差分正演模拟(图 6b)。第一层(0~20m)、第二层(20~40m)、第三层(40~60m)的速度依次为800、1600、2000m/s,采用主频为30Hz的雷克子波,时间采样间隔为0.5ms,炮间距为5m,道间距为5m。在正演数据中加入不同程度的高斯随机噪声,模拟不同信噪比时的初至拾取。
|
图 6 水平层状模型(a)及其正演模拟数据(b) |
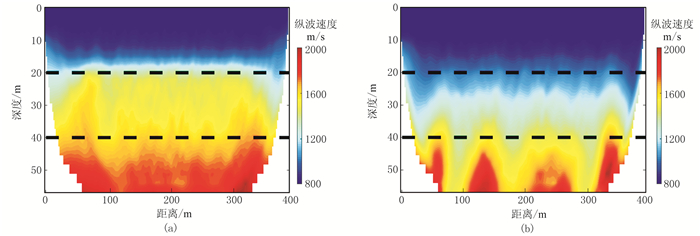
图 7为当原始记录SNR=25dB时的FCM方法和STA/LTA方法的单炮初至拾取结果(蓝色圆点)。图 8为使用基于射线追踪方法的层析成像方法对两种方法拾取结果进行纵波速度层析成像,图中黑色虚线为真实模型的速度分界面。可见当噪声不太强时,FCM方法能较准确地拾取初至,反演结果也与实际模型较相符;而STA/LTA方法的拾取虽大致准确,但由于参数选择固定,存在一定误差;纵波速度成像结果与真实模型不能较好匹配。

|
图 7 SNR=25dB时FCM(a)和STA/LTA(b)方法地震记录初至拾取结果 |
|
图 8 FCM(a)和STA/LTA(b)方法纵波速度层析成像结果 |
当SNR=15dB时(图 9),FCM和STA/LTA方法初至拾取都不准确,FCM方法只能拾取信噪比较高的近炮检距信号,而STA/LTA方法受噪声影响更严重,错误拾取非常多。

|
图 9 SNR=15dB时FCM(a)和STA/LTA(b)方法地震记录初至拾取结果 |
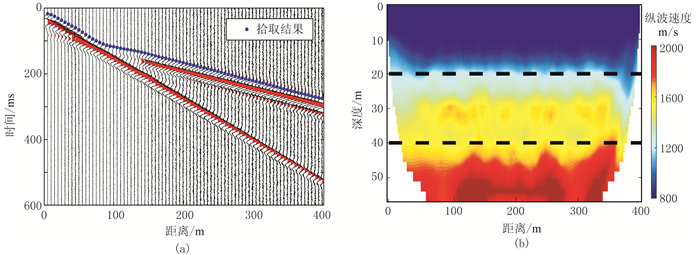
使用基于SVI的FCM方法进行拾取(图 10a),经过SVI处理后,折射波能量明显加强,噪声受到压制,远炮检距信噪比明显提高,可有效判定并识别真实的初至信号。从其反演结果(图 10b)看出,与真实速度模型较为匹配,进一步说明拾取的准确性。
|
图 10 SNR=15dB时基于SVI的FCM初至拾取结果(a)和纵波速度层析成像结果(b) |
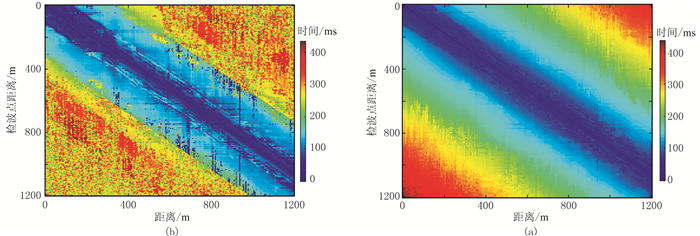
图 11a和图 11b分别为对原始数据使用FCM拾取和使用基于SVI的FCM拾取的初至时间二维图。在原始数据中只能拾取近炮检距信号,远炮检距无法拾取,但经SVI处理后,远炮检距拾取效果明显改善。

|
图 11 针对原始数据单独FCM(a)和基于SVI的FCM(b)方法初至时间二维图 |
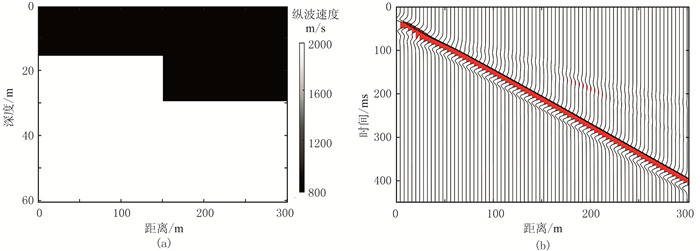
为进一步验证本文方法的有效性,建立如图 12a所示的台阶速度模型。其上层速度为800m/s,左侧深度为15m,右侧深度为30m,台阶在150m处,下层速度为2000m/s,时间采样间隔为0.5ms,采用主频为30Hz的雷克子波,炮间距为4m,道间距为4m。正演得到的地震记录如图 12b所示。
|
图 12 台阶理论模型(a)及其正演模拟数据(b) |
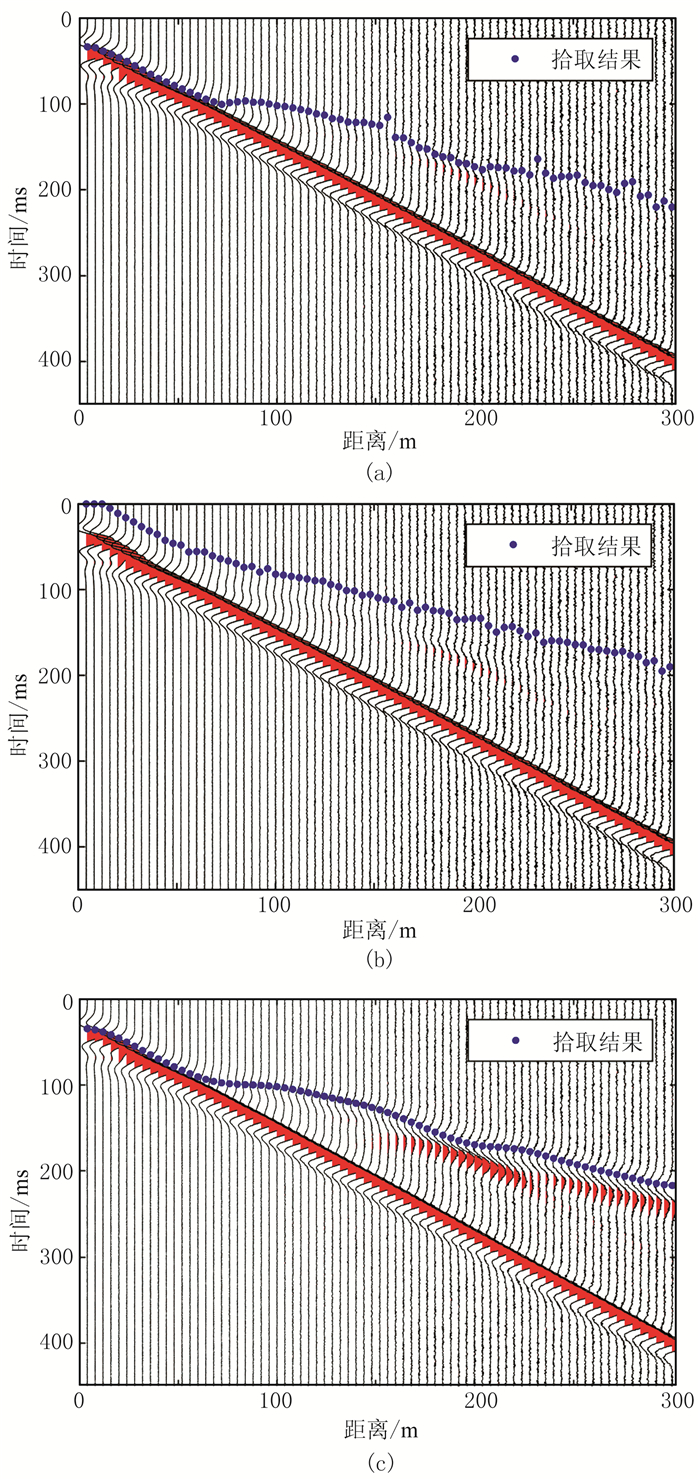
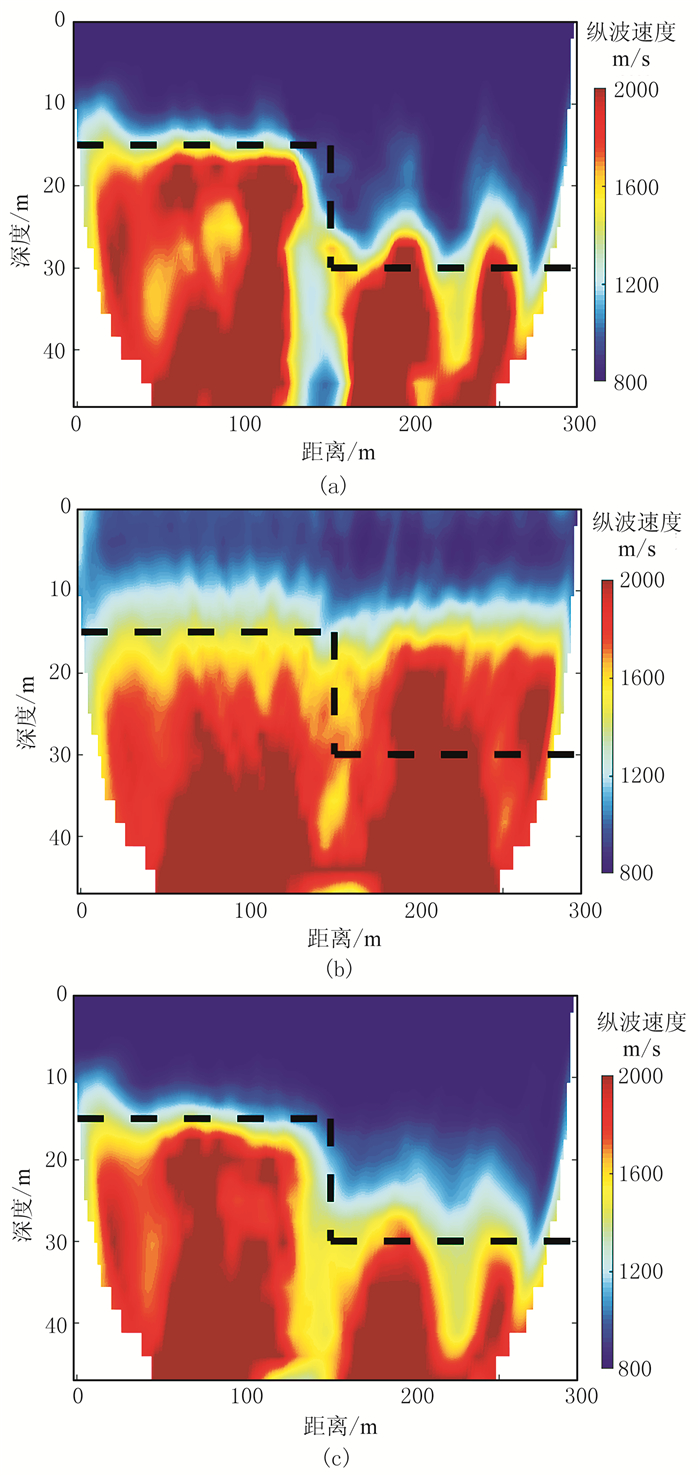
在该数据中加入不同程度的高斯随机噪声。图 13a和图 13b分别为当原始记录SNR=25dB时的FCM方法和STA/LTA方法的单炮初至拾取结果(蓝色圆点)。图 14a和图 14b为使用基于射线追踪方法的初至层析对两种方法的拾取结果进行层析成像,黑色虚线为真实模型的速度分界面。可知当噪声强度不太强时,FCM方法能较准确拾取初至,反演结果也与实际模型较为匹配,只在右侧分界面稍上移,原因是200m炮检距后的拾取不够准确。而STA/LTA方法的拾取在近炮检距也大致准确,但远炮检距的拾取结果不准确,基本变成直线,无细节变化,从反演结果(图 14b)可见,导致台阶右侧的反演结果与实际模型不能匹配。
|
图 13 SNR=25dB时地震记录初至拾取结果 (a)FCM;(b)STA/LTA;(c)基于SVI的FCM |
使用基于SVI的FCM方法进行初至拾取,结果见图 13c。与只使用FCM方法拾取相比,远炮检距拾取更准确,从反演结果(图 14c)可知,右侧高速层反演效果明显改善,与实际模型较吻合。
|
图 14 纵波速度层析成像结果 (a)FCM;(b)STA/LTA;(c)基于SVI的FCM |
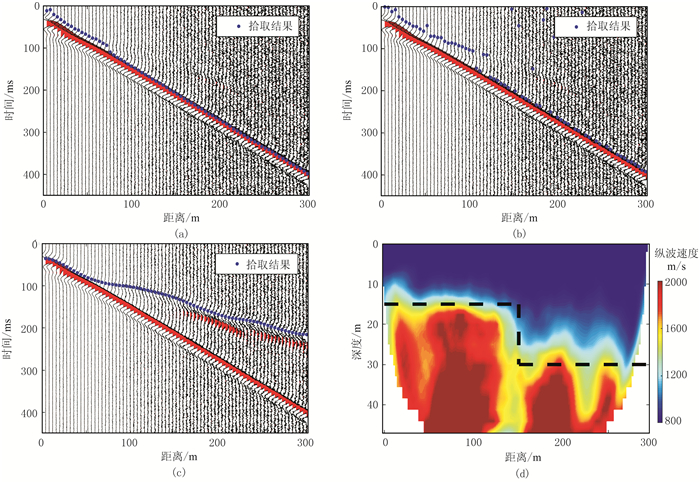
当SNR=15dB时(图 15),远炮检距的初至信号已经无法分辨。FCM方法和STA/LTA方法初至拾取都不准确,远炮检距都只能错误地拾取到直达波上。使用基于SVI的FCM方法进行拾取,经过SVI处理后(图 15c),初至信号能量明显加强,噪声受到压制,信噪比明显提高,可准确地拾取初至信号。由反演结果图(图 15d)看出,反演模型较为匹配,进一步说明拾取结果的准确性。
|
图 15 SNR=15dB时地震记录初至拾取结果及基于SVI的FCM拾取后层析成像结果 (a)FCM;(b)STA/LTA;(c)基于SVI的FCM;(d)基于SVI的FCM拾取后纵波速度层析成像 |
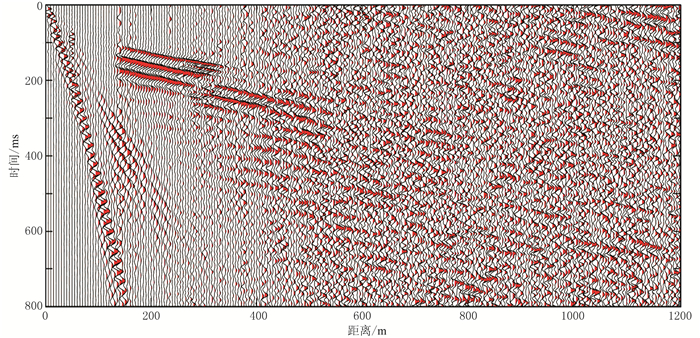
选取沙特吉达地区实际地震资料进行应用测试。数据剖面长度为1200m,采样间隔为1ms,共包含212炮记录,每炮240道接收,道间距和炮间距均为5m。图 16为该资料的单炮记录,该资料远炮检距初至信号极弱,信噪比极低,噪声干扰非常严重,初至难以准确拾取。
|
图 16 实际地震数据单炮记录 |
原始地震数据经过SVI处理后(图 17),远炮检距的噪声得到有效压制,初至同相轴清晰可辨。由于信噪比的提高,能够拾取远炮检距的初至信号。图 18a和图 18b分别为使用基于SVI的FCM拾取的和只使用FCM拾取的初至二维图,对比看出SVI处理后远炮检距信息拾取效果明显提高。

|
图 17 基于SVI的FCM初至拾取结果 |
|
图 18 针对实际资料单独FCM(a)和基于SVI的FCM(b)方法初至时间二维图 |
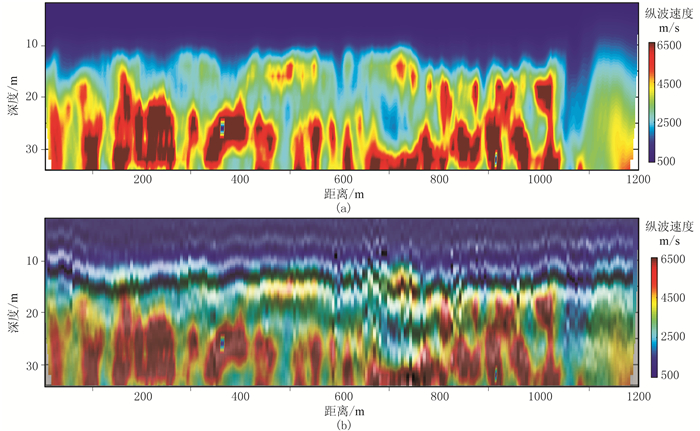
图 19a为利用SVI处理后的初至拾取结果进行层析成像的速度成像结果。根据前期在该区域开展的地质调查和相关地球物理研究成果[27],测线横跨一条南北向的Qademah断层,该断层缘于红海海域隆起形成的不连续速度结构。根据前人研究成果,在测线300m附近是断层位置。图 19a所示的速度成像结果中的低速下凹与地质情况吻合。为了验证反演结果的可靠性,与共炮检距剖面(图 19b)进行对比。在缺少钻井资料情况下,可认为共炮检距剖面能够反映重要的地下结构分布特征[28]。图 19b所示的共炮检距剖面水平方向不连续分布与速度成像高低速变化带有很好的一致性,特别是在横向300m和700m附近的低速不连续带吻合很好。
|
图 19 实际地震纵波速度层析成像(a)及共炮检距剖面与速度成像剖面拟合图(b) |
本文针对低信噪比地震资料中,特别是远炮检距初至信号弱、噪声强,无法准确地自动拾取初至信号的问题,提出了利用基于SVI约束的FCM聚类分析初至自动拾取方法。其基本思路是首先通过SVI方法提高地震记录远炮检距信号的信噪比,在此基础上,利用FCM算法的初至拾取方法对加强后的信号进行自动拾取。理论模型正演数据和实际地震资料对方法的有效性和适用性进行了验证,即实现了在低信噪比数据条件下,自动、快速拾取地震记录初至,达到了满意的计算效率和计算精度。通过层析成像速度反演结果也验证了拾取结果的可靠性。本文研究方法为地震数据处理提供了一种稳健、可靠的技术手段。
| [1] |
Senkaya M, Karsli H. A semi-automatic approach to identify first arrival time:the cross-correlation technique (CCT)[J]. Earth Sciences Research Journal, 2014, 18(2): 107-113. |
| [2] |
Peraldi R, Clement A. Digital processing of refraction data study of first arrival[J]. Geophysical Prospecting, 1972, 20(3): 529-548. DOI:10.1111/j.1365-2478.1972.tb00653.x |
| [3] |
Coppens F. First arrival picking on common-offset trace collections for automatic estimation of static corrections[J]. Geophysical Prospecting, 1985, 33(8): 1212-1231. DOI:10.1111/j.1365-2478.1985.tb01360.x |
| [4] |
Withers M, Aster R, Young C, et al. A comparison of select trigger algorithms for automated global seismic phase and event detection[J]. Bulletin of the Seismological Society of America, 1998, 88(1): 95-106. |
| [5] |
左国平, 王彦春, 隋荣亮. 利用能量比法拾取地震初至的一种改进方法[J]. 石油物探, 2004, 43(4): 345-347. ZUO Guoping, WANG Yanchun, SUI Rongliang. An improved method for first arrival pickup using energy ratio[J]. Geophysical Prospecting for Petroleum, 2004, 43(4): 345-347. |
| [6] |
徐钰, 曾维辉, 宋建国, 等. 浅层折射波勘探中初至自动拾取新算法[J]. 石油地球物理勘探, 2012, 47(2): 218-224. XU Yu, ZENG Weihui, SONG Jianguo, et al. A new method for first-break picking in refraction exploration[J]. Oil Geophysical Prospecting, 2012, 47(2): 218-224. |
| [7] |
Kalkan E. An automatic P-phase arrival-time picker[J]. Bulletin of the Seismological Society of America, 2016, 106(3): 971-986. DOI:10.1785/0120150111 |
| [8] |
Boschetti F, Dentith M D, List R D. A fractal-based algorithm for detecting first arrivals on seismic traces[J]. Geophysics, 1996, 61(4): 1095-1102. |
| [9] |
韩小俊, 施泽进, 李亚林. 利用分形维拾取地震波初至的一种改进算法[J]. 石油地球物理勘探, 2002, 37(1): 60-63. HAN Xiaojun, SHI Zejin, LI Yalin. An improved algorithm for picking up seismic first arrivals by using fractal dimension[J]. Oil Geophysical Prospecting, 2002, 37(1): 60-63. |
| [10] |
李辉峰, 邹强, 金文昱. 基于边缘检测的初至波自动拾取方法[J]. 石油地球物理勘探, 2006, 41(2): 150-155, 159. LI Huifeng, ZOU Qiang, JIN Wenyu. Method of automatic first breaks pick-up based on edge detection[J]. Oil Geophysical Prospecting, 2006, 41(2): 150-155, 159. |
| [11] |
谭玉阳, 于静, 冯刚, 等. 微地震事件初至拾取SLPEA算法[J]. 地球物理学报, 2016, 59(1): 185-196. TAN Yuyang, YU Jing, FENG Gang, et al. Arrival picking of microseismic events using the SLPEA algorithm[J]. Chinese Journal of Geophysics, 2016, 59(1): 185-196. |
| [12] |
胡瑞卿, 王彦春, 尹志恒, 等. 结合CEEMDAN和主成分分析的低信噪比微地震初至信号检测[J]. 石油地球物理勘探, 2019, 54(1): 45-53. HU Ruiqing, WANG Yanchun, YIN Zhiheng, et al. A first arrival detection method in low SNR microseismic signals based on CEEMDAN-PCA[J]. Oil Geophysical Prospecting, 2019, 54(1): 45-53. |
| [13] |
Comaniciu D, Meer P. Distribution free decomposition of multivariate data[J]. Pattern Analysis and Application, 1999, 2(1): 22-30. DOI:10.1007/s100440050011 |
| [14] |
Mallinson I, Bharadwaj P, Schuster G, et al. Enhanced refractor imaging by supervirtual interferometry[J]. The Leading Edge, 2011, 30(5): 546-550. DOI:10.1190/1.3589113 |
| [15] |
安圣培, 梁向豪, 彭更新, 等. 低信噪比地震数据折射初至的判定与识别[J]. 石油地球物理勘探, 2015, 50(3): 451-459. AN Shengpei, LIANG Xianghao, PENG Gengxin, et al. Recognization and identification of first arrival refractions in low SNR prestack seismic data[J]. Oil Geophysical Prospecting, 2015, 50(3): 451-459. |
| [16] |
Li J, Hanafy S, Schuster G T. Parsimonious surface wave interferometry[J]. Geophysical Journal International, 2018, 212(3): 1536-1545. DOI:10.1093/gji/ggx467 |
| [17] |
Chen Yangkang. Automatic microseismic event pick-ing via unsupervised machine learning[J]. Geophysical Journal International, 2018, 212(1): 88-102. DOI:10.1093/gji/ggx420 |
| [18] |
Bezdek J C, Hathaway R J, Sabin M J, et al. Convergence theory for fuzzy c-means:counter examples and repairs[J]. IEEE Transactions on Systems, Man, and Cybernetics, 1987, 17(5): 873-877. DOI:10.1109/TSMC.1987.6499296 |
| [19] |
Dunn J C. A fuzzy relative of the ISODATA process and its use in detecting compact well-separated clusters[J]. Journal of Cybernetics, 1973, 3(3): 32-57. DOI:10.1080/01969727308546046 |
| [20] |
Bezdek J C. Cluster validity with fuzzy sets[J]. Cybernetics and Systems, 1973, 3(3): 58-74. |
| [21] |
Bezdek J C.Pattern Recognition with Fuzzy ObjectiveFunction Algorithms[M]. Plenum Press, 1981.
|
| [22] |
吕雪梅, 安圣培, 胡天跃, 等. 相似度加权的超虚干涉法加强初至波信号[J]. 北京大学学报(自然科学版), 2018, 54(1): 87-93. LYU Xuemei, AN Shengpei, WU Tianyue, et al. Similarity-weighted super-virtual interferometry to enhance first breaks[J]. Acta Scientiarum Naturalium Universitatis Pekinensis, 2018, 54(1): 87-93. |
| [23] |
Li J, Lu K, Hanafy S, et al. Two robust imaging metho-dologies for challenging environments:Wave-equation dispersion inversion of surface waves and guided waves and supervirtual interferometry+tomography for far-offset refractions[J]. Interpretation, 2018, 6(4): SM27-SM37. DOI:10.1190/INT-2017-0229.1 |
| [24] |
Nakata N, Snieder R, Tsuji T, et al. Shear wave imaging from traffic noise using seismic interferometry by cross-coherence[J]. Geophysics, 2011, 76(6): SA97-SA106. DOI:10.1190/geo2010-0188.1 |
| [25] |
Place J, Draganov D, Malehmir A, et al. Crosscohe-rence based interferometry for the retrieval of first arrivals and subsequent tomographic imaging of differential weathering[J]. Geophysics, 2019, 84(4): Q37-Q48. |
| [26] |
梁上林, 胡天跃, 崔栋, 等. 初至拾取中基于超级虚折射干涉的信号加强[J]. 石油物探, 2019, 58(4): 509-516. LIANG Shanglin, HU Tianyue, CUI Dong, et al. Signal enhancement based on super-virtual refraction interferometry in first arrival pickup[J]. Geophysical Prospecting for Petroleum, 2019, 58(4): 509-516. |
| [27] |
Li J, Hanafy S. Skeletonized inversion of surface wave:Active source versus controlled noise comparison[J]. Interpretation, 2016, 4(3): SH11-SH19. DOI:10.1190/INT-2015-0174.1 |
| [28] |
Li J, Hanafy S, Schuster G T. Dispersion inversion of guided P-waves in a waveguide of arbitrary geometry[J]. Journal of Geophysical Research:Solid Earth, 2018, 123(9): 7760-7774. DOI:10.1029/2018JB016127 |



 李静, 吉林省长春市西民主大街938号吉林大学地球探测科学与技术学院, 130021。Email:
李静, 吉林省长春市西民主大街938号吉林大学地球探测科学与技术学院, 130021。Email: