空间采样间隔直接影响所采集原始地震数据的质量,进而影响地震数据处理及解释效果[1-3]。Vermeer[1]在三维地震勘探设计中认为采样间隔Δxs和Δxr不大于最小波长的半个周期时,就能精确地重建地下连续波场,即存在
| $ \Delta {x_{\rm{s}}} = \Delta {x_{\rm{r}}} \le \frac{1}{{2{k_{{\rm{max}}}}}} = \frac{{{v_{{\rm{min}}}}}}{{2{f_{{\rm{max}}}}}} $ | (1) |
式中:kmax为地震波传播的最大波数;vmin为最小传播速度;fmax为最高频率。据此,他提出空间采样间隔只有在对偏移孔径内的绕射达到无假频采样时,才能不损害期望波场的高频成分。
秦广胜等[4]将偏移算子去假频准则定义为地震数据中算子轨迹与地震道相交处不产生假频的最大时间频率,并且它是局部算子倾角和道间距的函数。为了不产生假频,沿算子轨迹求和的地震道采样序列必须满足尼奎斯特采样准则,即
| $ \Delta \rho \le \frac{{{v^2}}}{{2{f_{{\rm{max}}}}}}{\left( {\frac{{{\rho _{\rm{s}}}}}{{{t_{\rm{s}}}}} + \frac{{{\rho _{\rm{r}}}}}{{{t_{\rm{r}}}}}} \right)^{ - 1}} $ | (2) |
式中:Δρ为对地下旅行时面的采样间隔,也就是面元中心点间距;ts是炮点到成像点的旅行时;tr为检波点到成像点的旅行时;ρs和ρr分别为炮点和检波点与成像点在同一水平投影面上的距离。对于叠前偏移不满足上式的空间采样准则会导致严重的偏移噪声。
王伟[5]通过对空间采样影响因素进行分析,认为空间采样间隔的减小对地震资料的分辨率、资料处理流程中静校正、动校正与速度分析、叠加和偏移等方面都有正面影响。
马在田[6]从算法理论的角度对偏移剖面中的假频、频散和横向分辨力做了系统论述,阐述了偏移剖面上的假频、横向分辨力与地震采样有关。夏洪瑞[7]指出道间距过大对偏移结果的影响主要是导致空间假频现象的出现、偏移速度场难以准确建立、偏移横向误差大及偏移信息量少,与具体偏移算法无关;并应用理论模型及实际资料对上述结论进行了验证。侯嵩等[8]研究了道间距的变化对地震数据偏移的影响, 认为道间距的大小必须满足空间采样定理,否则会产生空间假频,且这些假频会带到偏移过程中从而影响成像质量;其次,采用近似差分算子或条件稳定差分格式的有限差分偏移算法对道间距有一定要求;否则迭代计算过程将不收敛,且产生频散,而对于其他格式的差分法偏移和积分法偏移,道间距越小,越有利于改善成像效果。
狄帮让等[9]讨论了面元尺寸对地震成像分辨率的影响并认为:对于平缓地层,面元尺寸不影响地震成像的纵向分辨率;对于倾斜地层,应做进一步的实验研究;减小面元尺寸可有限地提高横向分辨率;在不同前提条件下,应优化选择不同大小的面元。张军华等[10]也认为面元尺寸会影响地质体的横向分辨率。熊金良等[11]指出小面元本身并未提高纵向分辨率,实质只是通过面元叠加提高高频段信噪比,进而提高纵向分辨率。钱荣钧[12]认为空间采样密度和分布的均匀性与偏移剖面的纵、横向分辨率有关,并且直接影响去噪效果和偏移噪声大小,进一步提出了要提高勘探精度,不仅需要增加空间采样的密度,而且需要空间采样均匀。
郭恺等[13]在地震采集面元尺度一般性设计的基础上,通过正演模拟成像,证明不同采集道距的成像解释结果差异较大。道距越大,解释难度越大,误差也越大;道距越小,成像解释结果与实际地质构造越接近。张媛等[14]结合哈山东的实际资料,分析不同面元的叠前时间偏移成像效果,证明小面元数据能够改善偏移成像的效果。刘军等[15]根据南海珠江口盆地实际资料,应用弹性波动方程实现纵波道集正演,模拟不同面元采集数据的成像,结果表明小面元采集能避免空间假频干扰,保护绕射弧的陡倾高频信息,降低反假频算子对砂体边界、陡倾地层能量归位的影响。
上述文章论述的空间采样都是基于以下两种地震成像理论:一是基于反射波同向叠加理论,要求空间采样满足无混叠假频;二是基于绕射点的偏移理论,要求空间采样满足无偏移假频,两种地震成像理论导出的计算公式形式均可表示为[16]
| $ \Delta x = \frac{{{v_{{\rm{int}}}}}}{{2{f_{{\rm{max}}}}{\rm{sin}}\theta }} $ | (3) |
式中:Δx为采样间隔(道间距或炮点距最小值);vint为目的层的层速度;fmax为最高无混叠频率;θ为地层倾角或偏移倾角。考虑空间采样无混叠假频时θ可理解为地层倾角,考虑空间采样满足无偏移假频时θ可理解为偏移倾角。偏移倾角一般取30°,这样能够收敛95%的绕射能量。因此,在地层倾角较小时,绕射波控制采样间隔,θ表示偏移倾角;在地层倾角大于30°时,倾角决定采样间隔,θ则表示地层倾角。
从以上公式可知,空间采样的选择只考虑对反射波的无假频采样,或只考虑对偏移孔径内的绕射无假频采样,则对于水平地层和倾斜地层上绕射点的偏移成像而言,空间采样间隔取决于绕射能量收敛;在地层倾角大于30°时,空间采样只与地层倾角有关,与偏移成像要求无关。这就表明以往空间采样间隔计算公式不适用于陡倾地层的地震偏移成像。因此,基于地倾斜地层绕射波场的分布特征,按照地震偏移成像对绕射波场保护的要求,选择满足地震偏移成像需要的空间采样参数具有实际意义。
2 地震波空间采样的理论推导 2.1 偏移的实质分析目前业界最常用的偏移成像方法是Kirchhoff时间偏移。Kirchhoff时间偏移的实现过程:将绕射波轨迹拉平,沿拉平轨迹进行波场求和[17];再将得到的值置于绕射点位置上,这就实现了绕射波场的偏移(图 1)[18]。为了简单起见,以绕射积分叠后偏移为例,偏移前地震波场是叠加数据,沿着绕射波轨迹求和,实际上是三种波场的叠加,即反射波、绕射波和随机噪声。随着绕射波轨迹的拉平,反射波变成与绕射波呈镜像关系的曲线。因此,偏移的实质就是:①绕射同相叠加;②随机干扰为满足统计规律的叠加;③反射波非同相叠加。对于同相叠加来说,一道与多道的叠加结果是一样的,即绕射波的偏移收敛与空间采样无关系。对于随机干扰而言,空间采样的非规则分布增加了随机干扰的随机性,有利于实现统计压噪[19]。但对于反射波来说,空间采样的非均匀性直接影响波场的水平方向求和结果,即是直接影响偏移成像效果。
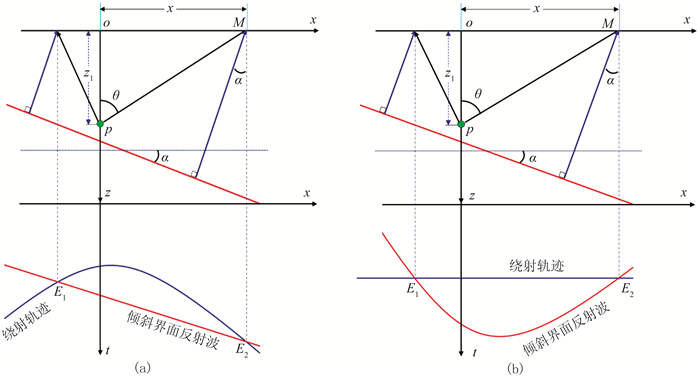
|
图 1 倾斜反射层与绕射点的时距曲线(a)及偏移过程(b)示意图 |
建立倾斜地层反射波场与绕射点波场的直角坐标系,简述一个绕射点和单地层反射波的偏移成像(图 2)。设绕射点p位于原点正下方;S、R分别为地表的一个激发点和接收点;M为S与R之间的中点;h为半炮检距;x为炮检距;θ为偏移倾角,即为y轴与和中点M连线的夹角;z1为绕射点深度;z2为坐标原点处倾斜地层深度;Δz为过M点铅垂线上倾斜地层深度与z2的差值;α为地层倾角,等于地层与x轴的夹角;v表示上覆地层的均方根速度;t1表示从炮点到绕射点、再从绕射点到接收点的传播时间;t2表示炮检距x处倾斜地层的自激自收时间。根据叠加理论,绕射波轨迹的时间方程表示为地表M点至p点的自激自收时间;从图 2坐标关系得到M点至绕射点p的时间距离方程表示为
| $ {t_1} = \frac{2}{v}\sqrt {{x^2} + z_1^2} $ | (4) |
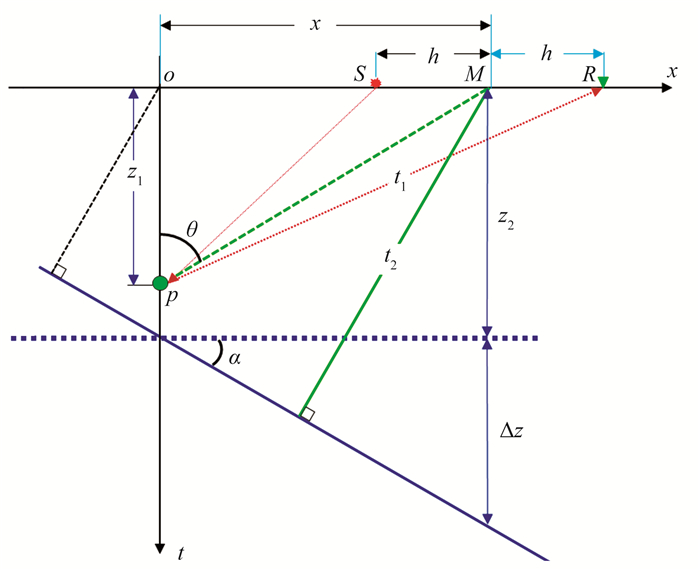
|
图 2 倾斜地层反射波场与点绕射波场直角坐标示意图 |
同理,倾斜地层在M点的时间距离方程也相当于M点到倾斜地层的自激自收时间,从图 2得到时间距离方程为
| $ \begin{array}{*{20}{l}} {{t_2} = \frac{2}{v}({z_2} \pm \Delta z){\rm{cos}}\alpha = \frac{2}{v}({z_2} + x{\rm{tan}}\alpha ){\rm{cos}}\alpha }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{2({z_2}{\rm{cos}}\alpha + x - {\rm{sin}}\alpha )}}{v}} \end{array} $ | (5) |
式中:当地层下倾方向和
结合地震偏移成像理论,根据式(4)的绕射波时距方程,可得绕射波的动校正时差公式
| $ \Delta t = \frac{2}{v}(\sqrt {{x^2} + z_1^2} - {z_1}) $ | (6) |
同理,对式(5)的反射波时距方程进行动校正,动校正后的反射波时间等于反射波时间减去绕射波动校时差,即
| $ t = \frac{2}{v}[({z_2}{\rm{cos}}\alpha + x{\rm{sin}}\alpha ) - \sqrt {{x^2} + z_1^2} + {z_1}] $ | (7) |
对动校正后反射波时间做空间采样微分,得到
| $ \begin{array}{*{20}{l}} {{\rm{d}}t = \frac{2}{v}\left| { \pm {\rm{sin}}\alpha - \frac{{ \pm x}}{{\sqrt {{x^2} + z_1^2} }}} \right|{\rm{d}}x}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{2}{v}|({\rm{sin}}\alpha \mp {\rm{sin}}\theta )|{\rm{d}}x} \end{array} $ | (8) |
根据同相叠加原理,动校正后的反射波时差应不大于反射波的最小半周期,即
| $ {\rm{d}}t = \frac{2}{v}|({\rm{sin}}\alpha \mp {\rm{sin}}\theta )|{\rm{d}}x \le \frac{{{T_{{\rm{min}}}}}}{2} = \frac{1}{{2{f_{{\rm{max}}}}}} $ | (9) |
由此得
| $ {\rm{d}}x \le \frac{v}{{4{f_{{\rm{max}}}}|({\rm{sin}}\alpha \mp {\rm{sin}}\theta )|}} $ | (10) |
地层倾角和偏移倾角都在(0,90°)范围内,但α和θ都具有方向性。当地层下倾方向和
当α与θ方向一致时,式(10)中分母的括号内取“-”号;当α与θ反向时,式(10)中分母的括号内取“+”号。
考虑空间采样间隔计算公式的通用性,sinα和sinθ都为正值,式(10)中分母的括号内取“+”号具有普遍意义,因此倾斜地层反射波的空间采样间隔计算公式表示为
| $ {\rm{d}}x \le \frac{v}{{4{f_{{\rm{max}}}}({\rm{sin}}\alpha + {\rm{sin}}\theta )}} $ | (11) |
当地层水平时,上式就变成了绕射波偏移归位对空间采样要求的计算公式。对于倾斜地层的反射波偏移来说,由于0° < α < 90°,则sinα>0,因此与原来计算空间采样间隔的公式(式(10))相比,更能反映倾斜地层地震偏移成像对空间采样的要求。
2.4 倾斜地层极限空间采样参数分析将式(11)按三角函数“和化积”的方式写成
| $ {\rm{d}}x \le \frac{v}{{8{f_{{\rm{max}}}}{\rm{sin}}\left( {\frac{{\alpha + \theta }}{2}} \right){\rm{cos}}\left( {\frac{{\alpha - \theta }}{2}} \right)}} $ | (12) |
对该式求地层倾角α的导数,当导数为0时,空间采样间隔取到最小值,即
| $ {\rm{cos}}\left( {\frac{{\alpha + \theta }}{2}} \right){\rm{cos}}\left( {\frac{{\alpha - \theta }}{2}} \right) = {\rm{sin}}\left( {\frac{{\alpha + \theta }}{2}} \right){\rm{sin}}\left( {\frac{{\alpha - \theta }}{2}} \right) $ | (13) |
可得cosα=0, 则α=90°。
显然,当地层倾角为90°,即地层直立时,空间采样间隔有极小值。通过以上分析可得对绕射波和反射波的偏移归位实现了理论的统一。地层倾角为零时,公式就退化为绕射波偏移归位的计算公式,即地层倾角越大,空间采样间隔越小;偏移倾角越大,要求的偏移孔径越大,空间采样间隔越小。
2.5 不同成像方式的空间采样间隔计算公式对比不同地震成像方式对地震采集的空间采样间隔要求也不一样:对于倾斜地层的叠加,空间采样间隔的大小取决于地层倾角;对于绕射点偏移,空间采样间隔取决于绕射收敛倾角(30°);对于倾斜地层偏移,空间采样间隔不仅取决于地层倾角,也取决于绕射收敛倾角(30°)。为了进一步说明面向倾斜地层叠加、绕射点偏移归位、倾斜地层偏移成像的空间采样间隔的区别,表 1列举了几种成像方式下各自计算公式,以及地层倾角分别为90°、60°、30°、10°且绕射偏移倾角为30°时的计算公式。
|
|
表 1 不同成像理论的空间采样间隔计算公式对比 |
假设地层倾角分别为0°、10°、30°的简单两层结构(上层速度为1000m/s,下层速度为2000m/s)地质模型,其上只有一个绕射点。绕射点速度为2000m/s,绕射点深度1000m,围岩速度为1000m/s。要保护主频50Hz(最高截止频率为70Hz)的反射信号,按偏移倾角为30°的理论计算,从图 3及表 2中可见:若要满足叠加成像,对于地层倾角为10°的平缓地层,空间采样间隔应不大于20.57m;对于倾角为30°的地层,空间采样间隔应为7.14m。但若要满足倾斜地层偏移成像,对于10°的平缓地层,空间采样间隔应为5.30m;对于倾角30°的地层,空间采样间隔最好不要大于3.57m。

|
图 3 不同成像方式的空间采样参数分析 |
|
|
表 2 不同倾角地层的偏移成像理论计算的空间采样 |
为了验证理论计算结果,选择地层倾角分别为0°、10°、30°,以主频为50Hz的雷克子波合成地震记录,采用绕射波轨迹或偏移算子的参数,对倾斜地层的反射波进行偏移归位,得到图 4所示的从上~下分别对应地层倾角为0°(水平地层)、10°、30°,从左~右空间采样间隔依次为5、10、15m的成像结果。可见当地层倾角为0°时,空间采样间隔10m的成像地震道基本没有假频噪声,采用15m在成像点上方有一些微弱噪声,但不影响成像效果。当地层倾角为10°时,空间采样间隔在10m以下,成像的地震道基本没有假频噪声,而采用15m在成像点上方有一些抖动的噪声,说明存在一定的假频信号。当地层倾角为30°时,要使50Hz的信号成像,空间采样间隔应小于5m。通过上面的对比分析,正演模拟结果与理论计算的空间采样结果吻合良好。
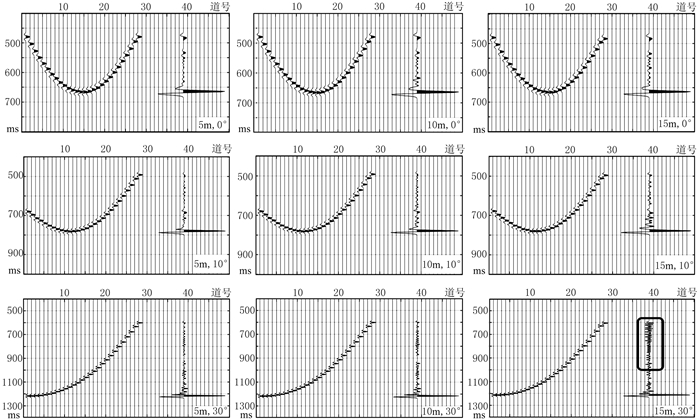
|
图 4 不同倾角倾斜地层在不同空间采样间距时的偏移成像结果 |
(1) 本文提出了满足倾斜地层偏移成像的空间采样间隔计算公式,完善了目前只适用于绕射波归位或水平地层反射波偏移的空间采样间隔计算公式,使基于绕射波和反射波的偏移归位理论的空间采样间隔公式实现了统一。
(2) 根据本文推导的空间采样间隔计算公式,当地层倾角为零时,即退化为绕射波偏移归位计算公式;随着地层倾角变大,所需空间采样间隔越小;随着偏移倾角变大,偏移孔径越大,所需空间采样间隔越小。
(3) 对地层倾角分别为0°、10°、30°的情形做对比分析得知,正演模拟结果与推导的空间采样间隔公式计算结果二者吻合良好。这样就验证了本文空间采样间隔计算公式的正确性,并为地震勘探设计中空间采样参数选择提供了可靠的理论依据。
| [1] |
Vermeer G J O著; 李培明, 何永清译.三维地震勘探设计[M].北京: 石油工业出版社, 2008, 80-82.
|
| [2] |
蔡希玲, 刘学伟, 勾丽敏. 地震采样波场的空间连续性分析方法[J]. 石油地球物理勘探, 2007, 42(4): 370-379. CAI Xiling, LIU Xuewei, GOU Limin. Analytic approaches for spatial continuity of seismic sampled wavefield[J]. Oil Geophysical Prospecting, 2007, 42(4): 370-379. |
| [3] |
Fred W S, Tim G F, Susan G B, et al. How fold and bin size impact data interpretability[J]. The Leading Edge, 1998, 17(9): 1274-1282. DOI:10.1190/1.1438123 |
| [4] |
秦广胜, 蔡其新, 刘学伟, 等. 满足叠前偏移要求的三维地震观测系统设计[J]. 石油地球物理勘探, 2010, 45(增刊1): 25-29. QIN Guangsheng, CAI Qixin, LIU Xuewei. 3D geometry designing for pre-stack migration[J]. Oil Geophysical Prospecting, 2010, 45(S1): 25-29. |
| [5] |
王伟. 谈空间采样对地震勘探资料的影响[J]. 山西建筑, 2016, 42(27): 83-85. WANG Wei. Discussion on the influence of spatial sampling to seismic exploration data[J]. Shanxi Architecture, 2016, 42(27): 83-85. |
| [6] |
马在田. 地震偏移剖面的假频、频散和横向分辨力[J]. 石油地球物理勘探, 1982, 21(4): 16-29. MA Zaitian. The alias, frequency dispersion and lateral resolution of migrated seismic section[J]. Oil Geophysical Prospecting, 1982, 21(4): 16-29. |
| [7] |
夏洪瑞. 道间距对偏移结果影响的讨论[J]. 勘探地球物理进展, 2007, 30(1): 33-38. XIA Hongrui. Effects of group interval on migration[J]. Progress in Exploration Geophysics, 2007, 30(1): 33-38. |
| [8] |
侯嵩, 尹军杰, 王赟, 等. 道间距对地震偏移的影响[J]. 石油地质与工程, 2009, 23(4): 32-34. HOU Song, YIN Junjie, WANG Yun. Effect of group interval on migration[J]. Petroleum Geology and Engineering, 2009, 23(4): 32-34. |
| [9] |
狄帮让, 熊金良, 岳英, 等. 面元大小对地震成像分辨率的影响分析[J]. 石油地球物理勘探, 2006, 41(4): 363-368. DI Bangrang, XIONG Jinliang, YUE Ying, et al. Ana-lysis on influence of bin size on resolution of seismic imaging:study of acquisition parameters based on seismic physical modeling[J]. Oil Geophysical Prospecting, 2006, 41(4): 363-368. |
| [10] |
张军华, 李军, 吴成, 等. 溶洞型储层地震采集参数与成像关系研究[J]. 石油地球物理勘探, 2015, 50(4): 573-579. ZHANG Junhua, LI Jun, WU Cheng, et al. The relationship between seismic acquisition parameters and data imaging in areas with cavern reservoirs[J]. Oil Geophysical Prospecting, 2015, 50(4): 573-579. |
| [11] |
熊金良, 岳英, 杨勇, 等. 面元大小与纵向分辨率关系[J]. 石油地球物理勘探, 2006, 41(4): 489-491. XIONG Jinliang, YUE Ying, YANG Yong, et al. Relationship between bin size and inline resolution[J]. Oil Geophysical Prospecting, 2006, 41(4): 489-491. |
| [12] |
钱荣钧. 关于地震采集空间采样密度和均匀性分析[J]. 石油地球物理勘探, 2007, 42(2): 235-243. QIAN Rongjun. Analysis on spatial sampling density and uniformity of seismic acquisition[J]. Oil Geophy-sical Prospecting, 2007, 42(2): 235-243. |
| [13] |
郭恺, 仝兆岐, 滕厚华. 地震采集面元尺度与成像横向分辨能力分析[J]. 石油与天然气地质, 2012, 33(1): 141-147. GUO Kai, TONG Zhaoqi, TENG Houhua. Analysis on bin size of seismic survey and lateral resolution of imaging[J]. Oil & Gas Geology, 2012, 33(1): 141-147. |
| [14] |
张媛, 莫延钢, 张丽娜, 等.基于叠前偏移的可控震源高密度采集观测系统属性分析[C]. SPG/SEG北京2016国际地球物理会议, 2016, 261-264. ZHANG Yuan, MO Yangang, ZHANG Lina, et al.Geometry attribute analysis of high-density vibroseis acquisition based on pre-stack migration[C]. SPG/SEG Beijing International Geophysical Conference, 2016, 261-264. |
| [15] |
刘军, 史文英, 支玲, 等. 面向砂体的地震采集面元与偏移成像关系研究[J]. 中国海上油气, 2018, 30(2): 54-64. LIU Jun, SHI Wenying, ZHI Ling, et al. Research on the relationship between seismic acquisition bin and migration imaging of sand bodies[J]. China Offshore Oil and Gas, 2018, 30(2): 54-64. |
| [16] |
Ebrom D, Li Xiaohua, McDonald J, et al. Bin spacing in land 3-D seismic surveys and horizontal resolution in time slices[J]. The Leading Edge, 1995, 14(1): 37-40. |
| [17] |
刘本晶, 梁兴, 侯艳, 等. 叠前道集优化技术在页岩储层预测中的应用[J]. 石油地球物理勘探, 2018, 53(增刊2): 189-196. LIU Benjing, LIANG Xing, HOU Yan, et al. Prestack gather conditioning in shale reservoir prediction[J]. Oil Geophysical Prospecting, 2018, 53(S2): 189-196. |
| [18] |
渥·伊尔马滋著; 黄绪德, 袁明德译.地震数据处理[M].北京: 石油工业出版社, 1994, 481-486.
|
| [19] |
臧胜涛, 苏勤, 王建华, 等. 山地复杂构造带地震资料处理方法[J]. 石油地球物理勘探, 2018, 53(增刊1): 62-68. ZANG Shengtao, SU Qin, WANG Jianhua, et al. Seismic data processing methods for complex mountai-nous areas[J]. Oil Geophysical Prospecting, 2018, 53(S1): 62-68. |



 张阳, 河北省涿州市华阳东路东方地球物理公司科技园采集技术中心, 072751。Email:
张阳, 河北省涿州市华阳东路东方地球物理公司科技园采集技术中心, 072751。Email: