2 中国石化胜利油田勘探开发研究院, 山东东营 257015
2 Research Institute of Exploration & Production, SINOPEC Shengli Oilfield, Dongying, Shandong 257015, China
实际地震数据由于采集仪器或者环境等因素的影响,往往存在非平稳随机噪声[1],在地震数据中以脉冲形式出现,具有较强的能量,主要包括猝发脉冲、异常扰动、声波干扰等[2],很难用人工方法完全剔除野值和串状干扰[3]。如果中、深层地震资料中存在强能量干扰,则叠前时间偏移剖面会出现不同程度的“画弧”现象[4]。现代地震资料处理的目标是既能衰减噪声、提高地震资料的信噪比,又能保留和增强有效不连续地震反射信息及储层流体信息[5]。常规滤波方法常常放大了噪声的影响,同时噪声的存在也限制了分辨率的提升[6],并“平滑”了地震数据中的不连续信息。通过自动识别地震记录中的强能量干扰,确定噪声出现的空间位置,根据定义的阈值和衰减系数用适当的方式压制非平稳随机噪声[7]。在动校正后或同相轴相对平直的地震剖面上,中值滤波器具有压制强能量干扰的能力[8-9],但很难选取合适的阈值算子兼顾保护有效信号和压制噪声[10]。由于异常噪声既不连续也不相关,采用局部中值简单地代替噪声位置处的数据,容易压制有效信号,尤其在同相轴弯曲和间断处[11]。为此,Boashash等[12]提出了一种瞬时频率估计算法——时频峰值滤波算法,基于时频分析理论压制非平稳随机噪声,将含噪信号调制为解析信号的瞬时频率信号,然后取解析信号时频分布的峰值估计有效信号,经时频峰值滤波后信号得到增强,噪声被压制。林红波等[13]提出了基于绝对级差统计量(ROAD)的径向时频峰值滤波非平稳随机噪声压制方法,结合局部时频峰值滤波和径向时频峰值滤波压制地震非平稳随机噪声。
近年来机器学习算法发展迅速,深度学习算法在数据去噪领域的应用也越来越广泛。Burger等[14]推出了具有三层网络的多层感知机模型(MLP),虽然网络结构不深,但是处理效果较好。Schmidt等[15]、Chen等[16]分别提出联合收缩方法(CSF)、反应扩散模型(TNRD),这两种方法的信噪比提高和边缘保护效果超过了块匹配方法(BM3D)。Mao等[17]利用机器学习算法实现了地震数据处理、属性提取、断层预测等方面的云地震数据分析平台。Zhang等[18]受迭代收缩阈值算法(ISTA)的启发,提出了一种新的结构化深度网络(Iterative Shrinkage-Threshold-ing Algorithm Network,ISTA-net),能快速、准确地实现数据的去噪和压缩感知重建。
本文利用深度学习算法中的监督数据驱动算法——迭代启发网络(Iterative scheme inspired network,IIN)压制非平稳随机噪声[19],该网络结构简单、紧凑。IIN由交替方向乘子算法(Alternating Direction of Method of Multipliers,ADMM)的迭代过程推导而来,利用L1范数优化变分模型。在训练阶段,通过增加一个新的辅助变量,将目标函数的极值转化为增广拉格朗日格式,使用L-BFGS算法判别、训练所有网络参数,最终得到最优去噪模型参数。在实验阶段,首先利用模型数据和实际数据建立训练数据库,使用训练阶段得到的去噪模型去噪。实验结果表明,与现有的压制非平稳随机噪声方法相比,文中方法具有明显的优势。
1 基本理论与技术流程 1.1 迭代收缩—阈值启发网络算法噪声消除的目的是从采集到的含噪数据y中恢复无噪数据。传统压缩感知(Compressive Sensing,CS)方法通过求解以下优化问题恢复无噪数据,其目标函数为[20]
| $ \mathit{\boldsymbol{x}} = \mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{x}} \frac{1}{2}\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPhi} x}} - \mathit{\boldsymbol{y}}} \right\|_2^2 + \lambda {\left\| {\mathit{\boldsymbol{ \boldsymbol{\varPsi} x}}} \right\|_1} $ | (1) |
式中:x为无噪数据的估计值;Φ为变化矩阵,将x变换到不同域;Ψ为非线性变换函数;λ为正则化参数。
ISTA-net网络算法结合CS算法,网络由固定的层数组成,每层中一次迭代采用传统ISTA算法,该网络结合了ISTA和CS的优势[21]。该网络通过迭代两个更新步骤
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{r}}^{(k)}} = {\mathit{\boldsymbol{x}}^{(k - 1)}} - {\mathit{\boldsymbol{s}}^{(k)}}{\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}^{\rm{T}}}[\mathit{\boldsymbol{ \boldsymbol{\varPhi} }}{\mathit{\boldsymbol{x}}^{(k - 1)}} - \mathit{\boldsymbol{y}}]}\\ {{\mathit{\boldsymbol{x}}^{(k)}} = {\rm{arg}}\mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{x}} \frac{1}{2}\left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{r}}^{(k)}}} \right\|_2^2 + T{{\left\| {F(\mathit{\boldsymbol{x}})} \right\|}_1}} \end{array}} \right. $ | (2) |
估计去噪数据[22]。式中:k为迭代次数;s(k)为步长,根据之前的步长参数由学习确定;T为软阈值算子的阈值;F(x)为参数可学习的非线性变换函数。
1.2 IIN算法非平稳随机噪声主要表现为脉冲噪声,以不规则脉冲或噪声“尖峰”的形式随机出现在地震数据中,持续时间短,具有谱密度较宽和振幅相对较高的特点[23]。由于L2范数对局部异常值的检测不稳定,在压制非平稳随机噪声时会限制算法的处理效果。因此本文采用的IIN算法在迭代收缩—阈值启发网络算法的基础上,采用L1范数优化噪声压制方程,增强对局部强能量噪声的敏感度[24],结合ADMM网络(ADMM-net)[25],通过优化问题
| $ \mathit{\boldsymbol{x}} = {\rm{arg}}\mathop {{\rm{min}}}\limits_\mathit{\boldsymbol{x}} ({\left\| {\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}}} \right\|_1} + \sum\limits_{l = 1}^L {{\lambda _l}} {\left\| {{\mathit{\boldsymbol{D}}_l}\mathit{\boldsymbol{x}}} \right\|_1}) $ | (3) |
得到去噪数据。式中l∈[1, 2, …, L]为滤波器序号,L为单层滤波器的总数。滤波器D的参数由网络进行训练。
引入变量t=x-y,z=Dx,则式(3)的增广拉格朗日函数为[26]
| $ \begin{array}{l} {\xi _{\varepsilon ,\rho }}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{t}},\mathit{\boldsymbol{z}},\mathit{\boldsymbol{\alpha }},\mathit{\boldsymbol{\omega }})\\ \begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {{\left\| \mathit{\boldsymbol{t}} \right\|}_1} + \frac{\varepsilon }{2}\left\| {\mathit{\boldsymbol{t}} - (\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}})} \right\|_2^2 - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \langle \mathit{\boldsymbol{\omega }},t - (\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{y}})\rangle + \sum\limits_{l = 1}^L {{\lambda _l}} {{\left\| {{\mathit{\boldsymbol{z}}_l}} \right\|}_1} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{l = 1}^L {\frac{{{\rho _l}}}{2}} \left\| {{\mathit{\boldsymbol{z}}_l} - {\mathit{\boldsymbol{D}}_l}\mathit{\boldsymbol{x}}} \right\|_2^2 - \sum\limits_{l = 1}^L {\langle {\mathit{\boldsymbol{\alpha }}_l},{\mathit{\boldsymbol{z}}_l} - {\mathit{\boldsymbol{D}}_l}\mathit{\boldsymbol{x}}\rangle } } \end{array} \end{array} $ | (4) |
式中:ε、ρ为权重系数;α、ω为拉格朗日乘数矩阵。根据ADMM算法,引入变量p=ω/ε,βl=αl/ρl,则式(4)分解为6个问题
| $ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{x}}^{(n)}} = {{[{\varepsilon ^{(n)}}\mathit{\boldsymbol{I}} + \sum\limits_{l = 1}^L {\rho _l^{(n)}} \mathit{\boldsymbol{H}}_l^{(n){\rm{T}}}\mathit{\boldsymbol{H}}_l^{(n)}]}^{ - 1}} \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left\{ {{\varepsilon ^{(n)}}[{\mathit{\boldsymbol{t}}^{(n - 1)}} - {\mathit{\boldsymbol{p}}^{(n - 1)}} + \mathit{\boldsymbol{y}}] + } \right.}\\ {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{l = 1}^L {\rho _l^{(n)}} \mathit{\boldsymbol{H}}_l^{(n){\rm{T}}}[\mathit{\boldsymbol{z}}_l^{(n - 1)} - \mathit{\boldsymbol{\beta }}_l^{(n - 1)}]} \right\}} \end{array} $ | (5a) |
| $ {\mathit{\boldsymbol{c}}_l^{(n)} = \mathit{\boldsymbol{D}}_l^{(n)}{\mathit{\boldsymbol{x}}^{(n)}}} $ | (5b) |
| $ {\mathit{\boldsymbol{z}}_l^{(n)} = S\left[ {\mathit{\boldsymbol{c}}_l^{(n)} + \mathit{\boldsymbol{\beta }}_l^{(n - 1)};\frac{{{\lambda _l}}}{{{\rho _l}}}} \right]} $ | (5c) |
| $ {\mathit{\boldsymbol{\beta }}_l^{(n)} = \mathit{\boldsymbol{\beta }}_l^{(n - 1)} + \eta _l^{(n)}[\mathit{\boldsymbol{c}}_l^{(n)} - \mathit{\boldsymbol{z}}_l^{(n)}]} $ | (5d) |
| $ {{\mathit{\boldsymbol{t}}^{(n)}} = S\left[ {{\mathit{\boldsymbol{x}}^{(n)}} - \mathit{\boldsymbol{y}} + {\mathit{\boldsymbol{p}}^{(n - 1)}};\frac{1}{\varepsilon }} \right]} $ | (5e) |
| $ {{\mathit{\boldsymbol{p}}^{(n)}} = {\mathit{\boldsymbol{p}}^{(n - 1)}} + {\tau ^{(n)}}[{\mathit{\boldsymbol{x}}^{(n)}} - {\mathit{\boldsymbol{t}}^{(n)}} - \mathit{\boldsymbol{y}}]} $ | (5f) |
式中:n为层数;S(·)为非线性收缩函数;I为各元素为1的矩阵;Hln为第n层中第l个滤波器矩阵;τ、η为可学习的权重参数,控制学习速率,在网络训练中逐层修正。
1.3 技术流程在IIN网络算法中,每层有6个计算节点(对应式(5)),具体步骤如下。
(1) 利用式(5a)重构输入的地震数据。若该层是第一层(n=1)时,式(5a)变为
| $ {\mathit{\boldsymbol{x}}^{(1)}} = {\left[ {{\varepsilon ^{(1)}}\mathit{\boldsymbol{I}} + \sum\limits_{l = 1}^L {\rho _l^{(1)}} \mathit{\boldsymbol{H}}_l^{(n){\rm{T}}}\mathit{\boldsymbol{H}}_l^{(1)}} \right]^{ - 1}}[{\varepsilon ^{(1)}}\mathit{\boldsymbol{y}}] $ | (6) |
(2) 对重构数据x(n)进行滤波处理。
(3) 根据式(5c)对滤波数据进行非线性变换,其中S[·]为分段函数,其形式为
| $ \begin{array}{l} S[a,{u_i},w_{l,i}^{(n)}]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left\{ {\begin{array}{*{20}{c}} {a + w_{l,1}^{(n)} - {u_1}}&{a < {u_1}}\\ {a + w_{l,{N_C}}^{(n)} - {u_{{N_c}}}}&{a > {u_{{N_C}}}}\\ {w_{l,m}^{(n)} + \frac{{(a - {u_m})[w_{l,m + 1}^{(n)} - w_{l,m}^{(n)}]}}{{{u_{m + 1}} - {u_k}}}}&{{u_1} \le a \le {u_{{N_C}}}} \end{array}} \right. \end{array} $ | (7) |
由于分段线性函数拟合性程度高,可以根据数据的特点,学习更加合适的非线性变换函数。其中
| $ m = \left\lfloor {\frac{{a - {u_1}}}{{{u_2} - {u_1}}}} \right\rfloor $ |
式中:
(4) 根据式(5d)更新乘数βl(n)。
(5) 对重构数据按步骤(3)进行非线性变换,如果n=1,即为第1层时,令p(n-1)=0。
(6) 根据式(5f)更新乘数p(n)。
图 1为第k层正向传播流程。
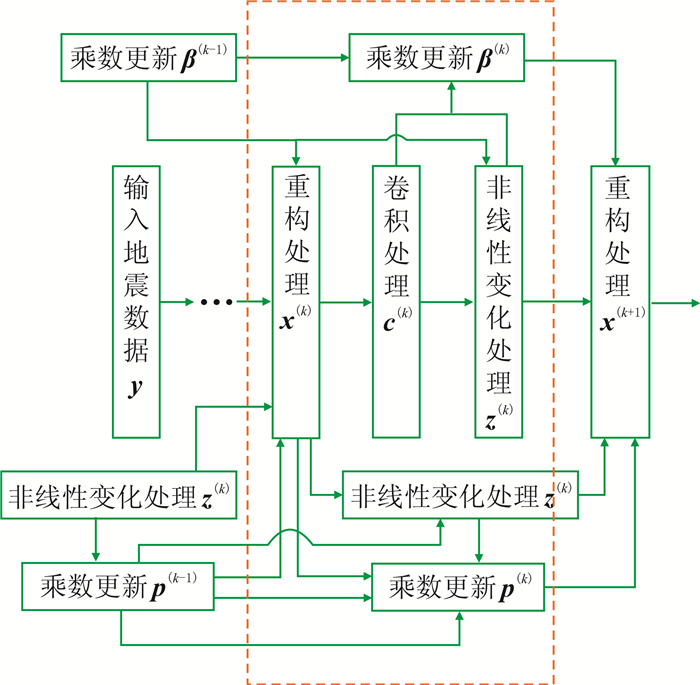
|
图 1 第k层正向传播流程 |
在网络训练过程中,通过计算估计数据与输入数据之间的误差作为损失函数
| $ E(\mathit{\boldsymbol{ \boldsymbol{\varTheta} }}) = {\left\{ {10\left| {{\rm{lg}}\frac{{\sum\limits_\mathit{\boldsymbol{y}} {\sum\limits_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }} {{{[\mathit{\boldsymbol{x}} - \mathit{\boldsymbol{\hat x}}(\mathit{\boldsymbol{y}},\mathit{\boldsymbol{ \boldsymbol{\varTheta} }})]}^2}} } }}{{\sum\limits_\mathit{\boldsymbol{y}} {\sum\limits_\mathit{\boldsymbol{ \boldsymbol{\varTheta} }} {{\mathit{\boldsymbol{x}}^2}} } }}} \right|} \right\}^{ - 1}} $ | (8) |
式中Θ表示上述流程中各个参数的集合。在反向传播过程中计算损失函数E(Θ)对参数集Θ的梯度,利用L-BFGS算法,通过最小化式(8)的取值,优化去噪数据
图 2为第k层反向传播流程。通过反向传播计算得到去噪网络参数模型,利用该模型对输入地震数据进行正向传播便可得到去噪后的地震数据。
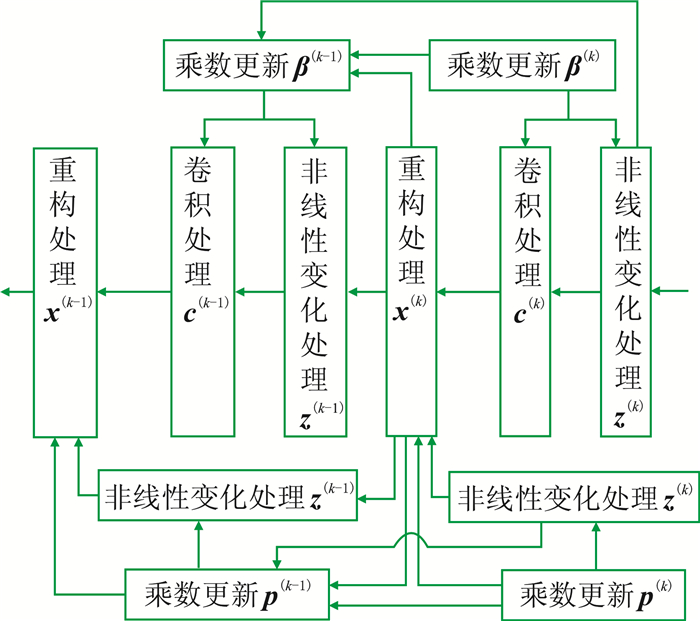
|
图 2 第k层反向传播流程 |
为了验证上述去噪算法的可行性和有效性,分别对模型数据和实际地震数据进行去噪实验。通过比较不同层数的网络处理效果设置网络总层数,过多的层容易导致过拟合,过少的层数不能有效去除噪声。综合去噪效果和计算时间设置单层滤波器总数目。根据经验设置NC值,关系到分段线性函数的拟合程度。合成地震数据添加了非平稳随机噪声,生成含噪数据作为输入数据,无噪数据作为输出数据;单炮叠前地震数据作为实际数据,存在大量的非平稳随机噪声,采用空变中值滤波和时变中值滤波去噪得到去噪后数据,再选择去噪效果理想的数据作为数据库数据。通过水平翻转和90°旋转将训练数据集扩充,以增加数据的多样性。然后对上述数据训练得到去噪模型。图 3为训练库部分数据。

|
图 3 训练库部分数据 |
图 4为损失函数曲线与峰值信噪比(PSNR)曲线。由图可见:①在第6次迭代之前,损失函数值呈明显下降趋势,当迭代次数大于6后,损失函数值收敛于小值,说明去噪误差达到最小值,并且其变化趋于平稳,证明训练模型去噪结果稳定(图 4a)。②前几次迭代生成的去噪模型的去噪能力不强,经过几次迭代之后,去噪能力趋于稳定,尤其在迭代次数大于7之后,去噪数据的PSNR较高且稳定(图 4b)。由于采用简单、紧凑的网络结构,因此曲线收敛速度较快,表明文中方法用相对较小的数据集和较少的训练时间得到了稳定的去噪模型。
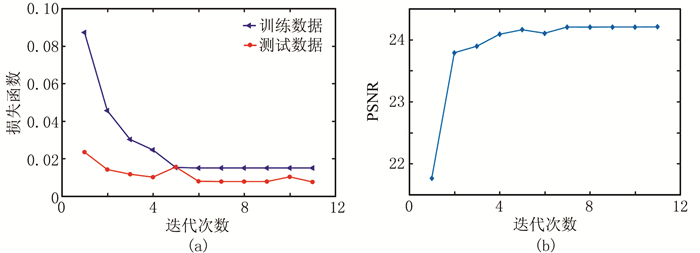
|
图 4 损失函数曲线(a)与峰值信噪比(PSNR)曲线(b) |
根据模型中有效信号的能量在合成数据(图 5a)加入非平稳随机噪声得到含噪数据(图 5b),再利用训练好的网络模型去噪得到去噪结果(图 5c)。可见,经过去噪后噪声被压制,去除的噪声(图 5d)中基本不存在有效信号,提高了信噪比。为了对比对叠后模型的去噪效果,分别利用本文方法与传统中值滤波方法对含噪模型(图 6a)去噪,结果表明:本文方法的去噪结果(图 6b)没有残留噪声,去除的噪设置网络总层数n=13,单层滤波器总数目L=8,单个滤波器矩阵设为3×3阶。根据经验将NC值设为501,即把[-1, 1]平均分成500段。训练库数据的单个大小为200×200,用2000组数据作为训练库,200组数据作为验证库,数据库中80%为实际地震数据,20%为合成地震数据。每组数据的左侧为含噪数据,右侧为无噪数据声(图 6c)中不存在有效信号;中值滤波方法的阈值设置影响了去噪结果(图 6d),部分有效信号被压制,如果阈值设置太大,则会残留噪声,很难选取合适的阈值有效地压制噪声。

|
图 5 数据模型的去噪效果 (a)合成数据;(b)含噪数据;(c)去噪结果;(d)图c与图b数据之差 |

|
图 6 对叠后模型的去噪效果 (a)含噪模型;(b)本文方法去噪结果;(c)图b与图a数据之差;(d)中值滤波去噪结果;(e)图d与图a数据之差 |
图 7为图 6第10道数据去噪前、后对比。由图可见:由于本文方法噪声压制方程的保真项采用L1范数,可更敏感地检测地震数据中的非平稳随机噪声并进行压制(图 7a);中值滤波去噪结果中有效信号也被压制,去噪效果不理想(图 7b)。

|
图 7 图 6第10道数据去噪前、后对比 (a)本文方法;(b)中值滤波 |
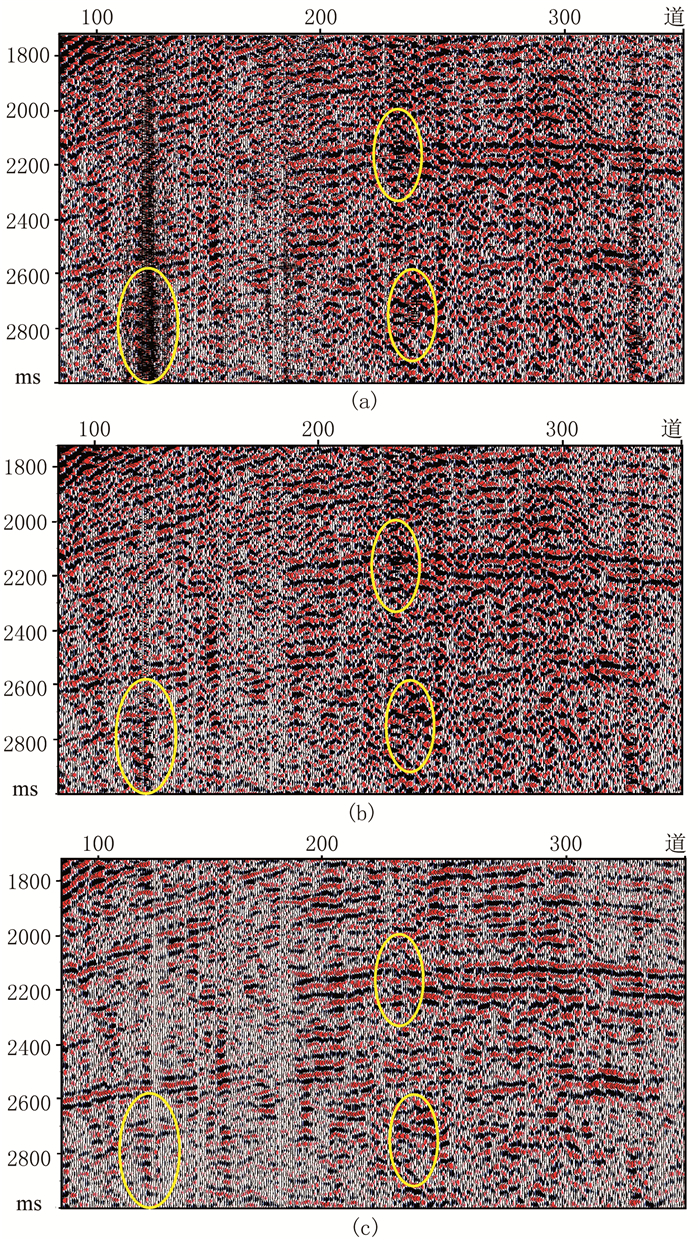
分别采用时频峰值滤波方法和本文方法对实际地震数据去噪并分析去噪结果。图 8为F区实际地震数据去噪结果。由图可见:86道实际地震记录中有几道含有较强的非平稳随机噪声,干扰有效信号并影响弱有效信号的拾取(图 8a);时频峰值滤波对图 8a的去噪结果中残留噪声(图 8b);经本文方法对图 8a去噪后有效压制了噪声,没有破坏有效信号且很好地保护了弱有效信号(图 8d)。

|
图 8 F区实际地震数据去噪结果 (a)实际地震数据;(b)时频峰值滤波;(c)图b与图a数据之差;(d)本文方法;(e)图d与图a数据之差 |
单点高密度地震资料信号频带宽、波场信息丰富,反映了地下真实的反射信息,但同时也存在大量的噪声,因此出现信噪比较低、有效信号与噪声混杂的问题,不易发挥高密度资料的潜在优势。为了检验本文方法对单点高密度地震数据的去噪效果,在训练库中增加相应的单点高密度数据,并选取G区的单点高密度单炮道集进行去噪实验。图 9为G区单点高密度地震数据去噪结果。由图可见:经本文方法对单点高密度地震数据(图 9a)去噪后,在压制非平稳随机噪声的同时,保护了有效信号(图 9d箭头处);时频峰值滤波方法对图 9a的去噪结果中残留噪声(图 9b箭头处)。图 10为图 9的局部放大。由图可见:时频峰值滤波处理结果中残留噪声(图 10b);本文方法去噪结果的同相轴清晰、连续,有效压制了噪声(图 10c)。

|
图 9 G区单点高密度地震数据去噪结果 (a)单点高密度地震数据;(b)时频峰值滤波;(c)图b与图a数据之差;(d)本文方法;(e)图d与图a数据之差。共有610道,采样时间为3s,时间采样间隔为0.01s |
理论模型试算和实际地震数据去噪结果表明,本文方法有效减小了信号畸变,较好地压制了各种非平稳随机干扰,且对实际数据具有较强适应性。
4 结束语针对地震数据中的非平稳随机噪声,本文提出了采用基于迭代启发网络算法的去噪方法,采用深度学习算法,利用L1范数对目标函数进行优化,可更敏感地检测并压制地震数据中的非平稳随机噪声,同时较好地保护有效信号。理论模型及实际资料的去噪结果表明:
(1) 利用迭代启发网络(IIN)算法,通过构建包含不同形态有效信号同相轴的数据,并结合实际地震数据建立训练数据库,由训练得到的去噪模型根据有效信号的特征,在去噪的同时可保留同相轴的形状特征;采用的迭代网络简单、紧凑,加快了网络的收敛速度,用相对较小的数据集和较少的训练时间快速训练去噪模型,去噪效果较好。
(2) 本文方法具有较强的适应性,有效压制了常规地震数据中的非平稳随机噪声。对于单点高密度地震数据,较传统的时频峰值滤波算法,可有效减小信号畸变,较好地压制各种非平稳随机干扰。
| [1] |
钟铁, 李月, 杨宝俊, 等. 陆地地震勘探随机噪声统计特性[J]. 地球物理学报, 2017, 60(2): 655-664. ZHONG Tie, LI Yue, YANG Baojun, et al. Statistical features of the random noise in land seismic prospecting[J]. Chinese Journal of Geophysics, 2017, 60(2): 655-664. |
| [2] |
邵婕, 孙成禹, 唐杰, 等. 基于字典训练的小波域稀疏表示微地震去噪方法[J]. 石油地球物理勘探, 2016, 51(2): 254-260. SHAO Jie, SUN Chengyu, TANG Jie, et al. Micro-seismic data denoising based on sparse representations over learned dictionary in the wavelet domain[J]. Oil Geophysical Prospecting, 2016, 51(2): 254-260. |
| [3] |
刘国昌, 蔡加铭, 闫海洋, 等. 利用稀疏约束非平稳多项式回归去除地震噪声及拾取初至[J]. 石油地球物理勘探, 2020, 55(3): 548-556. LIU Guochang, CAI Jiaming, YAN Haiyang, et al. Using sparse-constrained nonstationary polynomial regression to remove seismic noises and picking up first arrival[J]. Oil Geophysical Prospecting, 2020, 55(3): 548-556. |
| [4] |
李海山, 陈德武, 吴杰, 等. 叠前随机噪声深度残差网络压制方法[J]. 石油地球物理勘探, 2020, 55(3): 493-503. LI Haishan, CHEN Dewu, WU Jie, et al. Pre-stack random noise suppression with deep residual network[J]. Oil Geophysical Prospecting, 2020, 55(3): 493-503. |
| [5] |
唐杰, 张文征, 戚瑞轩, 等. 基于噪声水平估计的加权核范数最小化噪声压制方法研究[J]. 石油物探, 2019, 58(5): 734-740. TANG Jie, ZHANG Wenzheng, QI Ruixuan, et al. Seismic data denoising by weighted nuclear norm mi-nimization based on noise estimation[J]. Geophysical Prospecting for Petroleum, 2019, 58(5): 734-740. |
| [6] |
王伟, 高静怀, 陈文超, 等. 基于结构自适应中值滤波器的随机噪声衰减方法[J]. 地球物理学报, 2012, 55(5): 1732-1741. WANG Wei, GAO Jinghuai, CHEN Wenchao, et al. Random seismic noise suppression via structure-adaptive median filter[J]. Chinese Journal of Geophysics, 2012, 55(5): 1732-1741. |
| [7] |
张岩, 任伟建, 唐国维. 利用多道相似组稀疏表示方法压制随机噪声[J]. 石油地球物理勘探, 2017, 52(3): 442-450. ZHANG Yan, REN Weijian, TANG Guowei. Random noise suppression based on sparse representation of multi-trace similarity group[J]. Oil Geophysical Prospecting, 2017, 52(3): 442-450. |
| [8] |
Nodes T, Gallagher N. Median filters:some modifications and their properties[J]. IEEE Transactions Acoustics Speech Signal Processing, 1982, 30(5): 739-746. DOI:10.1109/TASSP.1982.1163951 |
| [9] |
林红波, 李月, 徐学纯. 压制地震勘探随机噪声的分段时频峰值滤波方法[J]. 地球物理学报, 2011, 54(5): 1358-1366. LIN Hongbo, LI Yue, XU Xuechun. Segmenting time-frequency peak filtering method to attenuation of seismic random noise[J]. Chinese Journal of Geophysics, 2011, 54(5): 1358-1366. |
| [10] |
唐杰, 张文征, 梁雨薇, 等. 自适应数据驱动的紧框架微地震数据随机噪声压制[J]. 石油地球物理勘探, 2019, 54(5): 954-961. TANG Jie, ZHANG Wenzheng, LIANG Yuwei, et al. A random-noise suppression approach with self-adaptive data-driven tight frame for micro-seismic data[J]. Oil Geophysical Prospecting, 2019, 54(5): 954-961. |
| [11] |
Deng X Y, Yang D, Liu T, et al. Study of least squares support vector regression filtering technology with a new 2D Ricker wavelet kernel[J]. Journal of Seismic Exploration, 2011, 20(2): 161-176. |
| [12] |
Boashash B, Mesbah M. Signal enhancement by time-frequency peak filtering[J]. IEEE Transactions on Signal Processing, 2004, 52(4): 929-937. DOI:10.1109/TSP.2004.823510 |
| [13] |
林红波, 马海涛, 许丽萍. 压制空间非平稳地震勘探随机噪声的ROAD径向时频峰值滤波算法[J]. 地球物理学报, 2015, 58(7): 2546-2555. LIN Hongbo, MA Haitao, XU Liping. A radial time-frequency peak filtering based on ROAD for suppressing spatially nonstationary random noise in seismic data[J]. Chinese Journal of Geophysics, 2015, 58(7): 2546-2555. |
| [14] |
Burger H C, Schuler C J, Harmeling S.Image denoising: Can plain neural networks compete with BM3D?[C]. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2012, 2392-2399.
|
| [15] |
Schmidt U, Roth S.Shrinkage fields for effective ima-ge restoration[C]. IEEE Conference on Computer Vision and Pattern Recognition (CVPR), 2014, 2774-2781.
|
| [16] |
Chen Y J, Yu W, Pock T.On learning optimized reaction diffusion processes for effective image restoration[C]. IEEE, Conference on Computer Vision & Patten Recognition, 2015, 5261-5269.
|
| [17] |
Mao X J, Shen C H, Yang Y B.Image restoration using very deep convolutional encoder-decoder networks with symmetric skip connections[C]. NIPS, 2016, 2802-2810.
|
| [18] |
Zhang J, Ghanem B.ISTA-Net: Interpretable optimization-inspired deep network for image compressive sensing[C]. IEEE Conference on Computer Vision and Pattern Recognition(CVPR), 2018, 1828-1837.
|
| [19] |
Zhang M, Liu Y, Li G, et al. Iterative scheme-inspired network for impulse noise removal[J]. Pattern Analysis and Applications, 2018, 23(2): 135-145. |
| [20] |
Mun S, Fowler J E.Block compressed sensing of images using directional transforms[C]. IEEE International Conference on Image Processing, 2010.
|
| [21] |
Beck A, Teboulle M. A fast iterative shrinkage-thre-sholding algorithm for linear inverse problems[J]. SIAM Journal on Imaging Sciences, 2009, 2(1): 183-202. DOI:10.1137/080716542 |
| [22] |
Blumensath T, Davies M E. Iterative hard thresho-lding for compressed sensing[J]. Applied & Computational Harmonic Analysis, 2009, 27(3): 265-274. |
| [23] |
张雅晨, 刘洋, 刘财, 等. 低信噪比地震资料FDOC-Seislet变换阈值消噪方法研究[J]. 地球物理学报, 2019, 62(3): 1181-1192. ZHANG Yachen, LIU Yang, LIU Cai, et al. Seismic random noise attenuation using FDOC-Seislet transform and threshold for seismic data with low SNR[J]. Chinese Journal of Geophysics, 2019, 62(3): 1181-1192. |
| [24] |
Jonas A, Ozan O. Solving ill-posed inverse problems using iterative deep neural networks[J]. Inverse Problems, 2017. DOI:10.1088/136-6420/aa9581 |
| [25] |
Yan Y, Huibin L, Zongben X, et al.Deep ADMM-Net for compressive sensing MRI[C]. NIPS, 2016, 10-18.
|
| [26] |
Boyd S, Parikh N, Chu E, et al. Distributed optimization and statistical learning via the alternating direction method of multipliers[J]. Foundations & Trends in Machine Learning, 2010, 3(1): 1-122. |



 唐杰, 山东省青岛市长江西路66号中国石油大学(华东)地球科学与技术学院, 266850。Email:
唐杰, 山东省青岛市长江西路66号中国石油大学(华东)地球科学与技术学院, 266850。Email: