断层是地下常见的地质构造,它对于油气勘探、工程施工、天然地震研究等具有重要意义,因此断层识别在地震资料解释中十分重要。当前已有很多断层识别和解释的方法,如相干体分析技术[1-3]、边缘增强属性分析技术[4]、蚂蚁追踪算法[5-6]、相似性传播聚类与主成分分析法[7]、构造导向滤波法[8]、基于熵的各向异性扩散保边滤波法[9]等。但是,这些方法都存在一定的局限性,如断层相关属性提取中存在噪声问题,不同工区存在参数优化与适应性问题等。
随着机器学习技术的快速发展与广泛应用,机器学习算法已经用于地震资料的断层识别。董守华等[10]、崔若飞[11]利用浅层全连接神经网络,通过学习断层的地震反射特征参数,实现了简单的断层识别。
随着Lecun等[12]提出卷积神经网络概念,多种基于卷积神经网络算法开始用于断层识别。Huang等[13]将卷积神经网络、传统机器学习算法与地震属性相结合实现了断层识别。Guitton[14]利用三维地震数据训练卷积神经网络实现了断层的三维识别。Wu等[15]利用人工合成的断层地震图像训练卷积神经网络实现了断层识别;Liu等[16]利用Smooth-Grad技术直观解释了卷积神经网络识别断层的过程;Xiong等[17]、Ma等[18]和Guo等[19]利用卷积神经网络实现了断层识别。Wu等[20]利用U-Net图像分割网络实现了断层识别。
Liu等[16]认为神经网络识别结果不如人工解释准确。Xiong等[17]和Ma等[18]认为神经网络识别结果优于相干体技术。尽管利用卷积神经网络可以实现断层识别,但是目前方法仍存在一定的局限性。地球物理领域没有大量可靠的实际断层样本用于训练,而人工合成断层地震图像虽然解决了训练样本问题,但合成的断层与实际断层仍存在较大的差异,并且无法包含所有的实际断层类型,导致断层识别结果不理想。因此,训练的断层识别网络模型仅在信噪比较高的测试数据上表现良好,应用于发育复杂、多样断层的实际地震数据时表现不佳,存在较多断层漏识别或错误识别。
针对上述问题,本文提出一种基于深度残差网络与迁移学习的断层识别改进方法。其中,深度残差网络是He等[21]提出的一种深度卷积神经网络,它解决了深度网络难以训练的问题[22],提升了网络性能,能更好地学习目标特征;迁移学习是运用已有知识对相关问题进行求解的一种新的机器学习方法[23],目的是迁移已有的知识以解决目标领域中仅有少量标签样本数据的学习问题[24]。本文利用深度残差网络增加网络复杂度,利用迁移学习增强网络的泛化能力,使网络能够学习更多的断层特征,更好地适应实际地震数据。
1 深度残差网络识别断层 1.1 训练样本构建神经网络识别断层本质是构建一个神经网络分类器,利用大量的断层样本训练网络,使网络能够将输入的断层准确分类。本文基于Wu等[15]提出的合成断层地震图像的方法,生成25万个训练样本,包括16万个断层样本与9万个非断层样本。样本共分为17类,其中断层样本16类,包括正角度断层(断层面向左倾斜)8类、负角度断层(断层面向右倾斜)8类,角度范围为[-85°, -64°]、[64°, 85°],每隔3°分为一类(图 1);非断层样本1类,分为“无断层”(图 1i、图 1j)和“断层不经过样本中心” (图 1k、图 1l)两种情况。每个样本大小均为48×32像素,所有样本的具体特征各不相同。

|
图 1 部分合成样本 断层样本角度:(a)-85°;(b)-79°;(c)-73°;(d)-67°;(e)85°;(f)79°;(g)73°;(h)67°。图i~图l为非断层样本 |
获得训练样本后,构建一个34层的深度残差网络,使用合成断层样本训练网络,达到目标条件后完成训练并保存网络参数。最后利用实际测试样本与实际地震数据进行测试。
1.2 残差学习模块构建增加神经网络的深度可以增加网络的参数种类,以便更好地学习目标特征。但是,简单地增加网络层数会出现梯度消失、梯度爆炸、过拟合等问题,造成网络退化。其具体表现为训练精度与测试精度的下降。
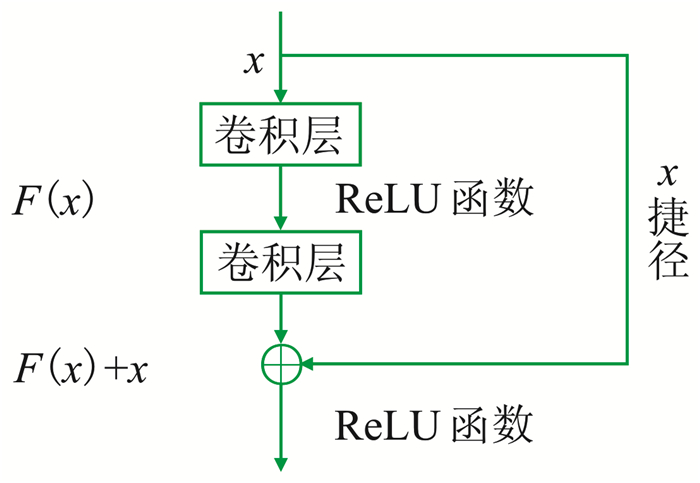
为了解决深层网络的退化问题,He等[21]提出了残差学习模块,如图 2所示。模块的输入为x,期望输出为H(x),实际输出为F(x),每个模块右侧都有捷径将输入值x直接传到输出处,输出时需要先使用激活函数激活。由于捷径的存在,残差学习模块的输出变为F(x)+x,学习目标变为F(x)=H(x)-x,即网络学习的内容变为残差。He等[21]指出,如果网络层数超过最佳层数,残差网络会将多余层训练为F(x)=0,即这些层的输入与输出相同,变为恒等映射,这样网络层数加深就不会造成网络退化。
|
图 2 残差学习模块结构示意图 ReLU函数为线性整流函数。图 3同 |
残差学习模块不仅解决了网络层数增加造成的退化问题,还使得网络的学习目标简化,难度降低,使深度神经网络的训练变得更加容易。
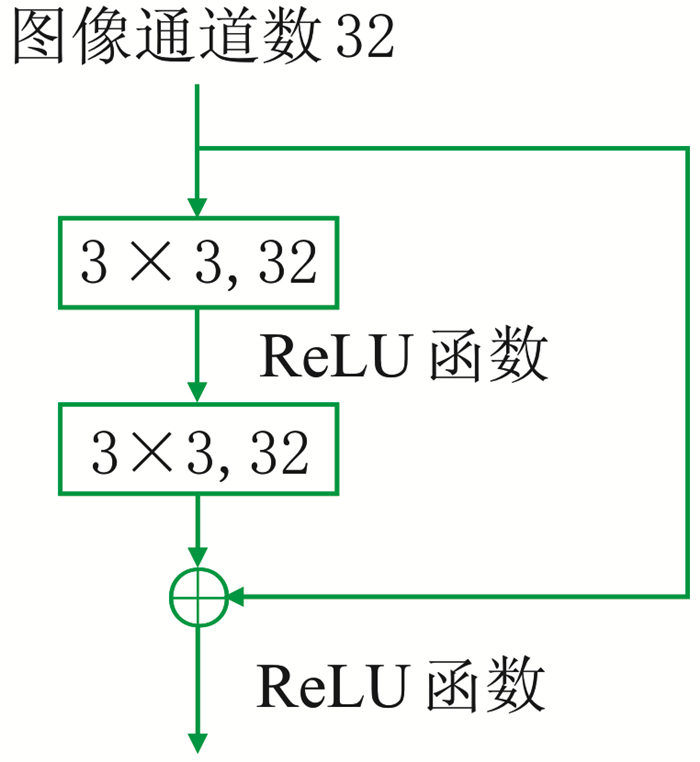
本文使用图 3所示的两层残差学习模块构建残差网络。两层残差学习模块中,卷积核的大小均为3×3,通过捷径输入的通道数与残差模块输出的通道数相同。每层卷积操作后的特征都需要使用激活函数激活才能输入到下一层。由于线性整流函数(Rectified Linear Unit, ReLU)相比于Sigmoid和双曲正切(Tanh)激活函数收敛速度更快,不容易发生梯度消失,更适合深度神经网络[25],因此在每层卷积操作后都使用ReLU[f(x)]=max(0, x)函数进行激活。
|
图 3 两层残差学习模块 |
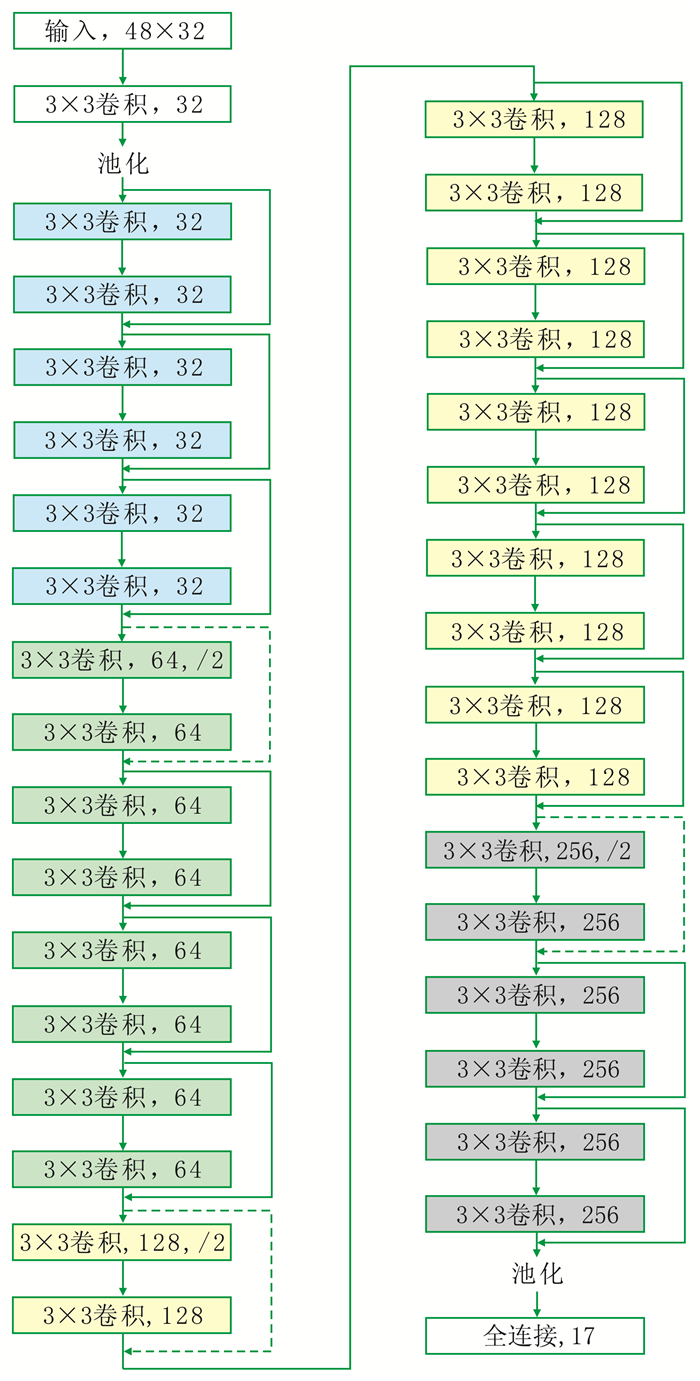
将输入层、卷积层、池化层、16个残差模块、池化层、输出层依次连接,构成34层深度残差网络(图 4)。其中,残差学习模块中捷径有实线和虚线两种。实线表示输入与输出通道数相同,可直接相加;虚线表示通道数不同,需要先使用1×1的卷积提升通道数,再相加。
|
图 4 34层深度残差网络结构示意图 |
网络输入层为48×32像素的断层图像,图像输入后,经过一次卷积与最大池化,提取断层图像的特征进一步学习[26]。残差模块的输入输出通道数依次为32、64、128、256。图 4中有三层网络出现“/2”标识,表示其卷积步长为2,卷积后会使图像大小变为原来的1/4,最终图像缩小为原来的1/64,压缩了数据特征图像与参数数量。输出前再次进行最大池化,然后对应不同的断层角度,用Softmax函数将输出结果分为17类
| $ \sigma \left( {{Z_j}} \right) = \frac{{{{\rm{e}}^{{Z_j}}}}}{{\sum\limits_{k = 1}^K {{{\rm{e}}^{{Z_k}}}} }} $ | (1) |
式中:σ(Zj)表示不同分类的概率分布,j为分类类别;k为分类数;本文K取17。
损失函数选用交叉熵(CrossEntropy)函数
| $ L = - \sum\limits_{i = 1}^n {{y_i}} \log {{\hat y}_i} $ | (2) |
式中:L为网络损失;yi为网络期望输出;
梯度下降选用自适应矩估计(Adaptive Moment Estimation,Adam)梯度最速下降法[27]。
1.4 网络训练与测试本文使用RTX2080Ti GPU训练网络。学习率设置为1×10-4,训练批次为256,数据循环训练5次,训练完成后保存网络参数并进行测试。网络对合成断层样本的识别准确率为99.56%;对1000个实际断层样本的识别准确率为73.45%。该结果表明合成数据与实际数据之间存在一定差异,由于实际数据含噪及地层产状复杂等原因,即使图像特征十分相似,数据特征也无法完全一致。
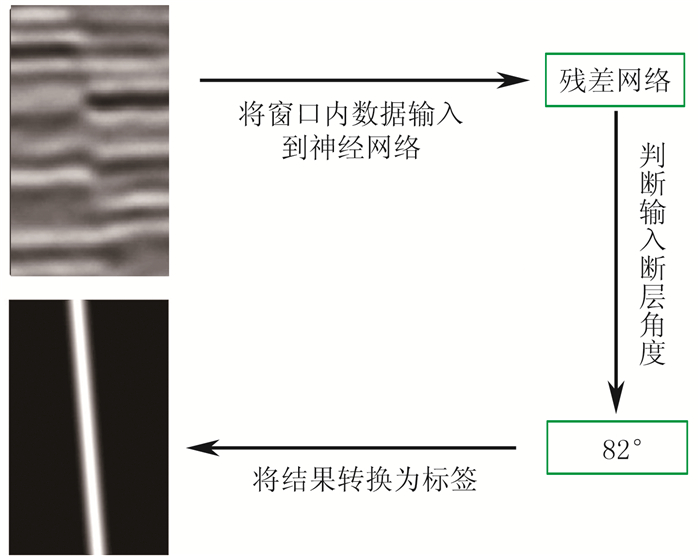
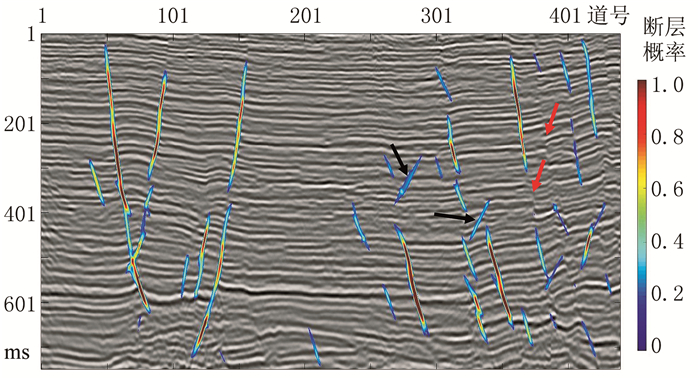
使用实际的二维地震剖面对该网络进一步测试。根据实际数据的大小,选择合适的窗口对数据滑动扫描并逐一识别,识别过程如图 5所示。数据扫描完成后,得到断层识别结果(图 6)。经过训练的深度残差网络能够准确识别出大多数断层,但也存在一定的漏识别与不准确识别,图 6中黑色箭头指示的位置为错误识别,红色箭头指示的位置为漏识别。
|
图 5 断层识别与标记过程 |
|
图 6 a测线34层的残差网络断层识别结果 |
为了解决上述问题,改进识别结果,本文引入迁移学习。
2 迁移学习迁移学习是利用数据、任务或网络模型之间的相似性,将在旧领域学习的网络模型应用于新领域的一种学习过程。迁移学习解决了大数据与少标注、普适化网络模型与个性化需求之间的矛盾[28]。
实际应用中,人工合成的断层图像为源领域,实际断层为目标领域。由于源领域与目标领域特征具有一定的相似性,因此迁移学习具有可行性。使用少量的实际断层样本对原有网络结构进行迁移学习,可以使神经网络拥有更好的适应性和泛化能力,提高神经网络在实际数据上的识别准确率。
2.1 数据实验通过人工合成25万个断层样本训练断层识别网络模型,只需少量实际断层训练样本即可进行迁移学习。手动提取4000个实际断层训练样本,实际样本中的断层与非断层的比例无需严格遵照合成样本的比例。实验发现:提取实际样本时,若提高其中断层样本的比例,则会提升网络对断层的识别能力,减少漏识别;若提高非断层的比例,则会提升网络对非断层的识别能力,减少错误识别。本文提取的实际训练样本中,断层与非断层的比例约为1:1。实际断层样本如图 7所示。

|
图 7 部分实际样本 断层样本角度:(a)-85°;(b)-79°;(c)-73°;(d)-67°;(e)85°;(f)79°;(g)73°;(h)67°。图i~图l为非断层样本 |
在迁移学习时,直接使用实际数据继续训练原有网络。由于实际断层样本数量较少,因此适当增大学习率至1×10-4、批次减小为128、数据循环次数增至50次,迁移完成后保存网络参数。
使用前述相同的1000个实际断层样本进行测试,迁移后的网络在实际断层样本上识别准确率由73.45%提高至95.54%。该结果表明网络成功由源领域迁移至目标领域,迁移学习效果明显,未发生负迁移[29-30]。
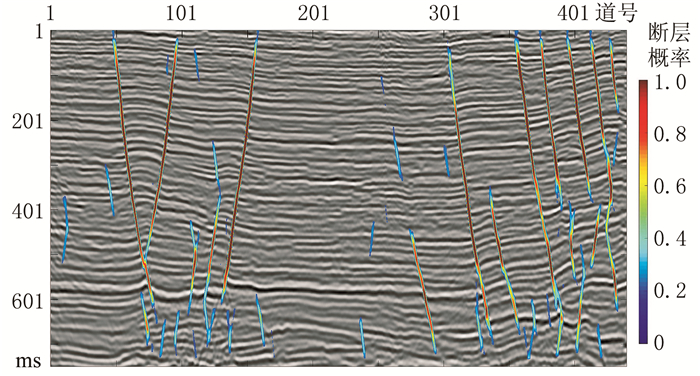
对图 6所示的二维地震剖面进行测试。结果(图 8)显示,迁移学习后残差网络减少了漏识别与错误识别,提高了识别准确率。
|
图 8 a测线迁移学习后的残差网络断层识别结果 |
为了进一步检验深度残差网络与迁移学习的效果,本文测试了更多的二维、三维实际地震资料。
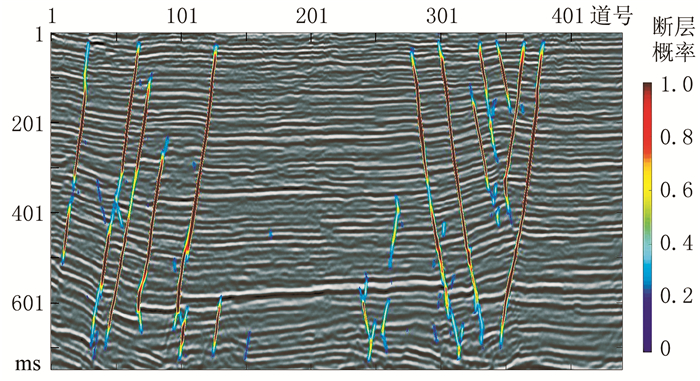
将改进后的网络应用于另一条测线(图 9,与图 6地震剖面为同一二维工区),迁移学习后残差网络准确地识别出了断层。相比于迁移前,减少了断层漏识别与错误识别,大断层识别连续性好,尺度较小的断层也能准确识别。这表明经过迁移学习后,网络学习到了实际地震资料中的断层特征。
|
图 9 b测线迁移学习后的残差网络断层识别结果 |
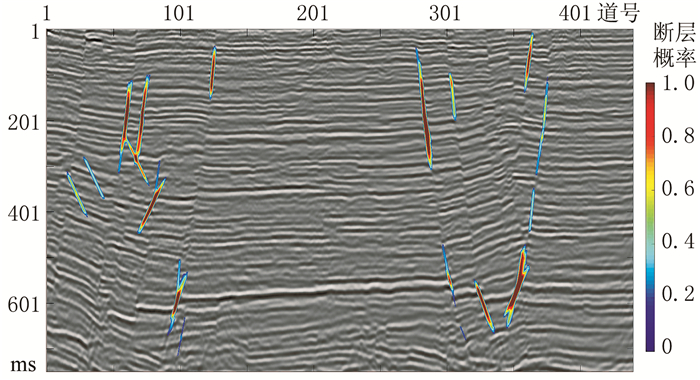
作为对比,本文训练6层卷积神经网络对图 9所示的二维地震测线数据进行识别,结果如图 10所示。训练该卷积神经网络时,训练数据、学习率、批次大小、数据循环次数都与训练34层残差网络时保持一致。对比图 9、图 10可以看出,残差网络与迁移学习结合识别结果明显优于6层卷积神经网络识别结果,断层漏识别明显减少。使用前述1000个实际断层样本进行测试,如表 1所示,6层卷积神经网络的识别准确率仅为57.87%,远低于残差网络与迁移学习结合的方法,与图 9、图 10识别结果相符。
|
图 10 b测线6层卷积神经网络的断层识别结果 |
|
|
表 1 不同结构神经网络的识别准确率 |
将迁移学习后残差网络应用于不同工区的三维地震资料,识别结果如图 11~图 13所示。
|
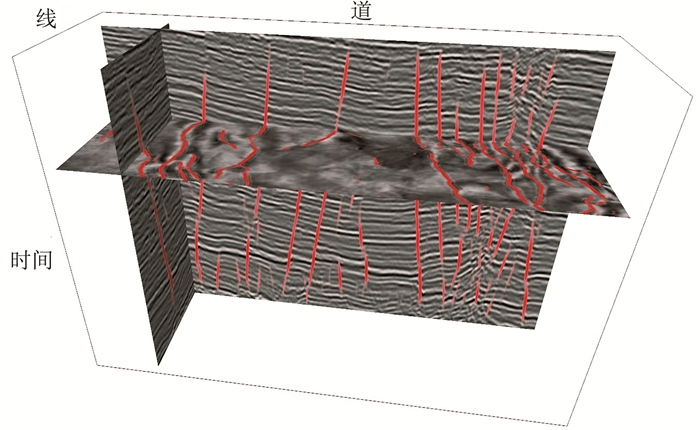
图 11 工区1三维地震资料本文方法断层识别结果 |

|
图 12 工区2三维地震资料本文方法断层识别结果 |
|
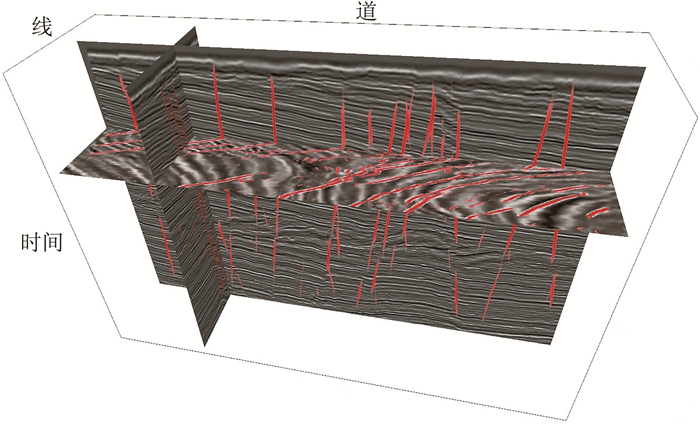
图 13 Kerry三维工区部分数据本文方法断层识别结果 |
其中,图 11为工区1的识别结果,该工区共201条测线,每条测线440道,采样间隔为4ms,采样点数为751;图 12为工区2的识别结果,该工区共441条测线,每条测线441道,采样间隔为4ms,采样点数为501;图 13为Kerry三维工区部分数据的识别结果,测试使用了191条测线,每条测线700道,采样间隔为4ms,采样点数为401。
测试结果表明,深度残差网络与迁移学习结合能够有效应用于不同工区的三维地震资料的识别。使用少量实际样本迁移后的网络,准确识别出了三维数据中的断层,并且大尺度断层在切片上也具有一定的连续性,能够直观地显示出三维地震资料上断层发育情况(图 11~图 13)。此外,这三组实际资料的断层倾角都在网络可识别的范围内,无需手动设置参数,能自动识别出不同倾角的断层。
4 结束语训练样本是神经网络识别断层的基础。少量的实际训练样本难以训练深度神经网络;人工合成的训练样本虽然数量庞大,但合成数据与实际数据存在特征差异。将合成数据的数量优势与实际数据的复杂特征相结合,可以提高神经网络断层识别准确率。
本文基于深度残差网络首先利用人工合成的大量断层及非断层样本进行训练,然后加上少量的实际断层样本进行迁移学习,提升了网络性能,增强了网络结构的泛化能力,从而提高了实际数据中断层识别的准确率。分析及应用表明,与仅使用合成数据训练的深度残差网络相比,迁移学习后的深度残差网络能够更加准确地识别断层,并且经过一次迁移学习后的网络可以适用于不同地区的实际资料。
本文方法依然存在不足之处,主要有:①断层识别及定位采用的是滑窗方式实现,与目标检测类的算法相比效率较低,对于本文中使用的实际数据,识别时间在1个小时左右;②由于在获取的地震数据中,断层基本都属于同一类型,因此无法检验本文方法对一些更为复杂类型的断层的识别准确率。
| [1] |
Bahorich M S, Farmer S L.3-D seismic discontinuity for faults and stratigraphic features: The coherence cube[C]. SEG Technical Program Expanded Abstracts, 1995, 14: 93-96.
|
| [2] |
Marfurt K J, Kirlin R L, Farmer S L, et al. 3-D seismic attributes using a semblance-based coherency algorithm[J]. Geophysics, 1998, 63(4): 1150-1165. DOI:10.1190/1.1444415 |
| [3] |
Gersztenkorn A, Marfurt K J. Eigenstructure-based coherence computations as an aid to 3-D structural and stratigraphic mapping[J]. Geophysics, 1999, 64(5): 1468-1479. DOI:10.1190/1.1444651 |
| [4] |
Rande T, Reymond B, Sjulstad H I, et al.New seismic attributes for automated stratigraphic facies boundary detection[C]. SEG Technical Program Expanded Abstracts, 1999, 18: 628-631.
|
| [5] |
严哲, 顾汉明, 蔡成国, 等. 利用方向约束蚁群算法识别断层[J]. 石油地球物理勘探, 2011, 46(4): 614-620. YAN Zhe, GU Hanming, CAI Chengguo, et al. Fault identification by orientation constraint ant colony algorithm[J]. Oil Geophysical Prospecting, 2011, 46(4): 614-620. |
| [6] |
李楠, 王龙颖, 黄胜兵, 等. 利用高清蚂蚁体精细解释复杂断裂带[J]. 石油地球物理勘探, 2019, 54(1): 182-190. LI Nan, WANG Longying, HUANG Shengbing, et al. 3D seismic fine structural interpretation in complex fault zones based on the high-definition ant-tracking attribute volume[J]. Oil Geophysical Prospecting, 2019, 54(1): 182-190. |
| [7] |
陈雷, 肖创柏, 禹晶, 等. 基于相似性传播聚类与主成分分析的断层识别方法[J]. 石油地球物理勘探, 2017, 52(4): 826-833. CHEN Lei, XIAO Chuangbai, YU Jing, et al. Fault recognition based on affinity propagation clustering and principal component analysis[J]. Oil Geophysical Prospecting, 2017, 52(4): 826-833. |
| [8] |
赵凤全, 崔德育, 康婷婷, 等. 构造导向滤波技术在断裂识别中的应用[J]. 石油地球物理勘探, 2018, 53(增刊1): 214-218, 227. ZHAO Fengquan, CUI Deyu, KANG Tingting, et al. Fault identification with structure-oriented filtering[J]. Oil Geophysical Prospecting, 2018, 53(S1): 214-218, 227. |
| [9] |
李军, 张军华, 刘杨, 等. 图像熵各向异性扩散保边滤波方法及在断层识别中的应用[J]. 石油地球物理勘探, 2019, 54(2): 365-370. LI Jun, ZHANG Junhua, LIU Yang, et al. Anisotropic diffusion edge-preserved filter based on image entropy and application in fault identification[J]. Oil Geophy-sical Prospecting, 2019, 54(2): 365-370. |
| [10] |
董守华, 石亚丁, 汪洋. 地震多参数BP人工神经网络自动识别小断层[J]. 中国矿业大学学报, 1997, 26(3): 16-20. DONG Shouhua, SHI Yading, WANG Yang. Automatic recognition of small fault by BP artificial ner-vous network from multiple seismic parameters[J]. Journal of China University of Mining & Technology, 1997, 26(3): 16-20. |
| [11] |
崔若飞. 神经网络技术在地震资料构造解释中的应用[J]. 地球物理学进展, 1997, 12(4): 67-75. CUI Ruofei. Application of structure interpretation with seismic data using artificial network[J]. Progress in Geophysics, 1997, 12(4): 67-75. |
| [12] |
Lecun Y, Kavukcuoglu K, Farabet C.Convolutional networks and applications in vision[C]. 2010 IEEE International Symposium on Circuits and Systems, 2010, 253-256.
|
| [13] |
Huang L, Dong X, Clee T E. A scalable deep learning platform for identifying geologic features from seismic attributes[J]. The Leading Edge, 2017, 36(3): 249-256. DOI:10.1190/tle36030249.1 |
| [14] |
Guitton A.3D Convolutional neural networks for fault interpretation[C]. Extended Abstracts of 80th EAGE Conference and Exhibition, 2018, 1-5.
|
| [15] |
Wu X M, Shi Y Z, Fomel S, et al.Convolutional neural networks for fault interpretation in seismic images[C]. SEG Technical Program Expanded Abstracts 2018, 37: 1946-1950.
|
| [16] |
Liu Z, Song C, She B, et al.Visual explanations from convolutional neural networks for fault detection[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 2226-2230.
|
| [17] |
Xiong W, Ji X, Ma Y, et al. Seismic fault detection with convolutional neural network[J]. Geophysics, 2018, 83(5): O97-O103. DOI:10.1190/geo2017-0666.1 |
| [18] |
Ma Y, Ji X, Nasher M, et al.Automatic fault detection with convolutional neural networks[C]. CPS/SEG International Geophysical Conference, Beijing, China, 2018, 786-790.
|
| [19] |
Guo B, Liu L, Luo Y.Automatic seismic fault detection with convolutional neural network[C]. CPS/SEG International Geophysical Conference, Beijing, China, 2018, 1786-1789.
|
| [20] |
Wu X M, Liang L M, Shi Y Z, et al. Fault Seg3D:using synthetic datasets to train an end-to-end convolutional neural network for 3D seismic fault segmentation[J]. Geophysics, 2019, 84(3): IM35-IM45. DOI:10.1190/geo2018-0646.1 |
| [21] |
He K, Zhang X, Ren S, et al.Deep residual learning for image recognition[C]. The IEEE Conference on Computer Vision and Pattern Recognition (CVPR), Las Vegas, USA, 2016, 770-778.
|
| [22] |
Michael N.Neural Networks and Deep Learning[EB/OL]. (2015)[2020-6-5]. http://neuralnetworksanddeeplearning.com/.
|
| [23] |
Pan S J, Yang Q. A survey on transfer learning[J]. IEEE Transactions on Knowledge and Data Enginee-ring, 2010, 22(10): 1345-1359. DOI:10.1109/TKDE.2009.191 |
| [24] |
庄福振, 罗平, 何清, 等. 迁移学习研究进展[J]. 软件学报, 2015, 26(1): 26-39. ZHUANG Fuzhen, LUO Ping, HE Qing, et al. Survey on transfer learning research[J]. Journal of Software, 2015, 26(1): 26-39. |
| [25] |
Krizhevsky A, Sutskever I, Hinton G E.Image net classification with deep convolutional neural networks[C]. Advances in Neural Information Processing Systems, 2012, 25(2): 1097-1105.
|
| [26] |
刘万军, 梁雪剑, 曲海成. 不同池化模型的卷积神经网络学习性能研究[J]. 中国图象图形学报, 2016, 21(9): 1178-1190. LIU Wanjun, LIANG Xuejian, QU Haicheng. Lear-ning performance of convolutional neural networks with different pooling models[J]. Journal of Image and Graphics, 2016, 21(9): 1178-1190. |
| [27] |
Kingma D, Ba J.Adam: A method for stochastic optimization[C]. International Conference for Learning Representations, San Diego, 2015.
|
| [28] |
Wang J, Jiang T, Cheung J.Transfer Learning Tutorial[EB/OL]. (2018)[2020-6-5]. https://github.com/jindongwang/transferlearning-tutorial.
|
| [29] |
Dai W, Jin O, Xue G, et al.EigenTransfer: a unified framework for transfer learning[C]. The 26th Annual International Conference on Machine Learning 2009, 193-200.
|
| [30] |
Rosenstein M T, Marx Z, Kaelbling L P, et al.To transfer or not to transfer[C]. NIPS 2005 Workshop on Transfer Learning.2005, 1-4.
|



 严哲, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院, 430074。Email:
严哲, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院, 430074。Email: