水力压裂微地震监测是非常规油气资源勘探、开发领域的一项重要技术[1]。水力压裂通过井筒向目标储层注入高压流体,使地层岩石破裂而释放能量级别很低的微地震信号[2-3],在水力压裂施工过程中进行微地震监测,通过处理监测数据,确定每个微地震事件的震源点,进而通过一系列震源点的分布描述压裂裂缝形态和分布规律[4-5]。因此,快速、准确地检测微地震事件是后期微地震数据处理的基础。
目前,微地震事件检测技术主要借鉴天然地震自动检测方法[6],发展了多种地震事件自动识别方法[7],包括长短时窗比(STA/LTA)、自回归Akaike信息准则(AR-AIC)等方法[8]。近年来,人们提出了诸多震相自动识别方法。张唤兰等[9]提出基于时窗能量比和AIC的微震初至拾取两步法。Shang等[10]组合STA/LTA、AIC、信号的峰度和偏度,提出了多种初至拾取算法,能处理信噪比更低的信号。曹俊海等[11]提出基于局部相关谱约束的多道匹配追踪算法识别微地震信号。
大规模的地面微地震监测阵列在水力压裂监测过程中产生了海量监测数据,而微地震事件的发生时刻是不确定的,需要研究从海量监测数据中自动识别有效微地震信号的算法,以提高数据处理效率。深度学习中的一些算法框架的特性特别适合处理海量数据并自动提取海量数据特征,其中以卷积神经网络(CNN)的应用最为广泛。由于微地震事件检测是一个从数据中提取特征的过程,因此可以将CNN用于微地震数据处理。陈润航等[12]从震源波形中提取梅尔倒谱系数(MFCC)图,基于CNN建立识别天然地震事件振动波形与爆破事件振动波形的分类器。赵明等[13]使用汶川地震余震事件波形构建数据集,搭建CNN训练和测试模型,成功实现了地震事件和噪声的分类,展示了CNN在实时地震监测方面的巨大潜力。在微地震事件检测方面,Bi等[14]提出了一种结合深度卷积神经网络(DCNN)和支持向量机(SVM)自动识别微震波形的方法,利用DCNN模型自动学习多通道波形图像数据的特征,结合SVM对多通道波形分类。
与前人研究不同,本文考虑地震事件与微地震事件在特征上的相似性,提出了一种通过统计同一事件各站点波形数据的分类结果判别微地震事件的方法。该方法使用由水力压裂实际监测数据训练和测试搭建的CNN模型,将待检测数据进行简单的预处理后直接输入到性能良好的模型中,以其各站点波形数据分割而成的样本数据分类为基础,统计同一事件的各站点波形数据的分类结果,投票决定该事件是否属于微地震事件。本文采用合成信号分析所提方法的抗噪性,采用川渝地区多口油气井加砂压裂地面微地震监测数据分析所提方法对不同井的泛化能力,结果证明所提方法可以自动识别实际微地震监测信号。
1 CNN 1.1 CNN介绍CNN是一种特殊的深度神经网络(图 1),其稀疏连接和权值共享的特性可以减少网络参数,降低网络模型的复杂度[15]。自Lecun等[16]提出CNN以来,在语音识别和自然语言处理等领域都取得了较好应用效果,其性能也在不断改进[17]。

|
图 1 CNN结构图 |
卷积层通过使用卷积核以固定步长遍历一次输入信号,对输入的局部区域进行卷积运算
| $ \mathit{\boldsymbol{x}}_j^l = f(z_j^l) = f\left( {\sum\limits_{i \in {\mathit{\boldsymbol{M}}_j}} {\mathit{\boldsymbol{x}}_i^{l - 1}} * \mathit{\boldsymbol{W}}_{ij}^l + \mathit{\boldsymbol{b}}_j^l} \right) $ | (1) |
并产生相应的特征[18]。式中:xjl为第l层第j个神经元的输出;xil-1为第l-1层第i个神经元的输出;f(zjl)为非线性激活函数; “*”表示卷积运算; Mj为第j个神经元对应的特征图子集; Wijl为卷积核; bjl为卷积后特征的偏置项。
卷积层后面周期性插入的池化层可以压缩输入的数据矩阵,从而简化从卷积层输出的信息,即
| $ {\mathit{\boldsymbol{x}}^l} = {\rm{down}} ({\mathit{\boldsymbol{x}}^{l - 1}}) $ | (2) |
式中down(·)表示下采样函数。
全连接层的作用是配合输出层将滤波级提取的特征进行分类,即
| $ {\mathit{\boldsymbol{x}}^l} = f({z^l}) = f({\mathit{\boldsymbol{W}}^l}{\mathit{\boldsymbol{x}}^{l - 1}} + {\mathit{\boldsymbol{b}}^l}) $ | (3) |
式中各符号含义同上。
1.2.2 CNN的反向传播在处理分类问题时,Softmax函数一般作为分类器的输出,表示n个不同类的概率分布。根据第i个样本的标签向量yi与模型预测的概率向量yi*构造损失函数,即
| $ C = - \frac{1}{m}\sum\limits_{i = 1}^m {\mathit{\boldsymbol{y}}_i^{\rm{T}}} {\rm{lg}}(\mathit{\boldsymbol{y}}_i^*) $ | (4) |
式中:m为样本个数;C为Softmax交叉熵。模型参数通过梯度下降算法更新,反向传播使损失函数的信息通过网络向后流动,完成梯度的快速计算[19]。对于单个样本,反向传播对于不同层的梯度计算步骤为:
(1) 首先定义灵敏度误差
| $ {\delta ^l} = \frac{{\partial C}}{{\partial {z^l}}} $ | (5) |
式中误差项δl表示第l层神经元输入对损失函数的影响。
(2) 根据不同情况计算不同层误差灵敏度
1) 如果当前第l层是卷积层,那么第l-1层的误差项为
| $ {\delta ^{l - 1}} = {\delta ^l} {\rm{rot}}{\kern 1pt} {\kern 1pt} {\kern 1pt} 180({\mathit{\boldsymbol{W}}^l}) \odot {f^\prime }({z^{l - 1}}) $ | (6) |
式中:f′(zl-1)=[f′(z1l-1)f′(z2l-1)…f′(zNl-1)]T,表示激活函数对各元素的导数值,N表示第l-1层的神经元个数;rot180(·)表示矩阵顺时针旋转180°操作;“⊙”表示哈达玛积运算。
2) 如果当前l层是池化层,那么第l-1层的误差灵敏度为
| $ {\delta ^{l - 1}} = {\rm{ upsample }}({\delta ^l}) \odot {f^\prime }({z^{l - 1}}) $ | (7) |
式中upsample(·)为上采样操作。
3) 如果当前l层是全连接层,那么第l-1层灵敏度误差为
| $ {\delta ^{l - 1}} = {({\mathit{\boldsymbol{W}}^l})^{\rm{T}}}{\delta ^l} \odot {f^\prime }({z^{l - 1}}) $ | (8) |
(3) 在确定各层灵敏度误差后,计算损失函数对权重W以及偏置b的梯度
| $ {\frac{{\partial C}}{{\partial {\mathit{\boldsymbol{W}}^l}}} = {\mathit{\boldsymbol{x}}^{l - 1}}{\delta ^l}} $ | (9) |
| $ {\frac{{\partial C}}{{\partial {\mathit{\boldsymbol{b}}^l}}} = {\delta ^l}} $ | (10) |
阵列式地面微地震监测系统包括几十个甚至上百个站点,使用高灵敏度三分量检波器采集微地震信号。实验数据分为实际数据和合成数据,均为垂直分量波形数据。实际数据为川渝地区多口油气井加砂压裂地面微地震监测数据,涉及不同类型的储层和井数据,其中LG172井是一口常规油井,实际压裂过程中监测的微地震信号较丰富。假设LG172井某个震源点发生破裂激发地震波,根据理论时差合成地面监测微地震数据——合成数据,可以模拟实际压裂过程中释放的微地震信号[20]。
将数据输入到CNN之前需要进行预处理。由于原始波形数据幅度波动较大,需要进行归一化处理[21],本文对每个通道数据均进行归一化操作。此外,有效微地震信号在整个监测波形数据中占据的比例非常小,导致正、负样本分布不均匀,致使神经网络无法有效学习[22],故采用分组处理的方法解决样本均衡问题。分组处理是截取固定长度的数据作为一个样本,其中包含微地震事件的为正样本,手动标注为1,只含背景噪声的为负样本,手动标注为0[23](图 2)。考虑到分组时要尽量保持正、负样本数目对等,同时样本数量不能太少,故将样本长度设置为256个数据点。需要说明的是,样本长度选择并不是固定的,在构建数据集时可根据不同数据量选取不同长度。为了使损失函数的计算更为合理,使用One-Hot编码(表 1)。

|
图 2 微地震波形数据分组处理 |
|
|
表 1 样本类型编码 |
本文采用微地震实际监测波形数据共849条(用于检测结果显示的数据不在此范围内),经过分组处理后得到含微地震事件的样本1420个,含背景噪声的样本1541个。随机抽取其中2000个样本作为训练集,961个样本作为测试集。
2.2 模型构建参考典型的CNN架构,搭建检测微地震事件的CNN模型(图 3),采用2个卷积层、2个池化层、1个全连接层和1个输出层的组合。这是由于输入数据只有两类,数据结构较简单,盲目增加网络层数会增大模型的存储需求,从而降低统计效率。由于微地震波形为一维数据,因此采用一维卷积处理。各层参数设置如表 2所示。
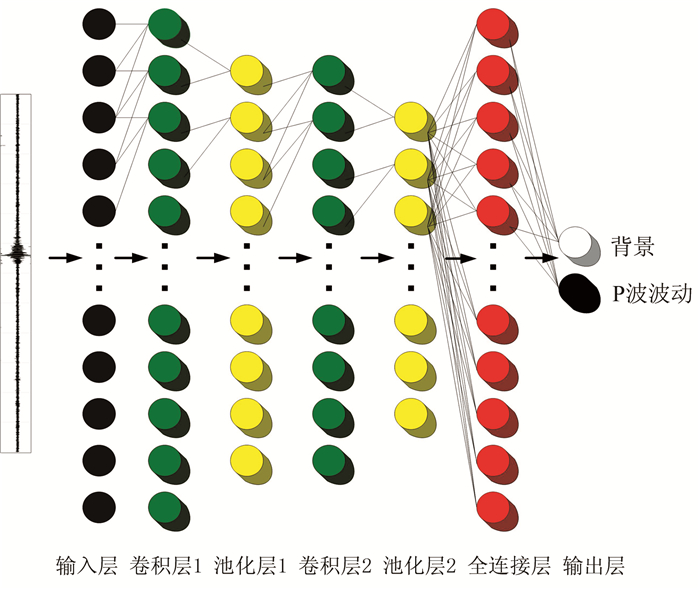
|
图 3 基于CNN的微地震事件检测模型构建 |
|
|
表 2 CNN模型参数设置 |
基于CNN的微地震事件检测方法主要分为数据处理、模型训练和实时数据检测三部分。如图 4所示,原始数据经过预处理后分为训练集样本和测试集样本。将训练集样本导入CNN模型训练,训练完成后将测试集样本输入到网络中评估模型性能。由于训练集和测试集无重复样本,因此可以模拟模型在实际部署之后的情况。如果模型性能表现较差,则返回调节样本长度和模型参数。如果模型性能良好,将多站点待检测数据归一化处理后截取为同样长度的待检测样本,然后按批输入到模型中,由此检测出各站点包含有效事件信号波动的样本号,根据各站点有效事件信号到时较接近的特点,通过统计同一事件各站点波形数据的分类结果判别微地震事件。

|
图 4 基于CNN的微地震事件检测流程 |
本文采用Python语言和Tensorflow架构作为编程环境,训练过程采用适用性估计(ADAM)优化算法,学习率为0.001。为了抑制过拟合同时加入了Dropout调整策略(训练时保留率为0.5,在测试时保留率为1.0,即所有隐层节点均参与运算)。在输入样本的过程中,引入了mini-batch(小批次,训练中设置为20个样本)降低运算复杂度。每次训练输入一个小批次样本,循环训练所有批次,将所有数据迭代一遍称为一个Epoch。本实验在配备Intel Core i5-74003.0GHz处理器和8GB内存的PC上训练20个Epoch(约1800次迭代),之后测试网络模型的性能。经过多次测试,最终得到的模型参数如表 2所示。训练过程中准确率和损失函数曲线分别如图 5和图 6所示。
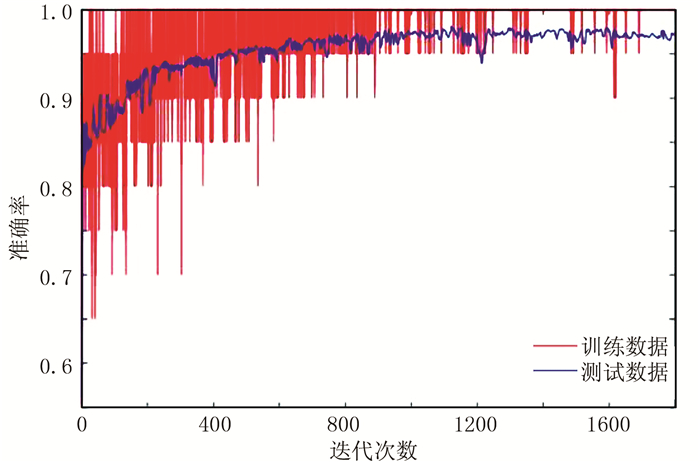
|
图 5 准确率变化曲线 |
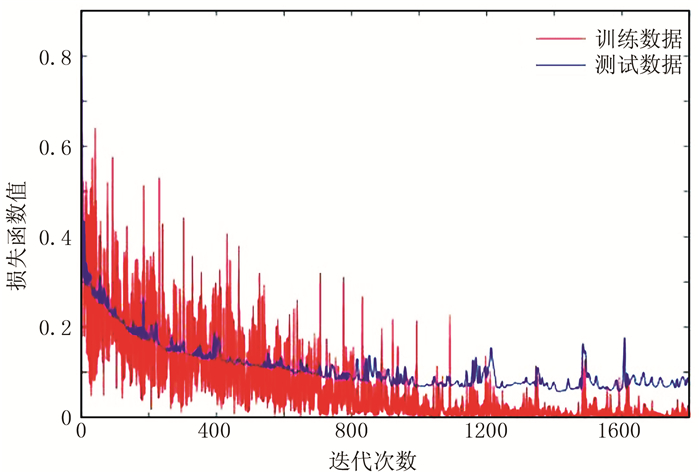
|
图 6 损失函数值变化曲线 |
由于阵列式地面微地震监测系统的检波器都埋设于地表的浅层土壤,易受各种干扰的影响[24],因此检验所提方法的抗噪性能非常必要。针对某个震源点,叠加雷克子波和高斯随机噪声生成合成信号,根据震源点到地面监测站点的正演走时偏移每一道雷克子波。定义信号信噪比为
| $ {\rm{SNR}} = 20{\kern 1pt} {\kern 1pt} {\rm{lg}}\left( {\frac{{\sum\limits_{k = 1}^N {{A^2}} ({t_k})}}{{\sum\limits_{k = 1}^N {{N^2}} ({t_k})}}} \right) $ | (11) |
式中:A(tk)为子波信号序列;N(tk)为噪声序列。
图 7为不同信噪比的合成信号。由图可见:当无噪声(图 7a)以及信噪比为15dB时(图 7b),合成信号的初至清晰,可直接判别为微地震事件;随着信噪比减小,噪声污染愈加严重,如当信噪比为6dB时(图 7c),噪声开始明显影响有效信号,当信噪比为0.5dB时(图 7d),有效信号几乎被噪声淹没,肉眼较难观察到有效信号,需要仔细甄别才能确定微地震事件(图 8)。
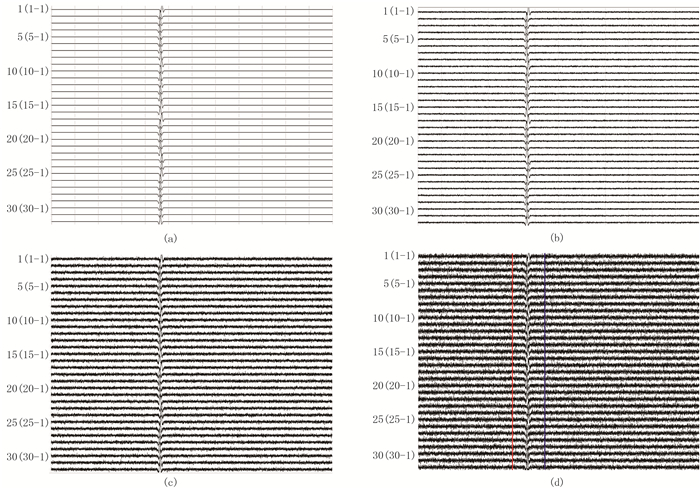
|
图 7 不同信噪比的合成信号 (a)无噪声; (b)SNR=15dB; (c)SNR=6dB; (d)SNR=0.5dB 纵向数字表示地面站点监测数据道数的标识,如30(30-1)表示第30道数据为站点30的垂直分量波形数据,下同 |

|
图 8 图 7d事件有效信号局部(红蓝标尺内多个数据道)放大 |
将图 7中的合成信号的波形数据分别输入到性能良好的CNN模型中,检测结果如表 3所示。表中事件检测通道比Mi定义为
| $ {M_i} = \frac{{{X_i}}}{Y} $ | (12) |
|
|
表 3 i=65时各合成信号检测结果 |
式中:Y为阵列式地面微地震监测系统中监测站点的总数;Xi为将第i个样本分类识别为包含有效事件信号的样本的站点数。对于第i个样本,遍历站点1~Y,若其中某个站点中该样本被分类识别为包含有效事件信号,则Xi=Xi+1。根据微地震事件的特点,并反复对比由该方法得到的微地震事件检测结果和人工标注的微地震事件,若以第i个样本为中心,左、右两个样本范围内的样本被分类识别为包含有效事件信号,则Xi=Xi+1,即
| $ {X_i} = \left\{ {\begin{array}{*{20}{l}} {{X_i} + 1}&{i \in [i - 2,i + 2]}\\ {{X_i}}&{{\rm{其他}}} \end{array}} \right. $ | (13) |
当实际压裂过程中发生微地震事件时,通常触发多个监测站点的检波器采集并存储相应的波形数据。同一事件各站点待检测波形分割的样本数据可能被分类识别为包含有效事件信号,也可能被识别为背景噪声。微地震事件的检测以其各站点波形数据分割而成的样本分类为基础,若高于一定比例(文中设定为50%,这个比例可根据实际信号质量情况而定)站点中的第i个样本(或者其左、右两个样本范围内的样本)被分类识别为包含有效事件信号,即Mi≥50%,就可认为该事件为微地震事件;反之为背景噪声。根据Mi值判别微地震事件类似投票表决的过程。
由表 3可见:当无噪声以及波形数据信噪比较高(15dB)时,65号样本的M值均为100%,即全部站点监测数据的65号样本均被识别为包含有效事件信号,因此可认为该事件为微地震事件;当波形数据信噪比降至0.5dB时,65号样本的M值也为100%。随着信噪比降低,检测过程中出现个别站点的背景噪声样本被误判为包含有效事件信号,如当信噪比为0.5dB时,几乎全部监测站点的波形数据都出现样本误判情况,但这些样本只被个别的监测站点共同包含,即这些噪声样本号对应的M < 50%。
图 9为数值模拟合成信号部分站点监测波形数据检测结果。由图可见:当无噪声(图 9a)以及波形数据信噪比为15dB(图 9b)时,得到的检测结果几乎相同,8个站点(图中为1~8道)的波形数据均在4400~4656数据点(65号样本)处检测到有效事件信号;当波形数据信噪比为6dB时,8个站点也均在4400个数据点附近检测到有效事件信号(图 9c),由于信噪比降低,在第3道的6100~6356数据点(72号样本)处以及第6道的8300~8556数据点(80号样本)处出现个别站点的背景噪声样本被误判为包含有效事件信号样本的情况;当信噪比为0.5dB(图 9d)时,8个站点中的7个站点的波形数据都出现噪声样本被误判为包含有效事件信号样本的情况。
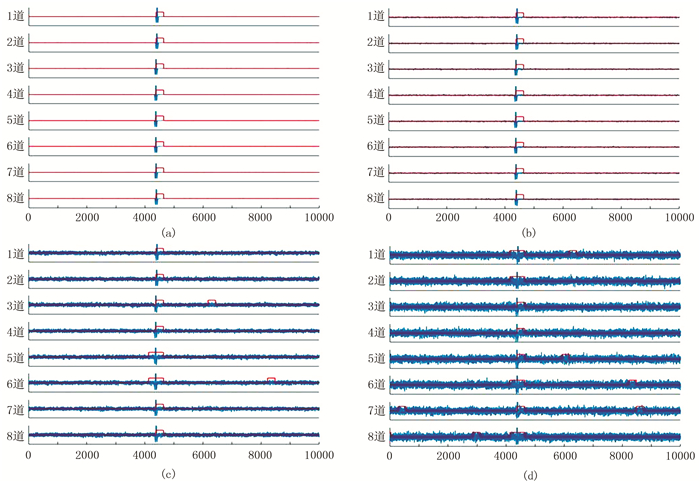
|
图 9 数值模拟合成信号部分站点监测波形数据检测结果 (a)无噪声;(b)SNR=15dB;(c)SNR=6dB;(d)SNR=0.5dB 图中只截取了10000个数据点显示,横坐标为数据点编号,下同 |
考虑到实际压裂过程中微地震事件的信号幅值波动较大,同时在上述实验中可能存在由于使用雷克子波振幅较大,导致有效信号容易识别。为此,将合成信号中的雷克子波的振幅分别降至13、10、7、5和3,分别随机叠加高斯白噪声,得到信噪比分别为15、6、2dB的波形数据,再使用相同的CNN模型进行测试。表 4为SNR=2dB、i=65时各合成信号检测结果。由表可见:①当子波振幅为15、13时,检测结果与上述实验相同。②随着子波振幅降低,模型将65号样本分类识别为包含有效事件信号的样本的站点数Xi逐渐减少,因此得到的M值也逐渐减小,但是当振幅为5时,65号样本的M值仍大于50%,仍可判断该事件为微地震事件;当振幅为3时,65号样本的M值仅为28.13%,故文中方法没有检测到微地震事件。
|
|
表 4 SNR=2dB、i=65时各合成信号检测结果 |
不同井的水力压裂微地震监测波形数据均存在差异,这些差异主要由储层岩石特性、压裂方式、地表土壤层厚度等因素决定。由于不同监测站点与井的距离、环境干扰强度均不同,在一口井压裂时,不同监测站点、不同时间段监测到的微地震信号也存在差异。为了检验所提方法对不同井的连续波形数据的泛化能力,在实际压裂微地震事件检测中使用多口井(包括普通油井和页岩气井)的阵列式地面微地震监测数据。在模型训练完成以及测试性能符合要求后,首先利用该模型检测LG172井其他时刻的微地震事件。图 10为LG172井地面监测站点不同样本号的波形数据。由图可见:①87号样本是一个31站点的微地震事件,其波形数据信噪比较高,信号明显(图 10a);96号样本显示的微地震事件虽然被噪声污染,但是其信号能量较强,持续时间长(图 10b);15号样本的微地震波形数据噪声污染严重,信噪比较低,信号微弱(图 10c);上述3个样本的M值均大于50%(表 5),故可判定为微地震事件。②113号样本是夜间安静环境下的背景信号(图 10d),全部监测站点中最多有5个站点的波形数据的背景噪声样本被误判为包含有效事件信号的样本,其M值仍小于50%(表 5),因此判定为非微地震事件。图 11为图 10对应的检测结果。
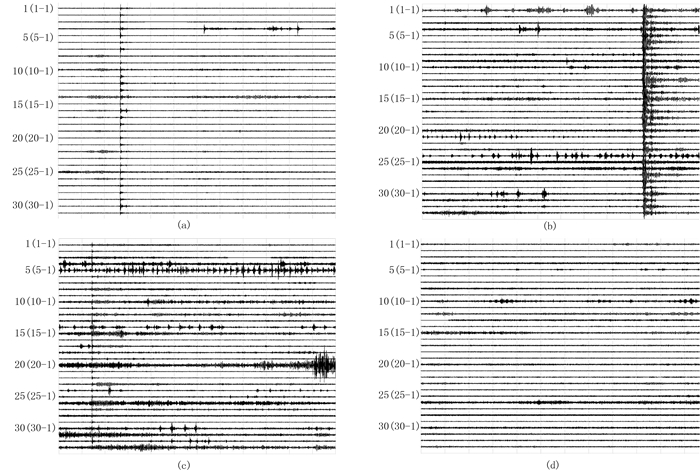
|
图 10 LG172井地面监测站点不同样本号的波形数据 (a)87;(b)96;(c)15;(d)113 |
|
|
表 5 LG172井监测波形数据的检测结果 |
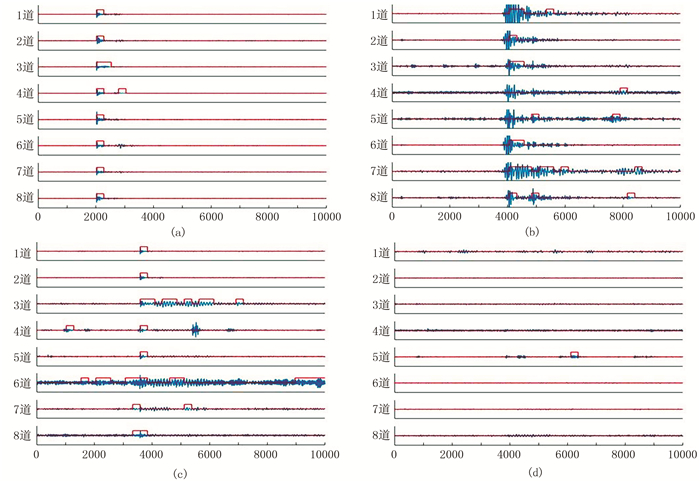
|
图 11 LG172井地面监测站点不同样本号的波形数据检测结果 (a)87;(b)96;(c)15;(d)113 |
再利用相同的模型检测N203井的部分微地震监测数据。图 12为N203井地面监测站点不同样本号的波形数据,图 13为图 12对应的检测结果。由图可见,相比于LG172井,N203井微地震信号初始幅度弱、中段幅度增强,同时持续时间较长。表现为:①76号样本(图 12a、图 13a)、70号样本(图 12b、图 13b)微地震事件的M的值均大于50%,可以被有效地检测。②69号样本(或其左、右两个样本范围内)(图 12c、图 13c)的微地震事件中仅有10个站点波形数据被模型分类识别为包含有效事件信号,这可能是由于部分地面监测站点采集的微地震信号波形较微弱所致,如第5道和第7道站点数据的有效信号波动几乎接近背景噪声;按照文中方法的原则,仍有半数监测站点的波形数据或其附近样本被分类识别为包含有效事件信号,因此也可判断该事件为微地震事件。③87号样本(图 12d、图 13d)的微地震事件中个别站点数据明显受噪声污染,出现模型将一些背景噪声样本误判为包含有效事件信号样本的情况,如第1道波形数据(图 13d)中大量的噪声样本被误判,但是这些被误判的背景噪声样本号仅被该站点数据包含,因此存在19个地面站点波形数据的87号样本被分类识别为包含有效事件,对应的M值为95%,因此可以判断该事件为微地震事件(表 6)。
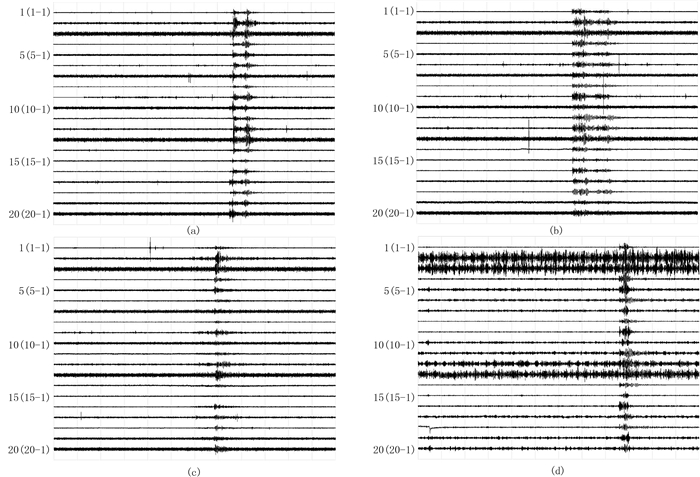
|
图 12 N203井地面监测站点不同样本号的波形数据 (a)76;(b)70;(c)69;(d)87 |

|
图 13 N203井地面监测站点不同样本号的波形数据检测结果 (a)76;(b)70;(c)69;(d)87 |
|
|
表 6 N203井监测波形数据的检测结果 |
利用相同模型对川渝地区其他几口井的典型波形数据进行微地震事件检测,检测结果表明所提方法均能有效判别微地震事件,因此具有良好的泛化能力。
4 结论以往人们主要基于单站点波形数据识别微地震事件,对于强干扰造成的低信噪比信号,可能出现微地震事件误判。文中方法根据阵列式地面微地震监测的特性,以单站点监测数据检测结果为基础,综合考虑事件发生时各站点波形数据的特点判别微地震事件。该方法经过训练确定合适的卷积神经网络模型参数之后,可直接输入实时采集的检波器数据。本文主要对合成信号和川渝地区不同井的实际监测数据进行微地震事件检测,得到以下认识:
(1) 对于叠加不同噪声的合成微地震信号,随着信噪比降低,信号质量越来越差。当信噪比降至2dB和0.5dB时,有效信号几乎被噪声淹没,虽然出现了一些样本被误判的情况,但是65号样本对应的M值仍大于50%,可确定为微地震事件,且合成信号中雷克子波振幅减小对检测结果的影响不大。因此本文所提方法对于噪声的容忍度高,能准确检测不同信噪比的微地震事件。
(2) 实际压裂过程中不同井采集的微地震波形数据存在一定差异。以川渝地区LG172井和N203井为例,对信噪比较高、有效信号明显,噪声污染严重、信号微弱以及只存在背景噪声的监测数据进行微地震事件检测,均能有效判别微地震事件。因此本文所提方法对于川渝地区不同的连续波形数据具有良好的泛化能力,可以在实际水力压裂过程中检测微地震事件。
此外,与常规方法相比,本文方法无需人工设定阈值,在训练过程中可自动提取特征和选择最优参数。所用的卷积神经网络模型在训练完成后,对于阵列式地面微地震监测系统的32个监测站点拼接的单站点长度为30000数据点的待检测波形数据,能够在1s内输出模型分类结果。同时,本文所用训练数据相对简单,通过增加训练数据,模型在现有基础上可以继续进行训练进而提高识别精度,这也是卷积神经网络的优势。
| [1] |
段银鹿, 李倩, 姚韦萍. 水力压裂微地震裂缝监测技术及其应用[J]. 断块油气田, 2013, 20(5): 644-648. DUAN Yinlu, LI Qian, YAO Weiping. Microseismic fracture monitoring technology of hydraulic fracturing and its application[J]. Fault-Block Oil & Gas Field, 2013, 20(5): 644-648. |
| [2] |
赵博雄, 王忠仁, 刘瑞, 等. 国内外微地震监测技术综述[J]. 地球物理学进展, 2014, 29(4): 1882-1888. ZHAO Boxiong, WANG Zhongren, LIU Rui, et al. Review of microseismic monitoring technology research[J]. Progress in Geophysics, 2014, 29(4): 1882-1888. |
| [3] |
储仿东, 焦亚军, 杨立峰, 等. 利用微地震识别水力压裂井旁天然裂缝[J]. 石油地球物理勘探, 2018, 53(增刊2): 143-147. CHU Fangdong, JIAO Yajun, YANG Lifeng, et al. Natural fracture identification at hydraulic fracturing wells with microseismic[J]. Oil Geophysical Prospecting, 2018, 53(S2): 143-147. |
| [4] |
王维波, 春兰, 桑宇, 等.气井压裂地面微地震监测系统开发及其应用[C].油气藏监测与管理国际会议, 2011, 325-329.
|
| [5] |
唐杰, 方兵, 蓝阳, 等. 压裂诱发的微地震震源机制及信号传播特性[J]. 石油地球物理勘探, 2015, 50(4): 643-649. TANG Jie, FANG Bing, LAN Yang, et al. Focal mechanism of micro-seismic induced by hydrofracture and its signal propagation characteristics[J]. Oil Geophysical Prospecting, 2015, 50(4): 643-649. |
| [6] |
宋维琪, 冯超. 微地震有效事件自动识别与定位方法[J]. 石油地球物理勘探, 2013, 48(2): 283-288. SONG Weiqi, FENG Chao. Automatic identification and localization of microseismic effective events[J]. Oil Geophysical Prospecting, 2013, 48(2): 283-288. |
| [7] |
刘翰林, 吴庆举. 地震自动识别及震相自动拾取方法研究进展[J]. 地球物理学进展, 2017, 32(3): 1000-1007. LIU Hanlin, WU Qingju. Developments of research on earthquake detection and seismic phases picking[J]. Progress in Geophysics, 2017, 32(3): 1000-1007. |
| [8] |
Wang H, Li M, Shang X F. Current developments on micro-seismic data processing[J]. Journal of Natural Gas Science and Engineering, 2016, 32(5): 521-537. |
| [9] |
张唤兰, 朱光明, 王云宏. 基于时窗能量比和AIC的两步法微震初至自动拾取[J]. 物探与化探, 2013, 37(2): 269-273. ZHANG Huanlan, ZHU Guangming, WANG Yunhong. Automatic microseismic event detection and picking method[J]. Geophysical and Geochemical Exploration, 2013, 37(2): 269-273. |
| [10] |
Shang X Y, Li X B, Esteban A M, et al. An improved P-phase arrival picking method S/L-K-A with an application to the Yongshaba mine in China[J]. Pure and Applied Geophysics, 2018, 175(6): 2121-2139. DOI:10.1007/s00024-018-1789-x |
| [11] |
曹俊海, 顾汉明, 尚新民. 基于局部相关谱约束的多道匹配追踪算法识别微地震信号[J]. 石油地球物理勘探, 2017, 52(4): 704-714. CAO Junhai, GU Hanming, SHANG Xinmin. Microseismic signal identification with multichannel ma-tching pursuit based on local coherence spectrum constraint[J]. Oil Geophysical Prospecting, 2017, 52(4): 704-714. |
| [12] |
陈润航, 黄汉明, 柴慧敏. 地震和爆破事件源波形信号的卷积神经网络分类研究[J]. 地球物理学进展, 2018, 33(4): 1331-1338. CHEN Runhang, HUANG Hanming, CHAI Huimin. Study on the discrimination of seismic waveform signals between earthquake and explosion events by convolutional neural network[J]. Progress in Geophy-sics, 2018, 33(4): 1331-1338. |
| [13] |
赵明, 陈石, Yuen D. 基于深度学习卷积神经网络的地震波形自动分类与识别[J]. 地球物理学报, 2019, 62(1): 380-388. ZHAO Ming, CHEN Shi, Yuen D. Waveform classification and seismic recognition by convolution neural network[J]. Chinese Journal of Geophysics, 2019, 62(1): 380-388. |
| [14] |
Bi L, Xie W, Zhao J J. Automatic recognition and classification of multi-channel microseismic waveform based on DCNN and SVM[J]. Computers & Geosciences, 2019, 123(2): 111-120. |
| [15] |
常亮, 邓小明, 周明全, 等. 图像理解中的卷积神经网络[J]. 自动化学报, 2016, 42(9): 1300-1312. CHANG Liang, DENG Xiaoming, ZHOU Mingquan, et al. Convolutional neural networks in image understanding[J]. Acta Automatica Sinica, 2016, 42(9): 1300-1312. |
| [16] |
Lecun Y, Boser B, Denker J, et al. Back propagation applied to handwritten zip code recognition[J]. Neural Computation, 1989, 1(4): 541-551. DOI:10.1162/neco.1989.1.4.541 |
| [17] |
Gu J X, Wang Z H, Kuen J, et al. Recent advances in convolutional neural networks[J]. Pattern Recognition, 2018, 77(5): 354-377. |
| [18] |
周飞燕, 金林鹏, 董军. 卷积神经网络研究综述[J]. 计算机学报, 2017, 40(6): 1229-1251. ZHOU Feiyan, JIN Linpeng, DONG Jun. Review of convolutional neural network[J]. Chinese Journal of Computers, 2017, 40(6): 1229-1251. |
| [19] |
Lecun Y, Bengio Y, Hinton G. Deep learning[J]. Nature, 2015, 521(5): 436-444. |
| [20] |
宋维琪, 杨晓东. 基于射线追踪的微地震多波场正演模拟[J]. 地球物理学进展, 2012, 27(4): 1501-1508. SONG Weiqi, YANG Xiaodong. The multi-wave field forward simulation of microseismic based on ray tra-cing[J]. Progress in Geophysics, 2012, 27(4): 1501-1508. |
| [21] |
于子叶, 储日升, 盛敏汉. 深度神经网络拾取地震P和S波到时[J]. 地球物理学报, 2018, 61(12): 4873-4886. YU Ziye, CHU Risheng, SHENG Minhan. Pick onset time of P and S phase by deep neural network[J]. Chinese Journal of Geophysics, 2018, 61(12): 4873-4886. |
| [22] |
曹鹏.不均衡数据分类方法的研究[D].辽宁沈阳: 东北大学, 2014.
|
| [23] |
姚开一, 李英玉. 基于神经网络的地震震相自动拾取方法[J]. 电子设计工程, 2018, 26(22): 7-11. YAO Kaiyi, LI Yingyu. Neural-network-based seismic phase automatic pickup method[J]. Electronic Design Engineering, 2018, 26(22): 7-11. |
| [24] |
刁瑞, 吴国忱, 尚新民, 等. 地面微地震有源噪声自动识别与匹配压制方法[J]. 石油地球物理勘探, 2018, 53(2): 311-319. DIAO Rui, WU Guochen, SHANG Xinmin, et al. Microseismic active noise automatic identification and matching denoising[J]. Oil Geophysical Prospecting, 2018, 53(2): 311-319. |



 盛立, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)控制科学与工程学院, 266580。Email:
盛立, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)控制科学与工程学院, 266580。Email: