② 中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 湖南长沙 410083;
③ 东方地球物理公司综合物化探处, 河北涿州 072751;
④ 桂林理工大学地球科学学院, 广西桂林 541006
② Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring, Ministry of Education, Changsha, Hunan 410083, China;
③ GME & Geochemical Surveys of BGP, CNPC, Zhuozhou, Hebei 072751, China;
④ College of Earth Sciences, Guilin University of Technology, Guilin, Guangxi 541006, China
重磁位场正演方法主要分为空间域方法和频率域方法。空间域方法又可以分为解析法和数值法。解析法是通过重磁异常场解析表达式直接求取空间任意点的精确异常场,其优点是原理简单、计算结果精确。解析法研究早期侧重于简单、规则模型的重磁场解析表达式的推导,如水平薄板、直立棱柱体、直立圆柱体等[1-4]。后来学者们逐步对均匀介质的多面体模型[5-9]和简单物性变化的任意三度体模型的重磁场解析式推导[10-11]、解析积分奇异点处理[9, 12]、边界场连续性问题[12]等开展了大量的研究。一般来说,解析法表达式比较复杂、适应性较差、计算量较大。数值法主要通过有限差分法[13]、有限体积法[14]、有限单元法[15-16]求解重磁异常满足的泊松方程,但是当计算大量位置点的异常场时,耗时较长。
频率域方法的原理是采用数值方法对场源在某条测线(或平面/三维空间)产生的重磁异常频谱(傅里叶变换解析表达式)进行计算,并通过反傅里叶变换得到异常场[17]。其优点是表达式简单,计算效率相对较高,但是傅里叶变换的截断效应限制了该方法的普遍适用性。Bhattacharyya[3]推导了任意磁化方向的长方体磁场频谱表达式;Pedersen[18]给出了直立圆柱体和多面体模型的重磁异常频率域表达式;熊光楚[19]给出了长方体模型重力位的三维傅里叶变换式;后来一些学者对物性连续变化模型的频率域解析式[20-24]、Parker模型频率域表达式[25-26]、偏移抽样方法提高反傅里叶变换数值精度[27]开展了大量研究。Tontini等[28]实现了重磁异常三维全空间频率域正演,并研究了FFT扩边法与误差的关系;Wu等[29-30]利用高斯FFT提高了反傅里叶变换的数值精度,降低了由于FFT引起的强制周期化、边界震荡效应等影响,并研究了地形对重磁异常的影响,分析了物性连续变化模型的梯度场;Ren等[31]提出一种基于非结构化网格的自适应快速多极子重磁场及其梯度张量正演方法,借助并行计算实现了快速、高精度的三维正演。
目前,随着计算机技术的不断发展和重磁异常正演算法的不断改进,频率域方法以其简捷、准确和高效等优势在数值模拟中的应用越来越广泛。但是,对于面向实际应用的超大规模复杂三维模型数值模拟问题,由于网格剖分单元数目剧增,计算量和存储量巨大,常规的空间域和频率域重磁异常正演方法已很难同时满足精度与效率上的要求。为此,本文提出一种重磁位场三维数值模拟方法,充分利用一维形函数积分的高精度性、不同波数之间高度并行性及傅里叶变换的高效性,实现高效、高精度、大规模的重磁位场数值模拟。
1 理论与方法弱磁性体的磁位V及重力位ϕ的空间域积分表达分别为[32]
| $ \left\{ {\begin{array}{*{20}{l}} {V(x,y,z) = - \mu \iiint\limits_V \mathit{\boldsymbol{M}} ({x^\prime },{y^\prime },{z^\prime }) \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \nabla G(x,y,z;{x^\prime },{y^\prime },{z^\prime }){\rm{d}}v}\\ {\phi (x,y,z) = 4\pi D\iiint\limits_V \rho ({x^\prime },{y^\prime },{z^\prime }) \cdot }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} G(x,y,z;{x^\prime },{y^\prime },{z^\prime }){\rm{d}}v} \end{array}} \right. $ | (1) |
式中:M为空间域磁化强度矢量;ρ为剩余密度;μ为真空磁导率,取值4π×10-7 H/m;D为万有引力常量,取值6.674×10-11 m3kg-1s-2;(x, y, z)为观测点坐标;(x′, y′, z′)为异常点坐标;为哈密顿算符;G为格林函数。
对式(1)沿x、y方向做二维傅里叶变换,分别得到磁力位和重力位一维积分公式
| $ \left\{ \begin{array}{l} \tilde V({k_x},{k_y},z) = - \frac{{{\rm{i}}{k_x}}}{{2k}}\mu \int {{{\tilde M}_x}} {{\rm{e}}^{ - k|z - {z^\prime }|}}{\rm{d}}{z^\prime } - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\rm{i}}{k_y}}}{{2k}}\mu \int {{{\tilde M}_y}} {{\rm{e}}^{ - k|z - {z^\prime }|}}{\rm{d}}{z^\prime } + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mu \int {{{\tilde M}_z}} \frac{{ {\rm{sign}} (z - {z^\prime })}}{2}{{\rm{e}}^{ - k|z - {z^\prime }|}}{\rm{d}}{z^\prime }\\ \tilde \phi ({k_x},{k_y},z) = \frac{{2\pi D}}{k}\int {\tilde \rho } ({k_x},{k_x},{z^\prime }){{\rm{e}}^{ - k|z - {z^\prime }|}}{\rm{d}}{z^\prime } \end{array} \right. $ | (2) |
式中:
式(2)的推导需利用波数域格林函数,其表达式为
| $ {\tilde G_{\rm{r}}} = \frac{{{{\rm{e}}^{ - k|z - {z^\prime }|}}}}{{2k}} $ | (3) |
磁位和重力位的一阶导数分别为
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{B}} = - \nabla V}\\ {\mathit{\boldsymbol{g}} = \nabla \phi } \end{array}} \right. $ | (4) |
对应的二阶导数分别为
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{T}}_{\rm{B}}} = - \nabla \nabla V}\\ {{\mathit{\boldsymbol{T}}_{\rm{g}}} = \nabla \nabla \phi } \end{array}} \right. $ | (5) |
式中下标“B”和“g”分别代表磁力场和重力场。
利用傅里叶变换的微分性质,对式(4)和式(5)做二维傅里叶变换,得到波数域重磁异常场和张量的表达式分别为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{\tilde B}} = \left[ {\begin{array}{*{20}{l}} {{{\tilde B}_x}}\\ {{{\tilde B}_y}}\\ {{{\tilde B}_z}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - {\rm{i}}{k_x}}\\ { - {\rm{i}}{k_y}}\\ { {\rm{sign}} (z - {z^\prime })k} \end{array}} \right]\tilde V\\ \mathit{\boldsymbol{\tilde g}} = \left[ {\begin{array}{*{20}{l}} {{{\tilde g}_x}}\\ {{{\tilde g}_y}}\\ {{{\tilde g}_z}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{\rm{i}}{k_x}}\\ {{\rm{i}}{k_y}}\\ { - {\rm{sign}} (z - {z^\prime })k} \end{array}} \right]\tilde \phi \end{array} \right. $ | (6) |
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\tilde T}}}_{\rm{B}}} = \left[ {\begin{array}{*{20}{l}} {\tilde T_{\rm{B}}^{xx}}&{\tilde T_{\rm{B}}^{xy}}&{\tilde T_{\rm{B}}^{xz}}\\ {\tilde T_{\rm{B}}^{3x}}&{\tilde T_{\rm{B}}^{yy}}&{\tilde T_{\rm{B}}^{yz}}\\ {\tilde T_{\rm{B}}^{zx}}&{\tilde T_{\rm{B}}^{zy}}&{\tilde T_{\rm{B}}^{zz}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {k_x^2}&{{k_x}{k_y}}&{[ {\rm{sign}} (z - {z^\prime })k]{\rm{i}}{k_x}}\\ {{k_x}{k_y}}&{k_y^2}&{[ {\rm{sign}} (z - {z^\prime })k]{\rm{i}}{k_y}}\\ {[ {\rm{sign}} (z - {z^\prime })k]{\rm{i}}{k_x}}&{[ {\rm{sign}} (z - {z^\prime })k]{\rm{i}}{k_y}}&{ - {k^2}} \end{array}} \right]\tilde V\\ {{\mathit{\boldsymbol{\tilde T}}}_{\rm{g}}} = \left[ {\begin{array}{*{20}{l}} {\tilde T_{\rm{g}}^{xx}}&{\tilde T_{\rm{g}}^{xy}}&{\tilde T_{\rm{g}}^{xz}}\\ {\tilde T_{\rm{g}}^{3x}}&{\tilde T_{\rm{g}}^{yy}}&{\tilde T_{\rm{g}}^{yz}}\\ {\tilde T_{\rm{g}}^{zx}}&{\tilde T_{\rm{g}}^{zy}}&{\tilde T_{\rm{g}}^{zz}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} { - k_x^2}&{ - {k_x}{k_y}}&{ - [ {\rm{sign}} (z - {z^\prime })k]{\rm{i}}{k_x}}\\ { - {k_x}{k_y}}&{ - k_y^2}&{ - [ {\rm{sign}} (z - {z^\prime })k]{\rm{i}}{k_y}}\\ { - [ {\rm{sign}} (z - {z^\prime })k]{\rm{i}}{k_x}}&{ - [ {\rm{sign}} (z - {z^\prime })k]{\rm{i}}{k_y}}&{ - {k^2}} \end{array}} \right]\tilde \phi \end{array} \right. $ | (7) |
式中:
式(2)为重磁位垂向一维积分表达式。从该表达式可以看出,不同波数一维空间域积分是相互独立的,可以并行计算;该一维积分深度方向可离散为多个单元积分之和,每个积分单元采用形函数法插值计算,得到单元积分的解析表达式,可提高计算精度和效率。
2 基于形函数的一维积分本文采用基于二次插值的形函数法[31]计算傅里叶变换后的一维积分。将一维积分沿垂直方向剖分为m个单元,采用二次形函数描述物性参数变化。从式(2)可以看出,重力位与磁位的积分表达式相似,只是系数不同;重力异常与磁异常积分中,不同方向的积分表达式也相似,只是系数不同。因此,下面以x方向磁位积分为例,介绍形函数法计算一维积分的具体过程。
对积分区域进行离散
| $ {I_x}({k_x},{k_y},z) = - \sum\limits_{i = 1}^m {\int_{z_i^\prime }^{z_{i + 2}^\prime } \mu } \frac{{{\rm{i}}{k_x}}}{{2k}}\tilde M_x^i({z^\prime }){{\rm{e}}^{ - k|z - {z^\prime }|}}{\rm{d}}{z^\prime } $ | (8) |
式中i表示积分单元。
对磁化强度在节点处采用二次形函数插值
| $ \tilde M_x^i({z^\prime }) = \tilde M_x^{{i_1}}{N_1} + \tilde M_x^{{i_2}}{N_2} + \tilde M_x^{{i_3}}{N_3} $ | (9) |
式中:N1、N2、N3为二次形函数;i1、i2、i3分别为积分单元i的3个插值节点。
将式(9)代入式(8)中,整理得
| $ {I_x}({k_x},{k_y},z) = - \sum\limits_{i = 1}^m {(\tilde M_x^{{i_1}}W_i^1 + \tilde M_x^{{i_2}}W_i^2 + \tilde M_x^{{i_3}}W_i^3)} $ | (10) |
式中Wi1、Wi2、Wi3为形函数单元积分系数,其解析表达式详细推导过程见附录A。
由式(10)离散后的一维单元积分可推导出解析表达式,该表达式计算精度较高,接近于解析解。对于物性参数满足二次变化的复杂形体,垂向单元剖分间隔可根据需要灵活选择。
3 算法流程本文按照如下流程进行重磁位场数值模拟计算。
(1) 网格剖分。给定计算区域,确定沿x、y、z方向的剖分单元个数C1、C2、C3。水平方向均匀剖分,垂直方向可任意剖分,得到三维离散坐标点(xm, yn, zl),给定计算的观测平面z。
(2) 模型参数设定。给所有的剖分单元赋予剩余密度或磁化率值。
(3) 离散波数计算。由FFT法的波数计算公式得出水平离散坐标(xm, yn)的离散波数(kx, ky)。
(4) 重磁空间域二维傅里叶变换。对空间域重磁位场剩余密度或者磁化强度进行水平二维离散傅里叶变换。
(5) 积分计算。采用形函数法计算垂向一维积分,得到波数谱。
(6) 重磁波数谱二维傅里叶反变换。利用FFT算法,对波数谱场或张量进行二维离散傅里叶反变换,得到空间域重磁位场或张量。
4 算例分析 4.1 正确性验证设计一个棱柱体模型,采用基于四个高斯点的高斯—FFT法[28]计算重磁异常场及张量的数值解,并与模型解析解[32]进行对比,验证该算法的正确性。
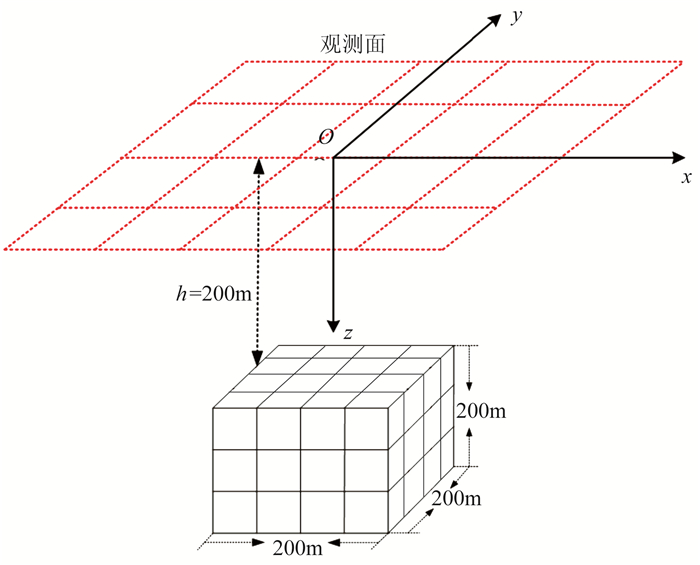
模型如图 1所示。异常体大小为200m×200m×200m,顶面埋深h为200m。观测面为z=0的水平面,模拟区域为800m×800m×400m,观测点个数为201×201。棱柱异常体与模拟区域水平中心点重合。模拟区域网格节点个数为201×201×201,空间采样间隔均为4m。设定异常体的磁化强度为0.01A/m,背景磁场为4500nT,磁倾角为45°,磁偏角为5°;设定其剩余密度为1000kg/m3。
|
图 1 棱柱体模型示意图 |
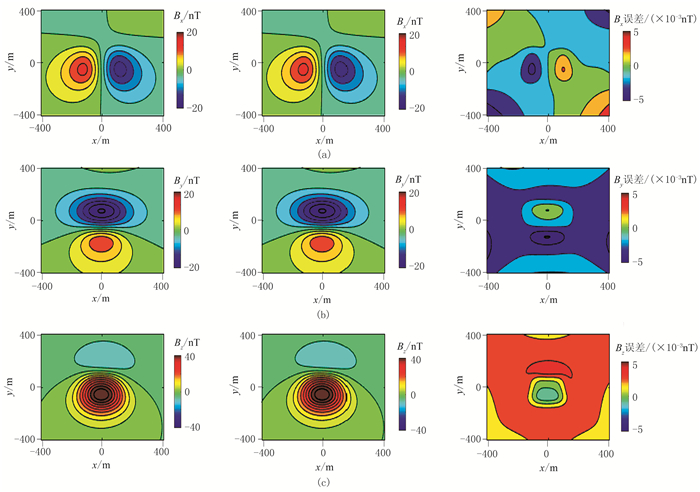
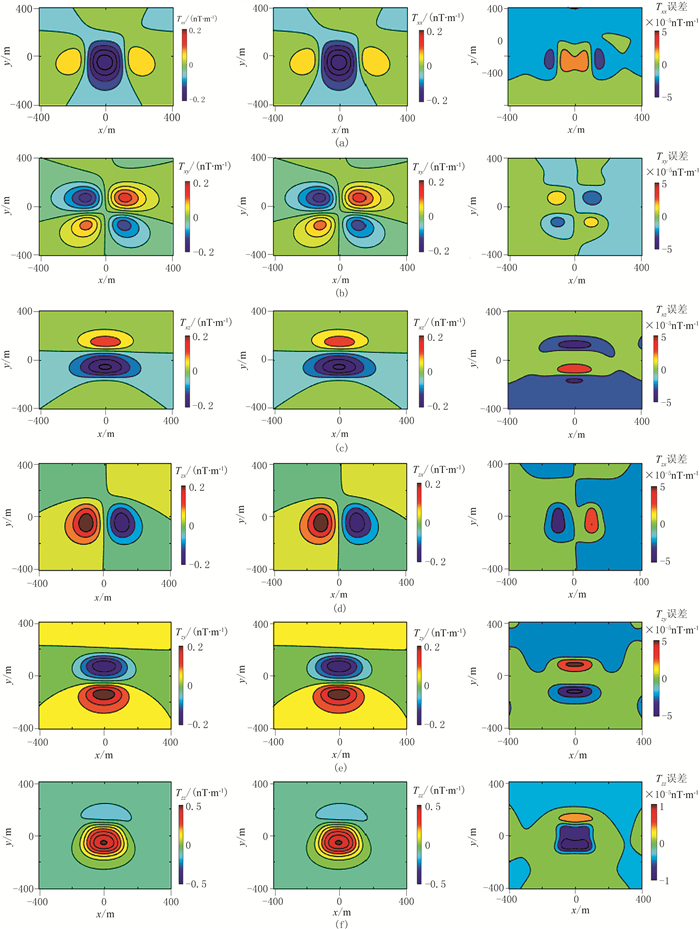
图 2为磁异常场在z=0平面的数值解、解析解与绝对误差。可以看出,磁异常场的绝对误差最大约为5×10-3nT。图 3为磁异常梯度张量在z=0平面的数值解、解析解与绝对误差,可以看出,磁异常梯度张量的绝对误差最大约为5×10-5nT/m。磁异常场和磁异常梯度张量的绝对误差均比相应解析解小三个数量级。
|
图 2 z=0平面磁异常场的数值解(左)、解析解(中)及绝对误差(右) (a)Bx; (b)By; (c)Bz |
|
图 3 z=0平面磁梯度张量的数值解(左)、解析解(中)及绝对误差(右) (a)Txx; (b)Txy; (c)Tyy; (d)Tzx; (e)Tzy; (f)Tzz; |
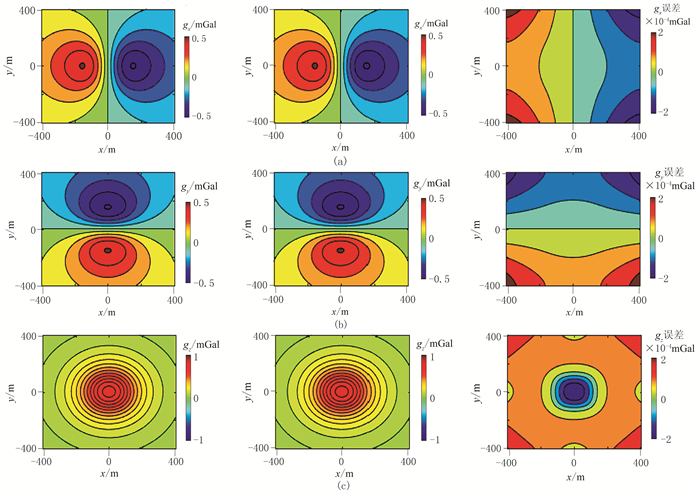
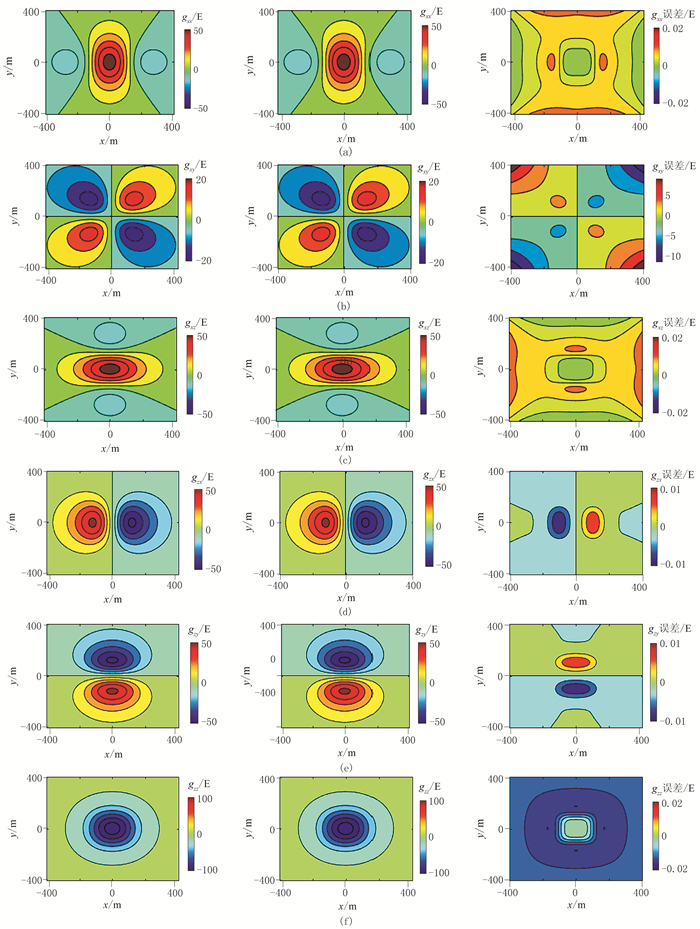
图 4为重力异常场在z=0平面的数值解、解析解与绝对误差。可以看出,重力异常场的绝对误差最大约为2×10-4mGal。图 5为重力异常梯度张量在z=0平面的数值解、解析解与绝对误差,可以看出,重力异常梯度张量的绝对误差最大约为0.02E。同样地,重力异常场和重力异常梯度张量的绝对误差值也均比相应解析解低三个数量级。重磁场数值模拟结果表明,本文算法正确,且精度高。
|
图 4 z=0平面重力异常场的数值解(左)、解析解(中)及绝对误差(右) |
|
图 5 z=0平面重力梯度张量的数值解(左)、解析解(中)及绝对误差(右) (a)gxx; (b)gxy; (c)gyy; (d)gzx; (e)gzy; (f)gzz |
对波数域的一维积分采用二次形函数法可得到每个单元的近似解析解,该方法计算精度较高,适用于复杂介质的数值模拟计算。以磁异常数值模拟为例设计一个复杂形体模型。异常体的水平方向磁化率不变,垂直方向磁化率呈二次变化。垂直方向分别采用均匀剖分与形函数插值两种方法获得数值解。通过数值解与解析解[25]的对比分析,可验证本文方法对于复杂模型的适用性。为了研究统计整个观测面的误差情况,引入相对均方根误差[30]
| $ {\rm{rrms}} = \frac{{\sqrt {\sum\limits_{i = 1}^P {\sum\limits_{j = 1}^N {{{({{\hat B}_{ij}} - {B_{ij}})}^2}} } } }}{{\sqrt {\sum\limits_{i = 1}^P {\sum\limits_{j = 1}^N {\hat B_{ij}^2} } } }} \times 100 $ | (11) |
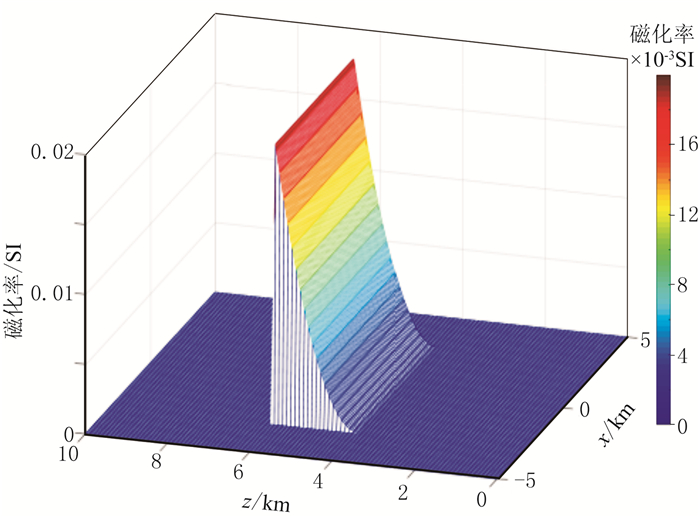
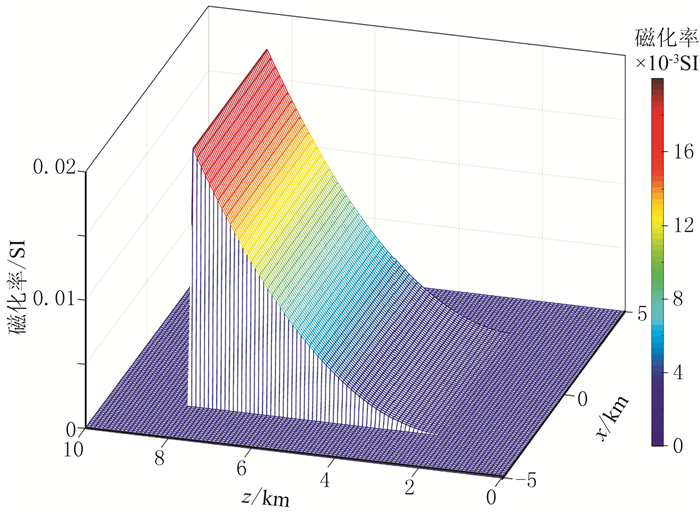
式中:P和N分别是x和y方向的节点数;Bij是磁场(张量)数值解;ij是磁场(张量)解析解。该误差统计方式能突出大异常值所占的比重。设计两个不同模型,水平方向磁化率均不变,垂向磁化率从0递增到0.02SI,其中模型1(图 6)垂直方向磁化率变化为0.02/60002(z-2000)2(2000≤z≤8000),模型2 (图 7)磁化率变化为0.02/20002(z-4000)2(4000≤z≤6000),水平方向采样间距均为100m。两个模型的背景磁感应强度均为45000nT,磁倾角为45°,磁偏角为5°。
|
图 6 模型1垂向磁化率变化趋势图 |
|
图 7 模型2垂向磁化率变化趋势图 |
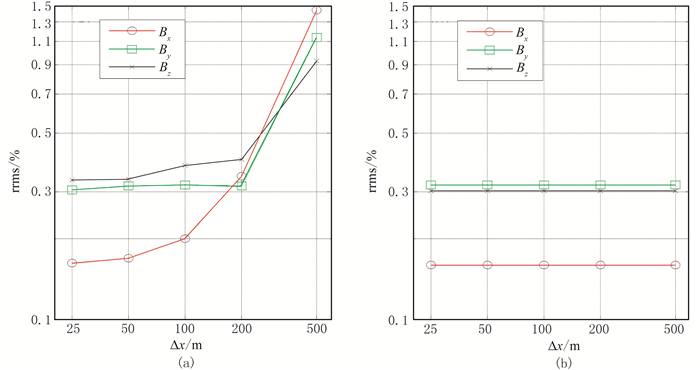
图 8和图 9分别为模型1磁场分量和磁张量随着采样间距变化的数值解与解析解的相对均方根误差变化图。可以看出,两种方法在垂直采样间距为25m时的计算精度相近,在积分单元内磁化率均匀剖分的误差随着采样间距的增大而增大,而形函数二次插值的计算精度基本保持不变。
|
图 8 模型1磁场分量相对均方根误差统计曲线 (a)单元内磁化率均匀剖分;(b)单元内磁化率形函数二次插值 |
|
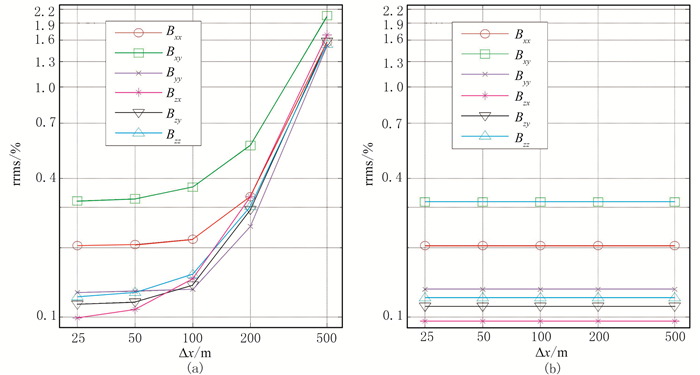
图 9 模型1磁张量相对均方根误差统计曲线 (a)单元内磁化率均匀剖分;(b)单元内磁化率形函数二次插值 |
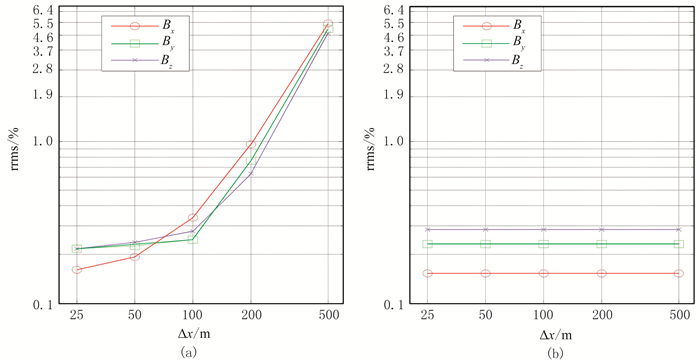
图 10和图 11分别为模型2磁场分量和磁张量随着采样间距变化的数值解与解析解的相对均方根误差变化图。
|
图 10 模型2磁场分量相对均方根误差 (a)单元内磁化率均匀剖分;(b)单元内磁化率形函数二次插值 |
|
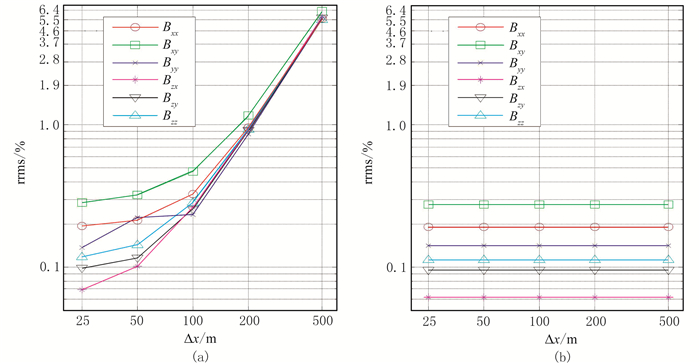
图 11 模型2磁张量相对均方根误差 (a)单元内磁化率均匀剖分;(b)单元内磁化率形函数二次插值 |
与模型算例1计算结果对比可以看出,两个模型在两种剖分方法下的误差变化趋势基本一致。但是与模型1相比,模型2中单元内磁化率均匀剖分的计算精度有所降低,这是由于模型2中模型介质磁化率的变化更剧烈,而单元内磁化率形函数二次插值的计算精度变化较小。这再次验证了该方法对于复杂介质模型具有较好的适用性。
对于模型区域剖分网格单元数为100×100×100、观测点数为101×101的三维正演计算,传统空间域累加算法耗时约800s,波数域Parker公式计算结果约耗时8.4s,本文算法约耗时5.1s,加速比分别为156.8与1.65,验证了本算法的高效性。
5 结论本文提出一种高效、高精度的重磁位场三维数值模拟方法。该方法沿水平方向进行二维傅里叶变换,把重磁位场三维积分转化为垂向一维积分问题。对于离散后的单元积分采用形函数二次插值计算,可得出单元积分的解析表达式,理论上具有较高的计算精度。
设计棱柱体模型,模型的解析解与本文方法的数值解对比表明,本文提出的重磁位场数值模拟方法正确且计算精度高。
设计复杂连续变化介质模型,模型解析解与数值解对比表明,本文提出的形函数插值计算一维积分与传统的棱柱体均匀剖分相比具有更高的计算精度,更适用于变化复杂的实际介质的模拟计算。
附录A 形函数单元积分系数推导过程
| $ {I_{x{\rm{e}}}}({k_x},{k_y},z) = \sum\limits_{i = 1}^m {\int_{z_i^\prime }^{z_{i + 2}^\prime } \mu } \frac{{{\rm{i}}{k_x}}}{{2k}}\tilde M_x^i({z^\prime }){{\rm{e}}^{ - k|z - {z^\prime }|}}{\rm{d}}{z^\prime } $ | (A-1) |
对第i个单元进行积分时,根据观测点与积分单元的相对位置,分三种情况进行讨论:
(1) 当观测点在该单元上方时,即z<z′,式(A-1)为
| $ {I_{x{\rm{e}}}}({k_x},{k_y},z) = \int_{z_i^\prime }^{z_{i + 2}^\prime } {\left( {\mu \frac{{{\rm{i}}{k_x}}}{{2k}}} \right)\tilde M_x^i({z^\prime })} {{\rm{e}}^{k(z - {z^\prime })}}{\rm{d}}{z^\prime } $ | (A-2) |
(2) 当观测点在该单元下方时,即z>z′i+2,式(A-1)为
| $ {I_{x{\rm{e}}}}({k_x},{k_y},z) = \int_{z_i^\prime }^{z_{i + 2}^\prime } {\left( {\mu \frac{{{\rm{i}}{k_x}}}{{2k}}} \right)\tilde M_x^i({z^\prime })} {{\rm{e}}^{ - k(z - {z^\prime })}}{\rm{d}}{z^\prime } $ | (A-3) |
(3) 当观测点在该单元内部时,即z′≤z≤z′ i+2,式(A-1)为
| $ \begin{array}{*{20}{l}} {{I_{x{\rm{e}}}}({k_x},{k_y},z) = \int_{z_i^\prime }^z {\left( {\mu \frac{{{\rm{i}}{k_x}}}{{2k}}} \right)\tilde M_x^i({z^\prime })} {{\rm{e}}^{ - k(z - {z^\prime })}}{\rm{d}}{z^\prime } + }\\ {\quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int_z^{z_{i + 2}^\prime } {\left( {\mu \frac{{{\rm{i}}{k_x}}}{{2k}}} \right)\tilde M_x^i({z^\prime })} {{\rm{e}}^{k(z - {z^\prime })}}{\rm{d}}{z^\prime }} \end{array} $ | (A-4) |
令γ=k,式(A-2)变为
| $ {I_{x{\rm{e}}}}({k_x},{k_y},z) = {{\rm{e}}^{\gamma z}}\mu \frac{{{\rm{i}}{k_x}}}{{2k}}\int_{z_i^\prime }^{z_{i + 2}^\prime } {\tilde M_x^i} ({z^\prime }){{\rm{e}}^{ - \gamma {z^\prime }}}{\rm{d}}{z^\prime } $ | (A-5) |
令
| $ {I_{x{\rm{e}}}}({k_x},{k_y},z) = {a_x}(z)\int_{z_i^\prime }^{z_{i + 2}^\prime } {\tilde M_x^i} ({z^\prime }){{\rm{e}}^{ - \gamma {z^\prime }}}{\rm{d}}{z^\prime } $ | (A-6) |
对于式(A-3),令γ=-k,式(A-3)变为
| $ {I_{x{\rm{e}}}}(z) = \left( {\mu \frac{{{\rm{i}}{k_x}}}{{2k}}} \right){{\rm{e}}^{\gamma z}}\int_{z_i^\prime }^{z_{i + 2}^\prime } {\tilde M_x^i} ({z^\prime }){{\rm{e}}^{ - \gamma {z^\prime }}}{\rm{d}}{z^\prime } $ | (A-7) |
令
| $ {I_{x{\rm{e}}}}({k_x},{k_y},z) = {a_x}(z)\int_{z_i^\prime }^{x_{i + 2}^\prime } {\tilde M_x^i} ({z^\prime }){{\rm{e}}^{ - \gamma {z^\prime }}}{\rm{d}}{z^\prime } $ | (A-8) |
对于式(A-4),在(zi, z)积分区域令γ=-k,
| $ \begin{array}{*{20}{c}} {{I_{x{\rm{e}}}}({k_x},{k_y},z) = {a_x}(z)\int_{z_i^\prime }^z {\tilde M_x^i} ({z^\prime }){{\rm{e}}^{ - \gamma {z^\prime }}}{\rm{d}}{z^\prime } + }\\ {a_x^\prime (z)\int_{{z^\prime }}^{z_{i + 2}^\prime } {\tilde M_x^i} ({z^\prime }){{\rm{e}}^{ - \gamma {z^\prime }}}{\rm{d}}{z^\prime }} \end{array} $ | (A-9) |
对式(A-6)或式(A-8)单元积分,采用形函数表示插值函数,有
| $ \tilde M_x^i({z^\prime }) = {N_1}\tilde M_x^{{i_1}}({z^\prime }) + {N_2}\tilde M_x^{{i_2}}({z^\prime }) + {N_3}\tilde M_x^{{i_3}} $ | (A-10) |
式中
| $ {{N_1} = (2{L_1} - 1){L_1}} $ | (A-11) |
| $ {{N_2} = 4{L_1}{L_3}} $ | (A-12) |
| $ {{N_3} = (2{L_3} - 1){L_3}} $ | (A-13) |
其中
| $ {{L_1} = \frac{{z_3^\prime - {z^\prime }}}{{z_3^\prime - z_1^\prime }}} $ | (A-14) |
| $ {{L_3} = \frac{{{z^\prime } - z_1^\prime }}{{z_3^\prime - z_1^\prime }}} $ | (A-15) |
得到单元积分
| $ \int_e {{a_x}} (z){\tilde M_x}({z^\prime }){{\rm{e}}^{ - \gamma {z^\prime }}}{\rm{d}}{z^\prime } = \tilde M_x^{{i_1}}W_i^1 + \tilde M_x^{{i_2}}W_i^2 + \tilde M_x^{{i_3}}W_i^3 $ | (A-16) |
式中
| $ {W_i^1 = {a_x}(z)\int_e {{N_1}} {{\rm{e}}^{ - \gamma {z^\prime }}}{\rm{d}}{z^\prime }} $ | (A-17) |
| $ {W_i^2 = {a_x}(z)\int_e {{N_2}} {{\rm{e}}^{ - \gamma {z^\prime }}}{\rm{d}}{z^\prime }} $ | (A-18) |
| $ {W_i^3 = {a_x}(z)\int_e {{N_3}} {{\rm{e}}^{ - \gamma {z^\prime }}}{\rm{d}}{z^\prime }} $ | (A-19) |
求解过程如下
| $ \begin{array}{*{20}{c}} {{N_1}{{\rm{e}}^{ - \gamma {z^\prime }}}{\rm{d}}{z^\prime } = \frac{1}{{{l^2}}}[2\int_e {{z^{\prime 2}}} {{\rm{e}}^{ - \gamma {z^\prime }}}{\rm{d}}{z^\prime } + (l - 4z_3^\prime ) \times }\\ {\int_e {{z^\prime }} {{\rm{e}}^{ - \gamma {z^\prime }}}{\rm{d}}{z^\prime } + (2z_3^\prime - l)z_3^\prime \int_e {{{\rm{e}}^{ - \gamma {z^\prime }}}} {\rm{d}}{z^\prime }]}\\ { = \frac{1}{{{l^2}}}[2{I_2} + (l - 4z_3^\prime ){I_1} + (2z_3^\prime - l)z_3^\prime {I_0}]} \end{array} $ | (A-20) |
| $ \begin{array}{*{20}{c}} {\int_e {{N_2}{{\rm{e}}^{ - \gamma {z^\prime }}}{\rm{d}}{z^\prime }} = - \frac{4}{{{l^2}}}[\int_e {{z^{\prime 2}}} {{\rm{e}}^{ - \gamma {z^\prime }}}{\rm{d}}{z^\prime } - (z_1^\prime + z_3^\prime ) \times }\\ {\quad \int_e^\prime {{z^\prime }{{\rm{e}}^{ - \gamma {z^\prime }}}} {\rm{d}}{z^\prime } + z_1^\prime z_3^\prime \int_e {{{\rm{e}}^{ - \gamma {z^\prime }}}} {\rm{d}}{z^\prime }]}\\ { = - \frac{4}{{{l^2}}}[2{I_2} - (z_1^\prime + z_3^\prime ){I_1} + z_1^\prime z_3^\prime {I_0}]} \end{array} $ | (A-21) |
| $ \begin{array}{*{20}{c}} {\int_e {{N_3}{{\rm{e}}^{ - \gamma {z^\prime }}}{\rm{d}}{z^\prime }} = \frac{1}{{{l^2}}}[2\int_e {{z^{\prime 2}}} {{\rm{e}}^{ - \gamma {z^\prime }}}{\rm{d}}{z^\prime } - (l + 4z_1^\prime ) \times }\\ {\quad \int_e^\prime {{{\rm{e}}^{ - \gamma {z^\prime }}}} {\rm{d}}{z^\prime } + (2z_1^\prime + l)z_1^\prime \int_e {{{\rm{e}}^{ - \gamma {z^\prime }}}} {\rm{d}}{z^\prime }]}\\ { = \frac{1}{{{l^2}}}[2{I_2} - (l + 4z_1^\prime ){I_1} + (2z_1^\prime + l)z_1^\prime {I_0}]} \end{array} $ | (A-22) |
其中
| $ {I_0} = \int_{z_1^\prime }^{z_3^\prime } {{{\rm{e}}^{ - \gamma {z^\prime }}}} {\rm{d}}{z^\prime } = \frac{1}{\gamma }({{\rm{e}}^{ - \gamma z_1^\prime }} - {{\rm{e}}^{ - \gamma z_3^\prime }}) $ | (A-23) |
| $ \begin{array}{*{20}{l}} {{I_1} = \int_{z_1^\prime }^{z_3^\prime } {{z^\prime }} {{\rm{e}}^{ - \gamma {z^\prime }}}{\rm{d}}{z^\prime } = \frac{1}{{{\gamma ^2}}}[(1 + \gamma z_1^\prime ){{\rm{e}}^{ - \gamma z_1^\prime }} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} (1 + \gamma z_3^\prime ){{\rm{e}}^{ - \gamma z_3^\prime }}]} \end{array} $ | (A-24) |
| $ \begin{array}{*{20}{l}} {{I_2} = \int_{z_1^\prime }^{z_3^\prime } {{z^{\prime 2}}} {{\rm{e}}^{ - \gamma {z^\prime }}}{\rm{d}}{z^\prime } = \frac{1}{{{\gamma ^3}}}\{ [{\gamma ^2}z_1^{\prime 2} + 2(1 + \gamma z_1^\prime )]{{\rm{e}}^{ - \gamma z_1^\prime }} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [{\gamma ^2}z_3^{\prime 2} + 2(1 + \gamma _z^\prime )]{{\rm{e}}^{ - \gamma _3^\prime }}\} } \end{array} $ | (A-25) |
式(A-9)的单元形函数展开与式(A-6)类似,只是积分的上、下限不同。
利用每个单元的插值函数,可将所求积分表示为
| $ \begin{array}{*{20}{l}} {{I_x}({k_x},{k_y},z)}\\ {\quad = \sum\limits_{i = 1}^m {{a_x}} (z)(\tilde M_i^{{i_2}}W_1^\prime + \tilde M_x^{{i_2}}W_2^\prime + \tilde M_x^{{i_3}}W_3^\prime )} \end{array} $ | (A-26) |
| [1] |
TalwaniM. Rapid computation of gravitational attra-ction of three-dimensional bodies of arbitrary shape[J]. Geophysics, 1960, 25(1): 203-225. |
| [2] |
Nagy D. The gravitational attraction of a right rectangular prism[J]. Geophysics, 1966, 31(2): 362-371. |
| [3] |
Bhattacharyya B K. Magnetic anomalies due to prism-shaped bodies with arbitrary polarization[J]. Geophysics, 1964, 29(4): 517-531. DOI:10.1190/1.1439386 |
| [4] |
Singh S K. Magnetic anomaly due to a vertical right circular cylinder with arbitrary polarization[J]. Geophysics, 1978, 43(1): 173-178. |
| [5] |
Paul M K. The gravity effect of a homogeneous polyhedron for three-dimensional interpretation[J]. Pure & Applied Geophysics, 1974, 112(3): 553-561. |
| [6] |
Furness P. A physical approach to computing magne-tic fields[J]. Geophysical Prospecting, 1994, 42(5): 405-416. DOI:10.1111/j.1365-2478.1994.tb00218.x |
| [7] |
Ivan M. Optimum expression for computation of the magnetic field of a homogeneous polyhedral body[J]. Geophysical Prospecting, 1996, 44(2): 279-288. DOI:10.1111/j.1365-2478.1996.tb00150.x |
| [8] |
Guptasarma D, Singh B. New scheme for computing the magnetic field resulting from a uniformly magne-tized arbitrary polyhedron[J]. Geophysics, 1999, 64(1): 70-74. |
| [9] |
Kwok Y K. Gravity gradient tensors due to a polyhe-dron with polygonal facets[J]. Geophysical Prospecting, 1991, 39(3): 435-443. DOI:10.1111/j.1365-2478.1991.tb00320.x |
| [10] |
Chakravarthi V, Raghuram H M, Singh S B. 3-D forward gravity modeling of basement interfaces above which the density contrast varies continuously with depth[J]. Computers & Geosciences, 2002, 28(1): 53-57. |
| [11] |
García-Abdeslem J. The gravitational attraction of a right rectangular prism with density varying with depth following a cubic polynomial[J]. Geophysics, 2005, 70(3): J39-J45. DOI:10.1190/1.1958090 |
| [12] |
Nagy D, Papp G, Benedek J. The gravitational potential and its derivatives for the prism[J]. Journal of Geodesy, 2000, 74(7-8): 552-560. DOI:10.1007/s001900000116 |
| [13] |
Farquharson C G, Mosher C R W. Three dimen-sional modelling of gravity data using finite diffe-rences[J]. Journal of Applied Geophysics, 2009, 68(3): 417-422. DOI:10.1016/j.jappgeo.2009.03.007 |
| [14] |
Jahandari H, Farquharson C G. Forward modeling of gravity data using finite-volume and finite-element methods on unstructured grids[J]. Geophysics, 2013, 78(3): G69-G80. |
| [15] |
Cai Y, Wang C Y. Fast finite-element calculation of gravity anomaly in complex geological regions[J]. Geophysical Journal International, 2005, 162(3): 696-708. DOI:10.1111/j.1365-246X.2005.02711.x |
| [16] |
Maag E, Capriotti J and Li Y.3D gravity inversion using the finite element method[C].SEG Technical Program Expanded Abstracts, 2017, 36: 1713-1717.
|
| [17] |
吴乐园.重磁位场频率域高精度正演方法: Gauss-FFT法[D].浙江杭州: 浙江大学, 2014.
|
| [18] |
Pedersen L B. The gravity and magnetic fields from ellipsoidal bodies in the wavenumber domain[J]. Geophysical Prospecting, 1985, 33(2): 263-281. DOI:10.1111/j.1365-2478.1985.tb00434.x |
| [19] |
熊光楚. 重、磁场三维傅里叶变换的若干问题[J]. 地球物理学报, 1984, 27(1): 103-109. XIONG Guangchu. Some problems about the 3-D Fourier transforms of the gravity and magnetic fields[J]. Acta Grophysica Sinica, 1984, 27(1): 103-109. |
| [20] |
吴宣志. 三度体(物性随深度变化模型)位场波谱的正演计算[J]. 地球物理学报, 1983, 26(2): 177-186. WU Xuanzhi. The computation of spectrum of potential field due to 3-D arbitrary bodies with physical parameters varying with depth[J]. Acta Grophysica Si-nica, 1983, 26(2): 177-186. |
| [21] |
冯锐. 三维物性分布的位场计算[J]. 地球物理学报, 1986, 29(4): 399-406. FENG Rui. A computation method of potential field with three-dimensional density and magnetization distributions[J]. Acta Grophysica Sinica, 1986, 29(4): 399-406. |
| [22] |
Granser H. Nonlinear inversion of gravity data using the Schmidt-Lichtenstein approach[J]. Geophysics, 1987, 52(1): 88-93. |
| [23] |
Rao D B, Prakash M J, Babu N R. Gravity interpretation using Fourier-transforms and simple geometrical models with exponential density[J]. Geophysics, 1993, 58(2): 1074-1083. |
| [24] |
Tontini F C. Magnetic-anomaly Fourier spectrum of a 3D Gaussian source[J]. The Leading Edge, 2005, 70(1): L1-L5. |
| [25] |
Parker R. The rapid calculation of potential anomalies[J]. Geophysical Journal of the Royal Astronomical Society, 1973, 31(4): 447-455. DOI:10.1111/j.1365-246X.1973.tb06513.x |
| [26] |
Forsberg R. Gravity field terrain effect computations by FFT[J]. Journal of Geodesy, 1985, 59(4): 342-360. |
| [27] |
柴玉璞. Fourier变换数值计算的偏移抽样理论[J]. 中国科学(E辑), 1997, 40(5): 68-74. CHAI Yupu. Shift sampling theory of Fourier transform computation[J]. Science in China(E), 1997, 40(1): 21-27. |
| [28] |
Tontini F C, Cocchi L, Carmisciano C. Rapid 3-D forward model of fields with application to the Palinuro seamount gravity anomaly(Sourthern Tyrrhenian Sea, Italy)[J]. Journal of Geophysical Research, 2009, 114: 1205-1222. |
| [29] |
Wu L, Tian G. High-precision Fourier forward modeling of potential fields[J]. Geophysics, 2014, 79(5): G59-G68. DOI:10.1190/geo2014-0039.1 |
| [30] |
Wu L. Efficient modelling of gravity effects due to topographic masses using the Gauss-FFT method[J]. Geophysical Journal International, 2016, 205(1): 160-178. DOI:10.1093/gji/ggw010 |
| [31] |
Ren Z, Tang J, Kalscheuer T, et al. Fast 3-D large-scale gravity and magnetic modeling using unstructured grids and an adaptive multilevel fast multipole method[J]. Journal of Geophysical Research, 2017, 122(1): 79-109. |
| [32] |
管志宁. 地磁场与磁力勘探[M]. 北京: 地质出版社, 2005.
|
| [33] |
徐世浙. 地球物理中的有限单元法[M]. 北京: 北京科学出版社, 1994.
|


