基于磁力异常确定磁性体埋深是磁法勘探需要研究的问题之一,对磁性矿藏、火成岩及磁性基底的研究具有重要意义。有多种方法可完成该任务,如重磁场梯度比值函数法[1]、特征点法、切线法[2-7]、线性反演法、解析信号法、局部波数法、维纳反褶积法、欧拉反褶积法[8]等,其中比较经典的当属切线法和欧拉反褶积法。
切线法是利用过异常曲线上的一些特征点(如极值点、拐点)的切线之间的交点计算磁性体产状要素的方法。该方法简单、快速、受正常场选择影响小,在航磁异常的定量解释中广泛应用。中国国土资源航空物探遥感中心自20世纪60年代便开始研究磁性体深度计算方法,积累了大量的经验,对切线法进行了改进和完善[3-4]。切线法虽然是一种经验方法,但由于能适应复杂磁异常的解释,且精度不低,常用于磁性基底深度的求取和解释[5]。该方法的主要不足是手动操作比较繁琐,对操作者的经验要求较高。自20世纪90年代起开始应用ΔT切线法自动计算磁性体深度[6-7]。
欧拉反褶积是一种能自动估算场源位置的位场反演方法,以欧拉齐次方程为基础,运用位场异常及其空间导数以及各种地质体具有的特定“构造指数”确定异常场源的位置[8]。该方法于1982年第一次运用于模型数据和实测数据处理[9],后又推广到三维数据领域,并应用于面积位场资料的处理和解释[10]。欧拉方法虽然有着严格的理论基础,但仍存在一些应用方面的问题。针对欧拉方法受导数阶次、噪声、构造指数选择等因素影响较大的缺点,研究人员从不同的角度对常规的欧拉反褶积方法进行改进,比如增加解的稳定性、减弱计算结果的随机性、消除构造指数选择的影响等,均取得了不错的效果[11-12]。
本文通过研究磁源深度在磁异常及其垂向导数中的不同表现特征,提出利用磁异常及其垂向导数极大值比值序列作为磁源深度计算的“因变量”,并借助当今比较流行的BP神经网络技术进行磁源深度预测,探索出一种“傻瓜式”的磁源顶埋深预测方法。通过大量理论长方体模型的磁异常数据及其垂向导数极值比序列与模型顶深形成样本对,对构建的BP神经网络进行训练,使BP神经网络“学会”并“记住”极值比序列与深度之间的非线性映射关系,从而达到预测目的。理论模型和实际应用结果均验证了本文方法的有效性和正确性。
本文方法与切线法和欧拉反褶积法相比,其优点在于预测过程不需要人为干预和输入各种参数,深度的预测完全依靠训练好的BP神经网络,是一种“黑盒式”的智能自动深度预测方法,神经网络的训练效果决定了最终的预测精度。
1 方法原理在具体叙述方法原理之前,首先给出利用BP神经网络进行磁性体顶深预测的流程,以便于更好理解本方法。BP神经网络磁性体顶面埋深预测流程如下:
(1) 对实测面积性磁异常数据进行网格化;
(2) 对网格化数据进行化极处理并去除背景场;
(3) 求取磁异常场的垂向一阶、二阶、三阶导数;
(4) 提取各个独立磁异常及各垂向导数极大值,并形成极值比序列;
(5) 将极值比序列输入到已训练好的神经网络;
(6) 输出深度预测值。
训练BP神经网络的步骤如下:
(1) 设计不同大小、深度的磁性长方体模型,正演其垂直磁化条件下的磁异常;
(2) 求取磁异常的垂向一阶、二阶、三阶导数;
(3) 提取极值比序列,并与模型顶深形成样本对集合;
(4) 进行BP神经网络训练;
(5) 判断网络是否训练好。如训练好则存储网络,训练过程结束;否则返回步骤(4),直至网络训练好。
1.1 磁异常特征的选取磁异常及其各种导数的特征有很多种,比如形状、走向、宽度、强度、梯度等,如何有效地选择这些特征并用来进行深度预测,是一个现实问题。相关研究表明,浅部磁源的异常强度大且异常较“尖锐”(梯度大),而深部磁源的异常强度小且异常较平缓(梯度小)。因此,可以从异常强度和梯度这两个因素对磁源的深度进行分析。
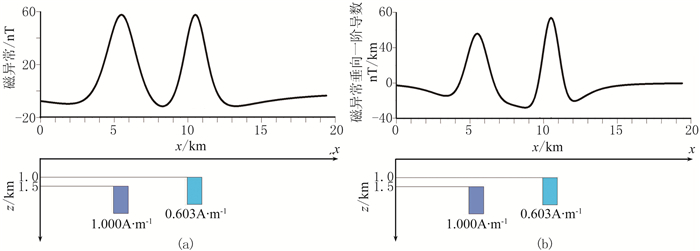
设计两个理论模型,如图 1a所示,两个大小相同(1.0km×1.5km)、磁化强度不同(1.000A/m、0.603A/m)、埋深不同(1.5km、1.0km)的长方形磁源体可产生相等极大值的磁异常,这说明单纯从异常的极大值对深度进行推测是多解的。图 1b为图 1a的垂向一阶导数曲线,可以看出,深、浅两个磁源所对应的磁异常极大值出现了明显的区别:深部磁源的垂向一阶导数极大值明显小于浅部磁源。
|
图 1 不同深度磁源体的磁异常(a)和垂向一阶导数(b) 下图为理论模型,上图为正演曲线 |
如果仅仅利用垂向一阶导数的极大值进行深度预测,同样存在多解性问题。因为地下磁源体的大小、形状、物性是千变万化的,总会有两个、甚至更多个顶深不同、磁化强度也不同的磁源体产生的垂向一阶导数极大值相等。这正是位场方法的典型特征。
解决这一问题的有效途径是,不仅要利用磁异常的极大值,而且还要利用其不同阶次垂向导数的极大值综合预测磁源深度。由于求导会放大噪声,本文最高只利用垂向三阶导数。这样在磁源深度预测的过程中,既考虑了磁异常的强度信息,也考虑了其梯度信息。选择磁异常及其垂向导数的极大值作为关键特征,好处是极大值的识别和提取比较容易。另外,极大值位于磁源体正上方,当磁源深度发生变化时,极大值的变化幅度最大,反应也最灵敏。
图 2为对相同大小、相同磁化强度的长方体模型,在垂直磁化条件下、不同顶深时模拟的磁力异常极大值(mag)、垂向一导极大值(magVz)、垂向二导极大值(magVzz)、垂向三导极大值(magVzzz)序列曲线图。长方体模型的参数:大小为2.0km(x)×0.2km(y) ×0.2km(z)、磁化强度为2.000A/m。观测面为z=0平面。从图中各曲线的规律来看,模型顶深越小,其极值序列曲线的变化(梯度)越大;反之则变化(梯度)越小。

|
图 2 不同顶深模型磁异常极值序列曲线 |
上面只是从经验的角度出发,似乎极值序列已经解决了深度预测的多解性问题,其实不然。为了论述方便,用球体的磁异常正演公式来说明。假设球心坐标为(0,0,r)(r为球体中心埋深),观测点位于(x,y,0)平面上。垂直均匀磁化球体的磁异常为
| $ \Delta T = \frac{{{\mu _0}}}{{4\pi }}\frac{{Mv\left( {2{r^2} + {x^2} + {y^2}} \right)}}{{{{\left( {{x^2} + {y^2} + {r^2}} \right)}^{\frac{5}{2}}}}} $ | (1) |
式中:μ0为真空中的磁导率;M为磁矩;υ为球体体积。
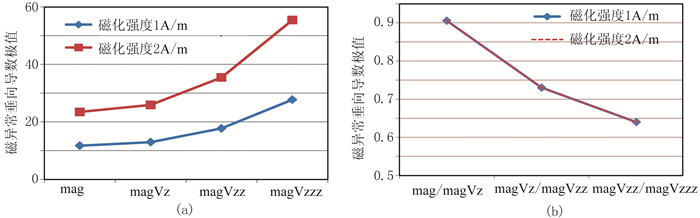
由式(1)可知,磁异常强度与观测点到磁源体的距离的平方成反比,与磁源体的磁化强度(忽略自退磁效应)成正比。也就是说,相同大小、形状、深度、不同磁化强度场源所产生的磁异常强度是不同的,必然会造成利用极值序列进行深度预测的多解性。图 3a为大小、形状、埋深相同但磁化强度不同的长方体磁源所产生的极值序列,可见两个不同的极值序列曲线对应同一个磁源深度,显然这个问题是多解的。那么, 一个重要的问题就是如何消除场源磁化强度的影响。从式(1)知道,磁化强度与磁异常强度呈线性正比关系,垂向导数依然是这种关系。因此,对于磁化强度的影响可以通过比值法进行消除,即利用mag/magVz、magVz/magVzz、magVzz/magVzzz极值比序列。
|
图 3 不同磁化强度对极值序列(a)和极值比序列(b)的影响 |
图 3b为极值比序列曲线,可以看出,相同大小、形状、埋深,不同磁化强度长方体磁源的极值比序列曲线完全重合,可见由于磁化强度不同所引起的多解性被完全消除。
1.3 BP网络构建人工神经网络因自学习、自组织、较好的容错性和优良的非线性逼近能力, 在诸多领域受到关注。勘探地球物理学家已经将神经网络引入地震、重磁、电磁法等诸领域,如地震道废道的自动剔除、自动编辑、初至拾取[13-15]、重磁电资料的反演[16-19]等,取得了良好的效果。
基于误差反向传播算法(BP算法)的多层前向神经网络,是目前应用最广的神经网络学习算法,在函数逼近、模式识别、数据压缩等领域有着广泛的应用[20]。
一个典型的BP神经网络一般由输入层、输出层和多个隐层(或称中间层)组成,而神经元是神经网络的最基本单元,它是对生物神经元的简化与模拟。图 4a为一个典型的、具有R维输入的神经元模型。图 4b为一个三层BP神经网络结构,包含一个隐层。构建一个BP神经网络,需要确定网络层数、神经元个数和传递函数等多方面的内容。

|
图 4 神经元(a)和三层BP网络(b)模型结构图 p1、p2、…、pR表示神经元的R个输入,P =(P1,P2,…,PR);w1, 1、w1, 2、…、w1, R表示网络权值,代表输入与神经元间的连接强度;b为神经元阈值,可以看作是一个输入恒为1的网络权值;n为求和单元对输入信号的加权求和结果;f为神经元传递函数;a为神经元输出 |
神经元传递函数为正切型(tanh)的隐层叫作S型隐含层。理论上已证明:具有偏差b和至少一个S型隐含层加上一个线性输出层的网络(三层网络),能够逼近任何一个具有有限间断点的非线性函数。增加层数可更进一步降低误差、提高精度,但同时也会使网络复杂化,增加网络权值的训练时间。对于本文研究而言,三层BP神经网络可满足要求[20]。
1.3.2 神经元个数神经网络输入层和输出层的神经元个数取决于所要解决的实际问题。对于本文研究的具体问题,其输入层和输出层神经元个数非常明确。输入向量为极值比序列mag/magVz、magVz/magVzz、magVzz/magVzzz,因此输入层包含3个神经元。目标为磁源体的顶深,因此输出层包含1个神经元。通过多次训练对比,确定隐层神经元个数为15~30即能取得好的效果。
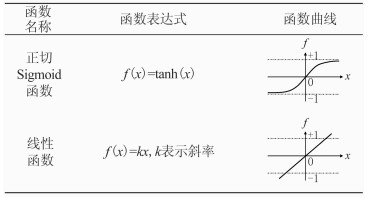
1.3.3 神经元传递函数BP神经元模型中的传递函数f通常选取可微的单调递增函数。结合本文具体问题,隐层神经元的传递函数选择正切Sigmoid函数,输出层神经元的传递函数选择线性函数。它们具体的函数表达式和图形详见表 1。
|
|
表 1 隐层和输出层的神经元传递函数 |
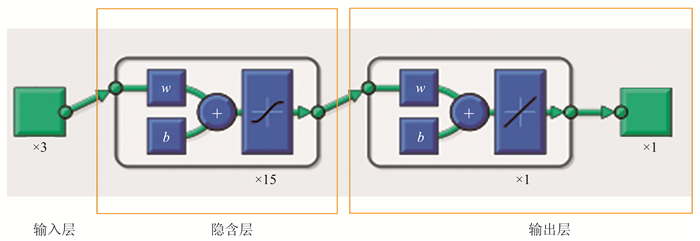
图 5为用于磁性体顶深预测的BP神经网络结构图,包括3个输入(mag/magVz、magVz/magVzz、magVzz/magVzzz)、1个输出(磁源顶深)、1个隐层,隐层包含15个神经元,所用的神经元传递函数为f(x)=tanh(x),输出层包含1个神经元,所用的神经元传递函数为f(x)=kx。
|
图 5 磁性体顶深预测的BP神经网络结构示意图 |
由于本文解决问题的思路是利用理论模型对网络进行训练,然后再利用训练结果预测实际资料,因此理论模型是否接近于实际模型,是影响预测精度的最大因素。设计的理论模型是否接近于实际地质模型,需要考虑如下几个方面的因素:形状、规模、深度等。
目前,利用磁力数据进行磁性体埋深解释大致涉及火山岩、侵入岩和铁磁性矿物。因此,所设计的模型主要关注如下几类地质模型。
(1) 薄层模型。薄层模型指纵向厚度小于横向尺寸的1/2倍,或者更小。这样的薄层模型可以用来模拟薄层火山岩和具有一定厚度但横向规模较大的磁性基底。本文设计的薄层模型横向规模为500~10000m,厚度为100~5000m,共设计335组模型。每组模型的埋深变化从500m到6000m,变化间隔为500m,这样335组模型共衍生出4020个模型。
(2) 柱状模型。柱状模型指纵向厚度大于或等于横向规模的2倍,或者更大。这样的柱状模型可以用来模拟柱状侵入的火成岩、柱状磁性岩脉等。本文设计的柱状模型的横向规模为500~5000m,厚度为1000~10000m,共设计116组模型。每组模型的埋深变化从500m到6000m,间隔为500m,这样116组模型共衍生出1356个模型。
(3) 等轴模型。根据上面两种模型的定义方式,等轴模型可以理解为纵、横向规模差别不大,除去上面两种模型外的模型都可以归到这一大组模型中。等轴模型的规模变化从500m到6000m,共设计290组模型,根据深度的不同共衍生出3480个模型。
利用上述三种模型正演的磁力异常及垂向导数获得极值比序列,并与顶深形成训练样本对,对神经网络进行训练。
1.4.2 数据归一化神经网络是统计归纳然后再演绎仿真的人工智能理论,归一化的目的是把事件的统计分布概率统一归纳在0~1灰色聚类的隶属性上。根据前文,BP神经网络主要利用S型传递函数,这种函数常常对0~1之间的数字比较敏感。另外,对“输入—目标”样本集数据进行归一化预处理,可以提高神经网络的训练效率。
归一化包含正归一化和反归一化:正归一化在训练和仿真(或预测)前进行;反归一化在仿真(或预测)后进行,主要是对输出向量进行反归一化,以使其恢复到正常值。
正归一化的公式为
| $ {P_{\rm{n}}} = 2\frac{{P - {P_{\min }}}}{{{P_{\max }} - {P_{\min }}}} - 1 $ | (2) |
| $ {T_{\rm{n}}} = 2\frac{{T - {T_{\min }}}}{{{T_{\max }} - {T_{\min }}}} - 1 $ | (3) |
式中:P为原始输入数据;Pn为归一化后的输入数据;T为原始目标数据;Tn是归一化后的目标数据;下标“max”、“min”分别代表极大值和极小值。对神经网络训练所用的“输入—目标”样本集数据需进行正归一化,对训练完的网络进行仿真(或预测)前的输入数据也需要进行正归一化。需要注意的是,归一化公式中的Pmax和Pmin要用训练时的最大值和最小值。
反归一化就是要恢复被归一化的数据。这里主要是对目标数据T进行反归一化,其公式为
| $ {{P^\prime } = 0.5\left( {{P_{\rm{n}}} + 1} \right)\left( {{P_{\max }} - {P_{\min }}} \right) + {P_{\min }}} $ | (4) |
| $ {{T^\prime } = 0.5\left( {{T_{\rm{n}}} + 1} \right)\left( {{T_{\max }} - {T_{\min }}} \right) + {T_{\min }}} $ | (5) |
式中P′和T′即分别为恢复后的输入数据和目标数据,Tmax和Tmin需用训练时的最大值和最小值,即式(2)和式(3)中的参数。
1.4.3 网络学习网络学习就是对BP神经网络进行训练所用的学习算法。对于不同的问题,不仅要考虑算法本身的性能,还要视问题的复杂度、样本集大小、网络规模、网络误差目标和所解决的问题类型(判断其属于“函数拟合”还是“模式分类”问题)而定。本文所要解决的磁源体深度预测问题属于“函数拟合”类型,经过多种模型的多次训练对比,最终选用贝叶斯正则化学习算法,其训练后的网络具有较好的推广能力。
利用设计的模型样本对上述BP神经网络程序进行训练。图 6是网络训练误差收敛曲线,可见经过2564次训练,最终收敛精度为0.06384。

|
图 6 样本的训练误差收敛曲线 |
上述的训练收敛精度,只能说明训练模型的整体收敛情况,不能说明个体的收敛程度。一个好的神经网络首先必须能对训练过的样本进行预测,否则很难期望它能预测未训练过的样本。
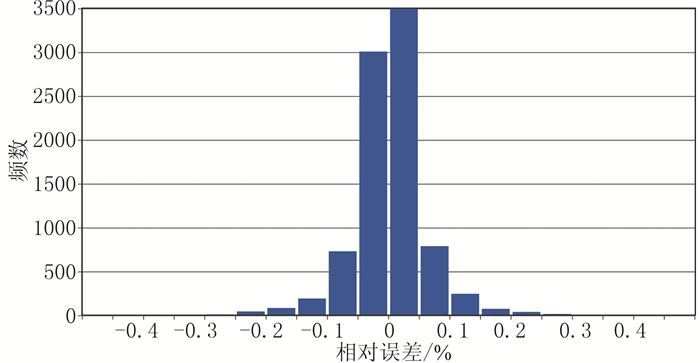
为了直观地检验学习过的神经网络对训练过的样本的预测能力,利用训练过的样本对神经网络进行仿真,利用概率分布直方图统计了样本预测的相对误差分布,如图 7所示。可见,相对误差概率基本呈正态分布特征:深度预测相对误差在±10%以内的样本占全体样本的比例约为91%;相对误差在±10%~±20%内的样本占比约为7%;相对误差大于±20%的样本占比约为2%,整体来说训练效果不错。
|
图 7 三类模型训练最终的相对误差分布直方图 |
统计发现,相对误差比较大的一般是那些顶深较小且具有一定横向规模的模型,这些模型的磁异常及垂向导数的极大值点不在模型的正上方,并且具有多个极大值。因而从这些模型中提取的极值比序列,不符合大多数模型的情况,故很难在训练中被神经网络“接受”,从而造成预测误差较大。这可以作为后续方法改进的一个方向。
2 模型测试为了验证前面训练好的BP神经网络的适应性和推广能力,设计了薄层、柱状、等轴三类长方体磁性模型共100个,利用这些模型的极值比序列作为训练好BP神经网络的输入,获得了相应模型的顶深预测值。为了更好地检验网络训练的效果,在设计这些理论模型埋深的时候,均避开了网络训练所用的模型深度。
图 8直观地展示了预测深度与理论顶深的差异。对各模型顶深预测的相对误差进行了详细统计,预测相对误差在±10%以内的样本有96个,相对误差在±10%~±20%内的样本有4个。由图 8可以看出,所训练的神经网络对未参加训练的模型顶深预测效果较好,达到了较高的准确度。

|
图 8 未参加训练模型的理论顶深与预测顶深对比 |
上文的测试模型都是垂直磁化,且未添加噪声。模拟某测区磁性体,设计了三类9个磁性体,其空间分布见图 9a所示。9个磁性体的详细参数见表 2。模拟测区范围80000m(x)×50000m(y),采样网距500m(x)×500m(y)。按中国东部的磁场参数(磁倾角60°,磁偏角-10°)对模拟测区内的9个磁性体进行了正演,并加入了±2nT的高斯噪声,模拟得到的磁异常分布见图 9b。

|
图 9 模拟测区内的磁性体分布(a)及加噪磁力异常(b) 图a中①~③号磁性体是层状模型,模拟水平层状的火山岩;④~⑥号磁性体是等轴模型,模拟等轴状的地质体;⑦~⑨号磁性体是柱状模型,模拟柱状的火成岩侵入体;红色点表示采样点 |
|
|
表 2 模拟测区内的磁性体参数及顶深预测情况统计表 |
为了得到9个磁性体的极值比序列,对图 9所示的磁异常按顺序进行一系列处理。
(1) 化极:化极处理是为了消除斜磁化的影响,使磁异常归位,这样可以使磁异常极大值位置与磁性体平面中心位置相对应,这是磁异常处理的常规步骤。
(2) 滤波:对化极处理后的磁异常进行插值切割法滤波,可以在求垂向各阶导数之前对采集噪声进行压制,减小噪声对求导的影响。
(3) 分别求取垂向一阶、垂向二阶、垂向三阶导数,并拾取各磁性体滤波后的化极磁异常及3个垂向导数的异常极大值,利用极大值的比值求得极值比序列。
(4) 以模型的类型和梯度极值比值序列为预测样本,作为输入进行深度预测。
表 2给出了神经网络方法预测的磁性体顶深的绝对误差。从绝对误差可以看出,预测结果精度较高,相对误差基本在10%以内。
对未化极、但经滤波的磁异常进行了欧拉反褶积预测,结果见图 10。可以看出,欧拉解大部分集中在场源体附近,在其他无场源的位置仅见零散分布。

|
图 10 滤波磁异常的欧拉反褶积预测解分布位置图 蓝色“+”为欧拉解的位置 |
为了比较本方法与欧拉方法的预测效果,统计了①~⑨号磁源体范围内的欧拉深度解的平均值,并与本文方法预测结果进行对比,详见表 2。可见,本文方法较欧拉方法预测磁源体深度的精度有明显提高,平均提高约49%。
3 实际应用YX洼陷隶属于中国东部渤海湾盆地济阳坳陷惠民凹陷。中国东部渤海湾盆地的中、新生代岩浆活动和火成岩比较发育,主力烃源层中常发育规模不等的喷发或侵入性基性岩浆。在这种背景下,YX洼陷主力烃源岩沙河街组沙三段和沙四段中火成岩与烃源岩广泛接触、相互作用,促进了油气的生成,并作为火成岩储层与沙三段泥岩一起形成了一类重要的油藏——火成岩油藏。对工区内钻遇火成岩的井数据进行统计,结果表明2000~3000m深度范围内广泛发育基性火山岩,岩性以辉绿岩和煌斑岩为主,磁性很强,厚度为50~300m,这些基性火山岩是本区磁异常的主要成因。
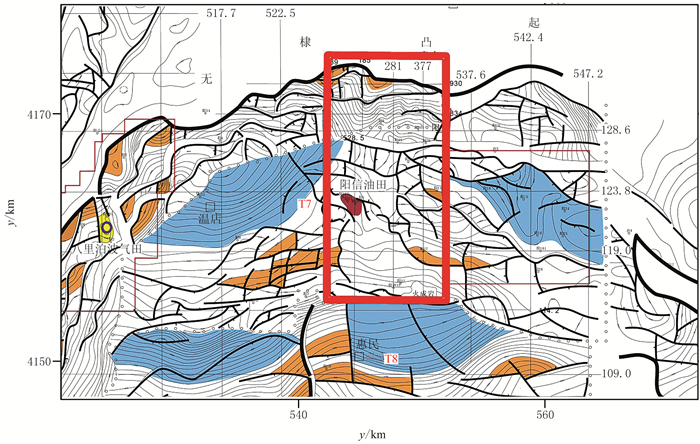
YX工区实测磁异常见图 11a。对磁异常场进行化极处理,结果见图 11b。训练所用的磁异常梯度值都来自单独磁源体,不存在区域背景的影响;而实际资料往往包含背景场,因此要尽量消除背景场的影响。利用插值切割方法[21]分离工区的化极磁异常,得到局部磁异常,结果如图 11c所示。可见基本消除了区域背景的影响,局部异常范围与钻遇火山岩井的位置吻合(见图 11c中红色圆圈标注的区域)。
|
图 11 工区实测磁异常图(a)、化极磁异常图(b)和局部磁异常图(c) |
对局部磁异常(图 11c)分别求取了垂向一次导数、垂向二次导数和垂向三次导数,结果见图 12。由图 12可见,随着求导次数的增加,局部磁异常的细节得到进一步凸显,磁异常高或异常低从整体形态逐步细化。

|
图 12 图 11c垂向一次导数(a)、垂向二次导数(b)和垂向三次导数(c) |
基于图 11c和图 12提取并计算了相应的磁异常梯度比值序列,共提取了6个序列样本,并输入前述训练好的BP神经网络进行深度预测,所提取的极值比序列以及预测结果见表 3。
|
|
表 3 工区磁源顶深预测结果统计表 |
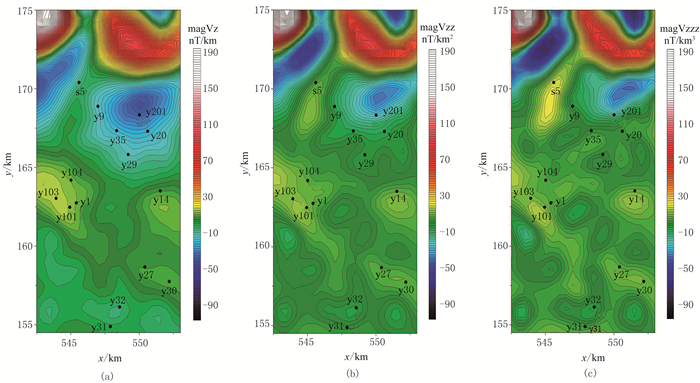
图 13是工区内钻遇火山岩钻井的顶深统计。对表 3的预测结果与图 13所示的钻井信息进行对比。图 13中的①、②号磁异常位于基岩隆起部位,深度约为700m;表 3中①、②号磁异常的预测深度分别为854m和882m,基本与钻井深度吻合,预测效果较好;③、⑤、⑥号磁异常位于洼陷区,具有完整的磁异常形态,根据表 3与附近钻遇火山岩的深度对比情况,这三个磁异常可靠度很高;④号磁异常属于③号磁异常的延续,没有完整的磁异常形态,预测的火成岩顶深明显偏小,预测效果不理想。主要是受到③号磁异常的影响,背景场未消除干净,使magVz的值受到了影响,导致极值比序列曲线发生畸变。
|
图 13 钻遇火山岩钻井的顶深统计图 图中背景等值线图是图 11c,圈码代表磁异常编号 |
本文探索了一种利用磁异常及其垂向导数极大值比值序列预测磁源深度的方法。该方法利用当今比较流行的BP神经网络技术进行磁源深度预测,提出了一种“傻瓜式”的磁顶埋深预测方法。通过大量理论长方体模型的磁异常及其垂向导数极值比序列与模型顶深形成样本对,对构建的BP神经网络进行训练,使BP神经网络“学会”并“记住”极值比序列与深度之间的非线性映射关系,从而达到预测目的。理论模型和实际资料的应用验证了方法的有效性,为磁源体顶面埋深的求取探索了一条新途径。
| [1] |
马国庆, 孟庆发, 李丽丽, 等. 利用重/磁场梯度比值函数计算地质体深度[J]. 石油地球物理勘探, 2019, 54(1): 229-234. MA Guoqing, MENG Qingfa, LI Lili, et al. Gradient ratio function of gravity and magnetic data for geolo-gical body depth calculation[J]. Oil Geophysical Pro-specting, 2019, 54(1): 229-234. |
| [2] |
罗孝宽, 郭绍雍. 应用地球物理教程-重力磁法[M]. 北京: 地质出版社, 1991.
|
| [3] |
朱英. 斜磁化切线法和特征点图解法[M]. 北京: 地质出版社, 1995.
|
| [4] |
郭志宏, 于长春, 周坚鑫. 低磁纬度区ΔT剖面磁异常场源深度计算的切线法[J]. 物探与化探, 2003, 27(5): 391-394. GUO Zhihong, YU Changchun, ZHOU Jianxin. The tangent technique of ΔT profile magnetic anomaly in the low magnetic latitude area[J]. Geophysical and Geochemical Exploration, 2003, 27(5): 391-394. |
| [5] |
吴顺和. 利用磁法资料直接解释基底起伏[J]. 石油地球物理勘探, 1980, 15(4): 55-61. WU Shunhe. Direct interpretation for basement relief using magnetic data[J]. Oil Geophysical Prospecting, 1980, 15(4): 55-61. |
| [6] |
韩守华, 赵晋芳, 蔡振京, 等. ΔT切线法自动计算深度及应用研究[M]. 北京: 中国国土资源航空物探遥感中心, 1990.
|
| [7] |
黄旭钊, 郭志宏, 徐昆. 交互式航磁异常切线法系统研制[J]. 物探与化探, 2007, 31(6): 572-576. HUANG Xuzhao, GUO Zhihong, XU Kun. The deve-lopment of the manual computer interaction aeromagnetic tangent method system[J]. Geophysical and Geochemical Exploration, 2007, 31(6): 572-576. |
| [8] |
郭志宏.航磁及梯度数据正反演解释方法技术实用化改进及应用[D].北京: 中国地质大学(北京), 2004. http://cdmd.cnki.com.cn/Article/CDMD-11415-2006056629.htm
|
| [9] |
Thompson D T. "EULDPH"-A new technique for making computer-assisted depth estimates from magnetic data[J]. Geophysics, 1982, 47(1): 31-37. |
| [10] |
Reid A B, Allsop J M, Granser H, et al. Magnetic interpretation in three dimensions using Euler deconvolution[J]. Geophysics, 1990, 55(1): 80-91. |
| [11] |
贾朔.磁异常欧拉反褶积方法的改进及在福建永定大排矿区的应用[D].北京: 中国地质大学(北京), 2017. http://cdmd.cnki.com.cn/Article/CDMD-11415-1017129799.htm
|
| [12] |
李青竹, 李志宁, 张英堂, 等. 基于二阶磁张量欧拉反褶积的磁源单点定位方法[J]. 石油地球物理勘探, 2019, 54(4): 915-924. LI Qingzhu, LI Zhining, ZHANG Yingtang, et al. Magnetic source single-point positioning based on se-cond-order magnetic tensor Euler deconvolution[J]. Oil Geophysical Prospecting, 2019, 54(4): 915-924. |
| [13] |
张学工, 李衍达. 用人工神经网络实现地震记录中的废道自动切除[J]. 地球物理学报, 1992, 35(5): 637-643. ZHANG Xuegong, LI Yanda. Automatic editing of noisy seismic data using an artificial neural network approach[J]. Chinese Journal of Geophysics, 1992, 35(5): 637-643. |
| [14] |
周竹生, 周熙襄. 一种用于地震道自动编辑的人工神经网络方法[J]. 石油地球物理勘探, 1994, 29(2): 147-155. ZHOU Zhusheng, ZHOU Xixiang. A neural network method for automatic seismic trace editing[J]. Oil Geophysical Prospecting, 1994, 29(2): 147-155. |
| [15] |
宋建国, 李赋真, 徐维秀, 等. 改进的神经网络级联相关算法及其在初至拾取中的应用[J]. 石油地球物理勘探, 2018, 53(1): 8-16. SONG Jianguo, LI Fuzhen, XU Weixiu, et al. An improved neural-network cascade-correlation algorithm and its application in seismic first break picking[J]. Oil Geophysical Prospecting, 2018, 53(1): 8-16. |
| [16] |
韩道范, 谢靖, 张文生, 等. BP神经网络在反演多层密度分界面中的应用研究[J]. 物探化探计算技术, 1994, 16(3): 249-252. HAN Daofan, XIE Jing, ZHANG Wensheng, et al. Research on BP neural network and its application to inversion of multi-density interfaces[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1994, 16(3): 249-252. |
| [17] |
耿喜哲, 刘天佑, 丁艳红, 等. 小波神经网络在重磁资料反演中的应用前景[J]. 物探与化探, 2001, 25(2): 102-108, 117. GENG Xizhe, LIU Tianyou, DING Yanhong, et al. The prospect of applying wavelet neural network to the inversion of gravitational and magnetic data[J]. Geophysical and Geochemical Exploration, 2001, 25(2): 102-108, 117. |
| [18] |
李创社, 张彦鹏, 李实, 等. 瞬变电磁勘探中的人工神经网络反演法[J]. 西安交通大学学报, 2001, 35(6): 604-615. LI Chuangshe, ZHANG Yanpeng, LI Shi, et al. New inversion method of artificial neural network in transient electromagnetic inversion[J]. Journal of Xi'an Jiaotong University, 2001, 35(6): 604-615. |
| [19] |
王鹤, 蒋欢, 王亮, 等. 大地电磁人工神经网络反演[J]. 中南大学学报(自然科学版), 2015, 46(5): 1707-1714. WANG He, JIANG Huan, WANG Liang, et al. Magnetotelluric inversion using artificial neural network[J]. Journal of Central South University(Science and Technology), 2015, 46(5): 1707-1714. |
| [20] |
许东, 吴铮编著.基于MATLAB6.x的系统分析与设计——神经网络[M].陕西西安: 西安电子科技大学出版社, 2002.
|
| [21] |
段本春, 徐世浙, 阎汉杰, 等. 划分磁异常场的插值切割法在研究火成岩体分布中的应用[J]. 石油地球物理勘探, 1998, 33(1): 125-131. DUAN Benchun, XU Shizhe, YAN Hanjie, et al. Application of interpolation-cut method for magnetic anomaly division to igneous mass investigation[J]. Oil Geophysical Prospecting, 1998, 33(1): 125-131. |



 赵文举, 河北省涿州市范阳中路307号东方地球物理公司综合物化探处, 072751。Email:
赵文举, 河北省涿州市范阳中路307号东方地球物理公司综合物化探处, 072751。Email: