② 油气资源与探测国家重点实验室, 北京 102249;
③ 海洋石油勘探国家工程实验室, 北京 102249;
④ 中国石化石油勘探开发研究院, 北京 100083
② State Key Laboratory of Petroleum Resources and Prospecting, Beijing 102249, China;
③ National Engineering Laboratory for Offshore Oil Exploration, Beijing 102249, China;
④ Sinopec Petroleum Exploration and Production Research Institute, Beijing 100083, China
地震反演技术可以利用地震数据的旅行时、振幅和波形等信息估计地下岩石的弹性参数[1-2],在储层预测与评价、油藏特征描述等方面得到了广泛的应用[3-4]。作为储层预测与表征的核心技术,叠后阻抗反演是应用最广、最成熟的反演方法[5-9]。该技术经历了从最初直接递推反演[5]到基于模型的迭代反演[7-10]的发展过程。
随着油气勘探开发的不断深入,要求阻抗反演结果达到一定的分辨率,便于更好地识别薄层[11]。然而,下列两个原因限制阻抗剖面的分辨率:①基于单一界面情形计算反射系数,正演方法不完备。假设地震数据仅包含一次波信息,忽略波的传播效应以及地层厚度的影响(调谐效应)。传播效应如透射损失以及调谐效应将造成地震记录的振幅异常,进而对反演结果的数值准确度以及分辨率造成影响。而层间多次波将会当作有效反射,造成错误的反演解释结果,特别是存在薄层且弹性参数差异较大的情况下[12]。同时,当前地震处理技术是无法完全消除透射损失、调谐效应、层间多次波的影响。②阻抗反演算法大多以最小二乘为基础,并加入合适的先验约束获取稳定的反演结果[13]。然而这些约束往往会使得反演结果过度光滑,无法清晰刻画地层的边界[14-16]。因此只有突破上述基本假设,才能得到分辨率更高的反演结果。
相对于常规阻抗褶积正演,将波动方程的解作为正演工具获取全波场响应,可以更为准确预测地下介质的弹性参数[17]。目前,波形阻抗反演方法有两种思路。一种是使用数值求解方法(有限差分、有限元等)近似求解波动方程,从而进行反问题求解获取阻抗结果,可称之为全波形反演(FWI)[18-19]。由于FWI对计算机储存能力以及计算效率要求极高,实际实施仍然存在困难。另一种是对层状假设下的波动方程解析求解并执行一维介质波形反演[20-21]。Ursin等[22]证明常规阻抗正演方法是解析解的零阶近似,因此利用解析解波形反演阻抗,结果将更为真实合理。
其次,可通过正则化约束获取高分辨且稳定的阻抗结果[17, 23]。稀疏和平滑约束在地震阻抗反演中广泛应用。平滑约束如高斯约束、L2范数约束等往往会忽略地下介质的分层特性,使得解过度光滑,无法清晰刻画地层的边界。稀疏约束如柯西约束、L1范数约束虽然可以获取高分辨率的解,但无法避免局部极小,从而引起某些地质假像[24]。借鉴图像处理中的图形锐化算法[25],Theune等[24]引入微分拉普拉斯块状约束,通过多道反演改善结果的垂直分辨率,但由于多道反演需要求解大型稀疏矩阵,将该约束简化到一维情况是更好的选择。
另外,叠前道集的优化过程中,特别是最为重要的角度道集提取环节[26],多数情况下基于声学介质假设,势必会导致道集趋向于声学AVO特征。而叠后成像、反演过程均忽略炮检距对反射系数的影响,部分叠加剖面未得到相应的重视。根据声波在界面的能量分配[27-28]可知,声波反射系数随入射角/炮检距变化,且随着入射角的增大而增大。借助于不同入射角度的反射信息,可更为准确反演弹性参数,尤其是速度信息。由于直接反演密度不稳定,需借鉴弹性阻抗反演技术[2],对部分叠加资料进行广义阻抗反演,进一步计算速度和密度信息,以避免密度反演的不稳定性。
借助上述三项关键技术,本文提出基于块状约束的一维声波波形广义声阻抗反演技术,用于提取更为真实、可靠且稳定的速度和密度参数。首先推导了两界面声波反射系统传播函数的递归表达式,最终获取不同入射角的反射响应和Fréchet导数。基于贝叶斯反演框架,在原始目标函数中加入块状约束,在压制病态数值噪声(即观测数据的小扰动对应的模型数据将产生巨大扰动的数值噪声)的同时保持地层的边界特征。针对目标函数是一个非线性问题,可利用高斯牛顿法求解,从而获得一个稳定的高分辨率波阻抗结果。利用广义声阻抗与入射角、速度和密度关系求解稳定的速度和密度。最终,通过模型以及实际数据验证新方法的有效性和实用性。
1 原理 1.1 声波方程反射响应解析求解声波方程的解析求解往往基于矩阵递归框架,但该算法框架需额外计算除反射响应以外的其他响应(如透射响应等),计算效率较低。另外,该算法的输入为速度和密度,无法直接输入声阻抗参数用于叠后反演。本文修改递归框架,将声阻抗作为算法输入,推导仅包含反射响应的递归计算公式,将矩阵运算简化为单元素运算,由于没有额外的计算量,可以迅速获取总的反射响应。
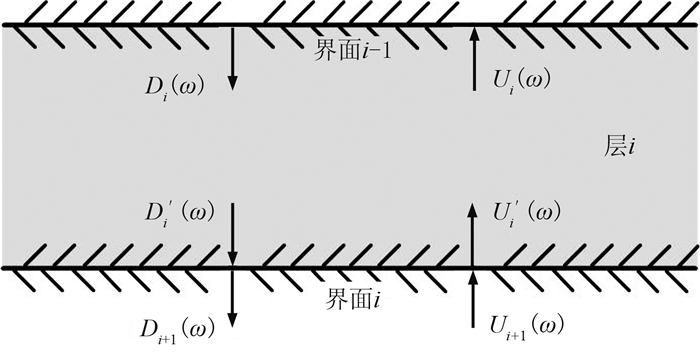
图 1为两个界面声波反射系统示意图,Di(ω)表示第i层顶界面的下行波,均匀介质中简谐波传播可表示为exp(-jωt),则第i层底界面的下行波可表示为
|
图 1 两个界面的上、下行波关系 |
| $ D_i^\prime (\omega ) = {D_i}(\omega ){\rm{exp}}\left( {\frac{{ - {\rm{j}}\omega {h_i}}}{{{v_i}}}} \right) $ | (1) |
式中hi和vi分别为第i层厚度、速度。同样第i层底界面的上行波可表示为
| $ U_i^\prime (\omega ) = {U_i}(\omega ){\rm{exp}}\left( {\frac{{{\rm{j}}\omega {h_i}}}{{{v_i}}}} \right) $ | (2) |
式中Ui(ω)表示第i层顶界面的上行波。
根据Treitel等[29]关于声波界面能量分配理论,可得
| $ \left\{ {\begin{array}{*{20}{l}} {U_i^\prime (\omega ) = {R_i}D_i^\prime (\omega ) + T_i^\prime {U_{i + 1}}(\omega )}\\ {{D_{i + 1}}(\omega ) = {T_i}D_i^\prime (\omega ) + R_i^\prime {U_{i + 1}}(\omega )} \end{array}} \right. $ | (3) |
式中:Ri、Ti分别为下行垂直入射时第i个反射界面的反射系数和透射系数;R′i、T′i分别为上行垂直入射时第i个反射界面的反射系数和透射系数。反射系数和透射系数满足
| $ \left\{ {\begin{array}{*{20}{l}} {{T_i} + {R_i} = T_i^\prime + R_i^\prime = 1}\\ {{R_i} = - R_i^\prime } \end{array}} \right. $ | (4) |
联立式(1)~式(4),可得
| $ {D_i}(\omega ) = [{D_{i + 1}}(\omega ) + {R_i}{U_{i + 1}}(\omega )]\frac{{{\rm{exp}}\left( {\frac{{{\rm{j}}\omega {h_i}}}{{{v_i}}}} \right)}}{{1 - {R_i}}} $ | (5) |
| $ {U_i}(\omega ) = [{U_{i + 1}}(\omega ) + {R_i}(\omega ){D_{i + 1}}(\omega )]\frac{{{\rm{exp}}\left( { - \frac{{{\rm{j}}\omega {h_i}}}{{{v_i}}}} \right)}}{{1 - {R_i}}} $ | (6) |
用式(6)除以式(5),有
| $ \frac{{{U_i}(\omega )}}{{{D_i}(\omega )}} = \frac{{{D_{i + 1}}(\omega ) + {R_i}{U_{i + 1}}(\omega )}}{{{U_{i + 1}}(\omega ) + {R_i}{D_{i + 1}}(\omega )}}{\rm{exp}}\left( {\frac{{ - 2{\rm{j}}\omega {h_i}}}{{{v_i}}}} \right) $ | (7) |
根据传播响应函数的定义ri(ω)=Ui(ω)/Di(ω),表示反射界面i以下的总反射响应。因此可得反射响应的递归计算公式为
| $ {r_i}(\omega ) = \frac{{1 + {R_i}{r_{i + 1}}(\omega )}}{{{r_{i + 1}}(\omega ) + {R_i}}}{\rm{exp}}\left( {\frac{{ - 2{\rm{j}}\omega {h_i}}}{{{v_i}}}} \right) $ | (8) |
垂直入射时反射系数为
| $ {R_i} = \frac{{{\rho _{i + 1}}{v_{i + 1}} - {\rho _i}{v_i}}}{{{\rho _{i + 1}}{v_{i + 1}} + {\rho _i}{v_i}}} $ | (9) |
根据声波在非垂直入射界面时能量分配规则[11],有
| $ {R_i}(\theta ) = \frac{{\frac{{{\rho _{i + 1}}{v_{i + 1}}}}{{{\rm{cos}}{\theta ^\prime }}} - \frac{{{\rho _i}{v_i}}}{{{\rm{cos}}\theta }}}}{{\frac{{{\rho _{i + 1}}{v_{i + 1}}}}{{{\rm{cos}}{\theta ^\prime }}} + \frac{{{\rho _i}{v_i}}}{{{\rm{cos}}\theta }}}} $ | (10) |
式中入射角θ与透射角θ′满足Snell定律p=sinθ/vi=sinθ′/vi+1,其中p为射线参数。
最深第M层不存在反射,因此rM=0。至此可由式(8)得到总反射响应函数r0。用r0乘以频率域子波s(ω),并进行傅里叶反变换,可获对应地震记录
| $ d(t) = \frac{1}{{2\pi }}\int_{ - \infty }^\infty s (\omega ){r_0}(\omega ){\rm{exp}}({\rm{j}}\omega t){\rm{d}}\omega $ | (11) |
此时整个算法的输入是速度、密度。将输入参数从深度域转换到时间域,并利用复双程旅行时间修改式(8),可得
| $ {r_i}(\omega ) = \frac{{1 + {R_i}{r_{i + 1}}}}{{{r_{i + 1}} + {R_i}}}{\rm{exp}}( - {\rm{j}}\omega {\tau _i}) $ | (12) |
式中τi=Δt,Δt为时间采样间隔。
定义广义声阻抗为
| $ {\bar I_i} = \frac{{{\rho _i}{v_i}}}{{{\rm{cos}}\theta }} = \frac{{{\rho _i}{v_i}}}{{\sqrt {1 - {{(p{v_i})}^2}} }} $ | (13) |
界面的反射系数为
| $ {R_i} = \frac{{{{\bar I}_{i + 1}} - {{\bar I}_i}}}{{{{\bar I}_{i + 1}} + {{\bar I}_i}}} $ | (14) |
则可将广义声阻抗作为算法的输入用于计算不同角度入射的地震响应。
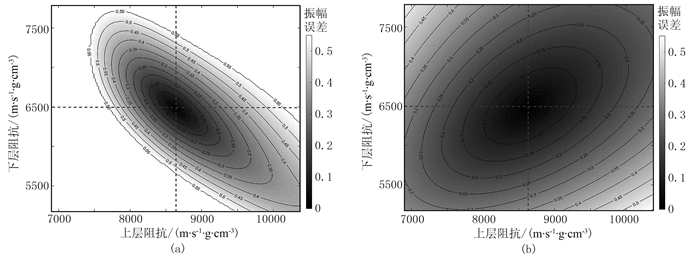
将输入参数从深度域转换到时间域,将算法与常规叠后反演预处理流程(建立初始模型)有机地结合在一起,便于对比。此外,还可以提高反演问题的稳定性,同时降低该问题非线性程度。本文借助残差函数图(RFM)作为转换前后反演问题的适定性评价标准[30]。通过对相邻层的波阻抗扰动,根据深度域和时间域扰动所建立的RFM如图 2所示。十字虚线的交点表示对应的真实值。等高线越密集,残差的扰动变化率越大,反演问题的稳定性越差;对应椭圆的离心率越大,该问题非线性程度越高。由此可见,当输入参数从深度域转换到时间域,反演问题的适定性会有所改善。
|
图 2 深度域(a)与时间域(b)RFM对比 |
上述反演问题的损失函数项(模型估计值与观测值之间的差异度量)是非线性的,对于非线性最优问题一般可通过全局优化算法如模拟退火、遗传算法等以及梯度类下降算法求解。全局优化算法可免于计算梯度但计算代价极大,本文使用梯度下降算法。该算法的关键在于求解Fréchet导数,即地震记录相对于模型参数的导数
| $ \frac{{\partial d(t)}}{{\partial \bar I}} = \frac{1}{{2\pi }}\int_{ - \infty }^\infty s (\omega )\frac{{\partial {r_0}(\omega )}}{{\partial \bar I}}{\rm{exp}}({\rm{j}}\omega t){\rm{d}}\omega $ | (15) |
由于子波与模型参数无关,仅需计算反射系数的Fréchet导数。可通过链式法则获取对应导数元素表达式
| $ \frac{{\partial {r_0}(\omega )}}{{\partial {{\bar I}_i}}} = \frac{{\partial {r_0}(\omega )}}{{\partial {r_1}(\omega )}}\frac{{\partial {r_1}(\omega )}}{{\partial {r_2}(\omega )}} \cdots \frac{{\partial {r_{i - 2}}(\omega )}}{{\partial {r_{i - 1}}(\omega )}}\frac{{\partial {r_{i - 1}}(\omega )}}{{\partial {{\bar I}_i}}} $ | (16) |
其中
| $ \frac{{\partial {r_{i - 2}}(\omega )}}{{\partial {r_{i - 1}}(\omega )}} = \frac{{1 - R_{i - 2}^2}}{{{{[1 - {R_{i - 2}}{r_{i - 1}}(\omega )]}^2}}}{\rm{exp}}[{\rm{j}}\omega {\tau _{i - 2}}(\omega )] $ | (17) |
| $ \begin{array}{l} \frac{{\partial {r_{i - 1}}(\omega )}}{{\partial {{\bar I}_i}}} = \frac{{\frac{{\partial {R_{i - 1}}}}{{\partial {{\bar I}_i}}}[1 - r_i^2(\omega )] + \frac{{\partial {r_i}(\omega )}}{{\partial {{\bar I}_i}}}(1 - R_{i - 1}^2)}}{{{{[1 + {R_{i - 1}}{r_i}(\omega )]}^2}}} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}[ - {\rm{j}}\omega {\tau _{i - 1}}(\omega )] \end{array} $ | (18) |
根据式(14),有
| $ \frac{{\partial {R_{i - 1}}}}{{\partial {{\bar I}_i}}} = \frac{{ - 2{{\bar I}_{i - 1}}}}{{{{({{\bar I}_{i - 1}} + {{\bar I}_i})}^2}}} $ | (19) |
由于
| $ \frac{{\partial {r_i}(\omega )}}{{\partial {{\bar I}_i}}} = \frac{{\frac{{\partial {R_i}}}{{\partial {{\bar I}_i}}}[1 - r_{i + 1}^2(\omega )]}}{{{{[1 + {R_i}{r_{i + 1}}(\omega )]}^2}}}{\rm{exp}}[ - {\rm{j}}\omega {\tau _{i - 1}}(\omega )] $ | (20) |
式中
| $ \frac{{\partial {R_i}}}{{\partial {{\bar I}_i}}} = \frac{{ - 2{{\bar I}_{i + 1}}}}{{{{({{\bar I}_{i + 1}} + {{\bar I}_i})}^2}}} $ | (21) |
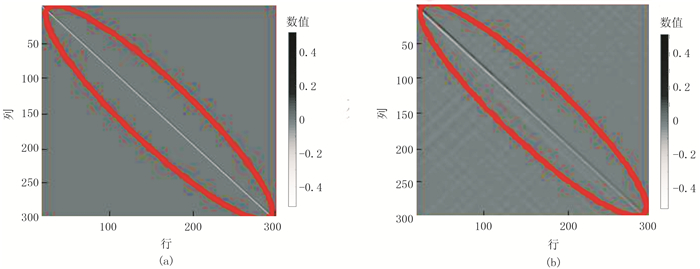
图 3为常规线性正演矩阵与反射系数的Fréchet导数矩阵对比。线性矩阵(图 3a)呈现条带状,带宽为2,随着深度变化其数值并未发生变化,除条带外其他元素均为0。这与线性假设一致,某点反射系数仅与相邻层的弹性参数有关。恰恰相反,导数矩阵(图 3b)呈现条带状,带宽为6~8个元素;受传播效应影响,随着深度变化矩阵数值逐渐变小;由于计算的全波场响应,条带周围元素不为0,说明某点反射系数与整个层状介质的弹性参数都有关,只是该点周围的几个层占主要因素。
|
图 3 线性矩阵(a)与导数矩阵(b)的对比 |
正演过程可表示为
| $ \mathit{\boldsymbol{d}} = \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{m}}) + \mathit{\boldsymbol{n}} $ | (22) |
式中:d为观测数据向量;m为模型参数向量;G为m映射到d的非线性算子,本文中G(m)为解析法正演的结果;n表示二者之间的误差。模型参数的先验概率分布为
| $ P(\mathit{\boldsymbol{m}}) = {P_{0m}}{\rm{exp}}[ - S(\mathit{\boldsymbol{m}})] $ | (23) |
式中:S(m)为模型参数的正则化项;P0m为模型参数的归一化常数。假设噪声相互独立并且服从高斯分布,利用贝叶斯公式可得模型参数的后验概率分布为
| $ \begin{array}{*{20}{l}} {P(\mathit{\boldsymbol{m}}|\mathit{\boldsymbol{d}}) = {\rm{exp}}\left\{ { - \frac{1}{{2\sigma _n^2}}{{[\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{m}})]}^{\rm{T}}} \times } \right.}\\ {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{m}})] - S(\mathit{\boldsymbol{m}})} \right\}} \end{array} $ | (24) |
式中:σn2表示噪声方差。式(24)对应的最大后验解(MAP)等效于下列目标函数的最优解
| $ J(\mathit{\boldsymbol{m}}) = \frac{1}{{2\sigma _n^2}}{[\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{m}})]^{\rm{T}}}[\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{m}})] + S(\mathit{\boldsymbol{m}}) $ | (25) |
当模型的先验信息服从高斯分布时,有
| $ S(\mathit{\boldsymbol{m}}) = {(\mathit{\boldsymbol{m}} - \mathit{\boldsymbol{\mu }})^{\rm{T}}}\sigma _{\rm{m}}^{ - 2}(\mathit{\boldsymbol{m}} - \mathit{\boldsymbol{\mu }}) $ | (26) |
式中:σm2为模型参数的方差;μ为模型的均值,可由构建的初始模型代替。
高斯分布约束是一个过度平滑的约束。地下介质的成层性要求反演结果的垂向梯度在层内为零,而层与层之间有个较大的值。这意味着概率分布函数集中在零点附近,而正负无穷处较小,微分拉普拉斯分布恰好满足这样的特征。因此可在平滑约束提供一个稳定解的基础上,再加上微分拉普拉斯约束项,从而更好地刻画地层边界。因此需要定义两个先验权重系数λs、λb,平衡反演结果的噪声、光滑度以及边界刻画能力。此时目标函数为
| $ \begin{array}{*{20}{l}} {J(\mathit{\boldsymbol{m}}) = {{[\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{m}})]}^{\rm{T}}}[\mathit{\boldsymbol{d}} - \mathit{\boldsymbol{G}}(\mathit{\boldsymbol{m}})] + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\lambda _{\rm{s}}}{{(\mathit{\boldsymbol{m}} - \mathit{\boldsymbol{\mu }})}^{\rm{T}}}\sigma _{\rm{m}}^{ - 2}(\mathit{\boldsymbol{m}} - \mathit{\boldsymbol{\mu }}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\lambda _{\rm{b}}}\{ \sqrt {1 + {{[D(\mathit{\boldsymbol{m}} - \mathit{\boldsymbol{\mu }})]}^2}} + 1\} } \end{array} $ | (27) |
式中最后一项就是微分拉普拉斯约束一维表达式,其中D是一阶差分矩阵
| $ \mathit{\boldsymbol{D}} = \left[ {\begin{array}{*{20}{l}} { - 1}&1&{}&{}&{}&{}\\ {}&{ - 1}&1&{}&{}&{}\\ {}&{}& \ddots & \ddots &{}&{}\\ {}&{}&{}&{ - 1}&1&{}\\ {}&{}&{}&{}&{ - 1}&1 \end{array}} \right] $ | (28) |
可使用高斯—牛顿算法求解该目标函数,即
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{H}}({\mathit{\boldsymbol{m}}^k})\Delta \mathit{\boldsymbol{m}} = - \mathit{\boldsymbol{\gamma }}({\mathit{\boldsymbol{m}}^k})}\\ {{\mathit{\boldsymbol{m}}^{k + 1}} = {\mathit{\boldsymbol{m}}^k} + \Delta \mathit{\boldsymbol{m}}} \end{array}} \right. $ | (29) |
式中:H为海森矩阵;k为迭代次数;梯度为
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\gamma }}({\mathit{\boldsymbol{m}}^k}) = {{({\mathit{\boldsymbol{g}}^k})}^{\rm{T}}}[\mathit{\boldsymbol{G}}({\mathit{\boldsymbol{m}}^k}) - \mathit{\boldsymbol{d}}] + {\lambda _{\rm{s}}}\sigma _{\rm{m}}^{ - 2}({\mathit{\boldsymbol{m}}^k} - \mathit{\boldsymbol{\mu }}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\lambda _{\rm{b}}}{\mathit{\boldsymbol{D}}^{\rm{T}}}\mathit{\boldsymbol{D}}({\mathit{\boldsymbol{m}}^k} - \mathit{\boldsymbol{\mu }})}}{{\sqrt {1 + [\mathit{\boldsymbol{D}}({\mathit{\boldsymbol{m}}^k} - \mathit{\boldsymbol{\mu }})} {]^2}}}} \end{array} $ | (30) |
式中第一项表示损失函数对模型的导数,其中gk=∂G(mk)/∂m,即对应正演问题的Fréchet导数矩阵;第二、第三项为平滑约束以及块状约束对模型的导数。如果问题的非线性程度不严重或者初始模型接近真实解时,海森矩阵H的二阶项可以忽略,则近似为
| $ \mathit{\boldsymbol{H}}({\mathit{\boldsymbol{m}}^k}) \approx {({\mathit{\boldsymbol{g}}^k})^{\rm{T}}}{\mathit{\boldsymbol{g}}^k} + {\lambda _{\rm{s}}}\sigma _{\rm{m}}^{ - 2}\mathit{\boldsymbol{E}} + {\lambda _{\rm{b}}}\mathit{\boldsymbol{Q}} $ | (31) |
式中:E是单位矩阵;Q表示块状约束的对模型二阶导数,即
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{Q}} = {{[{\mathit{\boldsymbol{D}}^{\rm{T}}}\mathit{\boldsymbol{D}}({\mathit{\boldsymbol{m}}^k} - \mathit{\boldsymbol{\mu }})]}^2}{{\{ 1 + {{[\mathit{\boldsymbol{D}}({\mathit{\boldsymbol{m}}^k} - \mathit{\boldsymbol{\mu }})]}^2}\} }^{ - \frac{3}{2}}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{\mathit{\boldsymbol{D}}^{\rm{T}}}\mathit{\boldsymbol{D}}}}{{\sqrt {1 + {{[\mathit{\boldsymbol{D}}({\mathit{\boldsymbol{m}}^k} - \mathit{\boldsymbol{\mu }})]}^2}} }}} \end{array} $ | (32) |
在实际资料反演中,一般情况下通过井旁道反演测试,人为选取最佳权重系数λs、λb。
1.4 速度、密度参数提取根据广义声波阻抗定义(式(13)),垂直入射和非垂直入射阻抗为
| $ \left\{ {\begin{array}{*{20}{l}} {{{\bar I}_i}(0) = {\rho _i}{v_i}}\\ {{{\bar I}_i}(\theta ) = {\rho _i}{v_i}{{\left[ {1 - {{\left( {\frac{{{\rm{sin}}\theta }}{{\bar v}}{v_i}} \right)}^2}} \right]}^{ - \frac{1}{2}}}} \end{array}} \right. $ | (33) |
则有
| $ \frac{{{{\bar I}_i}(\theta )}}{{{{\bar I}_i}(0)}} = {\left[ {1 - {{\left( {\frac{{{\rm{sin}}\theta }}{{\bar v}}{v_i}} \right)}^2}} \right]^{ - \frac{1}{2}}} $ | (34) |
式中v为低频背景速度。
通过上式可提取速度信息,进一步应用Ii(0)可获得密度信息。对于上述过程可能产生的数值噪声,可通过Garder公式ρi=0.31vi0.25,进行先验信息约束。
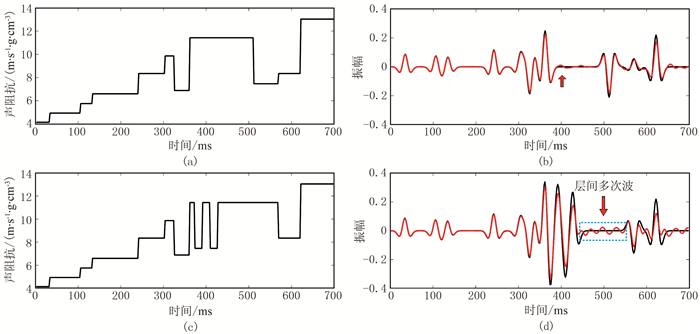
2 数值模拟测试 2.1 正演模拟分析为突出解析解正演方法的优势,首先使用厚层模型验证传播效应对一次反射波的影响。图 4a为对应的厚层阻抗模型,利用主频为30Hz的Ricker子波合成零炮检距地震记录,对比常规阻抗正演方法与弹性声波解析解方法结果(图 4b)。由于常规正演方法,只计算一次波,未考虑多次波以及透射损失,可以发现,透射损失的影响主要体现在振幅衰减上,随着深度增加,透射损失将越来越严重,400ms处也存在少许多次波。在400ms处加入一组薄互层(图 4c)突出多次波,合成记录如图 4d所示。可以看出,多次波(蓝色方框所示)以及调谐效应都相当严重,400ms以下的一次反射均受到多次波干涉。由于薄层存在,透射效应加剧。当弹性参数差异较大时,传播效应强烈影响一次反射波,深部反射受到强烈“污染”,并且当前地震处理技术无法完全消除这些影响。因此采用具有理论完备的正演方法,计算一次波的同时考虑层间多次波以及透射损失效应,有利于解决薄层问题。
|
图 4 常规阻抗正演方法(黑线)与声波解析解方法(红线)模拟的厚层和薄互层模型零炮检距记录对比 (a)厚层阻抗模型;(b)厚层模型零炮检距记录;(c)薄互层阻抗模型;(d)薄互层模型零炮检距记录 |
计算不同速度变化率及密度变化率为40%的声波界面反射系数随入射角的变化曲线(图 5),可见:随着入射角增大,速度变化导致的界面反射增强;速度差异越大,“AVO”效应越明显;但40%的密度变化率并不会产生AVO效应,即地震记录对密度变化不敏感,这也是常常将介质假设为常密度的原因。图 6左为利用薄互层模型(图 4c)合成的声波角度道集,其中子波主频为30Hz,角度范围为0~33°,角度间隔为3°。沿图 6左红色虚线处提取的均方根振幅曲线如图 6中所示,其变化特征与图 5一致。将不同角度的记录与零入射角道相减,如图 6右所示,可见:当角度较小时,“AVO”效应可以忽略;当角度较大时则不能忽略。利用“AVO”效应可以提高速度信息的准确度,同时密度可根据阻抗和速度获取,间接提高密度参数的精度。因此,通过近、远部分叠加剖面振幅信息获取较为准确的速度、密度信息是可行的。

|
图 5 声波介质反射系数随入射角的变化曲线 |

|
图 6 薄互层模型声波角度道集分析 左为角道集;中为左图虚线处两个界面的均方根振幅曲线;右为左图与零入射角道的残差 |
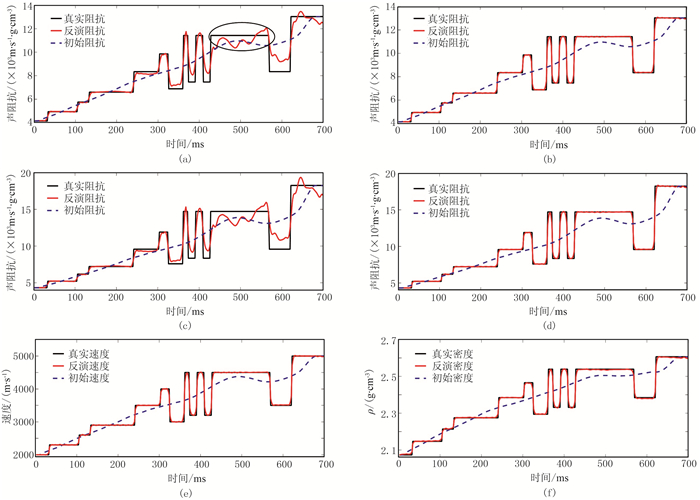
为验证本文构建的反演算法的有效性,利用薄互层模型进行反演测试。将声波解析解模拟结果作为输入,假定其为尚未消除传播效应影响的真实地震数据。分别使用常规和本文方法进行零入射角数据声阻抗反演,结果如图 7a和图 7b所示。由于传播效应以及调谐效应使得地震记录振幅异常,常规声阻抗反演结果误差大,对分界面的刻画不够清晰。如图 7a黑色椭圆所示,由于层间反射无法消除,常规声阻抗反演过程中,将其当作有效的一次反射,产生错误的反演结果。恰好相反,本文方法获取了一个更为准确且边界刻画清晰的阻抗估计结果(图 7b)。与真实阻抗相比,二者残差的归一化均方根误差为0.02。图 7c、图 7d为入射角为20°时常规和本文方法的广义声阻抗反演结果,与零角度阻抗反演结果相似。与之不同的是,阻抗在数值上变大。进一步提取的速度密度曲线如图 7e、图 7f所示,与真实速度、密度模型有较好的一致性。
|
图 7 模型数据反演结果 (a)垂直入射常规方法反演结果;(b)垂直入射本文方法反演结果;(c)θ=20°常规方法反演结果;(d)θ=20°本文方法反演结果;(e)速度曲线;(f)密度曲线 |
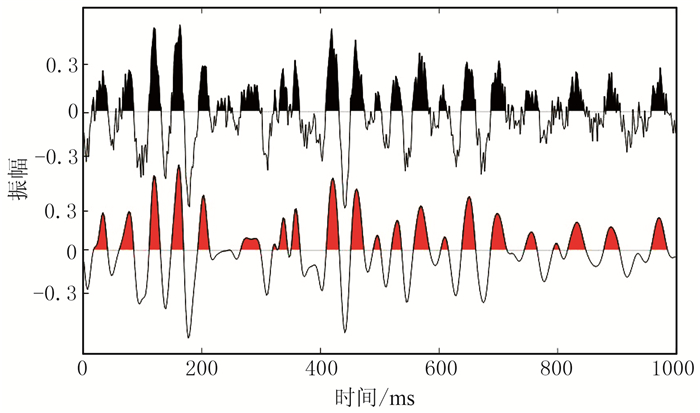
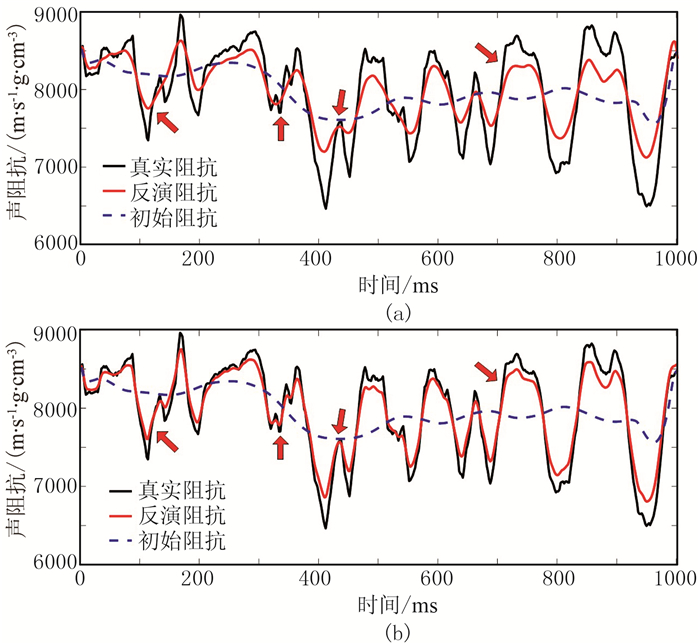
利用阻抗井数据(图 9黑线所示)合成地震记录,并对地震数据加入噪声测试算法的鲁棒性。该模型数据在500ms以下阻抗参数的成层性较好,可用于验证块状约束的有效性。图 8为加噪前、后地震记录对比(噪声与地震记录最大绝对值之比,An/s=36%)。图 9a、图 9b分别为相同条件下(相同初始模型、迭代次数等)高斯平滑约束以及块状约束的声阻抗反演结果。明显可见,平滑约束的反演结果分辨率低于块状约束的反演结果;块状约束对边界刻画更为清晰(箭头所示)。为更好说明该问题,在不同噪声水平(An/s)情况下,不加约束、平滑约束以及块状约束的情况下进行反演测试,计算反演结果与真实结果的相对误差如图 10所示。当噪声水平为零时,算法是稳定的,因此相对误差几乎为零;随着噪声水平的增加,相对误差均会增大;不加约束时的相对误差较大,高斯约束和块状约束都能获取较为稳定的结果,但块状约束的相对误差小于高斯约束。因此本文反演方法在高噪声情况下依然稳定可靠。
|
图 8 加噪前(红色)、后(黑色)地震记录对比 |
|
图 9 不同约束条件的含噪数据反演结果 (a)高斯约束;(b)块状约束 |

|
图 10 不同约束条件反演结果相对误差随信噪比变化曲线 |
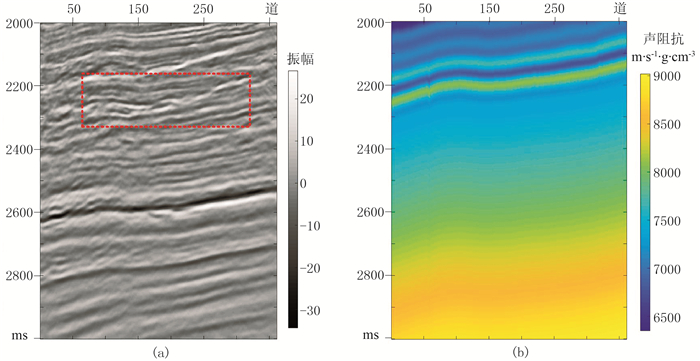
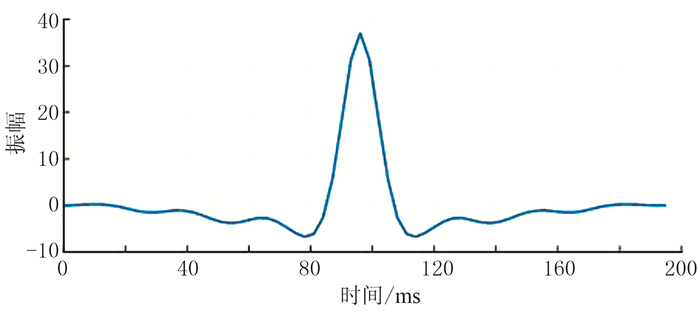
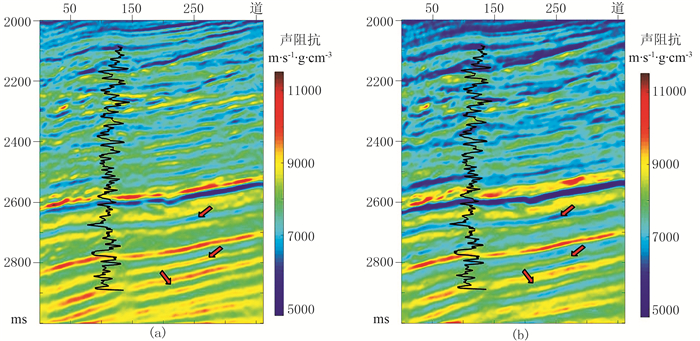
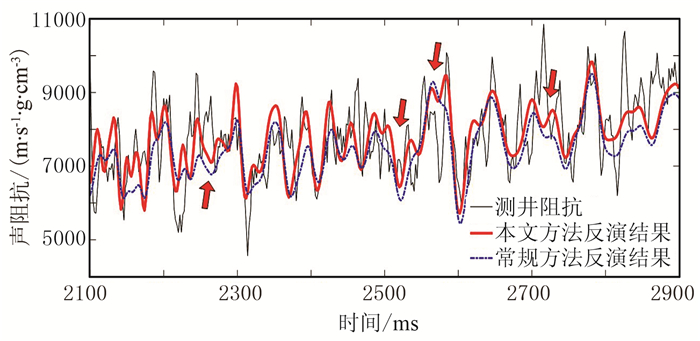
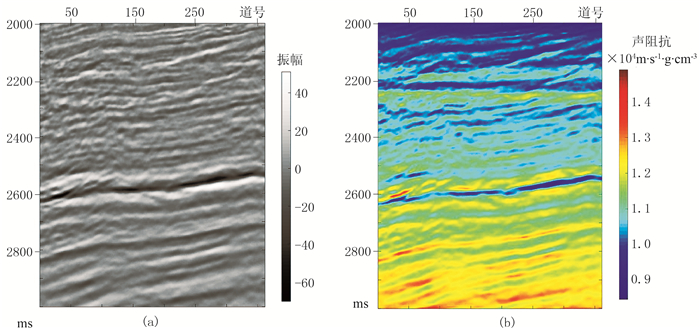
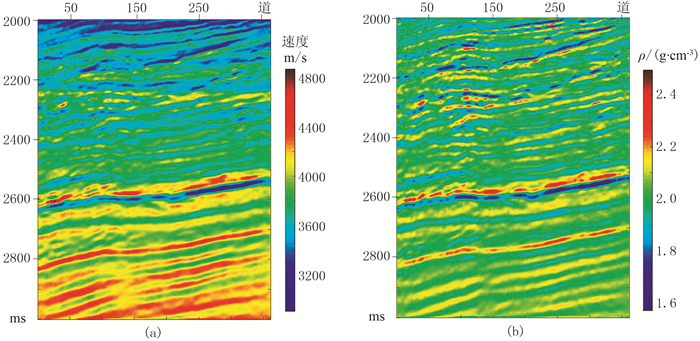
实际数据近炮检距部分叠加剖面如图 11a所示,勘探目标是2300~2500ms附近的浊积扇砂体(红色矩形框所示)。基于拾取的层位插值得到的初始阻抗模型,如图 11b所示。图 12为利用统计原理提取的子波。图 13为本文方法和常规方法反演的声阻抗结果,其中图上黑色曲线为根据测井数据计算的结果。图 14为实际地震记录与声波反演结果正演记录的对比,二者之间残差较小。图 15为测井数据(黑色,经Backus平均处理)与井旁地震数据反演结果(道号为100)对比,可以发现,本文方法反演结果(红色)与测井数据匹配度更髙,与Backus平均后测井数据相关系数高达92.5%,而常规反演结果(蓝色)与之相关系数仅为84.6%。与常规反演方法相比,本文方法提高了薄层的数值精度,且边界刻画更为清晰,分辨率更高(图 13、图 15红色箭头所示)。图 16a为远炮检距部分叠加剖面,由于复杂的地下传播效应影响,远炮检距叠加剖面分辨率低于近炮检距叠加剖面,导致对应的广义声阻抗反演结果分辨率(图 16b)也较低。应用Gardner公式作为低频先验信息,根据近、远炮检距反演结果提取稳定的速度和密度结果如图 17所示,与地震记录有良好的一致性,但分辨率高于地震记录,尤其是密度剖面。
|
图 11 近炮检距部分叠加剖面(a)及初始阻抗模型(b) |
|
图 12 基于统计理论估计的子波 |
|
图 13 本文方法(a)和常规方法(b)的阻抗反演结果 |

|
图 14 实际地震记录(上)、反演结果的正演地震记录(中)及其残差(下) |
|
图 15 两种方法反演结果与测井曲线的对比 |
|
图 16 远炮检距部分叠加剖面(a)和本文方法的广义阻抗反演结果(b) |
|
图 17 提取的速度(a)和密度剖面(b) |
本文基于一维声波方程解析解,提出非线性声阻抗反演方法。该方法充分考虑了透射损失、多次波的影响,是对常规声阻抗反演方法的补充和发展。借鉴于图形锐化技术,本文引入块状约束获取高分辨率的稳定解。模型以及实际资料反演结果均表明,新方法可以提供更准确且分辨率更高的反演结果,且边界刻画清晰。利用广义声波阻抗反演结果,可进一步提取速度与密度信息,也可将其作为一种地震属性用于流体识别。
本文反演方法不需要去除层间多次波,但需去除与表层相关的多次波,考虑横向变化的球面扩散补偿技术是必须的处理流程。
虽然本文推导的递归算法比递归矩阵正演算法快10倍左右,但执行单道反演仍然需数秒时间,可通过三个途径提高计算效率:首先,通过井旁道反演选取最优反演迭代次数;其次由于常规正演方法是解析解的零阶近似,可将常规反演结果作为初始模型减少迭代次数,加快收敛;最后,该方法为单道反演算法,易于并行计算,可通过OpenMP实现并行加速。
基于广义声波阻抗反演方法具有理论完备性,考虑了全波场信息,可将其推广到弹性波阻抗反演和相应弹性参数的提取。
| [1] |
Buland A, Omre H. Bayesian linearized AVO inver-sion[J]. Geophysics, 2003, 68(1): 185-198. |
| [2] |
马劲风. 地震勘探中广义弹性阻抗的正反演[J]. 地球物理学报, 2003, 46(1): 118-124. MA Jinfeng. Forward modeling and inversion method of generalized elastic impedance in seismic exploration[J]. Chinese Journal of Geophysics, 2003, 46(1): 118-124. |
| [3] |
Bosch M, Mukerji T, Gonzalez E F. Seismic inversion for reservoir properties combining statistical rock physics and geostatistics:A review[J]. Geophysics, 2010, 75(5): A165-A176. |
| [4] |
罗鑫, 陈学华, 张杰, 等. 基于依赖频率AVO反演的高含气饱和度储层预测方法[J]. 石油地球物理勘探, 2019, 54(2): 356-364. LUO Xin, CHEN Xuehua, ZHANG Jie, et al. High gas-saturation reservoir prediction based on frequency-dependent AVO inversion[J]. Oil Geophysical Prospecting, 2019, 54(2): 356-364. |
| [5] |
Lindseth R O. Synthetic sonic logs:A process for stratigraphic interpretation[J]. Geophysics, 1979, 44(1): 3-26. |
| [6] |
Walker C, Ulrych T J. Autoregressive recovery of the acoustic impedance[J]. Geophysics, 1983, 48(10): 1338-1350. DOI:10.1190/1.1441414 |
| [7] |
Ma X Q. A constrained global inversion method using an over-parameterized scheme:Application to post-stack seismic data[J]. Geophysics, 2001, 66(2): 613-626. DOI:10.1190/1.1444952 |
| [8] |
吕铁良.波阻抗约束反演中的约束方法研究[D].山东青岛: 中国石油大学(华东), 2007.
|
| [9] |
Cooke D A, Schneider W A. Generalized linear inversion of reflection seismic data[J]. Geophysics, 1983, 48(6): 665-676. DOI:10.1190/1.1441497 |
| [10] |
Oldenburg D W, Scheuer T, Levy S. Recovery of the acoustic impedance from reflection seismograms[J]. Geophysics, 1983, 48(10): 1318-1337. DOI:10.1190/1.1441413 |
| [11] |
雍学善, 余建平, 石兰亭. 一种三维高精度储层参数反演方法[J]. 石油地球物理勘探, 1997, 32(6): 852-856. YONG Xueshan, YU Jianping, SHI Lanting. A three-dimensional high precision reservoir parameter inversion method[J]. Oil Geophysical Prospecting, 1997, 32(6): 852-856. |
| [12] |
Oliveira S A M, Braga I L S, Lacerda M B, et al. Extending the useful angle range for elastic inversion through the amplitude-versus-angle full-waveform inversion method[J]. Geophysics, 2018, 83(3): R213-R226. |
| [13] |
杨文采. 非线性地震反演方法的补充及比较[J]. 石油物探, 1995, 34(4): 109-116. YANG Wencai. Supplement and comparison of nonlinear seismic inversion methods[J]. Geophysical Prospecting for Petroleum, 1995, 34(4): 109-116. |
| [14] |
Gholami A. Nonlinear multichannel impedance inversion by total-variation regularization[J]. Geophysics, 2015, 80(5): R217-R224. DOI:10.1190/geo2015-0004.1 |
| [15] |
王治强, 曹思远, 陈红灵, 等. 基于TV约束和Zoeppritz矩阵分解的波阻抗反演[J]. 石油地球物理勘探, 2017, 52(6): 1193-1199. WANG Zhiqiang, CAO Siyuan, CHEN Hongling, et al. Wave impedance inversion based on TV regularization and Zoeppritz-sparse matrix factorization[J]. Oil Geophysical Prospecting, 2017, 52(6): 1193-1199. |
| [16] |
林恬, 孟小红, 张致付. 基于约束最小二乘与信赖域的储层参数反演方法[J]. 地球物理学报, 2017, 60(10): 3969-3983. LIN Tian, MENG Xiaohong, ZHANG Zhifu. The petrophysical parameter inversion method based on constrained least squares and trust region domain[J]. Chinese Journal of Geophysics, 2017, 60(10): 3969-3983. |
| [17] |
Tarantola A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [18] |
Virieux J, Operto S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1-WCC26. |
| [19] |
杨午阳, 王西文, 雍学善, 等. 地震全波形反演方法研究综述[J]. 地球物理学进展, 2013, 28(2): 766-776. YANG Wuyang, WANG Xiwen, YONG Xueshan, et al. The review of seismic full waveform inversion method[J]. Progress in Geophysics, 2013, 28(2): 766-776. |
| [20] |
McAulay A D. Prestack inversion with plane-layer point source modeling[J]. Geophysics, 1985, 50(1): 77-89. |
| [21] |
Oliveira S, Loures L, Moraes F, et al. Nonlinear impedance inversion for attenuating media[J]. Geophy-sics, 2009, 74(6): R111-R117. |
| [22] |
Ursin B, Stovas A. Reflection and transmission responses of a layered isotropic viscoelastic medium[J]. Geophysics, 2002, 67(1): 307-323. |
| [23] |
Alemie W, Sacchi M D. High-resolution three-term AVO inversion by means of a Trivariate Cauchy probability distribution[J]. Geophysics, 2011, 76(3): R43-R55. |
| [24] |
Theune U, Jensås I Ø, Eidsvik J. Analysis of prior models for a blocky inversion of seismic AVA data[J]. Geophysics, 2010, 75(3): C25-C35. DOI:10.1190/1.3427538 |
| [25] |
Charbonnier P, Blanc-Féraud L, Aubert G, et al. Deterministic edge-preserving regularization in computed imaging[J]. IEEE Transactions on Image Processing, 1997, 6(2): 298-311. |
| [26] |
刘本晶, 梁兴, 侯艳, 等. 叠前道集优化技术在页岩储层预测中的应用[J]. 石油地球物理勘探, 2018, 53(增刊2): 189-196. LIU Bengjing, LIANG Xing, HOU Yan, et al. Pre-stack gather conditioning in shale reservoir prediction[J]. Oil Geophysical Prospecting, 2018, 53(S2): 189-196. |
| [27] |
Crowe C, Alhilali K.Attenuation of seismic reflections as a key to lithology and pore filler[C].60th Annual Meeting of AAPG, 1975.
|
| [28] |
Baysal E, Kosloff D D, Sherwood J W C. Reverse time migration[J]. Geophysics, 1983, 48(11): 1514-1524. DOI:10.1190/1.1441434 |
| [29] |
Treitel S, Robinson E A. Seismic wave propagation in layered media in terms of communication theory[J]. Geophysics, 1966, 31(1): 17-32. |
| [30] |
Macdonald C, Davis P M, Jackson D D. Inversion of reflection traveltimes and amplitudes[J]. Geophysics, 1987, 52(5): 606-617. DOI:10.1190/1.1442330 |



 李景叶, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院, 102249。Email:
李景叶, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院, 102249。Email: