② 东方地球物理公司物探技术研究中心, 河北涿州 072751;
③ 中国石化西北油田分公司勘探开发研究院, 乌鲁木齐 830011;
④ 中国地质大学(北京)地球物理与信息技术学院, 北京 100083
② Geophysical Research and Development Center, BGP, CNPC, Zhuozhou, Hebei 072751, China;
③ Petroleum Exploration and Production Research Institute, Sinopec Northwest Oilfield Company, Urumqi, Xinjiang 830011, China;
④ School of Geophysics and Information Technology, China University of Geosciences(Beijing), Beijing 100083, China;
中国陆相沉积岩大多具有薄互层特征,当受到构造运动的影响时,会发育垂向或近似垂向的高角度裂缝,呈现出典型的正交各向异性特征。作为一种重要的含油气储层,裂缝型储层中发育的裂缝既可以作为油气储集空间,又可以作为渗流通道[1]。研究正交各向异性的AVO响应对裂缝型储层的精细刻画有重要意义。
裂缝储层的各向异性是指含裂缝地层的弹性性质在不同方向上具有差异,且与诱导裂缝的构造应力有关[2]。国外学者在各向异性领域的研究起步较早,Christoffel[3]提出用弹性张量描述介质的各向异性,因此各向异性波动方程称为Christoffel方程。Crampin[4]首次发现各向异性介质中的地震横波分裂现象,并分析了地球上常见的各向异性介质的种类与特征。在此基础上,Hudson[5-6]推导了由于裂缝存在而产生的一阶和二阶扰动量,给出了含定向裂缝介质的弹性模量的计算方法,但只适用于高频情况。Schoenberg等[7-8]在位移不连续和旋转不变性的假设下,忽略裂缝的形状与结构,提出了线性滑移理论,并对多组裂缝尺度进行了数值模拟。Thomsen[9]提出了弱各向异性理论,给出了表征弱各向异性VTI介质的参数,并据此推导了相速度和群速度的近似表达式。当介质中存在与地层走向垂直的裂隙时,使用正交各向异性模型描述更合理。Tsvankin[10]基于Thomsen的TI介质参数,分别在三个对称面内求解Christoffel方程,给出了正交各向异性介质的参数化方法,并推导了弱正交各向异性介质中qP波相速度近似表达式。基于Tsvankin提出的正交各向异性参数,Bakulin等[11-13]对两种正交各向异性模型进行了研究,分别在VTI背景下嵌入一组垂直裂缝和两组相互垂直的裂缝,运用Schoenberg的柔度建模理论构建刚度系数矩阵。Rokhlin[14]基于Christoffel方程和边界条件提出了一种计算一般各向异性介质反射系数和透射系数的方法;Rüger[15-17]推导了弱各向异性介质中反射系数近似公式,并运用纵波方位AVO检测裂缝。
国内学者在各向异性领域的研究起步较晚,但是在正交各向异性方面的研究也有一些进展,傅旦丹等[18]研究了伪谱法在正交各向异性介质中的应用,分析了伪谱法的稳定性,并将Backus方法与Hudson理论结合,推出了周期性薄互层(PTL)与广泛扩容各向异性(EDA)组合的等效正交各向异性弹性常数的计算公式。张文生等[19]利用有限差分方法模拟正交各向异性介质中地震波场;魏建新[20]应用物理模拟方法研究了正交各向异性介质的波场特征;李娜[21]基于Tsvankin的各向异性参数研究了正交各向异性介质的相速度和群速度。许茜茹等[22]通过耦合S波射线理论和基于迭代的各向异性相速度与偏振矢量的高阶近似解,得到了适用于正交各向异性介质以qP波入射产生的二阶反射、透射系数的计算公式。张繁昌等[23]针对两组裂缝垂直的正交各向异性介质,基于Schoenberg的柔度建模理论构建刚度矩阵,推导了反射系数公式,并运用Fourier级数预测了裂缝方位。唐杰等[24]以两组垂直裂缝的正交各向异性介质为研究对象,研究了干燥和完全水饱和的地震波响应特征。郭恺等[25]研究了正交各向异性介质的多参数建模方法;单俊臻等[26]推导了一种新的PP波HTI介质反射系数一阶扰动公式,突破了传统反射系数近似公式仅适用于小炮间距的局限。秦海旭等[27]将两组裂缝垂直斜交的各向异性地层等效为单斜介质,推导了qP波方程并进行了正演模拟。
在上述研究中,基于波动方程的正演模拟方法得到的正交各向异性的地震波场非常复杂,多种模式的波相互混杂,再加上难以完全消除的数值频散与边界效应,无法用于定量分析正交各向异性介质的AVO响应特征。另外,弱正交各向异性假设下的反射系数近似公式的精度没有得到有效验证,无法适用于裂缝发育程度高或者VTI背景各向异性程度较强的地层。
针对上述问题,本文针对VTI背景介质中发育的一组直立裂缝诱导的正交各向异性,采用Tsvankin提出的各向异性参数构建刚度系数矩阵,再根据Christoffel方程求解出慢度矢量和偏振矢量,并结合弹性波传播理论的边界位移连续条件和应力连续条件,导出了计算精确反射系数和透射系数的方法。使用十二个各向异性模型分析背景VTI介质各向异性强度和裂缝发育程度对正交各向异性介质反射系数的影响。为了验证本文计算结果的正确性,与Rüger的反射系数近似公式的计算结果进行了对比。
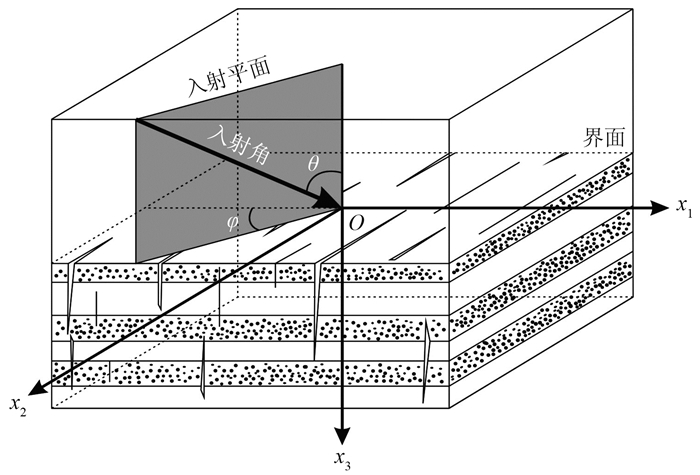
1 正交各向异性介质弹性刚度矩阵本文的正交各向异性介质是指在VTI背景介质中发育有一组垂直裂缝,如图 1的下层所示。
|
图 1 正交各向异性介质模型示意图 |
图 1中x1轴垂直于裂缝面,对称面x2Ox3平行于裂缝面,x1Ox3垂直于裂缝面,x1Ox2平行于水平界面,θ为入射波传播方向与x3轴的夹角(入射角),φ为入射平面与x1轴的夹角(方位角)。文中用上标“U、L”分别代表上层介质和下层介质,下标“1、2、3”对应轴x1、x2、x3轴向。相速度传播方向为波前法向,慢度为相速度的倒数。
正交各向异性介质的弹性刚度系数矩阵为
| $ \mathit{\boldsymbol{C}} = \left( {\begin{array}{*{20}{c}} {{c_{11}}}&{{c_{12}}}&{{c_{13}}}&0&0&0\\ {{c_{12}}}&{{c_{22}}}&{{c_{23}}}&0&0&0\\ {{c_{13}}}&{{c_{23}}}&{{c_{33}}}&0&0&0\\ 0&0&0&{{c_{44}}}&0&0\\ 0&0&0&0&{{c_{55}}}&0\\ 0&0&0&0&0&{{c_{66}}} \end{array}} \right) $ | (1) |
Tsvankin[9]定义的正交各向异性介质中三个不同的正交对称面上的各向异性参数为
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{V_{{\rm{P0}}}} = \sqrt {\frac{{{c_{33}}}}{\rho }} }\\ {{V_{{\rm{S0}}}} = \sqrt {\frac{{{c_{55}}}}{\rho }} }\\ {{\varepsilon ^{(1)}} = \frac{{{c_{22}} - {c_{33}}}}{{2{c_{33}}}}}\\ {{\gamma ^{(1)}} = \frac{{{c_{66}} - {c_{55}}}}{{2{c_{55}}}}} \end{array}\\ \begin{array}{*{20}{l}} {{\delta ^{(1)}} = \frac{{{{({c_{23}} + {c_{44}})}^2} - {{({c_{33}} - {c_{44}})}^2}}}{{2{c_{33}}({c_{33}} - {c_{44}})}}}\\ {{\varepsilon ^{(2)}} = \frac{{{c_{11}} - {c_{33}}}}{{{c_{33}}}}}\\ {{\gamma ^{(2)}} = \frac{{{c_{66}} - {c_{44}}}}{{2{c_{44}}}}} \end{array}\\ \begin{array}{*{20}{l}} {{\delta ^{(2)}} = \frac{{{{({c_{13}} + {c_{55}})}^2} - {{({c_{33}} - {c_{55}})}^2}}}{{2{c_{33}}({c_{33}} - {c_{55}})}}}\\ {{\delta ^{(3)}} = \frac{{{{({c_{12}} + {c_{66}})}^2} - {{({c_{11}} - {c_{66}})}^2}}}{{2{c_{11}}({c_{11}} - {c_{66}})}}} \end{array} \end{array} \right. $ | (2) |
式中:VP0为沿着垂直方向(x3方向)传播的P波速度;VS0为沿着垂直方向传播且沿着x2方向偏振的S波速度;ε(1,2)、γ(1,2)、δ(1,2,3)表示不同平面内的Thomsen型各向异性参数,其中上标“1、2、3”分别代表x2Ox3、x1Ox3和x1Ox2平面[11]。
可根据以上Tsvankin的各向异性参数构建弹性刚度系数矩阵,即
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{c_{11}} = [1 + 2{\varepsilon ^{(2)}}]\rho V_{{\rm{P0}}}^2}\\ {{c_{22}} = [1 + 2{\varepsilon ^{(1)}}]\rho V_{{\rm{S0}}}^2}\\ {{c_{33}} = \rho V_{{\rm{P0}}}^2}\\ {{c_{44}} = \frac{{1 + 2{\gamma ^{(1)}}}}{{1 + 2{\gamma ^{(2)}}}}\rho V_{{\rm{S0}}}^2}\\ {{c_{55}} = \rho V_{{\rm{S0}}}^2}\\ {{c_{66}} = [1 + 2{\gamma ^{(1)}}]\rho V_{{\rm{S0}}}^2} \end{array}\\ \begin{array}{*{20}{l}} {{c_{12}} = \left\{ {{{\{ {{[1 + 2{\varepsilon ^{(2)}}]}_\rho }V_{{\rm{P0}}}^2 - [1 + 2{\gamma ^{(1)}}]\rho V_{{\rm{S0}}}^2\} }^2} + } \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2{\delta ^{(3)}}{\rho ^2}V_{{\rm{P0}}}^2[1 + {\varepsilon ^{(2)}}]\{ [1 + 2{\varepsilon ^{(2)}}]V_{{\rm{P0}}}^2 - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\left. {{\kern 1pt} [1 + 2{\gamma ^{(1)}}]V_{{\rm{S0}}}^2\} } \right\}}^{\frac{1}{2}}} - [1 + 2{\gamma ^{(1)}}]\rho V_{{\rm{S0}}}^2} \end{array}\\ {c_{13}} = {[{(\rho V_{{\rm{P0}}}^2 - \rho V_{{\rm{S0}}}^2)^2} + 2{\delta ^{(2)}}{\rho ^2}V_{{\rm{P0}}}^2(V_{{\rm{P0}}}^2 - V_{{\rm{S0}}}^2)]^{\frac{1}{2}}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \rho V_{{\rm{S0}}}^2\\ \begin{array}{*{20}{l}} {{c_{23}} = \left\{ {{{\left[ {\rho V_{{\rm{P0}}}^2 - \frac{{1 + 2{\gamma ^{(1)}}}}{{1 + 2{\gamma ^{(2)}}\rho V_{{\rm{S0}}}^2}}} \right]}^2} + 2{\delta ^{(1)}}{\rho ^2}V_{{\rm{P0}}}^2 \times } \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\left. {\left[ {V_{{\rm{P0}}}^2 - \frac{{1 + 2{\gamma ^{(1)}}}}{{1 + 2{\gamma ^{(2)}}}}V_{{\rm{S0}}}^2} \right]} \right\}}^{\frac{1}{2}}} - \frac{{1 + 2{\gamma ^{(1)}}}}{{1 + 2{\gamma ^{(2)}}}}\rho V_{{\rm{S0}}}^2} \end{array} \end{array} \right. $ | (3) |
Christoffel方程是由波动方程导出,用于研究地震波的慢度和偏振矢量等传播特征[28]。基于Christoffel方程及其变形,结合Snell定律求解出反射波和透射波的慢度矢量和偏振矢量,并根据边界的位移连续条件和应力连续条件,求出反射系数和透射系数精确解。
2.1 入射P波的慢度矢量计算一般均匀完全弹性各向异性介质中地震波时间域Christoffel方程[3]为
| $ (\mathit{\boldsymbol{ \boldsymbol{\varGamma} }} - \rho \mathit{\boldsymbol{E}})\mathit{\boldsymbol{P}} = 0 $ | (4) |
即
| $ \left[ {\begin{array}{*{20}{c}} {{\varGamma _{11}} - \rho }&{{\varGamma _{12}}}&{{\varGamma _{13}}}\\ {{\varGamma _{21}}}&{{\varGamma _{22}} - \rho }&{{\varGamma _{23}}}\\ {{\varGamma _{31}}}&{{\varGamma _{32}}}&{{\varGamma _{33}} - \rho } \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{P_1}}\\ {{P_2}}\\ {{P_3}} \end{array}} \right] = 0 $ | (5) |
式中:E为单位矩阵;ρ为介质的密度;P为波的偏振矢量。
根据广义虎克定律,可得
| $ \left\{ {\begin{array}{*{20}{l}} {{\varGamma _{11}} = {c_{11}}s_1^2 + {c_{66}}s_2^2 + {c_{55}}s_3^2}\\ {{\varGamma _{22}} = {c_{66}}s_1^2 + {c_{22}}s_2^2 + {c_{44}}s_3^2}\\ {{\varGamma _{33}} = {c_{55}}s_1^2 + {c_{44}}s_2^2 + {c_{33}}s_3^2}\\ {{\varGamma _{12}} = {\varGamma _{21}} = ({c_{12}} + {c_{66}}){s_1}{s_2}}\\ {{\varGamma _{13}} = {\varGamma _{31}} = ({c_{13}} + {c_{55}}){s_1}{s_3}}\\ {{\varGamma _{23}} = {\varGamma _{32}} = ({c_{23}} + {c_{44}}){s_2}{s_3}} \end{array}} \right. $ | (6) |
式中s1、s2、s3为慢度矢量的三个分量。
当界面上、下介质为正交各向异性或是更高对称性的介质时,假设入射波以图 1方式入射,则入射波波前的法向单位矢量为
| $ \mathit{\boldsymbol{n}} = [{n_1},{n_2},{n_3}] = [{\rm{sin}}\theta {\rm{cos}}\varphi ,{\rm{sin}}\theta {\rm{sin}}\varphi ,{\rm{cos}}\theta ] $ | (7) |
式(4)两边同乘V2/ρ可得[29]
| $ ({\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}^{\rm{U}}} - {V^2}\mathit{\boldsymbol{E}})\mathit{\boldsymbol{P}} = 0 $ | (8) |
其展开形式为
| $ \left[ {\begin{array}{*{20}{c}} {\varLambda _{11}^{\rm{U}} - {V^2}}&{\varLambda _{12}^{\rm{U}}}&{\varLambda _{13}^{\rm{U}}}\\ {\varLambda _{21}^{\rm{U}}}&{\varLambda _{22}^{\rm{U}} - {V^2}}&{\varLambda _{23}^{\rm{U}}}\\ {\varLambda _{31}^{\rm{U}}}&{\varLambda _{32}^{\rm{U}}}&{\varLambda _{33}^{\rm{U}} - {V^2}} \end{array}} \right]\left[ {\begin{array}{*{20}{l}} {{P_1}}\\ {{P_2}}\\ {{P_3}} \end{array}} \right] = 0 $ | (9) |
式中
| $ \left\{ {\begin{array}{*{20}{l}} {\varLambda _{11}^{\rm{U}} = \frac{{c_{11}^{\rm{U}}n_1^2 + c_{66}^{\rm{U}}n_2^2 + c_{55}^{\rm{U}}n_3^2}}{{{\rho ^{\rm{U}}}}}}\\ {\varLambda _{22}^{\rm{U}} = \frac{{c_{66}^{\rm{U}}n_1^2 + c_{22}^{\rm{U}}n_2^2 + c_{44}^{\rm{U}}n_3^2}}{{{\rho ^{\rm{U}}}}}} \end{array}} \right. $ | (10a) |
| $ \left\{ {\begin{array}{*{20}{l}} {\varLambda _{33}^{\rm{U}} = \frac{{c_{55}^{\rm{U}}n_1^2 + c_{44}^{\rm{U}}n_2^2 + c_{33}^{\rm{U}}n_3^2}}{{{\rho ^{\rm{U}}}}}}\\ {\varLambda _{12}^{\rm{U}} = \varLambda _{21}^{\rm{U}} = \frac{{(c_{12}^{\rm{U}} + c_{66}^{\rm{U}}){n_1}{n_2}}}{{{\rho ^{\rm{U}}}}}}\\ {\varLambda _{13}^{\rm{U}} = \varLambda _{31}^{\rm{U}} = \frac{{(c_{13}^{\rm{U}} + c_{55}^{\rm{U}}){n_1}{n_3}}}{{{\rho ^{\rm{U}}}}}}\\ {\varLambda _{23}^{\rm{U}} = \varLambda _{32}^{\rm{U}} = \frac{{(c_{23}^{\rm{U}} + c_{44}^{\rm{U}}){n_2}{n_3}}}{{{\rho ^{\rm{U}}}}}} \end{array}} \right. $ | (10b) |
此时求解式(8)就等价于相速度V(特征值)和偏振矢量P(特征向量)的求解问题。为满足非零解条件,Christoffel矩阵的行列式值为零,即变成求解V2的一元三次方程
| $ {G_3}{({V^2})^3} + {G_2}{({V^2})^2} + {G_1}{V^2} + {G_0} = 0 $ | (11) |
若定义
| $ \left\{ {\begin{array}{*{20}{l}} {{G_0} = {B_{11}}{B_{22}}{B_{33}} + {B_{12}}{B_{23}}{B_{31}} + {B_{13}}{B_{21}}{B_{32}} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {B_{31}}{B_{13}}{B_{22}} - {B_{23}}{B_{32}}{B_{11}} - {B_{21}}{B_{12}}{B_{33}}}\\ {{G_1} = {B_{31}}{B_{13}} + {B_{23}}{B_{32}} + {B_{21}}{B_{12}} - {B_{11}}{B_{33}} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {B_{33}}{B_{22}} - {B_{22}}{B_{11}}}\\ {{G_2} = {B_{11}} + {B_{22}} + {B_{33}}}\\ {{G_3} = - 1} \end{array}} \right. $ | (12) |
解式(11)可得入射波的相速度VP、VS1、VS2(VP>VS1>VS2),则入射P波的慢度为
| $ {\mathit{\boldsymbol{s}}_0} = \left[ {\frac{{{n_1}}}{{{V_{\rm{P}}}}},\frac{{{n_2}}}{{{V_{\rm{P}}}}},\frac{{{n_3}}}{{{V_{\rm{P}}}}}} \right] $ | (13) |
若用si表示不同波的慢度矢量(i=0、1、…、6,分别代表入射P波、反射P、S1、S2波、透射P、S1、S2波),则
| $ {\mathit{\boldsymbol{s}}_i} = [{s_{i1}},{s_{i2}},{s_{i3}}] $ | (14) |
根据Snell定律,对于所有的入射、反射和透射波,与界面平行的两个慢度矢量的分量是相等的,即
| $ \left\{ {\begin{array}{*{20}{l}} {{s_{01}} = {s_{11}} = \cdots = {s_{61}}}\\ {{s_{02}} = {s_{12}} = \cdots = {s_{62}}} \end{array}} \right. $ | (15) |
式(4)的未知解是慢度矢量和偏振矢量,对于反射波和透射波慢度矢量的分量si3,为满足非零解条件,则需求解方程
| $ {\rm{det}} |\mathit{\boldsymbol{ \boldsymbol{\varGamma} }} - \rho \mathit{\boldsymbol{E}}| = 0 $ | (16) |
把上层介质和下层介质的参数以及已知的si1和si2代入式(16),可以解出上、下介质中的六个si3。
2.3 反射波和透射波的偏振矢量计算若用Pi表示偏振矢量(i=0、1、…、6,分别代表入射P波、反射P、S1、S2波、透射P、S1、S2波),即
| $ {\mathit{\boldsymbol{P}}_i} = [{P_{i1}},{P_{i2}},{P_{i3}}] $ | (17) |
式(16)已求得慢度矢量,再结合偏振矢量的归一化,对于上层介质有
| $ \left\{ {\begin{array}{*{20}{l}} {({\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^{\rm{U}}} - {\rho ^{\rm{U}}}\mathit{\boldsymbol{E}}){\mathit{\boldsymbol{P}}_i} = 0}\\ {P_{i1}^2 + P_{i2}^2 + P_{i3}^2 = 1} \end{array}} \right. $ | (18) |
对于下层介质有
| $ \left\{ {\begin{array}{*{20}{l}} {({\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}^L} - {\rho ^L}\mathit{\boldsymbol{E}}){\mathit{\boldsymbol{P}}_i} = 0}\\ {P_{i1}^2 + P_{i2}^2 + P_{i3}^2 = 1} \end{array}} \right. $ | (19) |
运用Zhou等[30]的方法求解式(18)和式(19),可得到反射波和透射波的偏振矢量。
对于求得的7个偏振矢量,需要通过其与相速度的关系进行偏振矢量符号的校正。根据Chen[31]的校正方法,对于入射、反射和透射的P波,若偏振矢量P与慢度矢量s的点乘大于0,则偏振矢量的符号为正;对于反射和透射的S波,入射面的法向量N为慢度矢量s与入射波波前法向矢量n的叉乘,若偏振矢量P与入射面法向量N的点乘为正,则偏振矢量的符号为正。
2.4 反射系数和透射系数的求解根据弹性波传播理论,当入射P波入射到界面时,应满足边界的位移连续条件和应力连续条件。根据Rokhlin[14]给出的边界条件可以导出反射系数和透射系数计算公式,即
| $ \left\{ {\begin{array}{*{20}{l}} {{P_{0l}} + \sum\limits_{i = 1} {{R_i}} {P_{il}} = 0}\\ {\sum\limits_{k = 1}^3 {\sum\limits_{l = 1}^3 {c_{j3kl}^{\rm{U}}} } {s_{0k}}{P_{0l}} + \sum\limits_{i = 1}^6 {{R_i}} (\sum\limits_{k = 1}^3 {\sum\limits_{l = 1}^3 {{c_{ij3kl}}} } {s_{ik}}{P_{il}}) = 0} \end{array}} \right. $ | (20) |
式中:Ri为反射系数或透射系数,i=1、2、…、6,分别表示反射P、S1、S2波和透射P、S1、S2波;j=0、1、2、3;cij3kl中当i=0~3时为cj3klU,i=4~6时为cj3klL。为了更直观地表达,将式(20)写为矩阵形式
| $ \left[ {\begin{array}{*{20}{c}} {{P_{01}}}&{{P_{11}}}&{{P_{21}}}&{{P_{31}}}&{ - {P_{41}}}&{ - {P_{51}}}&{ - {P_{61}}}\\ {{P_{02}}}&{{P_{12}}}&{{P_{22}}}&{{P_{32}}}&{ - {P_{42}}}&{ - {P_{52}}}&{ - {P_{62}}}\\ {{P_{03}}}&{{P_{13}}}&{{P_{23}}}&{{P_{33}}}&{ - {P_{43}}}&{ - {P_{53}}}&{ - {P_{63}}}\\ {{I_{01}}}&{{I_{11}}}&{{I_{21}}}&{{I_{31}}}&{{I_{41}}}&{{I_{51}}}&{{I_{61}}}\\ {{I_{02}}}&{{I_{12}}}&{{I_{22}}}&{{I_{32}}}&{{I_{42}}}&{{I_{52}}}&{{I_{62}}}\\ {{I_{03}}}&{{I_{13}}}&{{I_{23}}}&{{I_{33}}}&{{I_{43}}}&{{I_{53}}}&{{I_{63}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} 1\\ {{R_{{\rm{PP}}}}}\\ {{R_{{\rm{PS1}}}}}\\ {{R_{{\rm{PS2}}}}}\\ {{T_{{\rm{PP}}}}}\\ {{T_{{\rm{PS1}}}}}\\ {{T_{{\rm{PS2}}}}} \end{array}} \right] = 0 $ | (21) |
式中
| $ \begin{array}{l} \begin{array}{*{20}{l}} {{I_{0j}} = \sum\limits_{k = 1}^3 {\sum\limits_{l = 1}^3 {c_{j3kl}^{\rm{U}}} } {s_{0k}}{P_{0l}}}\\ {{I_{1j}} = \sum\limits_{k = 1}^3 {\sum\limits_{l = 1}^3 {c_{j3kl}^{\rm{U}}} } {s_{1k}}{P_{1l}}}\\ {{I_{2j}} = \sum\limits_{k = 1}^3 {\sum\limits_{l = 1}^3 {c_{j3kl}^{\rm{U}}} } {s_{2k}}{P_{2l}}}\\ {{I_{3j}} = \sum\limits_{k = 1}^3 {\sum\limits_{l = 1}^3 {c_{j3kl}^{\rm{U}}} } {s_{3k}}{P_{3l}}} \end{array}\\ \begin{array}{*{20}{l}} {{I_{4j}} = - \sum\limits_{k = 1}^3 {\sum\limits_{l = 1}^3 {c_{j3kl}^{\rm{L}}} } {s_{4k}}{P_{4l}}}\\ {{I_{5j}} = - \sum\limits_{k = 1}^3 {\sum\limits_{l = 1}^3 {c_{j3kl}^{\rm{L}}} } {s_{5k}}{P_{5l}}}\\ {{I_{6j}} = - \sum\limits_{k = 1}^3 {\sum\limits_{l = 1}^3 {c_{j3kl}^{\rm{L}}} } {s_{6k}}{P_{6l}}} \end{array} \end{array} $ | (22) |
为了分析不同类型各向异性参数对反射系数的影响,先将正交各向异性分别退化到用单组裂缝弱度参数描述的HTI介质和用Thomsen参数描述的VTI介质。然后,分两种情况进行数值分析:①固定裂缝弱度参数不变,变化背景介质的VTI各向异性参数;②固定背景VTI各向异性参数不变,变化裂缝弱度参数。
为了验证本文中正交各向异性反射系数计算方法的有效性,将计算结果与Rüger在正交各向异性介质中x1Ox3与x2Ox3面的PP波近似反射系数进行对比;再将退化的HTI和VTI介质的反射系数与Rüger近似公式所得到的反射系数进行对比。
3.1 正交各向异性参数与VTI各向异性参数和裂缝弱度参数的关系Bakulin等[12]给出了正交各向异性参数与背景介质的VTI各向异性参数以及裂缝弱度参数的关系为
| $ \left\{ {\begin{array}{*{20}{l}} {{\varepsilon ^{(1)}} = {\varepsilon _{\rm{b}}}}\\ {{\delta ^{(1)}} = {\delta _{\rm{b}}}}\\ {{\gamma ^{(1)}} = {\gamma _{\rm{b}}} + \frac{{{Z_{\rm{V}}} - {Z_{\rm{H}}}}}{2}}\\ {{\varepsilon ^{(2)}} = {\varepsilon _{\rm{b}}} - 2g(1 - g){Z_{\rm{N}}}}\\ {{\delta ^{(2)}} = {\delta _{\rm{b}}} - 2g[(1 - 2g){Z_{\rm{N}}} + {Z_{\rm{V}}}]}\\ {{\gamma ^{(2)}} = {\gamma _{\rm{b}}} - \frac{{{Z_{\rm{H}}}}}{2}}\\ {{\delta ^{(3)}} = 2g({Z_{\rm{N}}} - {Z_{\rm{H}}})} \end{array}} \right. $ | (23) |
式中:下标“b”表示VTI背景介质;g=VS02/VP02;ZN、ZV和ZH是无量纲参数,分别表示裂缝的法向弱度、垂直切向弱度以及水平切向弱度[32]。
3.2 P波从低阻抗介质入射到高阻抗介质假设模型的上层为低阻抗各向同性介质,下层为高阻抗的正交各向异性介质。根据式(3),刚度系数矩阵可以用P波垂直速度VP0、S波垂直速度VS0、密度ρ以及各向异性参数表示。
模型上层介质参数为:VP0=3150m/s,VS0=1615m/s,ρ=2322kg/m3,ε(1)=ε(2)=γ(1)=γ(2)=δ(1)=δ(2)=δ(3)=0。
模型下层介质参数为:VP0=3310m/s,VS0=1697m/s,ρ=2351kg/m3,其各向异性参数如表 1或表 2所示。
|
|
表 1 裂缝弱度参数不变、背景介质的VTI各向异性参数变化时的正交各向异性参数 |
|
|
表 2 背景VTI各向异性参数不变、裂缝弱度参数变化时的正交各向异性参数 |
首先,固定三个裂缝弱度参数不变,改变背景介质的VTI各向异性参数,分析其对反射系数的影响。表 1参数由式(23)计算得到,裂缝弱度参数ZN、ZV和ZH分别为0.215、0.120、0.090;VTI各向异性参数由弱变强:模型A1的背景为各向同性介质,εb=0、γb=0、δb=0,此时正交各向异性介质退化为HTI介质;模型A2的背景为弱各向异性VTI介质,εb=0.1、γb=0.12、δb=0.07;模型A3的背景为强各向异性VTI介质,εb=0.3、γb=0.25、δb=0.15。
固定θ=20°,φ从0°变化到90°时模型A1、A2、A3的反射系数RPP、RPS1、RPS2曲线如图 2所示。可以看出:

|
图 2 θ=20°时模型A1、A2和A3的RPP(a)、RPS1(b)、RPS2(c)随φ的变化曲线 |
(1) PP波反射系数的方位各向异性较弱;从模型A1到模型A3,VTI各向异性的增强导致RPP增大,模型A2比模型A1增大了40%,模型A3比模型A1增大了86%。
(2) 反射系数RPS1方位各向异性很强,且随方位角增大而减小;从模型A1到模型A3,VTI各向异性的增强导致RPS1减小,最大时模型A2比模型A1减小了33%,模型A3比模型A1减小了83%;
(3) 反射系数RPS2也具有很强的方位各向异性,曲线变化趋势与RPS1沿着方位呈大体镜像关系,但是量值上有差异;从模型A1到模型A3,VTI各向异性的增强导致RPS2减小,最大时模型A2比模型A1减小了30%,模型A3比模型A1减小了70%。
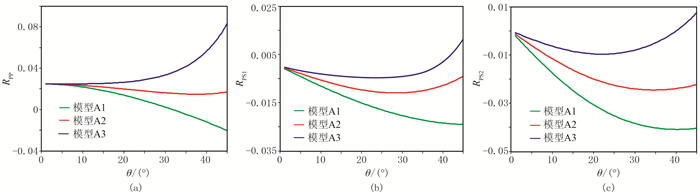
固定φ=60°,模型A1、A2、A3的反射系数RPP、RPS1、RPS2随θ的变化曲线如图 3所示。由图可知:
|
图 3 φ=60°时模型A1、A2和A3的RPP(a)、RPS1(b)、RPS2(c)随θ的变化曲线 |
(1) 小入射角时(θ < 10°),反射系数RPP受背景介质VTI各向异性参数的影响不大。但是,随着θ的增大,模型A1的RPP随θ增大而减小,且在θ≈35°时发生极性转变;从模型A1到模型A3,VTI各向异性增强导致大入射角的RPP增大。
(2) 随着θ的增大,反射系数RPS1在θ < 30°时都呈增大的趋势,而在30°~45°范围内模型A2、A3开始减小,模型A3在θ≈35°出现了极性转变;从模型A1到模型A3,VTI各向异性参数的增大导致RPS1减小,在θ=30°时模型A2比模型A1减小了50%,模型A3比模型A1减小了75%。
(3) 随着θ的增大,反射系数RPS2与RPS1变化趋势一致;从模型A1到模型A3,VTI各向异性系数的增大导致RPS2减小,在θ=30°时模型A2比模型A1减小了37.5%,模型A3比模型A1减小了75%。
φ在0°~90°内变化、θ在临界角范围以内,P波由各向同性介质入射到正交各向异性模型A1、A2和A3时的反射系数RPP、RPS1和RPS2的等值线图分别如图 4、图 5、图 6所示,可以看出:

|
图 4 入射P波由各向同性到各向异性模型A1(a)、A2(b)、A3(c)反射系数RPP等值线图 |
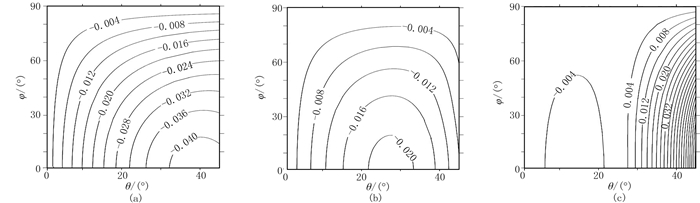
|
图 5 入射P波由各向同性到各向异性模型A1(a)、A2(b)、A3(c)反射系数RPS1等值线图 |
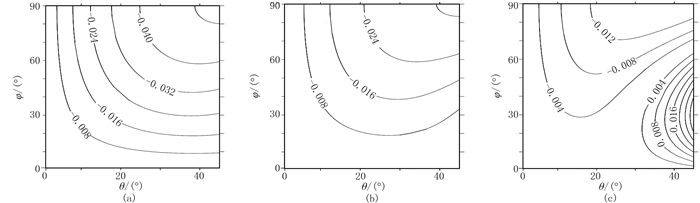
|
图 6 入射P波由各向同性到各向异性模型A1(a)、A2(b)、A3(c)反射系数RPS2等值线图 |
(1) 随着VTI背景各向异性程度的增强,RPP等值线曲率变化不大,只在反射系数的量值上有整体增大,且靠近临界角时增加幅度最大。
(2) RPS1和RPS2随方位变化的程度远大于RPP,都有随着背景介质VTI各向异性强度增强而减小的趋势,且等值线曲率变化也较大。
由于背景介质中插入的裂缝弱度值不大,裂缝诱导的HTI各向异性属于弱各向异性。针对此类正交各向异性介质的AVO分析,单纯的PP波对裂缝的发育以及背景介质的VTI各向异性程度的敏感度远小于PS1波和PS2波。
3.2.2 背景介质VTI各向异性系数固定不变,变化裂缝弱度参数由式(23)可知,当固定背景VTI介质的三个各向异性参数不变(εb=0.1,γb=0.12,δb=0.07,与表 1中模型A2的背景介质VTI各向异性参数取值相同)时,改变三个裂缝弱度值会影响HTI各向异性的强弱,弱度越大则HTI各向异性越强。表 2为下层高阻抗介质的背景VTI各向异性参数固定不变、变化裂缝弱度参数计算的正交各向异性参数值。模型B1的裂缝弱度参数ZN=ZV=ZH=0,此时正交各向异性介质退化为VTI各向异性介质;模型B2的裂缝弱度参数ZN=0.215、ZV=0.120、ZH=0.090,呈弱HTI各向异性,等同于表 1中的模型A2;模型B3的裂缝弱度参数ZN=0.215、ZV=0.120、ZH=0.090,裂缝发育程度较高,HTI各向异性也较强。
固定θ=20°,φ在0°~90°变化时模型B1、B2、B3的反射系数RPP、RPS1、RPS2曲线如图 7所示。由图 7可知:

|
图 7 θ=20°时模型B1、B2和B3的反射系数RPP(a)、RPS1(b)、RPS2(c)随φ的变化曲线 |
(1) 裂缝的发育会导致PP波的反射系数变小,模型B2比模型B1减小了32%,模型B3比模型B1减小了64%;即使在裂缝弱度较强的情况下,PP波的反射系数的方位各向异性也是比较微弱的。
(2) 反射系数RPS1受φ的影响较大,在φ=0°时,即平行裂缝面时,RPS1最大;在φ=90°时,即垂直裂缝面时,RPS1为0;从模型B1到模型B3,裂缝弱度的增强导致RPS1增大,最大时模型B2比模型B1增加了300%,模型B3比模型B1增加了600%。当裂缝不发育时(模型B1),RPS1不存在方位各向异性,等同于PSV波的反射系数。
(3) 反射系数RPS2在φ=0°时最小,φ=90°时最大;从模型B1到模型B3,裂缝弱度的增强导致RPS2增加,最大时模型B3比模型B2增加了100%。
固定φ=60°时,模型B1、B2、B3的反射系数RPP、RPS1、RPS2随θ的变化曲线如图 8所示,由图可知:

|
图 8 φ=60°时模型B1、B2和B3的反射系数RPP(a)、RPS1(b)、RPS2(c)随θ的变化曲线 |
(1) θ在0°~45°(临界角以内)范围内,反射系数RPP在θ < 5°时无明显差别,随着θ增大,RPP表现不同,裂缝弱度越大,RPP减小越快;最大时模型B2比模型B1减小了75%,模型B3比模型B1减小了100%。
(2) 随着θ增大,RPS1在θ < 25°时都呈增大的趋势,而在25°~45°范围内模型B1、B2开始减小,模型B1在θ≈30°出现了极性转变;从模型B1到模型B3,裂缝弱度的增强导致RPS1增大,θ=25°时模型B2比模型B1增大了100%,模型B3比模型B1增大了300%。
(3) 随着θ增大,当裂缝发育时,RPS2都呈负极性方向增大的趋势,在θ=0°时最小,在θ=45°时最大;从模型B1到模型B3,裂缝弱度的增强导致RPS2增大,最大时模型B3比模型B2增大了100%。
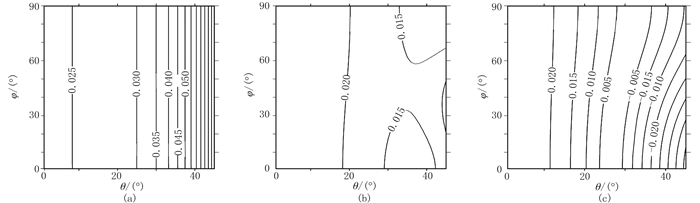
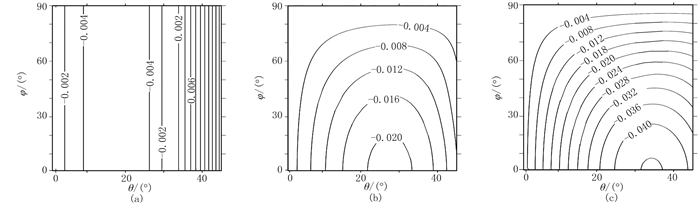
φ在0°~90°内变化、θ在临界角范围以内,P波由各向同性介质入射到正交各向异性模型B1、B2和B3时的反射系数RPP、RPS1和RPS2的等值线图分别如图 9、图 10、图 11所示,可以看出:随着裂缝弱度的增强,RPP在正极性方向减小,RPS1和RPS2在负极性方向增大。总体上,即使裂缝诱导的HTI各向异性较强,RPP的方位各向异性也比较弱,其对于裂缝发育的敏感度远小于RPS1和RPS2。
|
图 9 入射P波由各向同性到各向异性模型B1(a)、B2(b)和B3(c)的反射系数RPP等值线图 |
|
图 10 入射P波由各向同性到各向异性模型B1(a)、B2(b)和B3(c)的反射系数RPS1等值线图 |

|
图 11 入射P波由各向同性到各向异性模型B1(a)、B2(b)和B3(c)的反射系数RPS2等值线图 |
为了进一步探讨界面上、下阻抗对反射系数的影响,将A、B系列模型的上、下层介质的纵横波速度和密度交换,下层的各向异性参数保持不变,可得模型C1、C2、C3(表 1,裂缝弱度不变,VTI各向异性强度变化)和模型D1、D2、D3(表 2,裂缝弱度变化,VTI各向异性参数不变)。
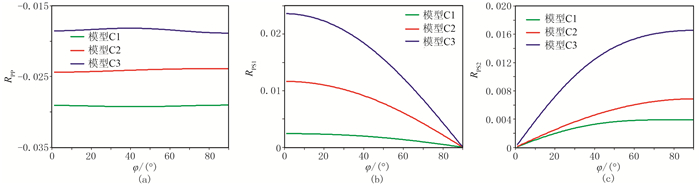
固定θ=20°,模型C1、C2、C3的反射系数RPP、RPS1、RPS2的随φ的变化曲线如图 12所示;固定φ=60°,模型C1、C2、C3的反射系数RPP、RPS1、RPS2随θ的变化曲线如图 13所示。对比图 12、图 13与图 2、图 3可知,与下层介质为高阻抗介质的情况相反,当下层介质为低阻抗介质时,背景介质的VTI各向异性强度越强,则PP波的反射系数在负极性方向越小,而PS1波与PS2波在正极性方向越大。
|
图 12 θ=20°时模型C1、C2和C3的反射系数RPP(a)、RPS1(b)、RPS2(c)随φ的变化曲线 |

|
图 13 φ=60°时模型C1、C2和C3的反射系数RPP(a)、RPS1(b)、RPS2(c)随θ的变化曲线 |
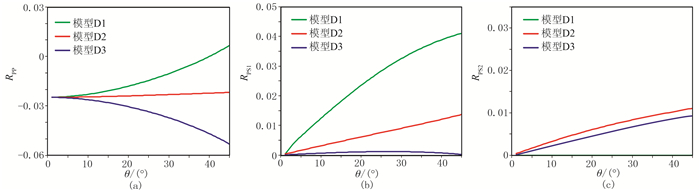
固定θ=20°,模型D1、D2、D3的反射系数RPP、RPS1、RPS2随φ的变化曲线如图 14所示;固定φ=60°,模型D1、D2、D3的反射系数RPP、RPS1、RPS2随θ的变化曲线如图 15所示。对比图 14、图 15与图 7、图 8可知,裂缝的发育会导致PP波的反射系数在负极性方向变大,而PS1波和PS2波的反射系数则在正极性方向变小,与下层介质为高阻抗介质的情况相反。

|
图 14 θ=20°时模型D1、D2和D3的反射系数RPP(a)、RPS1(b)、RPS2(c)随φ的变化曲线 |
|
图 15 φ=60°时模型D1、D2和D3的反射系数RPP(a)、RPS1(b)、RPS2(c)随θ的变化曲线 |
无论是从低阻抗介质入射,还是高阻抗介质入射,PP波反射系数的方位各向异性都远小于PS1波和PS2波。
3.4 与Rüger近似反射系数公式的对比为了验证本文反射系数计算结果的正确性,与Rüger近似公式计算的正交各向异性反射系数、HTI介质反射系数和VTI介质反射系数进行对比。
3.4.1 正交各向异性介质对于P波入射,Rüger[17]仅推导了正交各向异性介质RPP在x1Ox3和x2Ox3面的近似反射系数公式。将模型A2的参数代入到其公式计算反射系数曲线,并与本文的反射系数精确解的计算结果进行对比(图 16)。在x1Ox3面,两条曲线变化趋势一致,当θ在0°~20°范围内时近乎重合(图 16a);在x2Ox3面,两条曲线变化趋势亦一致,当θ在0°~25°范围内时近乎重合(图 16b)。

|
图 16 正交各向异性介质Rüger近似公式与本文方法计算的反射系数曲线对比 (a)x1Ox3面;(b)x2Ox3面 |
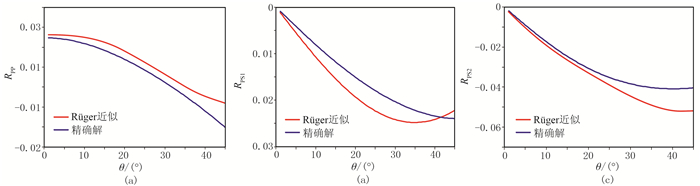
依据式(23)可以将正交各向异性介质退化到HTI介质。将模型A1代入Rüger[17]的HTI介质反射系数近似公式计算反射系数曲线,并与本文的反射系数精确解对比(图 17)。由图 17可以看出RPP、RPS1和RPS2的Rüger近似解与本文精确解变化趋势一致;RPS2在0°~20°范围内近乎重合。
|
图 17 HTI介质Rüger近似公式与本文方法计算的反射系数曲线对比 (a)RPP; (b)RPS1; (c)RPS2 |
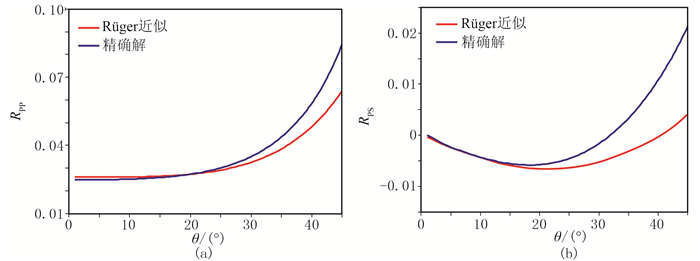
依据式(23)可以将正交各向异性介质退化到VTI介质。将模型B1参数代入Rüger的VTI介质反射系数近似公式,并与本文的反射系数精确解对比(图 18)。从图 18可以看出,RPP和RPS的近似解与精确解变化趋势一致,RPP在0°~25°范围内完全重合,RPS在0°~15°内近乎重合。
|
图 18 VTI介质Rüger近似公式与本文方法计算的反射系数曲线对比 (a)RPP; (b)RPS |
由以上分析可知,本文反射系数精确解与Rüger近似公式在中、小角度范围内近乎重合,整体趋势一致。因此,本文反射系数精确解计算方法正确。
4 结论针对互层背景中发育一组裂缝的正交各向异性介质模型,本文基于Christoffel方程及弹性界面的位移连续条件和应力连续条件,推导了反射系数和透射系数精确求解方法,建立了正交各向异性参数与背景介质VTI各向异性参数系数和裂缝参数之间的关联。通过与Rüger反射系数近似公式计算结果的对比,验证了本文计算结果的正确性。理论模型计算结果表明:
(1) 当P波从低阻抗介质入射至高阻抗介质时,背景介质VTI各向异性参数的变大会导致PP波反射系数增大、PS1波和PS2波的反射系数减小;而裂缝弱度的增强会导致PP波反射系数的减小及PS1波和PS2波的反射系数的增大。
(2) 当从高阻抗介质入射至低阻抗介质时,背景介质VTI各向异性系数的变大会导致PP波反射系数减小、PS1波和PS2波的反射系数增大;而裂缝弱度的增强会导致PP波反射系数的增大、PS1波和PS2波的反射系数的减小。
(3) PP波反射系数的方位各向异性要远小于PS1波与PS2波。
| [1] |
杨帅, 芦俊, 杨春. 含裂缝致密砂岩多波AVO响应分析[J]. 石油地球物理勘探, 2018, 53(4): 798-804. YANG Shuai, LU Jun, YANG Chun. Multi-wave AVO responses in fractured tight sandstone[J]. Oil Geophysical Prospecting, 2018, 53(4): 798-804. |
| [2] |
王赟, 刘媛媛, 张美根. 裂缝各向异性地震等效介质理论[M]. 北京: 科学出版社, 2017.
|
| [3] |
Christoffel E B. Ueber die Fortpflanzung von Stössen durch elastische feste Körper[J]. Annali Di Matematica Pura Ed Applicata, 1877, 8(1): 193-243. DOI:10.1007/BF02420789 |
| [4] |
Crampin S. Seismic wave propagation through a cracked solid:Polarization as a possible dilatancy diagnostic[J]. Geophysical Journal of the Royal Astronomical Society, 1978, 53(3): 467-496. DOI:10.1111/j.1365-246X.1978.tb03754.x |
| [5] |
Hudson J A. A higher order approximation to the wave propagation constants for cracked solid[J]. Geophysical Journal International, 1986, 87(1): 265-274. DOI:10.1111/j.1365-246X.1986.tb04556.x |
| [6] |
Hudson J A. Crack distribution which account for a given seismic anisotropy[J]. Geophysical Journal International, 1991, 104(3): 517-521. |
| [7] |
Schoenberg M. Reflection of elastic waves from perio-dically stratified media with interfacial slip[J]. Geophysical Prospecting, 1983, 31(2): 265-292. DOI:10.1111/j.1365-2478.1983.tb01054.x |
| [8] |
Schoenberg M, Sayers C M. Seismic anisotropy of fractured rocks[J]. Geophysics, 1995, 60(1): 204-211. |
| [9] |
Thomsen L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [10] |
Tsvankin I. Anisotropic parameters and P-wave velo-city for orthorhombic media[J]. Geophysics, 1997, 62(4): 1292-1309. DOI:10.1190/1.1444231 |
| [11] |
Bakulin A, Grechka V, Tsvankin I. Estimation of fracture parameters from reflection seismic data-Part Ⅰ:HTI model due to a single fracture set[J]. Geophy-sics, 2000, 65(6): 1788-1802. |
| [12] |
Bakulin A, Grechka V, Tsvankin I. Estimation of fracture parameters from reflection seismic data-Part Ⅱ:Fractured models with orthorhombic symmetry[J]. Geophysics, 2000, 65(6): 1803-1817. DOI:10.1190/1.1444864 |
| [13] |
Bakulin A, Grechka V, Tsvankin I. Estimation of fracture parameters from reflection seismic data-Part Ⅲ:Fractured models with monoclinic symmetry[J]. Geophysics, 2000, 65(6): 1818-1830. DOI:10.1190/1.1444865 |
| [14] |
Rokhlin S I. Reflection and refraction of elastic waves on a plane interface between two generally anisotropic media[J]. The Journal of the Acoustical Society of America, 1986, 79(4): 906-918. DOI:10.1121/1.393764 |
| [15] |
Rüger A. P-ware reflection coefficients for transversely isotropic models with vertical and horizontal axis of symmetry[J]. Geophysics, 1997, 62(3): 713-721. DOI:10.1190/1.1444181 |
| [16] |
Rüger A. Variation of P-wave reflectivity with offset and azimuth in anisotropic media[J]. Geophysics, 1998, 63(3): 935-947. DOI:10.1190/1.1444405 |
| [17] |
Rüger A. Reflection Coefficients and Azimuthal AVO Analysis in Anisotropic Media[M]. Tulsa: SEG, 2002.
|
| [18] |
傅旦丹, 何樵登. 含垂直裂隙PTL介质长波长等效正交各向异性弹性常数[J]. 地球物理学报, 2002, 45(增刊): 307-320. FU Dandan, HE Qiaodeng. Elastic constants of long-wavelength effective orthorhombic anisotropy for PTL media containing vertical cracks[J]. Chinese Journal of Geophysics, 2002, 45(S): 307-320. |
| [19] |
张文生, 宋海斌. 三维正交各向异性介质三分量高精度有限差分正演模拟[J]. 石油地球物理勘探, 2001, 36(4): 422-432. ZHANG Wensheng, SONG Haibin. Finite-difference forward modeling of three component records with high precision in 3-D orthorhombic anisotropic media[J]. Oil Geophysical Prospecting, 2001, 36(4): 422-432. |
| [20] |
魏建新.正交各向异性介质波场特性的物理模拟研究[D].北京: 中国地震局地球物理研究所, 2003.
|
| [21] |
李娜.正交各向异性介质正演模拟方法及波场特征分析[D].山东青岛: 中国石油大学(华东), 2014.
|
| [22] |
许茜茹, 毛伟建. 正交各向异性介质中qP波入射的二阶近似反射系数与透射系数[J]. 地球物理学报, 2019, 62(1): 266-281. XU Qianru, MAO Weijian. Reflection and transmi-ssion coefficients based on second-order approximation in orthorhombic anisotropic media[J]. Chinese Journal of Geophysics, 2019, 62(1): 266-281. |
| [23] |
张繁昌, 路亚威, 桑凯恒, 等. 正交介质方位傅里叶反射系数及裂缝密度预测[J]. 中国石油大学学报(自然科学版), 2019, 43(2): 37-44. ZHANG Fanchang, LU Yawei, SANG Kaiheng, et al. Azimuthal Fourier reflected coefficients in prediction of orthogonal fracture parameters[J]. Journal of China University of Petroleum(Edition of Natural Science), 2019, 43(2): 37-44. |
| [24] |
唐杰, 温雷, 王浩, 等. 正交各向异性介质中的剪张源震源机制与矩张量特征[J]. 石油地球物理勘探, 2018, 53(6): 1247-1255. TANG Jie, WEN Lei, WANG Hao, et al. Focal mecha-nisms and moment tensor in orthorhombic anisotropic media[J]. Oil Geophysical Prospecting, 2018, 53(6): 1247-1255. |
| [25] |
郭恺, 张永升, 冯彦彬. 正交各向异性介质多参数建模方法研究[J]. 石油物探, 2019, 58(6): 874-881. GUO Kai, ZHANG Yongsheng, FENG Yanbin. Multi-parameter modeling of orthotropic media[J]. Geophysical Prospecting for Petroleum, 2019, 58(6): 874-881. |
| [26] |
单俊臻, 吴国忱, 龚诚诚. HTI介质方位观测PP波反射系数一阶扰动近似[J]. 石油地球物理勘探, 2019, 54(2): 371-379. SHAN Junzhen, WU Guochen, GONG Chengcheng. First-order perturbation approximation of PP wave reflection coefficient for HTI medium[J]. Oil Geophysical Prospecting, 2019, 54(2): 371-379. |
| [27] |
秦海旭, 吴国忱, 刘争平. 裂缝单斜介质qP波正演模拟方法[J]. 石油地球物理勘探, 2015, 50(6): 1118-1126. QIN Haixu, WU Guochen, LIU Zhengping. qP wave forward modeling in fracture media with monoclinic symmetry[J]. Oil Geophysical Prospecting, 2015, 50(6): 1118-1126. |
| [28] |
李春鹏, 印兴耀, 张峰. HTI介质饱和流体特性和裂缝密度对方位反射系数的影响[J]. 石油物探, 2013, 52(1): 1-10. LI Chunpeng, YIN Xingyao, ZHANG Feng. Influence of HTI medium saturated fluid properties and fracture density on azimuthal reflectivity[J]. Geophysical Prospecting for Petroleum, 2013, 52(1): 1-10. |
| [29] |
Schoenberg M, Protázio J. "Zoeppritz" rationalized and generalized to anisotropy[J]. Journal of the Seismic Exploration, 1992, 1(2): 125-144. |
| [30] |
Zhou B, Greenhalgh S. On the computation of elastic wave group velocities for a general anisotropic me-dium[J]. Journal of Geophysics and Engineering, 2004, 1(3): 205-215. DOI:10.1088/1742-2132/1/3/005 |
| [31] |
Chen H.Anisotropic Effects upon Amplitude-vs-offset Response in Realistic Earth Models[D].University of Oklahoma Graduate College, 2000.
|
| [32] |
Schoenberg I, Helbig K. Orthorhombic media:mode-ling elastic wave behavior in a vertically fractured earth[J]. Geophysics, 1997, 62(5): 1954-1974. |



 芦俊, 北京市海淀区学院路29号中国地质大学(北京)地球物理与信息技术学院, 100083。Email:
芦俊, 北京市海淀区学院路29号中国地质大学(北京)地球物理与信息技术学院, 100083。Email: