② 中国石化石油工程地球物理有限公司胜利分公司, 山东东营 257000
② Shengli Branch of Sinopec Geophysical Corporation, Dongying, Shandong 257000, China
随着地震勘探技术的发展,各种成像技术不断涌现,如逆时偏移技术。但这些技术的成像质量很大程度上取决于初始速度模型的精度。全波形反演(FWI)是从记录的数据集中检索地下模型参数的一种有效方法。通过最优化算法不断更新介质模型参数,使模拟地震记录与实际观测记录间残差达到最小,从而得到与实际介质参数最接近的模型[1]。
与射线类反演方法相比,FWI充分利用地震波动力学和运动学信息,具有更高反演精度,但也存在过于依赖初始模型、多解性、计算量大等不足[2]。
为了规避FWI对初始模型的强依赖性,多种基于不同思路的算法被提出。如利用旅行时层析成像、偏移速度分析等其他方法构建更准确的初始速度模型[3]。近年来,在应用瞬时属性提高FWI初始速度模型精度方面也卓有成效。Bozda等[3]利用包络信息和瞬时相位信息辅助设计FWI初始速度模型。Luo等[4]、罗静蕊等[2, 5]剖析了地震包络反演对局部极小值的抑制特性;在利用时域声波FWI中的指数相位信息建立初始速度模型过程中,通过解决相位卷绕问题克服了局部极小问题;进而利用时域弹性波FWI中的瞬时相位信息构建FWI初始速度模型。迄今为止,瞬时频率属性还未被应用于时域FWI中。
在FWI中,深层信号弱,对目标函数的贡献较小,因此FWI难以得到精确的深层速度信息。为了取得较好的深层反演结果,亟待提高深层反演精度的新方法的提出。在实际地震记录上,任何时刻的瞬时频率是唯一存在的,瞬时频率的单调性有明显实用意义,如确定地震记录中不同反射层的地震波到达时间、划分不同的反射层段(尤其能精确划分深层速度)[1]。因此,本文将瞬时频率属性与FWI相结合,提出一种全新的时间域声波FWI方法[6],并加入梯度衰减因子以提高深层反演效果(该方法简称为FRE-FWI)。文中首先推导出时间域基于一阶近似瞬时频率的目标函数和伴随震源项方程,采用梯度阻尼因子进行剥离分层以防止深层与浅层相互干涉。通过模型和实际资料测试,验证了该方法在提高深层速度模型的精度方面的可行性和有效性。
1 FRE-FWI原理FWI通过极小化观测数据和模拟数据的误差获取地下模型参数。其伴随方程和梯度公式可通过伴随方法得到。建立如下极小化目标泛函[1]
| $ {\rm{min}}E(v) = \frac{1}{2}\int_0^T {{{\left\| {{d_{{\rm{cal}}}} - {d_{{\rm{obs}}}}} \right\|}^2}} {\rm{d}}t $ | (1) |
式中:T为记录时长;v为介质传播速度;dcal和dobs分别为模拟数据和观测数据。用数据残差替换原来的震源项,得到相应的伴随方程震源项为[2]
| $ B = \frac{{\partial E(v)}}{{\partial v}} $ | (2) |
在FWI初始速度建模中,目标函数的类型只影响伴随方程的震源项,故只需更新式(1)和式(2)即可。
一般情况下,可从解析信号中获得时域瞬时相位。没有负频率分量的信号被称为解析信号
| $ \tilde f(t) = f(t) + {\rm{iH}}[f(t)] $ | (3) |
也可写成以下形式
| $ \tilde f(t) = A(t){{\rm{e}}^{{\rm{i}}\phi (t)}} $ | (4) |
式中:A(t)为瞬时振幅或包络;ϕ(t)为瞬时相位。
解析信号不仅包含瞬时振幅信息,还包含与波传播的运动学特性相关的瞬时相位信息,可应用于反演中。通常,以下式获得瞬时相位
| $ \phi (t) = {\rm{arctan}}\frac{{{\rm{H}}[f(t)]}}{{f(t)}} $ | (5) |
然而,这种计算方式将引入相位展开问题。除非设计了较准确的初始速度模型,否则FWI中的相位缠绕问题会产生一个与局部最小值相对应的结果,通常远离真实解,特别是在深层。因此,Luo等[4]开发了一种基于时空域非展开相位的反演算法,并利用指数阻尼减小反射的非线性。
在地震勘探中,当多个事件相互干扰时,相位图中会形成残留。因此,相位图中的复杂数据值在干扰位置接近于零。换言之,相位信息中的残差数量与波场(或地下速度模型)的复杂性有关。若只有一个事件且没有干扰,则相位图没有残留。由于使用了强指数阻尼抑制了后到达事件,消除了多个事件(或波场的复杂性)之间的干扰,所以相位图中的残留物即使在高频下也会被消除。Luo等[4]使用(强)指数阻尼消除波场的复杂性,即为相位导数的反演提供了一种无低频信息的长波长结构;最后对未展开相位进行反演,利用反传播算法计算梯度,除新的残差矢量外,与传统FWI相似。所用强指数阻尼e-at算子中,a为表征阻尼强弱的参数。为了避免相位展开,并以简单方式实现反演,选择使用指数相位,即
| $ {{\rm{e}}^{{\rm{i}}\phi (t)}} = \frac{{f(t) + {\rm{iH}}[f(t)]}}{{\sqrt {{f^2}(t) + {{\{ {\rm{H}}[f(t)]\} }^2}} }} $ | (6) |
在这种形式中,从分析信号中剥离振幅信息,且仅留下相位信息。因相位ϕ(t)可取连续的值,则eiϕ(t)也可取连续值,因此不需以式(5)做相位展开,就可消除相位跳变,从而避免了相位展开过程。
加入强指数阻尼后,有
| $ {{\rm{e}}^{{\rm{i}}\phi (t)}}{{\rm{e}}^{ - at}} = \frac{{f(t) + {\rm{iH}}[f(t)]}}{{\sqrt {{f^2}(t) + {{\{ {\rm{H}}[f(t)]\} }^2}} }} \cdot {{\rm{e}}^{ - at}} $ | (7) |
即目标函数[4]为
| $ \sigma (m) = \sum\limits_{sr} {\int_0^T | } {\rm{e}}_{{\rm{cal}}}^{{\rm{i}}\phi (t)}{{\rm{e}}^{ - at}} - {\rm{e}}_{{\rm{obs}}}^{{\rm{i}}\phi (t)}{{\rm{e}}^{ - at}}{|^2}{\rm{d}}t $ | (8) |
直观地讲,瞬时频率为相位的微分,但在常规处理流程中,没有任何限制条件的时间信号计算出的瞬时频率可能是不正确的结果[7]。只有对于平均值为零的局部对称信号而言,前述瞬时频率才具有物理意义。虽然通过HHT算法[8]能正确求取瞬时频率,但该方法计算量极大。通过调研了解到当瞬时频率为一阶时间函数(即为常数)时可使用傅里叶变换做信号分析[9-11],在此条件下信号为满足平均值为零的局部对称信号,即转换为地震波复数道[12],同时计算量也会相对较小。因此,由指数相位得到的瞬时频率的一阶近似表示为
| $ {\rm{ Im}} ({{\rm{e}}^{{\rm{i}}\omega }}) \approx {\rm{ Im }}\left( {{{\rm{e}}^{\frac{{{\rm{i}}{\phi _{j + \Delta T}} - {\rm{i}}{\phi _j}}}{{{\Delta ^T}}}}}} \right) \approx {\rm{Im}} \left( {\frac{{{{\rm{e}}^{{\rm{i}}{\phi _{j + \Delta T}}}}}}{{{{\rm{e}}^{{\rm{i}}{\phi _j}}}}}} \right) $ | (9) |
式中:ω为角频率;Im(·)为求虚部;j为某一时刻;ΔT为时间采样间隔(定值),对反演计算无影响。
为了解一阶近似瞬时频率属性的作用,对层状模型正演得到地震记录[13]及其一阶近似瞬时频率属性。模型计算区域为2000m×1000m,空间间隔为10m。观测系统为:在地表距离边界1000m处激发,地表检波点(共200个)间距为10m。计算参数为:纵波源是主频为10Hz的雷克子波,时间采样间隔为2ms,总采样时长为1.024s。本次使用有限差分法做正演[14-15],以完美匹配层作为边界条件[16]。
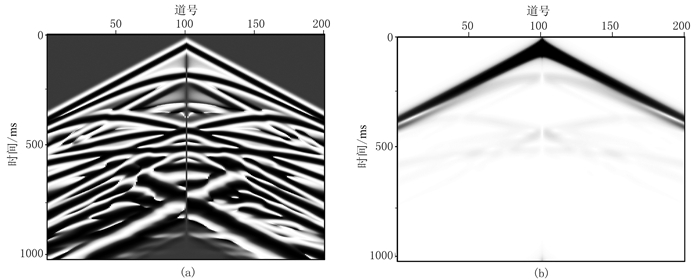
从正演结果可知,一阶近似瞬时频率属性(图 1a)在提取深层相对较弱信号的同时保持了地震记录的连续性,但也可看出该属性的频带高于瞬时振幅属性[17](图 1b)。
|
图 1 层状模型地震记录的一阶近似瞬时频率属性(a)和瞬时振幅属性(b) |
图 2为10Hz时层状模型单道提取一阶近似瞬时频率属性[18-19]、瞬时振幅属性与地震记录频谱对比图。可见瞬时振幅属性(蓝虚线)的频带与一阶近似瞬时频率属性(红线)的频带相近,一阶近似瞬时频率属性和瞬时振幅属性都能提供地震记录(黑线)中所不具有的低频成分。

|
图 2 10Hz时层状模型单道提取瞬时振幅属性、一阶近似瞬时频率属性与地震记录频谱对比图 |
综上所述,可得出一阶近似瞬时频率属性能为FWI提供低频成分,提取深层弱信号,实现更精确的深层速度恢复。
根据一阶近似瞬时频率属性的特性,更新残差公式为
| $ E(v) = \sum\limits_{sr} {\int_0^T {{{\left\| {{\rm{e}}_{{\rm{cal}}}^{{\rm{i}}\omega }{{\rm{e}}^{ - at}} - {\rm{e}}_{{\rm{obs}}}^{{\rm{i}}\omega }{{\rm{e}}^{ - at}}} \right\|}^2}} } {\rm{d}}t $ | (10) |
该式即为基于一阶近似瞬时频率的FWI初始速度建模目标函数。
将式(10)展开后取虚部,可得具体公式
| $ \begin{array}{l} E\left( v \right) = \sum\limits_{sr} {\mathop \smallint \nolimits_0^T \left[ {\frac{{{d_j}{\rm{H}}({d_{j + \Delta T}}) - {d_{j + \Delta T}}{\rm{H}}({d_j})}}{{A({d_{j + \Delta T}})A({d_j})}} - } \right.} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{\kern 1pt} \frac{{{u_j}{\rm{H}}({u_{j + \Delta T}}) - {u_{j + \Delta T}}{\rm{H}}({u_j})}}{{A({u_{j + \Delta T}})A({u_j})}}} \right]{\rm{d}}t\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \sum\limits_{sr} {\int_0^T {{F^2}} } {\rm{d}}t\quad j = 0, \cdots , T/\Delta T \end{array} $ | (11) |
式中:d、u分别为模拟地震记录和原始地震记录;H(d)、H(u)分别为其希尔伯特变换;A(d)、A(u)分别为模拟地震记录和原始地震记录的包络。其中
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{F}} = \frac{{{d_j}{\rm{H}}({d_{j + \Delta T}}) - {d_{j + \Delta T}}{\rm{H}}({d_j})}}{{A({d_{j + \Delta T}})A({d_j})}} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{u_j}{\rm{H}}({u_{j + \Delta T}}) - {u_{j + \Delta T}}{\rm{H}}({u_j})}}{{A({u_{j + \Delta T}})A({u_j})}}} \end{array} $ | (12) |
每道地震记录信号可看成由采样点相连而成的折线段所近似的离散曲线,则每两个采样点之间的直线段上前一时刻地震记录对时间的偏导数值与下一时刻地震记录对时间的偏导数值相近,于是可假设每两个采样点之间的直线段上前一时刻地震记录对时间的偏导数值与下一时刻地震记录对时间的偏导数值相等,即每个直线段边界处的值对时间的偏导数相等,即
| $ \begin{array}{l} \frac{{\partial E(v)}}{{\partial m}} = \sum\limits_{sr} {\int_0^T \mathit{\boldsymbol{F}} } \left\{ {\frac{{{\rm{H}}({d_{j + \Delta T}}) - {\rm{H}}({d_j})}}{{A({d_{j + \Delta T}})A({d_j})}} - \frac{{d_j^2{\rm{H}}({d_{j + \Delta T}}) - {d_{j + \Delta T}}{d_j}{\rm{H}}({d_j})}}{{A({d_{j + \Delta T}}){A^3}({d_j})}} - \frac{{{d_{j + \Delta T}}{d_j}{\rm{H}}({d_{j + \Delta T}}) - d_{j + \Delta T}^2{\rm{H}}({d_j})}}{{A({d_{j + \Delta T}}){A^3}({d_j})}} + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{\rm{H}}\left[ {\frac{{{d_{j + \Delta T}} + {d_j}}}{{A({d_{j + \Delta T}})A({d_j})}} + \frac{{{d_j}{\rm{H}}({d_{j + \Delta T}}){\rm{H}}({d_j}) - {d_{j + \Delta T}}{{\rm{H}}^2}({d_j})}}{{A({d_{j + \Delta T}}){A^3}({d_j})}} + \frac{{{d_j}{{\rm{H}}^2}({d_{j + \Delta T}}){\rm{H}}({d_j}) - {d_{j + \Delta T}}{\rm{H}}({d_j}){\rm{H}}({d_{j + \Delta T}})}}{{A({d_{j + \Delta T}}){A^3}({d_j})}}} \right]} \right\}{\rm{d}}t \end{array} $ | (13) |
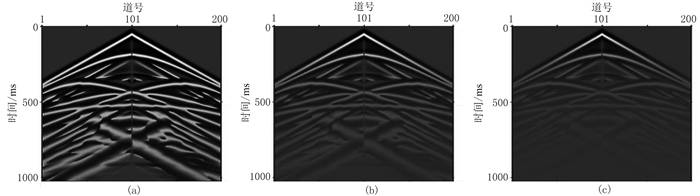
引入梯度衰减因子也是提高深层反演效果、防止深浅层间互相干涉的有效方法。本文沿用e-at算子[21],将其定义为梯度衰减因子,显然常量a为衰减系数。梯度衰减因子[22]可使地震信号随时间衰减,因此通过调节衰减系数a控制反演层位并做逐层反演,避免深、浅层同时反演带来的层间干涉,以提高深层反演效果。图 3为衰减系数a分别为1、3、5时一阶近似瞬时指数频率属性,可知衰减系数a越大,对深层的数值压制越强,由此达到提高深层反演效果,防止深、浅层之间互相干涉的目的。
|
图 3 衰减系数a=1(a)、a=3(b)、a=5(c)时一阶近似瞬时指数频率属性 |
带梯度衰减因子的基于一阶近似瞬时频率的FWI初始速度建模目标函数为
| $ \begin{array}{l} \mathit{\boldsymbol{ }}E\mathit{\boldsymbol{ }}(\mathit{\boldsymbol{ }}v\mathit{\boldsymbol{ }})\mathit{\boldsymbol{ }} = \sum\limits_{sr} {\mathop \smallint \nolimits_0^T \left[ {\frac{{{d_j}{\rm{H}}({d_{j + \Delta T}}) - {d_{j + \Delta T}}{\rm{H}}({d_j})}}{{A({d_{j + \Delta T}})A({d_j})}} - } \right.} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\frac{{{u_j}{\rm{H}}({u_{j + \Delta T}}) - {u_{j + \Delta T}}{\rm{H}}({u_j})}}{{A({u_{j + \Delta T}})A({u_j})}}} \right]{\rm{d}}t\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \sum\limits_{sr} {\int_0^T {{\mathit{\boldsymbol{F}}^2}} } {{\rm{e}}^{ - 2at}}{\rm{d}}t \end{array} $ | (14) |
由该式进一步可推得带梯度衰减因子的基于一阶近似瞬时频率的FWI梯度公式
| $ \begin{array}{l} \frac{{\partial E(v)}}{{\partial m}} = \sum\limits_{sr} {\int_0^T \mathit{\boldsymbol{F}} } {{\rm{e}}^{ - 2at}}\left\{ {\frac{{{\rm{H}}({d_{j + \Delta T}}) - {\rm{H}}({d_j})}}{{A({d_{j + \Delta T}})A({d_j})}}} \right. - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{d_j^2{\rm{H}}({d_{j + \Delta T}}) - {d_{j + \Delta T}}{d_j}{\rm{H}}({d_j})}}{{A({d_{j + \Delta T}}){A^3}({d_j})}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{d_{j + \Delta T}}{d_j}{\rm{H}}({d_{j + \Delta T}}) - d_{j + \Delta T}^2{\rm{H}}({d_j})}}{{A({d_{j + \Delta T}}){A^3}({d_j})}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{H}}\left[ {\frac{{{d_{j + \Delta T}} + {d_j}}}{{A({d_{j + \Delta T}})A({d_j})}} + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{{d_j}{\rm{H}}({d_{j + \Delta T}}){\rm{H}}({d_j}) - {d_{j + \Delta T}}{{\rm{H}}^2}({d_j})}}{{A({d_{j + \Delta T}}){A^3}({d_j})}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\left. {\frac{{{d_j}{{\rm{H}}^2}({d_{j + \Delta T}}){\rm{H}}({d_j}) - {d_{j + \Delta T}}{\rm{H}}({d_j}){\rm{H}}({d_{j + \Delta T}})}}{{A({d_{j + \Delta T}}){A^3}({d_j})}}} \right]} \right\}{\rm{d}}t \end{array} $ | (15) |
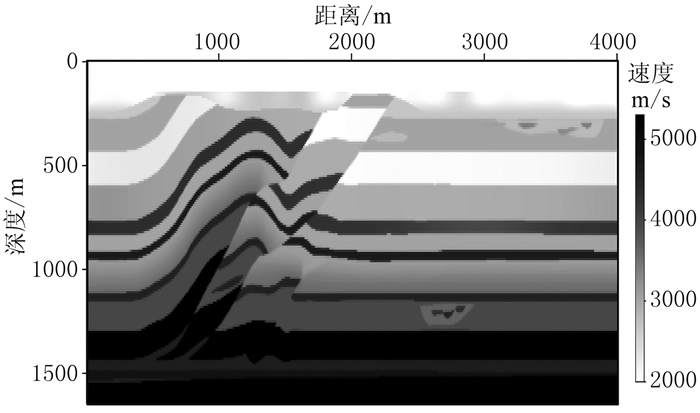
针对推覆体模型(图 4)检验FRE-FWI方法效果。模型计算区域为4000m×1650m,空间间隔为10m。观测系统设计:地表炮点间距为120m,总共激发32炮,检波点间距为10m,共计400个。计算参数为:震源采用主频为20Hz的雷克子波,同时切掉5Hz以下的频率成分,时间采样间隔为1ms,总采样时长为2.048s。
|
图 4 推覆体模型 |
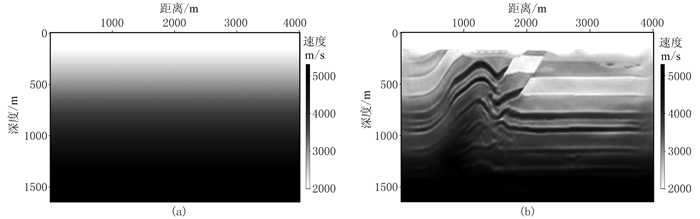
图 5a为初始速度模型,即图 4的一维线性深度模型。应用FRE-FWI方法迭代30次的反演结果如图 5b所示,对该反演结果应用常规FWI方法再迭代30次,得到图 6a。图 6b是对图 5a预设模型直接应用常规FWI方法迭代60次的反演结果。对比可见:仅用常规FWI方法的反演结果(图 6b)因初始速度模型较差,明显不如图 6a;因深层信号对常规FWI的贡献较低,深层效果更差,但FRE-FWI方法提取了深层信息后在初始模型较差时反演效果仍较好,如图 6a深层速度得到较好还原。
|
图 5 推覆体反演初始速度模型(a)及其应用FRE-FWI方法迭代30次的反演结果(b) |
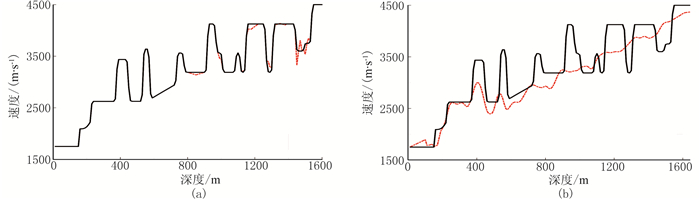
将上述针对推覆体模型得到的FRE-FWI、常规FWI方法反演结果(红线)与真实速度模型单道(黑线)进行对比,可知FRE-FWI方法(图 7a)相对常规FWI方法(图 7b)对浅层和深层速度还原更加精确。同时证明了基于瞬时频率属性的时间域初始速度建模方法可有效提高FWI的深层速度反演精度。
|
图 7 推覆体模型FRE-FWI方法(a)、常规FWI方法(b)反演结果(红线)与真实速度模型(黑线)单道对比 |
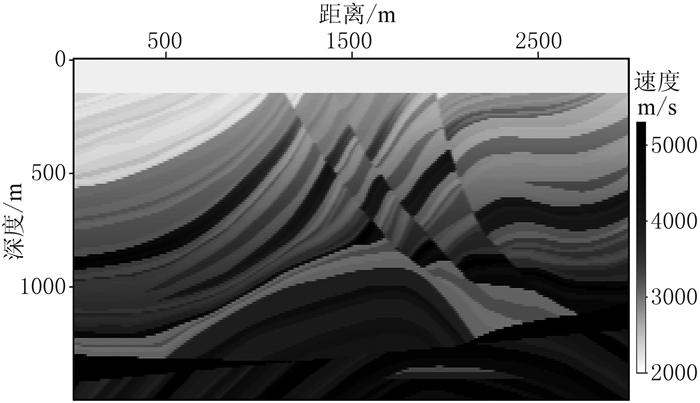
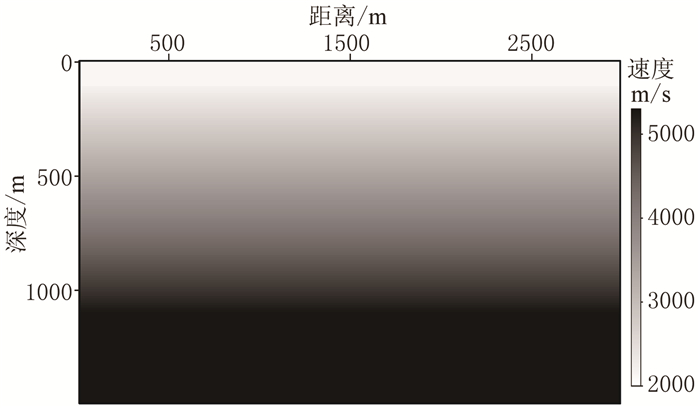
图 8为Marmousi速度模型的纵波速度。图 9为初始速度模型,即图 8的一维线性深度模型。
|
图 8 Marmousi纵波速度模型 |
|
图 9 Marmousi初始速度模型 |
模型计算区域有298×150个网格,空间间隔为10m。观测系统为:地表炮点间隔为90m,总共激发32炮,检波点间隔为10m,共布设298个。震源子波、下截频率、时间采样间隔及总采样时长同上述推覆体模型。
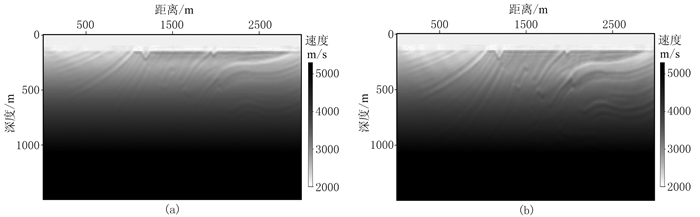
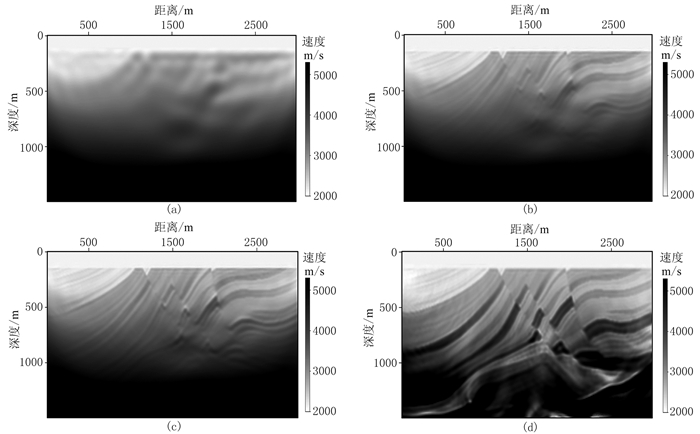
图 10a~图 10c分别为梯度阻尼因子a=5、3、0时FRE-FWI方法迭代10次的反演结果,图 10d则是对图 10c应用常规FWI再迭代30次的反演结果。图 11为梯度阻尼因子a=5、3时常规FWI方法迭代10次反演结果;图 12为梯度阻尼因子a=0时常规FWI方法迭代40次反演结果。图 13a、图 13b为梯度阻尼因子a=5、3时以包络FWI方法迭代10次的结果图;图 13c为a=0时以包络FWI方法迭代10次的FWI结果图;图 13d为以包络FWI方法所得反演结果为初始模型通过常规FWI方法迭代30次反演结果。对比时保持迭代次数一致,且环境变量一致。

|
图 10 Marmousi模型FRE-FWI方法的反演结果 (a)、(b)、(c)对应a=5、3、0时FRE-FWI方法迭代10次;(d)以a=0时FRE-FWI方法反演结果为初始模型再用FWI迭代30次 |
|
图 11 Marmousi模型在a=5(a)和a=3(b)时常规FWI方法迭代10次的反演结果 |

|
图 12 Marmousi模型在a=0时常规FWI方法迭代40次的反演结果 |
|
图 13 Marmousi模型包络FWI方法的反演结果 (a)、(b)对应a=5、3时包络FWI方法迭代10次;(c)a=0时包络FWI方法迭代10次的FWI;(d)以包络FWI方法得出的反演结果为初始模型再利用常规FWI方法迭代30次 |
对比图 10~图 13可见,其中包络FWI方法和FRE-FWI方法的成像效果优于常规FWI方法,与推覆体模型类似,深层信号对常规FWI的贡献较低,深层效果较差,但FRE-FWI方法提取了深层信息后在初始模型较差时反演效果依然较好,而包络FWI方法浅层效果优于FRE-FWI方法,但FRE-FWI方法深层效果更佳,证明基于瞬时频率属性的时间域初始速度建模方法可有效提高FWI的深层速度收敛精度。
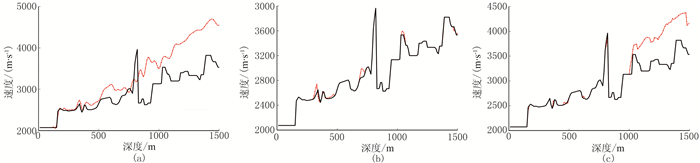
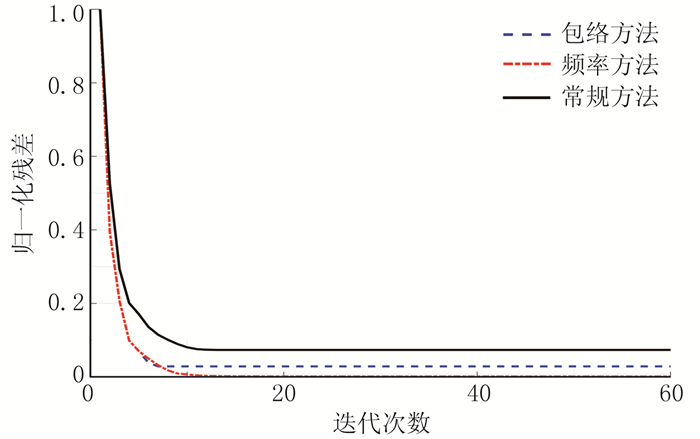
从常规FWI(图 14a)、FRE-FWI(图 14b)、包络FWI(图 14c)方法反演结果与真实速度模型的单道对比图可见,FRE-FWI方法对深层速度的反演效果更好,但浅层效果相比包络方法还有一定差距。从这三种方法的反演结果收敛曲线对比(图 15)可见,FRE-FWI相对常规FWI的残差下降更快,与包络FWI方法(蓝线)接近。
|
图 14 常规FWI(a)、FRE-FWI(b)、包络FWI(c)结果(红线)与真实速度模型(黑线)单道对比 |
|
图 15 常规FWI、包络FWI和FRE-FWI方法的残差下降率对比 |
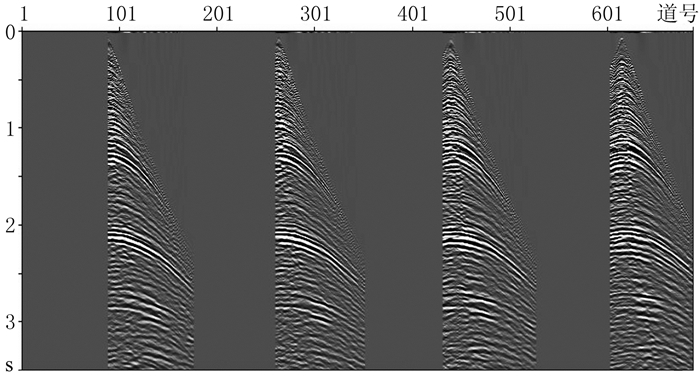
选取M油田实际资料(图 16):炮线长度为6890m,炮间距为176m,共有42炮;空间采样间隔为10m,每道3500个采样点7168道;时间采样间隔为1ms。截取其中一部分(6500m×2000m)进行测试。
|
图 16 M油田实际资料炮集 |
在梯度阻尼因子a=5、3、0时,采用FRE-FWI方法迭代10次进行反演(图 17a~图 17c),然后以a=0时FRE-FWI方法反演结果为初始模型,采用常规FWI方法再迭代30次(图 17d),并以常规FWI方法同时采取与上文相同的层剥离方法总计迭代60次(图 17e)。对比反演结果可知,FRE-FWI方法相对常规FWI方法对地下层状介质从浅到深的反演效果都更好。

|
图 17 M油田实际资料反演结果 (a)、(b)、(c)对应a=5、3、0时FRE-FWI方法迭代10次;(d)以a=0时FRE-FWI方法反演结果为初始模型再迭代30次的FWI;(e)以常规FWI方法同时进行层剥离迭代60次 |
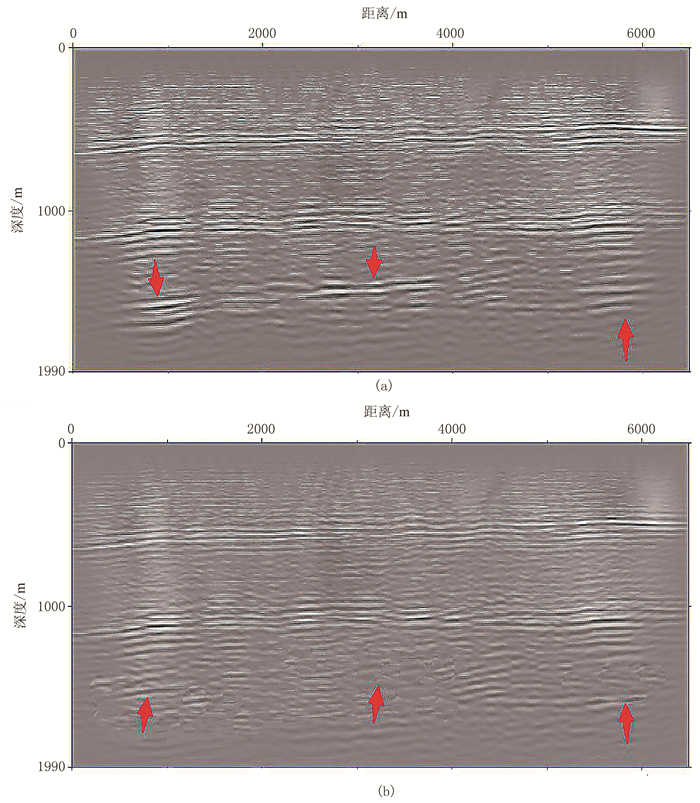
对比用FRE-FWI方法(图 18a)和常规FWI方法(图 18b)反演结果进行逆时偏移所得剖面可知,FRE-FWI方法提供的速度场所得逆时偏移剖面的深层效果比对常规FWI方法更好,剖面上地层更细致、清晰。
|
图 18 M油田实际资料FRE-FWI方法(a)和常规FWI方法(b)反演结果进行逆时偏移所得剖面 |
本文提出一种提高FWI深部速度收敛效果的初始速度建模新方法。首先推导出时间域基于一阶近似瞬时频率的目标函数和伴随震源项方程,并采用梯度阻尼因子进行层剥离分层以防止深层与浅层相互干涉,为反演提供较精确的深层速度,模型和实际资料测试检验了方法的可行性和有效性。
虽然所提方法对地下深部地层有较好的还原能力,但其求取瞬时频率的方法欠精确,假设导致的数学问题尚待解决,且对浅层速度还原还存在不足,因此在计算瞬时频率的方法、浅层速度还原等方面还有待更深入探究。
感谢中国石油大学(华东)地球科学与技术学院谷丙洛等老师的无私教诲,感谢该学院黄少华等同学的热情支持,感谢中国石化胜利物探研究院徐梅高工的悉心指导。
| [1] |
任志明.声波和弹性波波动方程有限差分正反演方法研究[D].北京: 中国石油大学(北京), 2016. REN Zhiming.Research on Finite-Difference Mode-ling and Inversion Methods Based on Acoustic and Elastic Wave Equations[D].China University of Petroleum(Beijing), Beijing, 2016. |
| [2] |
罗静蕊, 吴如山, 高静怀. 地震包络反演对局部极小值的抑制特性[J]. 地球物理学报, 2016, 59(7): 2510-2518. LUO Jingrui, WU Rushan, GAO Jinghuai. Local minima reduction of seismic envelope inversion[J]. Chinese Journal of Geophysics, 2016, 59(7): 2510-2518. |
| [3] |
Bozda E, Trampert J, Tromp J. Misfit functions for full waveform inversion based on instantaneous phase and envelope measurements[J]. Geophysical Journal International, 2011, 185(2): 845-870. DOI:10.1111/j.1365-246X.2011.04970.x |
| [4] |
Luo J R, Wu R S and Gao F C.Time domain full waveform inversion using instantaneous phase with damping[C].SEG Technical Program Expended Abstracts, 2018, 37: 1472-1476.
|
| [5] |
罗静蕊, 曹玉玲. 应用包络反演为弹性全波形反演构建初始模型[J]. 油气地球物理, 2017, 15(2): 60-63. LUO Jingrui, CAO Yuling. Applying envelope inversion to build initial model for elastic full waveform inversion[J]. Pretroleum Geophysics, 2017, 15(2): 60-63. |
| [6] |
董良国, 迟本鑫, 陶纪霞, 等. 声波全波形反演目标函数性态[J]. 地球物理学报, 2013, 56(10): 3445-3460. DONG Liangguo, CHI Benxin, TAO Jixia, et al. Ob-jective function behavior in acoustic full-waveform inversion[J]. Chinese Journal of Geophysics, 2013, 56(10): 3445-3460. |
| [7] |
张海勇. 瞬时频率的一种估计方法[J]. 系统工程与电子技术, 2002, 20(9): 5-6. ZHANG Haiyong. A method for estimating instantaneous frequency[J]. Systems Engineering and Electronics, 2002, 20(9): 5-6. |
| [8] |
钟佑明, 秦树人, 汤宝平. Hilbert-Huang变换中的理论研究[J]. 振动与冲击, 2002, 12(4): 15-19. ZHONG Youming, QIN Shuren, TANG Baoping. Theoretical research on Hilbert-Huang transformation[J]. Journal of Vibration and Shock, 2002, 12(4): 15-19. |
| [9] |
Kosloff D, Baysal E. Forward modeling by a Fourier method[J]. Geophysics, 1982, 47(10): 1402-1412. DOI:10.1190/1.1441288 |
| [10] |
Reshef M, Kosloff D, Edwards M, et al. Three-dimension acoustic modeling by the Fourier method[J]. Geophysics, 1988, 53(9): 1175-1183. DOI:10.1190/1.1442557 |
| [11] |
程乾生. 希尔伯特变换与信号的包络、瞬时相位和瞬时频率[J]. 石油地球物理勘探, 1979, 14(3): 1-14. CHENG Qiansheng. Hilbert transform and envelope, instantaneous phase and instantaneous frequency of signals[J]. Oil Geophysical Prospecting, 1979, 14(3): 1-14. |
| [12] |
贺振华. 地震波复数道分析的计算方法[J]. 石油物探, 1980, 19(4): 64-80. HE Zhenhua. Calculation method of seismic complex trace analysis[J]. Geophysical Prospecting for Petroleum, 1980, 19(4): 64-80. |
| [13] |
Furumura T, Kennett B, Takenaka H. Parallel 3-D pseudospectral simulation of seismic wave propaga-tion[J]. Geophysics, 1998, 63(1): 279-288. DOI:10.1190/1.1444322 |
| [14] |
Bartolo L D, Dors C, Mansur W J, et al. A new family of finite-difference schemes to solve the heterogeneous acoustic wave equation[J]. Geophysics, 2012, 77(5): T187-T199. DOI:10.1190/geo2011-0345.1 |
| [15] |
Fornberg B. The pseudospectral method:Comparisons with finite differences for the elastic wave equation[J]. Geophysics, 1987, 52(4): 483-501. DOI:10.1190/1.1442319 |
| [16] |
成景旺, 毛宁波, 吕晓春, 等. 非分裂完全匹配层边界存储时间域全波形反演[J]. 石油地球物理勘探, 2018, 53(4): 754-764. CHENG Jingwang, MAO Ningbo, LYU Xiaochun, et al. Time domain full waveform inversion with CFS-NPML boundary storage[J]. Oil Geophysical Prospecting, 2018, 53(4): 754-764. |
| [17] |
Luo J R, Wu R S. Seismic envelope inversion:reduction of local minima and noise resistance[J]. Geophy-sical Prospecting, 2015, 63(3): 597-614. DOI:10.1111/1365-2478.12208 |
| [18] |
Pratt R G. Frequency-domain elastic wave modeling by finite differences:A tool for crosshole seismic imaging[J]. Geophysics, 1990, 55(5): 626-632. DOI:10.1190/1.1442874 |
| [19] |
任德玉. 地震记录与瞬时频率初探[J]. 石油地球物理勘探, 1980, 15(1): 7-21. REN Deyu. Preliminary reseacrch on seismic record and instantaneous frequency[J]. Oil Geophysical Prospecting, 1980, 15(1): 7-21. |
| [20] |
Wu R S, Luo J R, Wu B Y. Seismic envelope inversion and modulation signal model[J]. Geophysics, 2014, 79(10): WA13-WA24. |
| [21] |
Alkhalifah T. Scattering-angle based filtering of the waveform inversion gradients[J]. Geophysical Journal International, 2015, 200: 363-373. |
| [22] |
史才旺, 何兵寿. 基于主成分分析和梯度重构的全波形反演[J]. 石油地球物理勘探, 2018, 53(1): 95-104. SHI Caiwang, HE Bingshou. Full waveform inversion based on principal component analysis and gradient reconstruction[J]. Oil Geophysical Prospecting, 2018, 53(1): 95-104. |



 任志明, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
任志明, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
