② 中国石油化工股份有限公司科技部油田处, 北京 100728
② Sinopec Science & Technology Department, Beijing 100728, China
实际地球介质复杂多样,传统的完全弹性介质理论受到严峻的挑战,越来越需要基于黏弹性介质理论研究实际介质中地震波的传播特征和衰减规律[1-2]。前人的研究表明,即使完成球面扩散和界面因素造成的衰减补偿之后,地震波在深层介质中传播的能量仍因介质的黏滞损耗远弱于浅层介质中的波场能量[3]。中国西部黄土塬区、沙漠覆盖区油气资源丰富,近地表介质疏松多孔、弹性差,地震波表现为强衰减、高频散、低分辨率等特征[4-5];若进一步考虑浅表介质孔隙、裂隙发育,孔隙空间中的流体多表现黏滞性时就需要考虑介质的强吸收衰减性。
对于地震波在实际介质传播中的衰减特征,目前最主要的研究理论包括黏弹性介质理论和孔隙双相介质理论[6]。黏弹性介质理论的发展始于Stokes方程的建立[7],之后基于弹性滞后和质点内摩擦等衰减机制,构建出多种符合实际的黏弹性介质模型[8]。例如线性流变模型、达朗贝尔模型以及常Q介质模型等都是在本构方程或运动方程中引入一定的非弹性衰减机理,进而使人们对黏滞波场特征和地震波非弹性衰减有更真实的认识[9-12]。描述孔隙介质双相性的重要理论包括宏观Biot理论[13]、微观喷射流理论[14]和BISQ理论[15],前两种理论分别是根据流体的宏观流动和微观喷射,研究介质的孔隙结构和流体效应对地震波传播衰减的影响,而最后一种理论是它们的有机统一。
杜启振等[16]发现,在地震频率范围内,地震波的衰减和频散特征的准确描述不能只考虑黏弹性介质理论和孔隙双相介质理论中的一种,还需要应用黏弹性模型刻画岩石骨架的性质。随后,Nie等[17]和凌云等[18]分别将Kelvin-Voigt体和标准Zener体的本构关系引入到BISQ模型中,建立了黏弹孔隙介质模型,研究地震波在黏弹孔隙介质中的衰减规律。强衰减模型是谢佩瑜等[19]在达朗贝尔模型的基础上,通过引入与孔隙度和渗透率等参数相关的黏滞项,并利用黏弹性拉梅系数替换弹性拉梅系数的方式建立的一种衰减介质模型。虽然强衰减模型是以运动方程描述介质的黏滞衰减特征,但是它能全面地考虑孔隙度、流体黏度和介质黏弹性等因素对地震波衰减和频散的影响。谢佩瑜等[19]还根据实际地震数据,验证了强衰减模型相比于带耗散的弹性Biot模型、BISQ模型以及黏弹性BISQ模型能更精确表征近地表介质衰减特征。
考虑到强衰减模型波动方程中的黏弹性拉梅系数是与频率相关的复数型参数,时间域数值算法显然不能用于强衰减模型的正演模拟。而且实际地震波是由多个单频简谐波组成的复合波,即地震波的传播与频率相关,不同频率成分具有不同的波场特征。若要实现强衰减模型介质的正演模拟,分析全频带范围内地震波的传播特征,需要采用频率—空间域数值算法。
频率—空间域数值模拟最先由Lysmer等[20]提出,之后相继出现5点、9点和25点有限差分算法。各种频率域正演方法都是对每一频率下所有空间网格整体求方程组,其计算误差分配到各网格点上,而且各单频切片的计算互相独立,因此能实现数值的并行计算,并不存在累计误差。随着加权平均思想和高精度模拟的深入研究,Min等[21]提出了优化的25点频率—空间域有限差分算法,与其他方法相比,该算法精度高、适用范围广,即只要满足每个横波波长达3.3个网格就能保证数值误差低于1%。有学者采用优化的25点有限差分法实现了黏弹各向异性介质和孔隙双相介质等的波场模拟,取得了不错的效果[22-25]。
在前人研究的基础上,本文将优化的25点有限差分法应用到强衰减模型波动方程的数值计算,研究强衰减模型介质中地震波的传播特征,以及孔隙度、流体黏度和介质黏弹性等因素的衰减机制。
1 强衰减介质模型 1.1 波动方程强衰减模型是一种综合性的黏弹性介质模型,不仅包括介质中流体流动引起的耗散,还包括介质自身的黏弹性所引起的耗散,其波动方程为
| $ \rho \mathit{\boldsymbol{\ddot u}} + \tilde \eta \mathit{\boldsymbol{\dot u}} = {\mu ^*}{\nabla ^2}\mathit{\boldsymbol{u}} + ({\lambda ^*} + {\mu ^*})\nabla (\nabla \cdot \mathit{\boldsymbol{u}}) $ | (1) |
式中:ρ为介质密度;u为位移向量;
| $ \tilde \eta = \eta {\phi ^2}/\kappa $ | (2) |
λ*、μ*是与频率相关的黏弹性拉梅系数,其具体表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {{\lambda ^*} = {\lambda ^\prime } + {\rm{i}}{\lambda ^{\prime \prime }}}\\ {{\lambda ^\prime } = {\lambda _0}\left( {1 + \frac{{{\rm{tan}}\gamma }}{\pi }{\rm{ln}}\frac{\omega }{{{\omega _0}}}} \right)}\\ {{\lambda ^{\prime \prime }} = {\lambda ^\prime }{\rm{tan}}\gamma } \end{array}} \right. $ | (3) |
| $ \left\{ {\begin{array}{*{20}{l}} {{\mu ^*} = {\mu ^\prime } + {\rm{i}}{\mu ^{\prime \prime }}}\\ {{\mu ^\prime } = {\mu _0}\left( {1 + \frac{{{\rm{tan}}\gamma }}{\pi }{\rm{ln}}\frac{\omega }{{{\omega _0}}}} \right)}\\ {{\mu ^{\prime \prime }} = {\mu ^\prime }{\rm{tan}}\gamma } \end{array}} \right. $ | (4) |
式中:λ0、μ0是弹性拉梅系数;ω0是基准圆频率;tanγ是介质的黏弹性参数,Yang等[26]给出了随频率线性变化的一般表达式
| $ {\rm{tan}}\gamma = \frac{{{\rm{tan}}{\gamma _2} - {\rm{tan}}{\gamma _1}}}{{{\omega _2} - {\omega _1}}}(\omega - {\omega _1}) + {\rm{tan}}{\gamma _1} $ | (5) |
其中:tanγ1、tanγ2是最低圆频率ω1和最高圆频率ω2对应的黏弹性参数。
1.2 地震波的衰减函数和频散函数振幅函数和相位函数是波动方程通解中的重要组成,可通过复波数确定,并能用于介质品质因子和等相位面速度的定义。为了研究强衰减模型介质中地震波的衰减和频散特征,谢佩瑜等[19]对波动方程(式(1))做纵、横波分离和傅里叶变换,分别得到纵波和横波的频散方程。由频散方程求解地震波的复波数,并根据Dvorkin等[15]的逆品质因子和相速度的计算公式,得出强衰减模型的逆品质因子和相速度
| $ \left\{ \begin{array}{l} Q_{\rm{P}}^{ - 1} = \frac{{2 {\rm{Im}} \left[ {\sqrt {\left( {1 + \frac{{{\rm{i}}\tilde \eta }}{{\rho \omega }}} \right)\frac{\rho }{{{\lambda ^*} + 2{\mu ^*}}}} } \right]}}{{ {\rm{Re}} \left[ {\sqrt {\left( {1 + \frac{{{\rm{i}}\tilde \eta }}{{\rho \omega }}} \right)\frac{\rho }{{{\lambda ^*} + 2{\mu ^*}}}} } \right]}}\\ {V_{\rm{P}}} = \frac{1}{{ {\rm{Re}} \left[ {\sqrt {\left( {1 + \frac{{{\rm{i}}\tilde \eta }}{{\rho \omega }}} \right)\frac{\rho }{{{\lambda ^*} + 2{\mu ^*}}}} } \right]}}\\ Q_{\rm{S}}^{ - 1} = \frac{{2 {\rm{Im}} \left[ {\sqrt {\left( {1 + \frac{{{\rm{i}}\tilde \eta }}{{\rho \omega }}} \right)\frac{\rho }{{{\mu ^*}}}} } \right]}}{{ {\rm{Re }}\left[ {\sqrt {\left( {1 + \frac{{{\rm{i}}\tilde \eta }}{{\rho \omega }}} \right)\frac{\rho }{{{\mu ^*}}}} } \right]}}\\ {V_{\rm{S}}} = \frac{1}{{ {\rm{Re}} \left[ {\sqrt {\left( {1 + \frac{{{\rm{i}}\tilde \eta }}{{\rho \omega }}} \right)\frac{\rho }{{{\mu ^*}}}} } \right]}} \end{array} \right. $ | (6) |
二维情况下,式(1)在频率—空间域可表示为
| $ \left\{ \begin{array}{l} \rho {\omega ^2}u - {\rm{i}}\tilde \eta \omega u + \frac{\partial }{{\partial x}}\left[ {{\lambda ^*}\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial z}}} \right) + 2{\mu ^*}\frac{{\partial u}}{{\partial x}}} \right] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{\partial }{{\partial z}}\left[ {{\mu ^*}\left( {\frac{{\partial u}}{{\partial z}} + \frac{{\partial v}}{{\partial x}}} \right)} \right] + {s_x}(\omega ) = 0\\ \rho {\omega ^2}v - {\rm{i}}\tilde \eta \omega v + \frac{\partial }{{\partial z}}\left[ {{\lambda ^*}\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial v}}{{\partial z}}} \right) + 2{\mu ^*}\frac{{\partial v}}{{\partial z}}} \right] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{\partial }{{\partial x}}\left[ {{\mu ^*}\left( {\frac{{\partial u}}{{\partial z}} + \frac{{\partial v}}{{\partial x}}} \right)} \right] + {s_z}(\omega ) = 0 \end{array} \right. $ | (7) |
式中:u、v分别为x和z方向的位移分量;sx(ω)、sz(ω)分别为x和z方向的频率域震源函数。
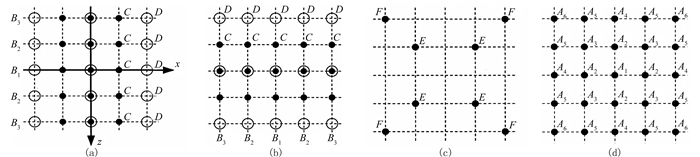
2.1 频率—空间域25点优化差分算子在25点优化差分格式的构造中,加权平均算子、平均加速项和加权系数是三项重要组成部分,其四种不同形式的差分网格如图 1所示。以水平位移u为例,式(7)中二阶空间偏导项
|
图 1 25点优化差分加权系数的网格分布
(a) |
| $ \begin{array}{l} \frac{{{\partial ^2}u}}{{\partial {x^2}}} \approx \frac{{{B_1}}}{{\Delta {x^2}}}\left[ {C({u_{i + 1, j}} - 2{u_{i, j}} + {u_{i - 1, j}}) + \frac{D}{4}({u_{i + 2, j}} - 2{u_{i, j}} + {u_{i - 2, j}})} \right] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {\frac{{{B_2}}}{{\Delta {x^2}}}\left[ {C({u_{i + 1, j + 1}} - 2{u_{i, j + 1}} + {u_{i - 1, j + 1}}) + \frac{D}{4}({u_{i + 2, j + 1}} - 2{u_{i, j + 1}} + {u_{i - 2, j + 1}})} \right] + }\\ {\frac{{{B_2}}}{{\Delta {x^2}}}\left[ {C({u_{i + 1, j - 1}} - 2{u_{i, j - 1}} + {u_{i - 1, j - 1}}) + \frac{D}{4}({u_{i + 2, j - 1}} - 2{u_{i, j - 1}} + {u_{i - 2, j - 1}})} \right] + } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {\frac{{{B_3}}}{{\Delta {x^2}}}\left[ {C({u_{i + 1, j + 2}} - 2{u_{i, j + 2}} + {u_{i - 1, j + 2}}) + \frac{D}{4}({u_{i + 2, j + 2}} - 2{u_{i, j + 2}} + {u_{i - 2, j + 2}})} \right] + }\\ {\frac{{{B_3}}}{{\Delta {x^2}}}\left[ {C({u_{i + 1, j - 2}} - 2{u_{i, j - 2}} + {u_{i - 1, j - 2}}) + \frac{D}{4}({u_{i + 2, j - 2}} - 2{u_{i, j - 2}} + {u_{i - 2, j - 2}})} \right]} \end{array} \end{array} $ | (8) |
| $ \begin{array}{l} \frac{{{\partial ^2}u}}{{\partial {z^2}}} \approx \frac{{{B_1}}}{{\Delta {z^2}}}\left[ {C({u_{i, j + 1}} - 2{u_{i, j}} + {u_{i, j - 1}}) + \frac{D}{4}({u_{i, j + 2}} - 2{u_{i, j}} + {u_{i, j - 2}})} \right] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {\frac{{{B_2}}}{{\Delta {z^2}}}\left[ {C({u_{i + 1, j + 1}} - 2{u_{i + 1, j}} + {u_{i + 1, j - 1}}) + \frac{D}{4}({u_{i + 1, j + 2}} - 2{u_{i + 1, j}} + {u_{i + 1, j - 2}})} \right] + }\\ {\frac{{{B_2}}}{{\Delta {z^2}}}\left[ {C({u_{i + 2, j + 1}} - 2{u_{i - 1, j}} + {u_{i - 1, j - 1}}) + \frac{D}{4}({u_{i - 1, j + 2}} - 2{u_{i - 1, j}} + {u_{i - 1, j - 2}})} \right] + } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {\frac{{{B_3}}}{{\Delta {z^2}}}\left[ {C({u_{i + 2, j + 1}} - 2{u_{i + 2, j}} + {u_{i + 2, j - 1}}) + \frac{D}{4}({u_{i + 2, j + 2}} - 2{u_{i + 2, j}} + {u_{i + 2, j - 2}})} \right] + }\\ {\frac{{{B_3}}}{{\Delta {z^2}}}\left[ {C({u_{i - 2, j + 1}} - 2{u_{i - 2, j}} + {u_{i - 2, j - 1}}) + \frac{D}{4}({u_{i - 2, j + 2}} - 2{u_{i - 2, j}} + {u_{i - 2, j - 2}})} \right]} \end{array} \end{array} $ | (9) |
| $ \frac{{{\partial ^2}u}}{{\partial x\partial z}} \approx \frac{E}{{4\Delta x\Delta z}}({u_{i + 1, j + 1}} - {u_{i + 1, j - 1}} - {u_{i - 1, j + 1}} + {u_{i - 1, j - 1}}) + \frac{F}{{16\Delta x\Delta z}}({u_{i + 2, j + 2}} - {u_{i + 2, j - 2}} - {u_{i - 2, j + 2}} + {u_{i - 2, j - 2}}) $ | (10) |
| $ \begin{array}{l} \begin{array}{*{20}{l}} {(\rho {\omega ^2} - {\rm{i}}\tilde \eta \omega )u \approx (\rho {\omega ^2} - {\rm{i}}\tilde \eta \omega )[{A_1}{u_{i, j}} + {A_2}({u_{i, j + 1}} + {u_{i + 1, j}} + {u_{i, j - 1}} + {u_{i - 1, j}}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {A_3}({u_{i + 1, j + 1}} + {u_{i + 1, j - 1}} + {u_{i - 1, j - 1}} + {u_{i - 1, j + 1}}) + {A_4}({u_{i, j + 2}} + {u_{i + 2, j}} + {u_{i, j - 2}} + {u_{i - 2, j}}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {A_5}({u_{i + 2, j + 1}} + {u_{i + 2, j - 1}} + {u_{i + 1, j - 2}} + {u_{i - 1, j - 2}} + {u_{i - 2, j - 1}} + {u_{i - 2, j + 1}} + {u_{i - 1, j + 2}} + {u_{i + 1, j + 2}}) + } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {A_6}({u_{i + 2, j + 2}} + {u_{i + 2, j - 2}} + {u_{i - 2, j - 2}} + {u_{i - 2, j + 2}})] \end{array} $ | (11) |
式中:(i,j)为网格中心点坐标;Am、Bn (m=1、2、…、6,n=1、2、3)以及C、D、E、F是频率—空间域25点优化差分算子的加权系数;Δx、Δz为空间网格步长。同理也可定义垂直分量v的差分算子。
对于上述差分算子加权系数,需要构造目标函数,使离散模型和连续模型的相速度相等,这是一个非线性优化问题,可利用Gauss-Newton法求解[27]。加权系数的具体取值参考Min等[21]的研究结果,该组优化的加权系数考虑到各种传播角度和所有泊松比情况,能适用各种模型的正演模拟,可以在α=vS/(f0Δx)≥3.3(其中f0为震源主频)的条件下保证数值算法的高精度[28]。
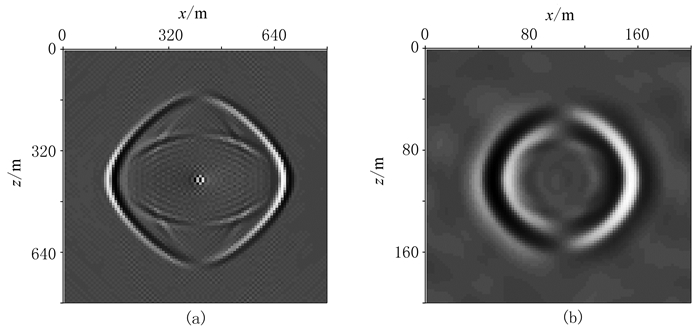
为了探讨优化的25点差分算法的稳定性,在vS=604m/s、f0=25Hz的情况下,分别设置Δx=8、2m(对应α=3.02<3.3和α=12.08>3.3)两种不同数值条件,下文将这两种数值条件依次称为第一数值条件和第二数值条件。在第一数值条件下,适当修改25点优化差分加权系数中的一些数值,如令B1=0.508781、B2=0.170898、B3=-0.015727、C=0.6596838、D=0.211686,使离散模型与连续模型的相速度不同,对比、分析优化的25点差分法在压制数值各向异性上的有效性。由第一数值条件和第二数值条件正演出的波场快照如图 2a、图 2b所示。对比图 2a与图 2b可见,当数值算法未能满足相应的稳定性条件时,波场快照上会表现出明显的数值频散和各向异性现象,所以波场模拟应首先考虑数值算法的稳定性条件。
|
图 2 不同数值条件下的波场快照 (a)第一数值条件;(b)第二数值条件 |
在正演模拟中,由于计算区域有限会不可避免地引入人为反射界面,严重影响最终模拟的效果,有必要构造边界条件压制边界反射[29]。常用的PML边界条件,吸收效果较好[30],其基本思想是在计算区域四周设置一定厚度的完全匹配层吸收衰减边界反射波的能量[31]。
若将PML边界应用于弹性波频率—空间域的正演模拟,需要将波动方程转换到复坐标系下。复坐标系变换可表示为
| $ {\tilde x_j} = \int_0^{{x_j}} {{e_j}} ({x_j}){\rm{d}}{x_j} $ | (12) |
式中:
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{\partial }{{\partial {{\tilde x}_j}}} = \frac{1}{{{e_j}}}\frac{\partial }{{\partial {x_j}}}}&{j = 1, 2}\\ {\frac{{{\partial ^2}}}{{\partial \tilde x_j^2}} = \frac{1}{{e_j^2}}\frac{{{\partial ^2}}}{{\partial x_j^2}}}&{j = 1, 2}\\ {\frac{{{\partial ^2}}}{{\partial {{\tilde x}_1}\partial {{\tilde x}_2}}} = \frac{1}{{{e_1}{e_2}}}\frac{{{\partial ^2}}}{{\partial {x_1}\partial {x_2}}}}&{} \end{array}} \right. $ | (13) |
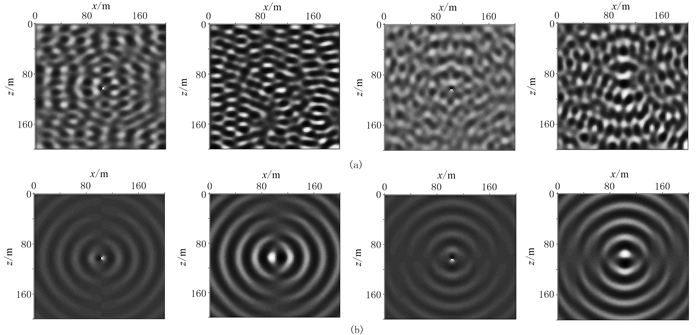
对比图 3中计算区域有、无PML边界的弹性波单频切片可见,当计算网格中不含PML层时,单频切片中的波场信息混乱,即全频段所有单频切片经反傅里叶变换之后,不能得到正确的时间域波场值;当计算边界含有一定厚度的PML层时,单频波场中的波前面自震源处向外传播,呈同心圆状,不受任何边界反射的影响。
|
图 3 无(a)、有(b)PML边界单频切片对比 从左至右依次为:水平分量实部、虚部,垂直分量实部、虚部 |
将式(8)~式(11)的差分格式代入式(7)中,应用式(13)能构造出含PML边界的频率—空间域弹性波离散化波动方程(以水平向为例)
| $ \begin{array}{*{20}{l}} {{p_1}{u_{i, j}} + {p_2}({u_{i + 1, j}} + {u_{i - 1, j}}) + {p_3}({u_{i, j + 1}} + {u_{i, j - 1}}) + }\\ {{p_4}({u_{i + 1, j + 1}} + {u_{i + 1, j - 1}} + {u_{i - 1, j + 1}} + {u_{i - 1, j - 1}}) + }\\ {{p_5}({u_{i + 2, j}} + {u_{i - 2, j}}) + {p_6}({u_{i, j + 2}} + {u_{i, j - 2}}) + }\\ {{p_7}({u_{i + 2, j + 1}} + {u_{i + 2, j - 1}} + {u_{i - 2, j - 1}} + {u_{i - 2, j + 1}}) + }\\ {{p_8}({u_{i + 1, j + 2}} + {u_{i + 1, j - 2}} + {u_{i - 1, j + 2}} + {u_{i - 1, j - 2}}) + }\\ {{p_9}({u_{i + 2, j + 2}} + {u_{i + 2, j - 2}} + {u_{i - 2, j + 2}} + {u_{i - 2, j - 2}}) + }\\ {{q_1}({v_{i + 1, j + 1}} - {v_{i + 1, j - 1}} - {v_{i - 1, j + 1}} + {v_{i - 1, j - 1}}) + }\\ {{q_2}({v_{i + 2, j + 2}} + {v_{i + 2, j - 2}} + {v_{i - 2, j + 2}} + {v_{i - 2, j - 2}}) + {s_x}(\omega ) = 0} \end{array} $ | (14) |
式中:系数p1~p9以及q1、q2是构造式(14)时合并所有同类项而得的系数。当所有网格点的波场值都按式(14)求解时,可建立线性方程组
| $ {\mathit{\boldsymbol{P}}_{N \times N}}\mathit{\boldsymbol{U}} = \mathit{\boldsymbol{S}} $ | (15) |
式中:P为N阶系数阻抗矩阵,对于二维情况下N=2Nx×Nz,Nx、Nz分别是x、z方向上的网格点数;U、S均为N维列向量,对应元素分别是各网格点频率—空间域波场值和震源函数值。频率—空间域波场模拟实则是大型线性方程组的求解过程[32],因此,本文在25点优化差分的基础上结合9点差分处理局部边界网格点,并采用LU分解法求解大型稀疏矩阵方程,计算出各网格点全频带范围内的波场值。一旦求出全频带波场值,就能通过反Fourier变换得到整个计算网格的时域波场值。
3 强衰减模型数值模拟 3.1 震源加载不同于时间域方法中直接在网格点的速度分量或应力分量上增加地震子波函数,频率—空间域波场模拟的震源加载需要构造与频率相关的震源矩阵。殷文等[33]总结几类频率域震源加载机制,并给出纵、横波震源在网格点上的加载公式,即
| $ \left\{ {\begin{array}{*{20}{l}} {{s_x}(\omega ) = {K_x}s(\omega )}\\ {{s_z}(\omega ) = {K_z}s(\omega )} \end{array}} \right. $ | (16) |
式中:s(ω)为频率域震源子波函数;Kx和Kz是震源的方向系数。本文利用四点网格模拟纵波源和横波源,若将网格左、右上角分别定义为0、1,左、右下角定义为2、3,纵、横波源的方向系数分别为
| $ \left\{ {\begin{array}{*{20}{l}} {{K_x} = - \delta (n) + \delta (n - 1) - \delta (n - 2) + \delta (n - 3)}\\ {{K_z} = - \delta (n) - \delta (n - 1) + \delta (n - 2) + \delta (n - 3)} \end{array}} \right. $ | (17) |
| $ \left\{ {\begin{array}{*{20}{l}} {{K_x} = \delta (n) + \delta (n - 1) - \delta (n - 2) - \delta (n - 3)}\\ {{K_z} = - \delta (n) + \delta (n - 1) - \delta (n - 2) + \delta (n - 3)} \end{array}} \right. $ | (18) |
为了验证优化的25点差分法在强衰减模型波场模拟中的有效性,本文首先设计一个符合近地表介质特征的均匀各向同性介质模型,网格数为100×100,PML层厚为50m,网格间距Δx=Δz=2m,其物性参数(表 1)的选择参考了Cui等[34]在胜利油田采集的微测井数据。根据这组实测数据计算的黏弹性参数为
|
|
表 1 均匀各向同性介质模型物性参数 |
| $ {\rm{tan}}\gamma = \frac{{0.0324 - 0.1092}}{{145 - 10}}(\omega - 10) + 0.1092 $ | (19) |
正演时间采样间隔Δt=1ms,采样点数为1024。为了对比波场信息,在模型中心分别加载纵波源和横波源。震源子波是主频为25Hz的Ricker子波。
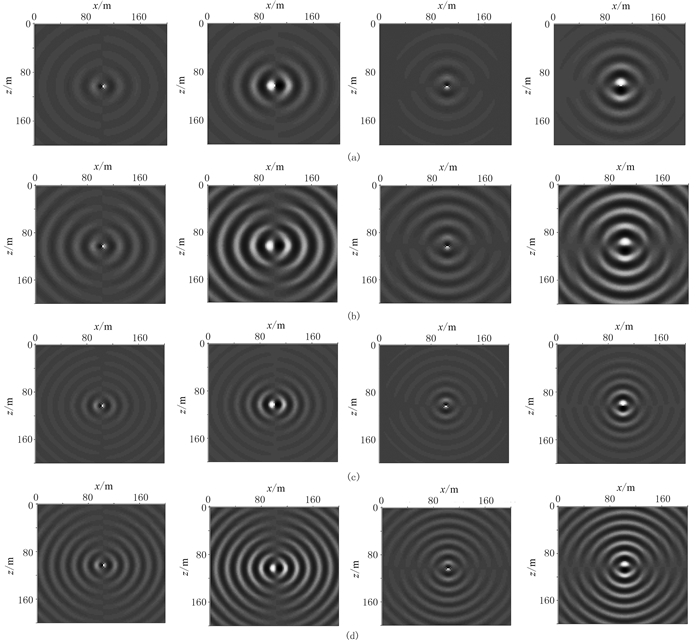
图 4、图 5分别为纵、横波源单频波场切片,波前面呈同心圆状,不同频率的地震波因为波长不同使单频切片上的“同心圆”间距不同,而且在相同频率的情况下,横波单频切片上的“同心圆”比纵波“同心圆”分布更为密集。与完全弹性介质相比(图 4b、图 4d、图 5b、图 5d),强衰减介质单频波场(图 4a、图 4c、图 5a、图 5c)的波前面能量比较弱,同心圆轨迹较模糊,表明地震波各频率成分受到严重的衰减,传播距离越远越严重。图 6为两种源激发的60ms波场快照,波前面也是以震源位置为中心的正圆形,其波前面与理论相符。
|
图 4 纵波源强衰减与完全弹性介质不同频率的单频波场切片对比 (a)强衰减模型,34.18Hz;(b)完全弹性模型,34.18Hz;(c)强衰减模型,48.83Hz;(d)完全弹性模型,48.83Hz从左至右依次为:水平分量实部、虚部,垂直分量实部、虚部 |
|
图 5 横波源强衰减与完全弹性介质不同频率的单频波场切片对比 (a)强衰减模型,34.18Hz;(b)完全弹性模型,34.18Hz;(c)强衰减模型,48.83Hz;(d)完全弹性模型,48.83Hz从左至右依次为:水平分量实部、虚部,垂直分量实部、虚部 |

|
图 6 强衰减介质模型60ms的波场快照 (a)纵波源,水平分量;(b)纵波源,垂直分量;(c)横波源,水平分量;(d)横波源,垂直分量 |
图 4、图 5单频切片及图 6的波场快照充分地描述了地震波在均匀各向同性、强衰减介质中的传播特征,表明优化的25点差分法模拟强衰减模型中地震波场的可行性。
强衰减模型全面地考虑了介质自身的黏弹性、孔隙度和黏性流体的流动作用,对近地表地震波衰减规律的预测和复杂黏弹性介质的描述更接近于实际[19]。在表 1所示物性参数的基础上,综合近地表介质孔隙结构、干燥疏松程度、黏滞性等适当地选择不同的物理参数,分析孔隙度、流体黏度和介质黏弹性对介质衰减特征的影响。当震源位于(90m,15m)处激发,在地表以3m的道间距设置一条排列接收,将纵、横波源模拟记录合并在一起,结果如图 7所示。图 7中的地震记录能清楚地显示纵波和横波在均匀半空间强衰减介质中的波场传播信息。

|
图 7 均匀强衰减介质地震记录 (a)水平分量;(b)垂直分量 |
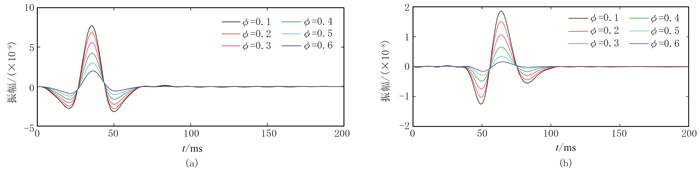
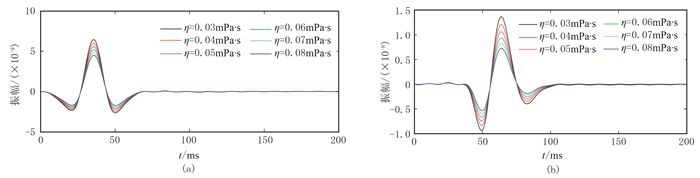
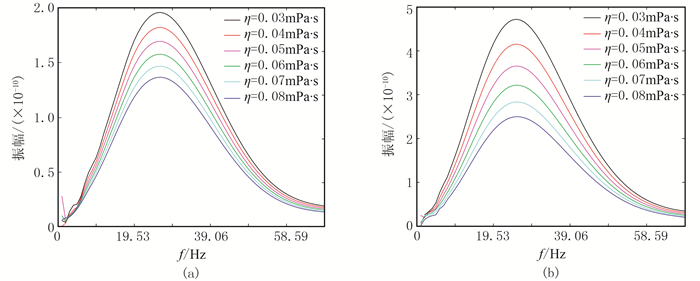
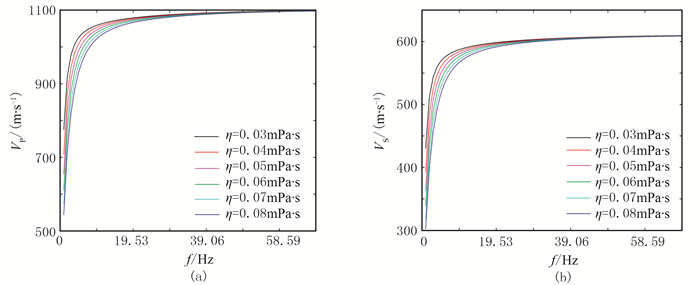
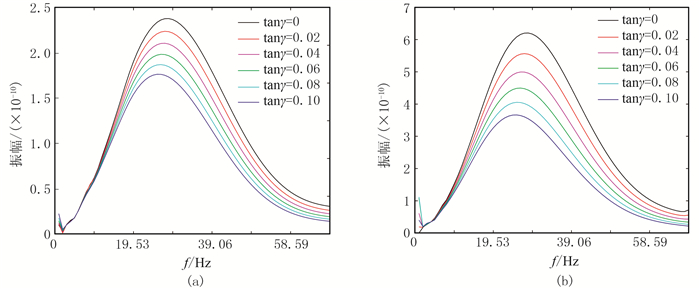
图 8~图 16展示了不同孔隙度、不同流体黏度和不同介质黏弹性条件下的x=120m处的单道地震记录及其振幅谱和地震波速度频散曲线。由图 8、图 11和图 14可清楚看出,随着介质孔隙度和流体黏度的增大以及介质自身黏滞性的增强,地震波的振幅值越来越小,即介质的任何一种物性条件变差时,介质对地震波的吸收衰减能力变强。在近地表介质条件下,孔隙度的变化所引起的地震波衰减幅度大于另外两种因素,说明近地表介质的疏松结构是造成介质强衰减性的关键。
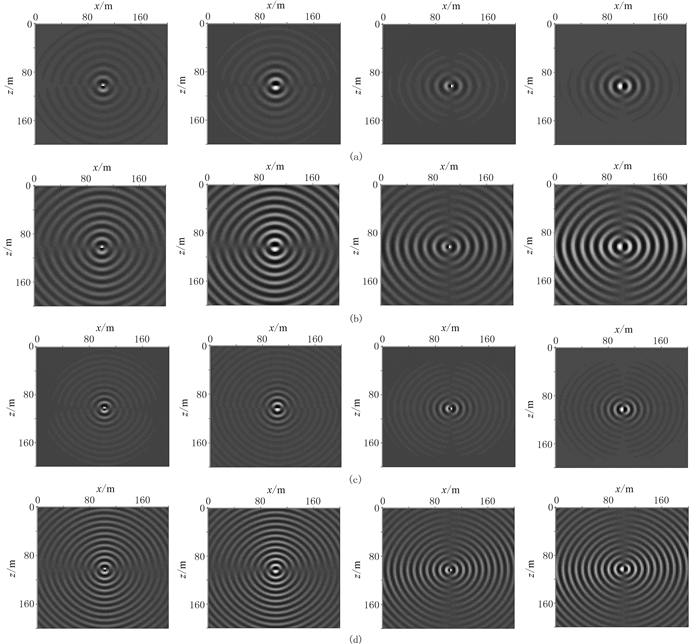
|
图 8 不同孔隙度条件下纵(a)、横波(b)单道记录对比 |

|
图 9 不同孔隙度条件下纵(a)、横波(b)单道振幅谱对比 |
|
图 10 不同孔隙度条件下纵(a)、横波(b)频散曲线对比 |
|
图 11 不同流体黏度条件下纵(a)、横波(b)单道记录对比 |
|
图 12 不同流体黏度条件下纵(a)、横波(b)单道振幅谱 |
|
图 13 不同流体黏度条件下纵(a)、横波(b)频散曲线 |

|
图 14 不同介质黏弹性条件下纵(a)、横波(b)单道记录对比 |
|
图 15 不同介质黏弹性条件下纵(a)、横波(b)单道振幅谱对比 |

|
图 16 不同介质黏弹性条件下纵(a)、横波(b)频散曲线对比 |
图 9、图 12和图 15分别为图 8、图 11和图 14单道地震记录对应的振幅谱,可见随着介质物性条件的变差,各频率成分的能量越来越弱,这就解释了图 4和图 5中强衰减单频切片相对于弹性单频切片较模糊的原因。而且还可以看出:①随介质自身黏滞性的增强,高频地震波能量衰减强于低频地震波,振幅谱呈现主频降低的现象;②介质孔隙度和流体黏度的增大能使整个地震频率范围内的波场能量发生衰减,其中有效频带内的能量衰减最强,但未出现主频降低的现象。
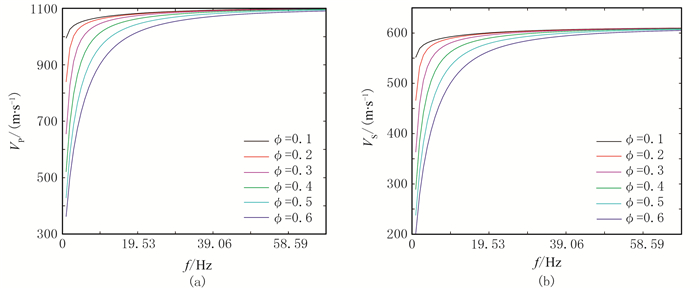
能量衰减和速度频散都是黏弹性介质地震波场重要特征,本文基于强衰减模型的相速度公式(式(5)),计算各条件下地震波的速度频散曲线如图 10、图 13和图 16所示。可以看出,介质孔隙度和流体黏度的增大以及介质黏弹性的增强,都能使地震波速度的频散特征表现更为明显,其中高频频散弱于低频频散。
综合对比图 8~图 16可以发现,介质的孔隙度、流体黏度以及介质黏弹性对纵波和横波传播衰减的影响不同,随着这三个参数的逐渐增大,横波振幅的递减幅度大于纵波。出现这种现象的原因为:
(1) 近地表介质结构疏松、多孔,当介质的孔隙度增大时,介质的抗剪切能力会变得越来越弱,导致横波的衰减随孔隙度的增大而变强。
(2) 强衰减模型波动方程(式(2))中的耗散系数与孔隙度、渗透率和流体黏度相关,其中流体黏度反应流体与固体骨架之间的黏滞作用,这种相互作用是导致地震波衰减的重要因素[35]。横波不能在流体中传播,在横波传播过程中流体相对于固体骨架的运动位移大于纵波,因此随流体黏度的逐渐增大,横波能量的递减幅度明显大于纵波。
(3) 近地表介质由于长期受风化、剥蚀等外力作用使固体骨架表现出明显的黏弹性,作为骨架波的横波受到的影响比较明显。
综上所述,强衰减模型考虑多种物理因素,以运动方程刻画介质的衰减规律是合理、有效的,而且它预测的纵、横波衰减机制与实际相符,值得在油气富集区推广应用。
3.3 含低速层的两层介质波场模拟为了研究近地表低速层介质对深层波场信息的影响机制,本文设计一个物性参数如表 2所示的两层介质模型:模型尺寸为175m×175m,其中上层是厚70m且疏松多孔的黏弹性介质,下层是致密弹性介质,选择主频为25Hz的Ricker子波作为纵波源在(87.5m,35.0m)处激发,50个检波器点以3.5m的间隔均匀分布在地表。
|
|
表 2 两层介质模型物性参数 |
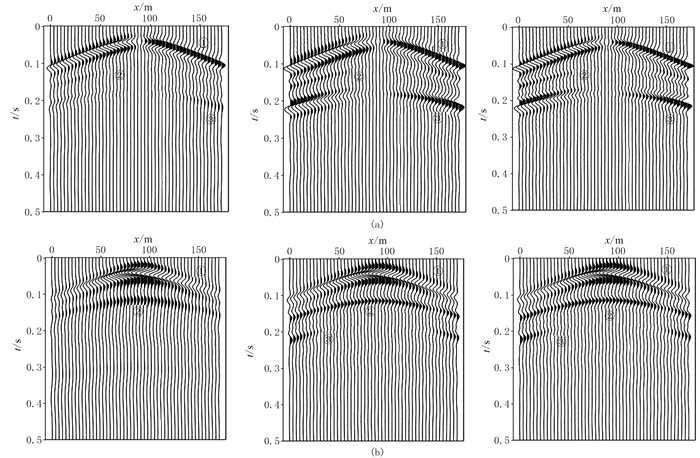
图 17展示了两层介质模型的近地表低速层分别由强衰减模型、一般黏弹性模型(达朗贝尔模型)和完全弹性介质理模型模拟的地震记录,图中可见直达波、反射纵波、转换横波。若近地表介质由完全弹性或由一般黏弹性模型描述时,各地震分量中携带深层介质信息的反射波和转换波能量较强、记录直观清楚,而且两种条件下的地震记录差异较小。但在基于强衰减模型所模拟的地震记录上,反射波和转换波的同相轴较模糊、能量弱。黄土塬、沙漠等地一般都会因表层覆盖较厚的低速层介质,对地震波的激发和接收产生巨大的影响[36]。
|
图 17 强衰减(左)、黏弹性(中)及完全弹性机制(右)下两层模型地震记录 (a)水平分量;(b)垂直分量。①直达波;②反射纵波;③转换横波 |
为了更直观地对比完全弹性、一般黏弹性和强衰减机制下的波场信息,抽取图 17地震记录中x=140m处水平分量单道信号,并计算其振幅谱(图 18)。由图可见:黏弹性介质较弹性介质对地震波高频成分有明显的黏滞损耗;强衰减介质中的地震波各频率成分的能量严重衰减。
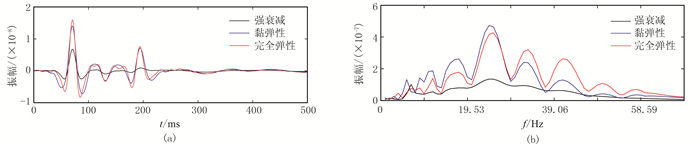
|
图 18 两层模型不同机制下单道记录(a)及振幅谱(b)对比 |
本文基于频率—空间域25点优化差分算法实现了强衰减模型波动方程的数值模拟,通过对比分析不同物性条件下地震波的衰减特征,模拟了浅表覆盖低速层的双层介质模型的地震波场,可以得出如下结论。
(1) 频率域波场模拟能得到全频带范围内包含所有时刻波场信息的单频切片,用于分析不同频率的波场特征。不同频率的单频切片由于地震波波长不同,其波场形态不同。相同频率的纵波和横波因传播速度的差异,单频切片中波前面的疏密程度差异很大。由于介质对地震波各频率成分的强吸收衰减作用,强衰减介质中地震波的频率—空间域波场相比于完全弹性波场信息变得模糊。
(2) 随着介质孔隙度和流体黏度的增大以及介质黏滞性的增强,地震波能量衰减和速度频散现象越来越明显。孔隙度、流体黏度和介质黏弹性对地震波吸收衰减的影响程度不同。对于近地表介质,孔隙度的影响最大,介质黏弹性次之。在三种影响因素中,介质黏弹性是导致地震波频带变窄、主频减小的关键,孔隙度和流体黏度对地震波主频的影响不大,主要导致地震波各频率成分尤其有效频带范围内能量的衰减。
(3) 基于强衰减模型所模拟的纵波和横波在不同孔隙度、不同流体黏度和不同介质黏弹性条件下的衰减规律存在差异,与实际情况相符。强衰减模型能有效克服达朗贝尔模型中纵波和横波衰减机制差异不大的缺陷。
(4) 对比上覆低速层分别为完全弹性、黏弹性和强衰减介质的两层介质模型的模拟波场可知,强衰减模型综合考虑了介质的多种物理因素,描述的近地表介质对深层波场信息的严重干扰更符合实际。所以基于强衰减模型研究近地表介质的强吸收衰减,能为地震数据处理中的Q值反演和衰减补偿提供理论基础。
| [1] |
Carcione J M. Seismic modeling in viscoelastic media[J]. Geophysics, 1933, 58(1): 110-120. |
| [2] |
牛滨华, 孙春岩. 地震波理论研究进展--介质模型与地震波传播[J]. 地球物理学进展, 2004, 19(2): 255-263. NIU Binhua, SUN Chunyan. Developing theory of propagation of seismic waves:medium model and propagation of seismic waves[J]. Progress in Geophysics, 2004, 19(2): 255-263. |
| [3] |
奚先, 姚姚. 二维黏弹性随机介质中的波场特征[J]. 石油地球物理勘探, 2004, 39(4): 381-387. XI Xian, YAO Yao. Characteristics of wavefield in 2-D viscoeiastic random medium[J]. Oil Geophysical Prospecting, 2004, 39(4): 381-387. |
| [4] |
李合群, 孟小红, 赵波, 等. 塔里木沙漠区地震数据品质与沙层Q吸收[J]. 石油地球物理勘探, 2010, 45(1): 28-34. LI Hequn, MENG Xiaohong, ZHAO Bo, et al. Seismic data quality and sand layer Q absorption in Tarim desert area[J]. Oil Geophysical Prospecting, 2010, 45(1): 28-34. |
| [5] |
宋吉杰, 禹金营, 王成, 等. 近地表介质Q估计及其在塔河北部油田的应用[J]. 石油物探, 2018, 57(3): 436-442. SONG Jijie, YU Jinying, WANG Cheng, et al. Q estimation for near-surface media and its application in the Northern Tahe Oilfield, China[J]. Geophysical Prospecting for Petroleum, 2018, 57(3): 436-442. |
| [6] |
牛滨华, 孙春岩. 黏弹性介质与地震波传播[M]. 北京: 地质出版社, 2007.
|
| [7] |
Stokes G G. On the aberration of light[J]. The London, Edinburgh, and Dublin Philosophical Magazine and Journal of Science, 1845, 27(177): 9-15. DOI:10.1080/14786444508645215 |
| [8] |
孙成禹. 地震波理论与方法[M]. 山东东营: 中国石油大学出版社, 2007.
|
| [9] |
Carcione J M, Kosloff D, Kosloff R. Wave propagation simulation in a linear viscoacoustic medium[J]. Geophysical Journal International, 1988, 93(2): 393-401. DOI:10.1111/j.1365-246X.1988.tb02010.x |
| [10] |
Carcione J M, Kosloff D, Kosloff R. Wave propagation simulation in a linear viscoacoustic medium[J]. Geophysical Journal International, 1988, 95(3): 597-611. DOI:10.1111/j.1365-246X.1988.tb06706.x |
| [11] |
张金波, 杨顶辉, 贺茜君, 等. 求解双相和黏弹性介质波传播方程的间断有限元方法及其波场模拟[J]. 地球物理学报, 2018, 61(3): 926-937. ZHANG Jinbo, YANG Dinghui, HE Qianjun, et al. Discontinuous Galerkin method for solving wave equations in two-phase and viscoelastic media[J]. Chinese Journal of Geophysics, 2018, 61(3): 926-937. |
| [12] |
刘财, 胡宁, 郭智奇, 等. 基于分数阶时间导数常Q黏弹本构关系的含黏滞流体双相VTI介质中波场数值模拟[J]. 地球物理学报, 2018, 61(6): 2446-2458. LIU Cai, HU Ning, GUO Zhiqi, et al. Numerical simulation of the wavefield in a viscous fluid-saturated two-phase VTI medium based on the constant-Q viscoela-stic constitutive relation with a fractional temporal derivative[J]. Chinese Journal of Geophysics, 2018, 61(6): 2446-2458. |
| [13] |
Biot M A. Theory of propagation of elastic waves in a fluid-saturated porous solid, I:Low-frequency range[J]. The Journal of the Acoustical Society of America, 1956, 28(2): 168-178. DOI:10.1121/1.1908239 |
| [14] |
Mavko G, Nur A. Melt squirt in the asthenosphere[J]. Journal of Geophysical Research, 1975, 80(11): 1444-1448. DOI:10.1029/JB080i011p01444 |
| [15] |
Dvorkin J, Nur A. Dynamic poroelasticity:A unified model with the squirt and the Biot mechanisms[J]. Geophysics, 1993, 58(4): 524-533. DOI:10.1190/1.1443435 |
| [16] |
杜启振, 刘莲莲, 孙晶波. 各向异性粘弹性孔隙介质伪谱法波场正演模拟[J]. 油气地球物理, 2007, 5(1): 22-26. DU Qizhen, LIU Lianlian, SUN Jingbo. Wavefield numerical modeling with the pseudo-spectral method in anisotropic viscoelastic porous media[J]. Petroleum Geophysics, 2007, 5(1): 22-26. |
| [17] |
Nie J X, Ba J, Yang D H, et al. BISQ model based on a Kelvin-Voigt viscoelastic frame in a partially satura-ted porous medium[J]. Applied Geophysics, 2012, 9(2): 213-222. DOI:10.1007/s11770-012-0332-6 |
| [18] |
凌云, 杜向东, 曹思远. 基于Zener线性体的黏弹孔隙介质衰减频散特征分析[J]. 地球物理学进展, 2017, 32(1): 205-209. LING Yun, DU Xiangdong, CAO Siyuan. Attenuation and dispersion characteristics analysis in visco-poroelastic medium based on Zener linear solid[J]. Progress in Geophysics, 2017, 32(1): 205-209. |
| [19] |
谢佩瑜, 杨顶辉. 近地表强衰减介质中的地震波传播模型[J]. 地球物理学报, 2018, 61(3): 917-925. XIE Peiyu, YANG Dinghui. Seismic wave propagation model in near-surface strong attehuation media[J]. Chinese Journal of Geophysics, 2018, 61(3): 917-925. |
| [20] |
Lysmer J, Lawrence A D. A finite element method for seismology[J]. Methods in Computational Physics, 1972, 11: 181-216. |
| [21] |
Min D J, Shin C, Changsoo S, et al. Improved frequency-domain elastic wave modeling using weighted-ave-raging difference operators[J]. Geophysics, 2000, 65(3): 884-895. |
| [22] |
李桂花, 冯建国, 朱光明. 黏弹性VTI介质频率空间域准P波正演模拟[J]. 地球物理学报, 2011, 54(1): 200-207. LI Guihua, FENG Jianguo, ZHU Guangming. Quasi-P wave forward modeling in viscoelastic VTI media in frequency-space domain[J]. Chinese Journal of Geophysics, 2011, 54(1): 200-207. |
| [23] |
Min D J, Shin C, Yoo H S. Free-surface boundary condition in finite-difference elastic wave modeling[J]. Bulletin of the Seismological Society of America, 2004, 94(1): 237-250. DOI:10.1785/0120020116 |
| [24] |
刘财, 杨庆节, 鹿琪, 等. 双相介质中地震波的频率-空间域数值模拟[J]. 地球物理学报, 2014, 57(9): 2885-2899. LIU Cai, YANG Qingjie, LU Qi, et al. Simulation of wave propagation in two-phase porous media using a frequency-space domain method[J]. Chinese Journal of Geophysics, 2014, 57(9): 2885-2899. |
| [25] |
周聪, 刘江平, 罗银河, 等. 二维频率域全波场有限差分数值模拟方法[J]. 石油地球物理勘探, 2014, 49(2): 278-287. ZHOU Cong, LIU Jiangping, LUO Yinhe, et al. 2D full-wavefield modeling in frequency domain using finite-difference[J]. Oil Geophysical Prospecting, 2014, 49(2): 278-287. |
| [26] |
Yang L, Yang D H, Nie J X. Wave dispersion and a-ttenuation in viscoelastic isotropic media containing multiphase flow and its application[J]. Science China:Physics, Mechanics & Astronomy, 2014, 57(6): 1068-1077. |
| [27] |
Lines L R, Treitel S. A review of least-squares inversion and its application to geophysical problems[J]. Geophysical Prospecting, 1984, 32(2): 159-186. DOI:10.1111/j.1365-2478.1984.tb00726.x |
| [28] |
杨庆节, 刘财, 郭智奇, 等. 基于BISQ模型双相各向同性介质弹性波传播的频率-空间域有限差分模拟[J]. 地球物理进展, 2015, 30(1): 249-260. YANG Qingjie, LIU Cai, GUO Zhiqi, et al. Wave propagation in two-phase isotropic medium based on BISQ model in frequency-space domain[J]. Progress in Geophysics, 2015, 30(1): 249-260. |
| [29] |
Collino F, Tsogka C. Application of the perfectly matched absorbing layer model to the linear elastodynamic problem in anisotropic heterogeneous media[J]. Geophysics, 2001, 66(1): 294-307. |
| [30] |
罗玉钦, 刘财. 多轴复频移近似完全匹配层弹性波模拟[J]. 石油地球物理勘探, 2019, 54(5): 1024-1033. LUO Yuqin, LIU Cai. Multi-axial compex-frequency shifting nearly perfectly matched layer for seismic forward modeling in elastic media[J]. Oil Geophysical Prospecting, 2019, 54(5): 1024-1033. |
| [31] |
Berenger J P. A perfectly matched layer for the ab-sorption of electromagnetic waves[J]. Journal of Computational Physics, 1994, 114(2): 185-200. |
| [32] |
高凤霞.频率域波动方程多参数全波形反演方法研究[D].吉林长春: 吉林大学, 2014.
|
| [33] |
殷文, 印兴耀, 吴国忱, 等. 高精度频率域弹性波方程有限差分方法及波场模拟[J]. 地球物理学报, 2006, 49(2): 561-568. YIN Wen, YIN Xingyao, WU Guochen, et al. The method of finite difference of high precision elastic wave equations in the frequency domain and wavefield simulation[J]. Chinese Journal of Geophysics, 2006, 49(2): 561-568. |
| [34] |
Cui Q H, Rui Y J, Shang X M.Near-surface absorption compensation technique and its application[C].Near Surface Geophysics Asia Pacific Conference, 2013, 517-520.
|
| [35] |
邹冠贵.孔隙介质地震波传播及衰减特征评价研究[D].北京: 中国矿业大学, 2010. ZOU Guangui.Propagation of Elastic Wave in a Fluid-saturated Porous Media and Attenuation Characteristic Evaluation[D].China University of Mining, Beijing, 2010. |
| [36] |
赵秋芳, 云美厚, 朱丽波, 等. 近地表Q值测试方法研究进展与展望[J]. 石油地球物理勘探, 2019, 54(6): 1397-1418. ZHAO Qiufang, YUN Meihou, ZHU Libo, et al. Progress and outlook of near-surface quality factor Q measurement and inversion[J]. Oil Geophysical Prospecting, 2019, 54(6): 1397-1418. |



 王赟, 北京市海淀区学院路29号中国地质大学(北京)地球物理与信息技术学院, 100083。Email:
王赟, 北京市海淀区学院路29号中国地质大学(北京)地球物理与信息技术学院, 100083。Email: