② 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580;
③ 东方地球物理公司西南物探分公司, 四川成都 610000
② School of Geosciences, China University of Petroleum(East China), Qingdao, Shandong 266580, China;
③ Southwest Geophysical Prospecting Branch, BGP, CNPC, Chengdu, Sichuan 610000, China
面波在原始地震记录中表现为能量强、频率低、扫帚状分布,是目前地震资料中最主要的噪声之一,严重影响了地震资料的品质,不利于地震资料处理与解释工作。因此,面波压制一直是地球物理工作者不断研究的课题。
针对面波压制,已经发展了许多相关技术,如频率域滤波、F-K滤波、F-X滤波、自适应相减、小波变换、Curvelet变换、S变换等[1-5]。这些方法都取得了一定的效果,但也存在一定的局限性。
频率域滤波根据面波与有效波的频率特征差异,利用傅里叶变换将地震数据变换到频率域,进行低通、高通或带通滤波,此方法容易损伤相应频带上的有效波。为了克服常规频率域滤波的缺点,李文杰等[6]针对不同的炮检距选用不同的低截频率,在选定的面波区域进行高通滤波,有效地压制了面波,最大限度地保护了非面波区域的有效信号,但对深层低频有效信息仍有不同程度的损伤。
F-K滤波是一种比较经典的面波压制技术,由于其简便、快捷,得到广泛应用。但是F-K滤波要求空间采样规则,当地震数据存在振幅差异或空间采样稀疏时,容易造成同相轴“蚯蚓化”等波形失真现象。同时,F-K滤波是将若干道记录作为一个整体进行处理,在衰减面波的同时,也会损伤重叠在面波中的部分低频有效信息。
自适应相减滤波技术的基本思想是从原始地震数据中估算面波干扰,通过振幅、相位的调整,使估算的面波干扰与实际地震数据中的面波特征一致,再从原始地震数据中减去估算的面波干扰,得到压制面波后的地震记录。其中,比较经典的是基于最小平方的自适应相减滤波技术。马振元等[7]利用扫描信号与滤波因子的褶积预测面波,然后应用最小平方二乘法从地震记录中减去预测的面波。王志农等[8]提出的区域自适应极化滤波技术、谢金娥等[9]提出的基于F-K域的自适应波束面波压制方法、董烈乾等[10]提出的基于Curvelet域的预测自适应滤波技术以及陈文超等[11]提出的基于连续小波变换的自适应滤波,都是一些与之相关的配套技术,应用也较为广泛。自适应相减滤波技术是一种相对保真的面波压制技术,其效果取决于预测的面波模型,通常为了最大限度地保护有效信号,往往会存在面波压制不足的缺点。
小波变换、Curvelet变换属于多尺度理论分析范畴,其较强的方向特征对面波有较好的压制效果。岳龙等[12]根据面波与有效波主要能量在小波域的分布区域不同,提出利用连续小波变换压制面波的方法。由于小波变换的基函数是各向同性的,对于高维奇异信号的表达,小波变换容易失效。Curvelet变换具有较强的方向特征,能够克服小波变换对高维奇异信号表达的不足。近年来发展出许多Curvelet变换压制面波的方法:如郑静静等[13]提出的基于第二代Curvelet变换压制面波技术;李继伟等[14]提出的基于能量比值的Curvelet阈值迭代面波压制方法;董烈乾等[15]基于Curvelet变换,通过多次分解压制面波。但是,Curvelet变换压制面波的效果受面波与有效波在Curvelet域中的重叠程度影响。因此,大多数基于Curvelet变换压制面波技术都通过层层迭代或层层分解,以提高地震数据在Curvelet域中的分辨率,达到良好的面波压制效果。
S变换充分吸取了短时傅里叶变换与小波变换各自的优点,通过灵活选取面波时窗,实现面波的压制。李杨等[16]基于广义S变换,将时间域的地震数据变换到时频域压制面波。
随着勘探向岩性油气藏、页岩气、火成岩等新领域的延伸,对地震数据处理提出了更高的要求——保真保幅。噪声压制技术总的发展趋势由单一特征差异向多特征差异发展,由频率时不变特性向频率时变特性发展。张金宝等[17]对地震资料去噪强度、去噪效率与振幅保真等问题进行了探讨,提出针对不同噪声的特点,采用不同的联合去噪方法,可以在提高信噪比的同时,达到相对保真保幅处理。徐颖等[18]根据噪声类型、不同域中的表现特征,采用六分法多域组合的去噪思路,在塔中奥陶系低信噪比区取得了较好的处理效果。
针对面波的压制,GeoEast软件中的自适应面波衰减模块应用较为广泛。该模块利用统计分析识别和压制面波,在时频域根据面波与有效波的频率、空间分布及能量等方面的差异判断面波分布范围,其最大的优势是对资料的高频信号和低频信号保护较好。陈娟等[19]、尹思等[20]分别在额济纳旗地区、柴达木盆地尖顶山地区应用此方法取得了良好应用效果。王维红等[21]对传统的区域滤波技术进行了改进和完善,应用减去法压制面波,形成了一套保护低频有效信号的面波压制流程,并应用于松辽盆地北部斜坡区,实用性较强。
本文结合自适应相减滤波的保真保幅特性和Curvelet变换的多方向特性,首先利用自适应相减滤波技术压制原始记录中大部分面波,再应用Curvelet变换压制残余面波。该方法是一种组合面波压制技术,流程简单,在提高地震资料信噪比的同时,可以做到相对保真保幅处理。实际数据处理结果证实了方法的有效性和实用性。
1 基本原理 1.1 自适应相减滤波技术自适应相减滤波技术基于预测的面波模型,利用减去法实现面波压制,其优点是只压制面波,对有效信息的保护较好。该方法的重点是求取滤波因子,首先根据原始地震数据和噪声模型计算滤波因子,然后将滤波因子与噪声模型褶积预测面波,最后从地震数据中减去预测的面波,实现面波压制。
假设z(t)为地震数据,x(t)为有效反射波,w(t)为噪声(特指面波),则有
| $ z\left( t \right) = x\left( t \right) + w\left( t \right)\;\;\;\;\;\;t = 1, 2, \cdots , T $ | (1) |
式中T为最大时间采样点。假设滤波因子为f(t),面波模型为s(t),则有
| $ w\left( t \right) = \sum\limits_{\tau = 0}^{n - 1} {f\left( \tau \right)} s\left( {t - \tau } \right) $ | (2) |
式中n为滤波因子长度。由于滤波因子来源于原始地震数据,所以求取滤波因子f就需要定义一个最小平方误差函数
| $ R = \sum\limits_t {{{\left[ {z\left( t \right) - w\left( t \right)} \right]}^2}} $ | (3) |
当R取最小值时可得最佳滤波因子f。将式(2)代入式(3),可得
| $ R = \sum\limits_t {{{\left[ {z\left( t \right) - \sum\limits_\tau {f\left( \tau \right)s\left( {t - \tau } \right)} } \right]}^2}} $ | (4) |
利用R对f求导并令导数为0,即可求得最佳滤波因子f。利用式(2),即可求得预测的面波。将预测的面波从地震数据中减去就可以得到面波压制后的有效波
| $ x\left( t \right) = z\left( t \right) - w\left( t \right) $ | (5) |
滤波因子为一个最佳的振幅、相位调整因子。将面波模型通过最佳滤波因子进行相位、振幅的调整与原始地震数据中的面波相匹配,达到保幅处理的目的。在进行自适应相减压制面波时,比较重要的一个步骤是定义时窗,在每一个时窗内计算滤波因子、预测面波,它是一种时变、空变的面波压制技术。
为了简便、快速得到面波模型,本文面波模型主要通过F-K域滤波法直接从原始地震数据中提取,面波模型更符合实际。
1.2 Curvelet变换面波压制技术Curvelet变换属于多尺度的理论范畴,由Candès等[22-24]基于Rideglet变换提出。由于其多方向特征,被广泛用于地震资料处理,包括随机噪声压制、面波压制、多次波预测、数据插值等,均取得了良好的应用效果。
Curvelet变换的实质是基函数与信号进行内积实现信号的多尺度表达,即
| $ C\left( {j, l, k} \right) = \left\langle {z, {\mathit{\Phi }_{j, l, k}}} \right\rangle = \int_{{R^2}} {z\left( t \right)\overline {{\mathit{\Phi }_{j, l, k}}\left( t \right)} } {\rm{d}}t $ | (6) |
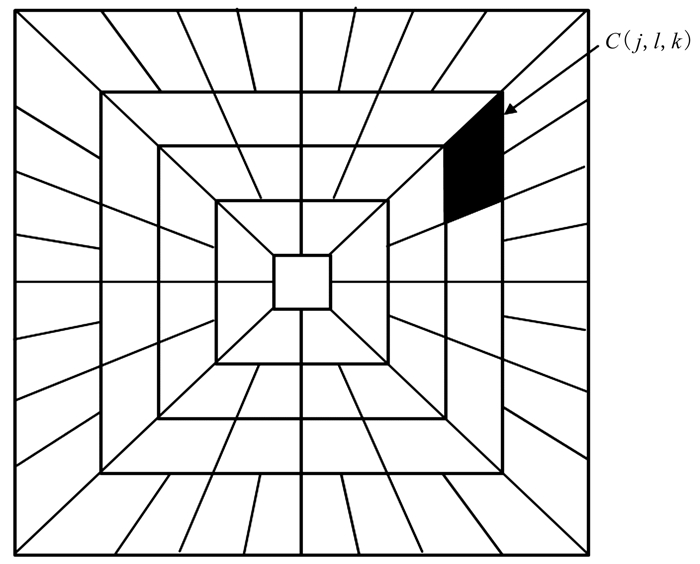
式中:Φj,l,k(t)为Curvelet基函数,Φ为Φ的共轭;z(t)∈L2(R2)为原始信号;C(j,l,k)为Curvelet域在尺度j、方向l、位置k处的系数。
由上式可知,Curvelet函数具有很强的方向敏感性。图 1是Curvelet变换频率域分割示意图,整个Curvelet变换按照频率由高到低划分尺度,可分为包含了低频、低波数信息的最内层粗尺度、用于信号分析的中间层精细尺度和包含了高频、高波数信息的最外层最佳尺度。每个尺度又沿着顺时针划分方向,每一个方向都由相应频率的Curvelet系数组成。图中黑色区为一个梯形,每一个梯形都对应的有一个Curvelet基函数,每一个Curvelet基函数都有一个特定的尺度、方向和位置表达,这些特定的因素可由式(6)中的下标(j,l,k)表征。
|
图 1 Curvelet频率域分割示意图 |
地震数据中,面波与有效波在频率和速度上存在差异。将其变换到Curvelet域中,面波与有效波的能量和分布也存在差异。其中,面波主要集中在图 1中的低频高波数区域(即横轴附近),这些区域的面波系数值较大,在其他区域的面波系数值较小或为零。利用Curvelet变换压制面波,主要是通过合适的层次分解,将面波与有效波在Curvelet域中进行分离,然后将较大的面波系数置零,以实现面波压制。
1.3 组合压制技术充分利用自适应相减滤波技术保真保幅特性和Curvelet变换多方向特征,进行有机组合压制面波,可以在保护有效信号的同时,有效压制面波。其处理流程(图 2)如下。

|
图 2 本文的面波压制处理流程 |
(1) 面波模型提取。首先根据面波与有效波的频率和速度差异,利用F-K滤波从原始地震数据中提取面波模型。由于F-K滤波的局限性,提取出的面波模型可能含有低频、低波数的有效信号。为了最大限度地保护有效信号,面波模型中应尽可能不包含有效信息。因此,需要对面波模型进行有效信号的回减处理,即利用倾角滤波滤出面波模型中的低倾角信号,获得最终不含有效信号的面波模型。
(2) 自适应相减滤波压制大部分面波。将不含有效波的面波模型与原始地震数据进行最小平方自适应相减,得到压制大部分面波后的地震数据体。
(3) Curvelet变换压制残余面波。由于大部分面波已经得到压制,残留的面波与有效波在Curvelet域中就更容易被分开。将压制大部分面波后的数据进行F-K谱分析,大致确定面波在F-K谱中分布区域;然后选择合适的Curvelet分解层次,使面波与有效波在Curvelet域中尽可能不重叠;最终选取主要含面波区域的尺度和方向,将其Curvelet系数置零,得到最终面波压制后的数据体。
1.4 与其他方法的对比为对本文方法的效果进行验证,分别选取了常用的F-X域滤波、非线性相关F-K域滤波、自适应相减滤波及Curvelet变换阈值迭代等面波压制方法与本文方法进行处理效果对比(图 3)。

|
图 3 不同面波压制方法对比 (a)原始数据;(b)F-X滤波;(c)F-K滤波;(d)自适应相减法;(e)Curvelet变换法;(f)本文方法 |
图 3a是包含面波的地震记录。从记录中可见,面波受近地表地质因素影响,呈现明显的散射特征,面波的相干特性不明显。
图 3b是利用F-X域进行两次面波压制后的记录。由于F-X域滤波是一种线性相干的面波压制方法,针对此类频散特征明显的面波,显然存在面波压制不足的缺陷,大部分相干性低的面波被保留,其面波压制的适用范围较窄。
图 3c是利用非线性相关F-K域滤波法面波压制后的记录,与F-X域滤波后的记录(图 3b)对比,大部分面波得到很好的压制。针对此类散射面波,非线性相关F-K域滤波技术有比较好的处理效果,但仍保留部分近炮检距的残留面波及反向线性噪声。
图 3d是基于自适应相减滤波面波压制后的记录。从处理效果上看,与F-K域滤波后的记录(图 3c)相比,整体上没有明显差异。文中自适应相减滤波的本质意义在于保真处理,它将F-K域滤波提取的面波模型进行了低频、低波数的有效信号回减,保证了在压制面波的同时,尽可能不损伤有效信号。
图 3e是利用Curvelet变换分别进行3次阈值迭代面波压制后的记录。从处理效果上看,面波压制彻底,特别是图 3c的近炮检距残留面波以及反向线性噪声都得到了很好的压制。但是,Curvelet变换流程参数设置繁琐,每一次迭代参数会随着面波的压制程度以及此时面波与有效波在Curvelet域中的特征差异进行重新设置。通常原始采集数据面波干扰较重,有效波与面波在Curvelet域中的差异性并非特别明显,需要进行逐步分离,提高二者在Curvelet域中的差异性,才能达到比较好的面波压制效果。本文方法在利用自适应相减压制大部分面波后,再利用Curvelet变换压制图 3d中的残留面波及反向线性噪声,其含量少,且特征明显,可以很好地利用Curvelet变换的多方向特性,将其在Curvelet域中与有效波分离。相对于单纯的利用Curvelet变换压制面波,本文利用Curvelet变换压制残留面波,流程参数设置更加简便,适用性更强。由图 3f可见,面波压制彻底,单炮信噪比明显提高,有效波同相轴连续性增强。
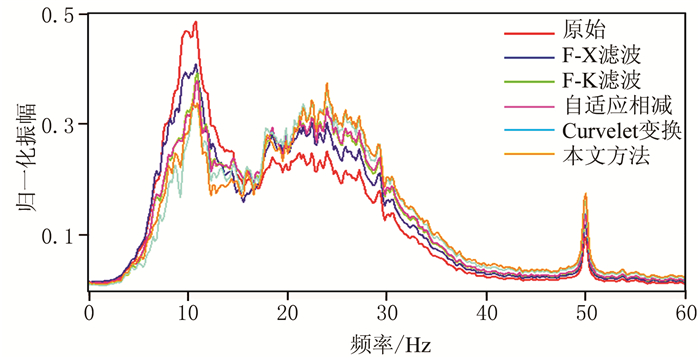
图 4是不同方法面波压制前后归一化频谱曲线,可见不同方法压制面波后,低频段强能量面波都得到了相应的衰减,且低频段信息保护较好,未见明显频谱泄露。
|
图 4 不同方法面波压制前、后频谱对比 |
实际资料来源于四川M工区。采集参数包括:记录长度为5s,采样间隔为2ms,道间距为30m,双边180道接收,炸药激发,激发岩性主要为灰岩、泥岩和砂岩,井深为5~20m。
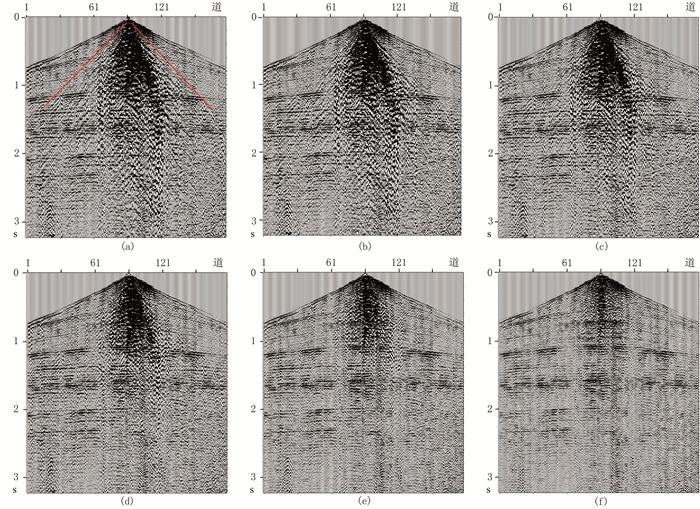
首先,对原始数据进行频率和速度分析。图 5是原始资料通过低截分频扫描后的单炮记录,可见低截扫描到18Hz时,仍能见部分面波,低截扫描到22Hz时,面波不明显。由此可初步判定面波的优势频带范围在20Hz以内。图 5a红色线是在原始单炮上进行的简单的线性速度测量示意图,通过初步测量得到面波的优势速度范围在1800m/s以内。
|
图 5 原始单炮与不同低截分频扫描记录的对比 (a)原始;(b)6Hz;(c)10Hz;(d)14Hz;(e)18Hz;(f)22Hz |
在对原始资料的频率—速度分析后,可基本确定面波在F-K域中的优势区域,然后通过F-K域滤波得到需要的面波模型。为了避免面波模型中含有有效信号,对F-K滤波后的面波做倾角滤波,将低倾角的有效波回减,最大限度地保护有效信号不受损伤。
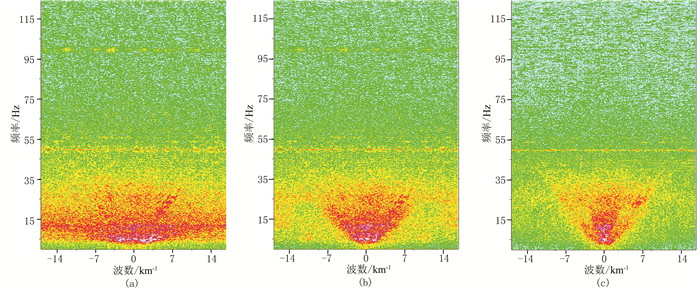
得到面波模型后,再与原始数据进行自适应相减,可得第一次面波压制后的地震数据及噪声,如图 6a所示。可见,原始记录中大部分面波被衰减,单炮记录未见空间假频、混波等波形失真现象,且噪声记录未见明显有效信号,相对保真保幅处理效果良好。但是,自适应相减面波压制后单炮近炮道存在部分面波残留,表现为线性相关性低、能量强、频率高等特点,同时还残留部分反向线性噪声。Curvelet变换的多方向特性及非线性特征,对这部分残留的噪声具有较好的压制效果。图 6b是将第一次面波压制后的单炮(图 6a左)变换到Curvelet域进行信噪分离后的单炮记录及噪声,可以看出,近炮检距残留的低线性相关面波得到有效的压制,且反向线性噪声也得到了衰减,噪声记录中未见明显有效信号。图 7是两次面波压制前、后的单炮记录的F-K谱,经过两次面波衰减后,F-K谱中噪声能量得到有效衰减。从整体处理效果看,本文提出的组合面波压制技术,在保真保幅处理的前提下,实现了面波的有效压制。

|
图 6 分步去噪后的单炮(左)及噪声(右)记录 (a)自适应相减滤波;(b)Curvelet变换 |
|
图 7 去噪前、后单炮记录的F-K谱对比 (a)原始;(b)自适应相减滤波;(c)Curvelet变换滤波 |
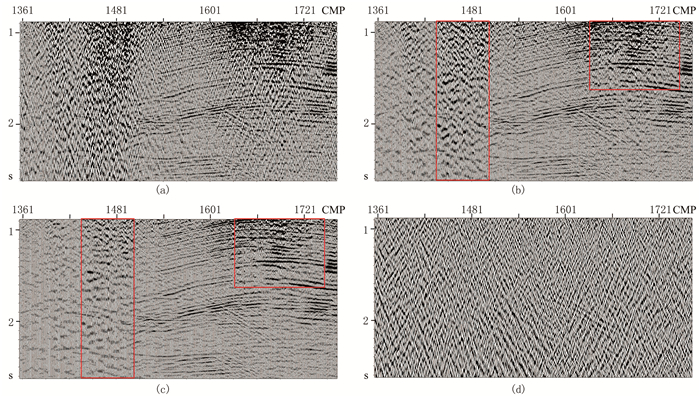
图 8是应用本文方法压制面波前、后的纯波叠加剖面及噪声叠加剖面(增益后)。由剖面可见,原始叠加剖面面波干扰严重,低信噪比区,有效波几乎被面波掩盖。通过自适应相减面波压制后,大部分面波被压制,但剖面上仍存在部分残留面波。这部分残留面波通过Curvelet变换滤波后,得到有效衰减,且低信噪比区低频面波被压制后,有效波的连续性增强(图 8b、图 8c巨形框所示)。为了验证本文方法的保真保幅性,将噪声剖面进行信号放大后(时窗为500ms的瞬时增益)的噪声剖面(图 8d)未见明显有效信号,表明本文方法在提高资料信噪比的同时,实现了面波的保真保幅压制。
|
图 8 面波压制前、后叠加剖面及噪声叠加剖面对比 (a)原始;(b)自适应滤波;(c)Curvelet变换;(d)噪声(增益后) |
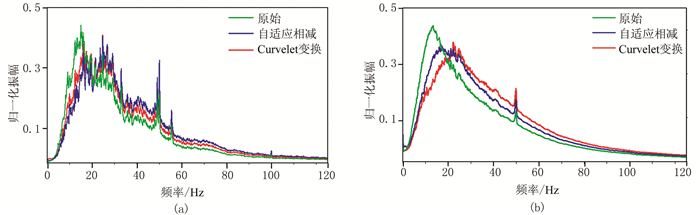
图 9为去噪前、后单炮记录和叠加剖面归一化后的频谱,去噪后低频面波得到衰减,主频向高频移动。
|
图 9 去噪前、后频谱对比 (a)单炮记录;(b)叠加剖面 |
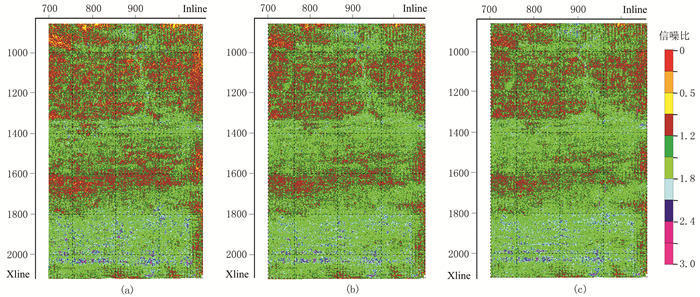
图 10为去噪前、后的叠加数据体信噪比统计,经过两次面波衰减后,信噪比逐步提高,且未见明显异常点,去噪效果明显。
|
图 10 去噪前、后叠加数据体信噪比统计结果 (a)原始;(b)自适应滤波;(c)Curvelet变换 |
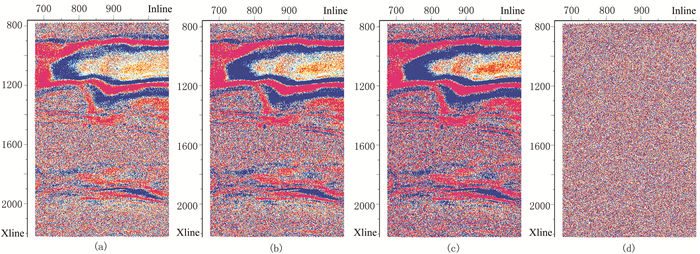
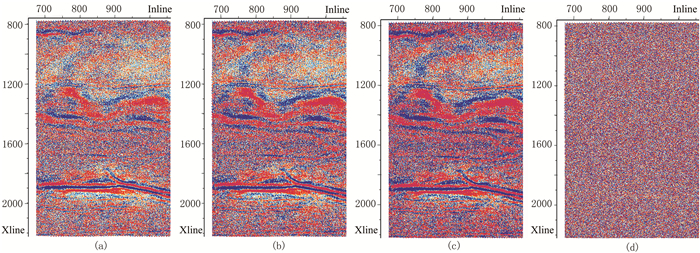
图 11和图 12为不同时刻叠加数据体的振幅切片,经过两轮面波压制后,切片更加光滑。从噪声切片上看,未见明显与有效信号相关的信息,面波压制效果良好。
|
图 11 去噪前、后及噪声叠加数据体振幅切片(2800ms) (a)原始;(b)自适应滤波;(c)Curvelet变换;(d)噪声 |
|
图 12 去噪前、后及噪声叠加数据体振幅切片(3200ms) (a)原始;(b)自适应滤波;(c)Curvelet变换;(d)噪声 |
图 13为原始数据经过两轮面波压制前、后局部叠加剖面低通分频扫描结果。自适应相减面波压制后,资料品质改善明显,大部分面波被衰减,有效波突出,但仍能看到部分残留面波,呈蚯蚓状,且存在挂条带现象。通过Curvelet变换进行第二次面波压制后,残留面波得到有效压制,剖面成像质量有所提升,0~4Hz扫描结果能隐约见到有效波同相轴,低频信息保护较好。

|
图 13 去噪前、后局部剖面分频扫描结果 (a)原始;(b)自适应滤波;(c)Curvelet变换。从左到右依次为:0~250Hz,0~4Hz,0~6Hz,0~8Hz,0~10Hz,0~12Hz |
基于已有的面波压制技术,本文结合自适应相减滤波技术的保真保幅特性与Curvelet变换的多方向特征,进行有机组合压制面波。与其他常用面波压制方法对比,验证了本文方法的优点。实际数据处理结果中未见明显空间假频、混波等波形失真现象,各平面属性图未见异常现象点,分频扫描记录中0~4Hz能隐约见到有效波同相轴,低频信息保护较好。噪声记录放大显示未见明显有效波信息,噪声切片亦未见明显与有效信号相关的信息,充分说明本文方法在提高资料信噪比的同时,能实现相对保真保幅面波压制。
| [1] |
李振春, 张军华. 地震数据处理方法[M]. 山东东营: 石油大学出版社, 2004: 23-54.
|
| [2] |
张军华, 吕宁, 田连玉, 等. 地震资料去噪方法技术综合评述[J]. 地球物理学进展, 2006, 21(2): 546-553. ZHANG Junhua, LYU Ning, TIAN Lianyu, et al. An overview of the methods and techniques for seismic data noise attenuation[J]. Progress in Geophysics, 2006, 21(2): 546-553. |
| [3] |
罗国安, 杜世通. 小波变换及信号重建在压制面波中的应用[J]. 石油地球物理勘探, 1996, 31(3): 337-349. LUO Guoan, DU Shitong. Application of wavelet transform and signal reconstruction in surface wave elimination[J]. Oil Geophysical Prospecting, 1996, 31(3): 337-349. |
| [4] |
毕云云, 汪金菊, 徐小红, 等. 基于离散曲波变换字典和二维局部离散余弦变换字典组合的面波压制[J]. 石油物探, 2017, 56(2): 222-231. BI Yunyun, WANG Jinju, XU Xiaohong, et al. Ground roll attenuation based on the combination of discrete curvelet transform dictionary and two-dimensional local discrete cosine transform dictionary[J]. Geophysical Prospecting for Petroleum, 2017, 56(2): 222-231. |
| [5] |
徐阳, 罗明璋, 王智, 等. 广义S变换与二维离散小波变换联合压制面波[J]. 石油物探, 2018, 57(3): 395-403. XU Yang, LUO Mingzhang, WANG Zhi, et al. Surface wave suppressing using generalized S-transform and 2D discrete wavelet transform[J]. Geophysical Pro-specting for Petroleum, 2018, 57(3): 395-403. |
| [6] |
李文杰, 魏修成, 宁俊瑞, 等. 基于频率衰减特性的面波压制方法[J]. 石油物探, 2008, 47(3): 225-227. LI Wenjie, WEI Xiucheng, NING Junrui, et al. A method for suppressing surface wave by considering the characteristic of frequency attenuation[J]. Geophysical Prospecting for Petroleum, 2008, 47(3): 225-227. |
| [7] |
马振元, 杜文凤, 卢勇旭, 等. 基于最小平方滤波的面波压制方法[J]. 物探与化探, 2016, 40(3): 561-567. MA Zhenyuan, DU Wenfeng, LU Yongxu, et al. A method based on least-squares filter of seismic ground-roll suppression[J]. Geophysical and Geochemical Exploration, 2016, 40(3): 561-567. |
| [8] |
王志农, 孙成禹, 伍敦仕, 等. 利用区域自适应极化滤波压制多分量面波干扰[J]. 石油地球物理勘探, 2019, 54(6): 1206-1216. WANG Zhinong, SUN Chengyu, WU Dunshi, et al. A surface wave suppression method based on area adaptive polarization filtering[J]. Oil Geophysical Prospecting, 2019, 54(6): 1206-1216. |
| [9] |
谢金娥, 郭全仕, 刘财, 等. 高密点地震资料面波压制的自适应波束方法[J]. 石油物探, 2009, 48(2): 110-114. XIE Jin'e, GUO Quanshi, LIU Cai, et al. Self-adaptive beam method for suppressing ground roll in high-density seismic data[J]. Geophysical Prospecting for Petroleum, 2009, 48(2): 110-114. |
| [10] |
董烈乾, 张慕刚, 张翊孟. 预测自适应相减面波压制方法[J]. 石油地球物理勘探, 2016, 51(6): 1089-1093. DONG Lieqian, ZHANG Mugang, ZHANG Yimeng. A ground roll suppression method based on predictive and adaptive subtraction[J]. Oil Geophysical Prospecting, 2016, 51(6): 1089-1093. |
| [11] |
陈文超, 高静怀, 包乾宗. 基于连续小波变换的自适应面波压制方法[J]. 地球物理学报, 2009, 52(11): 2854-2861. CHEN Wenchao, GAO Jinghuai, BAO Qianzong. Adaptive attenuation of ground roll via continuous wavelet transform[J]. Chinese Journal of Geophysics, 2009, 52(11): 2854-2861. |
| [12] |
岳龙, 刘怀山, 尹燕欣, 等. 基于连续小波变换的面波衰减方法研究[J]. 石油物探, 2016, 55(2): 214-222. YUE Long, LIU Huaishan, YIN Yanxin, et al. Atte-nuation of ground roll based on continuous wavelet transform[J]. Geophysical Prospecting for Petro-leum, 2016, 55(2): 214-222. |
| [13] |
郑静静, 印兴耀, 张广智, 等. 基于第二代Curvelet变换的面波压制[J]. 应用地球物理, 2010, 7(4): 325-335. ZHENG Jingjing, YIN Xingyao, ZHANG Guangzhi, et al. The surface wave suppression using the second generation Curvelet transform[J]. Applied Geophy-sics, 2010, 7(4): 325-335. |
| [14] |
李继伟, 刘晓兵, 周俊骅, 等. 基于能量比的Curvelet阈值迭代面波压制[J]. 石油地球物理勘探, 2019, 54(5): 997-1004. LI Jiwei, LIU Xiaobing, ZHOU Junhua, et al. A Curvelet threshold iteration method based on energy ratio for surface-wave suppression[J]. Oil Geophysical Prospecting, 2019, 54(5): 997-1004. |
| [15] |
董烈乾, 李振春, 王德营, 等. 第二代Curvelet变换压制面波方法[J]. 石油地球物理勘探, 2011, 46(6): 897-904. DONG Lieqian, LI Zhenchun, WANG Deying, et al. Ground-roll suppression based on the second generation Curvelet transform[J]. Oil Geophysical Prospecting, 2011, 46(6): 897-904. |
| [16] |
李杨, 董守华, 杜顺庆. 基于广义S变换的面波压制技术研究[J]. 能源技术与管理, 2009, 5(3): 116-118. LI Yang, DONG Shouhua, DU Shunqing. Surface wave suppression technique based on generalized S-transform analysis[J]. Energy Technology and Ma-nagement, 2009, 5(3): 116-118. |
| [17] |
张金宝, 成谷, 王云专, 等. 去噪强度、去噪效率与振幅保真[J]. 石油地球物理勘探, 2002, 37(1): 1-5. ZHANG Jinbao, CHENG Gu, WANG Yunzhuan, et al. Intensity and efficiency of noise attenuation and amplitude fidelity[J]. Oil Geophysical Prospecting, 2002, 37(1): 1-5. |
| [18] |
徐颖, 刘晨, 吕秋玲, 等. 多域组合去噪技术在塔中奥陶系低信噪比资料处理中的应用[J]. 石油物探, 2015, 54(2): 172-179. XU Ying, LIU Chen, LYU Qiuling, et al. Application of multi-domain composite denoising technology for the processing of Ordovician low SNR seismic data in Tazhong Area[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 172-179. |
| [19] |
陈娟, 赵玉华, 胡剑, 等. 叠前保真去噪技术在额济纳旗及邻区的应用[J]. 地球物理学进展, 2014, 29(5): 2157-2163. CHEN Juan, ZHAO Yuhua, HU Jian, et al. Application of prestack preserved amplitude denoising technology in Ejin Banner and its vicinities[J]. Progress in Geophysics, 2014, 29(5): 2157-2163. |
| [20] |
尹思, 王传武, 董永苍, 等. 利用保幅去噪技术提高地震资料分辨率--以柴达木盆地尖顶山地区为例[J]. 石油地球物理勘探, 2018, 53(增刊2): 7-11. YIN Si, WANG Chuanwu, DONG Yongcang, et al. Preserved-amplitude denoising for seismic resolution improvement:an example of Jiandingshan area in Qaidam Basin[J]. Oil Geophysical Prospecting, 2018, 53(S2): 7-11. |
| [21] |
王维红, 林春华, 张振. 保幅低频面波压制方法与应用[J]. 地球物理学进展, 2015, 30(3): 1190-1194. WANG Weihong, LIN Chunhua, ZHANG Zhen. Amplitude preserved low frequency surface wave suppression and its application[J]. Progress in Geophy-sics, 2015, 30(3): 1190-1194. |
| [22] |
Candès E J, Donoho D J. Curvelets:A Surprisingly Effective Nonadaptive Representation of Objects with Edges[M]. Nashville: Vanderbilt University Press, 1999.
|
| [23] |
Candès E J, Donoho D L. New tight frames of Curvelets and optimal representations of objects with piecewise-C2 singularities[J]. Communications on Pure and Applied Mathematics, 2004, 57(2): 219-266. DOI:10.1002/cpa.10116 |
| [24] |
Candès E J, Demanet L, Donoho D L, et al. Fast discrete curvelet transforms[J]. SIAM Multiscale Mo-deling and Simulation, 2006, 5(3): 861-899. DOI:10.1137/05064182X |



 李继伟, 四川省成都市华阳大道一段216号东方地球物理公司西南物探研究院, 610000。Email:
李继伟, 四川省成都市华阳大道一段216号东方地球物理公司西南物探研究院, 610000。Email: