非垂直向下的磁化强度(矢量)和非垂直向下的磁异常场强度(矢量),致使磁异常形态复杂化,从而使磁异常与其场源的关系变得很不直观。随着磁倾角变小,此问题越来越严重,给磁异常解释带来许多困难。Baranov[1]提出的磁异常化极概念(非垂直向下的磁化强度和磁异常场强度均转换为垂直向下,就像将磁源体搬到北极所产生的磁异常场一样,故称化极),奠定了解决这一问题的理论基础;Bhattacharyya[2]提出的位场波数域转换理论和方法,使磁异常化极得以实现。然而,随着磁倾角的减小,化极过程不稳定现象越发严重,使低纬度磁异常化极效果很不理想。于是各种低纬度波数域化极方法相继出现。这些方法可分为三类:①波数域压制型化极法,如伪倾角化极法[3]、平方余弦压制化极法[4]、维纳滤波化极法[5]及双曲正弦压制化极法[6]等;②波数域反演化极法[7];③波数域偏移抽样化极法[8-10]。
本文主要讨论三个问题:①从理论上证明压制型化极法肯定不能用于低纬度磁异常定量解释,但可用于定性解释;②从理论上揭示,采用等效源法实现的波数域反演化极和采用理论化极算子实现的波数域反演化极,前者效果总是优于后者的根本原因,给出该方法难以用于低纬度磁测资料定量解释的功能定位;③阐明波数域偏移抽样化极法的基本思想和方法原理,指出该方法相当苛刻的应用条件。
1 可用于定性解释的低纬度化极方法——压制型化极法从位场波数域转换算法误差方程[8-10]出发,导出了实用含噪磁异常波数域化极算法误差方程[9](附录A)
| $ \begin{array}{l} {\rm{Re}} \{ {\rm{IDFT}} \{ {R^\prime }(\mathit{\boldsymbol{md}}){\rm{DFT}}[g_1^\prime (\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})]\} \} \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {g_2}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }}) - {\rm{Re}} \left\{ {{\rm{IDFT}}\left\{ { \left[ {1 - \frac{{{R^\prime }(\mathit{\boldsymbol{md}})}}{{R(\mathit{\boldsymbol{md}})}}} \right] \times } \right.} \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{DFT}} [{g_2}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})]\} \} + {\rm{Re}} \{ {\rm{IDFT}} \{ {R^\prime }(\mathit{\boldsymbol{md}}) \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{DFT}} [e(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})]\} \} \end{array} $ | (1) |
式中:Re(·)表示取实部;DFT(·)、IDFT(·)分别表示正、反离散傅里叶变换;R(·)、R′(·)分别为理论化极算子和实用化极算子;g′1(nΔ)、g2(nΔ)分别为含噪待化极磁异常场和理论化极磁异常场;n(n1, n2)、m(m1, m2)分别为空间域和波数域坐标矢量,n1=1, 2, …, N1表示空间域x方向的离散坐标点,n2=1, 2, …, N2表示空间域y方向的离散坐标点,m1=1, 2, …, N1表示波数域u方向的离散坐标点,m2=1, 2, …, N2表示波数域v方向的离散坐标点;
利用式(1),可分析各种压制型化极法的基本功能。式中左端是以R′(md)为化极算子的实用化极算法表达式;右端第一项是理论化极异常场,第二项是化极损失项,第三项是观测误差。在低纬度区,理论化极算子R(md)实际是一放大作用极强的扇通滤波器,其中心线方位角θ0=90°+D(D为磁偏角);实用化极算子R′(md)是R(md)经压制的结果,也是一放大作用很强的扇通滤波器,中心线与R(md)的中心线重合。数学推导和计算可证明
| $ {1 - \frac{{{R^\prime }(\mathit{\boldsymbol{md}})}}{{R(\mathit{\boldsymbol{md}})}}} $ | (2) |
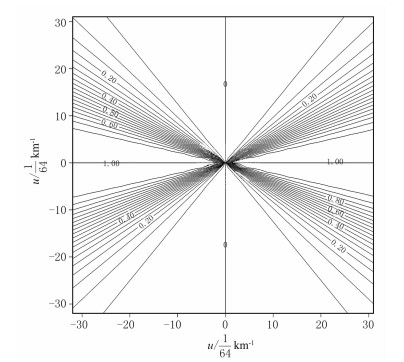
也是一种滤波器。不过,式(2)对伪倾角化极法[3]和平方余弦压制化极法[4]而言是扇通滤波器(图 1),对维纳滤波化极法[5]和双曲正弦压制化极法[6]而言是准扇通滤波器。这四个滤波器的中心线都与R(md)、R′(md)的中心线重合,但滤波强度弱很多。
|
图 1 扇通滤波器 |
笔者在研究磁异常化极中的误差规律时发现,像理论化极算子R(md)这类扇通滤波器,可分解为一个方向低通滤波器(中心线方位角为θ0=90°+D)和两个高通滤波器(其中滤波作用较强的滤波器中心方位角为θ0=90°+D,滤波作用较弱的滤波器中心方位角为θ0=D)[10]。其实实用化极算子R′(md)也可做同样的分解。扇通滤波器
下面对分解出的各个滤波器的功能及其对化极结果的影响作分析。
(1) 滤波器
(2) 滤波器
(3) 滤波器R′(md)中较强的方向低通滤波器(滤波器3),会导致化极结果图中出现沿磁偏角方向、正负相间的平行线状等值线。这是滤波器3对随机误差所形成的、遍布全图的正负等值线小圈沿磁偏角方向极度拉长的结果。因为随机误差所形成的小圈,高频成分较弱,所以R′(md)中的两个高通滤波器表现不明显。
上述三个滤波器的滤波强度都与压制因子的强度相关。压制因子增强,则滤波器3的作用减弱,滤波器1和滤波器2的作用增强。也就是说,压制因子增强,会削弱随机误差对化极结果的干扰,但同时会使化极损失效应增强。据此可得如下结论。
(1) 当增强压制强度,使滤波器3所产生的平行线异常减弱到可忽略不计的情况下,滤波器2将大幅度降低化极结果中正异常幅度,而小幅度地增强磁偏角方向上的边部负异常。
(2) 此种情况下,滤波器1对化极结果在垂直于磁偏角方向上有一定程度的圆滑作用。
(3) 在上述条件下,滤波器1、滤波器2将一定程度地影响化极异常的形态,但不影响化极异常的中心,也基本不影响化极结果中正异常的分布范围。
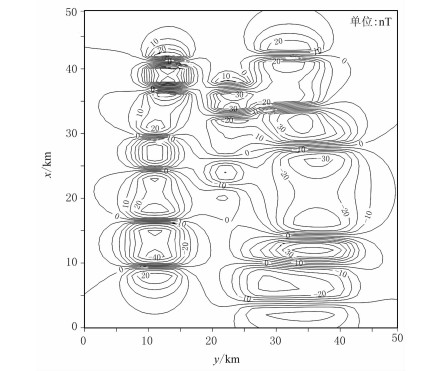
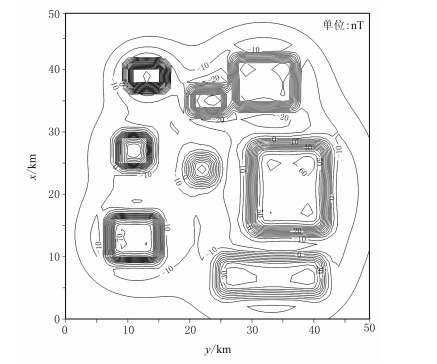
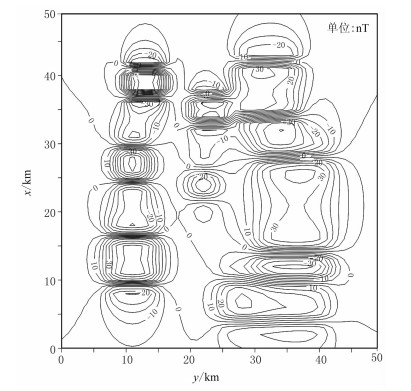
为了验证上述理论的正确性,设计一方柱体组合模型进行试验,模型参数见文献[11]。模型的磁倾角和磁偏角均为0°,观测范围为50km×50km,点、线距均为1km。图 2是该模型的总磁异常(ΔT),图 3是磁倾角为90°的理论化极异常。图 4是采用伪倾角法[3]计算的化极结果,其余三种压制型化极方法的化极结果与伪倾角法化极结果大同小异,故本文未展示。粗看上去,图 3与图 4差异非常大:图 4中化极结果的正异常幅值比图 3小得多,而磁偏角方向上的边部负异常则比图 3强;此外,垂直于磁偏角方向上的异常等值线出现一定程度的圆滑,而且变得稀疏。然而仔细观察可以发现,图 4所示的化极结果中正异常的中心位置和分布范围与图 3基本一致。
|
图 2 方柱体组合模型磁源的总磁异常(ΔT)分布图 |
|
图 3 图 2的理论化极异常(磁倾角为90°) |
|
图 4 采用伪倾角法对图 2磁异常的化极结果 |
理论分析和模型计算结果表明:各种波数域压制型化极法不能用于低纬度磁异常数据的定量解释,因为这些方法的化极结果与理论化极结果,无论异常形态还是量值,差异都相当大;但是这些方法完全可用于定性解释,因为化极结果中正异常的中心位置和分布范围与理论化极异常的基本一致。
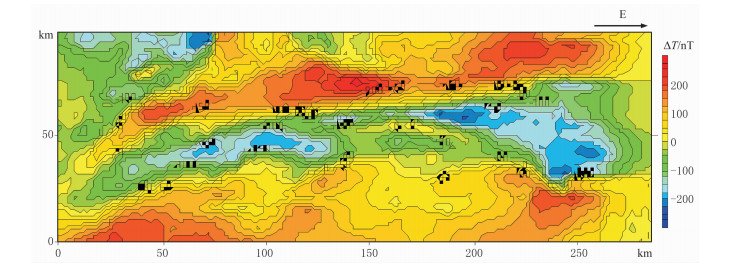
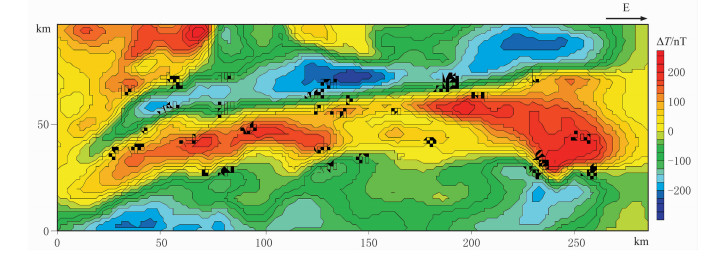
图 5是秘鲁A地区实测磁异常(ΔT)。该地区的地磁倾角和磁偏角分别为-2°和0°,观测点、线距均为2km,资料覆盖范围为100km×288km。图 6是图 5采用伪倾角法的化极结果,该图为秘鲁A地区的地质勘探提供了重要信息。
|
图 5 秘鲁A地区实测磁异常图 |
|
图 6 利用伪倾角法对图 5的化极异常图 |
从原理上看,波数域反演化极法[7]可用于低纬度磁异常数据的定量解释。该方法的核心是求解依据基本关系
| $ {\mathit{\boldsymbol{G}}{\mathit{\boldsymbol{m}}^\prime } = {\mathit{\boldsymbol{d}}^\prime }} $ | (3) |
建立的方程组
| $ {({\mathit{\boldsymbol{G}}^{\rm{H}}}\mathit{\boldsymbol{G}} + \mu {\mathit{\boldsymbol{S}}^{\rm{T}}}{\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{WS}}){\mathit{\boldsymbol{m}}^\prime } = {\mathit{\boldsymbol{G}}^{\rm{H}}}{\mathit{\boldsymbol{d}}^\prime }} $ | (4) |
式中:G是以1/R(md)为元素的对角矩阵;m′和d′分别为模型向量和观测值向量;W为加权函数矩阵;S为加权差分矩阵;上标“H”和“T”分别表示复共轭转置和转置;μ表示正则化参数。由理论化极算法误差方程[10]可知,式(3)严格成立的条件是G以T(md)为元素,而不是1/R(md),因为式(3)中的d′和m′分别是待化极异常的有限离散谱和化极目标异常的有限离散谱。T(md)与1/R(md)的关系(推导过程详见附录A)为
| $ \begin{array}{l} T(\mathit{\boldsymbol{md}}) = \frac{{ {\rm{DFT}} [{g_1}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})]}}{{ {\rm{DFT}} [{g_2}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})]}} = \frac{1}{{R(\mathit{\boldsymbol{md}})}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{{R(\mathit{\boldsymbol{md}})}}\frac{{ {\rm{DFT}} \left\{ {\sum\limits_{\mathit{\boldsymbol{k}} = - \propto ,\mathit{\boldsymbol{k}} \ne 0}^ \propto {{g_2}} [(\mathit{\boldsymbol{n}} + \mathit{\boldsymbol{kN}})\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}]} \right\}}}{{ {\rm{DFT}} [{g_2}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})]}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\sum\limits_{\mathit{\boldsymbol{l}} = - \propto ,\mathit{\boldsymbol{l}} \ne 0}^ \propto {{G_1}} [(\mathit{\boldsymbol{m}} + \mathit{\boldsymbol{lN}})\mathit{\boldsymbol{d}}]}}{{ {\rm{DFT}} [{g_2}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})]}} - \frac{1}{{R(\mathit{\boldsymbol{md}})}} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\sum\limits_{\mathit{\boldsymbol{l}} = - \propto ,\mathit{\boldsymbol{l}} \ne 0}^ \propto {{G_2}} [(\mathit{\boldsymbol{m}} + \mathit{\boldsymbol{lN}})\mathit{\boldsymbol{d}}]}}{{ {\rm{DFT}} [{g_2}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})]}} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{ {\rm{DFT}} \left\{ {\sum\limits_{\mathit{\boldsymbol{k}} = - \propto ,\mathit{\boldsymbol{k}} \ne 0}^ \propto {{g_1}} [(\mathit{\boldsymbol{n}} + \mathit{\boldsymbol{kN}})\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}]} \right\}}}{{ {\rm{DFT}} [{g_2}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})]}} \end{array} $ | (5) |
式中:g1[(n+kN)Δ]和G1[(m+lN)d]分别表示平面上无限延伸的待化极异常(无噪)及其谱的离散值;g2[(n+kN)Δ]和G2[(m+lN)d]分别表示平面上无限延伸的化极目标异常及其谱的离散值;l(l1, l2)、k(k1, k2)均为二维向量,l1、l2、k1、k2均为-∞到+∞的整数;g1(nΔ)为g1[(n+kN)Δ]的计算窗内部分,即无噪待化极磁异常场。式中的求和符号
Li等[7]用1/R(md)作为G的元素所获得的化极结果不理想,改用等效源法计算G的元素,结果大为改善。式(5)从理论上解释了这一现象产生的原因:采用等效源法得到的G中,至少包含了计算窗外数据的部分影响,而采用1/R(md)计算的G,则完全忽略了计算窗外数据的影响。文献[7]中的模型算例是对一直立方柱体的斜磁化磁异常场进行化极,所以采用一小直立方柱体为等效源计算G的元素,化极效果相当好。因为小方柱体磁异常的窗外数据与大方柱体磁异常的窗数据有很强的相似性。
由理论化极算法误差方程导出的式(5),为波数域反演化极过程中采用等效源法计算G的元素,提供了理论依据。然而对实际资料而言,窗外数据难以较精确地模拟。这可能就是该方法难以应用于实际资料处理的根本原因。
2.2 波数域偏移抽样化极法由含噪实用化极算法方程的推导过程(附录A)可知:式(1)中,若将DFT替换为移样离散傅里叶正变换算子DFT0η,将IDFT替换为移样离散傅里叶反变换算子IDFT0η(下标“0η”表示仅波数域偏移抽样,偏移参数η为二维行向量),将m替换为m+η,并令R′[(m+η)d]=R[(m+η)d],即得波数域偏移抽样化极算法方程
| $ \begin{array}{*{20}{l}} {{\rm{Re}}\{ {\rm{IDF}}{{\rm{T}}_{0\mathit{\boldsymbol{\eta }}}}\{ R[(\mathit{\boldsymbol{m}} + \mathit{\boldsymbol{\eta }})\mathit{\boldsymbol{d}}] \cdot {\rm{DF}}{{\rm{T}}_{0\mathit{\boldsymbol{\eta }}}}[g_1^\prime (\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})]\} \} }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {g_2}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }}) + {\rm{Re}}\{ {\rm{IDF}}{{\rm{T}}_{0\mathit{\boldsymbol{\eta }}}}\{ R[(\mathit{\boldsymbol{m}} + \mathit{\boldsymbol{\eta }})\mathit{\boldsymbol{d}}] \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{DF}}{{\rm{T}}_{0\mathit{\boldsymbol{\eta }}}}[e(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})]\} \} } \end{array} $ | (6) |
式中,左端为化极算法表达式,右端第一项为理论化极结果项,第二项为随机误差。波数域偏移抽样化极方法的基本思想是:测线沿磁偏角方向布设,使磁偏角为0°,然后通过沿u轴方向偏移v轴半个采样间隔(0.5d1)抽样,大大减小化极算子的量值,以控制随机误差对化极结果的影响。
由上述基本思想和式(6)的化极算法表达式可知,波数域偏移抽样化极法的具体做法包括如下步骤:
(1) 对磁偏角为0°的磁测资料做DFT0η变换,偏移抽样参数η=(0.5,0);
(2) 将步骤(1)的结果乘以理论化极算子R[(m+η)d];
(3) 对步骤(2)的结果做IDFT0η变换,偏移参数η=(0.5,0);
(4)对步骤(3)的结果取实部,即得偏移抽样化极结果。
波数域偏移抽样化极算法方程右端只有两项,一项是理论化极结果项,一项是观测误差项。因此把观测误差项的量值减至可忽略的程度,是该方法成功的关键。而误差项量值的减小,是通过沿u轴方向偏移v轴半个采样间隔(0.5d1)抽样实现的(d1越大,减小量越大)。这种抽样方式可使化极算子的量值大大减小,而且随着N1(d1=1/N1Δ1)的减小,量值还会进一步减小。然而当沿磁偏角方向上的网格数N1降至64时,化极算子的量值仍然相当大,以至于要求资料相对精度高于0.2%,才能保证观测误差项量值小到可忽略不计。
由上述分析可以看出,波数域偏移抽样化极法可用于低纬度磁异常的定量解释,但条件相当苛刻:磁偏角方向上网格数受限,且资料精度要求很高。因此在目前资料精度条件下,波数域偏移抽样化极法不可能用于低纬度区大面积磁测资料的定量解释。随着资料精度的不断提高,将来该方法有可能用于低纬度区小面积高精度磁测资料的定量解释。
3 结论(1) 理论研究表明,各种波数域压制型化极法不能应用于低纬度磁测资料的定量解释,但可以成为低纬度磁测资料定性解释的有效工具。这一理论成果的获得,实用化极算法误差方程的导出是基础,扇通滤波器定性分解(可分解为一个方向低通滤波器和两个或一个高通滤波器)观点的提出和运用是关键。这一源于化极问题的原创性概念和观点,为其他涉及扇通滤波器问题的解决提供了新的思路和方法。
(2) 文中的式(5)为波数域反演化极中采用等效源法计算G的元素,提供了严格的理论依据。理论上,该方法可用于低纬度磁测资料的定量解释,然而实际资料的窗外数据难以较精确地模拟。因此,该方法难以应用于实际数据的化极。该方法需求解超大型方程组,可能是难以实用化的另一原因。
(3) 波数域偏移抽样化极法,理论上可用于低纬度磁测资料的定量解释,但由于应用条件过于苛刻,在目前数据精度条件下不可能用于低纬度、大面积磁测资料的定量解释。但是随着未来资料精度的提高,该方法有可能用于低纬度区、小面积、高精度磁测资料的定量解释。
感谢中国石油集团东方地球物理公司贾继军高级工程师在研究初期在编程方面给予的帮助,杨战军高级工程师在图件绘制方面的帮助,以及孙喜明高级工程师在资料准备方面提供的帮助!
附录A 实用化极算法方程及T(md)表达式的推导假设g1(x, y)和G1(u, v)分别表示无噪待化极异常及其谱,g2(x, y)和G2(u, v)分别表示化极目标异常及其谱,那么g2(x, y)和G2(u, v)的二维IDFT算法误差方程[9]为
| $ \begin{array}{l} \begin{array}{*{20}{l}} {{\rm{IDFT}}[{G_2}(\mathit{\boldsymbol{md}})] - {g_2}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \sum\limits_{k = - \propto ,k \ne 0}^ \propto {{g_2}} [(\mathit{\boldsymbol{n}} + \mathit{\boldsymbol{kN}})\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}] - } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{IDFT}} \{ \sum\limits_{\mathit{\boldsymbol{l}} = - \propto ,\mathit{\boldsymbol{l}} \ne 0}^ \propto {{G_2}} [(\mathit{\boldsymbol{m}} + \mathit{\boldsymbol{lN}})\mathit{\boldsymbol{d}}]\} \end{array} $ | (A-1) |
g1(x, y)和G1(u, v)的二维DFT算法误差方程[9]可写作
| $ \begin{array}{*{20}{l}} {{G_1}(\mathit{\boldsymbol{md}}) = {\rm{DFT}} \{ {g_1}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})\} - \sum\limits_{\mathit{\boldsymbol{l}} = - \propto ,\mathit{\boldsymbol{l}} \ne 0}^ \propto {{G_1}} [(\mathit{\boldsymbol{m}} + \mathit{\boldsymbol{lN}})\mathit{\boldsymbol{d}}] + }\\ { {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{DFT}} \left\{ {\sum\limits_{\mathit{\boldsymbol{k}} = - \propto ,\mathit{\boldsymbol{k}} \ne 0}^ \propto {{g_1}} [(\mathit{\boldsymbol{n}} + \mathit{\boldsymbol{kN}})\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}]} \right\}} \end{array} $ | (A-2) |
式(A-2)两边乘以R(md), 并利用关系
| $ {G_2}(\mathit{\boldsymbol{md}}) = {G_1}(\mathit{\boldsymbol{md}})R(\mathit{\boldsymbol{md}}) $ | (A-3) |
可得
| $ \begin{array}{*{20}{l}} {{G_2}(\mathit{\boldsymbol{md}}) = R(\mathit{\boldsymbol{md}}){\rm{DFT}}\{ {g_1}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})\} - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} R(\mathit{\boldsymbol{md}})\sum\limits_{\mathit{\boldsymbol{l}} = - \propto ,\mathit{\boldsymbol{l}} \ne 0}^ \propto {{G_1}} [(\mathit{\boldsymbol{m}} + \mathit{\boldsymbol{lN}})\mathit{\boldsymbol{d}}] + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} R(\mathit{\boldsymbol{md}}){\rm{DFT}}\left\{ {\sum\limits_{\mathit{\boldsymbol{k}} = - \propto ,\mathit{\boldsymbol{k}} \ne 0}^ \propto {{g_1}} [(\mathit{\boldsymbol{n}} + \mathit{\boldsymbol{kN}})\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}]} \right\}} \end{array} $ | (A-4) |
将式(A-4)代入式(A-1),并移项,得理论化极算法误差方程
| $ \begin{array}{l} \begin{array}{*{20}{l}} {{\rm{IDFT}} \{ R(\mathit{\boldsymbol{md}}) {\rm{DFT}} [{g_1}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})]\} - {g_2}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})}\\ { = \sum\limits_{\mathit{\boldsymbol{k}} = - \propto ,\mathit{\boldsymbol{k}} \ne 0}^ \propto {{g_2}} [(\mathit{\boldsymbol{n}} + \mathit{\boldsymbol{kN}})\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}] + } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{IDFT}} \left\{ {R(\mathit{\boldsymbol{md}})\sum\limits_{\mathit{\boldsymbol{l}} = - \propto ,\mathit{\boldsymbol{l}} \ne 0}^ \propto {{G_1}} [(\mathit{\boldsymbol{m}} + \mathit{\boldsymbol{lN}})\mathit{\boldsymbol{d}}]} \right\} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{IDFT}} \left\{ {\sum\limits_{\mathit{\boldsymbol{l}} = - \propto ,\mathit{\boldsymbol{l}} \ne 0}^ \propto {{G_2}} [(\mathit{\boldsymbol{m}} + \mathit{\boldsymbol{lN}})\mathit{\boldsymbol{d}}]} \right\} - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{IDFT}} \left\{ {R(\mathit{\boldsymbol{md}}) {\rm{DFT}} \left\{ {\sum\limits_{\mathit{\boldsymbol{k}} = - \propto ,\mathit{\boldsymbol{k}} \ne 0}^ \propto {{g_1}} [(\mathit{\boldsymbol{n}} + \mathit{\boldsymbol{kN}})\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}]} \right\}} \right\} \end{array} $ | (A-5) |
对式(A-5)两端进行DFT后,乘以
| $ \begin{array}{l} \begin{array}{*{20}{l}} {{\rm{Re}} \{ {\rm{IDFT}} \{ {R^\prime }(\mathit{\boldsymbol{md}}) {\rm{DFT}} [{g_1}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})]\} \} - {g_2}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\rm{Re}} \left\{ {{\rm{IDFT}} \left\{ {\frac{{{R^\prime }(\mathit{\boldsymbol{md}})}}{{R(\mathit{\boldsymbol{md}})}} \times } \right.} \right.} \end{array}\\ \left. {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{DFT}}\left\{ {\sum\limits_{\mathit{\boldsymbol{k}} = - \propto ,\mathit{\boldsymbol{k}} \ne 0}^ \propto {{g_2}} [(\mathit{\boldsymbol{n}} + \mathit{\boldsymbol{kN}})\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}]} \right\}} \right\}} \right\} + \\ \begin{array}{*{20}{l}} { {\rm{Re}} \left\{ { {\rm{IDFT}} \left\{ {{R^\prime }(\mathit{\boldsymbol{md}})\sum\limits_{\mathit{\boldsymbol{l}} = - \propto ,\mathit{\boldsymbol{l}} \ne 0}^ \propto {{G_1}} [(\mathit{\boldsymbol{m}} + \mathit{\boldsymbol{lN}})\mathit{\boldsymbol{d}}]} \right\}} \right\} - }\\ { {\rm{Re}} \left\{ { {\rm{IDFT}} \left\{ {\frac{{{R^\prime }(\mathit{\boldsymbol{md}})}}{{R(\mathit{\boldsymbol{md}})}}\sum\limits_{\mathit{\boldsymbol{l}} = - \propto ,\mathit{\boldsymbol{l}} \ne 0}^ \propto {{G_2}} [(\mathit{\boldsymbol{m}} + \mathit{\boldsymbol{lN}})\mathit{\boldsymbol{d}}]} \right\}} \right\} - } \end{array}\\ \begin{array}{*{20}{l}} { {\rm{Re}} \left\{ {{\rm{IDFT}} \left\{ {{R^\prime }(\mathit{\boldsymbol{md}}){\rm{ DFT }}\left\{ {\sum\limits_{\mathit{\boldsymbol{k}} = - \propto ,\mathit{\boldsymbol{k}} \ne 0}^ \propto {{g_1}} [(\mathit{\boldsymbol{n}} + \mathit{\boldsymbol{kN}})\mathit{\boldsymbol{ \boldsymbol{\varDelta} }}]} \right\}} \right\}} \right\} - }\\ { {\rm{Re}} \left\{ { {\rm{IDFT}} \left\{ {\left[ {1 - \frac{{{R^\prime }(\mathit{\boldsymbol{md}})}}{{R(\mathit{\boldsymbol{md}})}}} \right] {\rm{DFT}} [{g_2}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})]} \right\}} \right\}} \end{array} \end{array} $ | (A-6) |
在采用实用化极算子的情况下,式(A-6)右端前四项量值很小,可忽略不计。所以实用无噪磁异常化极算法误差方程简化为
| $ \begin{array}{*{20}{l}} {{\rm{Re}} \{ {\rm{IDFT}} \{ {R^\prime }(\mathit{\boldsymbol{md}}) {\rm{DFT}} [{g_1}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})]\} \} - {g_2}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})}\\ {\;\: = - {\rm{Re}} \left\{ { {\rm{IDFT}} \left\{ {\left[ {1 - \frac{{{R^\prime }(\mathit{\boldsymbol{md}})}}{{R(\mathit{\boldsymbol{md}})}}} \right] {\rm{DFT}} [{g_2}(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})]} \right\}} \right\}} \end{array} $ | (A-7) |
上式两端同时加上
| $ {\rm{Re}}\{ {\rm{IDFT}} \{ {R^\prime }(\mathit{\boldsymbol{md}}){\rm{DFT}}[e(\mathit{\boldsymbol{n \boldsymbol{\varDelta} }})]\} $ | (A-8) |
并将g2(nΔ)由方程左端移到右端,即得正文中的式(1),即含噪实用化极算法方程。
对式(A-5)做如下变换:①将左端的g2(nΔ)移到右端;②对方程两端作DFT;③方程两端同除以R(md)DFT[g2(nΔ)],可得正文中的式(5),即T(md)的表达式。
| [1] |
Baranov V. A new method for interpretation of aeromagnetic maps[J]. Geophysics, 1957, 22(2): 359-383. |
| [2] |
Bhattacharyya B K. Two-dimensional harmonic analysis as a tool for magnetic interpretation[J]. Geophy-sics, 1965, 30(4): 829-857. |
| [3] |
Macleod I N, Jones K, Dai T F. 3-D analytic signal in the interpretation of total magnetic field data in low magnetic latitudes[J]. Exploration Geophysics, 1993, 24(3): 679-688. |
| [4] |
姚长利. 低纬度磁异常化极方法——压制因子法[J]. 地球物理学报, 2003, 46(5): 690-696. YAO Changli. Reduction-to-the-pole of magnetic anomalies at low latitude with suppression filter[J]. Chinese Journal of Geophysics, 2003, 46(5): 690-696. DOI:10.3321/j.issn:0001-5733.2003.05.017 |
| [5] |
Hansen R O, Pawlowski R S. Reduction to the pole at low latitudes by Wiener filtering[J]. Geophy-sics, 1989, 54(9): 1607-1613. |
| [6] |
张培琴, 赵群友. 低纬度区航磁异常变倾角磁化方向转换方法[J]. 物化探计算技术, 1996, 18(3): 206-211. ZHANG Peiqin, ZHAO Qunyou. Methods of the magnetic direction transform of aeromagnetic anomalies with differential inclinations at low magnetic latitudes[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1996, 18(3): 206-211. |
| [7] |
Li Y G, Oldenburg D W S. Reduction to the pole at the equator[J]. Geophysics, 2001, 66(2): 571-578. |
| [8] |
柴玉璞. 偏移抽样理论及其应用[M]. 北京: 石油工业出版社, 1997.
|
| [9] |
柴玉璞. Fourier变换数值计算的偏移抽样理论[J]. 中国科学(E辑), 1997, 40(5): 68-74. CHAI Yupu. Shift Sampling Theory of Fourier Transform Computation[J]. Science in China(E), 1997, 40(1): 21-27. |
| [10] |
Chai Y P. A-E equation of potential field transformation in the wavenumber domain and its application[J]. Applied Geophysics, 2009, 6(3): 205-216. |
| [11] |
柴玉璞. 从化极算法误差方程看各种波数域低纬度化极方法[J]. 石油地球物理勘探, 2012, 47(3): 496-505. CHAI Yupu. Evaluating the wavenumber domain RTP methods of magnetic anomaly at low latitudes from the RTP A-E equation[J]. Oil Geophysical Prospecting, 2012, 47(3): 496-505. |



 柴玉璞, 河北省涿州市范阳中路国际部大楼117室, 072751。Email:
柴玉璞, 河北省涿州市范阳中路国际部大楼117室, 072751。Email: