2 西安电子科技大学计算机科学与技术学院, 陕西西安 710071;
3 浙江大学地球科学学院, 浙江杭州 310027;
4 哈尔滨工业大学数学学院, 黑龙江哈尔滨 150001
2 School of Computer Science and Technology, Xidian University, Xi'an, Shaanxi 710071, China;
3 School of Earth Sciences, Zhejiang University, Hang-zhou, Zhejiang 310027, China;
4 School of Mathematics, Harbin Institute of Techno-logy, Harbin, Heilongjiang 150001, China
在位场数据解释中,场源边界识别是不可或缺的内容[1]。事实上,构造单元划分、断裂构造带位置的确定、岩性识别与地层分布解释、物性填图等,均需确定边界位置[2]。
边界识别方法的发展可分为三个阶段。第一阶段的研究大多基于位场异常表面不同阶次、不同方向上的导数及其组合,包括垂直导数[3]、水平总导数和二维解析信号[4]等。由于位场表面的导数随场源深度的增加衰减较快,且处理实际数据时求导计算会放大噪声,所以该阶段方法的主要缺点是对异常幅值较小的场源识别能力较差且抗噪能力差。第二阶段的方法主要针对边界均衡识别,包括倾斜角法(Tilt angle)[5]、倾斜角的水平总导数法[6]、自动增益控制法[7]等。这类方法能同时识别浅部与深部的地质体,但是提取的边界比较发散,定位不够准确。在第三阶段,学者们致力于在均衡识别的基础上增强所提取的边界,同时提高方法的抗噪能力,如Theta map法[8]、归一化标准差(NSTD)法[9]、增强型均衡滤波器法[10]、水平总导数的倾斜角(TAHG)法[11]等。由此可见,边界识别方法向更均衡、更收敛和更稳定的方向发展。
各阶谱矩及其统计不变量能够详细地描述表面几何特征,早先被广泛应用于工程领域的表面形貌识别,目前已被引入地球物理学领域并取得了良好的应用效果。孙艳云等[12]和杨文采等[13-14]基于二阶谱矩定义了脊形化系数和边界脊形化系数,从重力场成功地提取了地壳变形带信息,其中边界脊形化系数在构造边界定位中效果显著。付丽华等[15]基于二阶谱矩提出了一种描述表面数据粗糙度的特征因子,可有效反映数据波动与变异特征。付丽华等[16]基于四阶谱矩,应用算术平均顶点曲率提取磁异常数据特征,并将所提取的信息用于场源深度反演,取得了很好的效果。因此,利用谱矩能够从位场数据中提取出与场源边界、埋深等有关的几何特征信息。
相较于其他方法,基于谱矩的位场几何特征分析方法能够更均衡、收敛地识别地质体的几何特征。二阶谱矩可用于提取线形刻痕[12],但不能很好地识别其他刻痕。应用四阶谱矩的几何特征分析方法则可以进一步完善对弧形等刻痕信息的识别。为此,提出四阶弧形刻痕系数,理论和真实数据试验证明了利用此方法提取弧形和交会线形刻痕的有效性。最后结合二阶谱矩的脊形化系数对塔里木盆地航磁数据进行特征提取,更为全面地解释了该区域的地壳构造信息。
1 方法原理 1.1 表面谱矩在笛卡尔直角坐标系中,可用二维随机过程函数z(x, y)表示位场表面,其中z为异常强度,(x, y)是平面直角坐标位置。连续位场表面的p+q阶谱矩定义为[17-19]
| $ {m_{pq}} = \int_{ - \infty }^{ + \infty } {\int_{ - \infty }^{ + \infty } G } ({f_x},{f_y})f_x^pf_y^q{\rm{d}}{f_x}{\rm{d}}{f_y} $ | (1) |
式中:G(fx, fy)是位场表面z(x, y)的二维功率谱密度;fx、fy分别表示x、y方向上的空间频率。
实际勘探中得到的位场数据是离散的、有限的。假定研究区域共有M×N个采样点,在x、y方向上分别以Δx、Δy等间距采样,此时位场表面函数可表示为z(xi, yj)(i=1, 2, …, M; j=1, 2, …, N),对这样的离散位场表面,需要用滑动窗口提取局部特征信息。孙艳云等[12]推导出离散位场表面的p+q阶谱矩的表达式为
| $ \begin{array}{l} {m_{pq}} = \sum\limits_{v = 1}^{{N_1}} {\sum\limits_{u = 1}^{{M_1}} G } ({f_u},{f_v})f_u^pf_v^q\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{1}{{{N_1}{M_1}\Delta x\Delta y}}\sum\limits_{v = 1}^{{N_1}} {\sum\limits_{u = 1}^{{M_1}} {[F({f_u},{f_v})f_u^{p/2}f_v^{q/2}] \times } } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [{F^*}({f_u},{f_v})f_u^{p/2}f_v^{q/2}] \end{array} $ | (2) |
式中:M1、N1分别为滑动窗口在x、y方向包含的点数;F(fu, fv)为z(x, y)的二维离散傅里叶变换,F*(fu, fv)是其共轭。F(fu, fv)的傅里叶逆变换有如下性质
| $ \begin{array}{*{20}{l}} {{\rm{IDFT}} [F({f_u},{f_v}){f_u}] = \frac{{\partial z({x_u},{y_v})}}{{\partial x}}}\\ {u = 1,2, \cdots ,{M_1};v = 1,2, \cdots ,{N_1}} \end{array} $ | (3) |
| $ \begin{array}{*{20}{l}} {{\rm{IDFT}} [F({f_u},{f_v}){f_v}] = \frac{{\partial z({x_u},{y_v})}}{{\partial y}}}\\ {u = 1,2, \cdots ,{M_1};v = 1,2, \cdots ,{N_1}} \end{array} $ | (4) |
式中IDFT表示离散傅里叶逆变换。因此窗口面元的二阶谱矩元可用褶积形式表示为
| $ \begin{array}{*{20}{l}} {{m_{20}} = {z_x}({x_u},{y_v}) * {z_x}( - {x_u}, - {y_v})}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \sum\limits_{k = 1}^{{N_1}} {\sum\limits_{i = 1}^{{M_1}} {z_x^2} } ({x_i},{y_k})} \end{array} $ | (5) |
| $ {m_{11}} = \sum\limits_{k = 1}^{{N_1}} {\sum\limits_{i = 1}^{{M_1}} {{z_x}} } ({x_i},{y_k}){z_y}({x_i},{y_k}) $ | (6) |
| $ {m_{02}} = \sum\limits_{k = 1}^{{N_1}} {\sum\limits_{i = 1}^{{M_1}} {z_y^2} } ({x_i},{y_k}) $ | (7) |
且有
| $ {{z_x}(x,y) = \frac{{\partial z(x,y)}}{{\partial x}}} $ |
| $ {{z_y}(x,y) = \frac{{\partial z(x,y)}}{{\partial y}}} $ |
式中:m20为表面x方向斜率的方差;m02为y方向斜率的方差;m11是x方向斜率与y方向斜率的协方差。类似地,可推导四阶谱矩元m40、m31、m22、m13和m04的离散空间域表达式
| $ {{m_{40}} = \sum\limits_{k = 1}^{{N_1}} {\sum\limits_{i = 1}^{{M_1}} {z_{xx}^2} } ({x_i},{y_k})} $ | (8) |
| $ {{m_{31}} = \sum\limits_{k = 1}^{{N_1}} {\sum\limits_{i = 1}^{{M_1}} {{z_{xx}}} } ({x_i},{y_k}){z_{xy}}({x_i},{y_k})} $ | (9) |
| $ {{m_{22}} = \sum\limits_{k = 1}^{{N_1}} {\sum\limits_{i = 1}^{{M_1}} {z_{xy}^2} } ({x_i},{y_k})} $ | (10) |
| $ {{m_{13}} = \sum\limits_{k = 1}^{{N_1}} {\sum\limits_{i = 1}^{{M_1}} {{z_{yy}}} } ({x_i},{y_k}){z_{xy}}({x_i},{y_k})} $ | (11) |
| $ {{m_{04}} = \sum\limits_{k = 1}^{{N_1}} {\sum\limits_{i = 1}^{{M_1}} {z_{yy}^2} } ({x_i},{y_k})} $ | (12) |
式中
| $ {{z_{xx}}(x,y) = \frac{{{\partial ^2}z(x,y)}}{{\partial {x^2}}}} $ |
| $ {{z_{xy}}(x,y) = \frac{{{\partial ^2}z(x,y)}}{{\partial x\partial y}}} $ |
| $ {{z_{yy}}(x,y) = \frac{{{\partial ^2}z(x,y)}}{{\partial {y^2}}}} $ |
四阶谱矩元中,m40为x方向二阶导数
对于二阶谱矩,位场表面可用统计不变量M2和Δ2表征[17, 20-21]
| $ {{M_2} = {m_{20}} + {m_{02}}} $ | (13) |
| $ {{\varDelta _2} = \left| {\begin{array}{*{20}{c}} {{m_{20}}}&{{m_{11}}}\\ {{m_{11}}}&{{m_{02}}} \end{array}} \right| = {m_{20}}{m_{02}} - m_{11}^2} $ | (14) |
式中M2表示位场表面斜率的方差,能够反映位场异常的刻痕强弱,因此定义为刻痕的强度系数;Δ2主要与场在局部区域的各向异性有关,反映表面刻痕脊形化的程度,且通常Δ2≥0[12, 22-23]。
为从位场表面准确识别地壳变形带,孙艳云等[12]提出了刻痕的脊形化系数
| $ {\varLambda _2} = \frac{{2\sqrt {{\varDelta _2}} }}{{{M_2}}} = \frac{{2\sqrt {{m_{20}}{m_{02}} - m_{11}^2} }}{{{m_{20}} + {m_{02}}}} $ | (15) |
Λ2变化区间为[0, 1],与位场表面各向异性程度呈正相关,与刻痕强度系数M2成反比,可增强对异常幅值较小的场源的识别能力[12, 22]。
类似地,四阶谱矩的统计不变量M4和Δ4的计算公式[20]为
| $ {{M_4} = {m_{40}} + 2{m_{22}} + {m_{04}}} $ | (16) |
| $ {{\varDelta _4} = \left| {\begin{array}{*{20}{l}} {{m_{40}}}&{{m_{31}}}&{{m_{22}}}\\ {{m_{31}}}&{{m_{22}}}&{{m_{13}}}\\ {{m_{22}}}&{{m_{13}}}&{{m_{04}}} \end{array}} \right|} $ | (17) |
式中:M4表示表面曲率的方差,可反映表面曲率变化的剧烈程度,数值大说明表面明显地尖锐,峰顶呈尖峰状,数值小说明表面有较小的粗糙度变化,峰顶较圆滑;Δ4度量表面曲率的方向性效应,对应位场表面呈现圆弧形或者交会线形刻痕的几何特征,值小表明位场表面这种特征不明显。
与二阶谱矩的脊形化系数不同,四阶谱矩反映的是表面曲率变化,可提取圆弧形或者交会线形刻痕的几何特征,这种特征不受位场幅度大小的影响。因此,可以用四阶谱矩提取位场中的弧形刻痕信息,尤其是弧形的弱信号。为此,弧形刻痕系数必须与统计不变量Δ4正相关,与M4负相关。根据归一化的要求,用四阶谱矩的统计不变量M4和Δ4定义弧形刻痕系数
| $ {\varLambda _4} = \frac{{3\sqrt[3]{{{\Delta _4}}}}}{{{M_4}}} $ | (18) |
Λ4的变化区间亦为[0, 1]。Λ4与
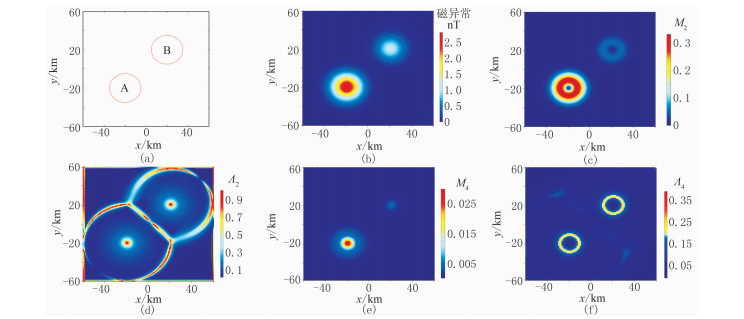
为检验谱矩方法提取弧形刻痕信息的有效性,设计图 1a所示模型。在大小为120km×120km、网格间距为1km×1km的区域内有两个半径均为15km、中心埋深均为20km的球状磁源体。球体A和B的球心坐标分别为(-20km,-20km)和(20km,20km),磁化强度分别为0.8A/m和0.3A/m。该模型的理论磁异常见图 1b。
|
图 1 球体模型及谱矩方法不同异常参数提取结果 (a)球体模型平面示意图;(b)理论磁异常;(c)M2;(d)Λ2;(e)M4;(f)Λ4 |
球体在地面的磁异常具有完整的弧形刻痕特征,是应用四阶谱矩提取位场中弧形刻痕信息的理想模型。采用3×3大小的滑动窗口对理论磁异常数据(图 1b)进行特征提取,结果如图 1c~图 1f所示。图 1c为刻痕的强度系数M2,由式(13)可知水平导数越大其值越大,主要反映较强磁异常的边界刻痕,对弱异常的识别能力较差,且提取的刻痕信息比较发散,不利于边界的准确定位。图 1d为脊形化系数Λ2,由图可知,Λ2能均衡识别强弱磁异常,可以确定两球体的中心位置,但是无法准确定位其弧形边界。图 1e为表面曲率的方差M4,主要反映较强磁异常的形状与位置信息,对弱异常的识别能力较差。由图 1f可知,弧形刻痕系数Λ4能均衡识别强弱磁异常,其高值清晰收敛地刻画出磁源体的边界。图中球体B因磁化强度较小而产生的异常较弱,但在Λ4的提取结果中,它的弧形刻痕信息和球体A的一样清晰,证明了应用四阶谱矩能够提取位场中的弧形刻痕的弱信号。
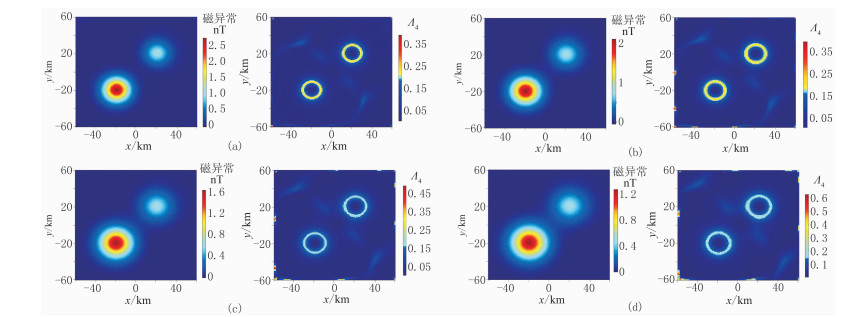
实际情况中地质体的埋深是未知的,因此边界识别方法对深度越不敏感越好,说明地质体埋深对提取效果的影响不大。为进一步检验弧形刻痕系数Λ4识别弧形边界的有效性,改变图 1a所示模型中球体的埋深,测试Λ4对深度的敏感程度。图 2a~图 2d是球体中心埋深分别为20、22、24、26km时的理论磁异常和Λ4提取结果。由于计算结果的范围变化较大,图中根据场值的大小采用不同的色标。
|
图 2 不同深度球体模型的理论磁异常(左)和弧形刻痕系数Λ4的提取结果(右) (a)20km;(b)22km;(c)24km;(d)26km |
由图 2可知,随着深度增加,原本独立的两磁异常范围渐渐扩大并产生交叠,场源强度逐渐变小,增加了边界识别的难度。分析Λ4的提取结果可知,弧形分布信息受场源强度影响较小,能稳定有效地反映不同深度地质体的弧形边界信息,对深度的敏感度较低。
为对比弧形刻痕系数Λ4与常用边界识别方法的效果,本文选取水平总导数(TDX)[9]、水平总导数的倾斜角TAHG[11]、Theta map[8]和归一化标准差(NSTD)方法[9]对模型(图 1a)进行边界信息提取,结果如图 3a~图 3d所示。

|
图 3 常用边界识别方法对球状地壳模型的提取结果(图中黑色虚线是球体边界) (a)TDX;(b)TAHG;(c)Theta map;(d)NSTD 图b~图d中各参数均为比值,无量纲,参数定义参见相关文献 |
由图 3可知,四种传统方法都能提取到两个球状磁源体的边界,但是均存在边界发散的问题,除TDX外的另外三种方法的提取结果中还存在干扰刻痕,难以准确分辨地质体的边界位置。对比图 1f可知,Λ4相较于传统方法能更准确、收敛地刻画球状磁源体的边界,且没有干扰刻痕。试验结果表明,Λ4的边界识别效果明显优于传统边界识别方法。
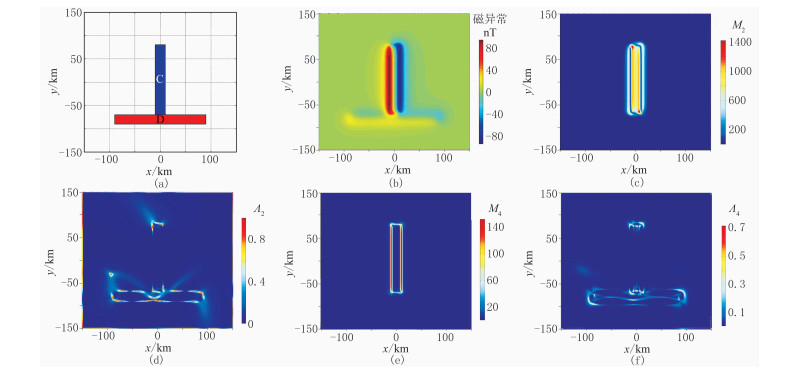
2.2 长方体模型为检验谱矩方法提取线形刻痕信息的有效性,设计图 4a所示包含两个长方体状磁源体(C和D)的组合模型进行理论试验。研究范围为300km× 300km、网格间距为1km×1km。磁源体C的中心坐标为(0,5.32km,9.00km),顶面埋深为4km,长、宽、高分别为150.00、20.22、10.00km,磁化强度为0.5A/m;磁源体D的中心坐标为(0,-79.79km,13.00km),顶面埋深为8km,长、宽、高分别为179.78、20.21、10.00km,磁化强度为0.2A/m。图 4b为该模型理论磁异常。
|
图 4 长方体模型及谱矩方法不同异常参数提取结果 (a)模型平面示意图;(b)理论磁异常图;(c)M2;(d)Λ2;(e)M4;(f)Λ4 |
据图 4可见,应用Λ2能够提取位场中的弱板形刻痕信号,应用Λ4也能够提取位场中的弱板形刻痕信号,不过边界不如Λ2清晰,这是因为Λ2主要反映的是磁异常表面斜率的变化,而Λ4主要反映的是曲率的变化,在长方体模型的平直边界处,磁异常斜率变化剧烈,曲率变化相对较小。仅仅利用Λ4,则可清晰地反映板形体的端角位置,而不是边界。板形体的端角呈现交会线形刻痕的几何特征,能够作为位场中的弧形刻痕信号被提取出来。
3 实际应用杨文采等[22]曾经介绍过塔里木盆地重力场的高阶谱矩分析,现在利用四阶谱矩的弧形刻痕系数分析该地区的航磁场。航空物探数据已经过标定和同化处理[24],经度和纬度方向点距分别为0.00886°和0.03380°,采样点数为678×356。磁力化极异常如图 5a所示。采用3×3的滑动窗口对其进行特征提取,Λ2和Λ4的提取结果分别见图 5b和图 5c。对比Λ2与Λ4的提取结果可见,二者有明显的区别,Λ2主要反映盆地基底中的线形构造,而Λ4主要反映出盆地内部主体为等轴状构造,如二叠纪古火山群等。

|
图 5 塔里木盆地磁异常(a)、Λ2(b)和Λ4(c)分布图 |
由于异常叠加及反演固有的多解性,准确解释区域磁异常非常困难,计算磁异常源的埋藏深度可以对地质成果的解释提供更准确的依据[25-27]。杨文采等[24]应用三维欧拉反褶积计算了区域磁异常源的埋藏深度。由于克拉通盆地地层通常具有上新下老的规律,将磁异常源分解为三个深度层次,分别为浅层2~5km、中层5~10km和深层10~20km。浅层磁异常源分布在盆地边缘,由中生代构造运动和海西期玄武岩侵位共同作用而成,在图 5a和图 5b中盆地边缘的线性构造中有明显反映。中层磁异常源分布在盆地内部,主要是海西期玄武岩侵位形成的,盆地内部5~10km的海相地层中常有发现。深层磁异常源主要是古老基底变质作用形成的,反映为图 5a和图 5b中盆地南部的线性构造。在磁异常图(图 5a)中,盆地内部深度为5~10km的海相地层中玄武岩侵位围绕古火山群分布,表现为等轴状构造的弱异常,淹没在古老变质基底的深层磁异常中,难以定位。在图 5c中Λ4强异常表现为红色圆圈状刻痕和圈点(如图中箭头所示),可能反映古火山群和其他等轴形状的地质体,说明应用四阶谱矩分析和信息提取技术成功地揭示了新的地壳组构。
4 结论(1) 基于谱矩的位场几何特征分析方法是近些年提出的一种新的自动边界识别方法,相较于传统方法能够更均衡、收敛地识别地质体的几何特征。二阶谱矩可用于提取线形刻痕,但不能很好地识别其他刻痕。应用四阶谱矩的几何特征分析方法可以进一步完善弧形等刻痕信息的识别。
(2) 与刻痕的脊形化系数不同,弧形刻痕系数反映的是圆弧形或者交会线形刻痕的几何特征,这种特征独立于位场的幅度。因此,可以应用四阶谱矩提取位场中的弧形刻痕信息,尤其是弧形的弱信号。
(3) 球体在地面的磁异常具有完整的弧形刻痕特征,是应用四阶谱矩来提取位场中弧形刻痕信息的理想模型。理论模型试验证明了应用四阶谱矩能够提取位场中的弧形刻痕的弱信号。
(4) 在塔里木盆地磁异常图中,盆地内部深度为5~10km的海相地层中玄武岩侵位围绕古火山群分布,表现为等轴状构造的弱异常,淹没在古老变质基底的深层磁异常中,难以定位。弧形刻痕系数强异常可反映古火山群和其他等轴形状的地质体,证明应用四阶谱矩分析和信息提取技术可以揭示特殊的地壳组构。
| [1] |
谭晓迪, 黄大年, 李丽丽, 等. 小波结合幂次变换方法在边界识别中的应用[J]. 吉林大学学报(地球科学版), 2018, 48(2): 420-432. TAN Xiaodi, HUANG Danian, LI Lili, et al. Application of wavelet transform combined with power transform method in edge detection[J]. Journal of Jilin University (Earth Science Edition), 2018, 48(2): 420-432. |
| [2] |
余钦范, 楼海. 水平梯度法提取重磁源边界位置[J]. 物探化探计算技术, 1994, 16(4): 363-367. YU Qinfan, LOU Hai. Extracting the boundary of magnetic and gravity sources using horizontal derivative method[J]. Computing Techniques for Geophysical and Geochemical Exploration, 1994, 16(4): 363-367. |
| [3] |
Evjen H M. The place of the vertical gradient in gra-vitational interpretations[J]. Geophysics, 1936, 1(1): 127-136. |
| [4] |
Nabighian M N. The analytic signal of two-dimensional magnetic bodies with polygonal cross-section:its properties and use for automated anomaly interpretation[J]. Geophysics, 1972, 37(3): 507-517. |
| [5] |
Miller H G, Singh V. Potential field tilt:a new concept for location of potential field sources[J]. Journal of Applied Geophysics, 1994, 32(2): 213-217. |
| [6] |
Verduzco B, Fairhead J D, Green C M, et al. New insights into magnetic derivatives for structural mapping[J]. The Leading Edge, 2004, 23(2): 116-119. DOI:10.1190/1.1651454 |
| [7] |
Rajagopalan S, Milligan P. Image enhancement of aeromagnetic data using automatic gain control[J]. Exploration Geophysics, 1995, 25(4): 173-178. |
| [8] |
Wijns C, Perez C, Kowalczyk P. Theta map:Edge detection in magnetic data[J]. Geophysics, 2005, 70(4): L39-L43. |
| [9] |
Cooper G R J, Cowan D R. Edge enhancement of potential-field data using normalized statistics[J]. Geophysics, 2008, 73(3): H1-H4. |
| [10] |
马国庆, 黄大年, 于平, 等. 改进的均衡滤波器在位场数据边界识别中的应用[J]. 地球物理学报, 2012, 55(12): 4288-4295. MA Guoqing, HUANG Danian, YU Ping, et al. Application of improved balancing filters to edge identification of potential field data[J]. Chinese Journal of Geophysics, 2012, 55(12): 4288-4295. DOI:10.6038/j.issn.0001-5733.2012.12.040 |
| [11] |
Ferreira F J F, De Souza J, Alessandra D B E S B, et al. Enhancement of the total horizontal gradient of magnetic anomalies using the tilt angle[J]. Geophy-sics, 2013, 78(3): J33-J41. |
| [12] |
孙艳云, 杨文采. 从重力场识别与提取地壳变形带信息的方法研究[J]. 地球物理学报, 2014, 57(5): 1578-1587. SUN Yanyun, YANG Wencai. Recognizing and extracting the information of crustal deformation belts from the gravity field[J]. Chinese Journal of Geophysics, 2014, 57(5): 1578-1587. |
| [13] |
杨文采, 孙艳云, 侯遵泽, 等. 用于区域重力场定量解释的多尺度刻痕分析方法[J]. 地球物理学报, 2015, 58(2): 520-531. YANG Wencai, SUN Yanyun, HOU Zunze, et al. An multi-scale scratch analysis method for quantitative interpretation of regional gravity fields[J]. Chinese Journal of Geophysics, 2015, 58(2): 520-531. |
| [14] |
杨文采, 孙艳云, 于常青, 等. 重力场多尺度刻痕分析与满加尔坳陷深层构造[J]. 地质学报, 2015, 89(2): 211-221. YANG Wencai, SUN Yanyun, YU Changqing, et al. Multi-scale scratch analysis of gravity field and deep structures in Manjar depression[J]. Acta Geologica Sinica, 2015, 89(2): 211-221. |
| [15] |
付丽华, 阮曙芬, 李宏伟, 等. 基于谱矩的地学特征因子提取方法及其应用[J]. 地质论评, 2017, 63(1): 246-255. FU Lihua, RUAN Shufen, LI Hongwei, et al. The spectrum moments-based approach to geo-science features extraction and its application[J]. Geological Review, 2017, 63(1): 246-255. |
| [16] |
付丽华, 杨文采. 谱矩方法在磁源体深度反演中的应用研究[J]. 地球物理学报, 2018, 61(7): 3044-3054. FU Lihua, YANG Wencai. Depth evaluation of magnetic sources by spectral moment analysis[J]. Chinese Journal of Geophysics, 2018, 61(7): 3044-3054. |
| [17] |
Thomas T R. Rough Surfaces[M]. London: Imperial College Press, 1999.
|
| [18] |
Longuet H M S. The statistical geometry of random surfaces[J]. Journal of the American Mathematics Society, 1962(13): 105-142. |
| [19] |
Yanagi K, Hara S, Endoh T. Summit identification of anisotropic surface texture and directionality assessment based on asperity tip geometry[J]. International Journal of Machine Tools and Manufacture, 2001, 41(13): 1863-1871. |
| [20] |
黄逸云. 三维随机表面形貌识别[J]. 浙江大学学报, 1984, 18(2): 138-148. HUANG Yiyun. The characterization of the three-dimensional random surface topography[J]. Journal of Zhejiang University, 1984, 18(2): 138-148. |
| [21] |
黄逸云. 随机表面二阶谱矩和统计不变量的几何解释及其图解法[J]. 浙江大学学报, 1985, 19(6): 143-153. HUANG Yiyun. Geometrical interpretation and graphical solution of second order spectrum moments and statistical invariants for random surface characterization[J]. Journal of Zhejiang University, 1985, 19(6): 143-153. |
| [22] |
杨文采, 孙艳云, 侯遵泽, 等. 用于塔里木地壳构造成像的重力场谱矩方法研究[J]. 地球物理学报, 2017, 60(8): 3140-3150. YANG Wencai, SUN Yanyun, HOU Zunze, et al. A study on spectral moments of gravity field with application to crustal structure imaging of Tarim basin[J]. Chinese Journal of Geophysics, 2017, 60(8): 3140-3150. |
| [23] |
孙艳云.从重力场提取地壳变形带信息的刻痕分析方法研究[D].北京: 中国地质大学(北京), 2015. SUN Yanyun.The Scratch Analysis Method for Information Extraction of Crustal Deformation Belts From Gravity Field[D]. Chinese University of Geo-sciences(Beijing), Beijing, 2015. |
| [24] |
杨文采, 王家林, 钟慧智, 等. 塔里木盆地航磁场分析与磁源体结构[J]. 地球物理学报, 2012, 55(4): 1278-1287. YANG Wencai, WANG Jialin, ZHONG Huizhi, et al. Analysis of regional magnetic field and source structure in Tarim Basin[J]. Chinese Journal of Geophy-sics, 2012, 55(4): 1278-1287. DOI:10.6038/j.issn.0001-5733.2012.04.023 |
| [25] |
王彦国, 罗潇, 邓居智, 等. 基于改进tilt梯度的三维磁异常解释技术[J]. 石油地球物理勘探, 2019, 54(3): 685-691. WANG Yanguo, LUO Xiao, DENG Juzhi, et al. 3D magnetic data interpretation based on improved tilt angle[J]. Oil Geophysical Prospecting, 2019, 54(3): 685-691. |
| [26] |
马国庆, 孟庆发, 李丽丽, 等. 利用重/磁场梯度比值函数计算地质体深度[J]. 石油地球物理勘探, 2019, 54(1): 229-234. MA Guoqing, MENG Qingfa, LI Lili, et al. Gradient ratio function of gravity and magnetic data for geolo-gical body depth calculation[J]. Oil Geophysical Prospecting, 2019, 54(1): 229-234. |
| [27] |
马国庆, 李丽丽, 杜晓娟. 磁张量数据的边界识别和解释方法[J]. 石油地球物理勘探, 2012, 47(5): 815-821. MA Guoqing, LI Lili, DU Xiaojuan. Boundary detection and interpretation by magnetic gradient tensor data[J]. Oil Geophysical Prospecting, 2012, 47(5): 815-821. |



 杨文采, 浙江省杭州市西湖区浙大路38号浙江大学玉泉校区第十一教学大楼244室, 310027。Email:
杨文采, 浙江省杭州市西湖区浙大路38号浙江大学玉泉校区第十一教学大楼244室, 310027。Email: