2 中国石油集团东方地球物理公司综合物化探处, 河北涿州 072751;
3 中南大学有色金属成矿预测与地质环境监测教育部重点实验室, 湖南长沙 410083;
4 南方科技大学前沿与交叉科学研究院, 广东深圳 51805;
5 青海省第三地质勘查院, 青海西宁 810029
2 GME & Geochemical Surveys of BGP, CNPC, Zhuozhou, Hebei 072751, China;
3 Key Laboratory of Metallogenic Prediction of Nonferrous Metals and Geological Environment Monitoring, Ministry of Education, Changsha, Hunan 410083, China;
4 SUSTech Academy for Advanced Interdisciplinary Studies, Shenzhen, Guangdong 518055, China;
5 The 3rd Geological Prospecting Institute of Qinghai Province, Xining, Qinghai 810029, China
20世纪60年代Rader[1]提出了一种快速离散傅里叶变换算法,极大提高了离散傅里叶变换的计算效率,使得快速傅里叶变换(FFT)算法得到了更加广泛的应用,被评为20世纪十大最优秀算法之一。早期FFT算法要求数据维数具有2n形式,随后针对数据维数为3n、2nK(n和K均为正整数)形式的FFT算法相继被提出[2-5]。而基于质数分解的FFT算法的出现,解除了对数据维数的要求。Frigo等[6]开发了FFTW软件包,集成各类FFT算法,实现了对任意维数数据的离散傅里叶变换快速计算。对于某些问题,空间或者频率域采样数据往往是不等间隔的,采用该采样方式的计算方法称为非规则采样数据离散傅里叶变换(NDFT,Non-Uniform Discrete Fourier Transform)。Dutt等[7]、Anderson[8]、Nguyen等[9]、Potts等[10]、Fessler等[11]、Greengard等[12]、Sørensen等[13]通过改进FFT算法实现了NDFT。
由于傅里叶变换算子的振荡性,傅里叶变换可以归为振荡函数的积分。高振荡函数积分的计算是计算科学领域的研究热点。目前求解振荡函数积分的方法大致可以分为三类:Filon型方法,Levin型方法和渐进展开法。对于傅里叶变换而言,由于算子e-ikx的矩已知,大多采用Filon型方法实现傅里叶变换[14-18]。Clendenin[14]采用的是线性函数;Piessens等[19]采用了更为复杂的Chebyshev多项式;Arieh[20]对基于Filon型方法的傅里叶变换算法中的积分点进行了分析,并在高震荡方程求解中取得良好的效果;Wu等[21]将高斯积分应用于核函数的积分中,取得了较高的计算精度;Li等[22]、Dai等[23]和戴世坤等[24]对高斯快速傅里叶变换与传统傅里叶变换在重、磁三维正演中的应用进行了对比研究。这些方法的区别在于剖分区间采用不同形式的多项式逼近核函数。
本文结合傅里叶变换积分与三次样条函数,提出一种快速傅里叶变换方法。该方法特点之一是能根据变换函数谱的变化趋势,任意地选取采样间距,提高了傅里叶变换剖分采样的灵活性,能兼顾计算精度和计算效率;特点之二是可根据离散后单元积分得到解析表达式,克服传统方法难以获得解析表达式的问题,进一步提高计算精度。
1 理论与方法 1.1 基于样条插值的一维傅里叶变换函数f(m)的一维傅里叶正变换公式为
| $ F(k) = \int_{ - \infty }^\infty {f(m)} {{\rm{e}}^{ - {\rm{i}}km}}{\rm{d}}m $ | (1) |
式中:k表示波数;F(k)为波数谱。对式(1)进行离散化
| $ F(k) = \sum\limits_{i = 1}^M {\int_{{m_i}}^{{m_{i + 1}}} {f(m)} } {{\rm{e}}^{ - {\rm{i}}km}}{\rm{d}}m $ | (2) |
式中M表示总单元数。
对单元i的内核函数进行三次样条插值[25]
| $ \begin{array}{*{20}{l}} {f{{(m)}_i} = {d_i}{{(m - {m_i})}^3} + {c_i}{{(m - {m_i})}^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {b_i}(m - {m_i}) + {a_i}} \end{array} $ | (3) |
式中系数ai、bi、ci、di可采用基于固定边界条件的样条插值计算得到。
将式(3)代入式(2),得到
| $ \begin{array}{l} F(k) = \mathop \sum \limits_{i = 1}^M \mathop \smallint \nolimits_{{m_i}}^{{m_{i + 1}}} [{d_i}{(m - {m_I})^3} + {c_i}{(m - {m_i})^2} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {b_i}(m - {m_i}) + {a_i}]{{\rm{e}}^{ - {\rm{i}}km}}{\rm{d}}m \end{array} $ | (4) |
令m′=m-mi,则式(4)变为
| $ F(k) = \mathop \sum \limits_{i = 1}^M \mathop \smallint \nolimits_0^L [{d_i}{m^{\prime 3}} + {c_i}{m^{\prime 2}} + {b_i}{m^\prime } + {a_i}]{{\rm{e}}^{ - {\rm{i}}k({m^\prime } + {m_i})}}{\rm{d}}{m^\prime } $ |
式中L表示单元长度。令单元积分为
| $ {I_{\rm{e}}} = (\int_0^L {{d_i}} {m^{\prime 3}} + {c_i}{m^{\prime 2}} + {b_i}{m^\prime } + {a_i}){{\rm{e}}^{ - {\rm{i}}k({m^\prime } + {m_i})}}{\rm{d}}{m^\prime } $ | (5) |
据式(5)可得解析积分表达式为
| $ {I_{\rm{e}}} = {d_i}{I_1} + {c_i}{I_2} + {b_i}{I_3} + {a_i}{I_4} $ | (6) |
其中
| $ \begin{array}{*{20}{l}} {{I_1} = \int_0^L {{m^{\prime 3}}} {{\rm{e}}^{ - {\rm{i}}k({m^\prime } + {m_i})}}{\rm{d}}{m^\prime }}\\ \begin{array}{l} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{1}{{{k^4}}}\{ - 6 + k{m^\prime }[ - 6i + k{m^\prime }(3 + ik{m^\prime })]\} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{\rm{e}}^{ - {\rm{i}}{k_x}({m^\prime } + {m_i})}}|_0^L \end{array} \end{array} $ |
| $ \begin{array}{*{20}{l}} {{I_2} = \int_0^L {{m^{\prime 2}}} {{\rm{e}}^{ - {\rm{i}}k({m^\prime } + {m_i})}}{\rm{d}}{m^\prime }}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{1}{{{k^3}}}[ - 2i + k{m^\prime }(2 + ik{m^\prime })]{{\rm{e}}^{ - {\rm{i}}k({m^\prime } + {m_i})}}|_0^L} \end{array} $ |
| $ {{I_3} = \int_0^L {{m^\prime }} {{\rm{e}}^{ - {\rm{i}}k({m^\prime } + {m_i})}}{\rm{d}}{m^\prime } = \frac{1}{{{k^2}}}(1 + ik{m^\prime }){{\rm{e}}^{ - {\rm{i}}k({m^\prime } + {m_i})}}|_0^L} $ |
| $ {{I_4} = \int_0^L {{{\rm{e}}^{ - {\rm{i}}k({m^\prime } + {m_i})}}} {\rm{d}}{m^\prime } = \frac{i}{k}{{\rm{e}}^{ - {\rm{i}}k({m^\prime } + {m_i})}}|_0^L} $ |
特别地,当波数k=0时,单元积分可简化为
| $ {I_{\rm{e}}} = \int_0^L {({d_i}{m^{\prime 3}} + {c_i}{m^{\prime 2}} + {b_i}{m^\prime } + {a_i})} {\rm{d}}{m^\prime } $ | (7) |
对式(7)积分可得解析表达式
| $ {I_{\rm{e}}} = {a_i}L + \frac{{{b_i}}}{2}{L^2} + \frac{{{c_i}}}{3}{L^3} + \frac{{{d_i}}}{4}{L^4} $ | (8) |
对函数f(x, y)进行二维傅里叶正变换
| $ F({k_x},{k_y}) = \int_{ - \infty }^\infty {\int_{ - \infty }^\infty {f(x,y)} } {{\rm{e}}^{ - {\rm{i}}({k_x}x + {k_y}y)}}{\rm{d}}x{\rm{d}}y $ | (9) |
式中:kx为x方向的波数;ky为y方向的波数;F(kx, ky)为波数谱。
式(9)的数值计算为二维积分,本文采取的策略是依次对x、y两个方向分别进行一维积分
| $ {F({k_x},y) = \int_{ - \infty }^\infty {f(x,y)} {{\rm{e}}^{ - {\rm{i}}{k_x}x}}{\rm{d}}x} $ | (10) |
| $ {F({k_x},{k_y}) = \int_{ - \infty }^\infty {F({k_x},y)} {{\rm{e}}^{ - {\rm{i}}{k_y}y}}{\rm{d}}y} $ | (11) |
为了分析误差,引入相对均方根误差[26],一维和二维的相对均方根误差公式分别为
| $ \left\{ {\begin{array}{*{20}{l}} {{\rm{rrms}} = \frac{{\sqrt {\sum\limits_{i = 1}^P {{{({{\hat B}_i} - {B_i})}^2}} } }}{{\sqrt {\sum\limits_{i = 1}^P {\hat B_i^2} } }} \times 100\% }\\ {{\rm{rrms }} = \frac{{\sqrt {\sum\limits_{i = 1}^P {\sum\limits_{i = j}^M {{{({{\hat B}_{ij}} - {B_{ij}})}^2}} } } }}{{\sqrt {\sum\limits_{i = 1}^P {\sum\limits_{i = j}^M {\hat B_{ij}^2} } } }} \times 100\% } \end{array}} \right. $ | (12) |
式中:P和M分别是x和y方向的节点数;Bi、Bij分别表示表示一维和二维数值解;
为了验证该方法的正确性,对高斯函数进行样条插值傅里叶变换,并与解析公式进行对比。其中,一维和二维高斯函数及其傅里叶变换解析公式分别为
| $ {f(x) = {{\rm{e}}^{ - \alpha {x^2}}} \Leftrightarrow F(k) = \sqrt {\frac{\pi }{\alpha }} {{\rm{e}}^{ - \frac{{{k^2}}}{{4a}}}}} $ | (13) |
| $ {f(x) = {{\rm{e}}^{ - \alpha ({x^2} + {y^2})}} \Leftrightarrow F({k_x},{k_y}) = \frac{\pi }{\alpha }{{\rm{e}}^{ - \frac{{k_x^2 + k_y^2}}{{4a}}}}} $ | (14) |
式中α是任意非零常数,本文令α=0.001。
设定一维傅里叶变换的取值范围为[-100m, 100m],采样点数为101,波数采样范围为[-0.3, 0.3],采样点数为101;二维变换x、y方向点坐标范围均为[-100m, 100m], 采样点数均为101个,两个方向波数范围均为[-0.3, 0.3], 采样点数均为101。一维和二维傅里叶变换的波数域和空间域采样均采用等间隔剖分。
图 1为一维正、反傅里叶变换数值解与解析解曲线。可以看出,正、反傅里叶变换的数值解与解析解吻合度很高,正、反傅里叶变换的相对均方根误差分别约为4.5×10-6和4.2×10-7,验证了本文一维傅里叶正、反变换理论的正确性。

|
图 1 一维傅里叶正(左)、反(右)变换数值解与解析解对比 |
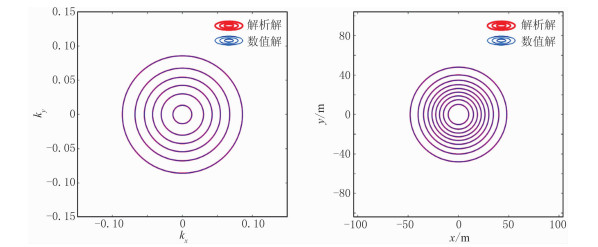
图 2为二维正、反傅里叶变换数值解与解析解等值线。可以看出,正、反傅里叶变换的数值解与解析解吻合度很高,正、反傅里叶变换的相对均方根误差分别约为6.0×10-6和1.4×10-5,验证了本文二维傅里叶正、反傅里叶变换理论的正确性。从计算结果可以看出,一维正反变换与二维正反变换的计算精度变化规律不同,这是由于不同的核函数谱的变化规律不同,因此其正、反傅里叶变换的计算精度不存在特定的规律性。
|
图 2 二维傅里叶正(左)、反(右)变换数值解与解析解 |
在频率域重磁场数值模拟中,傅里叶变换是关键步骤之一。设计连续介质模型,对基于样条插值傅里叶变换的重磁场三维数值模拟的计算效率与精度进行了研究,其中重磁场三维数值模拟采用空间波数混合域三维数值模拟方法[22-24]。文献[25]表明基于高斯—FFT的重磁场数值模拟具有较高的计算精度,本文算例将高斯点数NG=4的高斯FFT法重磁场数值模拟结果作为连续介质的解析解。本文算例中,令kx=ky=K。测试计算机配置为CPU-Inter Core i5-4590, 主频为3.3GHz, 内存为16GB。
3.1 重力场数值模拟设计连续介质模型,其垂直方向密度不变,水平方向剩余密度ρ的空间变化可表示为
| $ \rho = 2000 \times {{\rm{e}}^{ - 5 \times {{10}^{ - 8}}({x^2} + {y^2})}} $ | (15) |
模拟区域大小为20km(x)×20km(y)×10km(z),坐标原点位于水平范围中心;异常体区域大小为20km(x)×20km(y)×3km(z),顶面埋深为3km。模拟区域水平采样间隔均为200m,垂向采样间隔为100m,网格剖分数为101×101×101;异常体区域波数采样范围为-1.5×1.0-2~1.5×1.0-2。
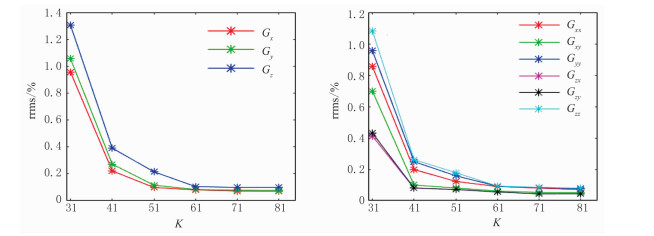
图 3为不同波数下模拟的地面重力异常场及其梯度张量的相对均方根误差。可以看出,随着波数的增大,重力异常场及梯度张量的相对均方根误差逐渐减小,当波数K为71时,其计算精度与高斯FFT计算结果接近。当K继续增大时,梯度张量的计算误差有增大趋势,原因在于随着波数的增大,基于样条插值傅里叶变换的计算精度逐渐高于4点高斯FFT的计算精度,若把高斯FFT作为解析解,误差缓慢增大。
|
图 3 模拟的重力异常场(左)及梯度张量(右)的相对均方根误差曲线 |
表 1所示为不同K时利用本文方法与高斯FFT方法计算地面重力场及其张量梯度耗时统计。可以看出,随着K的增大,样条插值FFT计算时间呈线性增长。在计算精度相近的情况下,即波数K=71时,样条插值FFT的计算时间为0.74s,高斯FFT的计算时间为4.85s,即前者约为后者的1/6。基于NG=4的高斯FFT计算时间相当于传统FFT计算量的16倍,而本文算法仅需计算一次积分,因而在相同的计算精度下,基于样条插值的傅里叶变换计算速度高于高斯FFT算法。
|
|
表 1 重力模型样条FFT与高斯FFT计算时间统计 |
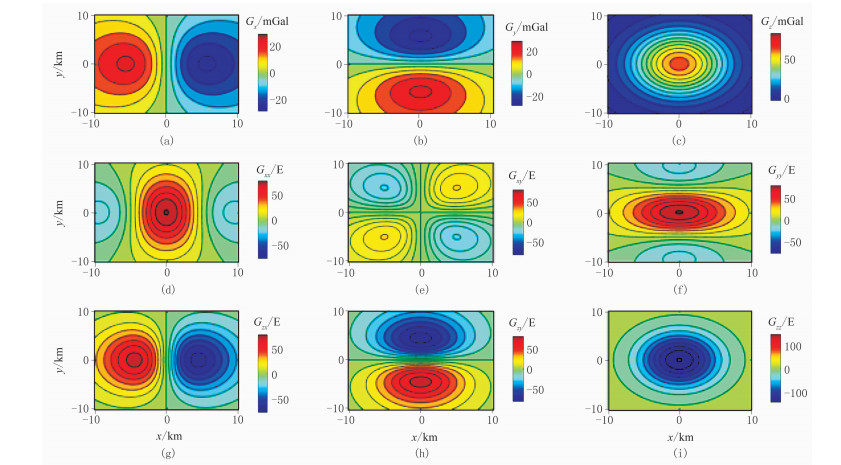
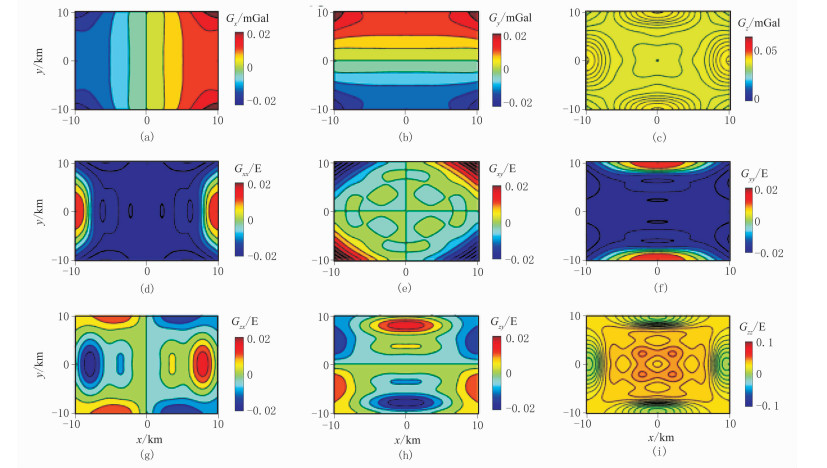
图 4为K=71时地面重力异常场及梯度张量的数值解,图 5为图 4数据的绝对误差。从图 4和图 5可以看出,重力异常场的绝对误差最大约为0.05mGal,重力梯度张量的绝对误差最大约为0.06E,均比数值解(图 4)低3个数量级,表明其计算精度高,K选取71是合适的。
|
图 4 K=71时重力异常Gx(a)、Gy(b)、Gz(c)及梯度张量Gxx(d)、Gxy(e)、Gyy(f)、Gzx(g)、Gzy(h)、Gzz(i)的数值解 |
|
图 5 K=71时重力异常Gx(a)、Gy(b)、Gz(c)及梯度张量Gxx(d)、Gxy(e)、Gyy(f)、Gzx(g)、Gzy(h)、Gzz(i)绝对误差分布 |
设计一个连续介质模型,垂直方向磁化率不变,水平方向磁化率κ的空间变化为
| $ \kappa = 0.02 \times {{\rm{e}}^{ - 5 \times {{10}^{ - 8}}x({x^2} + {y^2})}} $ | (16) |
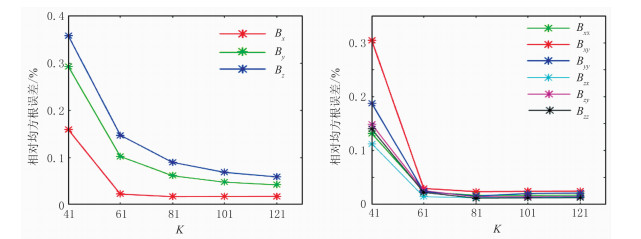
模拟区域为20km(x)×20km(y)×10km(z),坐标原点位于水平范围中心;异常区域大小为20km(x)×20km(y)×3km(z),顶面埋深为3km。模拟区域网格剖分数为101×101×101;异常区域空间水平采样间隔均为200m,垂向采样间隔为100m。背景磁异常场为35A/m,磁倾角为45°,磁偏角为5°,波数K采样范围为-1.5×1.0-2~1.5×1.0-2。图 6所示为不同K时,采用样条插值FFT计算的地面磁异常场及其梯度张量的相对均方根误差。可以看出,随着K的增加,磁异常场及梯度张量的相对均方根误差逐渐减小;当K=101时,磁异常场及梯度张量的相对均方根误差小于0.1%,其计算精度与高斯FFT接近,当波数继续增大时,均方根误差降低的趋势变缓。
|
图 6 不同K时本文方法计算的磁异常场(左)及梯度张量(右)相对均方根误差 |
表 2所示为不同K时分别用本文方法及高斯FFT计算地面磁场及其梯度张量所耗时间对比。可以看出,随着K的增加,样条插值FFT计算时间呈线性增长。在计算精度相近的情况下,即K=101时本文方法耗时1.52s,高斯插值FFT算法耗时6.77s,即样条插值FFT耗时约为高斯插值FFT的1/4。
|
|
表 2 磁力数据样条FFT与高斯FFT计算时间对比 |
图 7为波数K=101时磁异常场及梯度张量的数值解,图 8为波数K=101时磁异常场及梯度张量的绝对误差。由图 7与图 8可以看出,磁异常场的绝对误差最大约为0.05nT,磁梯度张量的绝对误差最大约为2×10-5nT/m,均比数值解(图 7)小2个数量级,表明本文方法计算精度高,且本实验中K选取101是合适的。

|
图 7 K=101时本文方法计算的磁异常场Bx(a)、By(b)、Bz(c)及梯度张量Bxx(d)、Bxy(e)、Byy(f)、Bzx(g)、Bzy(h)、Bzz(i)的数值解 |

|
图 8 K=101时本文方法计算的磁异常场Bx(a)、By(b)、Bz(c)及梯度张量Bxx(d)、Bxy(e)、Byy(f)、Bzx(g)、Bzy(h)、Bzz(i)绝对误差 |
为了进一步验证基于样条插值FFT方法对实测数据的应用效果,笔者利用“地理空间数据云”平台下载了安徽省数字高程数据(经度为117.6°~118.4°,纬度为30.5°~31.2°),对此数据进行数值模拟。该区地形如图 9所示,境内中部丘陵、岗地起伏,呈北东向展布。假设该地区地下地层为水平层状介质[26],采用基于样条插值FFT的空间波数混合域三维数值模拟方法计算其重力异常场,结果如图 10所示。可以看出,重力高的区域与图 9所示起伏地形范围吻合很好,说明基于样条插值FFT方法应用于实际数据的处理是可靠的,具有较好的适应性。

|
图 9 安徽省数字高程数据图 红色框内为研究区域 |

|
图 10 本文方法计算的重力异常场图 |
针对传统FFT存在截断效应的问题,本文结合FFT与三次样条插值算法,提出了一种基于样条插值的FFT算法。该方法充分利用样条插值拟合的高阶连续性及采样灵活的优点,兼顾计算精度和计算效率,实现了高效、高精度的FFT。得到如下结论:
(1) 利用高斯函数FFT,对比了数值解与解析解,验证了基于样条插值算法的一维、二维FFT的正确性。
(2) 将算法应用于频率域重、磁位场的计算,设计连续介质模型,对比基于样条插值FFT与高斯插值FFT的数值解,前者的计算精度更高。
(3) 对于连续介质模型,在计算精度相近的情况下,利用基于样条插值FFT进行重、磁场模拟计算,耗时统计数据表明,样条FFT的计算效率明显高于高斯FFT,前者的计算时间约为后者的1/6(重力数据)和1/4(磁力数据)。
| [1] |
Rader C M. Discrete Fourier transforms when the number of data samples is prime[J]. Proceedings of the IEEE, 1968, 56(6): 1107-1108. DOI:10.1109/PROC.1968.6477 |
| [2] |
Winograd S. On computing the discrete Fourier transform[J]. Proceedings of National Academy of Sciences, USA, 1976, 73(4): 1005-1006. DOI:10.1073/pnas.73.4.1005 |
| [3] |
Winograd S. On computing the discrete Fourier transform[J]. Mathematics of Computation, 1978, 32(141): 175-199. DOI:10.1090/S0025-5718-1978-0468306-4 |
| [4] |
Chu S, Burrus C S. A prime factor FTT algorithm using distributed arithmetic[J]. IEEE Transactions on Acoustic, Speech, and Signal Processing, 1982, 30(2): 217-226. DOI:10.1109/TASSP.1982.1163875 |
| [5] |
Duhamel P, Hollmann H. Split-radix FFT algorithm[J]. Electronics Letters, 1984, 20(1): 14-16. |
| [6] |
Frigo M, Johnson S G. The design and implementation of FFTW3[J]. Proceedings of the IEEE, 2005, 93(2): 216-231. |
| [7] |
Dutt A, Rokhlin V. Fast Fourier transforms for nonequispaced data[J]. SIAM Journal on Scientific Computing, 1993, 14(6): 1368-1393. |
| [8] |
Anderson M D D. Rapid computation of the discrete Fourier transform[J]. SIAM Journal on Scientific Computing, 1996, 17(4): 913-919. |
| [9] |
Nguyen N, Liu Q H. The regular Fourier matrics and nonuniform fast Fourier transforms[J]. SIAM Journal on Scientific Computing, 1999, 20(1): 283-293. |
| [10] |
Potts G S, Tasche M. Fast Fourier transforms for nonequispaced data:A tutorial, in modern sampling theory[J]. Applied & Numerical Harmonic Analysis, 2001, 14(6): 247-270. |
| [11] |
Fessler J A, Sutton B P. Nonuniform fast Fourier transforms using min-max interpolation[J]. IEEE Transaction Signal Processing, 2003, 51(2): 560-574. |
| [12] |
Greengard L, Lee J Y. Accelerating the nonuni-form fast Fourier transform[J]. SIAM Review, 2004, 46(3): 443-454. DOI:10.1137/S003614450343200X |
| [13] |
Sørensen T S, Schaeffter K N, Hansen M S. Accelerating the nonequispaced fast Fourier transform on commodity graphics hardware[J]. IEEE Transaction on Medical Imaging, 2008, 27(4): 538-547. |
| [14] |
Clendenin W W. A method for numerical calculation of Fourier integral[J]. Numerische Mathematik, 1966, 8(5): 422-436. DOI:10.1007/BF02166668 |
| [15] |
Piessens R, Poleunis F. A numerical method for the integration of oscillatory functions[J]. BIT Numerical Mathematics, 1971, 11(3): 317-327. |
| [16] |
匡斌, 王华忠. 傅里叶有限差分深度偏移成像方法研究和应用[J]. 石油地球物理勘探, 2001, 36(6): 698-703. KUANG Bin, WANG Huazhong. Research and application of Fourier finite difference depth migration ima-ging method[J]. Oil Geophysical Prospecting, 2001, 36(6): 698-703. DOI:10.3321/j.issn:1000-7210.2001.06.006 |
| [17] |
陈双全, 李向阳. 应用傅里叶尺度变换提高地震资料分辨率[J]. 石油地球物理勘探, 2015, 50(2): 213-218. CHEN Shuangquan, LI Xiangyang. Application of Fourier scale transform to improve resolution of seismic data[J]. Oil Geophysical Prospecting, 2015, 50(2): 213-218. |
| [18] |
严海滔, 周怀来, 牛聪, 等. 同步挤压改进短时傅里叶变换分频相干技术在断裂识别中的应用[J]. 石油地球物理勘探, 2019, 54(4): 860-868. YAN Haitao, ZHOU Huailai, Niu Cong, et al. The application of improved STFT frequency division cohe-rent technology in fault identification by synchronous extrusion[J]. Oil Geophysical Prospecting, 2019, 54(4): 860-868. |
| [19] |
Piessens R, Branders M. Computation of Fourier transform integrals using Chebyshev series expansions[J]. Computing, 1984, 32(2): 177-186. |
| [20] |
Arieh I. On the numerical quadrature of highly-oscillating integrals, I:Fourier transforms[J]. IMA Journal of Numerical Analysis, 2004, 24(3): 365-391. |
| [21] |
Wu L Y, Tian G. High-precision Fourier forward mode-ling of potential fields[J]. Geophysics, 2014, 79(5): G59-G68. |
| [22] |
Li K, Chen L W, Chen Q R, et al. Fast 3D forward modeling of the magnetic field and gradient tensor on an undulated surface[J]. Applied Geophysics, 2018, 15(S1): 138-150, 207. |
| [23] |
Dai S K, Zhao D D, Zhang Q J, et al. Three-dimensio-nal numerical modeling of gravity anomalies based on Poisson equation in space-wavenumber mixed domain[J]. Applied Geophysics, 2018, 15(S1): 151-161, 207. |
| [24] |
戴世坤, 王旭龙, 赵东东, 等. 空间-波数混合域二度体重力异常正演[J]. 石油地球物理勘探, 2019, 54(6): 1383-1389. DAI Shikun, WANG Xulong, ZHAO Dongdong, et al. Forward modeling of two-dimensional gravity anomaly in space wavenumber mixing domain[J]. Oil Geophysical Prospecting, 2019, 54(6): 1383-1389. |
| [25] |
Wu L Y. Efficient modelling of gravity effects due to topographic masses using the Gauss-FFT method[J]. Geophysical Journal International, 2016, 205(1): 160-178. DOI:10.1093/gji/ggw010 |
| [26] |
Ren Z Y, Tang J T, Kalscheuer T, et al. Fast 3-D large-scale gravity and magnetic modeling using unstructured grids and an adaptive multilevel fast multipole method[J]. Journal of Geophysical Research: Solid Earth, 2017, 122(1): 79-109. DOI:10.1002/2016JB012987 |



 戴世坤, 湖南省长沙市岳麓区麓山南路932号中南大学地球科学与信息物理学院, 410083。Email:
戴世坤, 湖南省长沙市岳麓区麓山南路932号中南大学地球科学与信息物理学院, 410083。Email: