2 东华理工大学地球物理与测控技术学院, 江西南昌 330013
2 School of Geophysics and Measurement-control Technology, East China University of Technology, Nanchang, Jiangxi 330013, China
Tikhonov正则化反演理论[1]适用于不适定的地球物理反问题。正则化因子的选取直接影响反演结果,故此,如何正确选取正则化因子一直是地球物理正则化反演领域的研究热点和难点。
利用一定的准则确定近似最佳正则化因子,且在整个反演过程中取值保持不变的方法,称为经验定值法。传统的定值方法包括:无偏风险估计法[2],广义交叉验证法[3-4]和L曲线法[5-6]。Lima等[7]考虑了噪声的随机性,提出解的不稳定性评价方式,结合解的稳定性确定正则化因子,并分别利用地震、重力和大地电磁测深(MT)数据反演试验验证了方法的有效性。由于该类方法操作复杂,需要开展大量的计算以确定近似最佳的正则化因子,故此,自适应正则化算法是正则化反演的发展趋势。
所谓自适应正则化算法,是指在反演过程中根据一定的准则自适应地调整正则化因子的取值的方法。Zhdanov[8]提出了一种根据初始数据拟合函数与模型约束函数的比值确定正则化因子的初值, 在数据拟合效率下降时对正则化因子进行衰减的自适应方法。陈小斌等[9]以MT反演为例,提出基于最平缓约束的自适应算法,该算法强调数据拟合项与模型稳定项的平衡,反演结果稳定性高。向阳等[10]以Zhdanov自适应算法为基本框架,提出了改进的自适应算法,该算法对Zhdanov算法所确定的正则化因子的初值做放大处理,并提出了衰减因子与数据拟合效率之间的关联方案,基于共轭梯度算法的MT数据光滑反演试验表明,该算法在一定程度上可以降低初始模型对反演结果的影响,提高解的稳定性。黄贤阳等[11]将向阳等[10]提出的自适应算法应用于基于光滑和聚焦约束的MT极值边界正则化反演,验证了该算法具有适用于其他稳定器的潜质。
需要指出是,以往关于正则化因子的文献大多是基于线性优化算法的。与线性优化算法不同,概率思想是非线性优化算法的核心,如模拟退火算法[12-13]按照概率接受“高能量”解;遗传算法[14]和差分进化算法[15]按照概率进行交叉和变异操作;粒子群算法[16]按照概率更新粒子的速度和位置。目前,鲜见文献在确定正则化因子时,对非线性优化算法中的随机性进行针对性的考量。
综上所述,从提高反演的稳定性方面考量而确定正则化因子取值是本文自适应正则化算法的思路。此外,以往的自适应算法对非线性算法中的随机性考虑不足,基于此,本文提出一种阶段式自适应正则化算法,并分别在MT线性和非线性反演试验中检验其适用性。
1 MT正则化反演 1.1 正则化目标函数MT数据的正则化反演目标函数为
| $ \begin{array}{*{20}{l}} {{P^\alpha }(\mathit{\boldsymbol{m}}) = \phi (\mathit{\boldsymbol{m}}) + \alpha S(\mathit{\boldsymbol{m}}) = {{\left\| {A(\mathit{\boldsymbol{m}}) - {\mathit{\boldsymbol{d}}_{{\rm{obs}}}}} \right\|}^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha {{\left\| {\mathit{\boldsymbol{W}}{\mathit{\boldsymbol{W}}_{\rm{e}}}(\mathit{\boldsymbol{m}} - {\mathit{\boldsymbol{m}}_{{\rm{apr}}}})} \right\|}^2}} \end{array} $ | (1) |
式中:α为正则化因子; m为待解模型;ϕ为数据拟合函数;S为模型约束函数;A为正演算子;dobs为观测数据;W为模型加权矩阵;We为约束函数矩阵;mapr为先验信息。本文采用有限元法实现MT数据正演。
1.2 阶段式自适应算法 1.2.1 Zhdanov自适应方案Zhdanov自适应方案是一种无需复杂计算的自适应正则化算法,其核心步骤包括计算正则化因子初值和自适应衰减两步[8, 17-18]。
正则化因子初值为
| $ {\alpha _0} = \frac{{\phi ({\mathit{\boldsymbol{m}}_0})}}{{S({\mathit{\boldsymbol{m}}_0})}} $ | (2) |
式中m0为初始模型。
若反演过程中数据拟合函数上升,或效率低于给定阈值,按照下式对正则化因子进行衰减
| $ {\alpha _n} = q{\alpha _{n - 1}} $ | (3) |
式中:n为迭代次数;q为衰减系数,取值参考区间为[0.5, 0.9]。
1.2.2 阶段式自适应方案阶段式自适应正则化算法的核心思想是,将反演的迭代过程分为若干“阶段”,利用“阶段”的平均拟合效率代替某次迭代的拟合效率,判断正则化因子的衰减,旨在降低正则化因子的衰减速度,降低非线性优化算法中随机性的影响,进而提高反演的稳定性。该算法基本流程如下。
(1) 将迭代反演过程设置为若干“阶段”。
(2) 将初始“阶段”模型m的平均数据拟合函数与平均模型约束函数之比值作为正则化因子的初值
| $ {\alpha _0} = \frac{{\overline {\phi ({\mathit{\boldsymbol{m}}_0})} }}{{\overline {S({\mathit{\boldsymbol{m}}_0})} }} $ | (4) |
式中上划线表示取均值。对于差分进化(DE)算法,则利用初始种群数据拟合函数的平均值和模型约束函数的平均值之比值作为正则化因子的初值。
(3) 利用当前“阶段”的平均数据拟合效率自适应调整下一阶段的正则化因子,即计算反演过程中相邻“阶段”的平均数据拟合下降效率,并按照下式确定下一“阶段”的正则化因子
| $ \left\{ {\begin{array}{*{20}{l}} {\overline {{\alpha _k}} = q \times \overline {{\alpha _{k - 1}}} }&{\overline {\Delta {\phi _k}} < \varepsilon }\\ {\overline {{\alpha _k}} = \overline {{\alpha _{k - 1}}} }&{\overline {\Delta {\phi _k}} \ge \varepsilon } \end{array}} \right. $ | (5) |
式中:k=1, 2, 3, …, Kmax为“阶段”数;
(4) 判断是否达到终止条件,若是,则结束迭代;若否,则返回步骤(3)。
1.3 目标函数优化为了验证本文提出的阶段式自适应算法在线性和非线性优化算法中的适用性,将其应用于二维MT共轭梯度反演和一维MT差分进化反演。
1.3.1 共轭梯度反演本文采用成熟通用的共轭梯度算法[10]实现二维MT反演,基本流程如下:
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{R}}_n} = A({\mathit{\boldsymbol{m}}_n}) - {\mathit{\boldsymbol{d}}_{{\rm{obs}}}}}\\ {\mathit{\boldsymbol{I}}_n^\alpha = \mathit{\boldsymbol{J}}_{{\mathit{\boldsymbol{m}}_n}}^{\rm{T}}{\mathit{\boldsymbol{R}}_n} + \alpha {\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{W}}({\mathit{\boldsymbol{m}}_n} - {\mathit{\boldsymbol{m}}_{{\rm{apr}}}})} \end{array}} \right. $ | (6) |
| $ \left\{ {\begin{array}{*{20}{l}} {\beta _n^a = \frac{{{{\left\| {\mathit{\boldsymbol{I}}_n^\alpha } \right\|}^2}}}{{{{\left\| {\mathit{\boldsymbol{I}}_{n - 1}^\alpha } \right\|}^2}}}}\\ {\mathit{\boldsymbol{\tilde I}}_n^\alpha = \mathit{\boldsymbol{I}}_n^\alpha + \beta _n^\alpha \mathit{\boldsymbol{\tilde I}}_{n - 1}^\alpha }\\ {\mathit{\boldsymbol{\tilde I}}_0^\alpha = \mathit{\boldsymbol{I}}_0^\alpha } \end{array}} \right. $ | (7) |
| $ \left\{ {\begin{array}{*{20}{l}} {\tilde s_n^\alpha = \frac{{ < \mathit{\boldsymbol{\tilde I}}_n^\alpha ,\mathit{\boldsymbol{I}}_n^\alpha > }}{{{{\left\| {\mathit{\boldsymbol{J\tilde I}}_n^\alpha } \right\|}^2} + \alpha {{\left\| {\mathit{\boldsymbol{W\tilde I}}_n^\alpha } \right\|}^2}}}}\\ {{\mathit{\boldsymbol{m}}_{n + 1}} = {\mathit{\boldsymbol{m}}_n} - \tilde s_n^\alpha \mathit{\boldsymbol{\tilde I}}_n^\alpha } \end{array}} \right. $ | (8) |
式中:Rn为第n次数据拟合残差;mn为待解模型;Inα为梯度方向;
DE(差分进化)算法是Storn等[19]基于遗传算法等进化思想提出的一种非线性全局优化算法,其本质是多目标函数优化算法,用于求解多维空间中的整体最优解。差分进化算法与遗传算法具有一定的相似性,都是利用随机的方式生成种群,主要都包括变异、交叉和选择三个步骤。由于DE算法具有受控参数少、原理简单、鲁棒性强的特点,受到越来越多的关注。但与成熟的非线性算法(如模拟退火、遗传算法)相比,该算法在地球物理反演领域的应用偏少。
本文采用全局寻优的DE算法[19-21]实现一维MT反演,该算法的核心环节如下。
(1) 变异操作
在当前种群中随机选择两个不同的个体,将它们的差向量缩放后与另外的个体进行向量运算,生成经过变异操作的中间种群为
| $ \mathit{\boldsymbol{V}}_i^{({\rm{it}} + 1)} = \mathit{\boldsymbol{X}}_{{r_1}}^{({\rm{it}})} + \mathit{\boldsymbol{F}} \times [\mathit{\boldsymbol{X}}_{{r_2}}^{({\rm{it}})} - \mathit{\boldsymbol{X}}_{{r_3}}^{({\rm{it}})}] $ | (9) |
式中:i=1, 2, 3, …, NP,NP为种群规模数;r1、r2和r3均为区间[1, NP]内的随机整数,且i≠r1≠r2≠r3;it表示进化代数;Vi(it+1)为中间种群的第i个个体;F表示变异因子;Xr1(it)表示当前种群的第i个个体。
(2) 交叉操作
利用下式开展交叉操作
| $ u_{i,j}^{({\rm{it}} + 1)} = \left\{ {\begin{array}{*{20}{c}} {v_{i,j}^{({\rm{it}} + 1)}}&{{\rm{ rand }} \le {\rm{CR 或 }}j = {j_{{\rm{rand}}}}}\\ {u_{i,j}^{({\rm{it}})}}&{{\rm{其他}}} \end{array}} \right. $ | (10) |
式中:
(3) 选择操作
采用贪婪算法,根据目标函数的大小选择进入新种群的个体
| $ \mathit{\boldsymbol{X}}_i^{({\rm{it}} + 1)} = \left\{ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{U}}_i^{({\rm{it}} + 1)}}&{f[\mathit{\boldsymbol{U}}_i^{({\rm{it}} + 1)}] \le f[\mathit{\boldsymbol{X}}_i^{({\rm{it}})}]}\\ {\mathit{\boldsymbol{X}}_i^{({\rm{it}})}}&{{\rm{其他}}} \end{array}} \right. $ | (11) |
式中:f为适应度函数, 即式(1)中的目标函数;Ui(it+1)为第it+1代的第i个交叉个体;Xi(it)为第it代新种群的第i个个体。
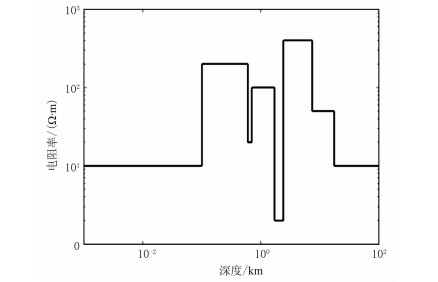
2 模型试验 2.1 模型一为了验证阶段式自适应算法在非线性算法中的可行性,选择文献[9]中的一维电阻率模型(图 1)开展试验。在1000~0.0001Hz选取40个对数等间距频点,采用随机生成的模型为初始模型。
|
图 1 一维电阻率模型[9] |
设计了两套对比试验方案:Zhdanov自适应正则化反演和阶段式自适应正则化反演。两种方案仅正则化因子确定方式不同,其余参数均一致,反演最大迭代次数为1000,衰减因子q=0.5,采用最小模型约束进行反演。反演结果见图 2。
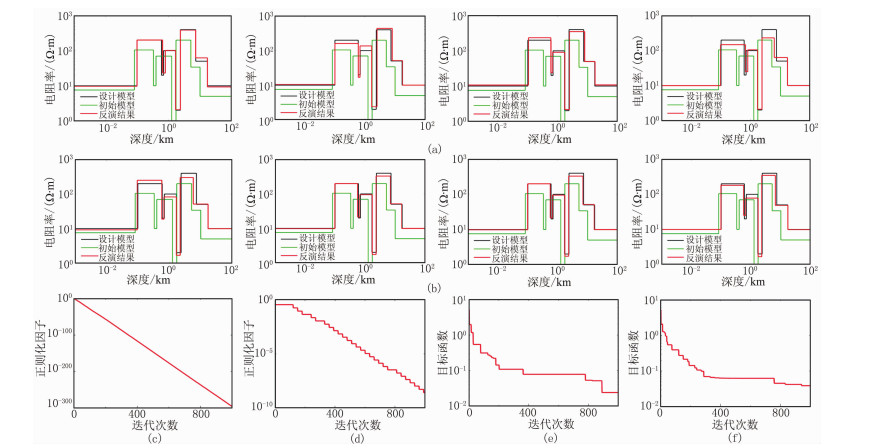
|
图 2 模型一Zhdanov自适应方案和阶段式自适应方案反演结果 (a)Zhdanov自适应方案反演结果(从左到右分别对应迭代100、300、500、1000次的反演结果,图b同);(b)阶段式自适应反演结果;(c)Zhdanov自适应方案的正则化因子衰减曲线;(d)阶段式自适应方案的正则化因子衰减曲线;(e)Zhdanov自适应方案的目标函数曲线;(f)阶段式自适应方案的目标函数曲线 |
需要指出的是,为了直观地对比不同正则化方案反演结果随迭代次数的变化,本次试验特意选择了较大的迭代次数。从图 2可以看出,即使Zhdanov自适应方案的目标函收敛效率较高,但其反演结果随迭代次数的增加出现了较大的波动,甚至逐渐变差;而阶段式自适应方案的目标函数曲线平稳下降,反演结果稳定性高,与真实模型偏离程度始终在可接受范围内。对比两个方案的正则化因子迭代曲线,可以看出阶段式自适应方案的正则化因子衰减速度更慢,可以更充分地发挥模型约束函数的作用,反演过程更加稳定。
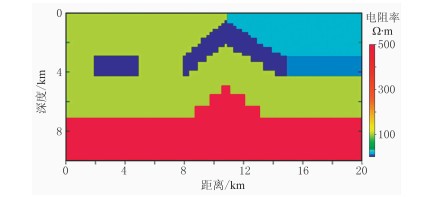
2.2 模型二选择文献[22]的二维电阻率模型(图 3)开展模型试验。在320~0.00055Hz范围内选取40个对数等间距频点,测点数共101个,用均匀半空间作为初始模型,利用共轭梯度算法进行光滑反演,最大迭代次数设为40。针对TE模式进行反演。
|
图 3 二维电阻率模型[22] |
本文对Zhdanov自适应正则化反演与阶段式自适应正则化反演进行对比。这两种方案仅正则化因子衰减方式不同,其余参数均一致。初始模型为均匀半空间(电阻率为100Ω·m), 采用光滑约束进行反演,以相邻两次迭代为一个阶段。选取衰减系数q为0.5,反演结果见图 4。
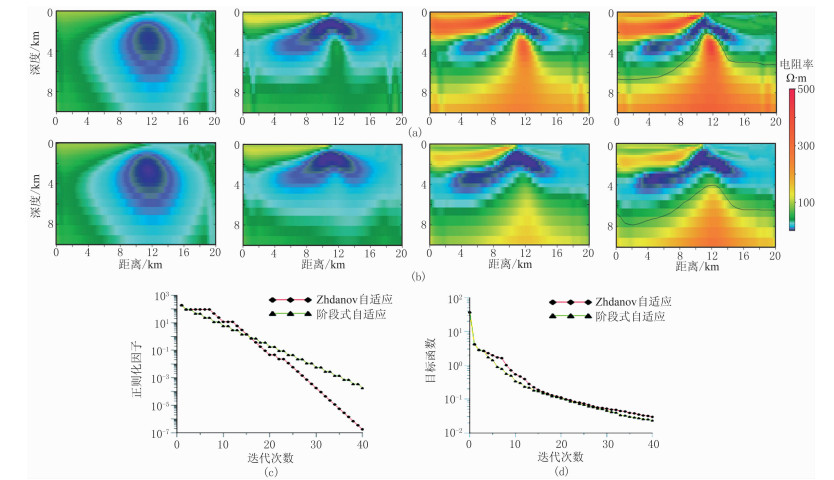
|
图 4 模型二q=0.5时Zhdanov自适应方案与阶段式自适应方案的反演结果 (a)Zhdanov自适应方案反演(从左到右分别对应迭代10、20、30、40次,图b同);(b)阶段式自适应反演;(c)正则化因子曲线;(d)目标函数曲线 |
分析图 4可以看出:q取0.5时,Zhdanov自适应方案反演结果中高阻隆起位置偏高,且两侧也存在虚假的低阻条带;而阶段式自适应方案反演结果中高阻隆起位置与模型更加接近,且反演模型更加光滑。另外,相对于Zhdanov自适应方案,阶段式自适应方案的目标函数曲线下降更平缓均匀,具有更强的反演稳定性。
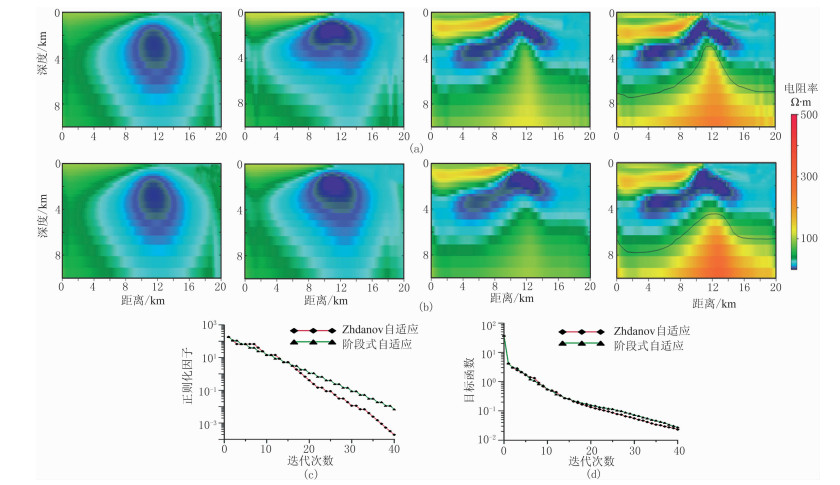
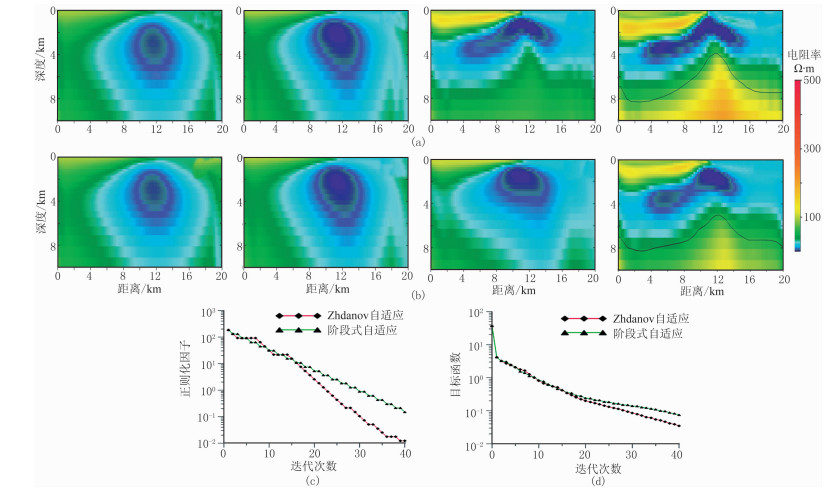
为了研究衰减系数q对反演结果的影响,进一步选取q=0.6和q=0.7,分别利用Zhdanov自适应方案与阶段式自适应方案进行反演,结果见图 5和图 6。
|
图 5 模型二q=0.6时Zhdanov自适应方案与阶段式自适应方案的反演结果 (a)Zhdanov自适应方案反演(从左到右分别对应迭代10、20、30、40次,图b同);(b)阶段式自适应反演;(c)正则化因子曲线;(d)目标函数曲线 |
|
图 6 模型二q=0.7时Zhdanov自适应方案与阶段式自适应方案的反演结果 (a)Zhdanov自适应方案反演(从左到右分别对应迭代10、20、30、40次,图b同);(b)阶段式自适应反演;(c)正则化因子曲线;(d)目标函数曲线 |
对比图 4和图 5,可以看出,Zhdanov自适应方案反演结果中高阻隆起位置依旧偏高,两侧出现了虚假的低阻条带,反演模型光滑性较差。而阶段式自适应方案反演结果两侧没有虚假的低阻条带,且高阻隆起位置与设计模型更加接近。相对于Zhdanov自适应方案,阶段式自适应方案的目标函数曲线下降更加稳定平缓。
综合分析图 4、图 5和图 6,不难发现,Zhdanov自适应反演的目标函数收敛效率更高,但阶段式自适应反演结果更加稳定,具体表现在:不同衰减因子取值条件下,阶段式自适应反演不存在Zhdanov自适应反演中一直存在的条带状假异常,而且其反演结果中高阻隆起位置与真实模型更加接近。这说明阶段式自适应算法在一定程度上为解决衰减因子不易确定的难题提供了新思路,也提示地球物理反演不能仅考虑目标函数的收敛速度。
为了定量评价反演结果与真实模型的偏离程度,根据反演结果解释了高阻隆起界面(图 4、图 5和图 6a和图 6b中最右图中的黑线),利用MATLAB进行线性插值获得界面起伏函数,并利用
| $ \frac{1}{l}\int_0^l | {Z_{{\rm{ real }}}} - {Z_{{\rm{ inv }}}}|{\rm{d}}x $ | (12) |
定量地计算了两种自适应算法在不同衰减因子条件下的反演结果与真实模型的偏离度。式中:l表示反演区域横向长度;Zreal表示真实高阻隆起界面函数;Zinv表示反演高阻隆起界面函数。计算结果见表 1。
|
|
表 1 解释的高阻隆起界面与真实界面的绝对平均偏差 |
通过表 1可以看出,在相同衰减因子条件下,阶段式自适应方案反演结果的高阻隆起位置与模型偏差更小,结果更准确。
此次试验模型中,高阻隆起的还原很困难。为了定量评价反演过程中的稳定性,记录了每一次迭代反演结果,记录了高阻隆起出现雏形时的数据拟合函数和模型约束函数,并按照式(13)计算了数据拟合函数绝对误差和模型约束函数绝对误差,利用式(14)计算了数据拟合函数相对误差和模型约束函数相对误差。
| $ \left\{ {\begin{array}{*{20}{l}} {\Delta {\phi _{\rm{前}}} = {\phi _{k + 1}} - {\phi _k}}\\ {\Delta {S_{\rm{前}}} = {S_{k + 1}} - {S_k}}\\ {\Delta {\phi _{\rm{后}}} = {\phi _k} - {\phi _{k - 1}}}\\ {\Delta {S_{\rm{后}}} = {S_k} - {S_{k - 1}}}\\ {\Delta {\phi _{\rm{均}}} = \frac{{{\phi _{k + 1}} - {\phi _{k - 1}}}}{2}}\\ {\Delta {S_{\rm{均}}} = \frac{{{S_{k + 1}} - {S_{k - 1}}}}{2}} \end{array}} \right. $ | (13) |
| $ \left\{ {\begin{array}{*{20}{l}} {\delta {\phi _{\rm{前}}} = \frac{{|{\phi _{k + 1}} - {\phi _k}|}}{{{\phi _k}}} \times 100\% }\\ {\delta {S_{\rm{前}}} = \frac{{|{S_{k + 1}} - {S_k}|}}{{{S_k}}} \times 100\% }\\ {\delta {\phi _{\rm{后}}} = \frac{{|{\phi _k} - {\phi _{k - 1}}|}}{{{\phi _k}}} \times 100\% }\\ {\delta {S_{\rm{后}}} = \frac{{|{S_k} - {S_{k - 1}}|}}{{{S_k}}} \times 100\% }\\ {\delta {\phi _{\rm{均}}} = \frac{{|{\phi _{k + 1}} - {\phi _{k - 1}}|}}{{2{\phi _k}}} \times 100\% }\\ {\delta {S_{\rm{均}}} = \frac{{|{S_{k + 1}} - {S_{k - 1}}|}}{{2{S_k}}} \times 100\% } \end{array}} \right. $ | (14) |
式中:“Δ”表示绝对误差;“δ”表示相对误差;k为迭代次数;下标“前”、“后”和“均”分别代表相关参数的当次迭代值与前一次迭代值、当次迭代值与后一次迭代值、以及前一次迭代值与后一次迭代值的绝对误差或相对误差。两种自适应方案反演结果中高阻隆起出现时的数据拟合函数和模型约束函数的变化情况参见表 2。
|
|
表 2 Zhdanov自适应方案与阶段自适应方案在高阻隆起出现时的数据拟合函数和模型约束函数的变化情况对比 |
此外,本文还尝试定义了模型改变与数据改变的匹配率,即模型稳定函数的改变率与数据拟合函数改变率之比值,来衡量反演过程中的不稳定性。为了规避量纲不一致的问题,采用模型稳定函数与数据拟合函数的相对改变率,采用下式计算匹配率
| $ \tau = \frac{{\delta S}}{{\delta \phi }} $ | (15) |
若匹配率较低,说明在同样的数据拟合函数相对改变率的条件下,模型的改变更小,即不容易出现反演不稳定的情况;反之亦然,若相对匹配率较高,说明在同样的数据拟合函数相对改变率的条件下,模型的改变更大,即更容易出现反演不稳定的情况。
根据表 2数据利用式(15)计算两种反演方案的匹配率见表 3。
|
|
表 3 反演结果出现高阻隆起时两种方案的匹配率 |
分析表 3,可以看出在不同的衰减因子条件下,本文提出的阶段式自适应算法的匹配率均小于Zhdanov自适应算法,说明阶段式自适应算法可以降低反演过程的不稳定性。
3 实测资料处理为了验证阶段式自适应算法的实用性,选取下扬子地区的某条测线进行处理。
下扬子地区海相地层具有较好的油气资源成藏条件,但该地区地质条件复杂、构造活动性强、埋深大,遭受多期强烈构造活动叠加,勘探难度较大。选取的测线长度约30km,MT测点14个,频点数为38,频率范围为320~0.001Hz。测线附近有一口钻井,钻孔深度为4060m,井底地层为下二叠统灰岩,自上而下地层包括第四系、新近系、古近系、白垩系和下二叠统[23]。
根据文献[24],整理出了研究区电阻率统计信息,如表 4所示。
|
|
表 4 测区电阻率信息统计表 |
根据该区域电阻率统计以及钻孔信息,可以看出,该区域的电性整体呈现“高—低—高”分布特征,即第四系—新近系(Q~N)为高阻层,古近系—白垩系泰州组(E-K2t)为低阻层,白垩系浦口组(K2p)及其下伏地层整体呈现高阻。
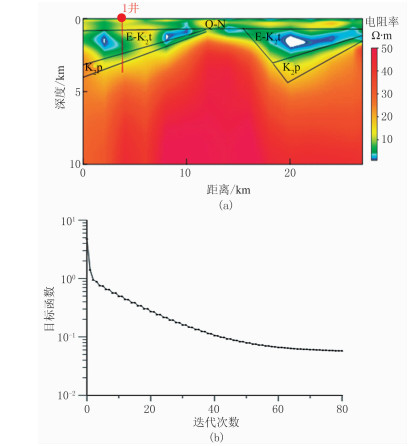
使用均匀半空间(10Ω·m)作为电阻率反演的初始模型,利用共轭梯度算法进行最小模型反演,最大迭代次数为80,衰减系数设置为0.8,以相邻两次迭代为一个“阶段”。选择TE模式进行反演,反演结果见图 7,图中黑线是根据电阻率反演结果、电阻率统计信息以及钻孔信息初步解释的电性界面。
|
图 7 阶段式自适应反演结果 (a)电阻率反演结果;(b)目标函数曲线 |
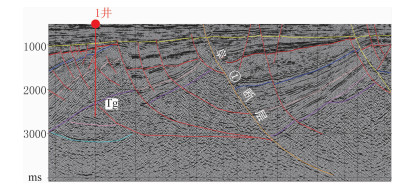
为了评价反演结果,搜集到一条与该MT测线平行的地震时间剖面[25](图 8)。
|
图 8 地震时间剖面 黄线为新近系底,红线为古近系底,粉线为白垩系底,紫线为印支面(Tg) |
综合图 7和图 8可以发现,电阻率反演结果所揭示的界面信息与地震剖面基本吻合,验证了本文电阻率反演结果的可靠性,也说明本文阶段式自适应算法具有实用性。
4 结论与展望与传统的自适应正则化算法按照“迭代次数”自适应调整正则化因子取值不同,阶段式自适应正则式算法按照“阶段”自适调整正则化因子。模型试验和实测资料处理表明:
(1) 阶段式自适应正则式算法,可更充分地发挥模型稳定函数的作用,提高解的稳定性,同时也在一定程度上为解决衰减因子不易确定的难题提供了新思路;
(2) 阶段式自适应正则式算法适用于线性和非线性优化算法,具有较高的推广前景;
(3) 通过实测资料处理,检验了算法的实用性。
需要指出的是,本文仅对一维MT差分进化算法和二维MT共轭梯度算法验证了阶段式自适应算法的可行性,如何将该算法推广至高维反演,以及合理地设计“阶段”是今后的研究方向。
| [1] |
Tikhonov A N.Regularization of Incorrectly Posed Problem[M]. Soviet Math, Dokl, 1963.
|
| [2] |
Wahba G.Spline Models for Observational Data[M]. SIAM, Philadelphia, 1990.
|
| [3] |
Wahba G. Practical approximate solutions to linear operator equations when the data are noisy[J]. SIAM Journal on Numerical Analysis, 1977, 14(4): 651-667. |
| [4] |
Golub G H, Heath M, Wahba G. Generalized cross-validation as a method for choosing a good ridge parameter[J]. Technometrics, 1979, 21(2): 215-223. DOI:10.1080/00401706.1979.10489751 |
| [5] |
Hansen P C, O'Leary D P. The use of the L-curve in the regularization of discrete ill-posed problems[J]. SIAM Journal on Scientific Computing, 1993, 14(6): 1487-1503. DOI:10.1137/0914086 |
| [6] |
Hansen P C. Regularization tools:a Matlab package for analysis and solution of discrete ill-posed problems[J]. Numerical algorithms, 1994, 6(1): 1-35. |
| [7] |
Lima W A, Silva J B C, Santos D F, et al. A robust interactive estimation of the regularization parameter[J]. Geophysics, 2019, 84(3): IM19-IM33. |
| [8] |
Zhdanov M S.Geophysical Inverse Theory and Regularization Problems[M]. Elsevier Science, Netherlands, 2002.
|
| [9] |
陈小斌, 赵国泽, 汤吉, 等. 大地电磁自适应正则化反演算法[J]. 地球物理学报, 2005, 48(4): 937-946. CHEN Xiaobin, ZHAO Guoze, TANG Ji, et al. An adaptive inversion algorithm for magnetotelluric data[J]. Chinese Journal of Geophysics, 2005, 48(4): 937-946. |
| [10] |
向阳, 于鹏, 陈晓, 等. 大地电磁反演中改进的自适应正则化因子选取[J]. 同济大学学报(自然科学版), 2013, 41(9): 1429-1434. XIANG Yang, YU Peng, CHEN Xiao, et al. An improve adaptive regularized parameter selection in magnetotelluric inversion[J]. Journal of Tongji University(Natural Science Edition), 2013, 41(9): 1429-1434. |
| [11] |
黄贤阳, 邓居智, 陈晓, 等. 基于不同稳定泛函约束的大地电磁极值边界反演研究及其在内蒙古塔木素测区的应用[J]. 应用地球物理学报, 2019, 16(3). HUANG Xianyang, DENG Juzhi, CHEN Xiao, et al. Magnetotelluric extremum boundary inversion based on different stabilizers and its application in Inner Mongolia Tamusu area[J]. Journal of Applied Geophysics, 2019, 16(3): 367-377. |
| [12] |
陈晓, 于鹏, 张罗磊, 等. 地震与大地电磁测深数据的自适应正则化同步联合反演[J]. 地球物理学报, 2011, 54(10): 2673-2681. CHEN Xiao, YU Peng, ZHANG Luolei, et al. Adaptive regularized synchronous joint inversion of MT and seismic data[J]. Chinese Journal of Geophysics, 2011, 54(10): 2673-2681. |
| [13] |
陈晓, 于鹏, 邓居智, 等. 基于宽范围岩石物性约束的大地电磁和地震联合反演[J]. 地球物理学报, 2016, 59(12): 4690-4700. CHEN Xiao, YU Peng, DENG Juzhi, et al. Joint inversion of MT and seismic data based on wide-range petrophysical constraints[J]. Chinese Journal of Geophysics, 2016, 59(12): 4690-4700. |
| [14] |
徐姣.基于快速遗传算法的速度反演研究及应用[D].四川成都: 成都理工大学, 2009. XU Jiao.The Research and Application in Velocity Inversion Based on Rapid Genetic Algorithm[D]. Chengdu University of Technology, Chengdu, Sichuan, 2009. |
| [15] |
Zeng Z W, Chen X, Liu X, et al.Joint inversion of MT and gravity based on differential evolution algorithm[C]. China International Geo-electromagnetism Workshop, 2019, 105-108.
|
| [16] |
赵德杨.地震波阻抗粒子群优化反演方法的研究[D].四川成都: 成都理工大学, 2014. ZHAO Deyang.Acoustic Impendence Inversion Based on Particle Swarm Optimization Algorithm[D]. Chengdu University of Technology, Chengdu, Sichuan, 2014. |
| [17] |
Kumar A, Wan L, Zhdanov M S.Regularization analysis of three-dimensional magnetotelluric inversion[C]. SEG Technical Program Expanded Abstracts, 2007, 26: 482-486.
|
| [18] |
Gribenko A, Zhdanov M. Rigorous 3D inversion of marine CSEM data based on the integral equation method[J]. Geophysics, 2007, 72(2). |
| [19] |
Storn R, Price K. Differential Evolution:A simple and efficient heuristic for global optimization over conti-nuous spaces[J]. Journal of Global Optimization, 1997, 11(4): 341-359. DOI:10.1023/A:1008202821328 |
| [20] |
王天意, 杨进, 颜廷杰, 等. 地球物理反演中的差分进化算法[J]. 地质与勘探, 2014, 50(5): 971-975. WANG Tianyi, YANG Jin, YAN Tingjie, et al. The differential evolution algorithm in geophysical inversion[J]. Geology and Exploration, 2014, 50(5): 971-975. |
| [21] |
余胜威. MATLAB优化算法案例分析与应用(进阶篇)[M]. 北京: 清华大学出版社, 2015.
|
| [22] |
张罗磊.OCCAM与SBI结合的MT二维反演方法[D].上海: 同济大学, 2008. ZHANG Luolei.OCCAM and SBI Based Two-Dimensional Magnetotelluric Inversion[D]. Tongji University, Shanghai, 2008. |
| [23] |
王家林, 钟慧智, 于鹏, 等.苏北中古生界MT精细处理及综合解释[R].上海: 同济大学, 2012.
|
| [24] |
王建.江苏盐阜地区中生界综合地球物理研究[D].上海: 同济大学, 2005. WANG Jian.Integrated Geophysical Research about Mesozoic in Yanfu, Jiangsu[D]. Tongji University, Shanghai, 2005. |
| [25] |
陈晓.大地电磁与地震正则化联合反演研究[D].上海: 同济大学, 2013. CHEN Xiao.Regularized Joint Inversion of MT and Seismic Data[D]. Tongji University, Shanghai, 2013. |



 陈晓, 江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院, 330013。Email:
陈晓, 江西省南昌市经开区广兰大道418号东华理工大学地球物理与测控技术学院, 330013。Email: