2 中国石油大学(北京)克拉玛依校区石油学院, 新疆克拉玛依 834000;
3 中国石油新疆油田分公司实验检测研究院, 新疆克拉玛依 834000
2 Karamay Campus, Faculty of Petroleum, China Unirersity of Petroleum(Beijing), Karamay, Xinjiang 834000, China;
3 Experiment Testing Institute, PetroChina Xinjiang Oilfield Company, Karamay, Xinjiang 834000, China
随着开发程度的不断提高,目前中国东部老油田综合含水率普遍达到90%以上,几乎全面进入特高含水阶段,挖潜难度不断加大,油田开发后劲严重不足。在现有经济技术条件下,25%~35%的油气是由于储层内部的非均质性,特别是储层构型(导致储层内部的渗流屏障和渗流差异)的影响而滞留于地下成为可动的宏观剩余油[1]。因此,应用储层构型研究以明确储层内部非均质特征、建立符合地下实际规律的地质模型,是特高含水期老油田科学开发的关键。储层构型研究是沉积相研究的进一步细化,视沉积相类型不同,沉积亚相、微相与构型级次有一定的可比性,但不具有一一对应的关系[2]。在现阶段研究过程中,非取心井单井储层构型划分主要借鉴了传统的沉积相研究方法,通过测井曲线形态定性、半定量地进行人工识别[3-4]。
近年来,随着人工智能技术的发展,沉积相的识别开始采用聚类分析、人工神经网络等数据挖掘算法[5-18]。聚类分析又称群分析,它以相似性为基础,是研究(样品或指标)分类问题的一种统计分析方法,该方法在辽河滩海地区沉积相的自动划分[13]以及川西某气田蓬莱镇组三角洲前缘亚相定量识别[14]中取得了较好的效果。人工神经网络是从信息处理角度对人脑神经元网络进行抽象,建立某种简单模型,按不同的连接方式组成不同的网络进行信息处理[15]。人工神经网络在沉积相判别中的应用较为广泛,Baneshi[16]、Aliakbar等[17]利用神经网络方法研究了伊朗陆上油气田岩相特征;Zhang等[18]根据水平井的测井曲线响应特征,利用多项式逻辑回归和人工神经网络,建立了测井沉积相的识别方法。人工智能技术在沉积相研究中的成功应用,为识别单井储层构型打下了良好的基础。
相比沉积相识别,单井储层构型划分具有自身的特点及难点。首先,储层构型研究整体更为复杂,在相同沉积背景的研究区内,如何应用取心井分析,建立能够推广、应用到非取心井的划分标准较为困难;其次,在特高含水期老油田中,开发井数量多,划分的层系多,单井构型划分工作量大,人工单井构型划分效率较低,主观性强;再次,划分结果准确性如何,缺乏直观的验证方法。因此,本文以沧东凹陷东部陡坡带冲积扇为例,基于岩心、测井、录井等资料,应用K-均值聚类及贝叶斯判别方法,提出了一种冲积扇单井储层构型自动划分及验证方法,希望能够提高单井储层构型识别的准确性及效率。
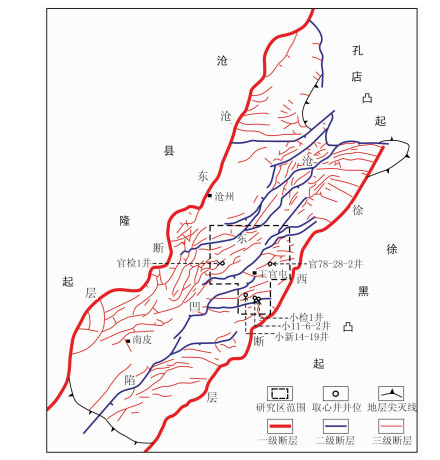
1 研究区概况沧东凹陷是渤海湾盆地黄骅坳陷的一个次级构造单元,位于孔店凸起以南,东西分别以徐西断层、沧东断层为界,内部断层较为复杂(图 1)。古近系孔店组一段(简称“孔一段”)沉积时期为亚热带半干旱—干旱气候,徐西断层开始强烈活动, 沧东凹陷湖盆沉积处于萎缩充填阶段,受控于古构造及古气候的影响,沉积环境由下伏孔店组二段(简称“孔二段”)的辫状河三角洲突变为孔一段下亚段的冲积扇沉积[19-20]。孔一段自下而上可划分为6个油组,依次为枣Ⅴ、枣Ⅳ、枣Ⅲ、枣Ⅱ、枣Ⅰ和枣0油组。
|
图 1 研究区位置 |
研究区位于沧东凹陷的东—中部,共有钻井1000余口,其中取心井40余口,取心层段主要为枣Ⅲ、枣Ⅱ油组。测井数据齐全,丰富的基础资料为冲积扇单井储层构型划分方法的研究提供了重要支撑。
2 研究方法单井储层构型的识别既包括单井构型的划分,也包括对划分结果的验证。本文以取心井岩心描述的构型划分结果与测井曲线的定性、定量关系作为桥梁,利用K-均值聚类方法建立构型单元的划分标准;应用贝叶斯判别规则形成构型单元的验证公式;将构型单元的划分标准和验证公式应用于非取心井,完成非取心井单井储层构型单元的识别。该方法流程如图 2所示,主要包括4个关键步骤。

|
图 2 单井储层构型识别流程 |
储层构型的研究最早源自于学者们针对曲流河野外露头的分析。对于地下油藏,岩心资料是识别沉积、储层构型的第一手资料。因此,通过对取心井精细描述,对取心井的储层构型划分,是非取心井储层构型划分标准及判别公式建立的基础。
在岩心观察、明确各级次构型单元沉积学成因、特征的同时,需要应用构型单元与测井曲线之间定性、半定量的关系辅助取心井构型单元的划分,形成相对准确且能够用测井曲线判别的取心井储层构型单元划分结果。
2.2 构型划分标准建立测井数据是取心井与非取心井之间对比、分析的桥梁。通过取心井储层构型划分结果,利用测井资料建立单井构型定量表征的标准,然后应用到具有相同类型测井资料的非取心井储层构型划分。具体过程如下。
首先是测井曲线的标准化。为了消除不同时间、不同仪器测量的测井资料之间的系统误差,需要对所有测井资料进行标准化。
其次是测井曲线类型的优选。测井曲线类型的优选主要依据有两个:一是单测井曲线表达的地质含义;二是几种测井曲线组合对不同级次构型单元的区分效果。优选出的测井曲线类型应能够反映储层构型的基本地质含义,并能通过合理组合有效区分不同级次的构型单元。
然后是构型划分标准的初步建立。对于储层构型的研究,适合研究区的构型单元划分方案是统一的研究平台,各级次构型单元类型是唯一确定的。因此,本文采用能够给定聚类数量的经典聚类算法,即K-均值聚类。K-均值聚类是一种迭代求解的聚类分析算法,具体步骤如下[21-24]:
(1) 选取聚类个数K;
(2) 从数据集中选定向量作为初始聚类中心,即C1,C2,…,CK,聚类中心的向量值可以任意设定,其取值会影响聚类结果;
(3) 逐个将需分类的样本Xi(i=1,2,…,n)按欧氏距离分配给某一个聚类中心Cj(0 < j≤K),
(4) 计算各个聚类中心的新的向量值
(5) 如果聚类中心不再变化,终止进程,否则返回步骤(3)。
最终完成构型划分标准建立。根据K-均值聚类方法初步建立的标准,对取心井进行构型划分,并与岩心观察划分结果对比,计算准确率。然后不断修正划分标准,直至准确率达到要求,建立最终的储层构型划分标准。
2.3 构型判别公式建立在建立构型划分标准之后,需要建立合理的验证方法以检验划分结果是否准确。本文采用在沉积、储层研究中有较好应用效果的贝叶斯判别法[25-28]。
贝叶斯判别法是利用已经确定的变量数据构建判别函数,使函数具有某种最优性质,以得到未知变量的后验概率,从而把属于不同类别的样本点尽可能地区别开[25]。
建立构型判别公式的原理:若有G个母体类,取Q个样品,每个样品必须属于这G个母体类中的一个母体。如果每个样品有p个观测指标(x1,x2,…,xp),则可把每个样品看作p维空间{T}中的一个点,Q个样品组成一个p维空间{T}。同时,把各样品视为相互独立的正态随机向量,于是有第g类xg{g =1,2,…,G}多元正态分布。若有一来自某类的新样品x=(x1,x2,…,xp),则可根据贝叶斯公式计算样品x归于第g类的后验概率
| $ \begin{aligned} p(g \mid \boldsymbol{x})=& \frac{p(\boldsymbol{x} \mid g)p(g)}{\sum\limits_{j=1}^{G} p\left(\boldsymbol{x} \mid G_{j}\right) p\left(G_{j}\right)} \end{aligned} $ | (1) |
式中:p(g)为第g类的先验概率;p(x|g)为x属于第g类的概率密度函数;p(Gj)为第Gj个数据点的先验概率;p(x|Gj)为x属于第Gj个数据点的概率密度函数。
在计算的G个后验概率中,如果x属于第k类的后验概率p(k|x)最大,则将样品x归于第k类[29]。
第g类的概率密度函数判别公式为
| $ p(\boldsymbol{x} \mid g)=\alpha_{g}+\sum\limits_{i=1}^{p} \alpha_{g} x_{g i} \quad i=1, 2, \cdots, p $ | (2) |
式中:αg为判别系数;xgi为第g类的第i个观测指标。
按照划分标准得到的构型划分结果,将测井数据分别代入各级次构型单元的判别公式中,得到其后验概率,进一步判断构型单元归属,计算准确率;修正判别公式,直至准确率满足要求,建立最终的构型判别公式。
2.4 非取心井储层构型识别将各级次构型单元判别标准应用到非取心井,形成非取心井构型单元的划分结果,应用贝叶斯判别公式对各级次构型单元进行验证,得到所有测井数据点的构型归属并计算准确率。对于准确率较小的构型单元可以根据专家经验进行适当的人工修改,直到准确率满足要求,最终完成非取心井储层构型单元的识别。
3 研究实例以沧东凹陷东部陡坡带冲积扇为例,进一步阐述基于K-均值聚类和贝叶斯判别的冲积扇单井储层构型单元识别方法。
3.1 取心井单井储层构型单元划分 3.1.1 岩心描述及测井曲线特征研究区早期冲积扇储层构型级次划分方案见表 1[2, 20],油气藏开发地质分层最小级别划分为单砂层,对应6级构型单元。本次研究通过5口取心井(官检1井、官78-28-2井、小新14-19井、小11-6-2井和小检1井等,井位置见图 1)400余米岩心描述,明确了单期复合砂体(7级构型单元)、单成因砂体(8级构型单元)和内部增生体、夹层(9级构型单元)的沉积和测井相特征,划分了取心井储层构型。下面以冲积扇扇中为例展开说明。
|
|
表 1 冲积扇储层构型级次划分 |
(1) 7级构型划分。研究区冲积扇扇中7级构型单元主要包括辫流带和漫流带。辫流带整体岩性较粗,以砾岩、砂岩、粉砂岩为主,可见碎屑流与牵引流沉积构造;SP(自然电位)曲线多呈箱型或钟型。漫流带岩性较细,多为泥质粉砂岩、砂质泥岩、泥岩,可见波状层理;泥岩多为块状,SP曲线接近基线,微电极幅度差最小。
(2) 8级构型划分。8级构型单元主要包括辫流水道、辫流砂岛、漫流细粒和漫流砂体。辫流水道岩性主要为细砾岩、含砾粗砂岩、粉细砂岩,单砂体厚度为2~6m,底部有冲刷面,可见粒序层理(图 3a)、平行层理、顺层分布的植物茎、有一定磨圆度的泥砾;SP、GR(伽马)曲线呈钟形,幅度较低(图 4a)。辫流砂岛岩性主要为中细砂岩、泥质粉砂岩、含砾砂岩等(图 3b),单砂体厚度通常大于4m,具不明显的正韵律或均质韵律,发育平行层理(图 3c)、交错层理(图 3d),韵律底部可见泥砾;SP、GR曲线呈箱形,电阻率幅度差大,较平滑(图 4a)。漫流细粒岩性最细,主要为泥质粉砂岩、粉砂质泥岩,颜色通常为灰绿色、紫红色或杂色(图 3e);SP曲线靠近泥岩基线,微电极曲线幅度差很小(图 4b);厚度为1.2~3.1m。

|
图 3 研究区冲积扇岩心照片 (a)小11-6-2井2877.9m粒序层理;(b)小新14-19井2638.4m含砾中粗砂岩;(c)官78-28-2井2681.4m平行层理;(d)官78-28-2井2725.5m交错层理,含油中砂岩;(e)小检1井2829.8m杂色泥质粉砂岩;(f)小新14-19井3097.3m生物扰动、平行层理;(g)小新14-19井3081.9m增生体顶部的冲刷面;(h)官78-28-2井2773.5m落淤层 |
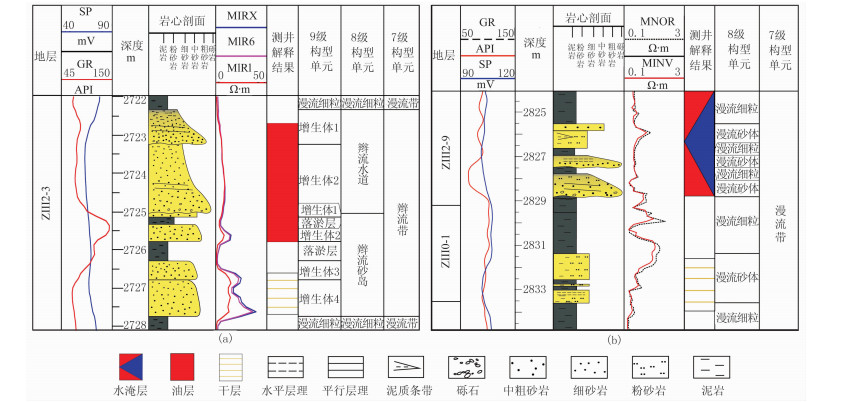
|
图 4 构型单元岩电响应特征 (a)辫流水道+辫流砂岛,官78-28-2井;(b)漫流砂体+漫流细粒,小检1井M1RX、M1R6、M1R1分别为120英寸、60英寸、10英寸电阻率测井;MNOR为微电位测井;MINV为微梯度测井 |
引入SP曲线回返率R可定量表征由于岩性变化引起的SP曲线的回返程度,在此进一步辅助表征以泥岩为主的构型单元测井相特征。
| $ R=\frac{\left(\frac{M_{1}+M_{2}}{2}-M_{3}\right) \times 100}{\frac{M_{1}+M_{2}}{2}} $ | (3) |
式中M1、M2、M3分别为夹层上部砂岩、下部砂岩、夹层SP曲线值。
漫流细粒SP曲线回返较强,回返率为46%~73%。漫流砂体由于辫流水道的频繁改道而保留较少,通常夹于厚层的漫流细粒泥岩之间,厚度横向分布不稳定,内部可见事件性砾石、生物扰动及平行层理等不同成因的沉积构造(图 3f)。漫流砂体自然电位曲线呈中低幅指状,有一定幅度差(图 4b)。
(3) 9级构型划分。9级构型单元主要包括增生体和夹层。增生体为在单一砂体内部由于水位变化形成的最大单一旋回沉积体。夹层为单一增生体顶部由于水动力条件变弱形成的细粒沉积。研究区内水动力较强且变化频繁,辫流水道单一增生体厚度小且横向分布不稳定,为0.15~0.90m;其上细粒沉积由于较强的水流冲刷而不易保存(图 3g),极为少见。辫流砂岛增生体厚度较大且分布较稳定,为0.20~1.00m;夹层(落淤层)(图 3h)分布稳定且非常多见,厚度集中在0.05~0.30m;SP曲线回返较弱,回返率为18%~43%。
3.1.2 测井类型优选针对各类测井数据,首先采用直方图法将其标准化;其次选取一组测井曲线对各级构型内所有构型单元做交会图,对比、分析不同组测井数据对构型单元的区分结果。以8级构型单元为例,电阻率(RT)、密度(DEN)、声波时差(AC)、补偿中子(CN)4种测井数据组合对辫流水道、辫流砂岛、漫流砂体等的区分效果较好(图 5)。因此,优选电阻率、密度、声波时差和补偿中子等4种测井数据用于研究区8级构型单元划分标准。按照同样方法,优选出孔隙度(φ)和泥质含量(SH)用于7级构型单元划分标准;优选电阻率、补偿中子、密度和声波时差等4种用于9级构型单元划分标准。
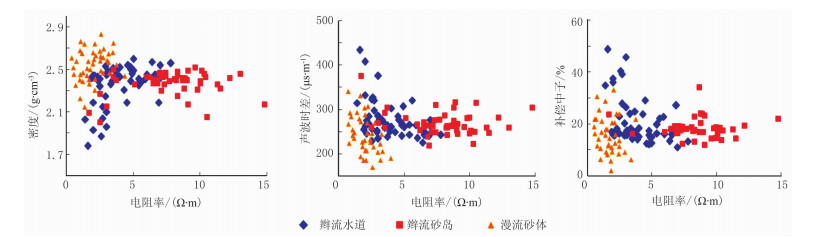
|
图 5 不同种类测井值交会图 |
为了使聚类结果更准确,统计各级次构型单元对应的优选测井类型数据的平均值作为给定的初始聚类中心,并根据各级次构型单元数量给定聚类种数,通过K-均值聚类的方法,得到不同级次构型单元的最终聚类结果(表 2)。
|
|
表 2 K-均值聚类初始聚类中心及最终聚类结果 |
将最终聚类结果作为构型单元的划分标准对取心井储层构型单元进行划分。以官78-28-2井2663.2~ 2680.0m取心段8级构型单元辫流砂岛和辫流水道为例,对比应用划分标准与根据岩心观察两种方法的划分结果(图 6)。

|
图 6 K-均值聚类与岩心观察两种方法划分取心井储层构型单元结果对比 |
辫流砂岛根据岩心观察划分厚度为6.7m,应用划分标准厚度为5.9m,准确率为88.1%。辫流水道根据岩心观察划分厚度为3.7m,应用划分标准厚度为5.2m,准确率为71.2%。应用划分标准辫流水道厚度准确率相对较低,一部分是由于将2667.9~2668.8m的辫流砂岛划分为辫流水道。岩心描述显示,该段位于辫流砂岛单砂体顶部,岩性较细,泥质含量较高,电阻率和密度值均较大,因此将辫流砂岛误划分为辫流水道;另一部分原因是将2672.1~2673.0m的辫流砂岛顶部及落淤层划分为辫流水道,该段为辫流砂岛与落淤层的过渡段,岩性为泥质粉—细砂岩,电阻率和密度相对较小,因此误将其划分为辫流水道。
图 7为应用划分标准对5口井400余米取心段各级次构型单元划分的准确率,可以看出,7级构型单元划分准确率最高,9级构型单元划分准确率最低,这主要是由于9级构型单元厚度较小造成的。一方面,部分落淤层、增生体仅几厘米厚,0.125m一个采样点的测井数据分辨率相对较低,无法对其识别;另一方面,由于落淤层、增生体厚度较小,而构型单元过渡带的厚度相对较大,岩性、物性均与主体位置差别较大,使划分结果出现较多异常点,准确率下降。

|
图 7 应用划分标准对取心段各级次储层构型单元划分的准确率 |
将岩心观察得到的构型划分结果作为参照,把不同级次构型单元优选的测井类型数据分类整理,通过贝叶斯判别法得到各级次构型单元的贝叶斯判别公式(表 3)。
|
|
表 3 各级次构型单元贝叶斯判别公式及其后验概率 |
以官78-28-2井2663.2~2680.0m取心段8级构型单元辫流砂岛和辫流水道(图 6)为例。辫流砂岛厚度为6.7m,辫流砂岛内共有54个测井数据点,经8级构型贝叶斯判别公式计算,45个点判别为辫流砂岛,占比为83.3%;7个点判别为辫流水道,占比为13.0%;2个点判别为漫流砂体,占比为3.7%;准确率为83.3%。辫流水道厚度为3.7m,辫流水道内共有30个测井数据点,经8级构型贝叶斯判别公式计算,24个点判别为辫流水道,占比为80.0%;5个点判别为辫流砂岛,占比为16.7%;1个点判别为漫流砂体,占比为3.3%;准确率为80.0%。
按照上述方法,判别5口取心井400余米取心段各级次构型单元内每个测井数据点的构型归属,得到构型归属占比及准确率(图 8)。可以看出,对于取心段,各级次构型单元贝叶斯判别归属准确率与应用划分标准对取心段各级次构型单元划分的准确率较为接近,证明该判别公式准确,可以应用到非取心井划分结果的检验。

|
图 8 贝叶斯判别公式判别各级次构型单元归属占比 |
利用交会图法优选的测井类型数据进行标准化处理后,以K-均值聚类方法得到的测井类型划分标准作为约束条件划分非取心井储层构型单元,将贝叶斯判别法得到的判别公式验证非取心井各级次储层构型单元划分结果准确率。
以非取心井小新11-13井、小新7-2-2井和小19-9井为例,分别统计三口井枣Ⅲ油组各构型单元识别准确率(表 4)及其厚度。其中,小新11-13井划分及检验结果如图 9所示,各单一构型单元识别准确率与其厚度关系如图 10所示。
|
|
表 4 三口非取心井各级次储层构型单元识别平均准确率 |

|
图 9 小新11-13井划分结果及识别准确率 |

|
图 10 小新11-13井储层构型单元厚度与划分准确率的关系 (a)7级构型单元;(b)8级构型单元;(c)9级构型单元。y为准确率,x为厚度 |
由表 4、图 9和图 10可知,各级次构型单元识别的平均准确率为78%~91%(表 4);各单一构型单元识别准确率整体分布为70%~95%,与厚度呈明显的正相关关系(图 9)。厚度大的7级构型单元识别准确率最高,厚度小的9级构型单元识别准确率最低,这是由于测井数据分辨率及岩性过渡带在不同厚度构型单元中的差异造成的。对于识别结果准确率较低的构型单元,可以根据专家经验适当调整划分结果以提高准确率。
4 结束语(1) 基于K-均值聚类和贝叶斯判别的冲积扇单井储层构型识别方法主要包括取心井储层构型划分、构型划分标准建立、构型判别公式建立以及非取心井储层构型识别四个步骤。该方法同样可以应用于其他研究工区多种沉积相类型的单井储层构型划分标准及判别公式的建立,为开发后期钻井资料丰富的老油田多种沉积相类型单井储层构型识别提供了一种新思路。
(2) 应用本文方法识别非取心井储层构型单元需注意三个主要问题:在岩心观察划分构型结果时,务必在合理构型级次划分方案基础上,对构型单元沉积特征有充分的认识;在建立划分标准时,需调整测井曲线组合及给定合适的初始聚类中心以得到准确率较高的聚类划分结果;在建立判别公式时,应将各级次构型单元判别准确率和构型单元划分准确率对比,两者接近才能说明判别公式准确。
(3) 由于测井数据的分辨率所限及构型单元过渡带的岩性变化两方面原因,该方法对于厚度较薄的构型单元以及构型单元过渡带的识别效果相对较差。非取心井储层构型识别准确率与构型单元厚度呈正相关关系,7级、8级、9级构型识别准确率依次降低。
| [1] |
吴胜和, 岳大力, 刘建民, 等. 地下古河道储层构型的层次建模研究[J]. 中国科学D辑:地球科学, 2008, 38(增刊1): 111-121. WU Shenghe, YUE Dali, LIU Jianmin, et al. Hierarchy modeling of subsurface palaeochannel reservoir architecture[J]. Science in China Series D:Earth Sciences, 2008, 38(S1): 111-121. |
| [2] |
吴胜和, 纪友亮, 岳大力, 等. 碎屑沉积地质体构型分级方案探讨[J]. 高校地质学报, 2013, 19(1): 12-22. WU Shenghe, JI Youliang, YUE Dali, et al. Discussion on hierarchical scheme of architectural units in clastic deposits[J]. Geological Journal of China Universities, 2013, 19(1): 12-22. DOI:10.3969/j.issn.1006-7493.2013.01.004 |
| [3] |
吴千然, 牟中海, 丁晓军, 等. 尕斯库勒油田N21油藏砂质辫状河储层构型研究[J]. 地质科技情报, 2019, 38(2): 151-160. WU Qianran, MOU Zhonghai, DING Xiaojun, et al. Reservoir architecture of sandy braided river in N21 reservoir of Gasikule Oilfield[J]. Geological Science and Technology Information, 2019, 38(2): 151-160. |
| [4] |
宋璠, 杨少春, 苏妮娜, 等. 扇三角洲前缘储层构型界面划分与识别——以辽河盆地欢喜岭油田锦99区块杜家台油层为例[J]. 西安石油大学学报(自然科学版), 2015, 30(1): 7-13. SONG Fan, YANG Shaochun, SU Nina, et al. Division and recognition of architecture interfaces of fan-delta front reservoir:taking Dujiatai reservoir of Jin-99 block in Huanxiling Oilfield, Liaohe Basin as an example[J]. Journal of Xi'an Shiyou University (Natural Science Edition), 2015, 30(1): 7-13. DOI:10.3969/j.issn.1673-064X.2015.01.002 |
| [5] |
张阳, 邱隆伟, 李际, 等. 基于模糊C均值地震属性聚类的沉积相分析[J]. 中国石油大学学报(自然科学版), 2015, 39(4): 53-61. ZHANG Yang, QIU Longwei, LI Ji, et al. Sedimentary facies analysis based on cluster of seismic attri-butes by fuzzy C-means algorithm[J]. Journal of China University of Petroleum, 2015, 39(4): 53-61. DOI:10.3969/j.issn.1673-5005.2015.04.007 |
| [6] |
刘洋. 基于相控神经网络的地震多属性储层厚度预测[J]. 成都理工大学学报(自然科学版), 2018, 45(2): 221-228. LIU Yang. Study on the reservoir thickness prediction by seismic multi-attributes based on facies-guided neural network[J]. Journal of Chengdu University of Technology (Science & Technology Edition), 2018, 45(2): 221-228. DOI:10.3969/j.issn.1671-9727.2018.02.09 |
| [7] |
Poultion M M. Neural networks as an intelligence amplication tool:A review of applications[J]. Geophy-sics, 2002, 67(3): 979-993. |
| [8] |
Tian Y, Xu H, Zhang X Y, et al. Multi-resolution graph-based clustering analysis for lithofacies identification from well log data:Case study of intraplatform bank gas fields, Amu Darya Basin[J]. Applied Geophysics, 2016, 13(4): 598-607. |
| [9] |
张艳, 张春雷, 成育红, 等. 基于机器学习的多地震属性沉积相分析[J]. 特种油气藏, 2018, 25(3): 13-17. ZHANG Yan, ZHANG Chunlei, CHENG Yuhong, et al. Multi-attribute seismic sedimentary facies analysis based on machine learning[J]. Special Oil and Gas Reservoirs, 2018, 25(3): 13-17. DOI:10.3969/j.issn.1006-6535.2018.03.003 |
| [10] |
Özdemir D, Akarun L. A fuzzy algorithm for color quantization of images[J]. Pattern Recognition, 2002, 35(8): 1785-1791. DOI:10.1016/S0031-3203(01)00170-4 |
| [11] |
许少华, 刘扬, 梁久祯, 等. 基于遗传-BP算法和图像处理的沉积微相识别[J]. 石油学报, 2002, 23(3): 48-52. XU Shaohua, LIU Yang, LIANG Jiuzhen, et al. Sedimentary facies identification based on genetic-BP algorithm and image process[J]. Acta Petrolei Sinica, 2002, 23(3): 48-52. |
| [12] |
何旭, 李忠伟, 刘昕, 等. 应用卷积神经网络识别测井相[J]. 石油地球物理勘探, 2019, 54(5): 1159-1165. HE Xu, LI Zhongwei, LIU Xin, et al. Log facies re-cognition based on convolutional neural network[J]. Oil Geophysical Prospecting, 2019, 54(5): 1159-1165. |
| [13] |
冯磊, 李光明. 多属性模糊聚类在辽河滩海沉积相研究中的应用[J]. 地球物理学进展, 2012, 27(6): 2622-2630. FENG Lei, LI Guangming. Application of multi-attribute fuzzy clustering on study of sedimentary facies of Liaohe beach area[J]. Progress in Geoghysics, 2012, 27(6): 2622-2630. |
| [14] |
张永成, 王洪辉, 谭桂花, 等. 基于模糊C均值聚类的沉积相定量识别——以川西某气田蓬莱镇组为例[J]. 科学技术与工程, 2012, 12(26): 6570-6574. ZHANG Yongcheng, WANG Honghui, TAN Guihua, et al. Quantitative identification of sedimentary facies based on fuzzy C-means clustering algorithm:A case study from Penglaizhen formation in the X gasfield in western Sichuan[J]. Science Technology and Engineering, 2012, 12(26): 6570-6574. DOI:10.3969/j.issn.1671-1815.2012.26.004 |
| [15] |
Howard W R. Pattern recognition and machine learn-ing[J]. Kybernetes, 2007, 36(2): 275. DOI:10.1108/03684920710743466 |
| [16] |
Baneshi M. The determination of lithofacies using an optimized neural network and well log data[J]. Petroleum Science and Technology, 2014, 32(8): 897-903. DOI:10.1080/10916466.2011.604056 |
| [17] |
Aliakbar K, Mohsen M, Behnam S S. Lithological facies identification in Iranian largest gas field:A comparative study of neural network methods[J]. Journal of the Geological Society of Indian, 2014, 84(3): 326-334. DOI:10.1007/s12594-014-0136-9 |
| [18] |
Zhang J L, Liu S S, Li J Z. Identification of sedimentary facies with well logs:an indirect approach with multinomial logistic regression and artificial neural network[J]. Arabian Journal of Geosciences, 2017, 10(11): 247. DOI:10.1007/s12517-017-3045-6 |
| [19] |
颜照坤.黄骅坳陷古近纪构造-沉积演化过程研究[D].四川成都: 成都理工大学, 2014.
|
| [20] |
张阳, 蔡明俊, 芦凤明, 等. 碎屑-牵引流控冲积扇储层构型特征及模式——以沧东凹陷小集油田为例[J]. 中国矿业大学学报, 2019, 48(3): 538-552. ZHANG Yang, CAI Mingjun, LU Fengming, et al. Reservoir architecture characteristics and mode of middle and edge alluvial fan controlled by debris flow and traction flow:A case study of Xiaoji oilfield, Cangdong sag[J]. Journal of China University of Mi-ning & Technology, 2019, 48(3): 538-552. |
| [21] |
Marco C, Aritz P, Jose A L. An efficient approximation to the K-means clustering for massive data[J]. Knowledge-Based Systems, 2017, 117: 56-69. DOI:10.1016/j.knosys.2016.06.031 |
| [22] |
Grigorios T, Aristidis L. The MinMax K-means clustering algorithm[J]. Pattern Recognition, 2014, 47(7): 2505-2516. DOI:10.1016/j.patcog.2014.01.015 |
| [23] |
Mahesh K K, Rama Mohan R A. An efficient K-means clustering filtering algorithm using density based initial cluster centers[J]. Information Sciences, 2017, 418. |
| [24] |
王祝文, 刘菁华, 任莉. 基于K均值动态聚类分析的地球物理测井岩性分类方法[J]. 东华理工大学学报(自然科学版), 2009, 32(2): 152-156. WANG Zhuwen, LIU Jinghua, REN Li. The method for lithology classification in geophysical well loggingbased on the K-means dynamic clustering analysis[J]. Journal of East China Institute of Technology, 2009, 32(2): 152-156. DOI:10.3969/j.issn.1674-3504.2009.02.009 |
| [25] |
袁照威, 陈龙, 高世臣, 等. 基于马尔科夫-贝叶斯模拟算法的多地震属性沉积相建模方法——以苏里格气田苏10区块为例[J]. 油气地质与采收率, 2017, 24(3): 37-43. YUAN Zhaowei, CHEN Long, GAO Shichen, et al. A method of sedimentary facies modeling through integration of multi-seismic attributes based on Markov-Bayes model:An example from Su10 area in the north of Sulige gas field[J]. Petroleum Geology and Reco-very Efficiency, 2017, 24(3): 37-43. |
| [26] |
刘兴业, 陈小宏, 李景叶, 等. 基于核贝叶斯判别法的储层物性参数预测[J]. 石油学报, 2016, 37(7): 878-886. LIU Xingye, CHEN Xiaohong, LI Jingye, et al. Re-servoir physical property prediction based on kernel-Bayes discriminant method[J]. Acta Petrolei Sinica, 2016, 37(7): 878-886. |
| [27] |
王芳芳, 李景叶, 陈小宏. 基于马尔科夫链先验模型的贝叶斯岩相识别[J]. 石油地球物理勘探, 2014, 49(1): 183-189. WANG Fangfang, LI Jingye, CHEN Xiaohong. Baye-sian facies identification based on Markov-chain prior model[J]. Oil Geophysical Prospecting, 2014, 49(1): 183-189. |
| [28] |
晏信飞, 曹宏, 姚逢昌, 等. 致密砂岩储层贝叶斯岩性判别与孔隙流体检测[J]. 石油地球物理勘探, 2012, 47(6): 945-950. YAN Xinfei, CAO Hong, YAO Fengchang, et al. Bayesian lithofacies discrimination and pore fluid detection in tight sandstone reservoirs[J]. Oil Geophysical Prospecting, 2012, 47(6): 945-950. |
| [29] |
丁帅伟, 姜汉桥, 陈民锋, 等. 基于模糊C均值聚类算法和贝叶斯判别函数研究深水油藏分类评价[J]. 西安石油大学学报(自然科学版), 2014, 29(2): 43-49. DING Shuaiwei, JIANG Hanqiao, CHEN Minfeng, et al. Classification and evaluation of deepwater oil reservoirs by combining clustering algorithm based on fuzzy C-mean with Bayesian discrimination function[J]. Journal of Xi'an Shiyou University(Natural Science Edition), 2014, 29(2): 43-49. DOI:10.3969/j.issn.1673-064X.2014.02.009 |



 张阳, 新疆克拉玛依市克拉玛依区安定路355号中国石油大学(北京)克拉玛依校区石油学院, 834000。Email:
张阳, 新疆克拉玛依市克拉玛依区安定路355号中国石油大学(北京)克拉玛依校区石油学院, 834000。Email: