② 中国石油长庆油田勘探开发研究院, 陕西西安 710021;
③ 中国石油勘探开发研究院, 北京 100083;
④ 中国石油塔里木油田公司勘探开发研究院, 新疆库尔勒 841000
② Research Institute of Exploration and Development, PetroChina Changqing Oilfield Company, Xi'an, Shaanxi 710021, China;
③ PetroChina Research Institute of Petroleum Exploration & Development, Beijing 100083, China;
④ Research Institute of Exploration and Development, PetroChina Tarim Oilfield Company, Korla, Xinjiang 841000, China
致密油气藏作为一种非常规油气资源,正成为现今国内外的研究热点。致密砂岩因其孔隙结构复杂、渗透率低、非均质性强等特点,利用常规测井解释方法往往得不到精确的流体渗流特性研究结果[1-2]。含水率是储层评价、油气开采及开发潜力评估的一项重要参数[3],且油水相对渗透率是精确求取该参数的关键参数[4],但致密砂岩的饱和度及渗透率等参数通常难以准确计算。近年兴起的神经网络为致密砂岩相对渗透率的研究提供了一种新方法[5-6]。
相对渗透率通常是通过实验方法获得,常用的方法有稳态法和非稳态法[7]。稳态法的原理是基于达西公式,其实验操作简单,但耗时较长,且对复杂储层无法真实模拟流体的运动;非稳态法是基于Buckley-Leverett驱油理论,实验耗时短,且可更真实地模拟岩石中流体的运动过程,因此被广泛应用。
针对计算模型,众多学者进行了相关探究。Burdine[8]早期导出润湿相和非润湿相的相对渗透率公式。Jones等[9]以作切线代替微分运算改进了计算油水相对渗透率的经典JBN方法,提出琼斯图解法。董平川等[10]提出一种非稳态油水相对渗透率计算方法。邓英尔等[11]综合考虑启动压力、毛管压力及重力情况下推导出油湿和水湿两种岩石的相对渗透率公式。王坤等[12]也兼顾启动压力、毛管压力及重力影响,构建了超低渗储层相对渗透率模型。Chima等[13]基于已有的裂缝性油藏相对渗透率模型,建立了气水相对渗透率的数学模型。
含水率是储层评价及指导油田开发的一项动态参数。目前,常用的含水率预测模型相对较少,主要有Logistic、Gompertz及Usher等三种[14]。童宪章[15]通过梳理采出程度和采收率与含水率的关系,建立了童氏图板,但实际生产数据常常无法按某条曲线规范地分布,使其实际应用受到限制。尹大庆等[16]针对油田不同开采阶段,通过回归分析绘制了修正童氏图板,其预测效果有所改善。同时,利用(四种常用的)水驱特征曲线也可研究累计产量与含水率之间的关系。Leverett在20世纪40年代推导的分流量方程也一直被广泛地应用于油田含水率的计算[17]。
上述几种方法虽都具有一定理论意义和应用价值,但也都存在一定局限。测井学者在持续探寻新的改进模型。Moody等[18]提出基于径向基函数(RBF)的神经网络结构。王炜等[19]将RBF神经网络法应用于地震预报专家系统ESEP3.0中,证明该方法具有理想预测效果和应用前景。Tan等[20]利用RBF神经网络法预测页岩气有机碳含量(TOC),并与经验公式法、多元回归法及ΔlogR法对比,验证了该方法预测TOC的可行性,同时也较准确地预测了其他矿物含量。邹友龙等[21]针对核磁共振实验的T2分布,采用RBF网络实现了岩石渗透率及流体组分的高精度预测。Komijani等[22]提出基于RBF神经网络的电化学阻抗斯奎特图的模拟与预测模型,证明了该方法的可行性和准确性。
诸多文献从不同角度论证了RBF神经网络方法的可行性。它具有全局最优逼近、非线性拟合能力强的优点,且学习简单、收敛速度快、便于实现。本文介绍了RBF网络原理;通过误差信息确定最优网络模型,实现对致密砂岩相对渗透率的预测;再利用预测结果计算含水率,从而为致密砂岩油气藏的预测和评价提供依据。
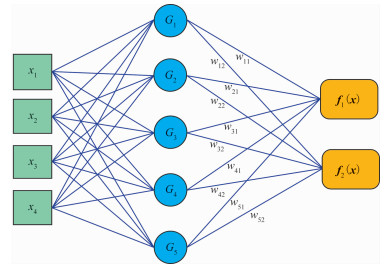
1 RBF网络原理 1.1 网络结构RBF神经网络为三层结构(图 1),即输入层、隐含层和输出层[21-22]。输入层节点传递输入信号到隐含层;隐含层节点是对输入信号在局部产生响应,常用函数是高斯函数;输出层节点通常是线性函数。从输入层空间到隐含层空间的变换是非线性的,而从隐含层空间到输出层空间的变换是线性的。通常选择测井数据或岩心分析数据作为网络模型的输入层,以输出层为待预测参数。
|
图 1 RBF神经网络结构图 |
相渗实验是获得相对渗透率的主要手段,以岩石物理实验数据作为网络的输入,将油、水相对渗透率作为输出,利用RBF神经网络实现对相对渗透率的预测。
1.2 基函数基函数是RBF神经网络隐含层节点的作用函数[21]。它有多种形式,其中最常用的是高斯函数。高斯函数表达式简单、解析性好、径向对称、任意阶导数均存在,便于理论分析。其表达式为
| $ {G_i}(\mathit{\boldsymbol{x}}) = {\rm{exp}}\left( {\frac{{ - {{\left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{c}}_i}} \right\|}^2}}}{{2\sigma _i^2}}} \right)\;\;\;\;\;\;\;\;\;\;\;i = 1, 2, \ldots , m $ | (1) |
式中:x是n维输入变量;ci是第i个基函数的中心,与x具有相同维数;σi是第i个感知变量(高斯宽度),可自由选择,它决定了基函数围绕中心点的宽度;m是感知单元的个数(隐含层节点数);‖x-ci‖是向量的范数,表示x与ci之间的距离。
RBF神经网络输入层实现从x→Gi(x)的非线性映射;输出层实现从Gi(x)→yk的线性映射[23]
| $ {\mathit{\boldsymbol{y}}_k} = \sum\limits_{i = 1}^m {{\mathit{\boldsymbol{w}}_{ik}}{G_i}(\mathit{\boldsymbol{x}})\;\;\;\;\;\;\;\;\;\;k = 1, 2, \ldots , m} $ | (2) |
式中:yk是输出节点;wik是RBF网络输出权值。
1.3 最近邻聚类学习算法RBF神经网络的学习算法主要有:随机算法、自组织学习算法和最近邻聚类学习算法,用来选取RBF的中心[20-22]。随机算法和自组织学习算法适用于静态模式的离线学习,必须提前获得所有可能的样本数据,且在学习前输入数据的中心个数。而最近邻聚类学习算法是一种在线自适应聚类学习算法,可在线学习且不需事先确定隐含层单元的个数,完成聚类所得到的RBF网络是最优的,所以本文选择更优的最近邻聚类学习算法构建模型,建立的RBF网络的输出为
| $ \mathit{\boldsymbol{f}}({x_k}) = \frac{{\sum\limits_{i = 1}^m {{\mathit{\boldsymbol{w}}_{ik}}{\rm{exp}}\left( {\frac{{ - {{\left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{c}}_i}} \right\|}^2}}}{{\sigma _{\rm{b}}^2}}} \right)} }}{{\sum\limits_{i = 1}^m {{\rm{exp}}\left( {\frac{{ - {{\left\| {\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{c}}_i}} \right\|}^2}}}{{\sigma _{\rm{b}}^2}}} \right)} }} $ | (3) |
式中σb为最佳高斯宽度,它表征RBF神经网络模型的复杂程度,一般可通过实验或误差信息来确定[23]。本文通过训练过程中产生的均方误差(MSE)和平均绝对误差(MAE)随高斯宽度的变化确定最佳高斯宽度。
2 RBF神经网络法相对渗透率预测利用RBF神经网络进行预测时,通常是将岩心随机分为两部分,即训练集和检验集。对训练集样本进行网络训练,而检验集则用于检验。这种方法样本的选取虽具有随机性,但不同分类方法训练的结果可能有差异。为了消除此影响,本文采用Leave-one-out[21]方法:假设样本总数为n,分别为s1、s2、…、sn,取出第一个样本s1,将其余的s2、s3、…、sn作为训练集,然后用s1进行检验,记录误差信息;再取出第二个样本s2,同样将剩下的s1、s3、…、sn作为训练集,用s2检验,记录误差信息;依此类推,取出第n个样本sn,将s1、s2、…、sn-1进行训练,用sn检验。该方法的优点是:所有的样本都进行了训练,同时每一个样本又各自作为检验集参与了验证,提高了预测的精确度;另外,也降低了分组不同的影响。
2.1 输入数据选取鄂尔多斯盆地陇东西部延长组30块岩心进行相渗实验,通过对比、分析实验结果,选择最优输入参数。
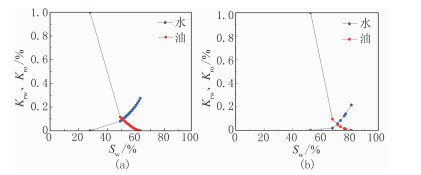
图 2是该区两种类型相渗曲线,从中可见油、水相对渗透率(Kro、Krw)是含水饱和度(Sw)的函数,含水饱和度的变化直接影响油、水相对渗透率,可将含水饱和度作为一个输入参数。含水饱和度与束缚水饱和度(Swi)相关,即包含可动水饱和度和束缚水饱和度两部分。通常,对于油层,Sw=Swi;而水层,则Sw>Swi。显然,束缚水饱和度也是影响相对渗透率的一个因素,可将束缚水饱和度作为第二个输入参数。此外,渗透率与孔隙结构有关,孔隙结构由孔隙结构指数
|
图 2 H300(a)和Y37(b)井岩心相渗曲线 |
|
|
表 1 RBF神经网络输入数据表(部分数据) |
高斯宽度是构建最佳网络模型的重要参数,其大小决定了动态自适应RBF网络模型的复杂程度[21-23]。通过记录均方误差(MSE)和平均绝对误差(MAE)随高斯宽度的变化规律,选取误差最小时的高斯宽度即为最佳高斯宽度。
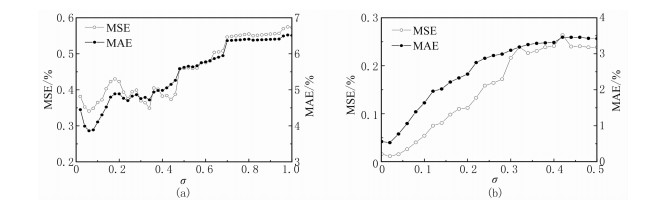
图 3为水和油的相对渗透率预测误差随高斯宽度的变化。从水的相对渗透率预测误差随高斯宽度的变化(图 3a)可知,在σ=0.05处的MSE(0.34%)和MAE(3.8%)最小,此时RBF网络的预测精度最高;从油的相对渗透率预测误差随高斯宽度的变化(图 3b)可知,当σ=0.02时,MSE(0.01%)和MAE(0.53%)呈现极小值。
|
图 3 水(a)和油(b)的相对渗透率预测精度随高斯宽度σ变化 |
图 4a、图 4b分别是测试集的油、水相对渗透率预测结果和测量结果的对比,对应的预测结果平均相对误差为14.55%和11.58%,精度较高。

|
图 4 水(a)和油(b)的相对渗透率预测结果与测量结果对比 |
含水率是产能预测和储层评价的重要参数,它是评价水驱油田开发效果、调整油田开发方案和分析油田开采动态的重要依据。计算含水率的现行方法很多,如图板法、水驱特征曲线法、数学模型预测法等。其中,分流量方程计算含水率是一种常见的数学模型预测法,其原理简单、易于实现、操作性强,被广泛应用[24]。其公式为
| $ {f_{\rm{w}}} = \frac{{{Q_{\rm{w}}}}}{{{Q_{\rm{o}}} + {Q_{\rm{w}}}}} = \frac{1}{{1 + \frac{{{K_{{\rm{ro}}}}}}{{{K_{{\rm{rw}}}}}} \cdot \frac{{{\mu _{\rm{w}}}}}{{{\mu _{\rm{o}}}}}}} $ | (4) |
式中:fw为含水率(无量纲);Qw、Qo分别为通过岩心的水和油的流量(cm3/s);μw、μo分别为水和油的黏度(mPa·s)。
基于达西公式, 推导出方程
| $ Q = \frac{{KA\Delta p}}{{\mu L}} $ | (5) |
式中:Q为单位时间内通过岩心的流量;K为岩石渗透率;μ为流体黏度;Δp为渗流截面间的压差;A为岩心截面积;L为岩心长度。
分析分流量方程,含水率计算的关键在于准确获得油、水相对渗透率。本文以鄂尔多斯盆地陇东地区延长组长8储层为例,利用分流量方程,基于RBF神经网络模型预测相对渗透率,计算了目的层的含水率,并用试油结果进行验证。
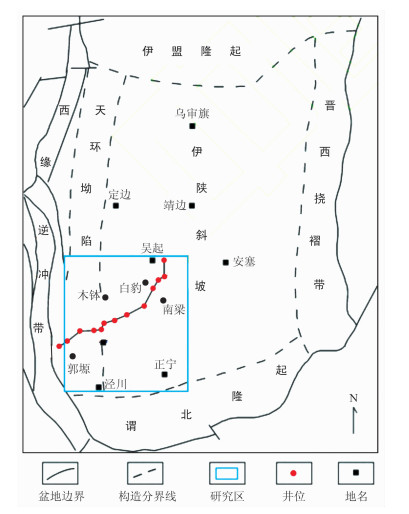
4 实例分析鄂尔多斯盆地是中国第二大沉积盆地,中生界三叠系延长组富含丰富的油气资源。陇东地区位于鄂尔多斯盆地西南部,区域横跨伊陕斜坡、天环坳陷和西缘逆冲带,地质构造复杂。沉积环境主要为三角洲平原和三角洲前缘亚相,发育岩性油气藏。储层主要为水下分流河道沉积的细砂岩,砂体分布范围广,且具有分区差异性,延长组长8段是该区重要的含油层系,研究区主体位于图 5蓝色框内。
|
图 5 研究区位置图 |
长8段储层以长石砂岩为主,填隙物主要为铁方解石和绿泥石,物性差,孔隙度主要集中在4%~12%,平均值为8.72%,渗透率主要分布范围是0.01~0.30mD,平均渗透率约为0.095mD,属于典型的低孔、特低渗储层。孔隙类型以粒间溶孔为主,还有其他各类溶孔,包括长石溶孔、岩屑溶孔以及晶间孔等,孔隙类型复杂多样。
束缚水饱和度对于相对渗透率的预测至关重要。通过核磁共振测井可得到准确的可动流体体积、束缚流体体积及束缚水饱和度等参数[25]。因此,在实际应用时,选择核磁共振计算的饱和度作为输入预测相对渗透率。
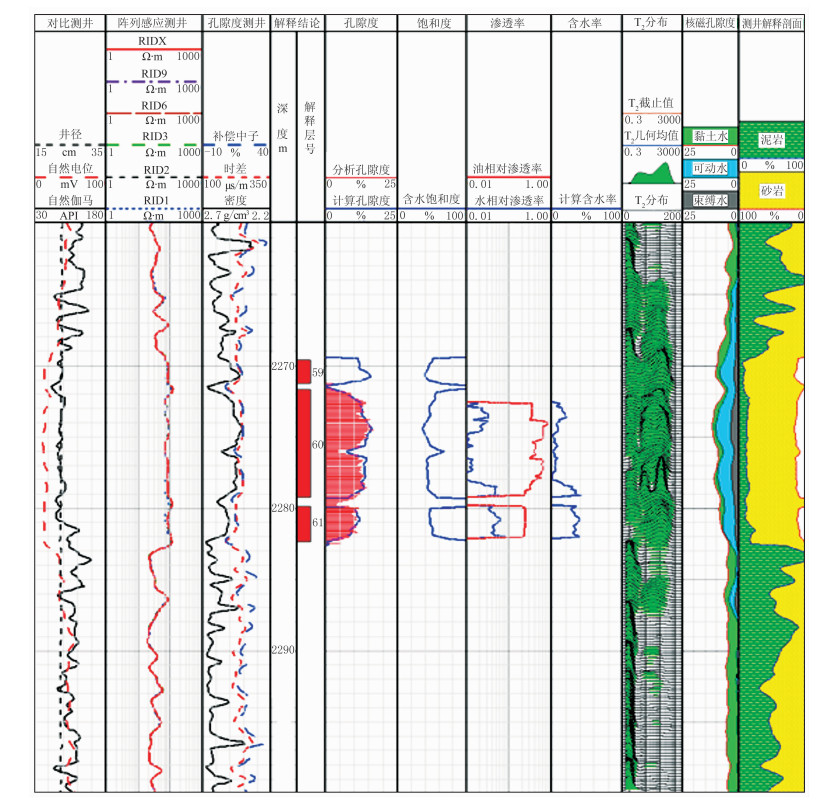
L124井是鄂尔多斯盆地陇东地区的一口勘探井,该井的测井解释成果图(图 6)上第7列是利用RBF网络预测的油和水的相对渗透率;第8列是分流量方程计算的含水率;第9列和第10列分别是核磁共振资料处理得到的T2分布和不同孔隙流体组分体积。该井试油层为2274~2278m,将本文方法应用到该井,计算该层含水率的平均值约为4.89%。试油显示该层日产油10.46t,日产水为0。因此,试油结论为油层,根据含水率定义,实际含水率为0,与预测结果接近。
|
图 6 L124井长8储层测井解释成果图 |
图 7是该区另一口C30井的长8层测井解释成果,其中第7~第10列显示的各项参数同图 6。该井分别在1984~1993m、2026~2029m、2032~2036m层段试油。利用本文方法预测相对渗透率,计算含水率约为70.89%。试油显示日产油6.12t,日产水13.8t,为油水同层,含水率约为69.28%。可见预测结果与试油数据接近。

|
图 7 C30井长8储层测井解释成果图 |
在利用RBF网络模型预测油水相对渗透率过程中,含水饱和度和束缚水饱和度是两个敏感性参数。通过岩电实验拟合岩电参数,利用阿尔奇公式计算含水饱和度,核磁共振束缚水饱和度与孔隙结构指数(
(1) 在利用RBF神经网络进行预测的过程中,选取Sw、ϕ、K、Swi四个敏感参数作为输入,实现对致密砂岩储层油水相对渗透率的预测。
(2) 通过误差信息随高斯宽度的变化可确定最佳高斯宽度,进而实施致密砂岩相对渗透率的预测,其平均相对误差分别为14.55%和11.68%,具有较高的精度。
(3) 将本文方法应用于鄂尔多斯盆地陇东地区的储层含水率计算,所得结果与试油数据吻合较好,证明了该方法的可行性和准确性。
利用RBF神经网络可实现对致密砂岩含水率的预测,但该方法过于依赖岩心实验数据,且训练样本受地区、层位的影响较大。在实际应用中,含水饱和度和束缚水饱和度两个参数在很大程度上决定了预测结果的精度。
附录A 最近邻聚类学习算法最近邻聚类学习算法的具体实现过程如下。
(1) 选择一个适当的高斯宽度σ0,定义矢量A(l)用于存放属于各类的输出矢量之和,定义一个计数器B(l)用于统计属于各类的样本个数,其中l为类别数。
(2) 从第1个数据对(x1,y1)开始,在x1上建立一个聚类中心,令c1=x1,A (1)=y1,B(1)=1。这样建立的RBF网络只有一个隐含单元,其中心是c1,该隐含单元到输出层的权重为w1=A(1)/B(1)。
(3) 考虑第2个样本数据对(x2,y2),求出x2到c1这个聚类中心的距离‖x2-c1‖。若‖x2-c1‖≤σ0,则c1为x2的最近聚类,且令A(1)=y1+y2,B(1)=2,w1=A(1)/B(1)。
(4) 如果‖x2-c1‖>σ0,则将x2作为一个新的聚类中心,且令c2=x2,A(2)=y2,B(2)=1。在上面建立的RBF神经网络中再添加一个隐含层单元,该隐含层单元到输出层的权重为w2=A(2)/B(2)。
(5) 针对第k个样本数据对(xk,yk),k=3、4、…、N,存在m个聚类中心,其中心点分别为c1、c2、…、cm,上述建立的RBF网络中已有m个隐含层单元,分别求出xk到m个聚类中心的距离‖xk-cj‖,j=1、2、…、m。
设‖xk-cj‖为这些距离中的最小值,即cj为xk的最近邻聚类。若‖xk-cj‖>σ0,则将xk作为一个新的聚类中心。可令cm+1=xk,m=m+1,A(m)=yk,B(m)=1,并保持A(i)、B(i)值不变,i=1、2、…、m-1。在上述已建立的RBF网络中再添加m个隐含层单元,该隐含层单元到输出层的权重为wm=A(m)/B(m)。若‖xk-cj‖≤σ0,则A(j)=A(j)+yk,B(j)=B(j)+1。当i≠j时,保持A(i)、B(i)的值不变。隐含层单元到输出层的权重为wi=A(i)/B(i),i=1、2、…、m。
| [1] |
邹存友, 玉立君. 中国水驱砂岩油田含水与采出程度的量化关系[J]. 石油学报, 2012, 33(2): 288-292. ZOU Cunyou, YU Lijun. A quantization relationship between water cut and degree of reserve recovery for waterflooding sandstone reservoirs in China[J]. Acta Petrolei Sinica, 2012, 33(2): 288-292. |
| [2] |
闫星宇, 顾汉明, 肖逸飞, 等. XGBoost算法在致密砂岩气储层测井解释中的应用[J]. 石油地球物理勘探, 2019, 54(2): 447-455. YAN Xingyu, GU Hanming, XIAO Yifei, et al. XGBoost algorithm applied in the interpretation of tight-sand gas reservoir on well logging data[J]. Oil Geophysical Prospecting, 2019, 54(2): 447-455. |
| [3] |
Xu J C, Guo C H, Jiang R Z, et al. Study on relative permeability characteristics affected by displacement pressure gradient:Experimental study and numerical simulation[J]. Fuel, 2016, 163(1): 314-323. |
| [4] |
周鹏. 新型水驱油田含水率预测模型的建立及其应用[J]. 新疆石油地质, 2016, 37(4): 452-455. ZHOU Peng. New model for water cut forecasting in water flooding oilfields establishment and application[J]. Xinjiang Petroleum Geology, 2016, 37(4): 452-455. |
| [5] |
季少聪, 杨香华, 朱红涛, 等. 下刚果盆地A区块Madingo组烃源岩TOC含量的地球物理定量预测[J]. 石油地球物理勘探, 2018, 53(2): 369-380. JI Shaocong, YANG Xianghua, ZHU Hongtao, et al. Geophysical quantitative prediction of TOC content in source rocks of Madingo Formation in Block A, Lower Congo Basin[J]. Oil Geophysical Prospecting, 2018, 53(2): 369-380. |
| [6] |
孙延风, 梁艳春, 孟庆福. 改进的神经网络最近邻聚类学习算法及其应用[J]. 吉林大学学报(信息科学版), 2002, 20(1): 63-66. SUN Yanfeng, LIANG Yanchun, MENG Qingfu. Improved neural network nearest neighbor clustering learning algorithm and its application[J]. Journal of Jilin University(Information Science Edition), 2002, 20(1): 63-66. DOI:10.3969/j.issn.1671-5896.2002.01.013 |
| [7] |
刘西雷. 基于分形理论计算相渗分流量曲线[J]. 大庆石油地质与开发, 2015, 34(1): 59-62. LIU Xilei. Relative permeability fractional flow curve calculation based on fractal theory[J]. Petroleum Geo-logy & Oilfield Development in Daqing, 2015, 34(1): 59-62. DOI:10.3969/J.ISSN.1000-3754.2015.01.012 |
| [8] |
Burdine N T. Relative permeability calculations from pore size distribution data[J]. Transactions of The Metallurgical Society of AIME, 1953, 19(8): 71-79. |
| [9] |
Jones S C, Roszelle W O. Graphical techniques for determining relative permeability from displacement experiments[J]. Journal of Petroleum Technology, 1978, 30(5): 807-817. DOI:10.2118/6045-PA |
| [10] |
董平川, 马志武, 赵常生. 储层相对渗透率评价方法[J]. 大庆石油地质与开发, 2008, 27(6): 55-58. DONG Pingchuan, MA Zhiwu, ZHAO Changsheng. Evaluating method of relative permeabilities of a reservoir[J]. Petroleum Geology & Oilfield Development in Daqing, 2008, 27(6): 55-58. DOI:10.3969/j.issn.1000-3754.2008.06.015 |
| [11] |
邓英尔, 刘慈群, 庞宏伟. 考虑多因素的低渗透岩石相对渗透率[J]. 新疆石油地质, 2003, 24(2): 152-154. DENG Yinger, LIU Ciqun, PANG Hongwei. Calculation of relative permeability of low permeability rock with multiple factors[J]. Xinjiang Petroleum Geology, 2003, 24(2): 152-154. DOI:10.3969/j.issn.1001-3873.2003.02.020 |
| [12] |
王坤, 张烈辉. 考虑应力敏感超低渗油藏油水相对渗透率的计算[J]. 石油天然气学报, 2011, 33(11): 117-119. WANG Kun, ZHANG Liehui. Calculation of relative permeability of extra-low permeability reservoirs considering stress sensitivity[J]. Journal of Oil and Gas Technology, 2011, 33(11): 117-119. DOI:10.3969/j.issn.1000-9752.2011.11.026 |
| [13] |
Chima A, Geiger S.An analytical equation to predict gas-water relative permeability curves in fracture[C]. SPE Latin America and Caribbean Petroleum Engineering Conference, 2012.
|
| [14] |
高文君, 徐冰涛, 黄瑜, 等. 水驱油田含水率预测方法研究及拓展[J]. 石油与天然气地质, 2017, 38(5): 993-999. GAO Wenjun, XU Bingtao, HUANG Yu, et al. Research on and development of prediction method of water cut in water flooding oilfield[J]. Oil & Gas Geology, 2017, 38(5): 993-999. |
| [15] |
童宪章. 油井产状和油藏动态分析[M]. 北京: 石油工业出版社, 1981: 37-60.
|
| [16] |
尹大庆, 林东维, 朱文波, 等. 水驱砂岩油藏修正童氏图版含水率预测方法[J]. 大庆石油地质与开发, 2014, 33(2): 54-57. YIN Daqing, LIN Dongwei, ZHU Wenbo, et al. Pre-diting method for the water cut of water flooded sandstone oil reservoirs by corrected Tong's chart board[J]. Petroleum Geology & Oilfield Development in Daqing, 2014, 33(2): 54-57. DOI:10.3969/J.ISSN.1000-3754.2014.02.011 |
| [17] |
李松泉, 程林松, 李秀生, 等. 特低渗透油藏非线性渗流模型[J]. 石油勘探与开发, 2008, 35(5): 606-612. LI Songquan, CHENG Linsong, LI Xiusheng, et al. Non-linear seepage flow models of ultra-low perme-ability reservoirs[J]. Petroleum Exploration and Deve-lopment, 2008, 35(5): 606-612. DOI:10.3321/j.issn:1000-0747.2008.05.013 |
| [18] |
Moody J, Darken J. Fast learning in networks of locally-tuned processing units[J]. Neural Computation, 1989, 1(2): 281-294. |
| [19] |
王炜, 吴耿峰, 张博锋, 等. 径向基函数(RBF)神经网络及其应用[J]. 地震, 2005, 25(2): 19-25. WANG Wei, WU Gengfeng, Zhang Bofeng, et al. Neural networks of radial basis function (RBF) and it's application to earthquake prediction[J]. Earthquake, 2005, 25(2): 19-25. |
| [20] |
Tan M J, Liu Q, Zhang S Y. A dynamic adaptive radial basis function approach for total organic carbon content prediction in organic shale[J]. Geophysics, 2013, 78(6): D445-D459. DOI:10.1190/geo2013-0154.1 |
| [21] |
邹友龙, 胡法龙, 李长喜, 等. 利用径向基函数预测岩石渗透率及流体分子组分[J]. 测井技术, 2012, 36(3): 225-229. ZOU Youlong, HU Falong, LI Changxi, et al. Prediction of rock permeability and fluid molecular composition using radial basis function[J]. Well Logging Technology, 2012, 36(3): 225-229. DOI:10.3969/j.issn.1004-1338.2012.03.002 |
| [22] |
Komijani H, Rezaeihassanabadi S, Parsaei R, et al. Radial basis function neural network for electroche-mical impedance prediction at presence of corrosion inhibitor[J]. Periodica Polytechnica-Chemical Engineering, 2017, 61(2): 128-132. |
| [23] |
谭茂金. 有机页岩测井岩石物理[M]. 北京: 石油工业出版社, 2015: 58-67. TAN Maojin. Petrophysics and Rock Physics of Organic Shale[M]. Beijing: Petroleum Industry Press, 2015: 58-67. |
| [24] |
张伟, 冯进, 胡文亮, 等. L油田古近系油藏含水率计算方法及其应用[J]. 石油钻探技术, 2016, 44(1): 105-110. ZHANG Wei, FENG Jin, HU Wenliang, et al. Calculation method and application for water content of paleogene reservoirs in L oilfield[J]. Petroleum Drilling Techniques, 2016, 44(1): 105-110. |
| [25] |
高楚桥, 何宗斌, 吴洪深, 等. 核磁共振T2截止值与毛细管压力的关系[J]. 石油地球物理勘探, 2004, 39(1): 117-120. GAO Chuqiao, HE Zongbin, WU Hongshen, et al. Relationship between NMR T2 cutoff and capillary pressure[J]. Oil Geophysical Prospecting, 2004, 39(1): 117-120. DOI:10.3321/j.issn:1000-7210.2004.01.022 |



 谭茂金, 北京市海淀区学院路29号中国地质大学(北京)地球物理与信息技术学院, 100083。Email:
谭茂金, 北京市海淀区学院路29号中国地质大学(北京)地球物理与信息技术学院, 100083。Email: