② 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071
② Laboratory for Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266071, China
叠前地震反问题作为储层地球物理学的核心内容,是解决复杂油气储层特征描述及油气判识的重要理论与方法,通常包括波动方程反演(层析成像、全波形反演等)、AVO(Amplitude Variation with Offsets,振幅随炮检距变化)、EI(Elastic Impedance,弹性阻抗)反演[1-4]。然而,由于带限地震数据缺失低频和高频信息,且受到噪声的干扰,叠前地震反问题表现出较强的不适定性,因此叠前地震反问题必须通过其他途径(如钻、测井数据、油藏建模数据等)补充缺失的模型信息。正则化和概率化反演(以贝叶斯理论为主)是缓解叠前地震反问题不适定性最重要的两种手段[5]。然而,随着油气藏类型日益复杂化,仅仅依靠单一的模型最优解,已经难以满足地球物理勘探人员对复杂油气储层岩性和含流体性质的精细描述的要求,故模型参数最优解、不确定度及置信区间等勘探风险评估逐渐引起储层地球物理学家的关注。
在地震反演的贝叶斯框架中,模型参数的先验信息可以通过随机变量的先验概率密度分布函数(Prior Probability Density Function,Prior PDF)定量表征。其认为地下介质模型参数是随机的,则地震反问题是指在多类型观测数据集的协同约束下匹配随机变量的随机实现过程[5]。目前,以贝叶斯推断为基础的反问题中,最大后验概率解(Maximum A Posteriori Estimation,MAP)[5-13]、后验PDF的显式解[14-20]及后验PDF的随机解(以马尔可夫链蒙特卡洛模型为主,MCMC)[21-27]是应用最广泛的三种概率解。贝叶斯MAP解是通过贝叶斯公式计算得到模型参数的后验概率密度分布,以最大化后验PDF获取模型参数的最优解。后验概率的显式解是指模型参数的后验统计特征(如均值和协方差等)可以通过显式表达式定量表征,以高斯型概率模型为应用典型。随机解是指通过随机采样的方式对后验PDF进行随机采样,利用大量随机样本点逼近理论后验PDF的求解方式。Hansen等[28]阐述了两类观测数据约束下高斯概率密度模型的地质统计模拟问题以及贝叶斯线性反问题的显式解。Grana等[14-15]在混合先验分布的基础上,采用序贯模拟方法对后验PDF的显式解进行单点模拟,实现了纵波阻抗、离散岩相的同步预测,该方法由于未引入模型参数的低频信息,需要在模拟相对纵波阻抗后补偿低频背景。Lang等[16]在高斯概率模型的基础上,通过后验概率模型的显式解实现了叠前地震纵、横波阻抗和密度的随机反演方法。Li等[27]联合马尔科夫链蒙特卡洛模型、混合高斯概率先验信息,提出了岩相驱动下的叠后地震随机反演方法,改善了叠后地震反演分辨率的同时,实现了“离散相态”与“弹性参数”的协同预测。
Hastie等[29]基于贝叶斯推断理论框架,系统阐述了混合概率模型在“离散变量”反演与分类领域的意义。混合概率模型在贝叶斯推断中是实现叠前地震“连续弹性参数”和“离散相态”协同预测的基础。基于此,本文依据岩性驱动的模型参数统计先验信息,把地层岩性(如砂、泥岩)与模型参数和观测地震数据联系在一起,提出了一种基于混合概率模型的时频联合域叠前地震概率化弹性阻抗反演方法;综合利用时域、频域地震、低频整合先验信息及已知模型点四类数据集实现对弹性阻抗、离散岩相的序贯协同预测;此外,将非线性边界修正算法引入叠前地震流体因子的直接提取过程,旨在提高叠前地震反演的稳定性,克服弹性参数提取过程中易出现“超界解”的问题。通过理论模型测试和实际勘探实例证实叠前地震概率化弹性阻抗反演方法的稳定性和可行性。
1 方法原理 1.1 时频联合域地震正演模型构建不同变换域地震反演是通过考虑不同域内地震响应与合成地震数据间的匹配程度以搜索最优模型参数的过程[5]。频率域反演相比时间域反演具有频率分量自动解耦、频率选择自由、多分量逐级寻优及分辨率高的特点。因此,将混合域卷积模型应用于地震数据的正演
| $ \begin{array}{*{20}{l}} {S(\omega ,{\theta _i}) = W(\omega ,{\theta _i})\int_0^{ + \infty } {{r_{{\rm{PP}}}}} (t,{\theta _i}) \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}( - {\rm{j}}\omega t){\rm{d}}t + N(\omega )} \end{array} $ | (1) |
式中:S(ω, θi)、W(ω, θi)分别为入射角为θi的地震频谱和子波频谱,ω为角频率;rPP(t, θi)为基于Biot-Gassmann孔隙弹性理论的Russell线性AVO近似方程[30-33];j为虚数单位;t为时间;N(ω)为噪声频谱。式(1)可以重组为矩阵形式
| $ \mathit{\boldsymbol{S}}_{{\theta _i}}^\omega = \mathit{\boldsymbol{W}}_{{\theta _i}}^\omega \mathit{\boldsymbol{ECm}} + {\mathit{\boldsymbol{N}}_\omega } $ | (2) |
式中:Sθiω为地震频谱;Wθiω=diag[W(ω, θi)]为地震子波的频谱矩阵;E为Fourier变换算子;C为一阶差分矩阵;
| $ \mathit{\boldsymbol{d}} = {\mathit{\boldsymbol{G}}_0}\mathit{\boldsymbol{m}} + \mathit{\boldsymbol{N}} $ | (3) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{d}} = \left[ {\begin{array}{*{20}{c}} {{\lambda _\omega }\mathit{\boldsymbol{S}}_{{\theta _i}}^\omega }\\ {{\lambda _t}\mathit{\boldsymbol{S}}_{{\theta _i}}^t} \end{array}} \right]}\\ {{\mathit{\boldsymbol{G}}_0} = \left[ {\begin{array}{*{20}{c}} {{\lambda _\omega }\mathit{\boldsymbol{W}}_{{\theta _i}}^\omega \mathit{\boldsymbol{EC}}}\\ {{\lambda _t}\mathit{\boldsymbol{W}}_{{\theta _i}}^t\mathit{\boldsymbol{C}}} \end{array}} \right]}\\ {\mathit{\boldsymbol{N}} = \left[ {\begin{array}{*{20}{c}} {{\lambda _\omega }{\mathit{\boldsymbol{N}}_\omega }}\\ {{\lambda _t}{\mathit{\boldsymbol{N}}_t}} \end{array}} \right]} \end{array}} \right. $ | (4) |
式中:Sθit、Wθit和Nt分别为时域地震数据、时域子波矩阵和随机噪声向量;λt和λω分别为时、频域地震反演的加权系数。在不同信噪比的情况下,通过调整λt、λω,选择高信噪比的频率分量,控制地震反演算法的稳定性和分辨率[12, 19, 27]。为了提高时频联合域地震反演的可靠性,将弹性阻抗的低频先验信息引入式(3),以补偿观测地震数据中缺失的低频分量。
假设η为利用实际测井数据构建的弹性阻抗低频先验数据,λL为低频背景的正则化因子,D为正则化对角矩阵。联合式(3)与η,可将正演模型改写为
| $ {\mathit{\boldsymbol{H}} = \mathit{\boldsymbol{Pm}}} $ | (5) |
其中
| $ {\mathit{\boldsymbol{H}} = \left[ {\begin{array}{*{20}{c}} {{\lambda _\omega }\mathit{\boldsymbol{S}}_{{\theta _i}}^\omega }\\ {{\lambda _t}\mathit{\boldsymbol{S}}_{{\theta _i}}^t}\\ {{\lambda _{\rm{L}}}\mathit{\boldsymbol{\eta }}} \end{array}} \right]} $ | (6a) |
| $ \mathit{\boldsymbol{P}} = \left[ {\begin{array}{*{20}{c}} {{\lambda _\omega }\mathit{\boldsymbol{W}}_{{\theta _i}}^\omega \mathit{\boldsymbol{EC}}}\\ {{\lambda _t}\mathit{\boldsymbol{W}}_{{\theta _i}}^t\mathit{\boldsymbol{C}}}\\ {{\lambda _{\rm{L}}}\mathit{\boldsymbol{D}}} \end{array}} \right] $ | (6b) |
| $ {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{H}}} = \left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{C}}_{\omega \omega }}}&{{\mathit{\boldsymbol{C}}_{\omega t}}}&{{\mathit{\boldsymbol{C}}_{\omega \eta }}}\\ {\mathit{\boldsymbol{C}}_{\omega t}^{\rm{T}}}&{{\mathit{\boldsymbol{C}}_{tt}}}&{{\mathit{\boldsymbol{C}}_{t\eta }}}\\ {\mathit{\boldsymbol{C}}_{\omega \eta }^{\rm{T}}}&{\mathit{\boldsymbol{C}}_{t\eta }^{\rm{T}}}&{{\mathit{\boldsymbol{C}}_{\eta \eta }}} \end{array}} \right] $ | (6c) |
式中:H为输入的三种类型已知数据集;P为正演核矩阵;Cωω、Ctt和Cηη分别是Sθiω、Sθit和η的协方差矩阵;Cωt、Cωη分别是Sθiω与Sθit、η之间的协方差矩阵;Ctη是Sθit与η之间的协方差矩阵;CH为三种数据集H的联合协方差矩阵。
1.2 混合概率模型驱动的弹性阻抗反演方法混合概率模型是多个“单峰”PDF的线性叠加,旨在量化待反演模型参数的“多峰”分布特征,是“单峰”PDF的推广形式[5]。待反演模型参数的先验概率密度分布往往受到储层岩性的影响,储层岩性不同将导致模型参数的统计特征差异[5, 15, 19, 27]。具有“多峰”分布特征的混合概率模型是实现“离散型”—“连续型”模型参数协同预测的关键。高斯型PDF是数学、物理及工程等领域中最普遍的统计分布,具有线性变换性质,易于求解地球物理反问题的显式解[16-18, 28-29]。因此,本文将高斯混合PDF作为弹性阻抗反演模型的先验PDF。其中,弹性阻抗的先验均值、方差及高斯混合PDF中的峰态数量由实际测井数据的解释结果和统计特征获得。
针对贝叶斯线性地震反问题,若目标工区中储层岩性类别的数量为M,将式(6)代入式(A-8)~式(A-9)(附录A),则模型最优解可用后验概率分布的显式解进行量化,推导得到三类数据集(即Sθiω、Sθit和η)协同约束下的第k个高斯概率分量pk(m|H)的显式解,其后验均值为
| $ \begin{array}{l} \mathit{\boldsymbol{\mu }}_{\mathit{\boldsymbol{m}}|\mathit{\boldsymbol{H}}}^k = \mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{m}}^k + \mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^k[\begin{array}{*{20}{c}} {{\lambda _\omega }{{(\mathit{\boldsymbol{W}}_{{\theta _i}}^\omega \mathit{\boldsymbol{EC}})}^{\rm{T}}}}&{{\lambda _t}{{(\mathit{\boldsymbol{W}}_{{\theta _i}}^t\mathit{\boldsymbol{C}})}^{\rm{T}}}}&{{\lambda _{\rm{L}}}{\mathit{\boldsymbol{D}}^{\rm{T}}}} \end{array}] \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_{\omega \omega }}}&{{\mathit{\boldsymbol{S}}_{\omega t}}}&{{\mathit{\boldsymbol{S}}_{\omega \eta }}}\\ {\mathit{\boldsymbol{S}}_{\omega t}^{\rm{T}}}&{{\mathit{\boldsymbol{S}}_{tt}}}&{{\mathit{\boldsymbol{S}}_{t\eta }}}\\ {\mathit{\boldsymbol{S}}_{\omega \eta }^{\rm{T}}}&{\mathit{\boldsymbol{S}}_{t\eta }^{\rm{T}}}&{{\mathit{\boldsymbol{S}}_{\eta \eta }}} \end{array}} \right]^{ - 1}}\left[ {\mathit{\boldsymbol{H}} - \left( {\begin{array}{*{20}{c}} {{\lambda _\omega }\mathit{\boldsymbol{W}}_{{\theta _i}}^\omega \mathit{\boldsymbol{EC}}}\\ {{\lambda _t}\mathit{\boldsymbol{W}}_{{\theta _i}}^t\mathit{\boldsymbol{C}}}\\ {{\lambda _{\rm{L}}}\mathit{\boldsymbol{D}}} \end{array}} \right)\mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{m}}^k} \right] \end{array} $ | (7) |
式中:μmk和Cmk分别为待反演模型参数m的先验均值和先验协方差;Sωω、Stt和Sηη分别是正演地震频谱数据、时域地震数据、弹性阻抗数据的协方差矩阵;Sωt、Sωη分别是正演频谱数据与正演时域地震数据、正演弹性阻抗数据之间的协方差矩阵;Stη是正演时域地震数据与正演弹性阻抗数据之间的协方差矩阵。另外,后验协方差为
| $ \begin{array}{l} \mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{m}}|\mathit{\boldsymbol{H}}}^k = \mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^k - \mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^k[\begin{array}{*{20}{c}} {{\lambda _\omega }{{(\mathit{\boldsymbol{W}}_{{\theta _i}}^\omega \mathit{\boldsymbol{EC}})}^{\rm{T}}}}&{{\lambda _t}{{(\mathit{\boldsymbol{W}}_{{\theta _i}}^t\mathit{\boldsymbol{C}})}^{\rm{T}}}}&{{\lambda _{\rm{L}}}{\mathit{\boldsymbol{D}}^{\rm{T}}}} \end{array}] \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_{\omega \omega }}}&{{\mathit{\boldsymbol{S}}_{\omega t}}}&{{\mathit{\boldsymbol{S}}_{\omega \eta }}}\\ {\mathit{\boldsymbol{S}}_{\omega t}^{\rm{T}}}&{{\mathit{\boldsymbol{S}}_{tt}}}&{{\mathit{\boldsymbol{S}}_{t\eta }}}\\ {\mathit{\boldsymbol{S}}_{\omega \eta }^{\rm{T}}}&{\mathit{\boldsymbol{S}}_{t\eta }^{\rm{T}}}&{{\mathit{\boldsymbol{S}}_{\eta \eta }}} \end{array}} \right]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{\lambda _\omega }\mathit{\boldsymbol{W}}_{{\theta _i}}^\omega \mathit{\boldsymbol{EC}}}\\ {{\lambda _t}\mathit{\boldsymbol{W}}_{{\theta _i}}^t\mathit{\boldsymbol{C}}}\\ {{\lambda _{\rm{L}}}\mathit{\boldsymbol{D}}} \end{array}} \right]\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^k \end{array} $ | (8) |
其中
| $ \begin{array}{l} \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{S}}_{\omega \omega }}}&{{\mathit{\boldsymbol{S}}_{\omega t}}}&{{\mathit{\boldsymbol{S}}_{\omega \eta }}}\\ {\mathit{\boldsymbol{S}}_{\omega t}^{\rm{T}}}&{{\mathit{\boldsymbol{S}}_{tt}}}&{{\mathit{\boldsymbol{S}}_{t\eta }}}\\ {\mathit{\boldsymbol{S}}_{\omega \eta }^{\rm{T}}}&{\mathit{\boldsymbol{S}}_{t\eta }^{\rm{T}}}&{{\mathit{\boldsymbol{S}}_{\eta \eta }}} \end{array}} \right] = {\kern 1pt} \left[ {\begin{array}{*{20}{c}} {{\lambda _\omega }\mathit{\boldsymbol{W}}_{{\theta _i}}^\omega \mathit{\boldsymbol{EC}}}\\ {{\lambda _t}\mathit{\boldsymbol{W}}_{{\theta _i}}^t\mathit{\boldsymbol{C}}}\\ {{\lambda _{\rm{L}}}\mathit{\boldsymbol{D}}} \end{array}} \right] \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^k[\begin{array}{*{20}{c}} {{\lambda _\omega }{{(\mathit{\boldsymbol{W}}_{{\theta _i}}^\omega \mathit{\boldsymbol{EC}})}^{\rm{T}}}}&{{\lambda _t}{{(\mathit{\boldsymbol{W}}_{{\theta _i}}^t\mathit{\boldsymbol{C}})}^{\rm{T}}}}&{{\lambda _{\rm{L}}}{\mathit{\boldsymbol{D}}^{\rm{T}}}} \end{array}] + {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{H}}} \end{array} $ | (9) |
由于高斯型PDF具有线性变换性质(附录A),待反演模型的混合后验PDF p(m|H)可以重新表征为高斯混合概率模型
| $ \gamma _{\mathit{\boldsymbol{m}}|\mathit{\boldsymbol{H}}}^k = \frac{{{\lambda _k}{N_k}(\mathit{\boldsymbol{H}};\mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{H}}^k,\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{H}}^k)}}{{\sum\limits_{k = 1}^M {{\lambda _k}} {N_k}(\mathit{\boldsymbol{H}};\mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{H}}^k,\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{H}}^k)}} $ | (10) |
式中:λk=p(zk)为第k种离散岩性zk的先验概率;Nk(H; μHk, CHk)表示均值为μHk、协方差为CHk的高斯PDF,μHk=
Pμmk、CHk=PCmkPT分别为已知数据集H的训练均值和训练协方差。针对实际工区可以通过测井解释数据统计获取
通过混合后验均值和后验协方差的显式表达式(式(7)、式(8)),即可计算三类已知数据集H约束下的待反演模型参数最优解。为了更好地分析待反演模型的不确定性,采用基于单点实现的序贯模拟算法(Sequential Simulation)(图 1)对后验PDF进行随机采样。此外,将先前的模拟点集ms作为贝叶斯地震反演中下一个模拟点mi的约束条件。因此,针对第k个高斯概率分量pk(m|H),在待模拟点位置的后验均值可改写为
| $ \begin{array}{l} \mathit{\boldsymbol{\mu }}_{{m_i}}^k{|_{({\mathit{\boldsymbol{m}}_{\rm{s}}},\mathit{\boldsymbol{s}}_{{\theta _i}}^\omega ,\mathit{\boldsymbol{s}}_{{\theta _i}}^t,\mathit{\boldsymbol{\eta }})}} = \mathit{\boldsymbol{\mu }}_{{m_i}}^k + [\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{U}}_i}\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{U}}^{\rm{T}}}}&{{\mathit{\boldsymbol{U}}_i}\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{P}}^{\rm{T}}}} \end{array}] \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {[\mathit{\boldsymbol{C}}_{({\mathit{\boldsymbol{m}}_{\rm{s}}},\mathit{\boldsymbol{s}}_{{\theta _i}}^\omega ,\mathit{\boldsymbol{s}}_{{\theta _i}}^t,\mathit{\boldsymbol{\eta }})}^k]^{ - 1}}\left[ {\begin{array}{*{20}{c}} {{\lambda _{{m_{\rm{s}}}}}({\mathit{\boldsymbol{m}}_{\rm{s}}} - \mathit{\boldsymbol{U\mu }}_\mathit{\boldsymbol{m}}^k)}\\ {{\lambda _\omega }(\mathit{\boldsymbol{S}}_{{\theta _i}}^\omega - \mathit{\boldsymbol{W}}_{{\theta _i}}^\omega \mathit{\boldsymbol{EC\mu }}_\mathit{\boldsymbol{m}}^k)}\\ {{\lambda _{\rm{L}}}(\mathit{\boldsymbol{\eta }} - \mathit{\boldsymbol{D\mu }}_\mathit{\boldsymbol{m}}^k)} \end{array}} \right] \end{array} $ | (11) |
式中:μmik为待模拟点mi的先验均值;ms表示先前的模拟点集;Ui=[0…0 1…0]为待模拟点mi的采样矩阵(即第i个元素为1,其余元素均为0),已知(或先前模拟)数据ms的提取矩阵为U=[Uj,Ul,…,Ui-1,…,Ue]T,j、l、e分别表示先前模拟点的位置;λms表示ms的权重系数。当λω=0、λt=0和λL=0的情况下,式(11)等价于序贯高斯模拟,待模拟点mi的后验方差改写为
| $ \begin{array}{l} \sigma _{{m_i}{|{({\mathit{\boldsymbol{m}}_{\rm{s}}},\mathit{\boldsymbol{s}}_{{\theta _i}}^\omega ,\mathit{\boldsymbol{s}}_{{\theta _i}}^t,\mathit{\boldsymbol{\eta }})}}}^k = \sigma _{{m_i}}^k + [\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{U}}_i}\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{U}}^{\rm{T}}}}&{{\mathit{\boldsymbol{U}}_i}\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{P}}^{\rm{T}}}} \end{array}] \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {[\mathit{\boldsymbol{C}}_{({\mathit{\boldsymbol{m}}_{\rm{s}}},\mathit{\boldsymbol{s}}_{{\theta _i}}^\omega ,\mathit{\boldsymbol{s}}_{{\theta _i}}^t,\mathit{\boldsymbol{\eta }})}^k]^{ - 1}}\left( {\begin{array}{*{20}{c}} {{\lambda _{{\mathit{\boldsymbol{m}}_{\rm{s}}}}}\mathit{\boldsymbol{UC}}_\mathit{\boldsymbol{m}}^k\mathit{\boldsymbol{U}}_i^{\rm{T}}}\\ {{\lambda _\omega }\mathit{\boldsymbol{W}}_{{\theta _i}}^\omega \mathit{\boldsymbol{ECC}}_\mathit{\boldsymbol{m}}^k\mathit{\boldsymbol{U}}_i^{\rm{T}}}\\ {{\lambda _t}\mathit{\boldsymbol{W}}_{{\theta _i}}^t\mathit{\boldsymbol{CC}}_\mathit{\boldsymbol{m}}^k\mathit{\boldsymbol{U}}_i^{\rm{T}}}\\ {{\lambda _{\rm{L}}}\mathit{\boldsymbol{DC}}_\mathit{\boldsymbol{m}}^k\mathit{\boldsymbol{U}}_i^{\rm{T}}} \end{array}} \right) \end{array} $ | (12) |
式中C(ms, Sθiω, Sθit, η)k为已知条件数据集(ms、Sθif、Sθit及η)的协方差矩阵,有
| $ \begin{array}{l} \mathit{\boldsymbol{C}}_{({\mathit{\boldsymbol{m}}_s},\mathit{\boldsymbol{S}}_{{\theta _i}}^k,\mathit{\boldsymbol{S}}_{{\theta _i}}^t,\mathit{\boldsymbol{\eta }})}^k = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{UC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{U}}^{\rm{T}}}}&{\mathit{\boldsymbol{UC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{P}}^{\rm{T}}}}\\ {\mathit{\boldsymbol{PC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{U}}^{\rm{T}}}}&{\mathit{\boldsymbol{PC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{P}}^{\rm{T}}} + {\mathit{\boldsymbol{C}}_\varepsilon }} \end{array}} \right]\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \left[ {\begin{array}{*{20}{c}} {\mathit{\boldsymbol{UC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{U}}^{\rm{T}}}}&{\mathit{\boldsymbol{UC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{F}}^{\rm{T}}}}&{\mathit{\boldsymbol{UC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{G}}^{\rm{T}}}}&{\mathit{\boldsymbol{UC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{D}}^{\rm{T}}}}\\ {\mathit{\boldsymbol{FC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{U}}^{\rm{T}}}}&{\mathit{\boldsymbol{FC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{F}}^{\rm{T}}}}&{\mathit{\boldsymbol{FC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{G}}^{\rm{T}}}}&{\mathit{\boldsymbol{FC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{D}}^{\rm{T}}}}\\ {\mathit{\boldsymbol{GC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{U}}^{\rm{T}}}}&{\mathit{\boldsymbol{GC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{F}}^{\rm{T}}}}&{\mathit{\boldsymbol{GC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{G}}^{\rm{T}}}}&{\mathit{\boldsymbol{GC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{D}}^{\rm{T}}}}\\ {\mathit{\boldsymbol{DC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{U}}^{\rm{T}}}}&{\mathit{\boldsymbol{DC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{F}}^{\rm{T}}}}&{\mathit{\boldsymbol{DC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{G}}^{\rm{T}}}}&{\mathit{\boldsymbol{DC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{D}}^{\rm{T}}}} \end{array}} \right] \end{array} $ | (13) |
式中:F=WθiωEC; G=WθitC。
在贝叶斯推断中,混合先验概率模型搭建了储层弹性阻抗与离散岩性之间的关系,在弹性阻抗、观测数据等特征属性的协同约束下,即可获得储层岩性的后验概率密度分布;然后,依据最大后验概率解获取储层岩性的最优解。基于此,从被优选的目标分量中随机采样得到岩相约束下的弹性阻抗数据。Hansen等[28]和Lang等[16]提出了2类条件数据约束下的地震反问题的线性解。基于贝叶斯分类,可以得到多类数据集协同约束的第k个高斯概率分量的后验权重
| $ \begin{array}{l} \gamma _{{m_i|({\mathit{\boldsymbol{m}}_{\rm{s}}},\mathit{\boldsymbol{H}})}}^k\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{{\lambda _k}{N_k}[{\mathit{\boldsymbol{m}}_{\rm{s}}},\mathit{\boldsymbol{S}}_{{\theta _i}}^\omega ,\mathit{\boldsymbol{S}}_{{\theta _i}}^t,\mathit{\boldsymbol{\eta }};{\mathit{\boldsymbol{\mu }}_{({\mathit{\boldsymbol{m}}_{\rm{s}}},\mathit{\boldsymbol{s}}_{{\theta _i}}^\omega ,\mathit{\boldsymbol{s}}_{{\theta _i}}^t,\mathit{\boldsymbol{\eta }})}},\mathit{\boldsymbol{C}}_{({\mathit{\boldsymbol{m}}_{\rm{s}}},\mathit{\boldsymbol{S}}_{{\theta _i}}^\omega ,\mathit{\boldsymbol{S}}_{{\theta _i}}^t,\mathit{\boldsymbol{\eta }})}^k]}}{{\sum\limits_{k = 1}^M {{\lambda _k}} {N_k}[{\mathit{\boldsymbol{m}}_{\rm{s}}},\mathit{\boldsymbol{S}}_{{\theta _i}}^\omega ,\mathit{\boldsymbol{S}}_{{\theta _i}}^t,\mathit{\boldsymbol{\eta }};{\mathit{\boldsymbol{\mu }}_{({\mathit{\boldsymbol{m}}_{\rm{s}}},\mathit{\boldsymbol{s}}_{{\theta _i}}^\omega ,\mathit{\boldsymbol{s}}_{{\theta _i}}^t,\mathit{\boldsymbol{\eta }})}},\mathit{\boldsymbol{C}}_{({\mathit{\boldsymbol{m}}_{\rm{s}}},\mathit{\boldsymbol{S}}_{{\theta _i}}^\omega ,\mathit{\boldsymbol{S}}_{{\theta _i}}^t,\mathit{\boldsymbol{\eta }})}^k]}} \end{array} $ | (14) |
式中
| $ \begin{array}{l} \mathit{\boldsymbol{\mu }}_{({\mathit{\boldsymbol{m}}_{\rm{s}}},\mathit{\boldsymbol{S}}_ {{\theta _i}}^\omega ,\mathit{\boldsymbol{S}}_{{\theta _i}}^t,\mathit{\boldsymbol{\eta }})}^k\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {[{\lambda _{{\mathit{\boldsymbol{m}}_{\rm{s}}}}}\mathit{\boldsymbol{U\mu }}_\mathit{\boldsymbol{m}}^k\;\:{\lambda _\omega }\mathit{\boldsymbol{W}}_{{\theta _i}}^\omega \mathit{\boldsymbol{EC\mu }}_\mathit{\boldsymbol{m}}^k\;\:{\lambda _t}\mathit{\boldsymbol{W}}_{{\theta _i}}^t\mathit{\boldsymbol{C\mu }}_\mathit{\boldsymbol{m}}^k\;\:{\lambda _{\rm{L}}}\mathit{\boldsymbol{D\mu }}_\mathit{\boldsymbol{m}}^k]^{\rm{T}}} \end{array} $ |
为序贯模拟过程中条件数据的先验均值。待模拟点mi的γmi|(ms, H)k可以用来判断、识别离散的储层岩性。当离散岩性分类(优选混合概率模型中的高斯分量)之后,待反演模型参数(即弹性阻抗)将从被选择的高斯分量中随机采样获得。值得注意的是,当访问下一个模拟点时,先前的模拟点被视为已知数据,且已知数据的邻域(矩形或圆形邻域)选择对于提高地震序贯模拟的计算效率具有重要意义,邻域半径通常设置为一个波长至两个波长之间。
1.3 叠前地震Gassmann流体参数反演方法复杂油气储层的饱和岩石为干岩石骨架与多种流体填充物构成的多孔双相介质,宏观岩石模量受干岩石骨架和孔隙流体的综合影响。Russell等[30-31]基于Biot-Gassmann孔隙弹性理论推导了岩石饱含流体情况下的线性地震AVO反射系数方程
| $ \begin{array}{*{20}{l}} {{R_{{\rm{PP}}}}(\theta ) = \left( {\frac{1}{4} - \frac{{\gamma _{{\rm{dry}}}^2}}{{4\gamma _{{\rm{sat}}}^2}}} \right){\rm{se}}{{\rm{c}}^2}\theta \Delta {\rm{ln}}f + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\frac{{\gamma _{{\rm{dry}}}^2}}{{4\gamma _{{\rm{sat}}}^2}}{\rm{se}}{{\rm{c}}^2}\theta - \frac{2}{{\gamma _{{\rm{sat}}}^2}}{\rm{si}}{{\rm{n}}^2}\theta } \right)\Delta {\rm{ln}}\mu + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {\frac{1}{2} - \frac{{{\rm{se}}{{\rm{c}}^2}\theta }}{4}} \right)\Delta {\rm{ln}}\rho } \end{array} $ | (15) |
式中:θ为入射角;f是Gassmann流体项,反映岩石孔隙流体的作用;μ为岩石剪切模量,反映岩石骨架的作用;ρ为饱和岩石密度;γdry2为干岩石骨架的纵横波速度平方比;γsat2是饱和岩石的纵横波速度平方比;Δlnf、Δlnμ和Δlnρ分别为Gassmann流体项、剪切模量和密度的地层反射率。
由式(15)可知,弹性阻抗反演比叠前地震AVO反演具有更高的计算效率和稳定性[1, 4],因此提出了基于模型正则化和边界约束的改进弹性阻抗反演方法,以预测表征油气储层含流体性质的Gass-mann流体项等弹性参数。与式(15)对应的流体弹性阻抗方程可以改写为
| $ {\rm{EI}}(\theta ) = {\rm{E}}{{\rm{I}}_0}{\left( {\frac{f}{{{f_0}}}} \right)^{a(\theta )}}{\left( {\frac{\mu }{{{\mu _0}}}} \right)^{b(\theta )}}{\left( {\frac{\rho }{{{\rho _0}}}} \right)^{c(\theta )}} $ | (16) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {a(\theta ) = \left( {\frac{1}{2} - \frac{{\gamma _{{\rm{dry}}}^2}}{{2{\gamma _{{\rm{sat}}}}}}} \right){\rm{se}}{{\rm{c}}^2}\theta }\\ {b(\theta ) = \frac{{\gamma _{{\rm{dry}}}^2}}{{2{\gamma _{{\rm{sat}}}}}}{\rm{se}}{{\rm{c}}^2}\theta - \frac{4}{{\gamma _{{\rm{sat}}}^2}}{\rm{si}}{{\rm{n}}^2}\theta }\\ {c(\theta ) = 1 - \frac{{{\rm{se}}{{\rm{c}}^2}\theta }}{2}} \end{array}} \right. $ | (17) |
式中:f0、μ0和ρ0是依据测井数据计算的弹性参数平均值;
| $ {\left[ {\begin{array}{*{20}{c}} {{\rm{ln}}\frac{\mathit{\boldsymbol{F}}}{{{f_0}}}}&{{\rm{ln}}\frac{\mathit{\boldsymbol{\mu }}}{{{\mu _0}}}}&{{\rm{ln}}\frac{\mathit{\boldsymbol{\rho }}}{{{\rho _0}}}} \end{array}} \right]_{n \times 3}}{\left[ {\begin{array}{*{20}{c}} {{a^\prime }({\theta _i})}\\ {{b^\prime }({\theta _i})}\\ {{c^\prime }({\theta _i})} \end{array}} \right]_{3 \times 1}}\;\: = \left[ {{\rm{ln}}\frac{{{\rm{EI}}({\theta _i})}}{{{\rm{E}}{{\rm{I}}_0}}}} \right] $ | (18) |
式中:F、μ和ρ分别表示井旁道实测Gassmann流体项、剪切模量和密度构成的向量;n为重采样后的测井数据样点数。
采用阻尼最小二乘法(或共轭梯度法)求解式(18),获得a′(θi)、b′(θi)和c′(θi)。令弹性参数的相对值表示为Rf、Rμ、Rρ和REI,即
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{R}}_f} = {{\left[ {\begin{array}{*{20}{c}} {{\rm{ln}}{{\left( {\frac{f}{{{f_0}}}} \right)}_1}}& \cdots &{{\rm{ln}}{{\left( {\frac{f}{{{f_0}}}} \right)}_N}} \end{array}} \right]}^{\rm{T}}}}&{}\\ {{\mathit{\boldsymbol{R}}_\mu } = {{\left[ {\begin{array}{*{20}{c}} {{\rm{ln}}{{\left( {\frac{\mu }{{{\mu _0}}}} \right)}_1}}& \cdots &{{\rm{ln}}{{\left( {\frac{\mu }{{{\mu _0}}}} \right)}_N}} \end{array}} \right]}^{\rm{T}}}}&{} \end{array}\\ \begin{array}{*{20}{l}} {{\mathit{\boldsymbol{R}}_\rho } = {{\left[ {\begin{array}{*{20}{c}} {{\rm{ln}}{{\left( {\frac{\rho }{{{\rho _0}}}} \right)}_1}}& \cdots &{{{\left( {{\rm{ln}}\frac{\rho }{{{\rho _0}}}} \right)}_N}} \end{array}} \right]}^{\rm{T}}}}\\ {{\mathit{\boldsymbol{R}}_{{\rm{EI}}}} = {{\left[ {\begin{array}{*{20}{c}} {{\rm{ln}}{{\left( {\frac{{{\rm{E}}{{\rm{I}}_{{\theta _i}}}}}{{{\rm{E}}{{\rm{I}}_0}}}} \right)}_1}}& \cdots &{{\rm{ln}}{{\left( {\frac{{{\rm{E}}{{\rm{I}}_{{\theta _i}}}}}{{{\rm{E}}{{\rm{I}}_0}}}} \right)}_N}} \end{array}} \right]}^{\rm{T}}}} \end{array} \end{array} \right. $ | (19) |
式中N为单道地震数据的样点数。为了实现非线性方程的线性化,对式(16)等号两边取自然对数,并将式(19)代入,得
| $ \underbrace {{{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{R}}_{{\rm{E}}{{\rm{I}}_{\rm{1}}}}}}\\ {{\mathit{\boldsymbol{R}}_{{\rm{E}}{{\rm{I}}_{\rm{2}}}}}}\\ \vdots \\ {{\mathit{\boldsymbol{R}}_{{\rm{E}}{{\rm{I}}_Q}}}} \end{array}} \right]}_{QN \times 1}}}_{{\mathit{\boldsymbol{R}}_{{\rm{EI}}}}} = \underbrace {{{\left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{A}}_{{\theta _1}}}}&{{\mathit{\boldsymbol{B}}_{{\theta _1}}}}&{{\mathit{\boldsymbol{C}}_{{\theta _1}}}}\\ {{\mathit{\boldsymbol{A}}_{{\theta _2}}}}&{{\mathit{\boldsymbol{B}}_{{\theta _2}}}}&{{\mathit{\boldsymbol{C}}_{{\theta _2}}}}\\ \vdots & \ddots & \vdots \\ {{\mathit{\boldsymbol{A}}_{{\theta _Q}}}}&{{\mathit{\boldsymbol{B}}_{{\theta _Q}}}}&{{\mathit{\boldsymbol{C}}_{{\theta _Q}}}} \end{array}} \right]}_{QN \times 3N}}}_\mathit{\boldsymbol{G}}\underbrace {{{\left[ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{R}}_f}}\\ {{\mathit{\boldsymbol{R}}_\mu }}\\ {{\mathit{\boldsymbol{R}}_\rho }} \end{array}} \right]}_{3N \times 1}}}_{{\mathit{\boldsymbol{R}}_{\rm{m}}}} $ | (20) |
式中:Aθi=diag[a(θi)]N;Bθi=diag[b(θi)]N;Cθi=diag[c(θi)]N;diag[·]表示对角矩阵运算;Q为入射角的数量。
考虑到Gassmann流体项、剪切模量及密度的大尺度先验背景可以从实际测井数据中获得,故将弹性参数的已知先验信息用L2范数表示,并引入到Gassmann流体项等参数的反演中,提高弹性参数反演的可靠性,则弹性参数反演的目标泛函和更新量分别为
| $ \begin{array}{*{20}{c}} {J(\Delta {\mathit{\boldsymbol{R}}_{\rm{m}}}) = \left\| {\Delta {\mathit{\boldsymbol{R}}_{{\rm{EI}}}} - \mathit{\boldsymbol{G}}\Delta {\mathit{\boldsymbol{R}}_{\rm{m}}}} \right\|_2^2 + {\lambda _f}\left\| {\Delta {\mathit{\boldsymbol{\xi }}_f} - {\mathit{\boldsymbol{D}}_f}\Delta {\mathit{\boldsymbol{R}}_f}} \right\|_2^2 + }\\ {{\lambda _\mu }\left\| {\Delta {\mathit{\boldsymbol{\xi }}_\mu } - {\mathit{\boldsymbol{D}}_\mu }\Delta {\mathit{\boldsymbol{R}}_\mu }} \right\|_2^2 + {\lambda _\rho }\left\| {\Delta {\mathit{\boldsymbol{\xi }}_\rho } - {\mathit{\boldsymbol{D}}_\rho }\Delta {\mathit{\boldsymbol{R}}_\rho }} \right\|_2^2} \end{array} $ | (21) |
和
| $ \begin{array}{*{20}{l}} {\Delta {\mathit{\boldsymbol{R}}_{\rm{m}}} = {{({\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{G}} + {\lambda _f}{\mathit{\boldsymbol{D}}_f}^{\rm{T}}{\mathit{\boldsymbol{D}}_f} + {\lambda _\mu }{\mathit{\boldsymbol{D}}_\mu }^{\rm{T}}{\mathit{\boldsymbol{D}}_\mu } + {\lambda _\rho }{\mathit{\boldsymbol{D}}_\rho }^{\rm{T}}{\mathit{\boldsymbol{D}}_\rho })}^{ - 1}} \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({\mathit{\boldsymbol{G}}^{\rm{T}}}\Delta {\mathit{\boldsymbol{R}}_{{\rm{EI}}}} + {\lambda _f}{\mathit{\boldsymbol{D}}_f}^{\rm{T}}\Delta {\mathit{\boldsymbol{\xi }}_f} + {\lambda _\mu }{\mathit{\boldsymbol{D}}_\mu }^{\rm{T}}\Delta {\mathit{\boldsymbol{\xi }}_\mu } + {\lambda _\rho }{\mathit{\boldsymbol{D}}_\rho }^{\rm{T}}\Delta {\mathit{\boldsymbol{\xi }}_\rho })} \end{array} $ | (22) |
式中:Δξf、Δξμ和Δξρ均为先验数据的迭代残差;先验信息的正则化算子Df、Dμ、Dρ是单位矩阵;ξf、ξμ和ξρ是弹性参数的先验背景;λf、λμ和λρ分别是Gassmann流体项、剪切模量和密度的先验约束权重。式(21)~式(22)未考虑待反演模型的下限和上限信息,然而实际地震数据受到噪声的干扰,反演结果往往会超出模型边界的解(固有不稳定性引起)。为了改善该问题,引入非线性边界转化算法。假定当前迭代次数为y,则中间变量的更新量为
| $ \begin{array}{*{20}{l}} {\Delta {\mathit{\boldsymbol{x}}^{(y)}} = \frac{{(\mathit{\boldsymbol{R}}_{\rm{m}}^{{\rm{max}}} - \mathit{\boldsymbol{R}}_{\rm{m}}^{{\rm{min}}})\Delta \mathit{\boldsymbol{R}}_{\rm{m}}^{(y)}}}{{\chi [\mathit{\boldsymbol{R}}_{\rm{m}}^{{\rm{max}}} - \mathit{\boldsymbol{R}}_{\rm{m}}^{(y - 1)}][\mathit{\boldsymbol{R}}_{\rm{m}}^{(y - 1)} - \mathit{\boldsymbol{R}}_{\rm{m}}^{{\rm{min}}}]}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{R}}_{\rm{m}}^{{\rm{min}}} \le {\mathit{\boldsymbol{R}}_{\rm{m}}} \le \mathit{\boldsymbol{R}}_{\rm{m}}^{{\rm{max}}}} \end{array} $ | (23) |
式中x、Rmmin、Rmmax和χ分别表示待反演模型的中间变量、先验模型下界、先验模型上界和决定转换梯度
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{R}}_{\rm{m}}^{(y)} = }\\ {\frac{{\mathit{\boldsymbol{R}}_{\rm{m}}^{{\rm{max}}}{\rm{exp}}[\chi \Delta {\mathit{\boldsymbol{x}}^{(y)}}][\mathit{\boldsymbol{R}}_{\rm{m}}^{(y - 1)} - \mathit{\boldsymbol{R}}_{\rm{m}}^{{\rm{min}}}] + \mathit{\boldsymbol{R}}_{\rm{m}}^{{\rm{min}}}[\mathit{\boldsymbol{R}}_{\rm{m}}^{{\rm{max}}} - \mathit{\boldsymbol{R}}_{\rm{m}}^{(y - 1)}]}}{{{\rm{exp}}[\chi \Delta {\mathit{\boldsymbol{x}}^{(y)}}][\mathit{\boldsymbol{R}}_{\rm{m}}^{(y - 1)} - \mathit{\boldsymbol{R}}_{\rm{m}}^{{\rm{min}}}] + [\mathit{\boldsymbol{R}}_{\rm{m}}^{{\rm{max}}} - \mathit{\boldsymbol{R}}_{\rm{m}}^{(y - 1)}]}}} \end{array} $ | (24) |
式中Rm(y-1)表示第y-1次迭代后的估计结果。式(24)计算得到第y次迭代的模型更新量ΔRm(y),代入式(23)计算Δx(y),将Δx(y)代入式(24),即计算得到被约束在上限和下限范围内的弹性模型,进而控制超过边界的预测结果的更新幅度。
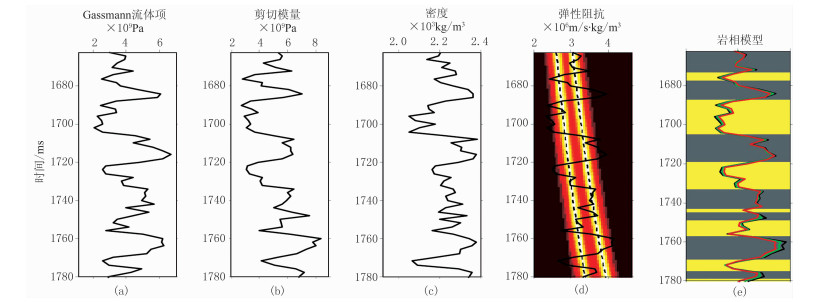
2 理论模型测试为了验证混合概率模型驱动的叠前地震概率化反演可行性,利用重采样后的测井数据设计了一维理论模型(图 2)。图 2展示了Gassmann流体项、剪切模量、密度、小角度弹性阻抗的先验概率密度分布及理论离散岩相。采用30Hz零相位Ricker小波、2ms采样间隔和精确Zoeppritz方程,合成了信噪比S/N=1情况下的AVO地震数据,AVO地震数据的入射角分别为10°、20°和30°(图 3)。
|
图 2 实际测井数据
(a)Gassmann流体项;(b)剪切模量;(c)密度;(d)小角度弹性阻抗;(e)离散岩相模型 图e中黄色代表砂岩,灰色代表泥岩 |
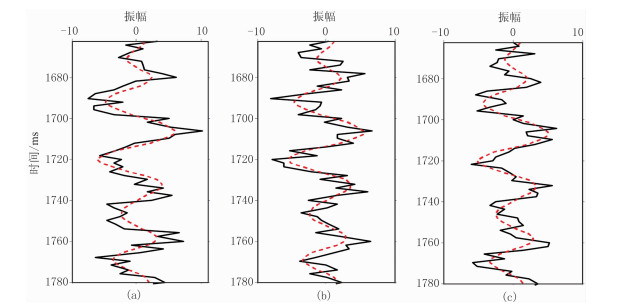
|
图 3 S/N=1情况下入射角为10°(a)、20°(b)和30°(c)的合成地震数据 黑线为S/N=1情况下的合成地震数据,红线为利用随机模拟实现均值解合成的地震数据 |
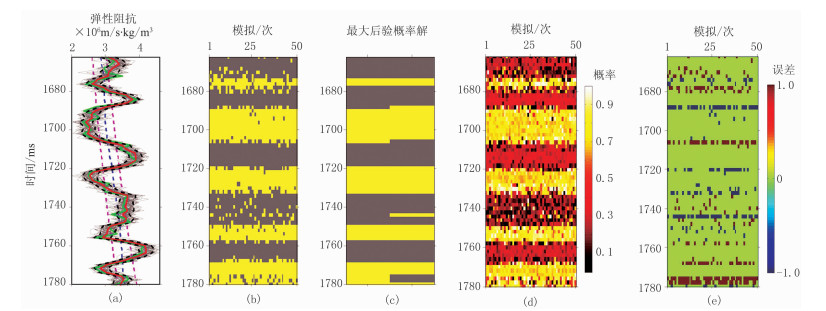
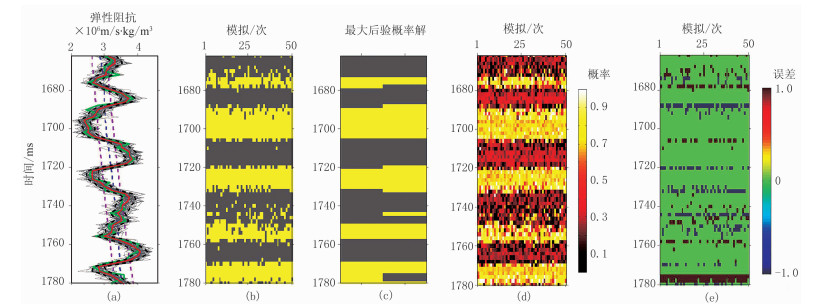
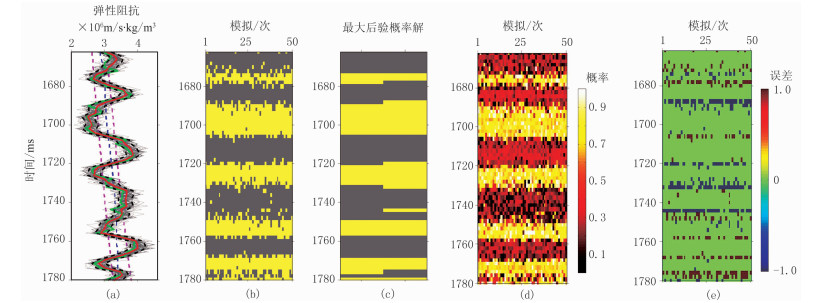
第一步是基于贝叶斯混合概率模型的地震弹性阻抗反演处理。不同角度(10°、20°和30°)的弹性阻抗与离散岩相的估计结果如图 4~图 6所示。从图 4~图 6可以看出,50次模拟实现(灰线)的均值解(红线)与理论模型(绿线)的拟合度较高。不同角度情况下,50次离散岩相判识的最大后验概率解(图 4c、图 5c和图 6c的左半部分)均与理论岩相(图 4c、图 5c和图 6c的右半部分)具有高度一致性。与之对应的,50次模拟实现的岩相误差主要出现在地层界面上及先验均值之间的模型参数过渡区,该现象产生的根本原因是这些区域的模型参数在不同后验PDF中的概率是相近的。因此,基于贝叶斯混合概率模型的地震弹性阻抗反演方法可以有效地实现弹性阻抗和离散岩相的概率化预测,为后续的边界约束叠前地震概率化弹性阻抗反演奠定了数据基础。
|
图 4 S/N=1情况下小角度(10°)弹性阻抗与离散岩相的估计结果
(a)弹性阻抗;(b)50次模拟的离散岩相;(c)最大后验概率解;(d)砂岩相的概率估计;(e)离散岩相的误差 图a中绿线表示真实模型,蓝线为弹性阻抗的低频背景,粉红色虚线表示弹性阻抗的先验均值,灰线表示弹性阻抗的50次模拟实现,红线表示50次模拟实现的均值解,黑色虚线表示50次随机模拟实现的置信区间。图 5~图 6同 |
|
图 5 S/N=1情况下中角度(20°)弹性阻抗与离散岩相的估计结果 (a)弹性阻抗;(b)50次模拟的离散岩相;(c)最大后验概率解;(d)砂岩相的概率估计;(e)离散岩相的误差 |
|
图 6 S/N=1情况下大角度(30°)弹性阻抗与离散岩相的估计结果 (a)弹性阻抗;(b)50次模拟的离散岩相;(c)最大后验概率解;(d)砂岩相的概率估计;(e)离散岩相的误差 |
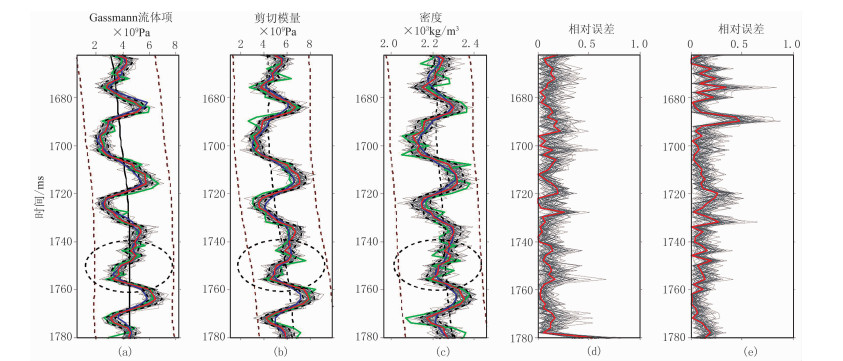
第二步是基于弹性阻抗的Gassmann流体项、剪切模量等弹性参数的同步反演。图 7展示了S/N=1情况下反演得到的f、μ和ρ。由图可见,本方法的50次模拟实现(灰线)的弹性参数预测结果被有效地限制在上、下限(棕色虚线)范围内,与理论模型高度一致;f预测结果的相对误差为12.8%,μ的相对误差为17.9%,证明了该边界约束弹性阻抗反演算法在参数提取方面的可行性;存在噪声干扰的情况下,f的估计结果受随机噪声的影响程度较小,μ的反演精度比f低,与理论分析相一致,主要是由于μ对地震AVO反射系数的贡献度低导致的。
|
图 7 S/N=1情况下50次随机模拟实现的弹性参数及其相对误差估计结果
(a)Gassmann流体项;(b)剪切模量;(c)岩石密度;(d)Gassmann流体项的相对误差;(e)剪切模量的相对误差 绿线表示真实模型,蓝线表示利用阻尼最小二乘方法的反演结果,灰线表示弹性参数的50次随机模拟实现,红线表示本文方法(50次随机模拟实现)反演得到的均值解,黑色虚线表示50次随机模拟实现的置信区间,棕色虚线为弹性参数的先验边界 |
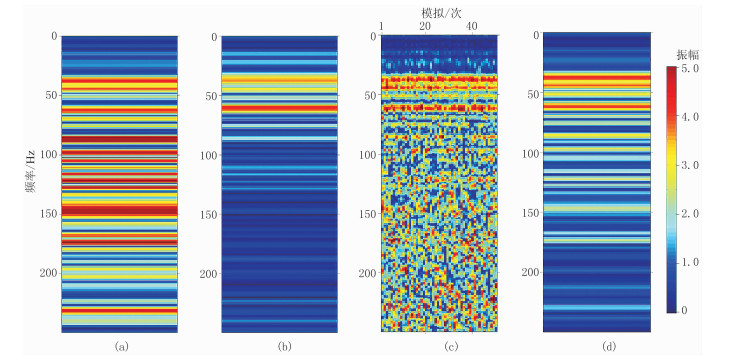
为了阐述基于弹性阻抗的Gassmann流体项、剪切模量等弹性参数的同步反演方法与常规反演方法之间的差异,图 8展示了不同反演方法得到的Gassmann流体项反射率的频谱计算结果。由图可见,最小二乘确定性反演方法仅能获取模型参数的“最优解”,反演结果的频带范围主要与输入地震数据的频宽有关,高频信息不能得到有效恢复(图 8b);本文方法反演结果的频谱(图 8c、图 8d)比常规最小二乘反演方法具有更宽的频带,尤其是在模型参数的高频信息恢复方面,该概率化反演方法可以更有效地恢复地下介质高频信息(图 8d)。
|
图 8 S/N=1情况下不同反演方法得到的Gassmann流体项反射率的频谱分析对比 (a)真实模型;(b)常规最小二乘反演;(c)本文方法50次随机模拟实现;(d)本文方法50次模拟实现的均值解 |
以中国华南地区Well-1井含油储层的地震勘探为例,验证本文混合概率模型驱动的叠前地震弹性阻抗反演方法的实用性。
研究区砂岩储层主要为含油层与油水同层。由图 9可以看出,小角度弹性阻抗可以较好地区分优质砂岩储层(含油砂岩、含油水砂岩,图 9a椭圆框)与泥岩(干层)(图 9a);相比中角度、大角度弹性阻抗,小角度弹性阻抗可以更好地区分砂岩储层(图 9b)。不同岩性情况下,小角度弹性阻抗的统计特征(先验均值、协方差)差异更大。然而,中角度与大角度弹性阻抗在砂岩储层和泥岩干层位置的先验均值却比较接近,故在概率化推断过程中将存在较强的不确定性。由于小、中、大角度弹性阻抗具有相似的统计特征“拐点”,因此本文将弹性阻抗岩相判识结果的“交集”作为目标工区岩相预测的依据。

|
图 9 弹性阻抗的岩石物理参数交会与统计 (a)小角度弹性阻抗与纵波速度交会;(b)小、中、大角度的弹性阻抗统计 |
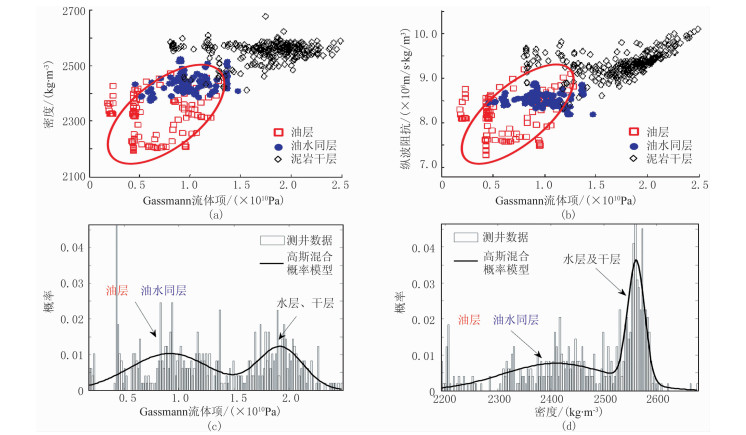
由图 10可见,Gassmann流体项较好地区分了油层、油水同层及泥岩干层,同时Gassmann流体项、密度等参数服从混合高斯概率密度分布,表现为“多峰”的概率统计特征。基于此,可将Russell近似公式作为“流体相”驱动叠前地震反演的地球物理映射关系,即模型参数为表征孔隙流体的Gassmann流体项、干岩石骨架的剪切模量、岩石密度及孔隙含流体类型(流体相)。
|
图 10 储层含流体性的岩石物理参数交会与统计 (a)Gassmann流体项与密度交会;(b)Gassmann流体项与纵波阻抗交会;(c)Gassmann流体项概率统计;(d)密度概率统计 |
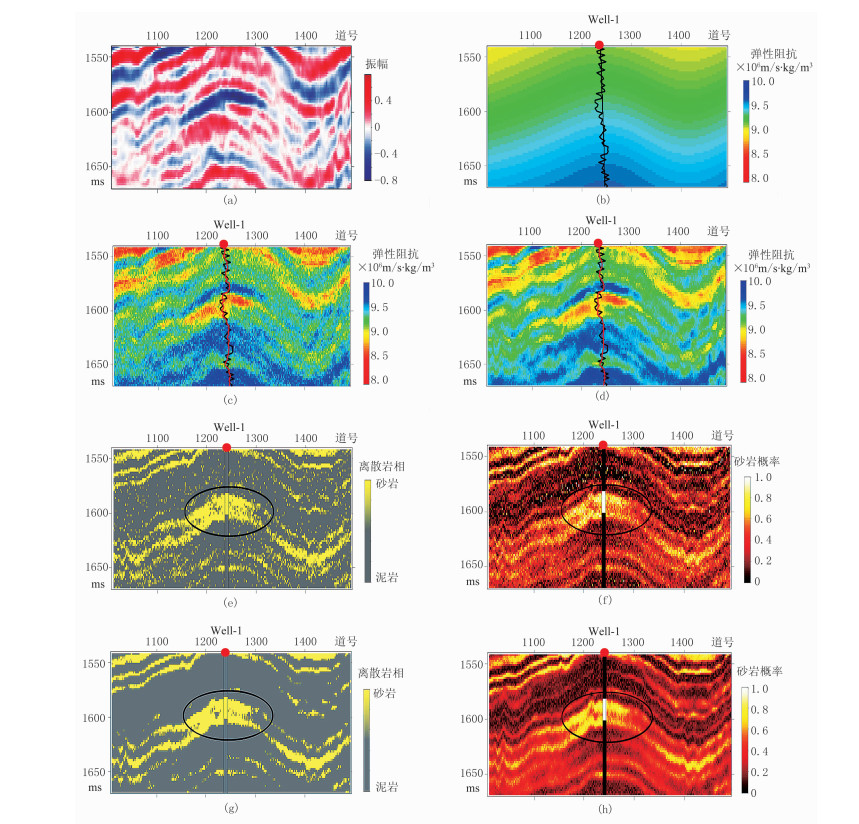
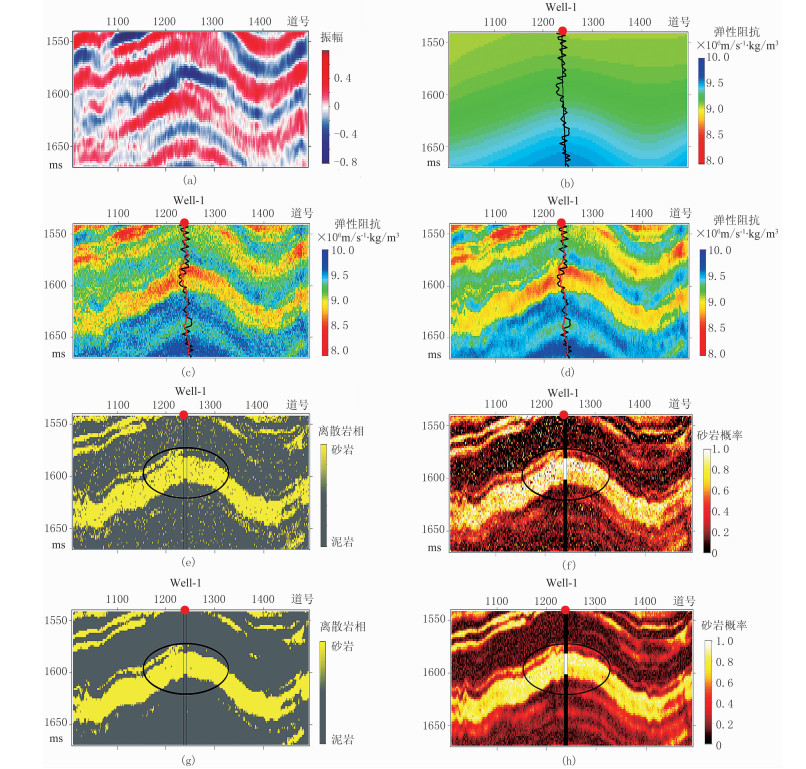
由图 11~图 13可以看出:①由于概率化地震反演的不确定性,单次模拟结果中仍存在序贯随机采样的干扰(图 11c~图 11d、图 12c~图 12d、图 13c~图 13d)。因此,地震概率化反演往往需要多次随机实现的均解或最大条件概率解(图 11d、图 12d、图 13d)。对比图 11c和图 11d,10次实现的均值解可以有效地抑制单次实现中的随机干扰。②井旁道的弹性阻抗估计结果(红线)和砂泥岩模型的岩性判识结果与实际测井弹性阻抗计算结果、砂岩储层解释结果高度一致,可以较准确地识别出砂岩油藏的发育位置(图 11e~图 11h、图 12e~图 12h、图 13e~图 13h)。
|
图 11 小角度(5°~16°)叠加的地震剖面、弹性阻抗及离散岩相的反演结果
(a)小角度地震记录道;(b)小角度初始弹性阻抗;(c)单次随机模拟实现结果;(d)10次随机模拟实现均值解;(e)单次随机模拟实现的岩相模拟;(f)单次随机模拟实现的砂岩相概率;(g)10次随机模拟实现的最大后验概率解;(h)10次随机模拟实现的概率均值 测井解释中黄色和白色为含油砂岩,灰色和黑色为泥岩或其他。红线是弹性阻抗估计结果;黑色椭圆表示油藏位置。图 12~图 13同 |

|
图 12 中角度(16°~26°)叠加的地震剖面、弹性阻抗及离散岩相的反演结果 (a)中角度地震记录道;(b)中角度初始弹性阻抗;(c)单次随机模拟实现结果;(d)10次随机模拟实现均值解;(e)单次随机模拟实现的岩相模拟;(f)单次随机模拟实现的砂岩相概率;(g)10次随机模拟实现的最大后验概率解;(h)10次随机模拟实现的概率均值 |
|
图 13 大角度(26°~30°)叠加的地震剖面、弹性阻抗及离散岩相的反演结果 (a)大角度地震记录道;(b)大角度初始弹性阻抗;(c)单次随机模拟实现结果;(d)10次随机模拟实现均值解;(e)单次随机模拟实现的岩相模拟;(f)单次随机模拟实现的砂岩相概率;(g)10次随机模拟实现的最大后验概率解;(h)10次随机模拟实现的概率均值 |
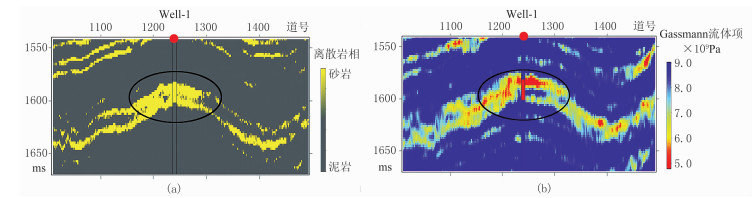
根据井旁道弹性阻抗的岩石物理参数交会与统计特征分析(图 9),角度弹性阻抗可以有效地识别砂岩储层,且将小、中、大3个角度弹性阻抗的岩相判识结果的“交集”作为砂泥岩中储层的最终判识结果(图 14a),可以降低岩相判识的不确定性,与实际砂岩油层解释结果吻合较好。图 14b展示了边界约束叠前弹性阻抗反演预测的Gassmann流体项f,从图中可以看出,Gassmann流体项在油砂储层位置存在明显低值异常,且砂泥岩-岩相与流体识别结果在预测位置上保持了较高的一致性,证明了本文混合概率模型驱动的叠前地震概率化反演方法在岩性预测和储层流体识别中具较好的实用性,应用前景广泛。
|
图 14 叠前地震概率化弹性阻抗反演的岩相和Gassmann流体项f的估算结果
(a)10次随机模拟实现的最大后验概率解;(b)预测Gassmann流体项 测井解释中黄色和红色为含油砂岩、灰色和紫色为泥岩或其他。反演结果中黄色为砂岩,灰色为泥岩 |
本文依据地下介质待反演模型参数的先验概率服从混合型概率密度模型,提出了基于时域、频域地震、低频整合先验信息及已知模型数据点四类条件数据集协同约束下的混合概率模型驱动的叠前地震时频联合域弹性阻抗反演方法。主要结论如下。
(1) 混合概率模型是实现“离散型”—“连续型”模型参数协同预测的关键,只有当不同离散相的待反演参数具有不同的统计特征时,才能够实现地震反演的离散相态判识。高斯混合PDF与高斯PDF的乘积仍可以表征为标准的混合高斯PDF,此时,“连续弹性参数”、“离散相态”的后验均值与后验协方差具有显式表达式,易于采用序贯模拟随机采样算法求解。
(2) 相比常规确定性反演方法,序贯模拟算法是通过逐点遍历的方式实现模型参数的随机采样,先前模拟点将作为下一个模拟点的约束条件,有助于实现“连续弹性参数”与“离散岩相”的概率化协同判识,便于实现和理解,使多数据协同约束的地球物理反问题变得清楚易懂。
(3) 理论测试和实际应用验证了该方法的可行性及稳定性。应用实例表明,混合概率模型驱动的叠前地震弹性阻抗反演的岩相和概率多重实现,与实际测井数据和油藏解释结果具有较高的一致性,有助于复杂岩性油气藏的储层刻画和流体直接检测,应用前景广泛。
附录A贝叶斯理论是在当前观测样本数据的情况下,结合对模型参数的先验认知,计算得到模型参数后验概率密度分布(PDF)的统计学习方法。
| $ p(\mathit{\boldsymbol{m}}|\mathit{\boldsymbol{H}}) = \frac{{p(\mathit{\boldsymbol{H}}|\mathit{\boldsymbol{m}})p(\mathit{\boldsymbol{m}})}}{{p(\mathit{\boldsymbol{H}})}} = \frac{{p(\mathit{\boldsymbol{H}}|\mathit{\boldsymbol{m}})p(\mathit{\boldsymbol{m}})}}{{\int_{ - \infty }^{ + \infty } p (\mathit{\boldsymbol{H}}|\mathit{\boldsymbol{m}})p(\mathit{\boldsymbol{m}}){\rm{d}}\mathit{\boldsymbol{m}}}} $ | (A-1) |
式中:p(m|H)表示后验概率密度分布;p(H|m)为观测数据的似然概率密度分布;m为表征该概率模型的未知参数;p(m)被称为未知参数的先验信息;p(H)为已知观测数据的PDF,与θ的取值无关[34]。若待反演模型参数服从高斯混合PDF
| $ \begin{array}{l} p(\mathit{\boldsymbol{m}}) = \sum\limits_{k = 1}^M {\left\{ {{\lambda _k}\frac{1}{{{{(\sqrt {2\pi } )}^n}}}\frac{1}{{\sqrt {|\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^k|} }} \times } \right.} \\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}\left[ { - \frac{1}{2}{{(\mathit{\boldsymbol{m}} - \mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{m}}^k)}^{\rm{T}}}{{(\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^k)}^{ - 1}}(\mathit{\boldsymbol{m}} - \mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{m}}^k} \right]} \right\} \end{array} $ | (A-2) |
式中:M为高斯混合概率模型中所包含概率分量的数量;
| $ \begin{array}{l} p(\mathit{\boldsymbol{H}}|\mathit{\boldsymbol{m}}) \propto \frac{1}{{{{(\sqrt {2\pi } )}^{2m + n}}\sqrt {|{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{H}}}|} }} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}\left[ { - \frac{1}{2}{{(\mathit{\boldsymbol{H}} - \mathit{\boldsymbol{Pm}})}^{\rm{T}}}\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{H}}^{ - 1}(\mathit{\boldsymbol{H}} - \mathit{\boldsymbol{Pm}})} \right] \end{array} $ | (A-3) |
式中:m为被选择频率分量的个数;H为观测地震数据;P为正演核矩阵;CH为协方差矩阵。利用贝叶斯公式(式(A-1))推导后验PDF(贝叶斯公式的分母与待估计模型参数无关,可忽略分母项)
| $ \begin{array}{*{20}{l}} {p(\mathit{\boldsymbol{m}}|\mathit{\boldsymbol{H}}) \propto \frac{1}{{\sqrt {|{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{H}}}|} {{(2\pi )}^{2m + n}}}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{k = 1}^M {\left\{ {\frac{{{\lambda _k}}}{{\sqrt {|\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^k|} }}{\rm{exp}}[ - \frac{1}{2}{{(\mathit{\boldsymbol{m}} - \mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{m}}^k)}^{\rm{T}}}{{(\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^k)}^{ - 1}}(\mathit{\boldsymbol{m}} - \mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{m}}^k)] \times } \right.} }\\ {\left. {\;\:{\rm{exp}}\left[ { - \frac{1}{2}{{(\mathit{\boldsymbol{H}} - \mathit{\boldsymbol{Pm}})}^{\rm{T}}}{{({\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{H}}})}^{ - 1}}(\mathit{\boldsymbol{H}} - \mathit{\boldsymbol{Pm}})} \right]} \right\}} \end{array} $ | (A-4) |
令
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{\kappa }}_k} = {\rm{ln}}({\lambda _k}\frac{1}{{\sqrt {|\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^k|} }}) - \frac{1}{2}\mathit{\boldsymbol{\eta }}_k^{\rm{T}}\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k^{ - 1}{\mathit{\boldsymbol{\eta }}_k}}\\ {{\mathit{\boldsymbol{\eta }}_k} = {{(\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^k)}^{ - 1}}\mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{m}}^k}\\ {{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k} = {{(\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^k)}^{ - 1}}}\\ {\mathit{\boldsymbol{n}} = \mathit{\boldsymbol{H}} - \mathit{\boldsymbol{Pm}}}\\ {\mathit{\boldsymbol{ \boldsymbol{\varPsi} }} = {{({\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{H}}})}^{ - 1}}} \end{array}} \right. $ | (A-5) |
则式(A-4)可以被改写为
| $ \begin{array}{l} p(\mathit{\boldsymbol{m}}|\mathit{\boldsymbol{H}}) \propto \frac{1}{{\sqrt {|{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{H}}}|} {{(2\pi )}^{2m + n}}}} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathop \sum \limits_{k = 1}^M \left[ {{\rm{exp}}\left( { - \frac{1}{2}{\mathit{\boldsymbol{n}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} n}}} \right){\rm{exp}}\left( {{\mathit{\boldsymbol{\kappa }}_k} + \mathit{\boldsymbol{\eta }}_k^{\rm{T}}\mathit{\boldsymbol{m}} - \frac{1}{2}{\mathit{\boldsymbol{m}}^{\rm{T}}}{\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k}\mathit{\boldsymbol{m}}} \right)} \right] \end{array} $ | (A-6) |
将式(A-6)改写为标准的高斯型PDF形式
| $ \begin{array}{l} p(\mathit{\boldsymbol{m}}|\mathit{\boldsymbol{H}}) \propto {\rm{exp}}\left[ {{\mathit{\boldsymbol{\kappa }}_k} - \frac{1}{2}{\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} H}} - } \right.\\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}{\mathit{\boldsymbol{m}}^{\rm{T}}}({\mathit{\boldsymbol{P}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} P}} + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k})\mathit{\boldsymbol{m}} + ({\mathit{\boldsymbol{H}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\varPsi} P}} + \mathit{\boldsymbol{\eta }}_k^{\rm{T}})\mathit{\boldsymbol{m}}} \right] \end{array} $ | (A-7) |
则式(A-7)所示的第k个标准型后验PDF分量的后验均值的显式解为
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\mu }}_{\mathit{\boldsymbol{m}}|\mathit{\boldsymbol{H}}}^k = {{({\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{H}}}^{ - 1}P + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k})}^{ - 1}}({\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{H}}}^{ - 1}\mathit{\boldsymbol{H}} + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k}\mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{m}}^k)}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{m}}^k + {{({\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{H}}}^{ - 1}\mathit{\boldsymbol{P}} + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k})}^{ - 1}}{\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{H}}}^{ - 1}(\mathit{\boldsymbol{H}} - \mathit{\boldsymbol{P\mu }}_\mathit{\boldsymbol{m}}^k)}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathit{\boldsymbol{\mu }}_\mathit{\boldsymbol{m}}^k + \mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^k{P^{\rm{T}}}{{(\mathit{\boldsymbol{PC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{P}}^{\rm{T}}} + {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{H}}})}^{ - 1}}(\mathit{\boldsymbol{H}} - \mathit{\boldsymbol{P\mu }}_\mathit{\boldsymbol{m}}^k)}\\ {} \end{array} $ | (A-8) |
后验协方差
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{C}}_{\mathit{\boldsymbol{m}}|\mathit{\boldsymbol{H}}}^k = {{({\mathit{\boldsymbol{P}}^{\rm{T}}}{\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{H}}}^{ - 1}\mathit{\boldsymbol{P}} + {\mathit{\boldsymbol{ \boldsymbol{\varGamma} }}_k})}^{ - 1}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^k - \mathit{\boldsymbol{C}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{P}}^{\rm{T}}}{{(\mathit{\boldsymbol{PC}}_\mathit{\boldsymbol{m}}^k{\mathit{\boldsymbol{P}}^{\rm{T}}} + {\mathit{\boldsymbol{C}}_\mathit{\boldsymbol{H}}})}^{ - 1}}\mathit{\boldsymbol{PC}}_\mathit{\boldsymbol{m}}^k} \end{array} $ | (A-9) |
式(A-8)、式(A-9)即描述了高斯混合概率模型驱动下的标准后验PDF的显式解。
| [1] |
宗兆云, 印兴耀, 张峰, 等. 杨氏模量和泊松比反射系数近似方程及叠前地震反演[J]. 地球物理学报, 2012, 55(11): 3786-3794. ZONG Zhaoyun, YIN Xingyao, ZHANG Feng, et al. Reflection coefficient equation and pre-stack seismic inversion with Young's modulus and Poisson ratio[J]. Chinese Journal of Geophysics, 2012, 55(11): 3786-3794. DOI:10.6038/j.issn.0001-5733.2012.11.025 |
| [2] |
印兴耀, 张世鑫, 张峰. 针对深层流体识别的两项弹性阻抗反演与Russell流体因子直接估算方法研究[J]. 地球物理学报, 2013, 56(7): 2378-2390. YIN Xingyao, ZHANG Shixin, ZHANG Feng. Two-term elastic impedance inversion and Russell fluid factor direct estimation method for deep reservoir fluid identification[J]. Chinese Journal of Geophysics, 2013, 56(7): 2378-2390. |
| [3] |
印兴耀, 曹丹平, 王保丽, 等. 基于叠前地震反演的流体识别方法研究进展[J]. 石油地球物理勘探, 2014, 49(1): 22-34. YIN Xingyao, CAO Danping, WANG Baoli, et al. Research progress of fluid discrimination with pre-stack seismic inversion[J]. Oil Geophysical Prospecting, 2014, 49(1): 22-34. |
| [4] |
印兴耀, 宗兆云, 吴国忱. 岩石物理驱动下地震流体识别研究[J]. 中国科学:地球科学, 2015, 45(1): 8-21. YIN Xingyao, ZONG Zhaoyun, WU Guochen. Research on seismic fluid identification driven by rock physics[J]. Scientia Sinica Terrae, 2015, 45(1): 8-21. |
| [5] |
李坤, 印兴耀, 宗兆云. 岩石物理驱动的相约束叠前地震概率化反演方法[J]. 中国科学:地球科学, 2020, 50(6): 832-850. LI Kun, YIN Xingyao, ZONG Zhaoyun. Facies-constrained prestack seismic probabilistic inversion dri-ven by rock physics[J]. Scientia Sinica Terrae, 2020, 50(6): 832-850. |
| [6] |
Downton J E.Seismic Parameter Estimation from AVO Inversion[D]. University of Calgary, Alberta, 2005.
|
| [7] |
Buland A, Omre H. Bayesian linearized AVO inver-sion[J]. Geophysics, 2003, 68(1): 185-198. |
| [8] |
Theune U, Jensås I Ø, Eidsvik J. Analysis of prior models for a blocky inversion of seismic AVA data[J]. Geophysics, 2010, 75(3): C25-C35. |
| [9] |
Alemie W, Sacchi M. High-resolution three-term AVO inversion by means of a trivariate Cauchy probability distribution[J]. Geophysics, 2011, 76(3): R43-R55. |
| [10] |
Zong Z Y, Yin X Y, Wu G C. AVO inversion and poroelasticity with P- and S-wave moduli[J]. Geophy-sics, 2012, 77(6): N17-N24. |
| [11] |
Yin X Y, Zong Z Y, Wu G C. Seismic wave scattering inversion for fluid factor of heterogeneous media[J]. Science China(Earth Sciences), 2014, 57(3): 542-549. DOI:10.1007/s11430-013-4783-2 |
| [12] |
Yin X Y, Li K, Zong Z Y. Resolution enhancement of robust Bayesian pre-stack inversion in the frequency domain[J]. Journal of Geophysics and Enginee-ring, 2016, 13(5): 646-656. DOI:10.1088/1742-2132/13/5/646 |
| [13] |
Li K, Yin X Y, Zong Z Y. Pre-stack Bayesian cascade AVA inversion in complex Laplace domain and its application to the broadband data acquired at East China[J]. Journal of Petroleum Science & Engineering, 2017, 158(4): 751-765. |
| [14] |
Grana D, Mukerji T, Dovera L, et al.Sequential Simulations of Mixed Discrete-Continuous Properties: Sequential Gaussian Mixture Simulation[M]. Springer, 2012.
|
| [15] |
Grana D, Paparozzi E, Mancini S, et al. Seismic driven probabilistic classification of reservoir facies for static reservoir modelling:a case history in the Barents Sea[J]. Geophysical Prospecting, 2013, 61(3): 613-629. DOI:10.1111/j.1365-2478.2012.01115.x |
| [16] |
Lang X, Grana D. Geostatistical inversion of prestack seismic data for the joint estimation of facies and impedances using stochastic sampling from Gaussian mixture posterior distributions[J]. Geophysics, 2017, 82(4): M55-M65. |
| [17] |
Lang X, Grana D. Bayesian linearized petrophysical AVO inversion[J]. Geophysics, 2018, 83(3): M1-M13. |
| [18] |
Fjeldstad T, Grana D. Joint probabilistic petrophysics seismic inversion based on Gaussian mixture and Markovchain prior models[J]. Geophysics, 2018, 83(1): R31-R42. |
| [19] |
李坤, 印兴耀, 宗兆云. 利用平滑模型约束的频率域多尺度地震反演[J]. 石油地球物理勘探, 2016, 51(4): 760-768. LI Kun, YIN Xingyao, ZONG Zhaoyun. Seismic multi-scale inversion in the frequency domain based on smooth model constraint[J]. Oil Geophysical Prospecting, 2016, 51(4): 760-768. |
| [20] |
Li K, Zhu M, Du J Y, et al.Direct estimation of lithofacies and geofluid parameters incorporating Gaussian mixture priori and prestack EVA inversion with bounding constraint[C]. SEG Technical Program Expanded Abstracts, 2018, 37: 560-564.
|
| [21] |
Metropolis N, Rosenbluth A, Rosenbluth M, et al. Equation of state calculations by fast computing machines[J]. The Journal of Chemical Physics, 1953, 21(6): 1087-1092. DOI:10.1063/1.1699114 |
| [22] |
Hastings W K. Monte Carlo sampling methods using Markov chains and their applications[J]. Biometrika, 1970, 57(1): 97-109. |
| [23] |
Malinverno A, Torres-Verdín C. Bayesian inversion of DC electrical measurements with uncertainties for re-servoir monitoring[J]. Inverse Problems, 2000, 16(5): 1343-1356. |
| [24] |
Braak C J F T. A Markov Chain Monte Carlo version of the genetic algorithm differential evolution:easy Bayesian computing for real parameter spaces[J]. Statistics and Computing, 2006, 16(3): 239-249. DOI:10.1007/s11222-006-8769-1 |
| [25] |
Bosch M, Cara L, Rodrigues J, et al. A Monte Carlo approach to the joint estimation of reservoir and elastic parameters from seismic amplitudes[J]. Geophy-sics, 2007, 72(6): O29-O39. |
| [26] |
张广智, 王丹阳, 印兴耀, 等. 基于MCMC的叠前地震反演方法研究[J]. 地球物理学报, 2011, 54(11): 2926-2932. ZHANG Guangzhi, WANG Danyang, YIN Xingyao, et al. Study on prestack seismic inversion using Markov Chain Monte Carlo[J]. Chinese Journal of Geophy-sics, 2011, 54(11): 2926-2932. DOI:10.3969/j.issn.0001-5733.2011.11.022 |
| [27] |
Li K, Yin X Y, Liu J, et al. An improved stochastic inversion for joint estimation of seismic impedance and lithofacies[J]. Journal of Geophysics and Engineering, 2019, 16(1): 62-76. |
| [28] |
Hansen T M, Journel A G, Tarantola A, et al. Linear inverse Gaussian theory and geostatistics[J]. Geophysics, 2006, 71(6): R101-R111. |
| [29] |
Hastie T, Tibshirani R, Friedman J.The Elements of Statistical Learning: Data Mining, Inference, and Prediction[M]. Springer Series in Statistics, 2009.
|
| [30] |
Russell B, Gray D, Hampson D. Linearized AVO and poroelasticity[J]. Geophysics, 2011, 76(3): C19-C29. |
| [31] |
Russell B, Hedlin K, Hilterman F, et al. Fluid-property discrimination with AVO:A Biot-Gassmann perspective[J]. Geophysics, 2003, 68(1): 29-39. |
| [32] |
印兴耀, 张世鑫, 张繁昌, 等. 利用基于Russell近似的弹性波阻抗反演进行储层描述和流体识别[J]. 石油地球物理勘探, 2010, 45(3): 373-380. YIN Xingyao, ZHANG Shixin, ZHANG Fanchang, et al. Utilizing Russell approximation-based elastic wave impedance inversion to conduct reservoir description and fluid identification[J]. Oil Geophysical Prospecting, 2010, 45(3): 373-380. |
| [33] |
印兴耀, 王慧欣, 曹丹平, 等. 利用三参数AVO近似方程的深层叠前地震反演[J]. 石油地球物理勘探, 2018, 53(1): 129-135. YIN Xingyao, WANG Huixin, CAO Danping, et al. Three term AVO approximation of Kf-fm-ρand prestack seismic inversion for deep reservoirs[J]. Oil Geophysical Prospecting, 2018, 53(1): 129-135. |
| [34] |
Tarantola A.Inverse Problem Theory and Methods for Model Parameter Estimation[M]. Society for Industrial and Applied Mathematics, 2005.
|



 李坤, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
李坤, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
