② 西南石油大学地球科学与技术学院, 四川成都 610500
② School of Geosciences and Technology, Southwest Petroleum University, Chengdu, Sichuan 610500, China
在非常规油气开发中,微地震监测已经成为水力压裂效果评估和方案调整的主要方法,在国内外非常规油气开发中得到了广泛应用[1-3]。根据检波器布设方式,微地震监测主要分为井中、地面以及井中和地面联合监测,不同的监测方式有着不同的适用条件,同时产生了不同的定位方法。地面微地震监测中检波器距离压裂段较远且噪声强,往往信噪比较低而无法拾取初至,通过大量检波器记录的叠加可压制噪声提高有效微地震信号的能量,因此以叠加能量扫描定位方法为主[4-5]。井中微地震监测由于检波器位于地下且距离压裂段较近,监测到的微地震信号信噪比较高,可准确拾取初至时间,因此井中微地震事件的定位方法多基于微地震事件的旅行时和偏振信息,利用微地震事件的初至信息确定震源深度和距离检波器的水平距离,利用检波器的三个分量确定震源的方位[6-7]。根据这一原理,大量的基于初至的定位方法被提出,既有经典的网格搜索法、Geiger定位法等线性反演方法,也有模拟退火、遗传算法、差分进化等非线性反演方法[8-10]。不少学者对这两类定位方法进行了比较,给出了各自的适用条件[11-14]。
井中微地震监测中,高信噪比微地震事件定位的方法已经较为成熟,通过准确拾取初至可得到准确的定位结果。对于无法拾取初至的低信噪比微地震事件的定位方法研究较少,何惺华[15]提出对井中检波器接收到的直达纵波计算三个分量能量之和,结合X、Y分量得到微地震事件的方位角,实现井中低信噪比微地震事件的定位;该方法直接利用三个分量的能量之和作为目标函数,在直井观测和水平层状介质模型下具有较强的多解性,虽然通过计算事件方位角可以减弱多解性,但是方位角的计算精度仍然受信噪比的影响。宋维琪等[16]对基于跟踪分量的井中微地震定位方法进行了研究,利用跟踪分量信噪比高并携带事件方位信息的优点,一定程度上降低了定位结果的多解性。
基于现有研究成果,本文将地面微地震的叠加能量扫描定位原理引入到井中低信噪比微地震事件的定位,根据井中微地震事件跟踪分量的性质,提出了基于跟踪分量扫描的井中微地震定位方法,应用加入实际噪声的模型数据验证方法的定位效果,通过对实际微地震监测数据的处理,验证了本文方法用于井中低信噪比微地震事件定位的有效性和可行性。
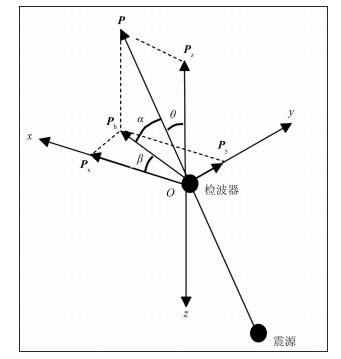
1 基本原理 1.1 跟踪分量图 1为质点位移向量的分解示意图。假设某一瞬间质点位移为P,与垂直方向的夹角为θ,与水平面夹角为α,则P可分解为垂向位移分量Pz和水平面上的位移分量Ph,即
| $ {\mathit{\boldsymbol{P}}_z} = \mathit{\boldsymbol{P}}{\rm{cos}}\theta $ | (1) |
| $ {\mathit{\boldsymbol{P}}_{\rm{h}}} = \mathit{\boldsymbol{P}}{\rm{cos}}\alpha $ | (2) |
|
图 1 质点位移的三分量分解示意图 |
Ph可进一步分解为
| $ {\mathit{\boldsymbol{P}}_x} = {\mathit{\boldsymbol{P}}_{\rm{h}}}{\rm{cos}}\beta = \mathit{\boldsymbol{P}}{\rm{cos}}\alpha {\rm{cos}}\beta $ | (3) |
| $ {\mathit{\boldsymbol{P}}_y} = {\mathit{\boldsymbol{P}}_{\rm{h}}}{\rm{cos}}\alpha {\rm{sin}}\beta $ | (4) |
式中β为Ph与x轴的夹角。
三分量检波器记录到的质点位移分别对应Px、Py、Pz,而P又称为三分量记录的跟踪分量[17]。x和y分量合成的所有水平面向量中Ph能量最强[18]。
在水平层状介质情况下,质点位移方向与震源和检波器连线方向并不一定相同,但二者在水平面内的投影方向始终是一致的,因此本文只使用跟踪分量在水平面的投影Ph,即后文中出现的跟踪分量。
1.2 叠加能量扫描定位原理基于旅行时的定位方法需要精确拾取微地震事件旅行时信息,旅行时拾取精度受信噪比影响很大,对于地面微地震事件和井中信噪比较低的微地震事件而言,很难精确读取P波或S波的旅行时,基于旅行时的定位方法受到限制[13],因此基于波形叠加能量扫描的定位方法在地面微地震监测中得到广泛应用。该方法最大的特点是不需要拾取微地震事件旅行时信息,需要极少的输入参数,能够实现微地震事件的自动化定位[19-20]。
常规的叠加能量扫描定位方法[4-5],首先对求解空间区域进行网格划分,根据地层速度模型计算出每个网格点到地面各检波器的理论旅行时,再对地面接收到的信号经过时差校正后拉平并叠加得到叠加道,然后计算叠加道能量值作为当前网格点的成像值,通过遍历所有网格点取最大成像值网格作为定位结果。为了提高计算效率,也有人采取动态网格、非线性优化等策略[21]。
叠加能量扫描定位方法也叫地震发射层析成像法(SET),王维波等[22]通过数值模拟和实际资料对该方法定位准确性与站点个数、信噪比、站点分布结构的关系等进行了研究。周德山等[23]提出了基于相对旅行时的地震发射层析成像算法,用相对旅行时代替绝对旅行时,减小了速度模型误差对定位结果的影响。常规能量扫描叠加基于单分量检波器,沈琛等[24]和梁北援等[25]在基于单分量检波器的基础上提出了微破裂向量扫描叠加定位方法,在常用的Semblance叠加中引入了向量叠加,利用三分量信息提高了微地震事件方位定位精度。梁北援等[25]还对这种定位方法的解释原则进行了研究。
1.3 井中叠加能量扫描定位方法对于信噪比较低的井中微地震事件,由于无法拾取初至或初至拾取精度较低,难以满足基于旅行时的定位方法需要。针对这一问题,宋维琪等[16]对基于跟踪分量的井中微地震定位方法进行了研究,将叠加能量扫描定位方法引入到井中微地震定位中,其基本原理是在计算某个网格点的叠加能量时,不是直接对三个分量进行叠加,而是将三个分量数据合成到当前网格点与检波器连线方向形成一个新的向量,再对该向量计算非均一化互相关值。根据跟踪分量的定义及性质,跟踪分量能量最强且各检波器间波形一致性最好,因此能够获得最大互相关值。该方法利用了井中三分量数据的振动方向信息,并提高了微地震事件的信噪比。沈琛等[24]和梁北援等[25]提出的应用于地面微地震的微破裂向量扫描定位方法也是基于该原理。只考虑质点振动的Ph分量,叠加能量定义为
| $ \begin{array}{l} {E_1}({x_i}, {y_j}, {z_k})\\ \;\;\;\;\; = {\sum\limits_{t = 1}^M {\left[ {\sum\limits_{n = 1}^N {{f_{{x_i}, {y_j}, {z_k}, n}}} ({t_0} + t + \Delta {t_{{x_i}, {y_j}, {z_k}, n}})} \right]} ^2} \end{array} $ | (5) |
式中:E1(xi,yj,zk)为网格点(xi,yj,zk)对应的所有检波器在水平面内的分量经时差校正后的叠加能量;N为检波器数量;t0为包含有效微地震事件时窗的起点; M为时窗内的样点数,M(时窗长度)采取固定窗口,根据射孔信号估算出微地震事件到达各检波器的最大时差L,以微地震事件触发时刻为中心,则窗长为2L,换算为M个采样点;Δtxi, yj, zk, n为网格点(xi, yj, zk)到第n个检波器旅行时相对于参考检波器的时差,其中i=1,2,…,Gx,j=1,2,…,Gy,k=1,2,…,Gz,分别为x、y、z方向上的网格序号;fxi, yj, zk, n为网格点(xi, yj, zk)对应的第n个检波器的Ph分量,即
| $ {f_{{x_i}, {y_j}, {z_k}, n}}\left( t \right) = {X_n}\left( t \right){\rm{cos}}{\beta _{{x_i}, {y_j}, {z_k}, n}} + {Y_n}\left( t \right){\rm{sin}}{\beta _{{x_i}, {y_j}, {z_k}, n}} $ | (6) |
式中:Xn(t)、Yn(t)分别为第n个检波器的X和Y分量记录;βxi, yj, zk, n为网格点(xi, yj, zk)和第n个检波器的连线在水平面投影与x轴的夹角。
基于叠加能量扫描的微地震定位精度受速度模型的精度和噪声的非随机性影响较大。速度模型精度影响了旅行时计算精度,进而影响各检波器微地震信号经时差校正后拉平效果。信噪比和噪声的非随机性影响了各检波器微地震信号经时差校正、拉平、叠加后能否有效压制噪声进而提高有效信号能量。受以上因素影响,同时由于具有相近方位角的两个位置在水平面的合成向量具有较大相似性,叠加能量对方位变化并不够敏感,定位结果在方位角上具有较强的多解性。
1.4 跟踪分量扫描定位方法为了增强叠加能量对于方位的敏感性,定义网格点(xi, yj, zk)对应的第n个检波器的Ph分量的叠加能量为
| $ {E_2}({x_i}, {y_j}, {z_k}) = \sum\limits_{n = 1}^N {\sum\limits_{t = 1}^M {f_{{x_i}, {y_j}, {z_k}, n}^2({t_0} + t)} } $ | (7) |
对比式(5)与式(7)可以看出:E1是先经过时差校正再进行波形叠加,最后计算叠加波形的能量,相对于方位引起的波形变化对叠加能量的影响,时差变化对叠加能量的影响更大。在水平层状介质假设下,时差变化主要反映了事件的径向距离和深度的变化,因此只通过E1定位会导致定位结果存在较大方位误差;E2是不进行时差校正,而是分别计算各个检波器水平面内合成向量的能量,然后再对所有检波器计算出的能量进行叠加,E2反映的只有方位信息,对方位变化更加敏感。计算过程上一个是先叠加再计算能量,另一个是先计算能量再进行叠加。
基于以上分析,本文通过在井中叠加能量扫描定位方法的基础上加入对方位角敏感的信息,强化叠加能量扫描结果对方位变化的敏感性,可进一步提高定位精度。联合式(5)和式(7)建立新的叠加能量公式为
| $ E({x_i}, {y_j}, {z_k}) = {E_1}({x_i}, {y_j}, {z_k}) + {E_2}({x_i}, {y_j}, {z_k}) $ | (8) |
按照上式对所有网格点计算叠加能量,具有最大叠加能量的网格即为震源位置。
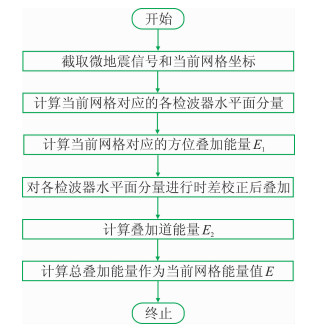
图 2为本文方法计算单个网格点总叠加能量值的流程,依此遍历所有网格点后取最大能量值的网格点作为定位结果。
|
图 2 联合叠加能量定位方法流程 |
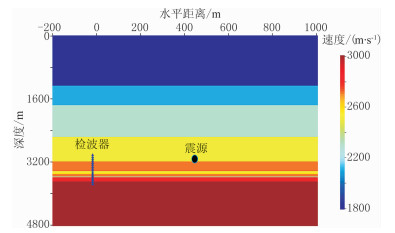
设计图 3所示的速度模型和观测系统:16个三分量检波器井中接收,检波器垂向间距为20m,第一个检波器深度为3000m,震源坐标为(424m,0,3000m),选择主频为50Hz、长度为100ms的Berlage子波利用射线追踪生成模拟三分量记录(图 4a)。
|
图 3 正演模型及观测系统 |
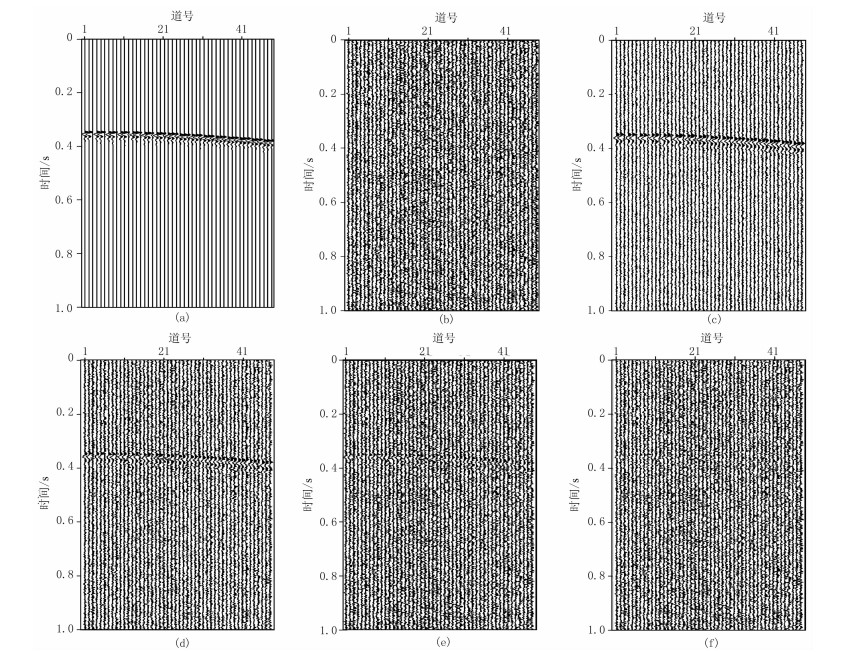
|
图 4 正演模拟数据及其加噪记录 (a)无噪;(b)噪声;(c)R=2;(d)R=1;(e)R=1/2;(f)R=1/4。每三道为一个检波器的X、Y、Z分量数据 |
为了验证本文方法对噪声的适应性,从实际微地震监测记录中提取压裂过程中产生的背景噪声(图 4b),以信号最大值与噪声最大值之比作为信噪比(R),分别以R=2、1、1/2、1/4加入到正演记录中,得到不同信噪比的正演模拟记录(图 4c~图 4f)。
本文定位方法的精度与设置的网格大小有关,网格越小定位精度越高,但计算量和内存需求要大幅增加。如果不考虑噪声、速度模型等其他影响因素,理论上可以将定位误差限制在网格间距的
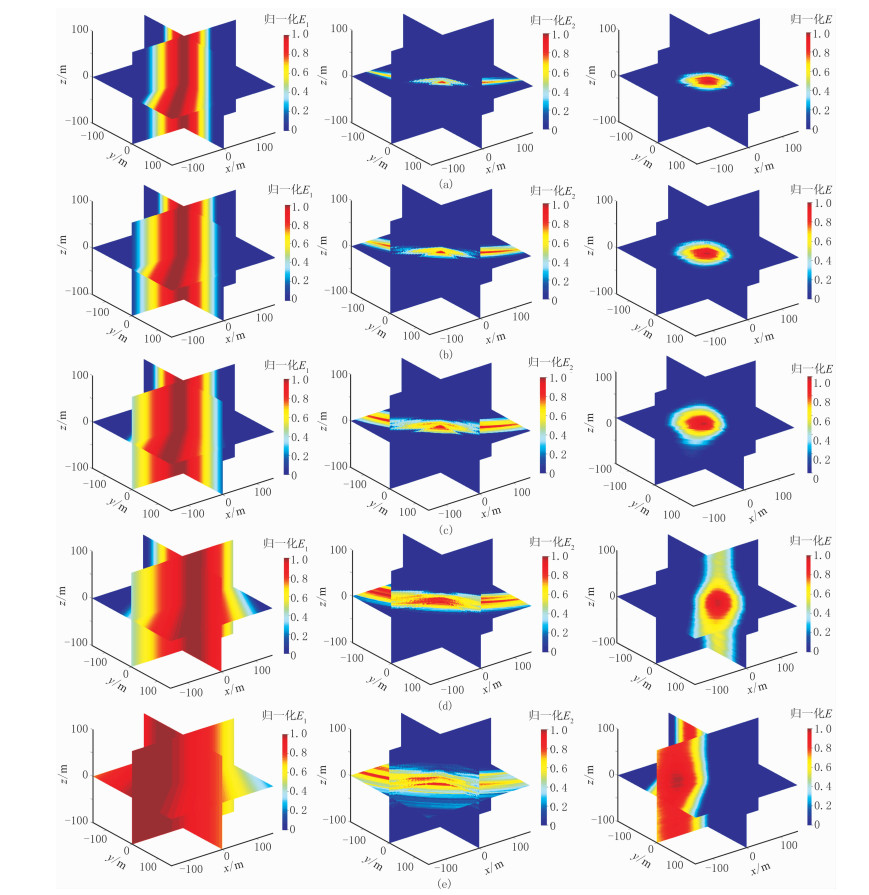
图 5为不同信噪比条件下计算的叠加能量E1、E2和E。从叠加能量切片上可看出:叠加能量E1随着网格的方位变化而变化,在指向震源的同一方向上不变;叠加能量E2随着网格深度和网格到震源的径向距离的变化而变化,与网格的方位无关;信噪比高于1/2时,总叠加能量E能够实现三维聚焦,随着信噪比的降低聚焦性变差;信噪比低于1/2时,总叠加能量E聚焦性很差,且能量团中心位置已经远离震源,尤其是水平方向偏差更大。
|
图 5 模拟数据不同信噪比下的叠加能量 (a)无噪;(b)R=2;(c)R=1;(d)R=1/2;(e)R=1/4 |
求取具有最大叠加能量的网格点即实现震源定位。表 1为不同信噪比时的定位误差,可以看出:①无噪声情况下,三个方向定位误差均为0。②在信噪比不小于1/2情况下,三个方向定位误差均基本能控制在10m之内,并且z方向定位误差小于x和y方向;定位误差随着信噪比的降低而明显增大,当信噪比低于1/2时,定位结果已经不可靠。③当信噪比为1/2时,即使信号已经淹没在噪声中,但定位结果仍具有较高可靠性。
|
|
表 1 不同信噪比情况下本文方法定位误差 |
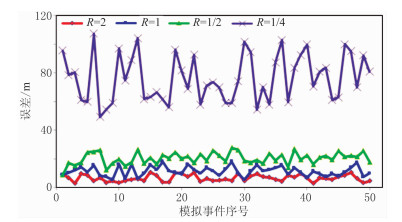
为了进一步验证上述结论的普遍性,在实际监测的背景噪声中随机截取50段作为噪声样本,采用同样方法模拟微地震信号并进行定位,以定位结果到震源的距离作为误差,通过统计得到图 6所示结果。结果表明:随着信噪比的降低,定位误差越来越大,在信噪比分别为2、1、1/2情况下,定位平均误差为6.7m、11.5m、19.4m;当信噪比降低到1/4时,平均定位误差迅速增加到76.5m,已经不能有效用于压裂监测。以上结果验证了本文提出的定位方法具有较高的抗噪能力,可实现低信噪比微地震事件的可靠定位。
|
图 6 50个模拟事件在不同信噪比下的定位误差统计 |
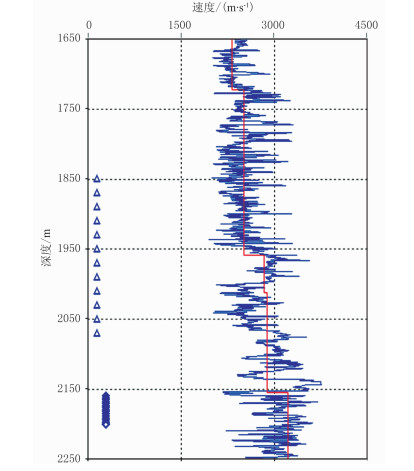
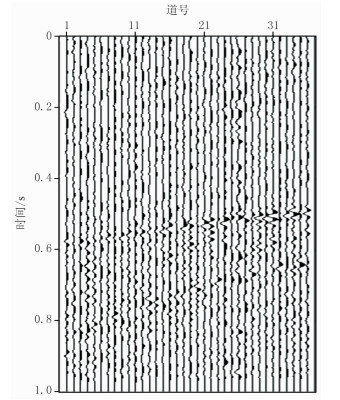
为了进一步验证本文方法的定位效果,对东部某油田的一口实际井中微地震监测数据进行定位。该数据已经进行了前期的滤波、方位校正等必要处理,并根据声波测井资料建立如图 7所示的水平层状介质模型。通过潘树林等[26]提出的多道互相关方法进行有效事件的识别,共识别出疑似有效事件86个,其中信噪比较高的事件有58个,信噪比较低的事件28个。图 8为其中的一个代表性的低信噪比事件,由于无法准确拾取初至信息,基于初至的常规定位方法不再适用。
|
图 7 测井曲线(蓝色)及速度模型(红色) |
|
图 8 实际微地震记录 每三道为一个检波器的X、Y、X分量数据 |
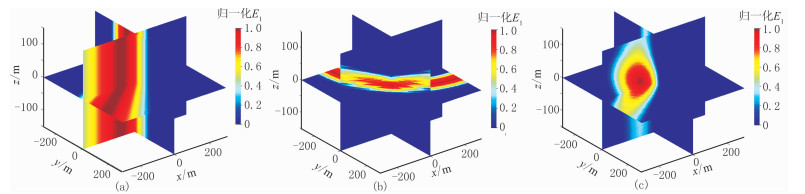
以压裂段为中心,建立一个x、y、z方向长度分别为600m、600m、300m的求解空间,将该空间以1m边长的正方体进行网格剖分,对该微地震事件进行定位。图 9为利用本文方法得到的叠加能量分布,总叠加能量在压裂段附近实现聚焦,通过求取最大叠加能量网格点得到震源位置。
|
图 9 实际微地震事件的叠加能量E1(a)、E2(b)和E(c) |
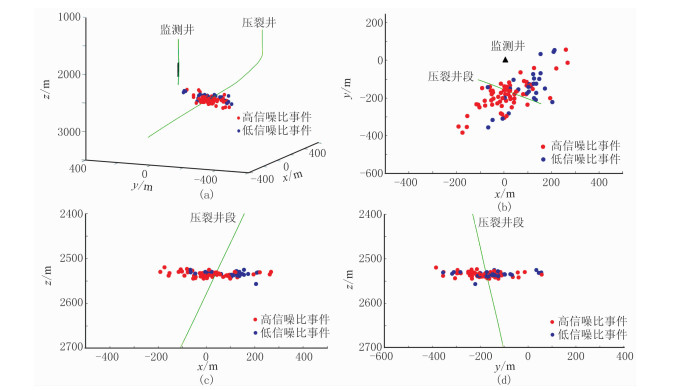
图 10为所有事件的定位结果,从结果可以清晰看出裂缝的形态,高信噪比事件和低信噪比事件的定位结果均可靠,证明本文方法可用于实际弱微地震事件的定位,通过该方法可实现对更多的微地震事件的定位,有助于对压裂效果进行更合理的评价。
|
图 10 实际微地震事件水平井压裂段定位结果 (a)三维显示;(b)俯视图;(c)y方向侧视图;(d)x方向侧视图 |
(1) 本文基于井中三分量检波器的跟踪分量原理,通过构造联合叠加能量函数,实现了井中监测微地震事件的向量扫描定位,模型数据和实际数据均验证了该方法的有效性。
(2) 文中方法对于低信噪比微地震事件的定位结果仍具有可靠性,在常规基于初至的定位方法无法适用的情况下具有明显优势;该方法不需要拾取微地震事件的初至信息,更适用于现场实时定位。
(3) 文中算例只利用了微地震事件的P波信息,通过网格遍历搜索完成定位,如何联合利用S波信息进一步提高定位的精度、应用模拟退火等非线性优化算法提高计算效率,值得进一步深入研究。
| [1] |
杜开元, 段国斌, 徐刚, 等. 深层页岩气井压裂加砂工艺优化的微地震评价[J]. 石油地球物理勘探, 2018, 53(增刊2): 148-155. DU Kaiyuan, DUAN Guobin, XU Gang, et al. Microseismic event evaluation for sand fracturing optimization in deep shale-gas wells[J]. Oil Geophysical Prospecting, 2018, 53(S2): 148-155. |
| [2] |
李晓峰, 张矿生, 卜向前, 等. 老井重复压裂效果评价[J]. 石油地球物理勘探, 2018, 53(增刊2): 162-167. LI Xiaofeng, ZHANG Kuangsheng, BU Xiangqian, et al. Evaluations of repeated fracturings in old wells[J]. Oil Geophysical Prospecting, 2018, 53(S2): 162-167. |
| [3] |
衡峰, 王刚, 刘博, 等. 应用微地震监测技术研究不同簇间距压裂效果[J]. 石油地球物理勘探, 2018, 53(增刊2): 137-142. HENG Feng, WANG Gang, LIU Bo, et al. Hydraulic fracturing with different cluster spacing based on microseismic monitoring[J]. Oil Geophysical Prospecting, 2018, 53(S2): 137-142. |
| [4] |
Duncan P M, Eisner L. Reservoir characterization using surface microseismic monitoring[J]. Geophysics, 2010, 75(5): A139-A146. |
| [5] |
Chambers K, Kendall J M, Brandberg-Dahl S, et al. Testing the ability of surface arrays to monitor microseismic activity[J]. Geophysical Prospecting, 2010, 58(5): 817-826. |
| [6] |
Maxwell S C, Rutledge J, Jones R, et al. Petroleum reservoir characterization using downhole microseismic monitoring[J]. Geophysics, 2010, 75(5): A129-A137. |
| [7] |
宋维琪, 冯超. 微地震有效事件自动识别与定位方法[J]. 石油地球物理勘探, 2013, 48(2): 283-288. SONG Weiqi, FENG Chao. Automatic identification and localization of micro seismic effective events[J]. Oil Geophysical Prospecting, 2013, 48(2): 283-288. |
| [8] |
宋维琪, 高艳珂, 朱海伟. 微地震资料贝叶斯理论差分进化反演方法[J]. 地球物理学报, 2013, 56(4): 1331-1339. SONG Weiqi, GAO Yanke, ZHU Haiwei. The diffe-rential evolution inversion method based on Bayesian theory for micro-seismic data[J]. Chinese Journal of Geophysics, 2013, 56(4): 1331-1339. |
| [9] |
谭玉阳, 李罗兰, 张鑫, 等. 一种改进的基于网格搜索的微地震震源定位方法[J]. 地球物理学报, 2017, 60(1): 293-304. TAN Yuyang, LI Luolan, ZHANG Xin, et al. An improved method for microseismic source location based on grid search[J]. Chinese Journal of Geophysics, 2017, 60(1): 293-304. |
| [10] |
尹奇峰, 潘冬明, 郭全仕, 等. 基于快速模拟退火算法的井中微地震事件定位反演[J]. 地球物理学进展, 2019, 34(5): 1954-1961. YIN Qifeng, PAN Dongming, GUO Quanshi, et al. Inversion of borehole microseismic event location based on fast simulated annealing algorithm[J]. Progress in Geophysics, 2019, 34(5): 1954-1961. |
| [11] |
Bardainne T, Gaucher E, Cerda F, et al.Comparison of picking based and waveform based location methods of microseismic events: Application to a fracturing job[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 1547-1551.
|
| [12] |
Pesicek J D, Child D, Artman B, et al. Picking versus stacking in modern microsearthquake location:Comparision of results from a surface passive seismic monitoring array in Oklahoma[J]. Geophysics, 2014, 79(6): KS61-KS68. DOI:10.1190/geo2013-0404.1 |
| [13] |
Maxsell S C. Microseismic location uncertainty[J]. CSEG Recorder, 2009, 34(4): 41-46. |
| [14] |
毛庆辉, 王鹏, 曾隽. 水力压裂微地震事件定位方法综述[J]. 地球物理学进展, 2019, 34(5): 1878-1886. MAO Qinghui, WANG Peng, ZENG Jun. Review of hydro-fracturing microseismic event location methods[J]. Progress in Geophysics, 2019, 34(5): 1878-1886. |
| [15] |
何惺华. 基于三分量的微地震震源反演方法与效果[J]. 石油地球物理勘探, 2013, 48(1): 71-76. HE Xinghua. A micro-source inversion method based on three component data[J]. Oil Geophysical Prospecting, 2013, 48(1): 71-76. |
| [16] |
宋维琪, 杨晓东. 解域约束下的微地震事件网格搜索法、遗传算法联合反演[J]. 石油地球物理勘探, 2011, 46(2): 259-266. SONG Weiqi, YANG Xiaodong. A joint inversion combining the grid-search algorithm and the genetic algorithm under solution-domain constraints for microseismic events[J]. Oil Geophysical Prospecting, 2011, 46(2): 259-266. |
| [17] |
加尔彼林 E H. 地震勘探偏振法[M]. 北京: 石油工业出版社, 1989: 38-41.
|
| [18] |
张文波, 李建峰, 孙鹏远, 等. 基于直达波偏振分析的三分量检波器定向方法[J]. 石油地球物理勘探, 2017, 52(增刊2): 19-25. ZHANG Wenbo, LI Jianfeng, SUN Pengyuan, et al. A three-component geophone orientation method based on direct P-wave polarization[J]. Oil Geophysical Prospecting, 2017, 52(S2): 19-25. |
| [19] |
Gajewski D, Anikiev D, Kashtan B, et al.Localization of seismic events by diffraction stacking[C]. SEG Technical Program Expanded Abstracts, 2007, 26, 1287-1291.
|
| [20] |
Zhebel O, Gajewski D, Vanelle C.Localization of seismic events in 3D media by diffraction stacking[C]. Extended Abstracts of 73rd EAGE Conference & Exhibition, 2011, 276-284.
|
| [21] |
徐克彬, 陈祖斌, 刘玉海, 等. 基于L-M算法的微地震定位方法[J]. 石油地球物理勘探, 2018, 53(4): 765-769, 790. XU Kebin, CHEN Zubin, LIU Yuhai, et al. A microseismic localization method based on L-M inversion algorithm[J]. Oil Geophysical Prospecting, 2018, 53(4): 765-769, 790. |
| [22] |
王维波, 周瑶琪, 春兰. 地面微地震监测SET震源定位特性研究[J]. 中国石油大学学报(自然科学版), 2012, 36(5): 45-50, 55. WANG Weibo, ZHOU Yaoqi, CHUN Lan. Characteristics of source localization by seismic emission tomo-graphy for surface based on microseismic monitoring[J]. Journal of China University of Petroleum(Natural Science Edition), 2012, 36(5): 45-50, 55. DOI:10.3969/j.issn.1673-5005.2012.05.008 |
| [23] |
周德山, 韩文功, 李振春, 等. 基于相对旅行时计算的地面微地震监测SET定位算法[J]. 地球物理学进展, 2016, 31(6): 2495-2500. ZHOU Deshan, HAN Wengong, LI Zhenchun, et al. Source location method for surface microseismic monitoring based on relative travel time calculation[J]. Progress in Geophysics, 2016, 31(6): 2495-2500. |
| [24] |
沈琛, 梁北援, 李田. 微破裂向量扫描技术原理[J]. 石油学报, 2009, 30(5): 744-748. SHEN Chen, LIANG Beiyuan, LI Tian. Principle of vector scanning technique for micro-fractures[J]. Acta Petrolei Sinica, 2009, 30(5): 744-748. DOI:10.3321/j.issn:0253-2697.2009.05.020 |
| [25] |
梁北援, 冷传波. 微破裂向量扫描原理的研发进展[J]. 地球物理学进展, 2016, 31(4): 1620-1627. LIANG Beiyuan, LENG Chuanbo. Development of vector scanning for microseismic[J]. Progress in Geophysics, 2016, 31(4): 1620-1627. |
| [26] |
潘树林, 崔庆辉, 秦子雨, 等. 基于多道信噪能量统计的微地震有效信号识别方法[J]. 物探化探计算技术, 2019, 41(4): 527-533. PAN Shulin, CUI Qinghui, QIN Ziyu, et al. Microseismic event identification method based on multi-channel[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2019, 41(4): 527-533. DOI:10.3969/j.issn.1001-1749.2019.04.13 |



 崔庆辉, 山东省东营市东营区北一路210号胜利油田物探研究院物探方法研究室, 257022。Email:
崔庆辉, 山东省东营市东营区北一路210号胜利油田物探研究院物探方法研究室, 257022。Email: