② 成都理工大学地球勘探与信息技术教育部重点实验室, 四川成都 610059
② Key Laboratory of Earth Exploration and Information Technology, Ministry of Education, Chengdu University of Technology, Chengdu, Sichuan 610059, China
研究地震波的频散和衰减现象对含流体孔隙介质中流体性质的评估具有重要意义。当地震波穿过饱含流体孔隙介质时,诱发的流体流动是造成地震波频散和衰减的主要原因[1]。实验室测量和理论模拟数据表明,当地震波穿过流体饱和的多孔岩石时,在低频范围内可观察到依赖频率的频散和衰减现象[2-3]。Batzle等[4]也曾在地震频段内观测到流体流动引起的频散现象。而储层中的流体类型及其分布特征对流体流动性有显著影响,进而也会影响地震波频散衰减及依赖频率的地震响应特征[5-6]。因此,研究双相不混溶流体饱和裂缝—孔隙岩石的频散衰减效应及依赖频率的地震响应具有重要意义。
为了更好地研究含流体介质中影响频散和衰减的因素,Chapman等[2, 7]提出了一种基于喷射流的模型,它是由孔隙、微裂隙及定向中尺度裂缝构成的局域流模型。通过对模型中敏感流体进行分析,发现饱含油气的储层的衰减通常高于衰减平均值。考虑到异常的频散和衰减特征在地震响应上也会有所体现,Chapman等[8]进一步分析了敏感流体的频散和衰减对AVO响应的影响。Chen等[9]引入Refutas方程计算多相混合流体的有效黏度,分析了多相流体饱和孔隙岩石依赖频率的衰减及地震响应特征。罗鑫等[10-11]进一步研究了含气饱和度对地震波频散和衰减的影响,并利用依赖频率的AVO反演实现了高含气饱和度储层的识别。
上述相关文献主要针对单一流体或多相流体均匀混合情况下的频散和衰减现象进行了分析,但孔隙岩石中所含的流体大多为部分饱和。为了模拟更符合实际储层流体情况,很多学者[12-15]对部分饱和岩石中弹性波的传播规律进行了研究。White理论[12]详细论述了弹性波在具有局部非均匀性的部分饱和模型中的传播规律。Johnson[13]对介观尺度的White模型做了改进和完善;Müller等[14]提出并发展了孔隙和流体任意分布的斑块饱和模型用于描述流体流动引起的频散和衰减现象;Amalokwu等[15]对包含定向裂缝的部分饱和合成岩石进行了实验测量,发现剪切波的各向异性与含水饱和度有关;Ghosh等[16]强调创建一种可将完全饱和与部分饱和相统一的岩石物理模型的重要性;赵正阳等[17]研究了纵波在部分饱和介质中传播时的频散和衰减特性。这些均为研究部分饱和孔隙介质中的地震波频散和衰减提供了方法、技术。
随着对部分饱和多孔介质中地震波传播研究的不断深入,综合考虑多种因素对速度频散和衰减的影响,将有助于更进一步了解裂缝—孔隙介质饱含流体情况下由“波致流”引起的频散和衰减机理。Papageorgiou等[18]研讨了毛细管压力为零时喷射流在两种流体饱和介质中的影响;进一步的研究[19]发现,毛细管压力与流体“斑块效应”之间存在相关性;在此基础上,提出了一种饱含两种不混溶流体的多孔各向同性模型[20]。Jin等[21]将该模型扩展应用于各向异性介质,通过改变毛细压力参数,研究了同时兼顾流体“均匀饱和”与“斑块饱和”两种情形的频散和衰减。
本文基于裂缝—孔隙岩石物理模型,分析了砂岩储层中两种不混溶流体流动所致的地震频散和衰减效应,通过双相流体间毛细压力参数变化间接表示流体饱和状态,研究了砂岩模型孔隙空间中两种流体饱和度及饱和状态差异对地震响应的影响,为实际地震数据的油气检测提供理论依据。
1 方法和原理 1.1 Chapman等效介质理论依赖频率的部分饱和各向异性模型是基于Chapman等效介质理论[22],假定孔隙空间由各向同性的球形孔隙和微裂隙以及定向排列的中尺度裂缝组成,裂缝半径大于颗粒尺度但小于地震波长。对含双相流体的介质进行模拟分析,计算模型的有效刚度矩阵,频率相关的刚度矩阵形式为
| $ {\mathit{\boldsymbol{C}}_{ijkl}} = \mathit{\boldsymbol{C}}_{ijkl}^0 - {\phi _{\rm{p}}}\mathit{\boldsymbol{C}}_{ijkl}^1 - {\varepsilon _{\rm{c}}}\mathit{\boldsymbol{C}}_{ijkl}^2 - {\varepsilon _{\rm{f}}}\mathit{\boldsymbol{C}}_{ijkl}^3 $ | (1) |
式中:Cijkl0表示通过拉梅系数λ和μ计算得到的各向同性介质的弹性常数矩阵;Cijkl1、Cijkl2和Cijkl3分别为与球形孔隙、微裂隙和中尺度裂缝相关的弹性矩阵校正量,对应由孔隙度ϕp、微裂隙密度εc和裂缝密度εf进行校正;i、j、k、l为矩阵元素的下标。
1.2 部分饱和模型中的流体计算理论模型中对流体流动的描述基于达西定律,当多孔介质饱和双相不混溶流体时,每种流体的流动将取决于流体的有效流动性和毛细管压力参数。Jin等[21]提出由于毛细管效应或饱和度不均匀性,导致双相流体之间压力存在差异。利用无量纲参数将双相流体系统中的流体压力相关联(以气水情况为例,但该模型适用于任何双相流体系统)
| $ {P_{\rm{g}}} = q{P_{\rm{w}}} $ | (2) |
式中:Pg和Pw分别表示气、水的压力;q表示毛细管压力量化参数,范围是[q0,1],且q0= Kg/Kw,其中Kg、Kw分别为气、水的体积模量,显然Kg<Kw。q值小于1表示流体间未达到均匀状态,尚处于所谓的“斑块饱和”;随着q值增大,两种流体间满足等应力条件形成“均匀饱和”状态。将以上影响纳入原有理论,并引入中间变量
| $ {\frac{1}{{{K_{\rm{f}}}}} = \frac{{{S_{\rm{w}}}}}{{\tilde q{K_{\rm{w}}}}} + \frac{{(1 - {S_{\rm{w}}})q}}{{\tilde q{K_{\rm{g}}}}}} $ | (3) |
| $ {{M_{\rm{f}}} = \frac{{{\kappa _{\rm{w}}}}}{{\tilde q}}{M_{\rm{w}}} + \frac{{q{\kappa _{\rm{g}}}}}{{\tilde q}}{M_{\rm{g}}}} $ | (4) |
且有
| $ {\left\{ {\begin{array}{*{20}{l}} {\tilde q = {S_{\rm{w}}} + q(1 - {S_{\rm{w}}})}\\ {{M_{\rm{w}}} = \frac{\kappa }{{{\eta _{\rm{w}}}}}}\\ {{M_{\rm{g}}} = \frac{\kappa }{{{\eta _{\rm{g}}}}}} \end{array}} \right.} $ | (5) |
式中:Sw是含水饱和度;ηw、ηg分别为水和气体的黏度,则Mw和Mg表征水和气体的流动性;κw和κg分别为水和气体的相对渗透率;κ表示岩石骨架的绝对渗透率。
式(3)表明,Kf是由参数q加权的两种流体体积模量的Reuss(空间平均波速模型)平均值,故该值将对有效流体刚度产生影响。式(4)给出的混合流体的有效流动性Mf是考虑两种流体迁移率的加权平均值。此处,水和气体的相对渗透率可由
| $ \left\{ {\begin{array}{*{20}{l}} {{\kappa _{\rm{w}}} = S_{\rm{w}}^3}\\ {{\kappa _{\rm{g}}} = {{(1 - {S_{\rm{w}}})}^2}} \end{array}} \right. $ | (6) |
计算。因此,速度频散和衰减的特征频率取决于流体饱和度与不均匀流体之间的压力。理论表明,在部分饱和裂缝岩石中,喷射流频率ωm和裂缝尺度特征频率ωf由下式给出
| $ \left\{ {\begin{array}{*{20}{l}} {{\omega _{\rm{m}}} = \frac{{{\omega _0}{M_{\rm{f}}}}}{{{M_{\rm{w}}}}}}\\ {{\omega _{\rm{f}}} = \frac{{\omega _0^\prime {M_{\rm{f}}}}}{{{M_{\rm{w}}}}}} \end{array}} \right. $ | (7) |
式中ω0和ω′0是含水饱和度为1时ωm和ωf的值。
根据式(7)可判断部分饱和与完全饱和情况之间的主要区别在于双流体混合物的有效流动性。低流动性导致流体较低的特征频率,可解释为低迁移率流体流动更慢,即需更多时间使压力梯度松弛。
1.3 依赖频率的速度和衰减及反射系数分布根据Chapman理论模型[7]计算的频率相关的各向异性弹性刚度矩阵为
| $ \left[ {\begin{array}{*{20}{c}} {{C_{11}}}&{{C_{12}}}&{{C_{13}}}&0&0&0\\ {{C_{12}}}&{{C_{11}}}&{{C_{13}}}&0&0&0\\ {{C_{13}}}&{{C_{13}}}&{{C_{33}}}&0&0&0\\ 0&0&0&{{C_{44}}}&0&0\\ 0&0&0&0&{{C_{44}}}&0\\ 0&0&0&0&0&{{C_{66}}} \end{array}} \right] $ | (8) |
利用此刚度矩阵可计算地震波的复数速度
| $ \left\{ {\begin{array}{*{20}{l}} {{V_1}(\omega ) = {{({C_{11}}{\rm{si}}{{\rm{n}}^2}\theta + {C_{33}}{\rm{co}}{{\rm{s}}^2}\theta + {C_{44}} + \sqrt N )}^{\frac{1}{2}}}{{(2\rho )}^{ - \frac{1}{2}}}}\\ {{V_2}(\omega ) = {{({C_{11}}{\rm{si}}{{\rm{n}}^2}\theta + {C_{33}}{\rm{co}}{{\rm{s}}^2}\theta + {C_{44}} - \sqrt N )}^{\frac{1}{2}}}{{(2\rho )}^{ - \frac{1}{2}}}} \end{array}} \right. $ | (9) |
式中:ρ为介质密度;θ为波向量与对称轴夹角;且有
| $ \begin{array}{*{20}{l}} {N = {{[({C_{11}} - {C_{44}}){\rm{si}}{{\rm{n}}^2}\theta - ({C_{33}} - {C_{44}}){\rm{co}}{{\rm{s}}^2}\theta ]}^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{({C_{13}} - {C_{44}})}^2}{\rm{si}}{{\rm{n}}^2}(2\theta )} \end{array} $ | (10) |
根据计算结果进而求得依赖频率的地震波速度VP(ω)、VS(ω)及逆品质因子1/QP(ω)
| $ \left\{ {\begin{array}{*{20}{l}} {{V_{\rm{P}}}(\omega ) = \frac{1}{{ {\rm{Re}} \frac{1}{{{V_1}(\omega )}}}}}\\ {{V_{\rm{S}}}(\omega ) = \frac{1}{{ {\rm{Re}} \frac{1}{{{V_2}(\omega )}}}}}\\ {\frac{1}{{{Q_{\rm{P}}}(\omega )}} = \frac{{ {\rm{Im}} [V_1^2(\omega )]}}{{ {\rm{Re}} [V_1^2(\omega )]}}} \end{array}} \right. $ | (11) |
将Wiggins等[23]提出的AVO三项(截距项A(ω)、斜率项B(ω)、曲率项C(ω))线性近似式拓展至入射角—频率域,进而建立依赖频率的AVO反射系数公式
| $ {R_{\rm{P}}}(\omega ,\theta ) = A(\omega ) + B(\omega ){\rm{si}}{{\rm{n}}^2}\theta + C(\omega ){\rm{ta}}{{\rm{n}}^2}\theta {\rm{si}}{{\rm{n}}^2}\theta $ | (12) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {A(\omega ) = \frac{1}{2}[\frac{{\Delta {V_{\rm{P}}}(\omega )}}{{V_{\rm{P}}^\prime (\omega )}} + \frac{{\Delta \rho }}{{{\rho ^\prime }}}]}\\ {B(\omega ) = \frac{1}{2}\frac{{\Delta {V_{\rm{P}}}(\omega )}}{{V_{\rm{P}}^\prime (\omega )}} - 4{{[\frac{{V_{\rm{S}}^\prime (\omega )}}{{V_{\rm{P}}^\prime (\omega )}}]}^2} \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\Delta {V_{\rm{S}}}(\omega )}}{{V_{\rm{S}}^\prime (\omega )}} - 2{{[\frac{{V_{\rm{S}}^\prime (\omega )}}{{V_{\rm{P}}^\prime (\omega )}}]}^2}\frac{{\Delta \rho }}{{{\rho ^\prime }}}}\\ {C(\omega ) = \frac{1}{2}\frac{{\Delta {V_{\rm{P}}}(\omega )}}{{V_{\rm{P}}^\prime (\omega )}}} \end{array}} \right. $ | (13) |
式中:ΔVP(ω)、ΔVS(ω)和Δρ分别表示界面两侧介质纵、横波速度和密度的差值;V′P(ω)、V′S(ω)和ρ′为界面两侧介质纵、横波速度和密度的平均值。
1.4 地震响应的数值模拟计算基于计算得到的依赖频率的速度和反射系数,利用相移法波动方程模拟依赖频率的地震响应[24]。为避免波场模拟中多次波等影响,采用一维波动方程
| $ \frac{{{\partial ^2}u}}{{\partial {t^2}}} - {V^2}\frac{{{\partial ^2}u}}{{\partial {z^2}}} = 0 $ | (14) |
式中:u表示介质的标量位移;z为深度;t表示双向旅行时间;V是依赖频率的纵波速度。其中平面波u可表示为u=e-ikzzeiωt,将该方程代入式(14)并对其进行傅里叶变换,获得依赖频率的与速度有关的垂直波数表达式
| $ {k_z}(\omega ) = \frac{\omega }{{V(\omega )}} $ | (15) |
在数值模拟中,基于相移法做波场延拓,相移式为
| $ u(z + \Delta z) = u(z,\omega ){{\rm{e}}^{{\rm{i}}{k_z}(\omega )\Delta z}} $ | (16) |
即得依赖频率的地震响应。
2 数值模拟分析 2.1 依赖频率的速度和衰减为了研讨双相不混溶流体的性质对速度频散和衰减的影响,本文根据文献[25]的砂岩样品数据,设计了由双相流体填充的砂岩储层模型,进行数值模拟。砂岩参数如表 1所示。岩石中填充流体的基本参数假定为在压力25MPa、温度50℃条件下由Ba-tzle等[26]的方程式计算得到,三种流体物理参数如表 2所示。通过Chapman等[22]的等效介质理论计算地震波依赖频率的速度和衰减,且数值模拟结果都是在与裂缝法线平面呈25°角时计算的。
|
|
表 1 砂岩模型参数 |
|
|
表 2 流体参数 |
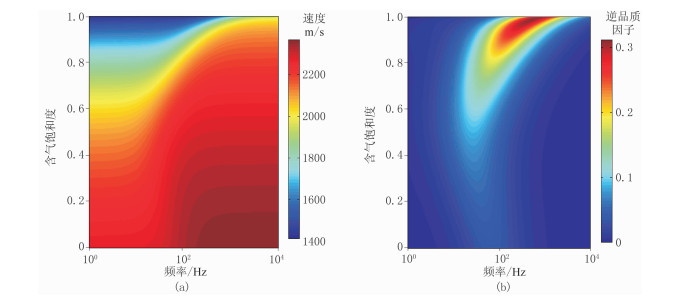
砂岩储层中双相流体间毛细压力为固定值时,双相流体介质依赖频率的速度和衰减与饱和度有关。从含气水砂岩的依赖频率的速度和衰减二维平面图(图 1)中可见:随着饱和度的变化,频散和衰减在整体变化趋势上存在差异;相同频率下纵波速度随含气饱和度的增加而降低,逆品质因子的值对饱和度变化的响应较复杂(细节见图 2)。
|
图 1 含气水砂岩储层随含气饱和度和频率变化的速度(a)和衰减(b) |
|
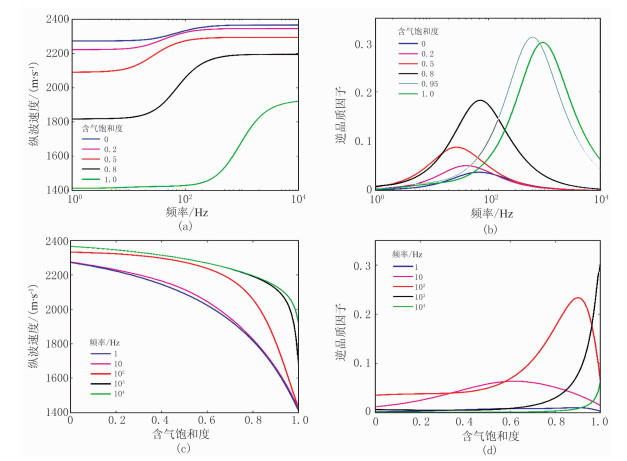
图 2 含气水砂岩储层随频率(a、b)或含气饱和度(c、d)变化的速度(a、c)和衰减曲线(b、d) |
为更清晰地对频散和衰减的变化进行分析,从中抽取几个固定频率和饱和度的速度和衰减曲线(图 2)进行分析。对比图 2a与图 2b可知,纵波速度在整个频段的变化差值随含气饱和度增加不断增大,衰减峰值对应的特征频率在较低(小于0.50)含气饱和度范围内随其增加而减小,在较高(大于0.50)饱和度范围内随其增加而增大;且从另外抽取的含气饱和度为0.95(图 2b中灰线)的衰减曲线同样可见其峰值存在增减性变化,随含气饱和度的增加峰值呈现先增后减的趋势。还可看到,在不同频段内纵波速度(图 2c)和衰减(图 2d)对饱和度的敏感性也存在差异。随着频率由低频段增至高频段,速度和衰减的变化更剧烈,且在近似地震频带的中间频段(100Hz)对饱和度的变化较敏感。在此频段,当含气饱和度大于0.60后,纵波速度开始急剧下降,衰减数值也发生剧烈变化。即在大约0.60~0.85区间,衰减值随含气饱和度增加首先呈较快上升,此后的高含气饱和度范围转为急剧下降。
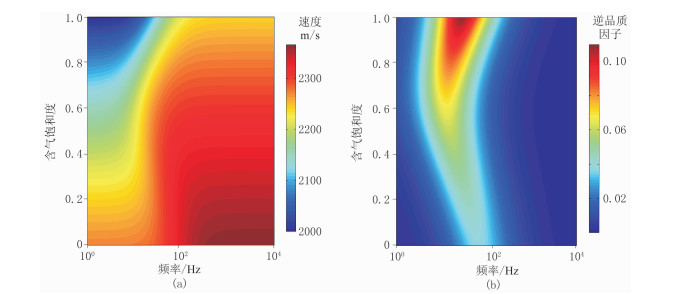
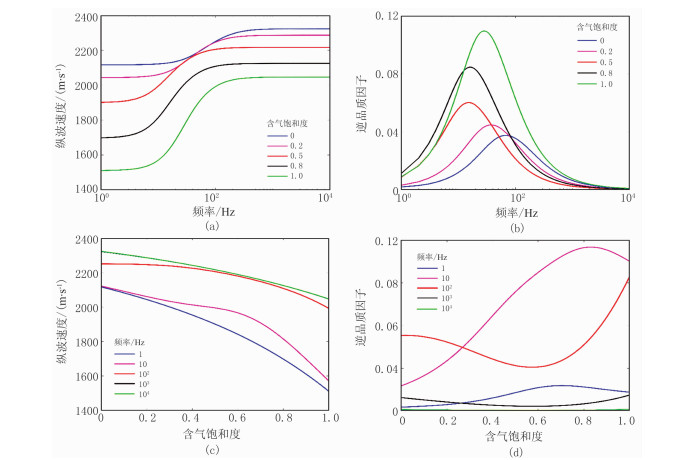
为了研究介质中存在不同双相流体系统时频散和衰减的差异,进一步针对含油水砂岩的频散和衰减进行分析。图 3为含油水砂岩依赖频率的速度和衰减二维平面图,相同频率下含油水砂岩的纵波速度随含油饱和度增加而减小,而特征频率随着含油饱和度增加先减小后增大。图 4为含油水砂岩固定饱和度或频率下的纵波速度和衰减曲线,图 4c中频率为103与104Hz的曲线基本重合。且通过对比发现在中低频段速度和衰减对于饱和度变化的响应较为敏感。由图 1、图 3对比可知,含油水砂岩的频散和衰减的变化差值远小于气水砂岩。气水和油水砂岩在高饱和度处的衰减特征存在明显差异,气水砂岩的衰减值在高饱和度时发生急剧降低,而油水砂岩衰减不存在此现象。此外,相对气水砂岩,油水砂岩随饱和度发生变化所对应的频率范围较低。
|
图 3 含油水砂岩储层随含油饱和度和频率变化的速度(a)和衰减(b) |
|
图 4 含油水砂岩储层随频率(a、b)或含油饱和度(c、d)变化的速度(a、c)和衰减(b、d)曲线 |
当介质中含有双相不混溶流体时,两种流体之间毛细压力差异所导致的流体饱和状态的不同也是需考虑的因素。q为衡量流体间压力的参数,取值范围设定为[q0,1]。随着q值的增加,流体之间由所谓不混溶的“斑块饱和”逐渐达到平衡的“均匀饱和”状态。由于气水砂岩的q值变化范围较大,本文对毛细压力参数变化的讨论针对气水砂岩展开。
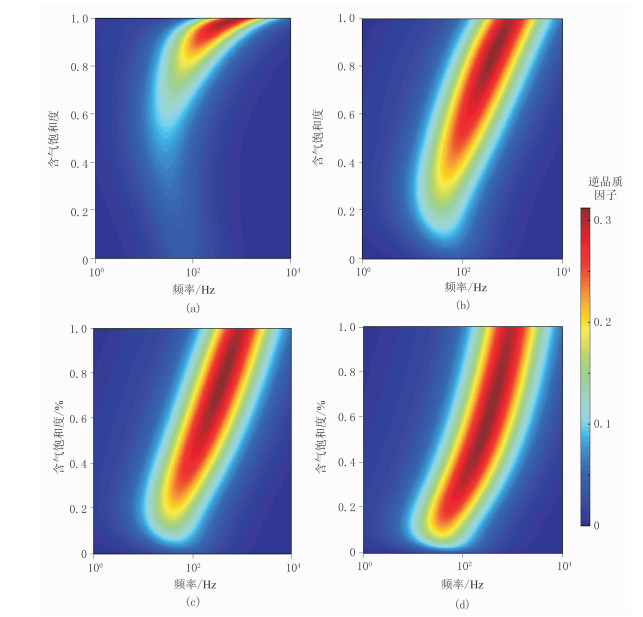
不同q值下气和水填充的砂岩的衰减结果如图 5所示,由图可知,q值的增加对于衰减值整体上的变化范围没有影响,衰减值变化速率最快的范围所对应的饱和度逐渐减小。随着q的增加,流体流动性变化由急剧逐渐趋于平缓,衰减整体上对饱和度的敏感性逐渐减弱。衰减的数值模拟结果对饱和度响应较为明显的频率仍为中间频段,但低频段的变化也有所增强。
|
图 5 不同q值下的气和水填充的砂岩储层衰减 (a)q=q0; (b)q=10q0; (c)q=20q0; (d)q=1 |
为了明确随q值增加时特征频率与饱和度的变化规律,从图 5中提取不同q值下衰减峰值对应的特征频率随含气饱和度的变化曲线(图 6)。由图可见,q值变化对特征频率的变化范围没有影响,但随着q值的增加,高含气饱和度处特征频率随饱和度的变化速率逐渐降低,在整个含气饱和度变化范围内的变化更均匀。

|
图 6 不同q值下的气和水填充的砂岩储层特征频率随含气饱和度的变化 |
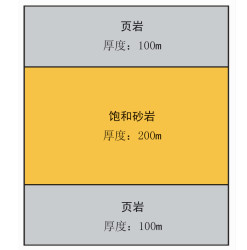
利用水平层状模型(图 7)模拟双相不混溶流体填充时砂岩储层的地震响应,地质模型中页岩的纵、横波速度分别为2755和2070m/s,密度为1402kg/m3。
|
图 7 三层地质模型 |
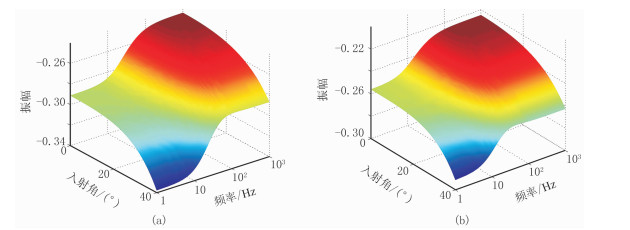
在计算出不同流体填充的砂岩储层依赖频率的地震波速度的基础上,模拟得到地质模型上层反射界面随入射角度和频率变化的反射系数分布(图 8),可见含气水与含油水砂岩的反射系数整体的变化特征相似。即随频率增加,反射系数值不断增大,变化速率先增大后减小,在中间频段的反射系数变化最明显;随入射角度增加,反射系数值不断减小,在30°~40°时变化差值较大;但气水砂岩的反射系数变化差值明显大于含油水砂岩。
|
图 8 随入射角和频率变化的含流体砂岩上界面反射系数分布 (a)气水;(b)油水 |
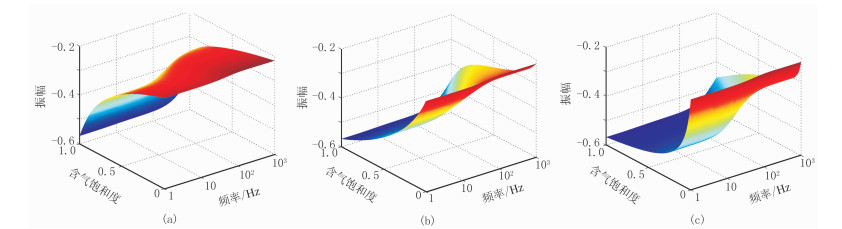
考虑流体之间分布状态变化的影响,在固定入射角(20°)下,对不同q值的气水砂岩反射系数随饱和度和频率的变化(图 9)进行分析。可知随着含气饱和度的增加,反射系数值不断减小。流体间压力的差异也对反射系数分布存在着影响。随着q值增加,双相流体由“部分饱和”转变为“均匀饱和”状态,反射系数的变化范围不受影响,变化速率的极值点对应频率不断升高,对应的饱和度值逐渐降低。
|
图 9 固定入射角度时不同流体饱和状态的气水储层上界面随含气饱和度和频率变化的反射系数分布 (a)q=q0; (b)q=10q0; (c)q=1 |
针对三层地质模型研究砂岩储层中含不同流体时的地震响应,讨论在不同饱和度及饱和状态下的响应差异。
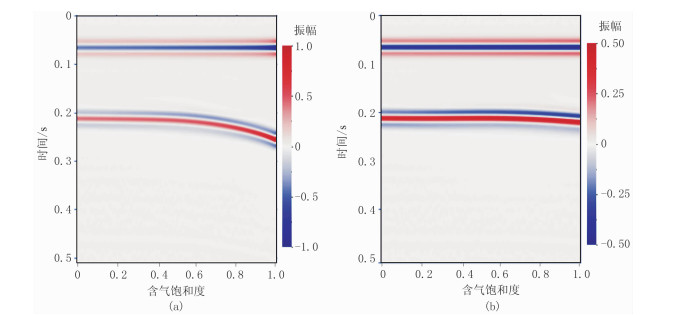
含气水和油水地质模型随饱和度变化的地震响应如图 10所示,可知含不同流体的介质模型在地震响应上存在差异。气水和油水填充模型的上层反射界面处,随着油气饱和度的增加,地震响应在时间上不发生延迟现象,这缘于假定上覆页岩不存在速度频散和衰减,页岩层纵波速度不受饱和度影响。但由于砂岩层速度随饱和度增加而发生变化,地震波振幅的绝对值随饱和度增加而增大。而在下层反射界面处,填充流体为油水和气水的储层模型地震响应都存在时间上的延迟和波形畸变现象,且随着油气饱和度增加,地震记录的延时时间不断增长,地震波形上也呈现出振幅绝对值与油气饱和度的正相关关系。对比图 10a与图 10b可知,相较于含油水模型,含气水模型在高含气饱和度时表现出更强敏感性,在传播时间上具体表现为存在明显的“下拉”现象,波形振幅值差异也更明显。
|
图 10 气水(a)、油水(b)双相流体储层三层模型地震响应 |
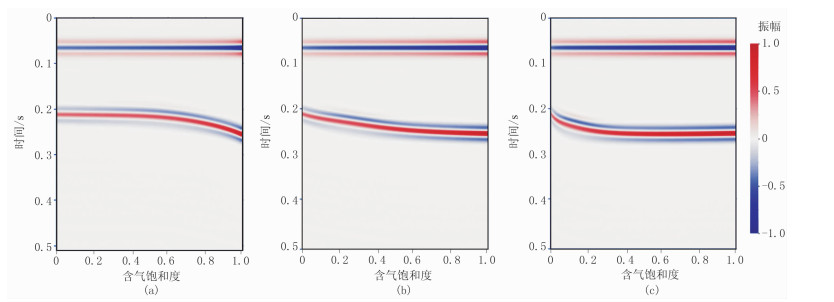
进一步分析表明,不同q值对储层地震响应结果也存在影响。从图 11可知,随着q值增加,上层界面相同含气饱和度时的地震波振幅值不断增加,在时间上无延迟现象。下层界面地震波振幅值变化最剧烈的位置对应的含气饱和度值逐渐减小,时间上变化速率的极值点也向低饱和度方向移动。
|
图 11 固定入射角度时不同流体饱和状态的气水储层上界面随含气饱和度变化的地震响应 (a)q=q0;(b)q=10q0;(c)q=1 |
本文对双相不混溶流体饱和裂缝—孔隙岩石的频散衰减效应及依赖频率的地震响应进行了研究,主要探讨了流体饱和度和毛管参数对频散衰减及地震响应的影响,得出以下认识与结论。
(1) 对含双相流体介质的频散衰减结果的分析发现,随着油气饱和度的增加,地震波速度降低,频散衰减的特征频率区别于单一流体呈先减后增的变化趋势;在中间频段(100Hz)频散衰减对饱和度变化的响应较为明显。
(2) 对比不同双相流体情形得知,若其中一种是气体时,其体积模量、密度和黏度等的显著差异引起流体流动性剧烈变化,进而导致地震波的频散和衰减在高含气饱和度时表现出强敏感性;衰减曲线峰值也区别于无气体情况,呈现先增后减的变化规律,地震响应上的时间延迟和振幅增强现象更明显。
(3) 两种流体间的毛细压力参数值q影响着两种流体的混合状态。随着q值增加,流体间从“斑块饱和”转变为“均匀混合”状态,地震波衰减对饱和度的敏感性逐渐减弱,反射系数变化速率的极值向着“高频低饱”移动,地震响应时间和振幅剧烈变化所对应的含气饱和度值逐渐降低。
| [1] |
Pride S R, Berryman J G, Harris J M. Seismic attenuation due to wave-induced flow[J]. Journal of Geo-physical Research, 2004, 109: B01201. |
| [2] |
Chapman M. Frequency-dependent anisotropy due to meso-scale fractures in the presence of equant porosity[J]. Geophysical Prospecting, 2010, 51(5): 369-379. |
| [3] |
勾彬彬, 陈学华, 瞿雷, 等. 依赖频率的裂缝孔隙介质弹性属性及参数影响[J]. 石油地球物理勘探, 2018, 53(6): 1235-1240. GOU Binbin, CHEN Xuehua, QU Lei, et al. The effects of elastic properties and parameters on frequency-dependent fractured porous media[J]. Oil Geo-physical Prospecting, 2018, 53(6): 1235-1240. |
| [4] |
Batzle M L, Han D H, Hofmann R. Fluid mobility and frequency-dependent seismic velocity-Direct measurement[J]. Geophysics, 2006, 71(1): N1-N9. |
| [5] |
王峣钧, 陈双全, 王磊, 等. 基于斑块饱和模型利用地震波频散特征分析含气饱和度[J]. 石油地球物理勘探, 2014, 49(4): 715-722. WANG Xiaojun, CHEN Shuangquan, WANG Lei, et al. Gas saturation analysis with seismic dispersion attribute based on patchy saturation model[J]. Oil Geophysical Prospecting, 2014, 49(4): 715-722. |
| [6] |
张繁昌, 桑凯恒, 路亚威. 硬币型裂缝介质的频散与衰减[J]. 石油地球物理勘探, 2019, 54(4): 836-843. ZHANG Fanchang, SANG Kaiheng, LU Yawei. Dispersion and attenuation of coin-type crack media[J]. Oil Geophysical Prospecting, 2019, 54(4): 836-843. |
| [7] |
Chapman M, Maultzsch S, Liu E, et al. The effect of fluid saturation in an anisotropic multi-scale equant porosity model[J]. Journal of Applied Geophysics, 2003, 54(3): 191-202. |
| [8] |
Chapman M, Liu E, Li X Y. The influence of fluid-sensitive dispersion and attenuation on AVO analysis[J]. Geophysical Journal International, 2006, 167(1): 89-105. |
| [9] |
Chen X H, Zhong W L, He Z H, et al. Frequency-dependent attenuation of compressional wave and seismic effects in porous reservoirs saturated with multi-phase fluids[J]. Journal of Petroleum Science and Engineering, 2016, 147: 371-380. |
| [10] |
罗鑫, 陈学华, 张杰, 等. 基于依赖频率AVO反演的高含气饱和度储层预测方法[J]. 石油地球物理勘探, 2019, 54(2): 356-364. LUO Xin, CHEN Xuehua, ZHANG Jie, et al. High gas saturation reservoir prediction method based on frequency-dependent AVO inversion[J]. Oil Geophy-sical Prospecting, 2019, 54(2): 356-364. |
| [11] |
罗鑫, 陈学华, 吕丙南, 等. 基于Gray反射系数的频变AVO反演[J]. 石油物探, 2018, 57(2): 292-301. LUO Xin, CHEN Xuehua, LYU Bingnan. Frequency- varying AVO inversion based on Gray reflection coefficient[J]. Geophysical Prospecting for Petroleum, 2018, 57(2): 292-301. |
| [12] |
White J. Computed seismic speeds and attenuation in rocks with partial gas saturation[J]. Geophysics, 1975, 40(2): 224-232. |
| [13] |
Johnson D L. Theory of frequency dependent acoustics in patchy-saturated porous media[J]. The Journal of the Acoustical Society of America, 2001, 110(2): 682-694. |
| [14] |
Müller T M, Gurevich B, Lebedev M. Seismic wave attenuation and dispersion resulting from wave-induced flow in porous rocks-A review[J]. Geophy-sics, 2010, 75(5): A147-A164. |
| [15] |
Amalokwu K, Chapman M, Best A I, et al. Experi-mental observation of water saturation effect on S-wave splitting in synthetic rock with fractures aligned at oblique angles[J]. Geophysical Journal Internatio-nal, 2014, 200(1): 17-24. |
| [16] |
Ghosh R, Sen M K, Vedanti N. Quantitative interpretation of CO2 plume from Sleipner (North Sea), using post-stack inversion and rock physics modeling[J]. International Journal of Greenhouse Gas Control, 2015, 32: 147-158. |
| [17] |
赵正阳, 印兴耀, 宗兆云. 含横向喷射流的部分饱和介质的纵波衰减和频散特性研究[J]. 石油物探, 2019, 58(1): 21-30. ZHAO Zhengyang, YIN Xingyao, ZONG Zhaoyun. Study on longitudinal wave attenuation and dispersion characteristics of partial saturated media with transverse jet[J]. Geophysical Prospecting for Petroleum, 2019, 58(1): 21-30. |
| [18] |
Papageorgiou G, Chapman M. Multifluid squirt flow and hysteresis effects on the bulk modulus-water sa-turation relationship[J]. Geophysical Journal International, 2015, 203(2): 814-817. |
| [19] |
Papageorgiou G, Amalokwu K, Chapman M. Theoretical derivation of a Brie-like fluid mixing law[J]. Geophysical Prospecting, 2016, 64(4): 1048-1053. |
| [20] |
Papageorgiou G, Chapman M. Wave-propagation in rocks saturated by two immiscile fluids[J]. Geophysical Journal International, 2017, 209(3): 1761-1767. |
| [21] |
Jin Z Y, Chapman M, Papageorgiou G. Frequency-dependent anisotropy in a partially saturated fractured rock[J]. Geophysical Journal International, 2018, 215(3): 1985-1998. |
| [22] |
Chapman M, Zatsepin S V, Crampin S. Derivation of a microstructural poroelastic model[J]. Geophysical Journal International, 2010, 151(2): 427-451. |
| [23] |
Wiggins R, Kenny G S, Mcclure C D.Method for de-termining and displaying the shear wave reflectivities of a geologic formation[P]. European, 0113944, 1983-01-17.
|
| [24] |
Chen X H, He Z H, Gao G, et al.A fast combined method for fluid flow related frequency-dependent AVO modeling[C]. SEG Technical Program Expan-ded Abstracts, 2013, 32: 3454-3459.
|
| [25] |
Rathore J S, Fjaer, Renlie, et al. P- and S-wave aniso-tropy of a synthetic sandstone with controlled crack geometry[J]. Geophysical Prospecting, 2010, 43(6): 711-728. |
| [26] |
Batzle M L, Wang Z. Seismic properties of pore fluids[J]. Geophysics, 1992, 57(11): 1396-1408. |



 陈学华, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室, 610059。Email:
陈学华, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室, 610059。Email: