② 中国海洋石油国际有限公司, 北京 100027;
③ 中国石油大学(华东), 青岛 266580
② CNOOC International Co., Ltd., Beijing 100027, China;
③ China University of Petroleum(East China), Qing-dao, Shandong 266580, China
随着勘探地球物理技术的进步,地震勘探由传统的单分量声波向多波、多分量勘探发展,勘探目标也逐渐转向复杂探区[1]。采用各向同性介质假设的常规偏移方法处理实际各向异性介质地震资料,导致绕射波不能完全收敛、反射波不能准确归位等问题,从而降低成像质量[2-3]。弹性波波场包含更丰富的地层岩性信息,弹性波偏移方法通过充分利用纵、横波信息成像,可降低传统的纵波勘探的多解性,提高成像分辨率,为非均质储层预测、复杂油气藏的精细描述提供有效支撑[1]。因此,研究一种基于各向异性介质的弹性波叠前深度偏移方法尤为重要。
现今弹性波偏移方法主要分为两大类。
(1) 波动方程类弹性波偏移方法。首先由Sun等[4]提出弹性波波动方程有限差分法,后来经过Jia等[5]的发展,得到了对观测系统适应性更强的各向同性介质角度域弹性波逆时偏移方法。弹性波逆时偏移方法计算精度高,然而其计算效率不够理想,如何处理实际海量数据还需要进一步研究。
(2) 射线类弹性波偏移方法。最早由Kuo等[6]提出,其基于Pao等[7]推导的弹性波Kirchhoff-Helmholtz类型的积分,然而仅适用于常速度介质[8];后来人们研究了利用多分量地震数据进行PP和PS波成像的方法[9-10],较好地解决了不同波型间的串扰问题。Sena等[11]提出了适用于各向异性介质的弹性波Kirchhoff偏移方法,Hokstad[12]进一步研究了各向异性弹性波和黏滞性弹性波偏移。弹性波Kirchhoff偏移方法计算方便、效率高,但其作为一种射线类方法,不能利用多波至进行成像,因而不适合复杂地质构造成像。
针对弹性波逆时偏移和弹性波Kirchhoff偏移中存在的问题和不足,有人提出了弹性波高斯束偏移方法[13-15]。后来,Katchalov等[16]研究了真振幅弹性波多分量高斯束偏移方法,作为一种延伸的射线类方法,不仅与波动方程类偏移方法的成像精度接近,还具有较高的计算效率。Alkhalifah[17]、Protasov[18]提出了适用于多分量数据的各向异性介质高斯束偏移方法。近年来,人们进一步研究了高斯束正演[19-21]、转换波高斯束偏移[22]、高斯束逆时偏移[23-24]等方法。然而,当前的研究多集中在各向同性介质声波、弹性波成像[25]和各向异性介质声波成像[3, 25-26],针对各向异性介质弹性波偏移的文献相对较少。
本文在前人的研究基础上[15, 27],发展了各向异性介质弹性波射线追踪方程,以二维各向异性弹性波Kirchhoff-Helmholtz积分为基础,推导了各向异性介质弹性波高斯束偏移成像公式,提出了一种各向异性介质弹性波高斯束偏移方法。该方法通过引入权函数,有效压制了弹性波成像中不同波型引起的串扰。通过引入符号函数,较好地解决了转换波成像中的极性反转问题。模型试算结果证明了本文方法的有效性。
1 基本原理 1.1 各向异性介质弹性波射线追踪实现各向异性介质弹性波高斯束偏移的关键在于运动学和动力学射线追踪。运动学射线追踪主要计算中心射线路径和走时,动力学射线追踪计算射线的振幅和波前。本文在Zhu等[28]的各向异性介质qP波射线追踪算法基础上,推导了各向异性介质多波运动学和动力学射线追踪方程,发展了各向异性介质弹性波射线追踪算法。
1.1.1 运动学射线追踪Cerveny[29]推导了基于弹性参数的运动学射线追踪方程,然而其计算过程需要求解特征值问题,因而较复杂。为此,Zhu等[28]以相速度的形式重新定义了广义各向异性介质中的运动学追踪方程。本文将Zhu等[28]的拟声波各向异性介质运动学射线追踪算法推广到弹性各向异性介质中
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}{x_i}}}{{{\rm{d}}\tau }} = {V_{{\rm{P}}i}}}\\ {\frac{{{\rm{d}}{p_{{\rm{P}}i}}}}{{{\rm{d}}\tau }} = - \frac{1}{{{v_{\rm{P}}}}}\frac{{\partial {v_{\rm{P}}}}}{{\partial {x_i}}}} \end{array}} \right. $ | (1) |
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}{x_i}}}{{{\rm{d}}\tau }} = {V_{{\rm{S}}i}}}\\ {\frac{{{\rm{d}}{p_{{\rm{S}}i}}}}{{{\rm{d}}\tau }} = - \frac{1}{{{v_{\rm{S}}}}}\frac{{\partial {v_{\rm{S}}}}}{{\partial {x_i}}}} \end{array}} \right. $ | (2) |
式中:xi为直角坐标系中的坐标分量;pPi、pSi分别为qP波和qSV波慢度矢量的分量,下标P表示qP波,S表示qSV波,i=1, 3;τ为沿射线的走时;VPi、VSi分别为qP波、qSV波群速度[30];vP、vS分别为qP波、qSV波相速度,在TTI介质中,有
| $ {v_{\rm{P}}} = {v_{{\rm{P0}}}}[1 + \frac{\delta }{4}{\rm{si}}{{\rm{n}}^2}2(\theta - \xi ) + \varepsilon {\rm{si}}{{\rm{n}}^4}(\theta - \xi )] $ | (3) |
| $ {v_{\rm{S}}} = {v_{{\rm{S0}}}}[1 + \frac{\sigma }{4}{\rm{si}}{{\rm{n}}^2}2(\theta - \xi )] $ | (4) |
式中:vP0、vS0分别为P波、S波垂直速度;
利用上述方程进行射线追踪,得到qP波和qSV波中心射线的走时和路径。
1.1.2 动力学射线追踪各向异性介质的动力学射线追踪相对复杂,Hanyga[32]推导了一种基于弹性参数的各向异性介质动力学射线追踪方程,求解过程较复杂。在Zhu等[28]的研究基础上,可以推导射线中心坐标系各向异性动力学射线追踪方程
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}{Q_{{\rm{P}}M}}}}{{{\rm{d}}\tau }} = {A_{MN}}{Q_{{\rm{P}}N}} + {B_{MN}}{P_{{\rm{P}}N}}}\\ {\frac{{{\rm{d}}{P_{{\rm{P}}N}}}}{{{\rm{d}}\tau }} = - {C_{MN}}{Q_{{\rm{P}}N}} - {D_{MN}}{P_{{\rm{P}}N}}} \end{array}} \right. $ | (5) |
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{{\rm{d}}{Q_{{\rm{S}}M}}}}{{{\rm{d}}\tau }} = A_{MN}^\prime {Q_{{\rm{S}}N}} + B_{MN}^\prime {P_{{\rm{S}}N}}}\\ {\frac{{{\rm{d}}{P_{{\rm{S}}N}}}}{{{\rm{d}}\tau }} = - C_{MN}^\prime {Q_{{\rm{S}}N}} - D_{MN}^\prime {P_{{\rm{S}}N}}} \end{array}} \right. $ | (6) |
式中:PPN、PSN、QPM、QSM为各向异性动力学射线追踪参数,下标M和N分别为1和3;相关系数为
| $ \left\{ {\begin{array}{*{20}{l}} {{A_{MN}} = \frac{{{\partial ^2}\text{ln} {v_\text{P}}}}{{\partial {y_N}\partial {q_M}}}}\\ {{B_{MN}} = \frac{{\partial {{\bar V}_{\text{P}N}}}}{{\partial {q_M}}}}\\ {{C_{MN}} = \frac{{v_\text{P}^{ - 1}{\partial ^2}{v_\text{P}}}}{{\partial {y_M}\partial {y_N}}}}\\ {{D_{MN}} = \frac{{{\partial ^2}\text{ln} {v_P}}}{{\partial {y_M}\partial {q_N}}}} \end{array}} \right. $ | (7) |
| $ \left\{ {\begin{array}{*{20}{l}} {A_{MN}^\prime = \frac{{{\partial ^2}{\rm{ln}}{v_{\rm{S}}}}}{{\partial {y_N}\partial {q_M}}}}\\ {B_{MN}^\prime = \frac{{\partial {{\bar V}_{{\rm{S}}N}}}}{{\partial {q_M}}}}\\ {C_{MN}^\prime = \frac{{v_{\rm{S}}^{ - 1}{\partial ^2}{v_{\rm{S}}}}}{{\partial {y_M}\partial {y_N}}}}\\ {D_{MN}^\prime = \frac{{{\partial ^2}{\rm{ln}}{v_{\rm{S}}}}}{{\partial {y_M}\partial {q_N}}}} \end{array}} \right. $ | (8) |
式中:VPN和VSN分别为射线中心坐标系中qP波和qSV波群速度矢量的分量;yM与yN为射线中心坐标系坐标;qN和qM为射线中心坐标系慢度矢量分量, 且
经过动力学射线追踪,可以得到复值的动力学射线参数,从而计算射线的振幅和波前。
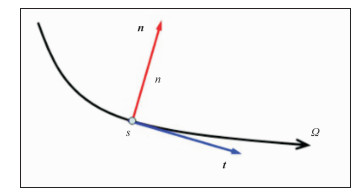
1.2 弹性波高斯束偏移成像的基本原理根据文献[33-34],得到射线中心坐标系(图 1)由原点x0出射、经过计算点x的各向异性介质高斯束位移矢量表达式
| $ \begin{array}{*{20}{l}} {{{\mathit{\boldsymbol{\hat u}}}^\nu }(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_0},\omega ) = \frac{{{\phi ^\nu }}}{{\sqrt {{v^\nu }(s)\rho (s)Q(s)} }}{\mathit{\boldsymbol{e}}^\nu } \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}\left[ {{\rm{i}}\omega \tau (s) + \frac{{{\rm{i}}\omega }}{2}\frac{{P(s)}}{{Q(s)}}{n^2}} \right]} \end{array} $ | (9) |
|
图 1 射线中心坐标系 在二维射线中心坐标系(y1,y3)下,对于任意射线Ω,n为Ω附近一点到参考点的距离,s为Ω上某点到选取的参考点的弧长,此时y1=n,y3=s;n为Ω的单位法向量,t为与Ω相切的单位切向量 |
式中:ϕν为不同波型的复值常数,上标ν表示不同波型,这里指qP波和qSV波;vν(s)为不同波型的相速度,对于qP波,vν(s)=vP(s),对于qSV波,vν(s)=vS(s);ρ(s)为介质密度;ω为角频率;τ(s)为旅行时;P(s)和Q(s)为复值的动力学射线参数;eν为x处的高斯束极化矢量,对于qP波,
假设Umν(x, x0, ω)为x点处接收到的由x0处ν型波震源引起的位移矢量,利用弹性动力学高斯束将Umν(x, x0, ω)通过一系列由x0点以不同角度出射的高斯束的叠加积分表示为
| $ \mathit{\boldsymbol{U}}_m^\nu (\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_0},\omega ) \approx {\varPsi ^\nu }\int {\frac{{{\rm{d}}{p_x}({\mathit{\boldsymbol{x}}_0})}}{{{p_z}({\mathit{\boldsymbol{x}}_0})}}} \mathit{\boldsymbol{\hat u}}_m^\nu (\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_0},\omega ) $ | (10) |
式中:px(x0)、pz(x0)分别为高斯束在x0处射线参数的水平和垂直分量;
| $ {\varPsi ^\nu } = \frac{{\rm{i}}}{{4\pi {{[{v^\nu }({\mathit{\boldsymbol{x}}_0})]}^2}}}\sqrt {\frac{{{\omega _{\rm{r}}}\omega _0^2}}{{\rho ({\mathit{\boldsymbol{x}}_0})}}} $ | (11) |
式中:vν(x0)为x0处ν型波的相速度;ρ(x0)为x0处介质密度;ωr为高斯束参考频率;ω0为高斯束初始宽度。
将震源位移波场通过弹性波动力学高斯束表示,可得高斯束正向延拓的波场公式
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{U}}_m^{{\rm{qP}}}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega ) = \frac{{\rm{i}}}{{4\pi {{[{v_{\rm{P}}}({\mathit{\boldsymbol{x}}_{\rm{s}}})]}^2}}}\sqrt {\frac{{{\omega _{\rm{r}}}\omega _0^2}}{{\rho ({\mathit{\boldsymbol{x}}_{\rm{s}}})}}} \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int {\frac{{{\rm{d}}p_x^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_{\rm{s}}})}}{{p_z^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_{\rm{s}}})}}} \mathit{\boldsymbol{\hat u}}_m^{{\rm{qP}}}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega )} \end{array} $ | (12) |
式中:vP(xs)为震源xs处qP波相速度;
根据Pao等[7]推导的不均匀各向异性介质弹性波Kirchhoff-Helmholtz积分方程,得到反向延拓的弹性波位移场
| $ \begin{array}{l} {\mathit{\boldsymbol{u}}_m}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ) = \int\limits_S {\left[ {{\mathit{\boldsymbol{t}}_i}({\mathit{\boldsymbol{x}}_{\rm{r}}},\omega )\mathit{\boldsymbol{G}}_{im}^*(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ) - } \right.} \\ \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{u}}_i}({\mathit{\boldsymbol{x}}_\text{r}},\omega )\varSigma_{im}^* {(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega )} } \right]{\rm{d}}{\mathit{\boldsymbol{x}}_{\rm{r}}} \end{array} $ | (13) |
式中:积分范围S代表自由地表面;ti(xr, ω)为接收点xr处应力;Gim(x, xr, ω)为xr处的i方向单位体力引起的x处位移的m方向分量,上标“*”表示取复值共轭;ui(xr, ω)为xs处激发、xr处接收的弹性波地震记录;Σim(x, xr, ω)为应力格林张量。Sena等[11]认为
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{t}}_i}({\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ) = {\mathit{\boldsymbol{n}}_j}{C_{ijkl}}\frac{{\partial {\mathit{\boldsymbol{u}}_l}}}{{\partial {x_k}}}}\\ {{\mathit{\boldsymbol{G}}_{im}}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ) = \sum\limits_v {g_{im}^\nu } (\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega )}\\ {\varSigma_{im} {(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega )} = {\mathit{\boldsymbol{n}}_j}{C_{ijkl}}\frac{{\partial {\mathit{\boldsymbol{G}}_{lm}}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega )}}{{\partial {x_k}}}} \end{array}} \right. $ | (14) |
式中:gimν(x, xr, ω)为ν型波的格林函数;ul为xs处激发、xr处接收的弹性波地震记录;nj为xr处沿外法线方向的单位矢量;Cijkl为刚度系数,i, j, k, l=1, 3;xk为直角坐标系中的坐标分量。
格林函数偏导数的近似解为[12]
| $ \frac{{\partial g_{lm}^\nu (\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega )}}{{\partial {\mathit{\boldsymbol{x}}_{\rm{r}}}}} \approx {\rm{i}}\omega \sum\limits_\nu {\mathit{\boldsymbol{p}}_k^\nu } ({\mathit{\boldsymbol{x}}_{\rm{r}}})g_{lm}^\nu (\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ) $ | (15) |
式中:
| $ g_{lm}^\nu (\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ) = \mathit{\boldsymbol{e}}_l^\nu ({\mathit{\boldsymbol{x}}_{\rm{r}}})\mathit{\boldsymbol{u}}_m^\nu (\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ) $ | (16) |
式中elν(xr)为xr处的极性矢量。假设到达自由地表时,在自由应力边界条件下,有
| $ {\mathit{\boldsymbol{t}}_i}({\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ) = 0 $ |
因此可将式(13)简化为
| $ (\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ) = \int\limits_S {[ - {\mathit{\boldsymbol{u}}_i}({\mathit{\boldsymbol{x}}_{\rm{r}}},\omega )\varSigma_{im}^* {(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega )} ]{\rm{d}}{\mathit{\boldsymbol{x}}_{\rm{r}}}} $ | (17) |
将式(14)~式(16)代入式(17),得到各向异性介质反向延拓的弹性波位移波场
| $ \begin{array}{l} {\mathit{\boldsymbol{u}}_m}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ) = \mathit{\boldsymbol{u}}_m^{\rm{P}}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ) + \mathit{\boldsymbol{u}}_m^{\rm{S}}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega )\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = - {\rm{i}}\omega \sum\limits_\nu {\int\limits_S {\mathit{\boldsymbol{u}}_m^{*\nu }} } (\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega )[{\mathit{\boldsymbol{u}}_x}({\mathit{\boldsymbol{x}}_{\rm{r}}},\omega )W_1^\nu ({\mathit{\boldsymbol{x}}_{\rm{r}}}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{u}}_z}({\mathit{\boldsymbol{x}}_{\rm{r}}},\omega )W_2^\nu ({\mathit{\boldsymbol{x}}_{\rm{r}}})]{\rm{d}}{\mathit{\boldsymbol{x}}_{\rm{r}}} \end{array} $ | (18) |
式中:umP(x, xr, ω)、umS(x, xr, ω)分别为qP波与qSV波位移场;ux(xr, ω)、uz(xr, ω)分别为xr处弹性波地震记录的x、z分量;系数W1ν(xr)、W2ν(xr)分别为
| $ \begin{array}{*{20}{l}} {W_1^\nu ({\mathit{\boldsymbol{x}}_{\rm{r}}}) = {C_{1113}}p_1^\nu ({\mathit{\boldsymbol{x}}_{\rm{r}}})\mathit{\boldsymbol{e}}_1^\nu ({\mathit{\boldsymbol{x}}_r}) + {C_{1313}}p_1^\nu ({\mathit{\boldsymbol{x}}_{\rm{r}}})\mathit{\boldsymbol{e}}_3^\nu ({\mathit{\boldsymbol{x}}_{\rm{r}}}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_{1313}}p_3^\nu ({\mathit{\boldsymbol{x}}_{\rm{r}}})\mathit{\boldsymbol{e}}_1^\nu ({\mathit{\boldsymbol{x}}_{\rm{r}}}) + {C_{3313}}p_3^\nu ({\mathit{\boldsymbol{x}}_{\rm{r}}})\mathit{\boldsymbol{e}}_3^\nu ({\mathit{\boldsymbol{x}}_{\rm{r}}})} \end{array} $ | (19) |
| $ \begin{array}{*{20}{l}} {W_2^\nu ({\mathit{\boldsymbol{x}}_{\rm{r}}}) = {C_{1113}}p_1^\nu ({\mathit{\boldsymbol{x}}_{\rm{r}}})\mathit{\boldsymbol{e}}_1^\nu ({\mathit{\boldsymbol{x}}_r}) + {C_{3313}}p_1^\nu ({\mathit{\boldsymbol{x}}_{\rm{r}}})\mathit{\boldsymbol{e}}_3^\nu ({\mathit{\boldsymbol{x}}_{\rm{r}}}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_{3313}}p_3^\nu ({\mathit{\boldsymbol{x}}_{\rm{r}}})\mathit{\boldsymbol{e}}_1^\nu ({\mathit{\boldsymbol{x}}_{\rm{r}}}) + {C_{3333}}p_3^\nu ({\mathit{\boldsymbol{x}}_{\rm{r}}})\mathit{\boldsymbol{e}}_3^\nu ({\mathit{\boldsymbol{x}}_{\rm{r}}})} \end{array} $ | (20) |
式中p1ν(xr)、p3ν(xr)分别为xr处ν型波在x、z方向的慢度。
由于高斯束的初始波前为平面,根据这一特性将多分量地震记录分解为不同波型、不同初始方向的局部平面波,利用相应的高斯束位移矢量波场进行波场延拓,经过相移校正和高斯窗分解[15],得到xL处出射的不同波型的反向延拓位移公式
| $ \begin{array}{l} \mathit{\boldsymbol{u}}_m^\nu (\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ) = - \frac{{\Delta L\omega }}{{4\pi }}\sum\limits_{{N_L}} {\int_S {\frac{{{\rm{d}}p_x^\nu }}{{p_z^\nu }}} } \sqrt {\rho ({\mathit{\boldsymbol{x}}_L})} \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{\hat u}}_m^{*\nu }(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_L},\omega )[W_x^\nu ({\mathit{\boldsymbol{x}}_L})D_x^\nu ({\mathit{\boldsymbol{x}}_L},p_x^\nu ,\omega ) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} W_z^\nu ({\mathit{\boldsymbol{x}}_L})D_z^\nu ({\mathit{\boldsymbol{x}}_L},p_x^\nu ,\omega )] \end{array} $ | (21) |
式中:ΔL为水平间隔;NL为高斯窗的数目;pxν、pzν分别为不同波型在水平和垂直方向的慢度;Dnν(xL, pxν, ω)为不同方向的多分量地震记录的加窗局部倾斜叠加, 即
| $ \begin{array}{l} D_n^{\nu }({\mathit{\boldsymbol{x}}_L},p_x^\nu ,\omega ) = \sqrt {\frac{{|\omega |}}{{2\pi }}} \int_S {{u_n}} ({\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ) \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}\left[ {{\rm{i}}\omega p_x^\nu ({\mathit{\boldsymbol{x}}_L})({\mathit{\boldsymbol{x}}_{\rm{r}}} - {\mathit{\boldsymbol{x}}_L}) - \left| {\frac{\omega }{{{\omega _{\rm{r}}}}}\frac{{{{({\mathit{\boldsymbol{x}}_{\rm{r}}} - {\mathit{\boldsymbol{x}}_L})}^2}}}{{2\omega _0^2}}} \right|} \right]{\rm{d}}{\mathit{\boldsymbol{x}}_{\rm{r}}} \end{array} $ | (22) |
权系数Wxν(xL)、Wzν(xL)分别为
| $ \begin{array}{l} W_x^\nu ({\mathit{\boldsymbol{x}}_L}) = {C_{1113}}p_x^\nu ({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_x^\nu ({\mathit{\boldsymbol{x}}_L}) + {C_{1313}}P_x^\nu ({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_z^\nu ({\mathit{\boldsymbol{x}}_L}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_{1313}}p_z^\nu ({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_1^\nu ({\mathit{\boldsymbol{x}}_L}) + {C_{3313}}p_z^\nu ({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_z^\nu ({\mathit{\boldsymbol{x}}_L}) \end{array} $ | (23) |
| $ \begin{array}{l} W_z^\nu ({\mathit{\boldsymbol{x}}_L}) = {C_{1113}}p_x^\nu ({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_x^\nu ({\mathit{\boldsymbol{x}}_L}) + {C_{3313}}P_x^\nu ({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_z^\nu ({\mathit{\boldsymbol{x}}_L}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_{3313}}p_z^\nu ({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_x^\nu ({\mathit{\boldsymbol{x}}_L}) + {C_{3333}}p_z^\nu ({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_z^\nu ({\mathit{\boldsymbol{x}}_L}) \end{array} $ | (24) |
根据Clearbout成像法则[35],结合式(21),得到qP—qP波及qP—qSV波互相关成像公式
| $ \begin{array}{l} \begin{array}{*{20}{c}} {{I_{{\rm{qP - qP}}}}(\mathit{\boldsymbol{x}}) = \int {\mathit{\boldsymbol{U}}_z^{{\rm{qP}}*}} (\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega )\mathit{\boldsymbol{u}}_z^{{\rm{qP}}}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ){\rm{d}}\omega }\\ { = \frac{{\Delta L\sqrt {{\omega _{\rm{r}}}\omega _0^2} }}{{16{\pi ^2}}}\sum\limits_{{N_L}} {\int {\frac{{{\rm{i}}\omega }}{{v_{\rm{P}}^2({\mathit{\boldsymbol{x}}_{\rm{s}}})}}} } \sqrt {\frac{{\rho ({\mathit{\boldsymbol{x}}_L})}}{{\rho ({\mathit{\boldsymbol{x}}_{\rm{s}}})}}} {\rm{d}}\omega \times } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int {\int {\frac{{{\rm{d}}p_x^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_{\rm{s}}}){\rm{d}}p_x^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L})}}{{p_z^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_{\rm{s}}})p_z^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L})}}} } \mathit{\boldsymbol{\hat u}}_z^{{\rm{*qP}}}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega ) \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {\hat u_x^{{\rm{*qP}}}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_L},\omega )[W_x^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L})D_x^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L},p_x^{{\rm{qP}}},\omega ) + }\\ {W_z^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L})D_z^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L},p_x^{{\rm{qP}}},\omega )]} \end{array} \end{array} $ | (25) |
| $ \begin{array}{l} \begin{array}{*{20}{c}} {{I_{{\rm{qP - qSV}}}}(\mathit{\boldsymbol{x}}) = \int {\mathit{\boldsymbol{U}}_z^{{\rm{qP}}*}} (\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega )\mathit{\boldsymbol{u}}_z^{{\rm{qSV}}}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{r}}},\omega ){\rm{d}}\omega }\\ { = \frac{{\Delta L\sqrt {{\omega _{\rm{r}}}\omega _0^2} }}{{16{\pi ^2}}}\sum\limits_{{N_L}} {\int {\frac{{{\rm{i}}\omega }}{{v_{\rm{P}}^2({\mathit{\boldsymbol{x}}_{\rm{s}}})}}} } \sqrt {\frac{{\rho ({\mathit{\boldsymbol{x}}_L})}}{{\rho ({\mathit{\boldsymbol{x}}_{\rm{s}}})}}} {\rm{d}}\omega \times } \end{array}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int {\int {\frac{{{\rm{d}}p_x^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_{\rm{s}}}){\rm{d}}p_x^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L})}}{{p_z^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_{\rm{s}}})p_z^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L})}}} } \mathit{\boldsymbol{\hat u}}_z^{{\rm{*qP}}}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},\omega ) \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \begin{array}{*{20}{l}} {\hat u_x^{{\rm{*qSV}}}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_L},\omega )[W_x^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L})D_x^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L},p_x^{{\rm{qSV}}},\omega ) + }\\ {W_z^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L})D_z^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L},p_x^{{\rm{qSV}}},\omega )]} \end{array} \end{array} $ | (26) |
式中:IqP—qP(x)、IqP—qSV(x)分别为qP—qP、qP—qSV波单炮成像值;权系数WxqP(xL)、WzqP(xL)、WxqSV(xL)、WzqSV(xL)分别为
| $ \left\{ \begin{array}{l} W_x^{{\rm{qP}}}({\boldsymbol{x}_L})\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {C_{1113}}p_x^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_x^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L}) + {C_{1313}}p_x^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_z^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_{1313}}p_z^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_x^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L}) + {C_{3313}}P_z^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_z^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L})\\ W_z^{{\rm{qP}}}({\boldsymbol{x}_L})\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {C_{1133}}p_x^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_x^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L}) + {C_{3313}}p_x^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_z^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_{3313}}p_z^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_x^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L}) + {C_{3333}}P_z^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_z^{{\rm{qP}}}({\mathit{\boldsymbol{x}}_L})\\ W_x^{{\rm{qSV}}}({\boldsymbol{x}_L})\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {C_{1113}}p_x^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_x^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L}) + {C_{1313}}p_x^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_z^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_{1313}}p_z^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_x^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L}) + {C_{3313}}P_z^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_z^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L})\\ W_z^{{\rm{qSV}}}({\boldsymbol{x}_L})\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {C_{1133}}p_x^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_x^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L}) + {C_{3313}}p_x^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_z^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {C_{3313}}p_z^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_x^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L}) + {C_{3333}}P_z^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L})\mathit{\boldsymbol{e}}_z^{{\rm{qSV}}}({\mathit{\boldsymbol{x}}_L}) \end{array} \right. $ | (27) |
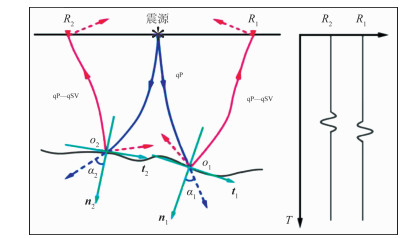
转换波成像时会出现极性反转(图 2),该现象由不同的转换波偏振方向引起。为此,本文通过判断qP波入射角α的正、负,引入符号函数校正成像结果[10]。
|
图 2 各向异性介质qP—qSV波在反射界面处的偏振 入射qP波具有不同符号的入射角,导致R1点的qP—qSV波位移分量为正水平方向,R2点的qP—qSV波位移分量为负水平方向,因而使R1、R2点记录到的x分量地震记录极性相反 |
为了证明文中方法的效果,通过TTI介质洼陷模型和TTI介质多层构造模型进行测试。
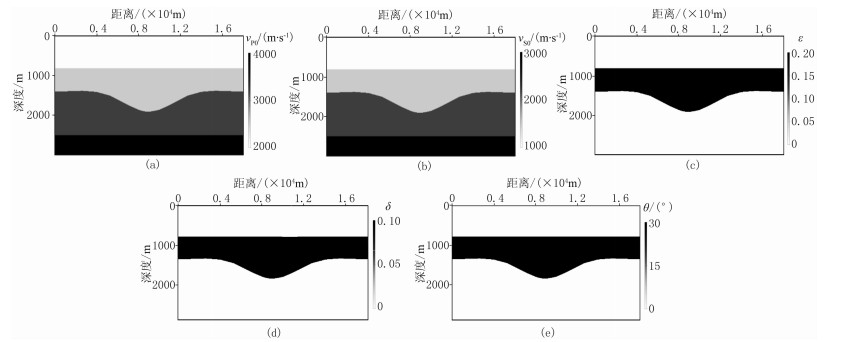
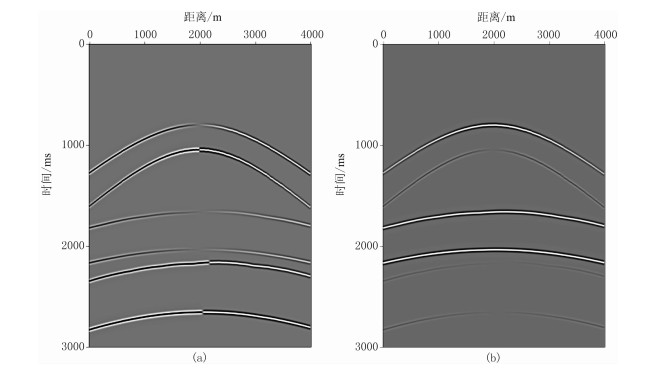
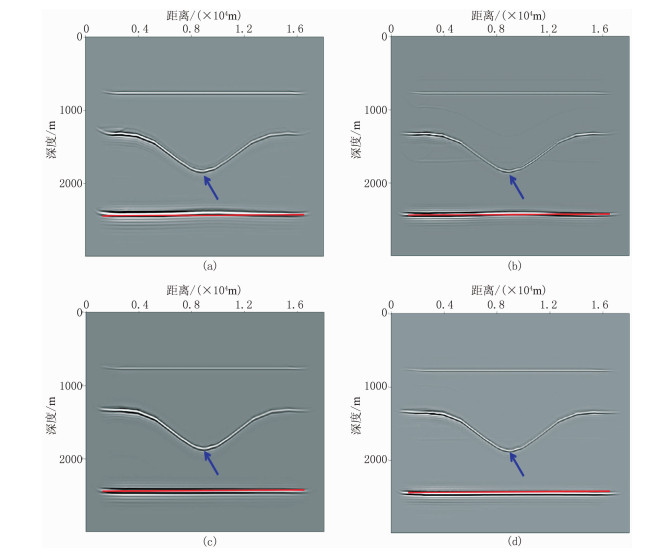
2.1 TTI介质洼陷模型图 3为TTI介质洼陷模型速度场及各向异性参数场,图 4为TTI介质洼陷模型地震记录。由图可见,x分量中qSV波能量较强,但混有qP波(图 4a),z分量中qP波能量较强,但混有qSV波(图 4b),因此不同波型间的相互影响导致串扰现象。图 5为弹性波高斯束偏移成像结果。由图可见:由于未考虑各向异性因素的影响,各向同性介质弹性波高斯束偏移成像结果的构造位置不准确,并且下部构造的能量不聚焦(图 5a、图 5b),出现“上翘”假象(箭头位置);TTI介质弹性波高斯束偏移成像结果的信噪比高、同相轴连续性好、构造位置准确(图 5c、图 5d)。TTI介质洼陷模型的试算结果证明了本文方法的有效性。
|
图 3 TTI介质洼陷模型速度场及各向异性参数场
(a)vP0;(b)vS0;(c)ε; (d)δ;(e)θ 模型尺寸为18010m×3000m,震源采用主频为25Hz的雷克子波,总炮数为281,炮间距为50m,检波器位于地表,每炮201道,道间距为20m。总记录时间为3s,采样间隔为1ms |
|
图 4 TTI介质洼陷模型地震记录 (a)x分量;(b)z分量 |
|
图 5 弹性波高斯束偏移成像结果 (a)各向同性介质PP波;(b)各向同性介质PS波;(c)TTI介质qP—qP波;(d)TTI介质qP—qSV波 |
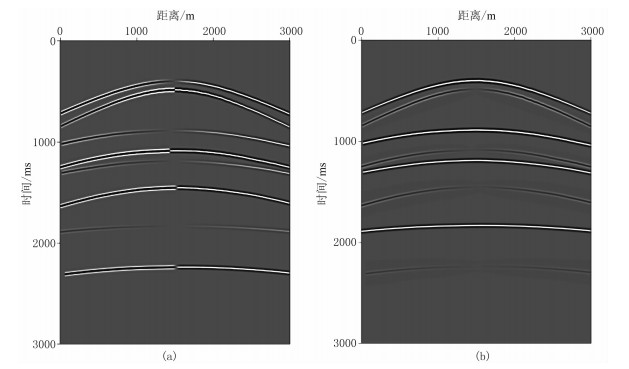
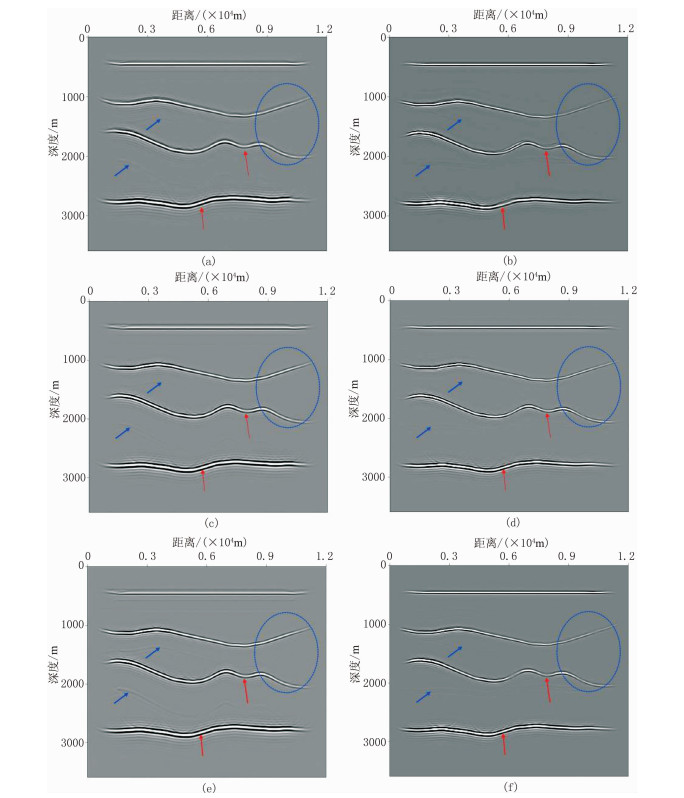
图 6为TTI介质多层构造模型速度场及各向异性参数场,图 7为TTI介质多层构造模型地震记录。由图 7可见,x分量中qSV波能量强于qP波(图 7a),z分量中qP波能量强于qSV波(图 7b),这将会对多分量弹性波成像产生较大影响。图 8为高斯束偏移成像结果。由图可见:①由于忽略各向异性影响,各向同性介质弹性波高斯束偏移成像结果的构造位置不准确,出现“上翘”假象,且下部同相轴受倾斜角度的影响,连续性不好,出现“上移”假象(红色箭头处),能量聚焦性不好(蓝圈处),整体成像品质较低(图 8a、图 8b)。②TTI介质弹性波高斯束偏移成像结果的能量聚焦性好、信噪比高、同相轴连续性好、构造位置准确(图 8c、图 8d)。③TTI介质qP—qP标量波(图 8c)成像结果的同相轴能量强于qP—qSV标量波(图 8d),由于后者的反射角大于前者,因此后者的成像孔径更大,且在成像中综合考虑了纵、横波波场信息,其成像分辨率高于前者,但存在串扰干扰(蓝箭头处);由于本文方法在成像中使用权函数,有效压制了串扰(蓝箭头处),整体成像剖面质量高(图 8c、图 8d)。TTI介质多层构造模型试算结果也证明了本文方法的有效性。
|
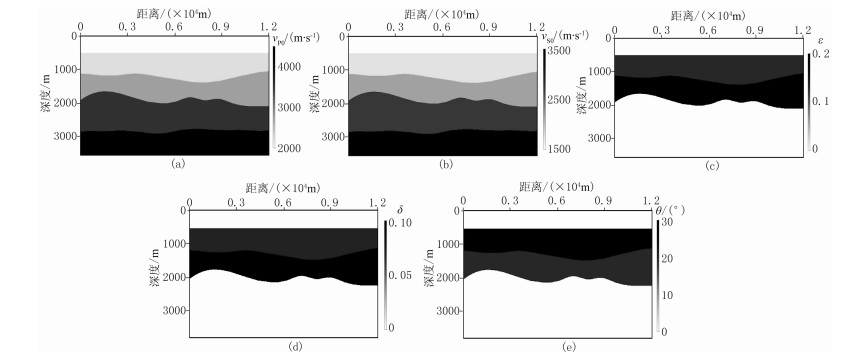
图 6 TTI介质多层构造模型速度场及各向异性参数场
(a)vP0;(b)vS0;(c)ε; (d)δ;(e)θ 模型尺寸为12010m×3600m,震源采用主频为25Hz的雷克子波,总炮数为181,炮间距为50m,检波器位于地表,每炮301道,道间距为10m。总记录时间为3s,采样间隔为1ms |
|
图 7 TTI介质多层构造模型地震记录 (a)x分量;(b)z分量 |
|
图 8 高斯束偏移成像结果 (a)各向同性介质弹性PP波;(b)各向同性介质弹性PS波;(c)TTI介质qP—qP波;(d)TTI介质qP—qSV波;(e)TTI介质qP—qP标量波;(f)TTI介质qP—qSV标量波 |
总体来说,利用各向异性介质弹性波高斯束偏移方法,通过对qP—qP波和qP—qSV波分别成像,从不同角度刻画地下构造,提高了整体成像质量,对复杂各向异性介质地质构造的成像效果优于各向同性算法。
3 结论本文通过修改各向异性介质射线追踪方程,给出了一种各向异性介质射线追踪算法,并将其应用于弹性波高斯束偏移,提出了一种适用于各向异性介质的弹性波高斯束偏移方法。通过在成像中引入符号函数,可以较好地解决转换波成像中的极性校正问题。通过修改权系数,可以有效压制成像中不同波型引起的串扰问题。
TTI介质洼陷模型和TTI介质多层构造模型试算结果表明,与各向同性介质弹性波高斯束偏移方法相比,各向异性介质弹性波高斯束偏移成像结果的信噪比较高、同相轴连续性较好、构造位置更准确。另外,使用多分量地震记录,利用纵、横波波场信息成像,可以有效提高成像分辨率,进而提供高质量的成像剖面。与传统的基于标量波场的成像方法相比,本文方法的适应性更强。
| [1] |
李振春. 地震偏移成像技术研究现状与发展趋势[J]. 石油地球物理勘探, 2014, 49(1): 1-21. LI Zhenchun. Research status and development trends for seismic migration technology[J]. Oil Geophysical Prospecting, 2014, 49(1): 1-21. |
| [2] |
吴国忱.各向异性介质地震波传播与成像[M].山东东营:中国石油大学出版社, 2006. WU Guochen.Seismic Wave Propagation and Imaging in Anisotropic Media[M]. China University of Petroleum Press, Dongying, Shandong, 2006. |
| [3] |
段新意, 李振春, 黄建平, 等. 各向异性介质共炮域高斯束叠前深度偏移[J]. 石油物探, 2014, 53(5): 579-586. DUAN Xinyi, LI Zhenchun, HUANG Jianping, et al. A prestack Gaussian beam migration in common-shot domain for anisotropic media[J]. Geophysical Prospecting for Petroleum, 2014, 53(5): 579-586. DOI:10.3969/j.issn.1000-1441.2014.05.011 |
| [4] |
Sun R, McMechan G A. Prestack reversetime migra-tion for elastic waves with application to synthetic offset vertical seismic profiles[J]. Proceedings of the IEEE, 1986, 74(3): 457-465. |
| [5] |
Jia Y, Paul S. Isotropic angle-domain elastic reverse time migration[J]. Geophysics, 2008, 73(6): S229-S239. DOI:10.1190/1.2981241 |
| [6] |
Kuo J T, Dai T F. Kirchhoff elastic wave migration for the case of noncoincident source and receiver[J]. Geophysics, 1984, 49(8): 1223-1238. DOI:10.1190/1.1441751 |
| [7] |
Pao Y H, Varatharajulu V. Huygen's principle, radiation conditions, and integral formulas for the scatte-ring of elastic waves[J]. Journal of the Acoustical Society of America, 1976, 59(6): 1361-1371. |
| [8] |
Sumner B, Bleistein N.Prestack elastic migration and parameter estimation[C]. SEG Technical Program Expanded Abstracts, 1988, 7: 963-965.
|
| [9] |
Zhe J P, Greenhalgh S A. Prestack multicomponent migration[J]. Geophysics, 1997, 62(2): 598-613. |
| [10] |
Xue A, McMechan G A.Prestack elastic Kirchhoff migration for multicomponent seismic data in variable velocity Media[C]. SEG Technical Program Expanded Abstracts, 2000, 19, doi: 10.1190/1.1816092.
|
| [11] |
Sena A G, Toksoz M N. Kirchhoff migration and velocity analysis for converted and nonconverted waves in anisotropic media[J]. Geophysics, 1993, 58(2): 265-276. |
| [12] |
Hokstad K. Multicomponent Kirchhoff migration[J]. Geophysics, 2000, 65(3): 861-873. |
| [13] |
Hill N R. Prestack Gaussian beam depth migration[J]. Geophysics, 2001, 66(4): 1240-1250. |
| [14] |
岳玉波, 李振春, 张平, 等. 复杂地表条件下高斯波束叠前深度偏移[J]. 应用地球物理, 2010, 7(2): 143-148. YUE Yubo, LI Zhenchun, ZHANG Ping, et al. Prestack Gaussian beam depth migration under complex surface conditions[J]. Applied Geophysics, 2010, 7(2): 143-148. |
| [15] |
岳玉波.复杂介质高斯束偏移成像方法研究[D].山东青岛: 中国石油大学(华东), 2011. YUE Yubo.Study on Gaussian Beam Migration Methods in Complex Medium[D]. China University of Petroleum(East China), Qingdao, Shandong, 2011. |
| [16] |
Katchalov A P, Popov M M. Application of the Gau-ssian beam method to elasticity theory[J]. Geophy-sical Journal of the Royal Astronomical Society, 1985, 81(1): 205-214. DOI:10.1111/j.1365-246X.1985.tb01359.x |
| [17] |
Alkhalifah T. Gaussian beam depth migration for anisotropic media[J]. Geophysics, 1995, 60(5): 1474-1484. DOI:10.1190/1.1443881 |
| [18] |
Protasov M I. 2-D Gaussian beam imaging of multicomponent seismic data in anisotropic media[J]. Geophysical Journal International, 2015, 203(3): 2021-2031. DOI:10.1093/gji/ggv408 |
| [19] |
周滨, 李振春, 刘强, 等. 各向异性介质弹性多波高斯束正演模拟[J]. 地球物理学进展, 2018, 33(1): 341-346. ZHOU Bin, LI Zhenchun, LIU Qiang, et al. Anisotropic Gaussian beam forward modeling for elastic multiple wave[J]. Progress in Geophysics, 2018, 33(1): 341-346. |
| [20] |
岳玉波, 钱忠平, 张旭东, 等. 声波介质一次散射波场高斯束Born正演[J]. 地球物理学报, 2019, 62(2): 648-656. YUE Yubo, QIAN Zhongping, ZHANG Xudong, et al. Gaussian beam based Born modeling method for single-scattering waves in acoustic medium[J]. Chinese Journal of Geophysics, 2019, 62(2): 648-656. |
| [21] |
岳玉波, 孙鹏飞, 王德营, 等. 弹性各向同性介质一次散射波场高斯束Born正演[J]. 地球物理学报, 2019, 62(2): 657-666. YUE Yubo, SUN Pengfei, WANG Deying, et al. Gaussian beam Born modeling method for single-scattering waves in elastic isotropic medium[J]. Chinese Journal of Geophysics, 2019, 62(2): 657-666. |
| [22] |
李振春, 刘强, 韩文功, 等. VTI介质角度域转换波高斯束偏移成像方法研究[J]. 地球物理学报, 2018, 61(4): 1471-1481. LI Zhenchun, LIU Qiang, HAN Wengong, et al. Angle domain converted wave Gaussian beam migration in VTI media[J]. Chinese Journal of Geophysics, 2018, 61(4): 1471-1481. |
| [23] |
肖建恩, 李振春, 张凯, 等. TI介质角度域高斯束逆时偏移方法[J]. 石油地球物理勘探, 2019, 54(5): 1067-1074. XIAO Jian'en, LI Zhenchun, ZHANG Kai, et al. Angle-domain reverse time migration with Gaussian beams for TI media[J]. Oil Geophysical Prospecting, 2019, 54(5): 1067-1074. |
| [24] |
张凯, 段新意, 李振春, 等. 角度域各向异性高斯束逆时偏移[J]. 石油地球物理勘探, 2015, 50(5): 912-918. ZHANG Kai, DUAN Xinyi, LI Zhenchun, et al. Angle domain reverse time migration with Gaussian beams in anisotropic media[J]. Oil Geophysical Prospecting, 2015, 50(5): 912-918. |
| [25] |
刘强, 张敏, 李振春, 等. 各向异性介质共炮域高斯束偏移[J]. 石油地球物理勘探, 2016, 51(5): 930-937. LIU Qiang, ZHANG Min, LI Zhenchun, et al. Common-shot domain Gaussian beam migration in anisotropic media[J]. Oil Geophysical Prospecting, 2016, 51(5): 930-937. |
| [26] |
张敏, 李振春, 刘强, 等. TI介质射线追踪及其高斯束成像应用[J]. 地球物理学进展, 2017, 32(4): 1721-1727. ZHANG Min, LI Zhenchun, LIU Qiang, et al. Ray tracing in TI media and its application of Gaussian beam migration[J]. Progress in Geophysics, 2017, 32(4): 1721-1727. |
| [27] |
Cerveny V.Seismic Ray Theory[M]. Cambridge University Press, 2001.
|
| [28] |
Zhu T, Gray S H, Wang D. Prestack Gaussian-beam depth migration in anisotropic media[J]. Geophysics, 2007, 72(3): S133-S138. |
| [29] |
Cerveny V. Seismic rays and ray intensities in inhomogeneous anisotropic media[J]. Geophysical Journal Royal Astronomical Society, 1972, 29(1): 1-13. DOI:10.1111/j.1365-246X.1972.tb06147.x |
| [30] |
Tsvankin I.Seismic Signatures and Analysis of Re-flection Data in Anisotropic Media[M]. Elsevier Science, 2005, 1-416.
|
| [31] |
Thomsen L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [32] |
Hanyga A. Gaussian beams in anisotropic elastic media[J]. Geophysical Journal of the Royal Astronomical Society, 1986, 85(3): 473-504. DOI:10.1111/j.1365-246X.1986.tb04528.x |
| [33] |
Babich V M, Kirpichnikova N J.Boundary Layer Me-thod in Diffration Problems[M]. Leningard University Press, Peterburg, 1974.
|
| [34] |
Cerveny V, Poppov M M, Psencik I. Computation of wave fields in inhomogeneous media Gaussian beam approach[J]. Geophysical Journal Royal Astronomical Society, 1982, 70(1): 109-128. DOI:10.1111/j.1365-246X.1982.tb06394.x |
| [35] |
Claerbout J F. Toward a unified theory of reflector mapping[J]. Geophysics, 1971, 36(3): 467-481. |



 杜向东, 北京市朝阳区太阳宫南街6号院中海油大厦, 100027。Email:
杜向东, 北京市朝阳区太阳宫南街6号院中海油大厦, 100027。Email: