② 中国石化弹性波理论与探测技术重点实验室, 北京 10008;
③ 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580;
④ 中国石化石油勘探开发研究院, 北京 100083;
⑤ 中国石油北京油气调控中心, 北京 100007
② SINOPEC Key Laboratory of Theory and Survey Technology for Seismic Elastic Waves, Beijing 100083, China;
③ School of Geosciences, China University of Petroleum(East China), Qingdao, Shandong 266580, China;
④ SINOPEC Research Institute of Petroleum Exploration & Production, Beijing 100083, China;
⑤ PetroChina Beijing Oil & Gas Pipeline Control Center, Beijing 100007, China
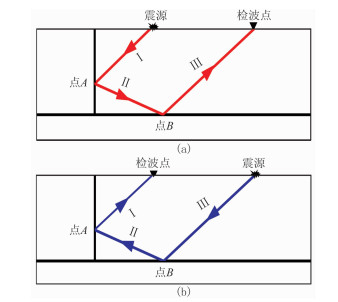
高陡盐丘和高陡断层等高陡构造给高分辨率地震成像带来了巨大挑战[1]。在常规地震成像方法中,棱柱波通常被当做噪声而压制[2],实际上棱柱波往往包含了很多从一次波中无法获取的高陡构造信息。因此,棱柱波可改善高陡构造的照明和成像效果[3-7]。Broto等[8]通过有限差分正演模拟描述了棱柱波的运动学特征,并提出了识别棱柱波的准则。棱柱波包含两个反射点和三条反射路径,根据传播路径将棱柱波分为FI和IF两类(图 1)。Marmalyevskyy等[9]提出了一种克希霍夫棱柱波成像方法描述高陡的盐丘侧面。
|
图 1 FI(a)、IF(b)型棱柱波 |
逆时偏移(RTM)[10-13]是20世纪80年代提出的高品质成像工具。Li等[14]、Dai[15]推出了棱柱波RTM方法,可以对高陡的盐丘侧面成像。黄建平等[16]将Poynting成像条件和平面波解构算子引入棱柱波RTM;刘金朋等[17]分析了棱柱波RTM效果;Qu等[7]利用棱柱波波形反演提高高陡构造速度反演精度。
上述棱柱波成像方法都是基于完全弹性假设,但实际地下介质存在严重的黏弹性,会发生地震波能量衰减[18-20],导致地下反射界面的弱振幅成像和错位。这种衰减现象对棱柱波的影响更严重,因为棱柱波的传播路径更长,在棱柱波成像时如果忽略地震波衰减,则会引起更严重的幅度损失和相位失真。为了补偿介质黏弹性引起的地震波衰减,可以考虑两种主要棱柱波成像方法:①反Q滤波方法,有效且计算效率高[20-25],但对复杂地质构造的成像精度不高。②Q补偿偏移方法,又分为基于射线理论的Q偏移[26-27]、基于单程波动方程的Q偏移[28-30]、黏声RTM(Q-RTM)[31-35]和黏声最小二乘RTM(Q-LSRTM)[36-38]。
文中使用RTM方法分别沿着传播路径FI、IF补偿Q衰减。为了提高高陡构造的成像精度,提出了一种面向高陡构造的黏声棱柱波RTM,并使用两个高陡模型验证所提方法的效果。
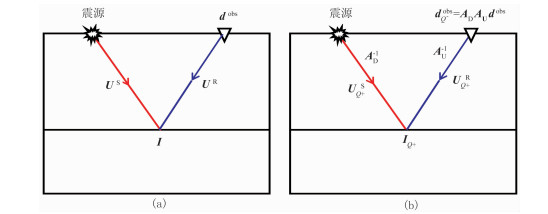
1 方法原理 1.1 黏声拟微分方程和离散形式在黏声介质成像过程中,需要沿着波场的正、反向传播路径补偿Q衰减[33](图 2b),即
| $ {(\mathit{\boldsymbol{A}}_{\rm{D}}^{ - 1}{\mathit{\boldsymbol{L}}_{{Q^ + }}})\mathit{\boldsymbol{U}}_{{Q^ + }}^{\rm{S}}(\mathit{\boldsymbol{x}},t) = \mathit{\boldsymbol{F}}} $ | (1) |
| $ {(\mathit{\boldsymbol{A}}_{\rm{U}}^{ - 1}{\mathit{\boldsymbol{L}}_{{Q^ + }}})\mathit{\boldsymbol{U}}_{{Q^ + }}^{\rm{R}}(\mathit{\boldsymbol{x}},T - t) = \mathit{\boldsymbol{d}}_{{Q^ - }}^{{\rm{obs}}}} $ | (2) |
|
图 2 声波(a)、黏声(b)RTM示意图 dobs为无衰减影响的观测数据,US和UR分别为声波正向和反向传播波场,AD和AU分别为下行波和上行波衰减算子,I和IQ+分别为声波逆时偏移和黏声逆时偏移成像结果 |
式中:AD-1和AU-1分别为下行波和上行波黏声补偿算子;LQ+为黏声补偿正演模拟算子;UQ+S(x, t)和UQ+R(x, t)分别为黏声补偿正向和反向传播波场,其中x为空间坐标,t为时间;F为源矩阵;T为总计算时间;dQ-obs为受衰减影响的观测数据。
将Bai等[39]提出的无记忆变量的黏声拟微分方程引入本文的黏声棱柱波RTM中
| $ \left( {\frac{{{\partial ^2}}}{{\partial {t^2}}} + \frac{{\tau v}}{2}\frac{\partial }{{\partial t}}\sqrt { - {\nabla ^2}} - {v^2}{\nabla ^2}} \right)p = 0 $ | (3) |
式中:p为压力;v为速度,即
| $ v = {v_0}|\frac{\omega }{{{\omega _0}}}{|^\gamma } $ | (4) |
式中:ω为角频率;v0为参考速度;ω0为参考角频率,文中取ω0=10Hz;而
| $ \gamma = \frac{1}{\pi }{\rm{ta}}{{\rm{n}}^{ - 1}}\left( {\frac{1}{Q}} \right) \approx \frac{1}{{\pi Q}} $ | (5) |
式中Q为品质因数。式(3)中
| $ \tau = \frac{{{\tau _\varepsilon }}}{{{\tau _\sigma }}} - 1 $ | (6) |
式中τε和τσ分别为应变松弛时间和应力松弛时间,即
| $ {{\tau _\sigma } = \frac{{\sqrt {{Q^2} + 1} - 1}}{{\omega Q}}} $ | (7) |
| $ {{\tau _\varepsilon } = \frac{{\sqrt {{Q^2} + 1} + 1}}{{\omega Q}}} $ | (8) |
利用有限差分方法求解式(3),并在波数域中处理分数拉普拉斯算子项(衰减项)。采用以下时间二阶、空间2M阶有限差分格式
| $ \frac{{{\partial ^2}p}}{{\partial {t^2}}}{|_{t = n\Delta t}} \approx \frac{1}{{{{(\Delta t)}^2}}}({p^{n + 1}} + {p^{n - 1}} - 2{p^n}) $ | (9) |
| $ {\frac{\partial }{{\partial t}}\sqrt { - {\nabla ^2}} p{|_{t = n\Delta t}} \approx \frac{1}{{\Delta t}}{{\rm{F}}^{ - 1}}[|k|{\rm{F}}({p^n} - {p^{n - 1}})]} $ | (10) |
| $ {{{\left. {\frac{{{\partial ^2}p}}{{\partial {x^2}}}} \right|}_{x = i\Delta x}} \approx \frac{1}{{{{(\Delta x)}^2}}}[{c_0}{p_i} + \sum\limits_{m = 1}^M {{c_m}} ({p_{i + m}} + {p_{i - m}})]} $ | (11) |
| $ {\left. {\frac{{{\partial ^2}p}}{{\partial {z^2}}}} \right|_{z = j\Delta z}} \approx \frac{1}{{{{(\Delta z)}^2}}}[{c_0}{p_j} + \sum\limits_{m = 1}^M {{c_m}} ({p_{j + m}} + {p_{j - m}})] $ | (12) |
式中:Δt为时间步长;Δx和Δz分别为水平和垂直方向的空间网格步长;p的上标和下标分别为时间和空间坐标,即i、j为空间坐标计数单位,n为时间计数单位;k为波数;F和F-1分别为傅里叶正、逆变换;c0, c1, …, cM为有限差分系数。
1.2 黏声波场延拓算子在实现衰减补偿时,只需将式(3)中衰减项的符号从正变为负即可。在衰减介质的Q补偿过程中,高频噪声随着时间呈指数增加,导致数值不稳定[19, 34, 36, 40-41]。为此,引入正则化项
| $ \left( {\frac{{{\partial ^2}}}{{\partial {t^2}}} - \frac{{\tau v}}{2}\frac{\partial }{{\partial t}}\sqrt { - {\nabla ^2}} - {v^2}{\nabla ^2} + \sigma \frac{{\tau {v^2}}}{2}\frac{\partial }{{\partial t}}{\nabla ^2}} \right){p^{{\rm{S + }}}} = \mathit{\boldsymbol{F}} $ | (13) |
式中pS+为黏声震源波场。基于伴随状态理论,由
| $ \begin{array}{*{20}{c}} {\left[ {\frac{{{\partial ^2}}}{{\partial {{(T - t)}^2}}} - \frac{{\tau v}}{2}\frac{\partial }{{\partial (T - t)}}\sqrt { - {\nabla ^2}} - {v^2}{\nabla ^2} + } \right.}\\ {\left. {\sigma \frac{{\tau {v^2}}}{2}\frac{\partial }{{\partial (T - t)}}{\nabla ^2}} \right]{p^{{\rm{R + }}}} = \mathit{\boldsymbol{d}}_{{Q^ - }}^{{\rm{obs}}}} \end{array} $ | (14) |
计算黏声检波点波场pR+。
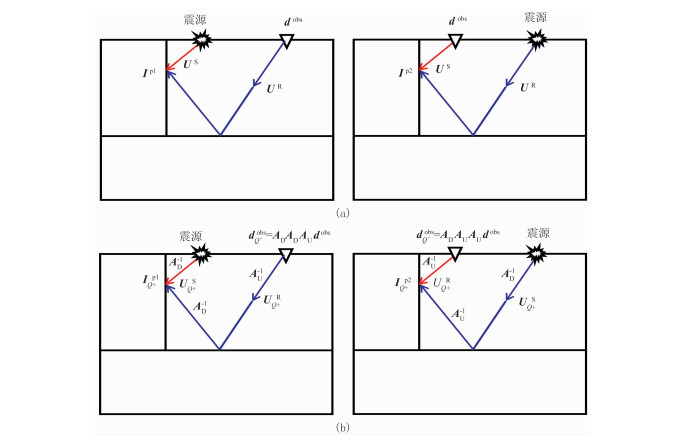
1.3 黏声棱柱波RTM基本原理当输入黏声数据进行棱柱波成像时,沿着3个反射路径均要进行黏声补偿(图 3)。
|
图 3 FI(左)、IF(右)声波RTM(a)和黏声RTM(b) Ip1和Ip2分别为声波介质棱柱波FI和IF的成像结果,IQ+p1和IQ+p2分别为黏声介质棱柱波FI和IF的成像结果 |
棱柱波FI和IF的正向延拓震源波场为
| $ \left\{ {\begin{array}{*{20}{l}} {(\mathit{\boldsymbol{A}}_{\rm{D}}^{ - 1}\mathit{\boldsymbol{L}}{{\rm{a}}_Q} + )\mathit{\boldsymbol{U}}{\rm{a}}_{{Q^ + }}^{\rm{S}} + (\mathit{\boldsymbol{x}},t) = \mathit{\boldsymbol{F}}}\\ {(\mathit{\boldsymbol{A}}_{\rm{U}}^{ - 1}\mathit{\boldsymbol{A}}_{\rm{D}}^{ - 1}\mathit{\boldsymbol{L}}{{\rm{b}}_{{Q^ + }}})\mathit{\boldsymbol{U}}b_{{Q^ + }}^{\rm{S}}(\mathit{\boldsymbol{x}},t) = \mathit{\boldsymbol{F}}} \end{array}} \right. $ | (15) |
式中:LaQ+和LbQ+分别为黏声补偿的FI和IF正演模拟算子;UaQ+S(x, t)和UbQ+S(x, t)分别为黏声补偿的FI和IF正向延拓震源波场。由
| $ \begin{array}{l} \left( {\frac{{{\partial ^2}}}{{\partial {t^2}}} - \frac{{\tau v}}{2}\frac{\partial }{{\partial t}}\sqrt { - {\nabla ^2}} - {v^2}{\nabla ^2} + \sigma \frac{{\tau {v^2}}}{2}\frac{\partial }{{\partial t}}{\nabla ^2}} \right)\mathit{\boldsymbol{U}}{\rm{a}}_{{Q^ + }}^{\rm{S}}(\mathit{\boldsymbol{x}},t)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathit{\boldsymbol{F}} \end{array} $ | (16) |
得到UaQ+S(x, t)。基于伯恩近似理论,由
| $ \begin{array}{l} \left( {\frac{1}{{{v^2}}}\frac{{{\partial ^2}}}{{\partial {t^2}}} - \frac{1}{v}\frac{{\tau \sqrt { - {\nabla ^2}} }}{2}\frac{\partial }{{\partial t}} - {\nabla ^2} + \sigma \frac{{\tau {v^2}}}{2}\frac{\partial }{{\partial t}}{\nabla ^2}} \right) \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{U}}{\rm{b}}_{{Q^ + }}^{\rm{S}}(\mathit{\boldsymbol{x}},t) = {\mathit{\boldsymbol{I}}_0}(\mathit{\boldsymbol{x}})\frac{1}{{{v^2}}}\left( {\frac{{{\partial ^2}}}{{\partial {t^2}}} - \frac{{\tau v}}{4}\sqrt { - {\nabla ^2}} \frac{\partial }{{\partial t}}} \right) \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{U}}{\rm{a}}_{{Q^ + }}^{\rm{S}}(\mathit{\boldsymbol{x}},t) \end{array} $ | (17) |
得到UbQ+S(x, t)(附录B)。式中I0表示由黏声RTM得到的成像结果。
黏声补偿的FI和IF反向延拓检波点波场由
| $ \left\{ {\begin{array}{*{20}{l}} {(\mathit{\boldsymbol{A}}_{\rm{D}}^{ - 1}\mathit{\boldsymbol{A}}_{\rm{U}}^{ - 1}\mathit{\boldsymbol{L}}_{{Q^ + }}^T)\mathit{\boldsymbol{U}}{\rm{a}}_{{Q^ + }}^{\rm{R}}(\mathit{\boldsymbol{x}},T - t) = \mathit{\boldsymbol{d}}_{{Q^ - }}^{{\rm{obs}}}}\\ {(\mathit{\boldsymbol{A}}_{\rm{U}}^{ - 1}\mathit{\boldsymbol{L}}{\rm{b}}_{Q}^T + )\mathit{\boldsymbol{U}}{\rm{b}}_{{Q^ + }}^{\rm{R}} + (\mathit{\boldsymbol{x}},T - t) = \mathit{\boldsymbol{d}}_{{Q^ - }}^{{\rm{obs}}}} \end{array}} \right. $ | (18) |
得到。式中:LaQ+T和LbQ+T分别为黏声补偿的FI和IF伴随算子;UaQ+R(x, t)和UbQ+R(x, t)分别为黏声补偿的FI和IF反向延拓检波点波场。由
| $ \begin{array}{l} \left[ {\frac{{{\partial ^2}}}{{\partial {{(T - t)}^2}}} - \frac{{\tau v}}{2}\frac{\partial }{{\partial (T - t)}}\sqrt { - {\nabla ^2}} - {v^2}{\nabla ^2} + } \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma \frac{{\tau {v^2}}}{2}\frac{\partial }{{\partial (T - t)}}{\nabla ^2}} \right]\mathit{\boldsymbol{U}}{\rm{b}}_{{Q^ + }}^{\rm{R}} + (\mathit{\boldsymbol{x}},t) = \delta {\mathit{\boldsymbol{d}}_{{Q^ - }}} \end{array} $ | (19) |
得到UbQ+R(x, t)。式中δdQ-为受衰减影响的观测数据与模拟数据之差。由
| $ \begin{array}{l} \left[ {\frac{1}{{{v^2}}}\frac{{{\partial ^2}}}{{\partial {{(T - t)}^2}}} - \frac{1}{v}\frac{{\tau \sqrt { - {\nabla ^2}} }}{2}\frac{\partial }{{\partial (T - t)}} - {\nabla ^2} + } \right.\\ {\kern 1pt} \left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sigma \frac{{\tau {v^2}}}{2}\frac{\partial }{{\partial (T - t)}}{\nabla ^2}} \right]\mathit{\boldsymbol{U}}{\rm{a}}_{{Q^ + }}^{\rm{R}}(\mathit{\boldsymbol{x}},t)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {\mathit{\boldsymbol{I}}_{{Q^ + }}}\frac{1}{{{v^2}}}\left[ {\frac{{{\partial ^2}}}{{\partial {{(T - t)}^2}}} - \frac{{\tau v}}{4}\sqrt { - {\nabla ^2}} \frac{\partial }{{\partial (T - t)}}} \right] \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{U}}{\rm{b}}_{{Q^ + }}^{\rm{R}}(\mathit{\boldsymbol{x}},t) \end{array} $ | (20) |
得到UaQ+R(x, t)。因此黏声棱柱波RTM的成像结果为
| $ \begin{array}{l} \mathit{\boldsymbol{I}}_{{Q^ + }}^{\rm{p}} = \mathop \smallint \nolimits_0^T [\mathit{\boldsymbol{U}}{\rm{a}}_{{Q^ + }}^{\rm{S}}(x,t)\mathit{\boldsymbol{U}}{\rm{a}}_{{Q^ + }}^{\rm{R}}(\mathit{\boldsymbol{x}},t) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \mathit{\boldsymbol{U}}{\rm{b}}_{{Q^ + }}^{\rm{S}}(\mathit{\boldsymbol{x}},t)\mathit{\boldsymbol{U}}{\rm{b}}_{{Q^ + }}^{\rm{R}}(\mathit{\boldsymbol{x}},t)]{\rm{d}}t \end{array} $ | (21) |
需要说明的是,利用式(21)计算UbQ+R(x, t)时,无法同时重构UaQ+S(x, t)、UaQ+R(x, t)和UbQ+S(x, t),因此每间隔10ms保存一个波场。
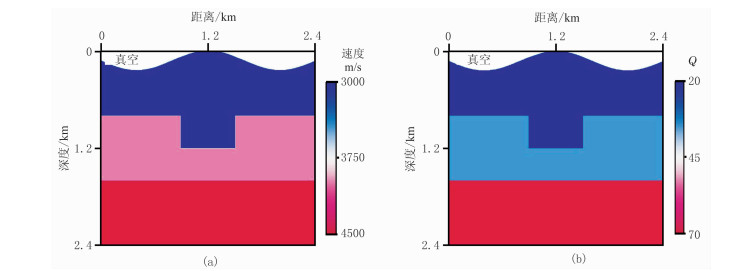
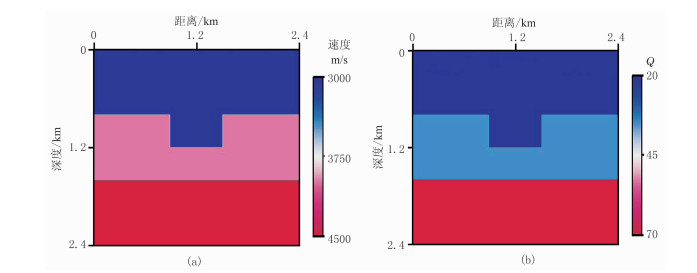
2 模型试算 2.1 简单起伏地表凹陷模型由笛卡尔坐标系的速度模型与Q模型(图 4)测试黏声棱柱波RTM的效果,采用贴体网格剖分(图 5)及坐标变换方法[34],得到曲线坐标系下的速度模型与Q模型(图 6)。在曲线坐标系下偏移成像可很好地校正起伏地表影响。
|
图 4 笛卡尔坐标系下的速度模型(a)与Q模型(b) 由上至下,3层介质的纵波速度分别为3000、4000、4500m/s,Q值分别为20、35、70模型尺寸为2.4km×2.4km,网格点数为301×301,空间网格步长为8m |

|
图 5 贴体网格剖分(a)及其局部放大(b) |
|
图 6 曲线坐标系下的速度模型(a)与Q模型(b) 主频为25Hz的30个雷克子波震源位于起伏地表,间隔为80m,301个检波器沿地表均匀分布,总记录时间为3.0s,采样间隔为0.6ms |
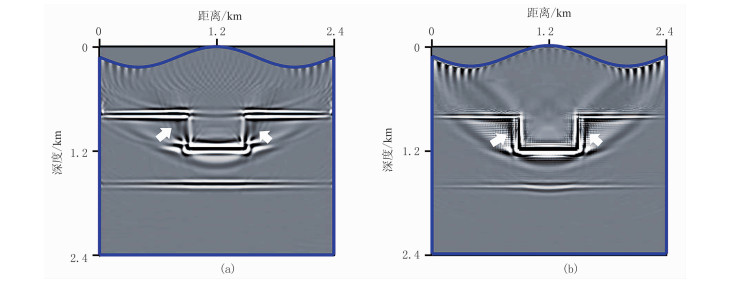
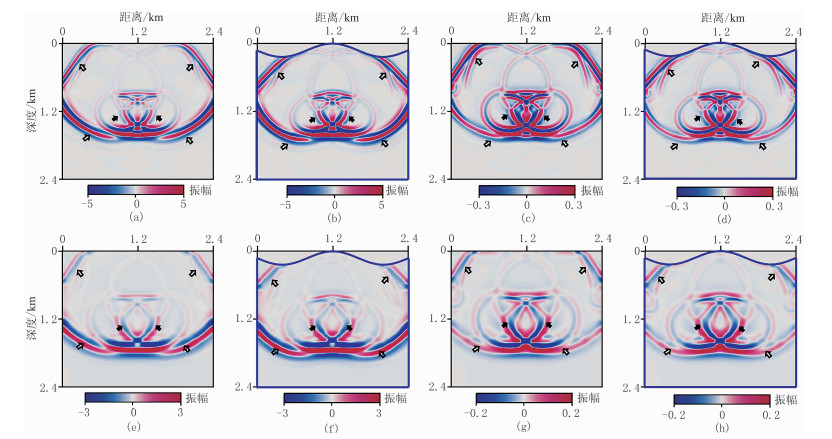
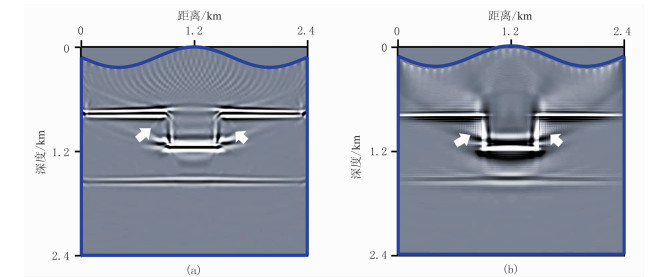
由模拟炮记录(图 7)可见,衰减记录存在明显的振幅衰减和相位频散(图 7a、图 7c)。由黏声RTM和黏声棱柱波RTM成像结果可见,黏声RTM对垂直反射层的成像效果不好(图 8a白色实线箭头处),黏声棱柱波RTM对水平反射层成像效果不如黏声RTM,但对垂直反射层的成像效果更好(图 8b),并出现少量高频噪声。原因为:因为利用规则化压制黏声衰减的本质是低通滤波,黏声棱柱波RTM需要对正向延拓及逆时延拓进行两次衰减补偿,相应地需要进行两次正则化处理,如果正则化滤波程度过大,则会损失较多有效能量,并遗留少量高频噪声。采用图 7a数据进行黏声RTM和黏声棱柱波RTM得到540ms的波场快照(图 9)。可见:①在曲线坐标系UaQ+S(x, t)中来自水平层的入射波、反射波(图 9a空心箭头处)能量比棱柱波(图 9a实线箭头处)强得多;在曲线坐标系UbQ+S(x, t)中棱柱波与入射波、反射波的能量更均衡(图 9c)。②在曲线坐标系UaS(x, t)、UbS(x, t)(未进行黏声补偿的波场)中入射波、反射波和棱柱波能量均较弱(图 9e、图 9g)。由声波RTM(图 10a)和声波棱柱波RTM(图 10b)成像结果可见,反射层的成像振幅和分辨率远低于黏声介质RTM(图 8),声波棱柱波RTM(图 10b)更是如此。上述模型试算结果表明,黏声棱柱波RTM对高陡构造的成像效果好于黏声RTM,与声波棱柱波RTM方法相比,振幅更均衡、分辨率更高。表 1为不同方法对简单起伏地表凹陷模型的成像时间对比。由表可见,黏声棱柱波RTM及声波棱柱波RTM的成像时间是黏声RTM和声波RTM的两倍多,黏声棱柱波RTM的成像时间约为声波棱柱波RTM的3.7倍。

|
图 7 模拟炮记录 (a)黏弹性介质;(b)声学介质;(c)图a左半部和图b右半部拼合 |
|
图 8 黏声RTM(a)和黏声棱柱波RTM(b)成像结果 |
|
图 9 540ms的波场快照 (a)曲线坐标系UaQ+S(x, t);(b)笛卡尔坐标系UaQ+S(x, t);(c)曲线坐标系UbQ+S(x, t);(d)笛卡尔坐标系UbQ+S(x, t);(e)曲线坐标系UaS(x, t);(f)笛卡尔坐标系UaS(x, t);(g)曲线坐标系UbS(x, t);(h)笛卡尔坐标系UbS(x, t) |
|
图 10 声波RTM(a)和声波棱柱波RTM(b)成像结果 |
|
|
表 1 不同方法对简单起伏地表凹陷模型的成像时间对比 |
利用高陡盐丘速度模型与Q模型(图 11)测试黏声棱柱波RTM的效果,模型具有垂直的盐丘结构,给成像带来巨大挑战。图 12为黏声介质与声波介质模拟炮记录。
|
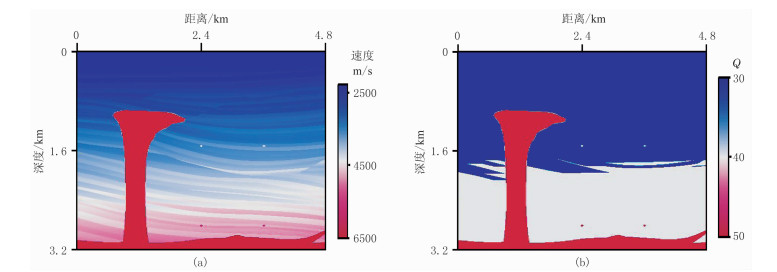
图 11 高陡盐丘速度模型(a)与Q模型(b) 模型由真实模型经过平滑处理得到。模型尺寸为4.8km×3.2km,网格尺寸为601×401,网格间隔为8m。纵波震源子波为主频为30Hz的雷克子波,位于地下8m处,震源个数为60,震源间隔为80m。每一条地震记录由600个检波器接收,检波器间隔为8m。计算时长达3.0s,采样间隔为0.6ms |
|
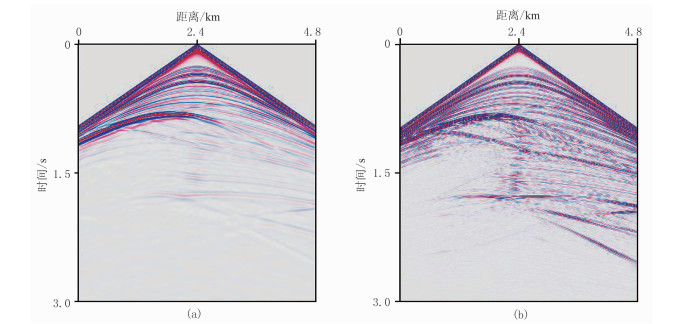
图 12 黏声介质(a)与声波介质(b)模拟炮记录 |
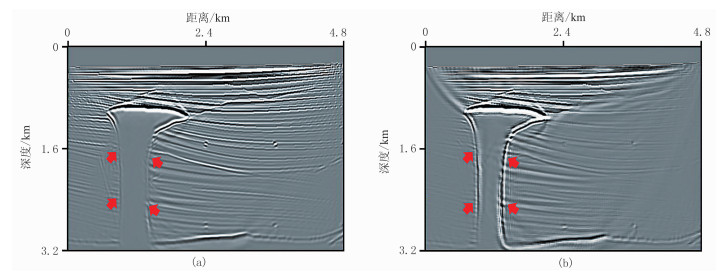
使用黏声介质模拟炮记录(图 12a)测试黏声棱柱波RTM的效果,得到600ms的波场快照(图 13)。可见:①在UaQ+S(x, t)(图 13a)中入射波(实线箭头处)能量明显强于棱柱波(空心箭头处),在UbQ+S(x, t)(图 13b)中棱柱波与入射波的能量更均衡;②在UaS(x, t)(图 13c)和UbS(x, t)(图 13d)中入射波、反射波和棱柱波的能量都非常弱。图 14为高陡盐丘模型黏声RTM和黏声棱柱波RTM成像结果。由图可见:黏声RTM对高陡盐丘侧面的成像效果不好(图 14a红色实线箭头处);黏声棱柱波RTM对层状沉积层成像分辨率较低,但对高陡盐丘侧面的成像效果更好(图 14b红色实线箭头处)。图 15为高陡盐丘模型声波RTM和声波棱柱波RTM成像结果。由图可见,高陡盐丘侧面和层状沉积层的成像能量和分辨率都远低于黏声RTM和黏声棱柱波RTM(图 14)。模型试算证明,黏声棱柱波RTM可对复杂高陡构造精确成像。表 2为不同方法对高陡盐丘模型的成像时间对比。由表可见,棱柱波RTM成像时间约为声波RTM的两倍。

|
图 13 600ms的波场快照 (a)UaQ+S(x, t);(b)UbQ+S(x, t);(c)UaS(x, t);(d)UbS(x, t) |
|
图 14 高陡盐丘模型黏声RTM(a)和黏声棱柱波RTM(b)成像结果 |

|
图 15 高陡盐丘模型声波RTM(a)和声波棱柱波RTM(b)成像结果 |
|
|
表 2 不同方法对高陡盐丘模型的成像时间对比 |
高陡构造给地震成像带来了巨大挑战,为此,本文提出了黏声棱柱波RTM方法,推导了黏声棱柱波正向延拓算子与逆时延拓伴随算子,并沿着棱柱波的传播方向补偿Q衰减。通过两个典型高陡构造模型试算证明,黏声棱柱波RTM对高陡构造的成像精度高于黏声RTM、声波棱柱波RTM,成像结果的能量更均衡、分辨率更高。
虽然黏声棱柱波RTM可以提高高陡构造的成像精度,但会牺牲低角度构造的成像分辨率,因此,需要联合黏声RTM和声波棱柱波RTM成像结果分析与解释地下构造。另外,黏声棱柱波RTM的计算时间约为黏声RTM的两倍,且因无法同时重构多个波场值,因此保存波场值需要大量的内存。
本文使用的黏声拟微分方程具有如下优点:①方程求解较简单;②可很容易地引入正则化算子,以保证黏声补偿的稳定性。但该方程也存在明显缺点,即它是基于弱黏弹性假设条件,因此在强黏弹性介质中不再适用。通过引入正则化算子,使计算量小于传统低通滤波方法,并减少了有效能量损失,但正则化方法的本质仍然是低通滤波。与黏声RTM相比,无论波场正向延拓还是逆时延拓,黏声棱柱波RTM均进行两次波场补偿,很难同时兼顾波场能量不损失及完全压制高频噪声。可替代的解决方法是利用最小二乘反演思想,推导稳定的黏声伴随算子,以保证黏声补偿的稳定性。
尚需指出,本文提出的黏声棱柱波RTM可改善高陡构造的成像效果,但需要考虑计算量与内存成本,与黏声RTM类似,对偏移速度场和品质因子场的精度要求较高。
附录A 黏声拟微分方程规则化算子无记忆变量的黏声拟微分方程为
| $ \left( {\frac{{{\partial ^2}}}{{\partial {t^2}}} - \frac{{\tau v}}{2}\frac{\partial }{{\partial t}}\sqrt { - {\nabla ^2}} - {v^2}{\nabla ^2}} \right)p = 0 $ | (A-1) |
式中:p为压力;v为速度;
| $ {\left( {\frac{{{\partial ^2}}}{{\partial {t^2}}} - \frac{{\varphi \tau }}{2}\frac{\partial }{{\partial t}} + {\varphi ^2}} \right)p = 0} $ | (A-2) |
令
| $ {{\varLambda _t} = {{\rm{e}}^{ - \frac{\pi }{4}t\tau }}} $ | (A-3) |
引入中间波场q(x, t)
| $ q(\mathit{\boldsymbol{x}},t) = {\varLambda _t}p(\mathit{\boldsymbol{x}},t) $ | (A-4) |
将式(A-4)代入式(A-2),得
| $ \left( {\frac{{{\partial ^2}}}{{\partial {t^2}}} - \frac{{\varphi \tau }}{2}\frac{\partial }{{\partial t}} + {\varphi ^2}} \right)\varLambda _t^{ - 1}q(\mathit{\boldsymbol{x}},t) = 0 $ | (A-5) |
Λt-1q(x, t)对t的一阶偏导数为
| $ \frac{\partial }{{\partial t}}[\varLambda _t^{ - 1}q(\mathit{\boldsymbol{x}},t)] = {{\rm{e}}^{\frac{{\varphi \tau }}{4}t}}\frac{{\partial q(\mathit{\boldsymbol{x}},t)}}{{\partial t}} + \frac{{\varphi \tau }}{4}{{\rm{e}}^{\frac{{\varphi \tau }}{4}t}}q(\mathit{\boldsymbol{x}},t) $ | (A-6) |
Λt-1q(x, t)对t的二阶偏导数为
| $ \begin{array}{l} \frac{{{\partial ^2}}}{{\partial {t^2}}}[\varLambda _t^{ - 1}q(\mathit{\boldsymbol{x}},t)] = {{\rm{e}}^{\frac{{\tau \varphi }}{4}}}t\frac{{{\partial ^2}q(\mathit{\boldsymbol{x}},t)}}{{\partial {t^2}}} + \frac{{\varphi \tau }}{4}{{\rm{e}}^{\frac{\varphi }{4}t\tau }}\frac{{\partial q(\mathit{\boldsymbol{x}},t)}}{{\partial t}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\varphi \tau }}{4}{{\rm{e}}^{\frac{{\varphi \tau }}{4}t}}\frac{{\partial q(\mathit{\boldsymbol{x}},t)}}{{\partial t}} + {\left( {\frac{{\varphi \tau }}{4}} \right)^2}{{\rm{e}}^{\frac{{\varphi \tau }}{4}t}}q(\mathit{\boldsymbol{x}},t) \end{array} $ | (A-7) |
将式(A-6)、式(A-7)代入式(A-5),得
| $ \begin{array}{l} \frac{{{\partial ^2}q(\mathit{\boldsymbol{x}},t)}}{{\partial {t^2}}} + \frac{{\varphi \tau }}{4}\frac{{\partial q(\mathit{\boldsymbol{x}},t)}}{{\partial t}} + \frac{{\varphi \tau }}{4}\frac{{\partial q(\mathit{\boldsymbol{x}},t)}}{{\partial t}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\left( {\frac{{\varphi \tau }}{4}} \right)^2}q(\mathit{\boldsymbol{x}},t) - \frac{{\varphi \tau }}{2}\left[ {\frac{{\partial q(\mathit{\boldsymbol{x}},t)}}{{\partial t}} + \frac{{\varphi \tau }}{4}q(\mathit{\boldsymbol{x}},t)} \right] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\varphi ^2}q(\mathit{\boldsymbol{x}},t) = 0 \end{array} $ | (A-8) |
化简式(A-8),得
| $ \left[ {\frac{{{\partial ^2}}}{{\partial {t^2}}} + \left( {1 - \frac{{{\tau ^2}}}{{16}}} \right){\varphi ^2}} \right]q(\mathit{\boldsymbol{x}},t) = 0 $ | (A-9) |
因此,可将式(A-1)改为
| $ \left\{ {\begin{array}{*{20}{l}} {\left[ {\frac{{{\partial ^2}}}{{\partial {t^2}}} + \left( {1 - \frac{{{\tau ^2}}}{{16}}} \right){\varphi ^2}} \right]q(\mathit{\boldsymbol{x}},t) = 0}\\ {p(\mathit{\boldsymbol{x}},t) = {{\rm{e}}^{\frac{{\varphi t\tau }}{4}}}q(\mathit{\boldsymbol{x}},t)} \end{array}} \right. $ | (A-10) |
由于p(x, t)随着t呈指数增长,由此引起的高频数值噪声导致计算不稳定。为此,引入规则化项σ,并重新整理式(A-10),得
| $ \left\{ {\begin{array}{*{20}{l}} {\left[ {\frac{{{\partial ^2}}}{{\partial {t^2}}} + \left( {1 - \frac{{{\tau ^2}}}{{16}}} \right){\varphi ^2}} \right]q(\mathit{\boldsymbol{x}},t) = 0}\\ {p(\mathit{\boldsymbol{x}},t) = {{\rm{e}}^{\frac{{\varphi - \sigma {\varphi ^2}}}{4}t\tau }}q(\mathit{\boldsymbol{x}},t)} \end{array}} \right. $ | (A-11) |
将式(A-11)的两个方程结合、化简,得
| $ \left[ {\frac{{{\partial ^2}}}{{\partial {t^2}}} - \frac{{(\varphi - \sigma {\varphi ^2})\tau }}{2}\frac{\partial }{{\partial t}} + {\varphi ^2}} \right]p(\mathit{\boldsymbol{x}},t) = 0 $ | (A-12) |
将φ代入式(A-12),得
| $ \begin{array}{l} \left( {\frac{{{\partial ^2}}}{{\partial {t^2}}} - \frac{{\tau v}}{2}\frac{\partial }{{\partial t}}\sqrt { - {\nabla ^2}} - {v^2}{\nabla ^2} - \sigma \frac{{\tau {v^2}}}{2}\frac{\partial }{{\partial t}}{\nabla ^2}} \right) \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} p(\mathit{\boldsymbol{x}},t) = 0 \end{array} $ | (A-13) |
黏声正演模拟方程为
| $ \begin{array}{*{20}{l}} {\left( {\frac{{{\partial ^2}}}{{\partial {t^2}}} - \frac{{\tau v}}{2}\frac{\partial }{{\partial t}}\sqrt { - {\nabla ^2}} - {v^2}{\nabla ^2} + \sigma \frac{{\tau {v^2}}}{2}\frac{\partial }{{\partial t}}{\nabla ^2}} \right){p^{{\rm{S + }}}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathit{\boldsymbol{F}}} \end{array} $ | (B-1) |
式中pS+为黏声震源波场。基于伯恩近似理论,模型参数的扰动将会引起波场的扰动,其中背景波场p0S+由
| $ \begin{array}{*{20}{l}} {\left( {\frac{1}{{v_0^2}}\frac{{{\partial ^2}}}{{\partial {t^2}}} - \frac{1}{{{v_0}}}\frac{{\tau \sqrt { - {\nabla ^2}} }}{2}\frac{\partial }{{\partial t}} - {\nabla ^2} + \sigma \frac{\tau }{2}\frac{\partial }{{\partial t}}{\nabla ^2}} \right)p_0^{{\rm{S + }}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathit{\boldsymbol{F}}} \end{array} $ | (B-2) |
求得。将
| $ \frac{1}{{{v^2}}} = \frac{1}{{v_0^2}} - \frac{{2{\rm{ \mathsf{ δ} }} v}}{{v_0^3}} + O({\rm{ \mathsf{ δ} }} v) $ | (B-3) |
式中O(δv)为速度扰动δv的高阶项。将式(B-1)与式(B-2)相减,得
| $ \begin{array}{*{20}{c}} {\left( {\frac{1}{{v_0^2}}\frac{{{\partial ^2}}}{{\partial {t^2}}} - \frac{\tau }{2}\frac{1}{{{v_0}}}\frac{\partial }{{\partial t}}\sqrt { - {\nabla ^2}} - {\nabla ^2} - \sigma \frac{\tau }{2}\frac{\partial }{{\partial t}}{\nabla ^2}} \right)p_s^{{\rm{S + }}}}\\ { = \frac{{2{\rm{ \mathsf{ δ} }} v}}{{{v_0}}}\left( {\frac{{{\partial ^2}}}{{\partial {t^2}}} - \frac{{\tau {v_0}}}{4}\frac{\partial }{{\partial t}}\sqrt { - {\nabla ^2}} } \right){p^{{\rm{S + }}}} + O({\rm{ \mathsf{ δ} }} v)} \end{array} $ | (B-4) |
式中psS+为黏声扰动波场。定义反射系数
| $ \mathit{\boldsymbol{I}}(\mathit{\boldsymbol{x}}) = \frac{{2{\rm{ \mathsf{ δ} }} v}}{{{v_0}}} $ | (B-5) |
将式(B-5)代入式(B-4)并忽略高阶项,得黏声伯恩近似方程
| $ \begin{array}{l} \left( {\frac{1}{{v_0^2}}\frac{{{\partial ^2}}}{{\partial {t^2}}} - \frac{\tau }{2}\frac{1}{{{v_0}}}\frac{\partial }{{\partial t}}\sqrt { - {\nabla ^2}} - {\nabla ^2} - \sigma \frac{\tau }{2}\frac{\partial }{{\partial t}}{\nabla ^2}} \right)p_s^{{\rm{S + }}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \mathit{\boldsymbol{I}}(\mathit{\boldsymbol{x}})\frac{1}{{v_0^2}}\left( {\frac{{{\partial ^2}}}{{\partial {t^2}}} - \frac{{\tau {v_0}}}{4}\frac{\partial }{{\partial t}}\sqrt { - {\nabla ^2}} } \right){p^{{\rm{S + }}}} \end{array} $ | (B-6) |
| [1] |
Hale D, Hill N R, Stefani J. Imaging salt with turning seismic waves[J]. Geophysics, 1992, 57(11): 1453-1462. |
| [2] |
Hawkins K. The challenge presented by North Sea Central Graden salt domes to all DMO algorithms[J]. First Break, 1994, 12(6): 327-343. |
| [3] |
Farmer P A, Jones I F, Zhou H, et al. Application of reverse time migration to complex imaging problems[J]. First Break, 2006, 24(9): 65-73. |
| [4] |
Jin S, Xu S and Walraven D.One-return wave equation migration: Imaging of duplex waves[C]. SEG Technical Program Expanded Abstracts, 2006, 25: 2338-2342.
|
| [5] |
Malcolm A E, Ursin B, De Hoop M V, et al. Seismic imaging and illumination with internal multiples[J]. Geophysical Journal International, 2009, 176(3): 847-864. |
| [6] |
Malcolm A E, De Hoop M V, Ursin B. Recursive imaging with multiply scattered waves using partial image regularization:A North Sea case study[J]. Geophysics, 2011, 76(2): B33-B42. |
| [7] |
Qu Y M, Li Z C, Huang J P, et al. Prismatic and full-waveform joint inversion[J]. Applied Geophysics, 2016, 13(3): 511-518. |
| [8] |
Broto K and Lailly P.Towards the tomogtaphic inversion of prismatic reflections[C]. SEG Technical Program Expanded Abstracts, 2001, 20: 726-729.
|
| [9] |
Marmalyevskyy N, Roganov Y, Gornyak Z, et al.Migration of duplex waves[C]. SEG Technical Program Expanded Abstracts, 2005, 24: 2025-2029.
|
| [10] |
Whitmore N.Iterative depth migration by backward time propagation[C]. SEG Technical Program Expanded Abstracts, 1983, 2: 382-385.
|
| [11] |
Baysal E, Kosloff D, Sherwood J. Reverse time migration[J]. Geophysics, 1983, 48(1): 1514-1524. |
| [12] |
Loewenthal D. Reverse time migration in spatial frequency domain[J]. Geophysics, 1983, 48(5): 627-635. |
| [13] |
McMechan G A. Migration by extrapolation of time-dependent boundary values[J]. Geophysical Prospecting, 1983, 31(3): 413-420. |
| [14] |
Li Y F, Agnihotri Y, Dy T.Prismatic wave imaging with dual flood RTM[C]. SEG Technical Program Expanded Abstracts, 2011, 30: 3290-3294.
|
| [15] |
Dai W.Multisource Least-Squares Migration and Prism Wave Reverse Time Migration[D]. The University of Utah, America, 2012.
|
| [16] |
黄建平, 刘培君, 李庆洋, 等. 一种棱柱波逆时偏移方法及优化[J]. 石油物探, 2016, 55(5): 719-727. HUANG Jianping, LIU Peijun, LI Qingyang, et al. An optimized reverse time migration approach for the prsim wave[J]. Geophysical Prospecting for Petro-leum, 2016, 55(5): 719-727. |
| [17] |
刘金朋, 王培培, 方中于, 等. 逆时偏移对棱柱波和回折波的成像效果分析[J]. 地球物理学进展, 2015, 30(3): 1396-1401. LIU Jinpeng, WANG Peipei, FANG Zhongyu, et al. Imaging effect analysis of the prism waves and the diving waves based on reverse-time migration[J]. Progress in Geophysics, 2015, 30(3): 1396-1401. |
| [18] |
Aki K, Richards P G.Quantitative Seismology(2nd Eiton)[M]. University Science Books, 2002.
|
| [19] |
Carcione J.Wave Fields in Real Media(2nd Eition)[M]. Elsevier, 2007.
|
| [20] |
Zhang X, Han L, Zhang F, et al. An inverse Q-filter algorithm based on stable wavefeild continuation[J]. Applied Geophysicis, 2007, 4(4): 263-270. |
| [21] |
Bickel S H, Natarajan R R. Plane-wave Q deconvolution[J]. Geophysics, 1985, 50(9): 1426-1439. |
| [22] |
Hargreaves N D, Calvert A J. Inverse Q filtering by Fourier transform[J]. Geophysics, 1991, 56(4): 519-527. |
| [23] |
高军, 凌云, 周兴元, 等. 时频域球面发散和吸收补偿[J]. 石油地球物理勘探, 1996, 31(6): 856-866, 905. GAO Jun, LING Yun, ZHOU Xingyuan, et al. Compenstion for spherical divergence and absorption in time-frequency domain[J]. Oil Geophysical Prospecting, 1996, 31(6): 856-866, 905. |
| [24] |
裴江云, 何樵登. 基于Kjartansson模型的反Q滤波[J]. 地球物理学进展, 1994, 9(1): 90-100. PEI Jiangyun, HE Qiaodeng. Inversion Q filtering according to Kjartansson model[J]. Progress in Geophysics, 1994, 9(1): 90-100. |
| [25] |
张瑾, 刘财, 冯晅, 等. 波场延拓反Q滤波的正则化方法[J]. 世界地质, 2013, 32(1): 123-129. ZHANG Jin, LIU Cai, FENG Xuan, et al. Regularization method of inver Q filtering based on wave field continuation[J]. Global Geology, 2013, 32(1): 123-129. |
| [26] |
Xie Y, Xin K, Sun J, et al.3D prestack depth migration with compensation for frequency dependent absorption and dispersion[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 2919-2922.
|
| [27] |
刘喜武, 年静波, 刘洪. 基于广义S变换的吸收衰减补偿方法[J]. 石油物探, 2006, 45(1): 9-14. LIU Xiwu, NIAN Jingbo, LIU Hong. Absorption attenuation compensation method based on generalized S transform[J]. Geophysical Prospecting for Petro-leum, 2006, 45(1): 9-14. |
| [28] |
Dai N, West G F.Inverse Q migration[C]. SEG Technical Program Expanded Abstracts, 1994, 13: 1418-1421.
|
| [29] |
郭恺, 娄婷婷. 双复杂介质条件下的反Q滤波偏移延拓算子研究[J]. 物探与化探, 2014, 38(3): 571-576. GUO Kai, LOU Tingting. A study of inverse Q continuation operator in dual complexity media[J]. Geophysical and Geochemical Exploration, 2014, 38(3): 571-576. |
| [30] |
Deng F, McMechan G A. True-amplitude prestack depth migration[J]. Geophysics, 2007, 72(3): S155-S166. |
| [31] |
马俊彦, 张龙, 罗昭洋, 等. 黏滞介质Q偏移技术在准噶尔盆地南缘低信噪比地区的应用[J]. 石油地球物理勘探, 2018, 53(1): 94-99. MA Junyan, ZHANG Long, LUO Zhaoyang, et al. Application of viscous medium Q migration technique in the low signal-to-noise ratio area of the southern margin of Junggar basin[J]. Oil Geophysical Prospecting, 2018, 53(1): 94-99. |
| [32] |
妥军军, 谭佳, 罗昭洋, 等. 叠前深度偏移技术在齐古复杂构造成像中的应用[J]. 石油地球物理勘探, 2018, 53(1): 100-106. TUO Junjun, TAN Jia, LUO Zhaoyang, et al. Application of prestack depth migration technique in the imaging of Qigu complex structure[J]. Oil Geophysical Prospecting, 2018, 53(1): 100-106. |
| [33] |
Zhu T Z, Harris J M, Biondi B. Q-compensated reverse-time migration[J]. Geophysics, 2014, 79(3): S77-S87. |
| [34] |
Qu Y, Li J. Q-compensated reverse time migration in viscoacoustic media including surface topography[J]. Geophysics, 2019, 84(4): S201-S217. |
| [35] |
周彤, 胡文毅, 宁杰远. 一种黏声波方程逆时偏移成像中的衰减补偿方法[J]. 地球物理学报, 2018, 61(6): 2433-2445. ZHOU Tong, HU Wenyi, Ning Jieyuan. An attenuation compensation method in reverse time migration for visco-acoustic media[J]. Chinese Journal of Geophysics, 2018, 61(6): 2433-2445. |
| [36] |
Qu Y M, Huang J P, Li Z C, et al. Attenuation compensation in anisotropic least-squares reverse time migration[J]. Geophysics, 2017, 82(6): S411-S423. |
| [37] |
Chen Y, Dutta G, Dai W, et al. Q-least-squares reverse time migration with viscoacoustic deblurring filters[J]. Geophysics, 2017, 82(6): S425-S438. |
| [38] |
姚振岸, 孙成禹, 喻志超, 等. 融合点扩散函数的预条件黏声最小二乘逆时偏移[J]. 石油地球物理勘探, 2019, 54(1): 73-83. YAO Zhenan, SUN Chengyu, YU Zhichao, et al. The pre-condition viscous least squares inverse time migration of the fusion point diffusion function[J]. Oil Geophysical Prospecting, 2019, 54(1): 73-83. |
| [39] |
Bai J, Chen G, Yingst D, et al.Attenuation compensation in viscoacoustic reverse time migration[C]. SEG Technical Program Expanded Abstracts, 2013, 32: 3825-3830.
|
| [40] |
Fletcher R P, Nichols D, Cavalca M.Wavepath-con-sistent effective Q estimation for Q compensated reserve-time migration[C]. Extended Abstracts of 74th EAGE Conference & Exhibition, 2012, WCA179-WCA187.
|
| [41] |
郭锐, 林鹤, 王前, 等. 改进的Capon2D Q值估计方法及其应用[J]. 石油地球物理勘探, 2018, 53(2): 182-188. GUO Rui, LIN He, WANG Qian, et al. An improved Capon2D Q estimation method and its application[J]. Oil Geophysical Prospecting, 2018, 53(2): 182-188. |



 曲英铭, 山东省青岛市黄岛区长江西路66号中国石油大学地球科学与技术学院, 266580。Email:
曲英铭, 山东省青岛市黄岛区长江西路66号中国石油大学地球科学与技术学院, 266580。Email: