② 贵州省石油学会, 贵州贵阳 550000
② Petroleum Society of Guizhou Province, Guiyang, Guizhou 550000, China
逆时偏移法自二十世纪七、八十年代提出以来,已经持续发展了近四十余年[1-2],作为当今对复杂构造成像中最为常用手段之一,因其较好的成像效果及实现容易等特点受到了青睐[3-5]a。逆时偏移可根据目标的不同及模型复杂程度分为声介质偏移、黏弹性介质偏移以及各向异性介质偏移等[6],黏弹性介质及各向异性介质的偏移目前尚处于探索实验阶段,基于声波的逆时偏移技术是当前的研究热点,但声波逆时偏移技术的推广和应用仍受较高的存储占用和较低的计算效率制约[7-8]。
与Kirchhoff偏移相比,基于双程波动方程的逆时偏移技术无成像倾角限制,且能够同时对回转波、多次波及棱柱波精确成像[9-10],可以在横向速度变化剧烈时取得不错的成像结果[11]。在正演及逆时偏移中,为保证薄层、缝洞及高倾角层位的有效信息精确获取,往往需取较小的模型网格,由此便导致了网格划分数目和计算量的增加。针对该问题,学者们提出了不同的网格划分优化方法:不规则网格法通过引入非规则网格差分算子,将规则四边形网格映射至任意形状四边形网格,对崎岖地表有较强适应能力[12-14];变网格法,通过对模型速度不同区域采用变网格步长的方式,在保证目标区域信息准确性的情况下,实现了网格数目的整体减少,能够有效降低存储占用和计算量[15-16];自适应网格法,通过阈值控制的方式,自动将原始模型均匀网格细化改造,使计算中所有网格误差值均处在设定阈值之内,有效地提高了计算效率及地层分辨能力[17-18]。但上述各种网格改进方法都是在笛卡尔坐标系下进行的,并不能彻底解决波场在不同速度层中采样不均匀的问题。
伪深度域法不同于传统的算法改进,通过引入曲坐标变换,将原始笛卡尔坐标系下模型速度场变换为纵向等间隔的单程旅行时速度场(又称伪深度域速度场或垂直时间域速度场),既避免了波场在高速度层中的过采样现象,又减少了模型纵向采样点数,从而达到降低计算量及提高计算效率的目的。伪深度域最早由Alkhailfah等[19]提出,Ma等[20]推导并分析了伪深度域下速度—应力方程,解决了纵向过采样问题。李庆洋等[21]为解决横向过采样问题,引入自适应差分算子计算横向空间微分,综合考虑了横、纵向空间采样问题,进一步提升了计算效率。但是,使用CPU(MPI并行)进行算法实现仍需消耗大量时间,使该方法仍然难以投入实际应用。因此,运用GPU并行就显得格外重要。GPU并行多采用CUDA和OpenCL两种架构。二者均有较强的数据并行处理能力,但都有编程环境配置繁复、编程语言不够精炼、初学者门槛较高等缺点。C++ AMP是基于DirectX技术实现的并行计算库,集成于微软VisualStudio软件开发工具中,用户无需进行复杂的环境配置,只需简单的引用相应头文件即可实现对应并行函数的调用,相比而言,上手难度低且加速效果并不差[22-23]。
本文将曲坐标变换引入到声波正演及逆时偏移,同时结合C++ AMP并行编程架构,实现了伪深度域下的声波方程正演及逆时偏移算法,通过标准盐丘模型、黔北页岩勘探区凤岗断块模型及复杂逆掩构造模型的试算,证实了本文方法在存储空间、I/O及计算成本上都具有显著的优势。
1 方法原理 1.1 伪深度域变换二维时空域一阶速度—应力声波方程可表示为
| $ \left\{ {\begin{array}{*{20}{l}} {\rho \frac{{\partial u}}{{\partial t}} = \frac{{\partial p}}{{\partial x}}}\\ {\rho \frac{{\partial w}}{{\partial t}} = \frac{{\partial p}}{{\partial z}}}\\ {\frac{{\partial p}}{{\partial t}} = \rho {v^2}\left( {\frac{{\partial u}}{{\partial x}} + \frac{{\partial w}}{{\partial z}}} \right) + S} \end{array}} \right. $ | (1) |
式中:p为压力波场;u、w分别为横、纵向振动速度分量场;ρ为介质密度;v为声波速度;S为震源函数。
伪深度域法需先利用积分公式
| $ \tau (x,t) = \int\limits_0^z {\frac{{{\rm{d}}z}}{{{v_{{\rm{sm}}}}(x,z)}}} $ | (2) |
将笛卡尔坐标系下平滑速度场模型进行纵向积分[19],以此得到单程旅行时间场τ(x,t),然后再将原速度模型用样条插值法插值成纵向等间隔(Δτ)的伪深度域速度模型。式中vsm为深度域平滑速度场。相应地,可再次利用样条插值法将伪深度域速度场反变换回深度域速度场(图 1)。

|
图 1 伪深度域与深度域正反变换示意图 |
在得到伪深度域速度模型后,还需将深度域声波方程改写为伪深度域声波方程。
将深度域波动方程转化到伪深度域时,对应的坐标转换为
| $ {\left\{ {\begin{array}{*{20}{l}} {\xi = x}\\ {\eta = \tau } \end{array}} \right.} $ | (3) |
引入微分算子
| $ {{f_x} = \frac{{\partial f}}{{\partial x}}} $ | (4) |
可得
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{\xi _x} = 1}\\ {{\xi _z} = 0} \end{array}\\ {\eta _x} = \frac{{\partial \tau }}{{\partial x}}\\ {\eta _z} = \frac{1}{{{v_{{\rm{sm}}}}}} \end{array} \right. $ | (5) |
为方便起见,将ηx记为α,则有
| $ \left\{ {\begin{array}{*{20}{l}} {{x_\xi } = 1}\\ {{x_\eta } = 0}\\ {{z_\xi } = - \alpha {v_{{\rm{sm}}}}}\\ {{z_\eta } = {v_{{\rm{sm}}}}} \end{array}} \right. $ | (6) |
假设笛卡尔坐标系x、z方向单位矢量为i、k;伪深度域坐标系中ξ、η方向的单位矢量为e1、e2,则其对应关系可表示为[24]
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{e}}_1} = {x_\xi }\mathit{\boldsymbol{i}} + {z_\xi }\mathit{\boldsymbol{k}} = \mathit{\boldsymbol{i}} - {v_{{\rm{sm}}}}\alpha \mathit{\boldsymbol{k}}}\\ {{\mathit{\boldsymbol{e}}_2} = {x_\eta }\mathit{\boldsymbol{i}} + {z_\eta }\mathit{\boldsymbol{k}} = {v_{{\rm{sm}}}}\mathit{\boldsymbol{k}}} \end{array}} \right. $ | (7) |
由散度定理可知,任意矢量场M在伪深度域坐标系下的散度和梯度的表达式分别为
| $ {\nabla \cdot \mathit{\boldsymbol{M}} = \frac{1}{{{v_{{\rm{sm}}}}}}[{{({v_{{\rm{sm}}}}{M_1})}_\xi } + {{({v_{{\rm{sm}}}}{M_2})}_\eta }]} $ | (8) |
| $ {\nabla \mathit{\boldsymbol{M}} = ({M_\xi } + \alpha {M_\eta }){\mathit{\boldsymbol{e}}_1} + \left( {{\alpha ^2}{M_\eta } + \frac{1}{{v_{{\rm{sm}}}^2}}{M_\xi }} \right){\mathit{\boldsymbol{e}}_2}} $ | (9) |
式中M1和M2分别为M的ξ和η方向分量。
将式(7)和式(8)代入式(1),在考虑密度为常值的情况下可得到伪深度域二维时空域一阶速度—应力方程
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial U}}{{\partial t}} = \frac{{\partial P}}{{\partial \xi }} + \alpha \frac{{\partial P}}{{\partial \eta }}}\\ {\frac{{\partial W}}{{\partial t}} = \alpha \frac{{\partial P}}{{\partial \xi }} + \left( {{\alpha ^2} + \frac{1}{{v_{{\rm{sm}}}^2}}} \right)\frac{{\partial P}}{{\partial \eta }}}\\ {\frac{{\partial P}}{{\partial t}} = \frac{{v_\tau ^2}}{{{v_{{\rm{sm}}}}}}\left[ {\frac{{\partial ({v_{{\rm{sm}}}}U)}}{{\partial \xi }} + \frac{{\partial ({v_{{\rm{sm}}}}W)}}{{\partial \eta }}} \right]} \end{array}} \right. $ | (10) |
式中:U、W分别为伪深度域中ξ、η方向对应速度分量;P为伪深度域的压力波场;vτ为伪深度域速度场。
在不考虑参数α(α=0)的影响时,式(10)可简化为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial U}}{{\partial t}} = \frac{{\partial P}}{{\partial \xi }}}\\ {\frac{{\partial W}}{{\partial t}} = \frac{1}{{v_{{\rm{sm}}}^2}}\frac{{\partial P}}{{\partial \eta }}}\\ {\frac{{\partial P}}{{\partial t}} = \frac{{v_\tau ^2}}{{{v_{{\rm{sm}}}}}}\left[ {\frac{{\partial ({v_{{\rm{sm}}}}U)}}{{\partial \xi }} + \frac{{\partial ({v_{{\rm{sm}}}}W)}}{{\partial \eta }}} \right]} \end{array}} \right. $ | (11) |
相比于声波方程(式(1)),简化后的伪深度域声波方程(式(11))只在纵向速度场更新中多乘了一个系数1/vsm2。这样只需更新更少的网格即可实现相同的正、反演效果,而计算量保持不变,从而减少存储空间占用和提高计算效率。
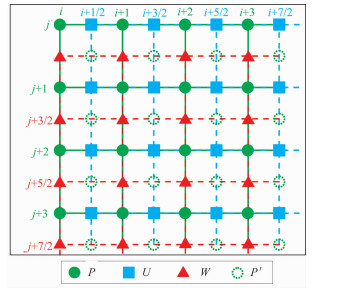
1.2 方程离散及吸收边界条件本文伪深度域声波方程离散和网格剖分与常规深度域声波方程所运用的有限差分交错网格法[25-26]相类似。但值得注意的是,在考虑式(10)中α参数不为零的情况时,为保证计算的合理性,在对伪深度域中U、W更新时需额外利用到压力场网格中间数据P′。因此,以四周压力场P的均值作为中间压力场P′,具体网格剖分方式如图 2所示。
|
图 2 伪深度域交错网格剖分示意图 |
对于时间和空间上的差分近似,采用与传统深度域交错网格法相同的离散规则,即压力和速度场的计算分别对应于t和t+Δt/2时刻进行。而空间差分近似则以高阶半网格方式实现,相应的空间差分系数如表 1所示。
|
|
表 1 交错网格法差分系数表[27] |
将伪深度域二维一阶速度—应力方程离散后可得
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {U|_{i + \frac{1}{2},j}^{t + \frac{1}{2}} = U|_{i + \frac{1}{2},j}^{t - \frac{1}{2}} + \frac{{\Delta t}}{{\Delta x}}\sum\limits_{l = 0}^{N - 1} {{C_{l + 1}}} (P|_{i + 1 + l,j}^t - P|_{i - l,j}^t) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha \frac{{\Delta t}}{{\Delta \tau }}\sum\limits_{l = 0}^{N - 1} {{C_{l + 1}}} ({P^\prime }|_{i,j + 1 + l}^t - {P^\prime }|_{i - l,j}^t)} \end{array}\\ \begin{array}{*{20}{l}} {W|_{i,j + \frac{1}{2}}^{t + \frac{1}{2}} = W|_{i,j + \frac{1}{2}}^{t - \frac{1}{2}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \alpha \frac{{\Delta t}}{{\Delta x}}\sum\limits_{l = 0}^{N - 1} {{C_{l + 1}}} ({P^\prime }|_{i + 1 + l,j}^t - {P^\prime }|_{i - l,j}^t) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {{\alpha ^2} + \frac{1}{{v_{{\rm{sm}}}^2}}} \right)\frac{{\Delta t}}{{\Delta \tau }}\sum\limits_{l = 0}^{N - 1} {{C_{l + 1}}} (P|_{i,j + 1 + l}^t - P|_{i,j - l}^t)} \end{array} \end{array} \right. $ | (12a) |
| $ \left\{ {\begin{array}{*{20}{l}} {P|_{i,j}^t = P|_{i,j}^{t - 1} + \frac{{v_\tau ^2}}{{v_{{\rm{sm}}}^2}}\frac{{\Delta t}}{{\Delta x}} \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{l = 0}^{N - 1} {{C_{l + 1}}} {v_{{\rm{sm}}}}(U|_{i + \frac{1}{2} + l,j}^{t - \frac{1}{2}} - U|_{i - \frac{1}{2} - l,j}^{t - \frac{1}{2}}) + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{v_\tau ^2}}{{{v_{{\rm{sm}}}}}}\frac{{\Delta t}}{{\Delta \tau }}\sum\limits_{l = 0}^{N - 1} {{C_{l + 1}}} {v_{{\rm{sm}}}}(W|_{i,j + \frac{1}{2} + l}^{t - \frac{1}{2}} - W|_{i,j - \frac{1}{2} - l}^{t - \frac{1}{2}})}\\ {P|_{i,j}^t = \frac{{P|_{i + 1,j}^t + P|_{i + 1,j + 1}^t + P|_{i,j + 1}^t + P|_{i,j}^t}}{4}} \end{array}} \right. $ | (12b) |
式中:Δx、Δτ分别为伪深度域纵横向采样间隔;Cl为有限差分系数;N为差分阶次的一半。
为解决人工引起的边界反射,本文采用分裂式PML吸收边界条件[28-29],将U、W和P分别沿ξ、η方向分解为两个部分
| $ \left\{ {\begin{array}{*{20}{l}} {U = {U_1} + {U_2}}\\ {W = {W_1} + {W_2}}\\ {P = {P_1} + {P_2}} \end{array}} \right. $ | (13) |
同时引入边界衰减因子σ1、σ2,对应带衰减因子的分裂式伪深度域声波方程可写为
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {U_1}}}{{\partial t}} + {\sigma _1} = \frac{{\partial P}}{{\partial \xi }}}\\ {\frac{{\partial {U_2}}}{{\partial t}} + {\sigma _2} = \alpha \frac{{\partial {P^\prime }}}{{\partial \eta }}}\\ {\frac{{\partial {W_1}}}{{\partial t}} + {\sigma _1} = \alpha \frac{{\partial {P^\prime }}}{{\partial \xi }}}\\ {\frac{{\partial {W_2}}}{{\partial t}} + {\sigma _2} = \left( {{\alpha ^2} + \frac{1}{{v_{{\rm{sm}}}^2}}} \right)\frac{{\partial P}}{{\partial \eta }}}\\ {\frac{{\partial {P_1}}}{{\partial t}} + {\sigma _1} = \frac{{v_\tau ^2}}{{{v_{{\rm{sm}}}}}}\frac{{\partial ({v_{{\rm{sm}}}}U)}}{{\partial \xi }}}\\ {\frac{{\partial {P_2}}}{{\partial t}} + {\sigma _2} = \frac{{v_\tau ^2}}{{{v_{{\rm{sm}}}}}}\frac{{\partial ({v_{{\rm{sm}}}}W)}}{{\partial \eta }}} \end{array}} \right. $ | (14) |
其中衰减因子σ1和σ2分别为
| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _1} = \frac{{3{v_{{\rm{max}}}}}}{{2\delta }}{\rm{ln}}\left( {\frac{1}{R}} \right){{\left( {\frac{{{\xi ^\prime }}}{\delta }} \right)}^2}}\\ {{\sigma _2} = \frac{{3{v_{{\rm{max}}}}}}{{2\delta }}{\rm{ln}}\left( {\frac{1}{R}} \right){{\left( {\frac{{{\eta ^\prime }}}{\delta }} \right)}^2}} \end{array}} \right. $ | (15) |
式中:vmax为速度场中最大速度值;δ为PML吸收层厚度;R为理想边界反射系数(通常取值10-6);ξ′和η′分别表示横、纵向计算点到正常计算区域之间的网格距离。
最终,得到带PML吸收边界条件的伪深度域二维时空域一阶速度—应力离散方程
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{U_1}|_{i + \frac{1}{2},j}^{t + \frac{1}{2}} = \frac{{2 - {\sigma _{1,i}}\Delta t}}{{2 + {\sigma _{1,i}}\Delta t}}{U_1}|_{i + \frac{1}{2},j}^{t - \frac{1}{2}} + \frac{2}{{2 + {\sigma _{1,i}}\Delta t}}\frac{{\Delta t}}{{\Delta x}} \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{l = 0}^{N - 1} {{C_{l + 1}}} (P|_{i + 1 + l,j}^t - P|_{i - l,j}^t)} \end{array}\\ \begin{array}{*{20}{l}} {{U_2}|_{i + \frac{1}{2},j}^{t + \frac{1}{2}} = \frac{{2 - {\sigma _{2,j}}\Delta t}}{{2 + {\sigma _{2,j}}\Delta t}}{U_2}|_{i + \frac{1}{2},j}^{t - \frac{1}{2}} + \frac{{2\alpha }}{{2 + {\sigma _{2,j}}\Delta t}}\frac{{\Delta t}}{{\Delta \tau }} \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{l = 0}^{N - 1} {{C_{l + 1}}} ({P^\prime }|_{i,j + 1 + l}^t - {P^\prime }|_{i,j - l}^t)} \end{array}\\ U|_{i + \frac{1}{2},j}^{t + \frac{1}{2}} = {U_1}|_{i + \frac{1}{2},j}^{t + \frac{1}{2}} + {U_2}|_{i + \frac{1}{2},j}^{t + \frac{1}{2}} \end{array} \right. $ | (16) |
| $ \begin{array}{*{20}{l}} {{W_1}|_{i,j + \frac{1}{2}}^{t + \frac{1}{2}} = \frac{{2 - {\sigma _{1,i}}\Delta t}}{{2 + {\sigma _{1,i}}\Delta t}}{W_1}|_{i,j + \frac{1}{2}}^{t + \frac{1}{2}} + \frac{{2\alpha }}{{2 + {\sigma _{1,i}}\Delta t}}\frac{{\Delta t}}{{\Delta x}} \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{l = 0}^{N - 1} {{C_{l + 1}}} ({P^\prime }|_{i + 1 + l,j}^t - {P^\prime }|_{i - l,j}^t)} \end{array} $ | (17a) |
| $ \left\{ {\begin{array}{*{20}{l}} {\begin{array}{*{20}{l}} {{W_2}|_{i,j + \frac{1}{2}}^{t + \frac{1}{2}} = \frac{{2 - {\sigma _{2,j}}\Delta t}}{{2 + {\sigma _{2,j}}\Delta t}}{W_2}|_{i,j + \frac{1}{2}}^{t + \frac{1}{2}} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {{\alpha ^2} + \frac{1}{{v_{{\rm{sm}}}^2}}} \right)\frac{2}{{2 + {\sigma _{2,j}}\Delta t}}\frac{{\Delta t}}{{\Delta \tau }}\sum\limits_{l = 0}^{N - 1} {{C_{l + 1}}} (P|_{i,j + 1 + l}^t - P|_{i,j - l}^t)}\\ {W|_{i,j + \frac{1}{2}}^{t + \frac{1}{2}} = {W_1}|_{i,j + \frac{1}{2}}^{t + \frac{1}{2}} + {W_2}|_{i,j + \frac{1}{2}}^{t + \frac{1}{2}}} \end{array}} \end{array}} \right. $ | (17b) |
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{P_1}|_{i,j}^t = \frac{{2 - {\sigma _{1,i}}\Delta t}}{{2 + {\sigma _{1,i}}\Delta t}}{P_1}|_{i,j}^{t - 1} + \frac{2}{{2 + {\sigma _{1,i}}\Delta t}}\frac{{v_\tau ^2}}{{{v_{{\rm{sm}}}}}}\frac{{\Delta t}}{{\Delta x}} \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{l = 0}^{N - 1} {{C_{l + 1}}} {v_{{\rm{sm}}}}(U|_{i + \frac{1}{2} + l,j}^{t - \frac{1}{2}} - U|_{i - \frac{1}{2} - l,j}^{t - \frac{1}{2}})} \end{array}\\ \begin{array}{*{20}{l}} {{P_2}|_{i,j}^t = \frac{{2 - {\sigma _{2,j}}\Delta t}}{{2 + {\sigma _{2,j}}\Delta t}}{P_2}|_{i,j}^{t - 1} + \frac{2}{{2 + {\sigma _{2,j}}\Delta t}}\frac{{v_\tau ^2}}{{{v_{{\rm{sm}}}}}}\frac{{\Delta t}}{{\Delta \tau }} \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{l = 0}^{N - 1} {{C_{l + 1}}} {v_{{\rm{sm}}}}(W|_{i,j + \frac{1}{2} + l}^{t - \frac{1}{2}} - W|_{i,j - \frac{1}{2} - l}^{t - \frac{1}{2}})} \end{array}\\ (P|_{i,j}^t = {P_1}|_{i,j}^t + {P_2}|_{i,j}^t + S|_{i,j}^t \end{array} \right. $ | (18) |
| $ {P^\prime }|_{i,j}^t = \frac{{P|_{i + 1,j}^t + P|_{i + 1,j + 1}^t + P|_{i,j + 1}^t + P|_{i,j}^t}}{4} $ | (19) |
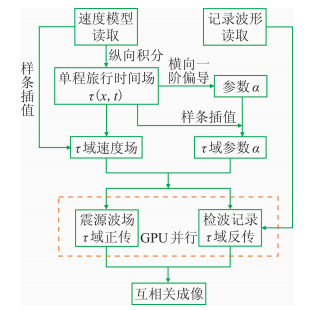
现阶段并行计算架构的选择有:MPI、OpenCL、CUDA和近几年出现的C++ AMP。其中MPI可以利用多个CPU并行协同处理同任务,而另外三种则属于GPU并行计算架构。与CPU并行架构相比,GPU并行架构计算效率更高,是当前的主要发展方向。三种GPU并行架构对比如表 2所示。C++ AMP并行计算架构相对容易实现且无过多限制,同时C++ AMP架构还提供了一定的显存及线程优化控制方法,其良好的硬件兼容性使代码能够在AMD及NVIDIA等不同硬件设备上运行,大大降低了并行成本,结合其简单易学及编程环境搭建简单等优势,C++ AMP并行架构成为Windows系统下并行计算的一个不错选择。本文在C++AMP架构下实现并行加速优化,具体实现过程可大致分为CPU端算法与GPU端算法两部分组成(图 3):①CPU端负责简单数据的处理及传递,如文件读取、写入及数据交换等;②GPU端负责大量数据的并行计算,如波场P、U、W的迭代更新等。
|
图 3 并行优化算法示意图 |
|
|
表 2 GPU端不同并行架构的优势及主要限制对比 |
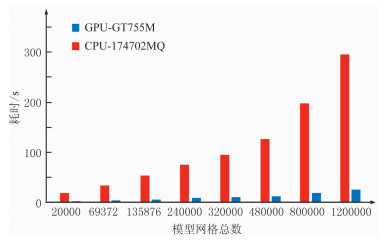
图 4对比了相同正演参数下CPU常规计算与C++AMP架构下并行计算耗时,可以看出,C++AMP架构下的并行计算效率约为并行前的10倍,且随着模型网格总数的增加而增高。当然,加速效果同样与所使用的GPU性能有关。同时需要指出的是,该测试仅是在完成算法且未进行编程优化的情况下得到的,在完成编程优化后加速效果有望进一步提高。
|
图 4 不同总网格数时C++ AMP GPU并行架构和与CPU常规正演计算耗时对比均统计相同参数下正演10000次总计算耗时 |
为了验证并行架构下伪深度域算法的可靠性,分别采用二维盐丘模型、黔北凤岗断块模型和复杂逆掩构造模型进行正演及逆时偏移成像试算,采用带照明补偿的成像条件。逆向波场重构采用边界存储法[30],相比直接储存每一时刻波场,可降低约90%~95%的存储空间,大大减少了数据读写量。
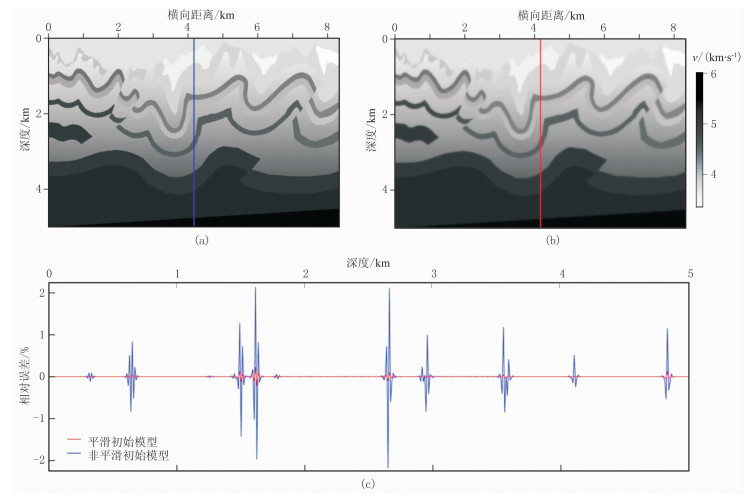
需要指出的是,若采用未平滑模型作为初始速度场,则会在变换过程中因初始速度模型纵向速度值变化不均匀导致变换结果存在一定插值误差,且正反变换两次的样条插值会导致一定的误差积累,在纵向速度变换剧烈处尤为严重。通过实验发现,采用低平滑速度模型作为正演、偏移速度场,高平滑速度模型作为积分速度场,能够有效减少变换带来的插值误差,同时也能减小参数α的横向变化,提高算法的稳定性。以复杂逆掩构造模型为例,对比低平滑初始速度场与非平滑初始速度场反变换结果(图 5)可看出,采用低平滑初始速度场较非平滑初始速度场反变换后结果误差较小、精度较高,能相对准确地将伪深度域成像结果反变换回深度域。
|
图 5 逆掩构造模型不同速度场反变换结果及其相对误差 (a)非平滑初始速度场;(b)低平滑初始速度场;(c)相对误差曲线 |
模型中盐丘与围岩速度差较大,能检验正演和偏移算法对高速异常体的适应性。该模型网格数为676×200,横、纵向间距均为3m。正演采样间隔为1ms、长度为1.2s,震源选择主频为25Hz的雷克子波;采用双边接收方式,最小炮检距为0,最大炮检距为1014m,道间距为3m。伪深度采样间隔Δτ=2ms,由
| $ {n_\tau } = {\rm{INT}} \left( {\frac{{{\tau _{{\rm{max}}}}}}{{\Delta \tau }}} \right) $ | (20) |
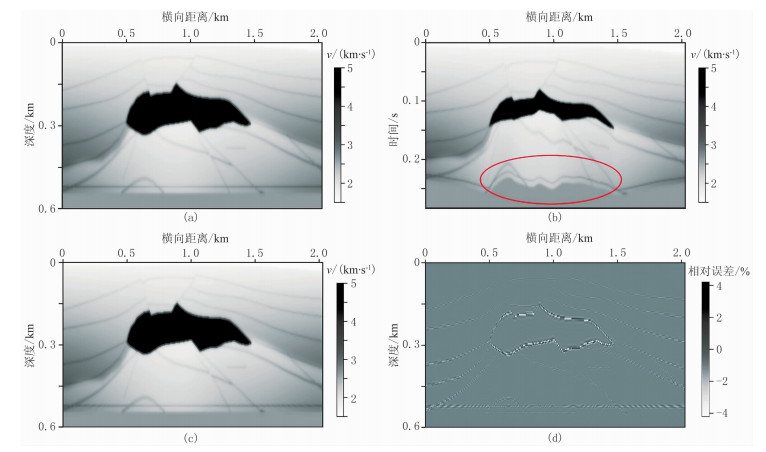
计算的伪深度网格点数nτ=142,可见伪深度变换可减少约29.0%的存储需求。式中:τmax为最大单程旅行时;INT(·)为向上取整函数。原始速度模型和伪深度域正、反变换模型如图 6所示,伪深度变换导致高速区抽稀采样、高速体下方呈现“界面上凸”现象(图 6b椭圆所示),做反变换后(图 6c)与原始速度场(图 6a)的相对误差(图 6d)最大约为4.2%。采用相同模拟参数,图 6a速度场的深度域正演记录如图 7a所示,伪深度域正演记录如图 7b所示,二者相对误差不超过1.5%(图 7c)。
|
图 6 盐丘模型 (a)深度域原始速度场;(b)伪深度域速度场;(c)反变换速度场;(d)图c的相对误差 |

|
图 7 盐丘模型常规深度域(a)与伪深度域(b)正演记录及其差值(c) |
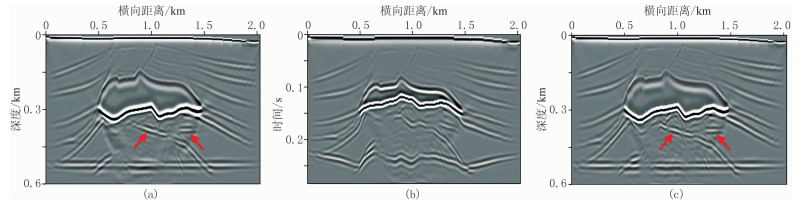
逆时偏移实验中,共计模拟169炮,起始炮点位于0,炮点距为12m,其他参数与正演保持一致,深度域和伪深度域成像结果如图 8所示。对比常规深度域与伪深度域反变换偏移结果可以看出伪深度域逆时偏移对高速异常体及其下方层位(红色箭头所示)均有较精确的成像效果。
|
图 8 盐丘模型逆时偏移结果 (a)深度域偏移结果;(b)伪深度域偏移结果;(c)伪深度域偏移结果的反变换 |
根据黔北凤岗页岩勘探区的前期钻孔及地震解释成果,设计了凤岗断块模型(图 9a)。该模型主要展示了研究区断层发育特征,其中上部多为高速灰岩地层,下部为低速泥页岩地层。模型网格数为737×275,横、纵向网格间距均为10m。时间采样间隔置为0.5ms,选择主频为25Hz的雷克子波为震源,模拟时长为1.8s;采用双边接收方式,最小炮检距为0,最大炮检距为3690m,道间距为10m。伪深度域采样间隔为3.76ms,伪深度网格点数为214(图 9b),可见伪深度域变换能节省22.18%的存储空间。

|
图 9 凤岗断块模型速度场变换结果 (a)深度域原始速度场;(b)伪深度域速度场 |
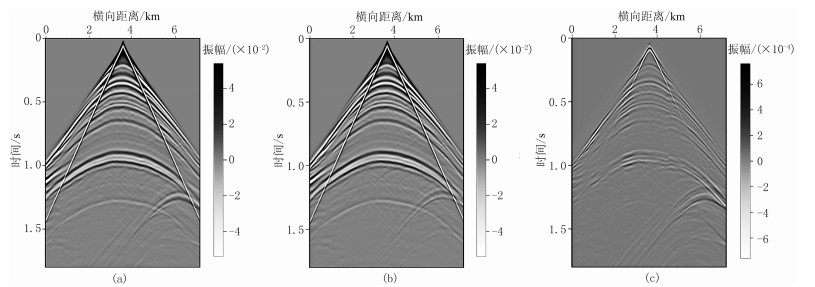
同样,由图 9b能很明显看出伪深度域速度场的变形现象,尤其是浅色低速地层(泥页岩层)导致下方地层呈现“下拽”现象(图中红圈所示),且其程度随着断层倾角的变大而增加。深度域和伪深度域模拟记录及差值如图 10所示,二者的相对误差约为1.5%。
|
图 10 凤岗断块模型常规深度域(a)与伪深度域(b)正演记录及其差值(c) |
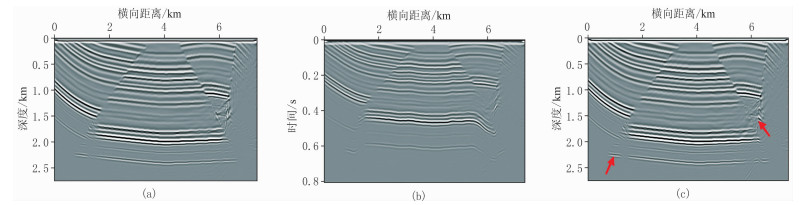
起始炮点位于0,炮点距为40m,共模拟184炮,其逆时偏移结果如图 11所示。凤岗断块模型深部低速页岩层的成像效果同样很好(图 11红色箭头所示),细节部分得以充分体现。
|
图 11 凤岗断块模型逆时偏移成像结果 (a)深度域偏移结果;(b)伪深度域偏移结果;(c)伪深度域反变换偏移结果 |
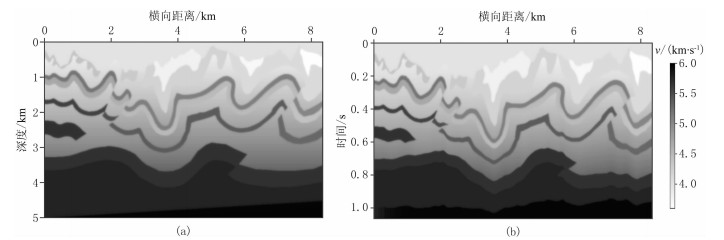
复杂逆掩断层模型(图 12a)浅、表层速度变化剧烈,褶皱构造、高陡构造及逆掩断层发育[31],能够检测不同模拟、偏移算法的适用性。该模型网格数为834×500,横纵向网格间距均为10m。时间采样间隔置为0.8ms,选择主频为30Hz的雷克子波为震源,模拟时长为4s;采用双边接收方式,最小炮检距为0m,最大炮检距为4170m,道间距为10m。伪深度域采样间隔为2.5ms,伪深度网格点数为426(图 12b),可见伪深度域变换能够减少14.8%的存储需求。同时,为减少速度变换过程中可能出现的抽样误差,正演及偏移成像均采用低平滑模型作为初始模型,高平滑模型作为变换速度场。
|
图 12 逆掩构造模型速度场变换结果 (a)深度域原始速度场;(b)伪深度域速度场 |
逆掩构造模型深度域和伪深度域模拟记录及差值如图 13所示,二者的相对误差约为2.2%,可忽略不计。417炮模拟记录(间隔20m)的逆时偏移结果如图 14所示,对比两种方法成像结果可知,对于复杂逆掩构造模型而言,常规深度域与伪深度域反变换成像结果均能很好对应。

|
图 13 逆掩构造模型常规深度域(a)与伪深度域(b)正演记录及其差值(c) |

|
图 14 逆掩构造模型逆时偏移结果 (a)深度域偏移结果;(b)伪深度域偏移结果;(c)伪深度域反变换偏移结果 |
由以上三个模型试算结果可以看出,伪深度域法对断层构造、深部薄互层、高速体边界及复杂高陡逆掩构造都有很好的成像效果,反变换后成像层位依然清晰准确,验证了算法的正确性和适用性。对比两种偏移方法(表 3)可以看出伪深度域节省约20%~35%的整体耗时,减少了15%~30%存储占用。
|
|
表 3 逆时偏移算法网格数目及耗时对比统计 |
本文通过引入曲坐标变换,推导了伪深度域声波方程及其离散形式,实现了伪深度域正、反向波场延拓。
(1) 相比传统深度域正演,伪深度域法可以起到波场“均衡采样”作用,变换后波场在伪深度域计算中任何位置都呈现出纵向上均匀采样的状态,能够避免深度域下高速层位波场的过采样,减少深度方向的样点数。在保证计算精度的情况下,降低存储空间需求及提高计算效率。标准盐丘模型以及黔北凤岗断块模型的逆时偏移试算表明,与深度域方法相比,伪深度域法能够节省15%~30%的数据存储量,效率提高了20%~35%。
(2) 将C++ AMP并行架构与伪深度域法正演、偏移算法相结合,大幅提高了计算效率,方便了算法的推广与应用。
(3) 采用低平滑速度场作为正演、偏移速度场能够有效降低正反变换中抽样插值带来的误差,增加成像结果反变换精度。
在考虑到现阶段实际工程中越发复杂的地下构造及更加精细化的成像需求,将该方法进一步推广到最小二乘法逆时偏移及全波形反演具有重要意义。
| [1] |
Mcmechan G A. Migration by extrapolation of time-dependent boundary values[J]. Geophysical Prospecting, 2006, 31(3): 413-420. |
| [2] |
Baysal E, Kosloff D, Sherwood J, et al. Reverse time migration[J]. Geophysics, 1983, 48(11): 1514-1524. |
| [3] |
李庆洋.复杂介质地震波正演模拟与最小二乘偏移研究[D].山东青岛: 中国石油大学(华东), 2017. http://cdmd.cnki.com.cn/Article/CDMD-10425-1019836689.htm
|
| [4] |
李庆洋, 黄建平, 李振春, 等. 基于L1范数正则化的三维多震源最小二乘逆时偏移[J]. 中国石油大学学报(自然科学版), 2019, 43(4): 52-59. LI Qingyang, HUANG Jianping, LI Zhenchun, et al. 3D multi-source least-squares reverse time migration based on L1 norm regularization[J]. Journal of China University of Petroleum(Edition of Natural Science), 2019, 43(4): 52-59. |
| [5] |
李振春, 周丽颖, 黄建平, 等. 最小二乘逆时偏移在碳酸盐岩缝洞型储层成像中的应用[J]. 地球物理学进展, 2017, 32(2): 664-671. LI Zhenchun, ZHOU Liying, HUANG Jianping, et al. Application of least square reverse time migration in the imaging of fractured-type carbonate reservoirs[J]. Progress in Geophysics, 2017, 32(2): 664-671. |
| [6] |
黄金强, 李振春. 基于Low-rank分解的复杂TI介质纯qP波正演模拟与逆时偏移[J]. 地球物理学报, 2017, 60(2): 704-721. HUANG Jinqiang, LI Zhenchun. Modeling and reverse time migration of pure quasi-P-waves in complex TI media with a low-rank decomposition[J]. Chinese Journal of Geophysics, 2017, 60(2): 704-721. |
| [7] |
李振春. 地震偏移成像技术研究现状与发展趋势[J]. 石油地球物理勘探, 2014, 49(1): 1-21. LI Zhenchun. Research status and development trends for seismic migration technology[J]. Oil Geophysical Prospecting, 2014, 49(1): 1-21. |
| [8] |
张春燕, 李振春, 孙小东. 逆时偏移方法技术进展综述[J]. 勘探地球物理进展, 2010, 33(5): 309-317. ZHANG Chunyan, LI Zhenchun, SUN Xiaodong. Review of reverse-time migration[J]. Progress in Exploration Geophysics, 2010, 33(5): 309-317. |
| [9] |
刘喜武, 刘洪. 波动方程地震偏移成像方法的现状与进展[J]. 地球物理学进展, 2002, 17(4): 582-591. LIU Xiwu, LIU Hong. Status and progress on wave equation migration methods[J]. Progress in Geophy-sics, 2002, 17(4): 582-591. |
| [10] |
黄金强, 李振春, 江文. TTI介质Low-rank有限差分法高效正演模拟及逆时偏移[J]. 石油地球物理勘探, 2018, 53(6): 1198-1209. HUANG Jinqiang, LI Zhenchun, Jiang Wen. An efficient forward modeling with the low-rank finite-difference algorithm for complex TTI media and its application in reverse time migration[J]. Oil Geophy-sical Prospecting, 2018, 53(6): 1198-1209. |
| [11] |
陈可洋. 地震波逆时偏移方法研究综述[J]. 勘探地球物理进展, 2010, 33(3): 153-159. CHEN Keyang. Review of seismic reverse time migration methods[J]. Progress in Exploration Geophysics, 2010, 33(3): 153-159. |
| [12] |
张剑锋. 弹性波数值模拟的非规则网格差分法[J]. 地球物理学报, 1998, 41(增刊1): 357-366. ZHANG Jianfeng. Non-orthogonal grid finite-diffe-rence method for numerical simulation of elastic wave propagation[J]. Chinese Journal of Geophysics, 1998, 41(S1): 357-366. |
| [13] |
朱生旺, 魏修成. 波动方程非规则网格任意阶精度差分法正演[J]. 石油地球物理勘探, 2005, 40(2): 149-153. ZHU Shengwang, Wei Xiucheng. Differential forward modeling of wave equation having irregular grid and any-order precision[J]. Oil Geophysical Prospecting, 2005, 40(2): 149-153. |
| [14] |
裴正林. 任意起伏地表弹性波方程交错网格高阶有限差分法数值模拟[J]. 石油地球物理勘探, 2004, 39(6): 629-634. PEI Zhenglin. Numerical modeling using staggered-grid high-order finite-difference of elastic wave equation on arbitrary relief surface[J]. Oil Geophysical Prospecting, 2004, 39(6): 629-634. |
| [15] |
李胜军, 孙成禹, 倪长宽, 等. 声波方程有限差分数值模拟的变网格步长算法[J]. 工程地球物理学报, 2007, 4(3): 207-212. LI Shengjun, SUN Chengyu, NI Changkuan, et al. Acoustic equation numerical modeling on a grid of va-rying spacing[J]. Chinese Journal of Engineering Geophysics, 2007, 4(3): 207-212. |
| [16] |
孙成禹, 李胜军, 倪长宽, 等. 波动方程变网格步长有限差分数值模拟[J]. 石油物探, 2008, 47(2): 123-127. SUN Chengyu, LI Shengjun, NI Changkuan, et al. Wave equation numerical modeling by finite difference method with varying grid spacing[J]. Geophysical Prospecting for Petroleum, 2008, 47(2): 123-127. |
| [17] |
刘志强, 孙建国, 孙辉, 等. 基于自适应网格的仿真型有限差分地震波数值模拟[J]. 地球物理学报, 2016, 59(12): 4654-4665. LIU Zhiqiang, SUN Jianguo, SUN Hui, et al. Mimetic finite-difference numerical simulation of seismic wave based on the adaptive grid[J]. Chinese Journal of Geophysics, 2016, 59(12): 4654-4665. |
| [18] |
宓铁良.自适应网格细化算法模拟地震波传播[D].北京: 清华大学, 2010.
|
| [19] |
Alkhalifah T, Fomel S, Biondi A B. The space-time domain:theory and modelling for anisotropic media[J]. Geophysical Journal of the Royal Astronomical Society, 2001, 144(1): 105-113. |
| [20] |
Ma X, Alkhalifah T. Wavefield extrapolation in pseudo depth domain[J]. Geophysics, 2013, 78(2): S81-S91. |
| [21] |
李庆洋, 黄建平, 李振春, 等. 伪深度域声波数值模拟方法及应用[J]. 石油地球物理勘探, 2015, 50(2): 283-289. LI Qingyang, HUANG Jianping, LI Zhenchun, et al. Acoustic wave numerical simulation in pseudo-depth domain[J]. Oil Geophysical Prospecting, 2015, 50(2): 283-289. |
| [22] |
柯璇, 石颖, 张伟, 等. 基于多线程多GPU并行加速的最小二乘逆时偏移算法[J]. 石油物探, 2019, 58(1): 88-102. KE Xuan, SHI Ying, ZHANG Wei, et al. Least-squares reverse time migration based on multi-thread and multi-GPU parallel acceleration[J]. Geophysical Prospecting for Petroleum, 2019, 58(1): 88-102. |
| [23] |
武泗海, 赵虎, 尹成, 等. 基于C++ AMP并行加速的三维弹性波波动方程数值模拟[J]. 物探化探计算技术, 2017, 39(5): 643-648. WU Sihai, ZHAO Hu, YIN Cheng, et al. Accelerated parallelism in numerical simulation for 3D elastic wave equation with C++AMP[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2017, 39(5): 643-648. |
| [24] |
段沛然, 谷丙洛, 李振春. 基于优化算子边界存储策略的高效逆时偏移方法[J]. 石油地球物理勘探, 2019, 54(1): 93-101. DUAN Peiran, GU Bingluo, LI Zhenchun. An efficient reverse time migration in the vertical time domain based on optimal operator boundary storage strategy[J]. Oil Geophysical Prospecting, 2019, 54(1): 93-101. |
| [25] |
裴正林, 牟永光. 非均匀介质地震波传播交错网格高阶有限差分法模拟[J]. 石油大学学报(自然科学版), 2003, 27(6): 17-21. PEI Zhenglin, MU Yongguang. A staggered-grid high-order difference method for modeling seismic wave propagation in inhomogeneous media[J]. Journal of China University of Petroleum (Edition of Natural Science), 2003, 27(6): 17-21. |
| [26] |
陈可洋. 标量声波波动方程高阶交错网格有限差分法[J]. 中国海上油气, 2009, 21(4): 232-236. CHEN Keyang. High-order staggered-grid finite difference scheme for scalar acoustic wave equation[J]. China Offshore Oil and Gas, 2009, 21(4): 232-236. |
| [27] |
董良国, 马在田, 曹景忠, 等. 一阶弹性波方程交错网格高阶差分解法[J]. 地球物理学报, 2000, 43(3): 411-419. DONG Liangguo, MA Zaitian, CAO Jingzhong, et al. A staggered-grid high-order difference method of one-order elastic wave equation[J]. Chinese Journal of Geophysics, 2000, 43(3): 411-419. |
| [28] |
李振春, 田坤, 黄建平, 等. 多轴完全匹配层的非分裂实现[J]. 地球物理学进展, 2013, 28(6): 2984-2992. LI Zhenchun, TIAN Kun, HUANG Jianping, et al. An unsplit implementation of the multiaxial perfectly matched layer[J]. Progress in Geophysics, 2013, 28(6): 2984-2992. |
| [29] |
董良国. 弹性波数值模拟中的吸收边界条件[J]. 石油地球物理勘探, 1999, 34(1): 45-56. DONG Liangguo. Absorptive boundary condition in elastic-wave numerical modeling[J]. Oil Geophysical Prospecting, 1999, 34(1): 45-56. |
| [30] |
王保利, 高静怀, 陈文超, 等. 地震叠前逆时偏移的有效边界存储策略[J]. 地球物理学报, 2012, 55(7): 2412-2421. WANG Baoli, GAO Jinghuai, CHEN Wenchao, et al. Efficient boundary storage strategies for seismic reverse time migration[J]. Chinese Journal of Geophy-sics, 2012, 55(7): 2412-2421. |
| [31] |
周东红, 黄金强, 李振春, 等. 各向异性介质一阶速度-应力方程平面波最小二乘逆时偏移[J]. 中国石油大学学报(自然科学版), 2019, 43(6): 48-58. ZHOU Donghong, HUANG Jinqiang, LI Zhenchun, et al. Plane-wave least-squares reverse time migration based on the first-order velocity-stress equation in anisotropic media[J]. Journal of China University of Petroleum (Edition of Natural Science), 2019, 43(6): 48-58. |



 王甘露, 贵州省贵阳市花溪区花溪大道南段2708号贵州大学西校区资源与环境工程学院, 550025。Email:
王甘露, 贵州省贵阳市花溪区花溪大道南段2708号贵州大学西校区资源与环境工程学院, 550025。Email: