② 国油伟泰(北京)科技有限公司, 北京 100176;
③ 中国石油新疆油田公司, 新疆克拉玛依 834000;
④ 中国石油集团东方地球物理公司, 河北涿州 072750
② GeoApex Technology(Beijing) Inc., Beijing 100176, China;
③ PetroChina Xinjiang Oilfield Company, Karamay, Xinjiang 834000, China;
④ BGP Inc., CNPC, Zhuozhou, Hebei 072751, China
逆时偏移成像效果取决于原始地震数据的质量、速度模型的精度和逆时偏移算法的精度。本文的研究基于陆上地震数据,主要讨论如何提高地震数据的质量和速度模型的精度。文中所阐述的空间地震子波一致性相位校正技术、近地表Q吸收补偿技术、基于模式的自适应频散面波衰减技术等确保了前期处理数据的质量[1-7],基于模式的全波形反演技术确保了速度模型精度,最终确保了逆时偏移成像的质量。空间地震子波一致性相位校正技术是基于叠加能量最大化通过最小平方迭代求解炮点、检波点的相位校正算子,使空间地震子波趋于一致。近地表Q吸收补偿技术是基于地震波传播吸收衰减规律,对近地表吸收造成的高频衰减进行补偿。基于模式的自适应频散面波衰减技术是首先通过正演模拟或基于相位变换法计算或预测频散面波模型,然后通过基于模式的自适应减去法去除地震记录中的频散面波,该技术在去除面波的同时不会伤及有效信号。
众所周知,全波形反演技术已广泛应用于高精度速度模型建立[8-16],遗憾的是目前的常规全波形反演技术存在较大的缺陷,比如“周期跳跃”现象导致目标函数的局部极值问题[2],以及严重依赖于地震数据的低频信息,而低频成分通常信噪比也较低,最终降低了速度模型的精度。自适应全波形反演通过使用自适应匹配滤波算子提供了一个较为稳健、高效地解决“周期跳跃”问题的手段[17-20],它通过使速度模型正演所得地震记录与实际接收地震记录之比接近1求解新的速度模型。为进一步提高自适应全波形反演的精度和效率,本文提出了基于模式的自适应全波形反演技术,通过使用基于模式的自适应匹配滤波算子取代常规自适应全波形反演中的自适应匹配滤波算子,提高最终逆时偏移的成像精度[8]。
将以上关键技术融合,提出了一个更加实用的提高逆时偏移成像精度的流程。对多块实际地震资料的处理结果表明,成像效果得到了较大改善,验证了本文技术和流程的有效性。
1 方法原理将包含以上关键技术的新流程分为如下四个主要部分:①近地表异常校正,它包括空间上地震子波相位畸变校正、空间振幅校正、静校正和近地表Q吸收校正等;②高保真噪声衰减,比如频散面波衰减、高分辨率多次波衰减和不伤害有效信号的强能量不规则干扰波衰减等;③提高分辨率的反褶积技术;④全波形反演算法的改进,比如不产生“周期跳跃”的可利用有效波主频带的基于模式的自适应全波形反演技术。本文主要讨论常规流程中没有的或者经过改进的关键处理技术。
1.1 空间地震子波一致性相位校正在实际地震资料处理过程中,如何处理好地震子波在空间方向上的一致性,即子波的相位变化是至关重要的。目前常规处理技术只是对空间子波相位做一个常相位的校正,不能满足子波任意相位变化的实际情况。也就是说,还没有对于子波的任意相位进行一致性校正的并可广泛应用实际的有效手段。本文采用一种叫做空间地震子波一致性相位校正的技术,以消除空间方向上地震子波相位的畸变,使地震子波波形在空间上保持一致,为后期全波形反演、逆时偏移准备统一的子波。首先求取炮点的相位校正算子,然后再求取检波点的相位校正算子。以求解炮点的相位校正算子为例,可通过下式迭代求解
| $ \begin{array}{l} \sum\limits_{k = - K}^K {{\phi _{{i_0}}}} (\tau ){A_{RR}}(\tau - k) = {B_{RR}}( - k)\\ k = - K, - K + 1, \cdots ,0, \cdots ,K - 1,K \end{array} $ | (1) |
式中:K为相位校正算子半支长度;ϕi0为第i0个炮点的相位校正算子;ARR和BRR的表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {{A_{RR}}(\tau - k) = \sum\limits_{l = {M_{{i_0}}}}^{M_{{i_0}}^\prime } {\sum\limits_t {{R_{E,D}}} } (t - k){R_{E,D}}(t - \tau )}\\ {{B_{RR}}( - k) = \sum\limits_{l = {M_{{i_0}}}}^{M_{{i_0}}^\prime } {\sum\limits_t {{R_{E,D}}} } (t - k){R_{\hat E,\hat D}}(t)} \end{array}} \right. $ | (2) |
其中:i0为正在计算的相位算子对应的炮序号;El, i0(t)为第l个CMP道集、不包含第i0炮的动校叠加道;
| $ \left\{ {\begin{array}{*{20}{l}} {{R_{E,D}}(t) = E_{l,{i_0}}^{(p)}(t) \otimes D_{{i_i},j}^{(p)}(t)}\\ {{R_{\hat E,\hat D}}(t) = \hat E_{l,{i_0}}^{(p)}(t) \otimes \hat D_{{i_i},j}^{(p)}(t)} \end{array}} \right. $ | (3) |
式中“⊗”表示互相关。
相位校正算子的初值可设为脉冲函数δ(t),通过迭代可计算炮点的相位校正算子ϕi0(t)。检波点的相位校正算子也可用相同的方式迭代求取。通过炮点、检波点相位校正算子的应用,空间方向上地震子波波形的一致性会得到较大改善。
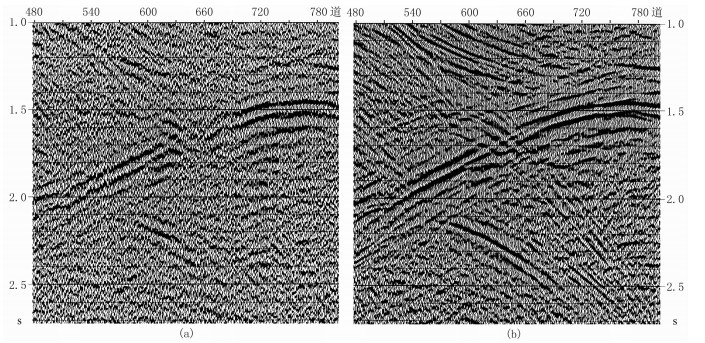
与空间地震子波相位校正前叠加剖面(图 1a)相比,在相位校正后的叠加剖面(图 1b)上,无论反射同相轴还是弱的绕射波同相轴的连续性都明显增强。
|
图 1 空间地震子波一致性相位校正前(a)、后(b)的叠加剖面 |
一般情况下近地表异常会导致地震记录的高频吸收能量衰减,从而降低地震记录的分辨率。由于近地表Q值在空间上的差异导致地震记录在空间上衰减程度不均,使地震记录在空间方向上频率特征差异较大,因此在处理时必须消除这种影响。首先通过Q层析求取近地表Q值体,然后再通过下式实现吸收补偿
| $ \begin{array}{*{20}{l}} {D(\tau + \Delta \tau ,\omega ) = D(\tau ,\omega ){\rm{exp}}\left[ {{{\left( {\frac{\omega }{{{\omega _{\rm{h}}}}}} \right)}^{ - \gamma }}\frac{{\omega t}}{{2Q}}} \right] \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}\left[ {{\rm{i}}{{\left( {\frac{\omega }{{{\omega _{\rm{h}}}}}} \right)}^{ - \gamma }}\omega t} \right]} \end{array} $ | (4) |
式中:
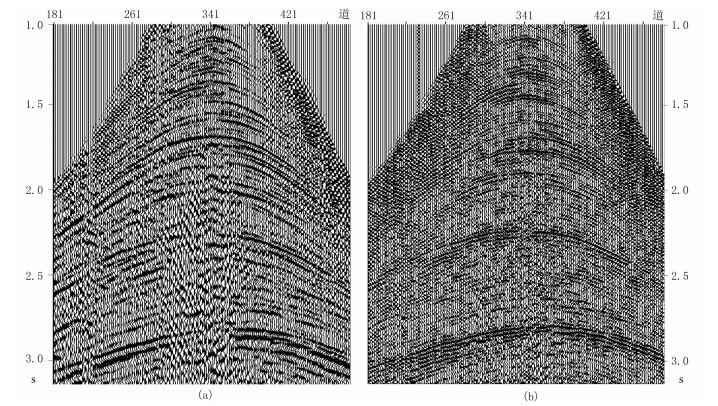
图 2为近地表Q吸收补偿前、后的单炮记录对比,可以清楚地看出,补偿后单炮记录的分辨率得到了明显提高,且道间的频率特征也趋于一致。图 3为近地表一致性吸收补偿前、后的逆时偏移剖面对比,从红圈中可以清楚地发现,近地表一致性吸收补偿提高了逆时偏移剖面分辨率、增强了同相轴的连续性和可追踪性。
|
图 2 近地表Q吸收补偿前(a)、后(b)的单炮记录 |

|
图 3 近地表Q吸收补偿前(a)、后(b)的逆时偏移剖面 |
对于陆上地震资料来说,全波形反演和逆时偏移都不能模拟面波,因此在全波形反演和逆时偏移之前必须先消除面波。一般情况下面波都以低速、低频率和强振幅形式出现,甚至出现很强的频散、假频等。常规全波形反演主要利用受面波影响较大的低频成分,因此必须在保证有效波低频成分不被损伤的情况下消除面波。本文消除频散面波策略为:首先通过面波模拟预测面波模型;然后通过相位匹配和基于模式的自适应减去法消除面波。
1.3.1 面波模型获取面波模型数据可通过面波正演模拟或相位匹配法获得。正演模拟是通过近地表速度反演方法得到较为精确的近地表速度模型,应用该速度模型正演模拟面波数据,其中包含了常规面波预测无法得到的散射部分。相位匹配法是在十字排列域做相位匹配获取面波模型。
对于陆上观测,三维炮集记录和模拟的面波一般情况下都不适合三维滤波,因为一般采集线距较大,所以空间假频比较严重。另外,面波在近炮线的排列上呈线性分布,而在远离炮线的排列上成双曲线形式出现,因此在炮集上采用基于线性滤波的算法进行滤波时失效。
为避免面波假频和同相轴非线性问题,本文将地震数据抽到十字排列域。在十字排列域面波是以椎体形状出现,并在时间等时切片上是圆环形,且在十字排列域面波的空间假频将明显减小,因为十字排列道集的空间采样是由炮点距和检波点距决定的。
为了进一步减少空间假频和频散效应,使用相位匹配的算法消除十字排列域面波的空间假频和频散效应,然后再通过使用基于模式的自适应减去法来消除面波。在十字排列域,面波的相位匹配过程可表示为与面波匹配的分量DL(x, y, ω)和不匹配的分量D0(x, y, ω)之和,具体表达式为
| $ \begin{array}{*{20}{c}} {D(x,y,\omega ){\rm{exp}}[{\rm{i}}({K_{x,L}}x + {K_{y,L}}y)]}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = {D_0}(x,y,\omega ) + {D_L}(x,y,\omega )} \end{array} $ | (5) |
| $ \begin{array}{*{20}{l}} {{D_0}(x,y,\omega ) = \frac{{\Delta S}}{{4{\pi ^2}}}\left\{ {\sum\limits_{m = 0,m \ne L}^M D ({k_{x,m}},{k_{y,m}},\omega ) \times } \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}\{ - {\rm{i}}[({k_{x,m}}x + {k_{y,m}}y) - }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} ({K_{x,L}}x + {K_{y,L}}y)]\} \} } \end{array} $ | (6) |
| $ \begin{array}{*{20}{l}} {{D_L}(x,y,\omega ) = \frac{{\Delta S}}{{4{\pi ^2}}}\{ D({k_{x,L}},{k_{y,L}},\omega ) \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\rm{exp}}\{ - {\rm{i}}[({k_{x,L}}x + {k_{y,L}}y) - ({K_{x,L}}x + {K_{y,L}}y)]\} \} } \end{array} $ | (7) |
式中:M为Fourier域总点数;L表示低波数分量;ΔS为Fourier域的面元面积;D(kx, ky, ω)为三维离散Fourier变换后的地震数据;D(x, y, ω)为频率空间域的地震数据;DL(x, y, ω)为需相位匹配的面波数据,主要由低波数分量构成;D0(x, y, ω)为除需相位匹配的面波以外的数据;kx, Lx+ky, Ly为面波匹配数据的近似相位,如果近似相位足够靠近真实的相位Kx, Lx+Ky, Ly,式(7)的指数项就很接近零,并且DL(x, y, ω)主要是由低波数分量构成。
1.3.2 基于模式的自适应减去法模拟的面波与地震数据中的真实面波不能完全吻合,需通过自适应匹配滤波减去法消除地震记录中的真实面波[2]。当信号与干扰波相互交叉干涉时,传统的自适应减去法在面波自适应衰减完成时往往导致信号畸变。
为克服常规自适应减去法的缺陷,提出了一种基于模式的自适应算法。该算法建立如下矩阵方程并求解
| $ \mathit{\boldsymbol{EB}}(\mathit{\boldsymbol{Nf}} - \mathit{\boldsymbol{D}}) \approx 0 $ | (8) |
式中:D为输入数据矩阵;N为模拟的面波数据矩阵;f为自适应匹配滤波算子矩阵;E为信号的投影预测误差滤波算子(PEF)矩阵;B为信号的投影预测滤波算子矩阵,其表达式为
| $ \mathit{\boldsymbol{B}} = {\varepsilon ^2}\mathit{\boldsymbol{I}}{(\mathit{\boldsymbol{E}}{\mathit{\boldsymbol{E}}^{\rm{H}}} + {\varepsilon ^2}\mathit{\boldsymbol{I}})^{ - 1}} $ | (9) |
其中:ε为白噪系数;I为单位矩阵;上标“H”表示矩阵共轭转置。
式(8)中Nf-D为有效信号和随机噪声。为减少随机噪声对求解过程的影响,对其进行投影预测滤波,也就是对Nf-D施加投影预测滤波算子B。为进一步优化并约束求解过程,再施加一个投影预测误差算子E,并求最小平方解。最终f的最小平方解可表示为
| $ \mathit{\boldsymbol{f}} = {({\mathit{\boldsymbol{N}}^{\rm{H}}}{\mathit{\boldsymbol{B}}^{\rm{H}}}{\mathit{\boldsymbol{E}}^{\rm{H}}}\mathit{\boldsymbol{EBN}})^{ - 1}}{\mathit{\boldsymbol{N}}^{\rm{H}}}{\mathit{\boldsymbol{B}}^{\rm{H}}}{\mathit{\boldsymbol{E}}^{\rm{H}}}\mathit{\boldsymbol{EBD}} $ | (10) |
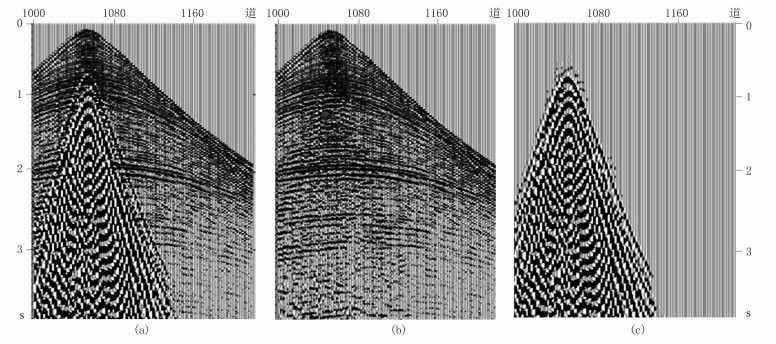
图 4a为从一个十字排列中抽出的共检波点道集,可见较强的面波,并且面波有很强的频散现象。图 4b为本文方法面波去除结果,无明显的面波剩余能量,恢复了被面波掩盖的有效信号。图 4c为本方法去除的面波,从中可以看出剔除的面波中无明显有效信号,说明去噪过程中没有伤及有效波,表明本文采用的基于模式的自适应面波衰减技术有较好的信号保真性。
|
图 4 面波去除前、后的共检波点道集 (a)原始地震记录;(b)去除面波后的记录;(c)去除的面波 |
全波形反演技术是目前建立高精度速度模型最有效的手段之一,而遗憾的是常规全波形反演存在“周期跳跃”和严重依赖于地震记录低频信息等的缺陷,为此提出了基于模式的自适应全波形反演技术。基于模式的自适应全波形反演的目标函数为
| $ F = \frac{{{{\left\| {\mathit{\boldsymbol{Tw}}} \right\|}^2}}}{{2{{\left\| \mathit{\boldsymbol{w}} \right\|}^2}}} $ | (11) |
式中:矩阵T是对w加权的对角矩阵;w为滤波算子,作用于模拟地震记录使其较好匹配实际地震记录,其表达式为
| $ \mathit{\boldsymbol{w}} = {({\mathit{\boldsymbol{P}}^{\rm{H}}}{\mathit{\boldsymbol{B}}^{\rm{H}}}{\mathit{\boldsymbol{E}}^{\rm{H}}}\mathit{\boldsymbol{EBP}})^{ - 1}}{\mathit{\boldsymbol{P}}^{\rm{H}}}{\mathit{\boldsymbol{B}}^{\rm{H}}}{\mathit{\boldsymbol{E}}^{\rm{H}}}\mathit{\boldsymbol{EBD}} $ | (12) |
其中P是模拟的地震数据的Toeplitz矩阵,即计算出的正传播波场。
式(11)是个线性最小平方问题,它有一个全局最小值,所以不存在常规全波形反演所存在的“周期跳跃”现象。通过速度模型m对式(11)中的目标函数F最小化,得到反传播波场与正传播波场的互相关,进而得到单炮对应的梯度
| $ \begin{array}{*{20}{l}} {\frac{{\partial F}}{{\partial \mathit{\boldsymbol{m}}}} = - {\mathit{\boldsymbol{u}}^{\rm{H}}}{{\left( {\frac{{\partial \mathit{\boldsymbol{A}}}}{{\partial \mathit{\boldsymbol{m}}}}} \right)}^{\rm{H}}}{\mathit{\boldsymbol{A}}^{{\rm{ - H}}}}{\mathit{\boldsymbol{r}}^{\rm{H}}}{\mathit{\boldsymbol{w}}^{\rm{H}}}\mathit{\boldsymbol{EBP}} \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {{({\mathit{\boldsymbol{P}}^{\rm{H}}}{\mathit{\boldsymbol{B}}^{\rm{H}}}{\mathit{\boldsymbol{E}}^{\rm{H}}}\mathit{\boldsymbol{EBP}})}^{ - 1}}\left( {\frac{{2\mathit{\boldsymbol{fI}} - {\mathit{\boldsymbol{T}}^2}}}{{{\mathit{\boldsymbol{w}}^{\rm{T}}}\mathit{\boldsymbol{w}}}}} \right)\mathit{\boldsymbol{w}}} \end{array} $ | (13) |
式中:矩阵A是波动方程正演模拟算子的矩阵表达式;r是选择检波点位置的波场限定算子;u表示震源s在速度模型m中在所有点和对应时间所产生的波场。
基于模式的自适应全波形反演技术实现过程与常规全波形反演技术实现过程类似,不再赘述。
通过以上所述方法,可避免常规全波形反演技术固有的“周期跳跃”现象,克服其高度依赖于地震记录的低频成分的缺陷[1, 18-20]。
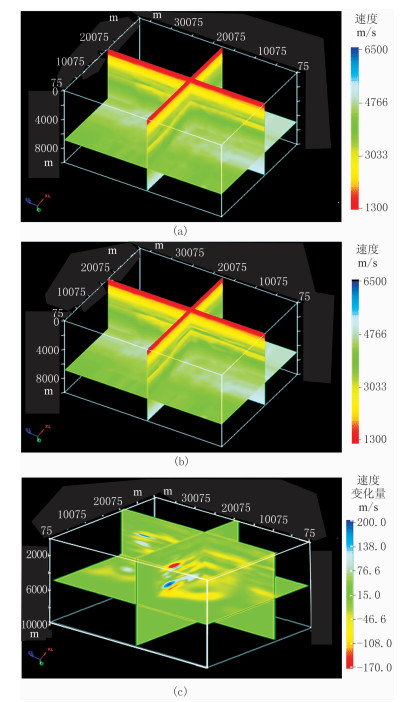
2 应用实例将上述关键技术应用于陆上地震资料处理,以验证其处理效果。图 5a为常规全波形反演得到的速度模型,将其作为本文基于模式的自适应全波形反演初始速度模型,反演结果如图 5b所示,图 5c为基于模式的自适应全波形反演得到的速度变化量。由图可见,基于模式的自适应全波形反演得到的速度模型细节更加丰富、准确,对于提高低幅度构造及复杂构造等的成像精度十分有利。
|
图 5 基于模式的自适应全波形反演与常规全波形反演结果 (a)常规全波形反演;(b)基于模式的自适应全波形反演;(c)二者的变化量 |
图 6a为用常规全波形反演速度模型(图 5a)的逆时偏移剖面,可以看出,由于速度模型的精度相对较低,导致目的层局部存在下弯现象(椭圆区域),与沉积规律不符,后来新钻井也证实不存在下弯现象。图 6b为用基于模式的自适应全波形反演速度模型(图 5b)的逆时偏移剖面,消除了目的层下弯现象,小断层、不整合等构造细节变得更加清楚,并且成像深度与实际钻井深度吻合较好(路7井)。

|
图 6 不同方法反演速度模型的逆时偏移剖面(一) (a)常规全波形反演;(b)基于模式的自适应全波形 |
图 7a为另一工区用常规全波形反演得到的速度模型的逆时偏移剖面,图 7b为用基于模式的自适应全波形反演的速度模型得到的逆时偏移剖面,对比可见,图 7a中的椭圆红圈内陡断面不聚焦。而图 7b中的椭圆红圈内的陡断面成像明显好于前者。另外,图 7a中方框内构造细节和小断面等不清晰,而图 7b中的方框内构造细节和小断面成像明显改善。

|
图 7 不同方法反演速度模型的逆时偏移剖面(二) (a)常规全波形反演;(b)基于模式的自适应全波形反演 |
本文通过使用空间地震子波一致性相位校正技术,使叠前数据的地震子波在空间上趋于一致。通过近地表Q吸收补偿技术使地震数据由于近地表吸收因素导致的高频衰减得到了补偿;通过应用基于模式的自适应频散面波衰减技术使陆上地震资料处理中难以去除的面波得到了有效去除,确保了用于逆时偏移的数据的质量。通过应用基于模式的自适应全波形反演技术得到了更为精确的速度模型,为逆时偏移奠定了速度模型基础,最终确保了逆时偏移的成像质量。
总之,通过在处理流程中使用文中介绍的三项前期处理新技术和基于模式的自适应全波形反演技术,地震数据的品质和速度模型的精度等都得到了较大提升,最终提高了逆时偏移成像精度。
致谢
在实际地震资料处理过程中使用了GeoApex Technology Inc.公司的系列先进技术,在此表示衷心感谢。
| [1] |
Zhang Y, Guo J.Challenges for improving the image of the igneous rock-related complex structures[C].Expanded Abstracts of SEG/Chinese Geophysical Society 2017 International Conference, 2017.
|
| [2] |
Zhang Y, Guo J.Ground-roll attenuation in cross-spread domain by phase matching and pattern-based adaptive subtraction[C].SEG Technical Program Expanded Abstracts, 2017, 36: 4965-4969.
|
| [3] |
Guo J, Zhou X.Surface-consistent phase correction[C].SEG Technical Program Expanded Abstracts, 2001, 20: 1839-1842.
|
| [4] |
高利东, 王大兴, 刘小亮, 等.黄土塬区表层Q值求取及补偿方法[C].CPS/SEG北京2018国际地球物理会议暨展览电子论文集, 2018, 224-227.
|
| [5] |
郝亚炬, 黄捍东, 文晓涛, 等. 广义S域Q值估计方法及油气检测中的应用[J]. 石油地球物理勘探, 2017, 52(5): 1059-1066. HAO Yaju, HUANG Handong, WEN Xiaotao, et al. Q estimation in the generalized S domain and its application in the hydrocarbon detection[J]. Oil Geophysical Prospecting, 2017, 52(5): 1059-1066. |
| [6] |
苏勤, 曾华会, 田彦灿, 等. 表层Q值确定性求取与空变补偿方法[J]. 石油地球物理勘探, 2019, 54(5): 988-996. SU Qin, ZENG Huahui, TIAN Yancan, et al. Near surface Q value computation and compensation with space-variant compensation[J]. Oil Geophysical Prospecting, 2019, 54(5): 988-996. |
| [7] |
王建民, 陈树民, 苏茂鑫, 等. 近地表高频补偿技术在三维地震勘探中的应用研究[J]. 地球物理学报, 2007, 50(6): 1837-1843. WANG Jianmin, CHEN Shumin, SU Maoxin, et al. A study of the near surface high-frequency compensation technology in 3-D seismic exploration[J]. Chinese Journal of Geophysics, 2007, 50(6): 1837-1843. DOI:10.3321/j.issn:0001-5733.2007.06.026 |
| [8] |
史才旺, 何兵寿. 基于主成份分析和梯度重构的全波形反演[J]. 石油地球物理勘探, 2018, 53(1): 95-104. SHI Caiwang, HE Bingshou. Full waveform inversion based on the main component analysis and gradient reconstruction[J]. Oil Geophysical Prospecting, 2018, 53(1): 95-104. |
| [9] |
Virieux J, Operto S. An overview of full waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1-WCC26. |
| [10] |
Brittan J, Jones I. FWI evolution-From a monolith to a toolkit[J]. The Leading Edge, 2019, 38(3): 179-184. |
| [11] |
Weglein A B. A timely and necessary antidote to indirect methods and so-called FWI evolution[J]. The Leading Edge, 2013, 32(10): 1192-1204. DOI:10.1190/tle32101192.1 |
| [12] |
Warner M, Ratcliffe A, Nangoo T, et al. Anisotropic full-waveform inversion[J]. Geophysics, 2013, 78(2): R59-R80. |
| [13] |
Warner M R and Guasch L.Robust adaptive waveform inversion[C].SEG Technical Program Expanded Abstracts, 2015, 34: 1059-1063.
|
| [14] |
Wray B, Chaazalnoel N, Zhao W, et al.Full-waveform inversion using broadband variable-depth streamer data in deep water, West Africa[C].Extended Abstracts of 76th EAGE Conference and Exhibition, 2014.
|
| [15] |
Tatantola A. Inversion of of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(2): 1259-1266. |
| [16] |
Leeuwen T V, Mulder W A. A correlation-based misfit criterion for wave-equation travel time tomography[J]. Geophysical Journal International, 2010, 182(3): 1383-1394. DOI:10.1111/j.1365-246X.2010.04681.x |
| [17] |
Vigh D, Starr B, Li H.3D full waveform inversion on a Gulf Mexico WAZ data set[C].SEG Technical Program Expanded Abstracts, 2010, 29: 957-961.
|
| [18] |
Warner M, Gauasch L.Adaptive waveform inversion-FWI without cycle skipping: Theory[C].Extended Abstracts of 76th EAGE Conference and Exhibition, 2014.
|
| [19] |
Warner M, Gauasch L. Adaptive waveform inversion:Theory[J]. Geophysics, 2016, 81(6): R429-R445. DOI:10.1190/geo2015-0387.1 |
| [20] |
Guasch L, Warner M R, Ravaut C. Adaptive waveform inversion:Practice[J]. Geophysics, 2019, 84(3): R447-R461. |



 国九英, 北京市北京经济技术开发区地盛西路6号国油伟泰(北京)科技有限公司, 100176。Email:
国九英, 北京市北京经济技术开发区地盛西路6号国油伟泰(北京)科技有限公司, 100176。Email: