② 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071
② Evaluation and Detection Technology Laboratory of Marine Mineral Resources, Qingdao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266071, China
在声波全波形反演(FWI)中,密度与速度高度耦合是密度反演最大的挑战[1],并且密度变化对地震波的振幅影响更大,而不能改变地震波的走时,因此在FWI研究中往往忽视密度反演。然而密度是重要的地下介质物性参数之一,可靠的速度、密度信息对储层评价、岩性解释和油藏描述等具有重要意义[2]。由于密度与速度参数之间存在耦合效应,选择不同参数化模式有利于降低二者间的串扰。何兵红等[3]列举了速度—密度、模量—密度、阻抗—密度、阻抗—速度、模量—速度及模量—阻抗等6种参数化模式,认为阻抗—速度参数化模式去耦合效果最佳,但是不能直接获取密度模型,无法避免速度和密度之间的耦合性。Köhn等[4]指出,在任何参数化模式下密度反演效果均最差,但速度—密度参数化模式优于模量—密度。由此可见,选取最优参数化模式反演密度的效果是有限的,因此期待以合理反演策略提高反演精度。Jeong等[5]在频率域组合多种参数化模式反演速度、密度参数精度较高,但其使用的超低频(0.167Hz)信息实际意义不大。Prieux等[6]首先用大炮检距地震数据反演速度,再用全炮检距地震数据反演速度和密度以提高密度反演的稳定性,并指出速度—密度参数化模式优于速度—阻抗。张广智等[7]首先固定密度反演出速度参数作为初始速度模型,再同时反演速度和密度的效果较好。Luo等[8]提出基于散射角分离的多尺度速度、密度反演方法,并获得良好的效果。
上述研究均认为速度—密度参数化模式是密度反演的最佳模式,其密度反演存在强烈的高波数偏移特性,即反演只聚焦于模型的高波数成分,因为小入射角反射波在密度反演中权重太大[9]。FWI需满足地震数据含低频信息、炮检距足够大和相对精确的初始模型[10]等条件。传统FWI明显依据低频数据和潜水波信息恢复模型参数的长波长分量[11-12],这种方法在密度反演中不适用,因为密度扰动对大炮检距反射信息不敏感,主要与中、小炮检距反射信息有关,实际上中等炮检距数据更常见。当前随着图形处理器(GPU)并行计算逐渐成熟及计算设备性能的提升,三维FWI发展迅速,而其庞大的数据和计算量对计算机内存和性能带来极大挑战[13]。
综上所述,常规FWI恢复密度模型的低波数信息难度较大[9]。针对反射波数据主导的低波数速度建模,Xu等[14]提出反射波波形反演(RWI),通过真振幅偏移/反偏移构建反射波能量[15],利用反射能量恢复模型深部背景速度。Wang等[16]实现了频率域RWI,指出低频信息对RWI不可或缺。Mora[17]认为FWI分为偏移过程和层析过程。Alkhalifah等[18]指出,传统RWI更利于更新模型短波长成分,通过分离反演梯度的长波长背景速度分量和短波长速度分量建立一个联合目标函数,同时更新背景速度和速度界面,从而有效增强层析效果。由于RWI对初始模型仍然具有一定的依赖性[19],因此Chi等[10]利用模拟记录与观测记录的互相关建立目标函数,提出互相关目标函数的RWI方法。Luo等[19]提出全旅行时反演,通过Rytov近似(一种常用的波动方程线性近似解,用于计算散射波场,与之并列的方法有Born近似、De Wolf近似、WKBJ近似等)分离振幅和旅行时信息,建立旅行时核函数,进一步提高反演的线性特征。Wang等[20]将RWI推广至弹性波反演,利用P-P波成像作为纵、横波偏移结果进行反偏移获取散射波场;随后,提出基于弹性波P/S分解的反射波旅行时反演,以此增强纵、横波速度反演的线性特征[21]。Wang等[22]通过波模式分解分析了弹性波旅行时反演的敏感核函数。Ren等[23]提出敏感核分解的反射波反演方法,获得了较好的实际效果。付继有等[24]研究了声介质的基于波形互相关的反射波反演方法,利用动态图像校正方法拾取旅行时差。崔超等[25]提出基于双差的波动方程反射波旅行时反演方法,提高了动态图像校正方法拾取旅行时的精度。
鉴于RWI能够反演密度模型的低波数分量,将其与FWI结合能够更准确地反演密度模型。但与常规速度反演不同,密度RWI提供了近乎全部的低波数信息。因此,本文提出基于互相关目标函数的反射波波形密度反演方法,建立了基于RWI+FWI的速度—密度双参数反演流程。首先回顾了传统声波变密度方程双参数反演,并利用辐射模式分析了密度反演的偏移特征;然后提出基于速度和密度经验公式的RWI方法;再结合传统FWI方法重建真实的速度、密度模型;最后通过简单双层模型和重采样的Sigsbee 2A模型进行反演测试,以验证方法的有效性。
1 理论 1.1 传统密度反演回顾与偏移特征分析时间域变密度声波方程为
| $ \begin{array}{l} \left\{ {\frac{1}{{\rho (\mathit{\boldsymbol{x}}){v^2}(\mathit{\boldsymbol{x}})}}\frac{{{\partial ^2}}}{{\partial {t^2}}} - \nabla \cdot \left[ {\frac{1}{{\rho (\mathit{\boldsymbol{x}})}}\nabla } \right]} \right\}p(\mathit{\boldsymbol{x}},t,{\mathit{\boldsymbol{x}}_{\rm{s}}})\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \delta (\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_{\rm{s}}})f(t) \end{array} $ | (1) |
式中:p(x, t, xs)为t时刻、空间位置x处的压力场,xs为震源位置;ρ(x)为密度;v(x)为速度;f(t)为震源函数。
声波FWI通过构建最小二乘约束使由初始模型得到的正演模拟记录pcal和观测记录dobs的波场残差最小,进而采用最优化方法获取地下介质的弹性参数m,目标函数为
| $ {\rm{E}}(\mathit{\boldsymbol{m}}) = \frac{1}{2}\sum\limits_{{\rm{s,g}}} {\int_t {{{[{p_{{\rm{cal}}}}({\mathit{\boldsymbol{x}}_{\rm{g}}},t,{\mathit{\boldsymbol{x}}_{\rm{s}}}) - {d_{{\rm{obs}}}}({\mathit{\boldsymbol{x}}_{\rm{g}}},t,{\mathit{\boldsymbol{x}}_{\rm{s}}})]}^2}{\rm{d}}t} } $ | (2) |
式中:xg为检波点位置;g、s分别表示检波点、炮点。
根据E(m)计算梯度即可迭代更新密度模型
| $ {\mathit{\boldsymbol{m}}^{n + 1}} = {\mathit{\boldsymbol{m}}^n} - {\alpha ^n}\nabla E_\mathit{\boldsymbol{m}}^n $ | (3) |
式中: n为当前迭代次数;α为迭代步长;Em为目标函数对密度的梯度。
李青阳等[26]根据伴随状态法[27]推导速度、密度梯度精确表达式,并借助等效交错网格[28-31]实现正、反演数值模拟。速度、密度梯度为
| $ \left\{ \begin{array}{l} \frac{{\partial E}}{{\partial v}} = \sum\limits_{{\rm{s,g}}} {\int_t {[f(t)*\frac{1}{{\rho (\mathit{\boldsymbol{x}}){v^3}(\mathit{\boldsymbol{x}})}}\frac{{{\partial ^2}}}{{\partial {t^2}}}G(\mathit{\boldsymbol{x}},t,{\mathit{\boldsymbol{x}}_{\rm{s}}}) \times } } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} G({\mathit{\boldsymbol{x}}_{\rm{g}}},t,\mathit{\boldsymbol{x}})*\Delta d]{\rm{d}}t\\ \frac{{\partial E}}{{\partial \rho }} = \sum\limits_{{\rm{s,g}}} {\int_t {\left\{ {f(t)*\left[ {\frac{1}{{{\rho ^2}(\mathit{\boldsymbol{x}}){v^2}(\mathit{\boldsymbol{x}})}}\frac{{{\partial ^2}}}{{\partial {t^2}}}G(\mathit{\boldsymbol{x}},t,{\mathit{\boldsymbol{x}}_{\rm{s}}}) - } \right.} \right.} } \\ \left. {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \nabla \cdot \left( {\frac{1}{{{\rho ^2}(\mathit{\boldsymbol{x}})}}\nabla G(\mathit{\boldsymbol{x}},t,{\mathit{\boldsymbol{x}}_{\rm{s}}})} \right)} \right]G({\mathit{\boldsymbol{x}}_{\rm{g}}},t,\mathit{\boldsymbol{x}})*\Delta d} \right\}{\rm{d}}t \end{array} \right. $ | (4) |
式中:G表示Green函数;“*”为褶积运算符;Δd=pcal(xg, t, xs)-dobs(xg, t, xs)为波场残差。
至此,已建立传统速度—密度FWI理论框架,然而要获得准确的密度反演结果难度较大。传统反演方法很难恢复密度模型的低波数分量,这是由于炮检距敏感性因素和频率因素所致。
1.1.1 炮检距敏感性因素在速度—密度FWI过程中,入射波穿过扰动介质产生散射波,而散射波场作用于模型更新量。因此首先分析速度—密度辐射模式[32]
| $ {R_{v,\rho }} = - 2\left( {1,{\rm{co}}{{\rm{s}}^2}\frac{\theta }{2}} \right) $ | (5) |
式中:θ为入射波方向与散射波方向的矢量夹角(开角);Rv, ρ为速度、密度辐射模式,表示介质单点扰动对应的散射波能量与入射、散射角度的关系,其物理意义为,当一束平面波传播至反射/散射体并发生反射/散射,其散射波场能量与开角的关系。
由速度、密度辐射模式可见:①速度辐射模式(图 1黑线)为一标准的圆形,物理意义是地下某一速度异常体扰动引起的波场扰动在各个方向上的振幅相同;②由地下某一密度异常体扰动引起的波场扰动能量只集中在小炮检距处,其振幅随着反射角的增大而减小(图 1红线);③在小炮检距范围内,速度辐射模式、密度辐射模式引起的波场扰动能量相近,耦合性很强,依靠小入射角地震数据难以区分速度和密度,同时密度贡献主要集中在小炮检距。因此在速度—密度参数化模式下,速度、密度之间的耦合性不可避免。图 2为速度、密度中心扰动介质散射波场。由图可见,二者的扰动波场振幅在小入射角时基本相同,密度扰动引起扰动波场振幅随着散射角增大逐渐衰减(图 2b),这与图 1的分析结果一致。

|
图 1 速度、密度辐射模式 黑线为速度辐射模式,红线为密度辐射模式 |

|
图 2 速度(a)、密度(b)中心扰动介质散射波场 模型网格点为200×200,空间采样步长为10m,背景速度、密度参数分别为3000m/s、2000kg/m3,速度和密度扰动点分别位于模型正中心,扰动值为背景值的1.2倍。震源采用主频为20Hz的雷克子波,位于扰动点的正上方 |
图 3为密度扰动下的散射波场振幅随炮检距变化。由图可见:当炮检距较大时,检波点位于次能量区域,即检波点无法接收有效的散射信息(图 3a);当炮检距较小时,散射波集中在主能量区域,此时密度扰动对散射波形影响极大,因此密度FWI主要依赖于小入射角反射/散射波(图 3b)。图 4为密度扰动介质散射波记录。由图可见,密度扰动引起的散射波能量随炮检距增大而减小,在远炮检距处振幅逐渐趋近于零,说明密度FWI只依赖于小入射角反射波。众所周知,大炮检距波形包含了丰富的折射波和潜水波信息,大炮检距数据驱动可为波形反演提供大尺度背景信息。因此仅仅依赖中、小炮检距信息的密度反演结果主要为高波数成分,类似于偏移剖面。
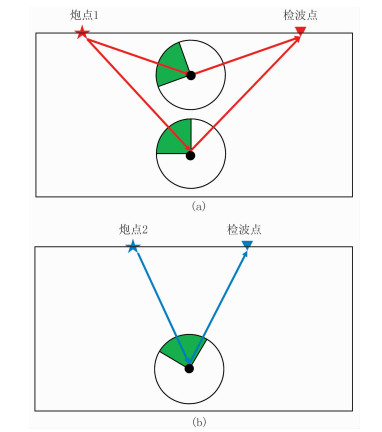
|
图 3 密度扰动下的散射波场振幅随炮检距变化 (a)炮检距较大;(b)炮检距较小 绿色部分为密度散射振幅主能量区域,其余部分为次能量区域 |

|
图 4 密度扰动介质散射波记录 速度、密度背景模型参数和密度扰动量同图 2,震源位于模型左上角,检波点位于地表 |
在有限炮检距情况下,恢复模型波数同样受频率影响,其直接表现为第一菲涅耳带宽度[33]。
Sirgue等[34]指出,地震波的低频对应于模型的低波数,二者呈线性关系。鉴于此,Jeong等[5]在频率域利用超低频信息(0.167Hz)扩大第一菲涅耳带的纵向范围恢复完整的低波数信息,最终通过多尺度反演得到精确的密度模型,但由于地震采集因素的限制,无法投入实际应用。当纵向深度小于或接近第一菲涅耳带半径时,密度敏感核仍然由低波数主导,虽然在垂直于波传播方向上密度敏感核振幅很小,但可在步长寻优过程中得到补偿,低波数更新量仍然可观。在时间域反演的梯度计算过程中,由于低频信息被梯度表达式中的惩罚函数[35]压制,仍难以恢复低波数。
1.2 互相关RWI由前文可知,传统密度波形反演只依赖于中、小炮检距的反射波数据,只能恢复模型的高波数成分。若要恢复低波数成分,只能依赖于RWI [14]。由于RWI方法主要反演大尺度背景模型而不考虑模型的扰动量,因此可以看作连续介质反演。针对模型的大尺度背景,依据Gadrner公式[36]
| $ \rho = \left\{ {\begin{array}{*{20}{l}} {1000}&{v \le 1500}\\ {310{v^{1/4}}}&{v > 1500} \end{array}} \right. $ | (6) |
同时反演两个参数。因此,文中以速度反演为主,通过式(6)更新密度。
根据式(4)得到速度敏感核函数
| $ K(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},{\mathit{\boldsymbol{x}}_{\rm{g}}}) = \Re G(\mathit{\boldsymbol{x}},t,{\mathit{\boldsymbol{x}}_{\rm{s}}})G({\mathit{\boldsymbol{x}}_{\rm{g}}},t,\mathit{\boldsymbol{x}}) $ | (7) |
其中
| $ \Re = \frac{1}{{\rho (\mathit{\boldsymbol{x}}){v^3}(\mathit{\boldsymbol{x}})}} $ | (8) |
沿着敏感核(波路径)反传数据残差同时更新速度模型的低波数和高波数成分,为了区分不同波场数据(直达波/潜水波和反射波等)对模型参数的贡献量,将当前FWI敏感核分解为
| $ G(\mathit{\boldsymbol{x}},t,{\mathit{\boldsymbol{x}}_{\rm{s}}}) = {G_0}(\mathit{\boldsymbol{x}},t,{\mathit{\boldsymbol{x}}_{\rm{s}}}) + {G_{\rm{s}}}(\mathit{\boldsymbol{x}},t,{\mathit{\boldsymbol{x}}_{\rm{s}}}) $ | (9) |
及
| $ G({\mathit{\boldsymbol{x}}_{\rm{g}}},t,\mathit{\boldsymbol{x}}) = {G_0}({\mathit{\boldsymbol{x}}_{\rm{g}}},t,\mathit{\boldsymbol{x}}) + {G_{\rm{s}}}({\mathit{\boldsymbol{x}}_{\rm{g}}},t,\mathit{\boldsymbol{x}}) $ | (10) |
式中:G0为背景介质的Green函数;Gs为扰动介质的Green函数,文中对应反射波。将式(9)和式(10)代入式(7)得
| $ \begin{array}{*{20}{c}} {K(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},{\mathit{\boldsymbol{x}}_{\rm{g}}}) = {K_1}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},{\mathit{\boldsymbol{x}}_{\rm{g}}}) + {K_2}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},{\mathit{\boldsymbol{x}}_{\rm{g}}}) + }\\ {{K_3}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},{\mathit{\boldsymbol{x}}_{\rm{g}}}) + {K_4}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},{\mathit{\boldsymbol{x}}_{\rm{g}}})} \end{array} $ | (11) |
其中
| $ \left\{ {\begin{array}{*{20}{l}} {{K_1}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},{\mathit{\boldsymbol{x}}_{\rm{g}}}) = \Re {G_0}(\mathit{\boldsymbol{x}},t,{\mathit{\boldsymbol{x}}_{\rm{s}}}){G_0}({\mathit{\boldsymbol{x}}_{\rm{g}}},t,\mathit{\boldsymbol{x}})}\\ {{K_2}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},{\mathit{\boldsymbol{x}}_{\rm{g}}}) = \Re {G_0}(\mathit{\boldsymbol{x}},t,{\mathit{\boldsymbol{x}}_{\rm{s}}}){G_{\rm{s}}}({\mathit{\boldsymbol{x}}_{\rm{g}}},t,\mathit{\boldsymbol{x}})}\\ {{K_3}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},{\mathit{\boldsymbol{x}}_{\rm{g}}}) = \Re {G_{\rm{s}}}(\mathit{\boldsymbol{x}},t,{\mathit{\boldsymbol{x}}_{\rm{s}}}){G_0}({\mathit{\boldsymbol{x}}_{\rm{g}}},t,\mathit{\boldsymbol{x}})}\\ {{K_4}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},{\mathit{\boldsymbol{x}}_{\rm{g}}}) = \Re {G_{\rm{s}}}(\mathit{\boldsymbol{x}},t,{\mathit{\boldsymbol{x}}_{\rm{s}}}){G_{\rm{s}}}({\mathit{\boldsymbol{x}}_{\rm{g}}},t,\mathit{\boldsymbol{x}})} \end{array}} \right. $ | (12) |
上述敏感核函数分解与传统全波场敏感核函数(式(7))相比,K1(x, xs, xg)表示炮点正传过程的入射波场与检波点反传过程的入射波场做零延迟互相关;K2(x, xs, xg)表示炮点正传过程的入射波场与检波点反传过程的反射(散射)波场做零延迟互相关;K3(x, xs, xg)表示炮点正传过程的反射(散射)波场与检波点反传过程的入射波场做零延迟互相关;K4(x, xs, xg)表示炮点正传过程的反射(散射)波场与检波点反传过程的反射(散射)波场做零延迟互相关。不同子核有相应的物理意义(图 5)。
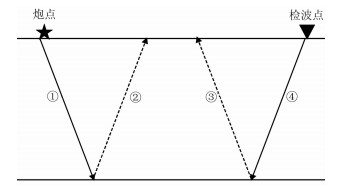
|
图 5 不同子核物理意义 K1=①+④, K2=①+③, K3=②+④, K4=②+③ |
Xu等[14]提出RWI策略,通过真振幅逆时偏移[15]/反偏移思想构建反射能量,利用反射能量恢复模型深部背景速度,在一定程度上克服了反演极易落入局部极值的现象。这里给出反射核函数
| $ {K^{{\rm{ref}}}}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},{\mathit{\boldsymbol{x}}_{\rm{g}}}) = {K_2}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},{\mathit{\boldsymbol{x}}_{\rm{g}}}) + {K_3}(\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{x}}_{\rm{s}}},{\mathit{\boldsymbol{x}}_{\rm{g}}}) $ | (13) |
根据Gadrner公式建立目标函数的速度—密度梯度
| $ \left\{ \begin{array}{l} \frac{{\partial E}}{{\partial v}} = \sum\limits_{{\rm{s,g}}} {\int_t {[f(t)*\Re {G_0}(\mathit{\boldsymbol{x}},t,{\mathit{\boldsymbol{x}}_{\rm{s}}}) \times } } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {G_{\rm{s}}}({\mathit{\boldsymbol{x}}_{\rm{g}}},t,\mathit{\boldsymbol{x}})*\Delta d]{\rm{d}}t + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \sum\limits_{{\rm{s,g}}} {\int_t {[f(t)*\Re {G_{\rm{s}}}(\mathit{\boldsymbol{x}},t,{\mathit{\boldsymbol{x}}_{\rm{s}}}) \times } } \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {G_0}({\mathit{\boldsymbol{x}}_{\rm{g}}},t,\mathit{\boldsymbol{x}})*\Delta d]{\rm{d}}t\\ \frac{{\partial E}}{{\partial \rho }} = 310 \times {\left( {\frac{{\partial E}}{{\partial v}}} \right)^{1/4}} \end{array} \right. $ | (14) |
式(14)包含正向背景波场G0(x, t, xs)、正向散射波场Gs(x, t, xs)、背向背景波场G0(xg, t, x)和背向散射波场Gs(xg, t, x),通过偏移/反偏移获得散射波场[10]。
在最小二乘目标函数下的波形反演方法中,为了得到真振幅正向和背向散射波场,在常规反演迭代循环中,每更新一次模型参数,都要额外增加一次最小二乘逆时偏移运算,因此其计算量远远超过传统波形反演。因此本文采用互相关目标函数替代传统的最小二乘目标函数,以避免每次迭代循环中由最小二乘逆时偏移带来的海量计算量。
重新定义观测记录与反偏移记录的互相关算子
| $ \eta ({\mathit{\boldsymbol{x}}_{\rm{g}}},\tau ,{\mathit{\boldsymbol{x}}_{\rm{s}}}) = \int_t {{d_{{\rm{demig}}}}} ({\mathit{\boldsymbol{x}}_{\rm{g}}},t + \tau ,{\mathit{\boldsymbol{x}}_{\rm{s}}}){d_{{\rm{obs}}}}({\mathit{\boldsymbol{x}}_{\rm{g}}},t,{\mathit{\boldsymbol{x}}_{\rm{s}}}){\rm{d}}t $ | (15) |
式中ddemig为反偏移记录,τ为时移量。考虑模拟记录与观测记录之间可能存在相位差异,选取以下目标函数[37]
| $ E = \frac{1}{2}\sum\limits_{{\rm{s,g}}} {\int {{{[\tau \eta ({\mathit{\boldsymbol{x}}_{\rm{g}}},\tau ,{\mathit{\boldsymbol{x}}_{\rm{s}}})]}^2}{\rm{d}}\tau } } $ | (16) |
则速度模型参数的梯度为[21]
| $ \begin{array}{l} \frac{{\partial E}}{{\partial v}} = \underbrace {\sum\limits_{{\rm{s,g}}} {\int \tau } {{[\eta ({\mathit{\boldsymbol{x}}_{\rm{g}}},\tau ,{\mathit{\boldsymbol{x}}_{\rm{s}}})]}^2}{\rm{d}}\tau \frac{{\partial \Delta \tau }}{{\partial p(\mathit{\boldsymbol{x}},t)}}\frac{{\partial p(\mathit{\boldsymbol{x}},t)}}{{\partial v}}{\rm{d}}\tau }_{{\rm{旅行时项}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \underbrace {\sum\limits_{{\rm{s,g}}} {\int {{\tau ^2}} } \eta ({\mathit{\boldsymbol{x}}_{\rm{g}}},\tau ,{\mathit{\boldsymbol{x}}_{\rm{s}}})\frac{{\partial \eta ({\mathit{\boldsymbol{x}}_{\rm{g}}},\tau ,{\mathit{\boldsymbol{x}}_{\rm{s}}})}}{{\partial p(\mathit{\boldsymbol{x}},t)}}\frac{{\partial p(\mathit{\boldsymbol{x}},t)}}{{\partial v}}{\rm{d}}\tau }_{{\rm{Born项}}} \end{array} $ | (17) |
Wang等[21]将上式定义为旅行时项和Born项两部分,其中旅行时项不仅反映数据振幅误差的影响,同时能够更新模型低波数分量,因此采用旅行时项作为梯度而忽略Born项。因此速度、密度梯度为如下Green函数形式
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial E}}{{\partial v}} = \sum\limits_{{\rm{s,g}}} {\int_t {f(t)} } *{K^{{\rm{ref}}}}*g(t){\rm{d}}t}\\ {\frac{{\partial E}}{{\partial \rho }} = 310 \times {{\left( {\frac{{\partial E}}{{\partial v}}} \right)}^{1/4}}} \end{array}} \right. $ | (18) |
式中g(t)为反传虚震源。基于波动方程的反演方法需要建立散射体和散射波场的线性关系(非线性关系求解难度较大),相应发展了Born近似和Rytov近似等方法。Born近似反映了速度扰动和波场扰动的线性关系,并综合考虑了振幅、相位等因素。Rytov近似反映了速度和波场相位的关系,反演的线性程度较Born近似更明显。为增强反演线性化,Luo等[19]基于Rytov近似,通过对数域波场分离振幅和相位,推出新的虚震源形式
| $ g(t) = \int {\frac{{\tau {\eta ^2}({\mathit{\boldsymbol{x}}_{\rm{g}}},\tau ,{\mathit{\boldsymbol{x}}_{\rm{s}}})\frac{{\partial {d_{{\rm{obs}}}}({\mathit{\boldsymbol{x}}_{\rm{g}}},t + \tau ,{\mathit{\boldsymbol{x}}_{\rm{s}}})}}{{\partial t}}}}{{\int {\frac{{\partial {d_{{\rm{obs}}}}({\mathit{\boldsymbol{x}}_{\rm{g}}},t + \tau ,{\mathit{\boldsymbol{x}}_{\rm{s}}})}}{{\partial t}}} \frac{{\partial {d_{{\rm{obs}}}}({\mathit{\boldsymbol{x}}_{\rm{g}}},t + \tau ,{\mathit{\boldsymbol{x}}_{\rm{s}}})}}{{\partial t}}{\rm{d}}t}}} {\rm{d}}t $ | (19) |
最后结合式(3)进行速度—密度双参数反演,在速度—密度同步反演迭代过程中,由该轮次迭代的速度更新量通过式(6)得到密度更新量,最终完成速度和密度低波数模型重建。需要指出,基于互相关目标函数的RWI必须同时反演密度和速度,因为大尺度密度背景差异不会改变地震波走时,走时信息仅依赖于背景速度。因此本文提出的互相关RWI是利用密度与速度的高度耦合性重建密度反演的低波数成分。表 1为基于RWI+FWI的速度—密度双参数反演流程。
|
|
表 1 基于RWI+FWI的速度—密度双参数反演流程 |
采用各向同性介质双层模型进行测试。首先分析传统FWI对于速度和密度模型的低波数反演能力,此处修正的上层速度和密度参数分别为2700m/s和1200kg/m3,得到背景速度、密度模型。由于主要沿着反射波路径更新低波数能量,而平滑模型造成正传、反传波场在弹性界面不产生反射(散射),进而引起迭代初期只更新界面、反射波路径能量在迭代多次才出现增强的现象,因此未对背景模型平滑处理。图 6为第1次迭代的FWI速度梯度与密度梯度剖面。由图可见:在速度梯度剖面中反射波路径低波数能量很强,呈2个“兔耳”形态,说明反射波数据具备恢复速度残差模型(真实模型速度与初始模型速度的差值)低波数分量的能力(图 6a);在密度梯度剖面中几乎观察不到“兔耳”形态,意味着反射波数据无法恢复密度残差模型低波数信息(图 6b)。在放弃以潜水波和折射波数据驱动的大尺度密度模型反演后,由反射波数据无法恢复低波数成分,这对于成功反演各尺度密度模型非常不利。
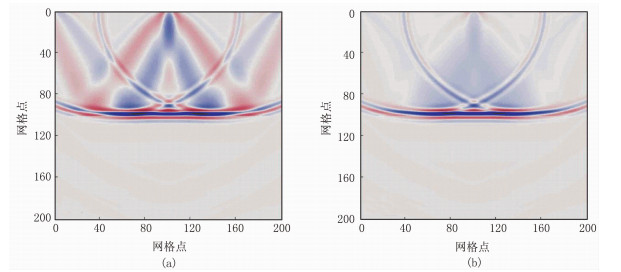
|
图 6 第1次迭代的FWI速度梯度(a)与密度梯度(b)剖面 模型网格点为200×200,界面位于纵向100网格处。空间采样步长为10m,震源采用主频为20Hz的雷克子波,位于(1000m, 50m),检波点覆盖模型表面。上、下层速度分别为3000、4000m/s,上、下层密度分别为1500、2000kg/m3。模型测试过程中切除了直达波 |
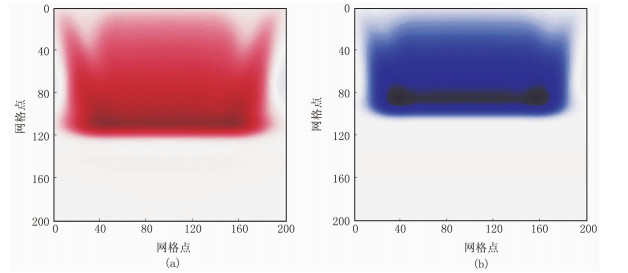
在速度RWI的同时,利用Gardner公式更新密度模型,因为RWI存在偏移/反偏移过程,无需初始模型提供界面信息,因此将初始速度和初始密度设置为参数统一的均匀模型,文中分别设置速度为3300m/s、密度为1800kg/m3和速度为2700m/s、密度为1200kg/m3两套参数。图 7为RWI单炮高、低密度梯度模型。由图可见,高、低密度梯度均仅存在沿着反射波路径的低频能量,并对应密度模型的低波数成分,同时正确指示了背景参数的偏高或偏低方向。图 8为RWI 20炮叠加高、低密度梯度平滑模型。由图可见,本文提出的反演策略有效恢复了密度低波数成分。
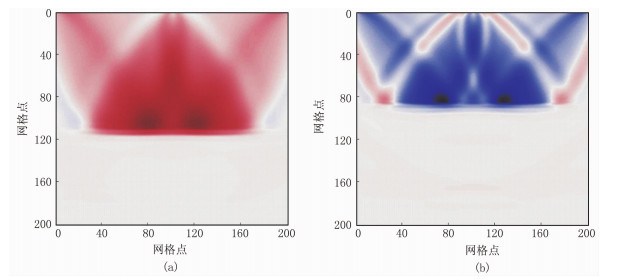
|
图 7 RWI单炮高(a)、低(b)密度梯度模型 图a中红色为正数,图b中蓝色为负数 |
|
图 8 RWI 20炮叠加高(a)、低(b)密度梯度平滑模型 炮间距为10m |
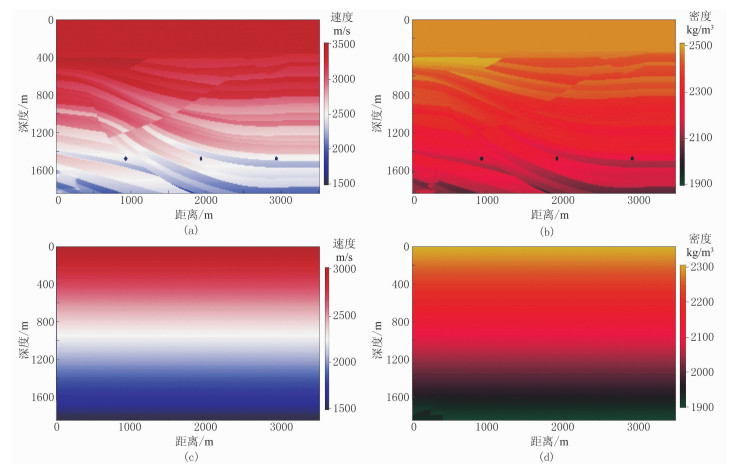
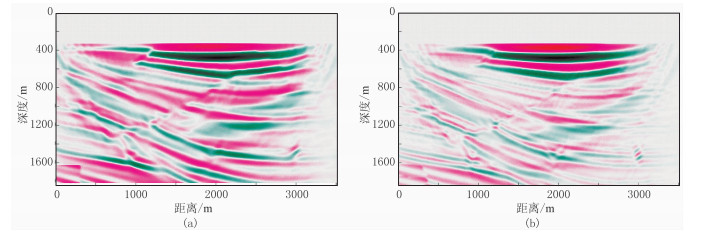
采用Sigsbee 2A重采样模型(图 9)进行数值试算。首先用初始线性速度(图 9c)、初始线性密度(图 9d)模型进行传统FWI测试,测试结果(图 10、图 11)表明:①初次迭代的密度梯度(图 10b)的高波数较速度梯度(图 10a)更明显。②迭代18次后陷入局部极值,虽然能看出构造轮廓,但是速度反演结果严重偏离真实模型(图 9a),整体地层界面明显下移,绕射点归位不好,存在“画弧”现象(图 11a);密度反演效果更差,仅更新了错误的高波数信息(图 11b)。
|
图 9 Sigsbee 2A重采样模型 (a)真实速度模型;(b)真实密度模型;(c)初始线性速度模型;(d)初始线性密度模型重采样后横向、垂向网格数分别为351、184,横向、垂向网格间距均为10m。震源采用主频为13Hz的雷克子波,共2500个时间采样点,时间采样间隔为0.8ms。炮点和检波点均匀分布在模型上表面,共35炮,炮间距为100m,检波点总数为350,检波点间距为10m。密度模型由计算Gardner公式得到。图c、图d的模型数值均从浅层到深层线性增加 |
|
图 10 传统FWI初次迭代的速度(a)、密度(b)梯度叠加剖面 |
|
图 11 传统FWI迭代18次的速度(a)、密度(b)结果 |
采用本文提出的速度—密度同步RWI方法重新迭代、更新初始速度、密度模型(共迭代39次),图 12为速度—密度同步RWI初次迭代、第20次迭代的密度梯度叠加剖面。由图可见:RWI初次迭代的密度梯度(图 12a)的能量主要集中在浅层,较传统FWI密度梯度(图 10b)更光滑,低波数能量更丰富;RWI迭代第20次的密度梯度(图 12b)的能量逐渐向中、深部转移,并且伴随着一些高波数信息(界面处)。由于RWI主要是为了提供残差模型的低波数信息,以修正地震波走时(针对速度而言)、相位等,人们一般在迭代中对梯度做适当平滑以消除界面能量,使模型更新主要以低波数为主。因此,在速度—密度双参数RWI中,文中对每次迭代的梯度均做轻微高斯平滑。最终反演结果(图 13)表明,与初始线性模型(图 9c、图 9d)相比,RWI最终结果明显存在低波数成分。

|
图 12 速度—密度同步RWI初次迭代(a)、第20次迭代(b)的密度梯度叠加剖面 |
|
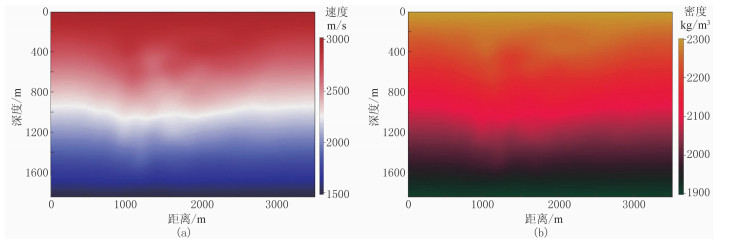
图 13 Sigsbee 2A模型最终RWI速度(a)、密度(b) |
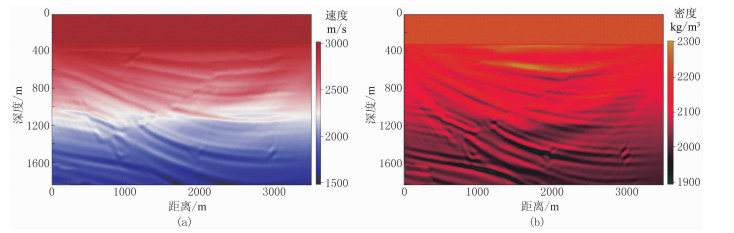
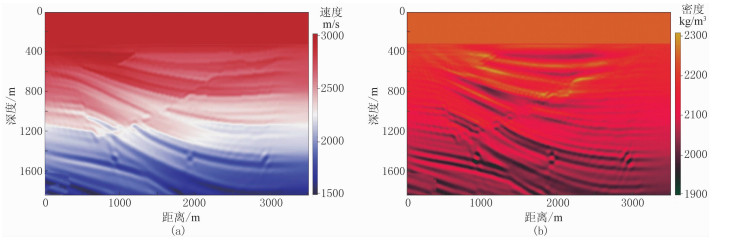
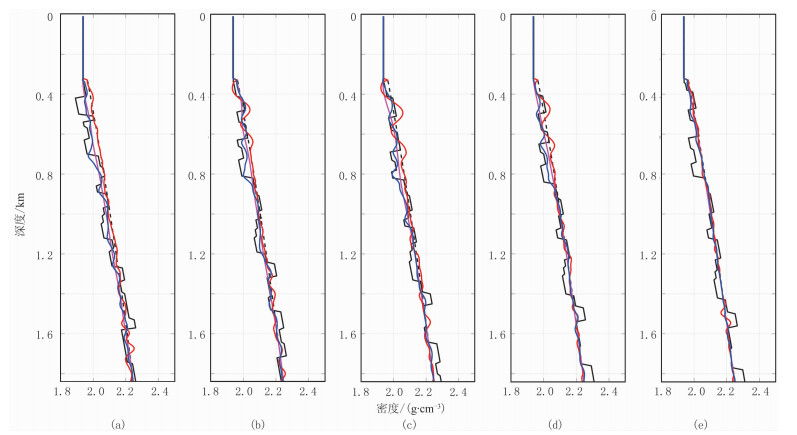
为检验RWI更新的低波数信息的准确性,在RWI速度、密度基础上,再次进行传统FWI测试,图 14为Sigsbee 2A模型RWI+FWI迭代39次的速度、密度。由图可见,速度(图 14a)和密度(图 14b)反演结果中层位清晰,绕射点准确归位并且没有绕射“画弧”现象。抽取真实速度(图 9a)、初始线性速度(图 9c)、传统FWI迭代18次的速度(图 11a)、RWI速度(图 13a)以及RWI+FWI迭代39次的速度(图 14a)在水平方向1.0、1.5、2.0、2.5、3.0km处的纵向曲线(图 15)可见:①由于初始线性速度与真实速度差异较大,传统FWI迭代18次的速度存在严重周波跳跃,导致反演很早落入局部极值,并且速度模型的更新也集中在初始线性速度附近,严重偏离真实值。②RWI速度明显接近真实速度,说明RWI提供了准确的低波数更新量,因此RWI+FWI速度基本与真实速度吻合,仅在深部(深度大于1.6km)与初始线性速度相近,这是由于模型深层无有效反射信息导致RWI速度不精确所致。抽取真实密度(图 9b)、初始线性密度(图 9d)、传统FWI迭代18次的密度(图 11b)、RWI密度(图 13b)以及RWI+FWI迭代39次的密度(图 14b)在水平方向1.0、1.5、2.0、2.5、3.0km处的纵向曲线(图 16)进行分析,结果与速度分析结果基本一致,由于密度反演固有的偏移特性,RWI为密度提供了唯一的低波数信息,加强了密度反演的层析特征,因此反演结果更准确。
|
图 14 Sigsbee 2A模型RWI+FWI迭代39次的速度(a)、密度(b) |

|
图 15 真实速度(黑色实线)、初始线性速度(黑色虚线)、传统FWI迭代18次的速度(红色实线)、RWI速度(粉色实线)以及RWI+FWI迭代39次的速度(蓝色实线)在水平方向1.0(a)、1.5(b)、2.0(c)、2.5(d)、3.0km(e)处的纵向曲线 |
|
图 16 真实密度(黑色实线)、初始线性密度(黑色虚线)、传统FWI迭代18次的密度(红色实线)、RWI密度(粉色实线)以及RWI+FWI迭代39次的密度(蓝色实线)在水平方向1.0(a)、1.5(b)、2.0(c)、2.5(d)、3.0km(e)处的纵向曲线 |
速度和密度双参数同时反演是目前相对有效的密度反演参数化模式,而二者之间的耦合性给传统FWI带来巨大挑战。此外,密度FWI还存在强偏移效应的问题,即传统FWI密度反演结果的层析分量严重不足。为此,本文提出了基于互相关目标函数的速度—密度双参数RWI方法,然后对RWI结果利用传统FWI最终得到较准确的速度、密度反演结果。通过理论分析和模型测试得到以下认识:
(1) 密度扰动对大炮检距信息的敏感性很低,因此只能利用中、小炮检距的地震反射数据反演密度,而小炮检距数据的密度反演结果的低波数成分严重缺失,进而导致同时反演陷入局部极值。此外,实际生产中还面临低频缺失、子波带限、观测孔径等问题,极易导致反演失败。RWI可克服反演局部极值以及减弱密度偏移特征。
(2) 速度、密度参数之间的强耦合效应(更新速度的同时根据经验公式同时更新密度)是大尺度背景模型RWI的理论基础。在实施RWI过程中利用Gardner经验公式同时对速度和密度进行更新,最终可精确地恢复速度、密度的低波数信息。
| [1] |
杨积忠, 刘玉柱, 董良国. 变密度声波方程多参数全波形反演策略[J]. 地球物理学报, 2014, 57(2): 628-643. YANG Jizhong, LIU Yuzhu, DONG Liangguo. A multi-parameter full waveform inversion strategy for acoustic media with variable density[J]. Chinese Journal of Geophysics, 2014, 57(2): 628-643. |
| [2] |
石玉梅, 张研, 姚逢昌, 等. 基于声学全波形反演的油气藏地震成像方法[J]. 地球物理学报, 2014, 57(2): 607-617. SHI Yumei, ZHANG Yan, Yao Fengchang, et al. Methodology of seismic imaging for hydrocarbon re-servoirs based on acoustic full waveform inversion[J]. Chinese Journal of Geophysics, 2014, 57(2): 607-617. |
| [3] |
何兵红, 方伍宝, 胡光辉, 等. 声波方程参数化模式及多参数全波形反演去耦合化策略[J]. 石油物探, 2018, 57(5): 73-84. HE Binghong, FANG Wubao, HU Guanghui, et al. Parameterization of acoustic wave equation and strategy for multi-parameter full waveform inversion[J]. Geophysical Prospecting for Petroleum, 2018, 57(5): 73-84. |
| [4] |
Köhn D, De Nil D, Kurzmann A, et al. On the influ-ence of model parametrization in elastic full waveform tomography[J]. Geophysical Journal International, 2012, 191(1): 325-345. DOI:10.1111/j.1365-246X.2012.05633.x |
| [5] |
Jeong W, Lee H Y, Min D J. Full waveform inversion strategy for density in the frequency domain[J]. Geophysical Journal International, 2012, 188(3): 1221-1242. DOI:10.1111/j.1365-246X.2011.05314.x |
| [6] |
Prieux V, Brossier R, Operto S, et al. Multiparameter full waveform inversion of multicomponent ocean-bottom-cable data from the Valhall field, Part 1:imaging compressional wave speed, density and attenuation[J]. Geophysical Journal International, 2013, 194(3): 1640-1664. DOI:10.1093/gji/ggt177 |
| [7] |
张广智, 孙昌路, 潘新朋, 等. 变密度声波全波形反演中密度影响因素及反演策略[J]. 吉林大学学报(地球科学版), 2016, 46(5): 1500-1560. ZHANG Guangzhi, SUN Changlu, PAN Xinpeng, et al. Influence factors and strategy of inversion for density of acoustic full waveform inversion with variable density[J]. Journal of Jilin University(Earth Science Edition), 2016, 46(5): 1500-1560. |
| [8] |
Luo J R, Wu R S. Velocity and density reconstruction based on scattering angle separation[J]. Pure and Applied Geophysics, 2018, 175(12): 4371-4387. DOI:10.1007/s00024-018-1916-8 |
| [9] |
郭振波.弹性介质波形反演方法研究[D].山东青岛: 中国石油大学(华东), 2014. GUO Zhenbo.Research on Waveform Inversion in Elastic Medium[D].China University of Petroleum(East China), Qingdao, Shandong, 2014. http://cdmd.cnki.com.cn/Article/CDMD-10425-1016711289.htm |
| [10] |
Chi B X, Dong L Q, Liu Y Z. Correlation-based reflection full-waveform inversion[J]. Geophysics, 2015, 80(4): R189-R202. |
| [11] |
Pratt R G, Goulty N R. Combining wave-equation i-maging with traveltime tomography to form high-resolution images from crosshole data[J]. Geophysics, 1991, 56(2): 208-224. |
| [12] |
Shipp R M, Singh S C. Two-dimensional full wavefield inversion of wide-aperture marine seismic streamer data[J]. Geophysical Journal International, 2002, 151(2): 325-344. DOI:10.1046/j.1365-246X.2002.01645.x |
| [13] |
姚刚, 吴迪. 反射波全波形反演[J]. 中国科学:地球科学, 2017, 47(10): 1220-1232. YAO Gang, WU Di. Reflection full waveform inversion[J]. Science China:Earth Sciences, 2017, 47(10): 1220-1232. |
| [14] |
Xu S, Wang S, Chen F, et al.Full waveform inversion for reflected seismic data[C].Extended Abstracts of 74th EAGE Conference & Exhibition, 2012, W024.
|
| [15] |
Zhang Y, Xu S, Bleistein N, et al. True-amplitude, angle-domain, common-image gathers from one-way wave-equation migrations[J]. Geophysics, 2007, 72(1): S49-S58. |
| [16] |
Wang S, Chen F, Zhang H, et al.Reflection-based full waveform inversion (RFWI) in the frequency domain[C].SEG Technical Program Expanded Abstracts, 2013, 32: 877-881.
|
| [17] |
Mora P. Inversion=migration+tomography[J]. Geophysics, 1989, 54(12): 1575-1586. DOI:10.1190/1.1442625 |
| [18] |
Alkhalifah T, Wu Z. The natural combination of full and image-based waveform inversion[J]. Geophysical Prospecting, 2016, 64(1): 19-30. DOI:10.1111/1365-2478.12264 |
| [19] |
Luo Y, Ma Y, Wu Y, et al. Full-traveltime inversion[J]. Geophysics, 2016, 81(5): R261-R274. |
| [20] |
Wang G C, Wang S X, Du Q Z, et al. Traveltime-based reflection full-waveform inversion for elastic medium[J]. Journal of Applied Geophysics, 2017, 141(1): 68-76. |
| [21] |
Wang G C, Wang S X, Song J, et al. Elastic reflection traveltime inversion with decoupled wave equation[J]. Geophysics, 2018, 83(5): R463-R474. DOI:10.1190/geo2017-0631.1 |
| [22] |
Wang T, Cheng J, Guo Q, et al. Elastic wave-equation-based reflection kernel analysis and traveltime inversion using wave mode decomposition[J]. Geophysical Journal International, 2018, 215(1): 450-470. DOI:10.1093/gji/ggy291 |
| [23] |
Ren Z, Li Z, Gu B. Elastic reflection waveform inversion based on the decomposition of sensitivity kernels[J]. Geophysics, 2019, 84(2): R235-R250. |
| [24] |
付继有, 李振春, 杨国权, 等. 声介质波动方程反射旅行时反演方法[J]. 石油地球物理勘探, 2015, 50(6): 1134-1140. FU Jiyou, LI Zhenchun, YANG Guoquan, et al. Wave equation reflection travel-time inversion in acoustic media[J]. Oil Geophysical Prospecting, 2015, 50(6): 1134-1140. |
| [25] |
崔超, 黄建平, 王自颖, 等. 基于双差的波动方程反射波旅行时反演方法[J]. 石油地球物理勘探, 2017, 52(4): 734-742. CUI Chao, HUANG Jianping, WANG Ziying, et al. Double difference wave-equation relection traveltime inversion[J]. Oil Geophysical Prospecting, 2017, 52(4): 734-742. |
| [26] |
李青阳, 吴国忱, 吴建鲁. 非均匀流-固边界耦合介质多参数全波形反演方法[J]. 地球物理学报, 2019, 62(9): 3557-3570. LI Qingyang, WU Guochen, WU Jianlu. A multi-parameter full waveform inversion method for a heterogeneous medium with a fluid-solid coupled boundary[J]. Chinese Journal of Geophysics, 2019, 62(9): 3557-3570. |
| [27] |
Plessix R E. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications[J]. Geophysical Journal Internatio-nal, 2006, 167(2): 495-503. DOI:10.1111/j.1365-246X.2006.02978.x |
| [28] |
Di B L, Dors C, Mansur W J. A new family of finite-difference schemes to solve the heterogeneous acoustic wave equation[J]. Geophysics, 2012, 77(5): T187-T199. DOI:10.1190/geo2011-0345.1 |
| [29] |
段沛然, 李青阳, 赵志强, 等. 等效交错网格高阶有限差分法标量波波场模拟[J]. 地球物理学进展, 2019, 34(3): 1032-1040. DUAN Peiran, LI Qingyang, ZHAO Zhiqiang, et al. High-order finite-difference method based on equivalent staggered grid scheme for scalar wavefield simulation[J]. Progress in Geophysics, 2019, 34(3): 1032-1040. |
| [30] |
李青阳, 吴国忱, 段沛然. 准规则网格高阶有限差分法非均质弹性波波场模拟[J]. 石油地球物理勘探, 2019, 54(3): 539-550. LI Qingyang, WU Guochen, DUAN Peiran. Elastic wavefield formodeling in heterogeneous media based on the quasi-regular grid high-order finite difference[J]. Oil Geophysical Prospecting, 2019, 54(3): 539-550. |
| [31] |
吴建鲁, 吴国忱, 王伟, 等. 基于等效交错网格的流固耦合介质地震波模拟[J]. 石油地球物理勘探, 2018, 53(2): 272-279. WU Jianlu, WU Guochen, WANG Wei, et al. Seismic forward modeling in fluid-solid media based on equi-valent staggered grid scheme[J]. Oil Geophysical Prospecting, 2018, 53(2): 272-279. |
| [32] |
Forgues E, Lambar G. Parameterization study for acoustic and elastic ray+Born inversion[J]. Journal of Seismic Exploration, 1997, 6(3): 253-277. |
| [33] |
Virieux J, Operto S. An overview of full-waveform inversion in exploration geophysics[J]. Geophysics, 2009, 74(6): WCC1-WCC26. |
| [34] |
Sirgue L, Pratt R G. Efficient waveform inversion and imaging:A strategy for selecting temporal frequencies[J]. Geophysics, 2014, 79(1): 231-248. |
| [35] |
Liang Z, Wu G, Zhang X. Time domain full waveform inversion with low frequency wavefield decompression[J]. Journal of Geophysics and Engineering, 2018, 15(6): 2330-2338. DOI:10.1088/1742-2140/aac62f |
| [36] |
Gardner G, Gardner L, Gregory A. Formation velocity and density-the diagnostics basics for stratigraphic traps[J]. Geophysics, 1974, 39(6): 770-780. DOI:10.1190/1.1440465 |
| [37] |
Van L T, Mulder W A. A correlation-based misfit criterion for wave-equation traveltime tomography[J]. Geophysical Journal International, 2010, 182(3): 1383-1394. DOI:10.1111/j.1365-246X.2010.04681.x |



 吴国忱, 山东青岛黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院工科楼C-629, 266580。Email:
吴国忱, 山东青岛黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院工科楼C-629, 266580。Email: