② 中海油研究总院有限责任公司, 北京 100028
② CNOOC Research Institute, Beijing 100028, China
由于实际地下介质充满流体、裂缝及裂隙,因而同时表现出各向异性与黏弹性特征,而这种黏弹各向异性的现象也在实验室和波场测量中被观测到[1],因此衰减和各向异性是地震波场数值模拟中越来越不容忽略的因素。
在进行弹性波数值模拟时,得到的混合波场通常同时含有纵波和横波,而在进行地震偏移成像,尤其是弹性波逆时偏移成像时,须将纵、横波解耦,以得到物理意义明确的成像剖面[2]。为此,Alkhalifah[3-4]提出了声学近似假设下的拟声波方程,人为设定沿对称轴方向的横波速度为零,推导出标量形式的四阶微分方程。为了简化方程,提高计算效率,Du等[5]和Zhou等[6]通过不同的降阶方法,推导出不同形式的二阶耦合qP波微分方程。Duveneck等[7]从胡克定律和运动方程出发,推导得到另一种形式的拟声波方程,且其波场具有明确的物理意义。程玖兵等[8-9]推导得到各向异性介质的伪纯模式波动方程,使其在运动学上同弹性波动方程等价。
考虑到衰减的影响,Zhang等[10]推导出时域拟微分算子的黏声各向同性方程,并成功地应用于逆时偏移中;随后,Suh等[11]将该方法拓展到各向异性介质中,补偿了各向异性介质中衰减的影响;Xu等[12]基于二阶拟微分方程,实现了黏声各向异性介质的正演模拟及逆时偏移;李金丽等[13]使用有限差分法进行黏弹VTI介质的正演模拟,并实现了该类介质的双程波照明分析方法。
上述各方法均存在拟声波方程的突出缺点,即当模型参数中有变化较大的倾角和方位角时,会出现不稳定现象[14]、残留横波假象[15],或只有在满足Thomsen参数ε≥δ时正演模拟才是稳定的[16]。
为了解决此类问题,有学者另辟蹊径。从qP波与qSV波的频散关系出发,直接解耦以构建纯qP波控制方程;要实现qP与qSV波的完全分离,关键在于导出简单、灵活的纯qP波控制方程和设计有效的拟微分求解算法。例如,Du等[5]和Zhang等[17]基于弱各向异性近似和平方根近似,推导出一种纯qP波解耦方程,其表现为时间—波数域形式,能较准确地描述TTI介质中的运动学特征;Zhan等[18]推导了一种新的解耦方程,将P波与qSV波完全分离,并成功将其应用于逆时偏移中;Xu等[19]提出了一种纯qP波椭圆微分方程,通过将微分方程分解成一个标量算子和一个微分算子,并用椭圆分解方法修正标量算子,达到校正振幅误差的目的;杨鹏等[20]改进了Xu等[19]所提方程,使其振幅更准确、更均衡;胡书华等[21]则将Xu等[19]二阶微分方程做降阶处理,通过Lebedev交错网格,得到TTI介质下纯qP波的稳定传播的波场;张庆朝等[22]利用近似相速度公式,导出TTI介质三维qP波频散方程及波动方程,并使用伪谱法做正演模拟。
时间递归积分延拓[23](Recursive integral time- extrapolation,RITE)是一类具有较高稳定性、可实现大时间步长条件下正演模拟的方法。在不同的RITE方法中,Low-rank波场延拓因其高效率和灵活的近似精度控制而尤为突显。Fomel等[24]首次使用Low-rank两步法波场延拓,实现了各向同性介质及各向异性介质的正演模拟,并指出该分解算法能准确描述地震波场的动力学特征;随后,Song等[25]将Low-rank应用于正交各向异性介质的正演模拟;Fang等[26]将交错网格有限差分与Low-rank相结合,实现了基于交错网格的Low-rank有限差分波场正演模拟,进一步提高了计算效率和计算精度;Sun等[27]结合Low-rank分解算法和一步法波场延拓,实现了黏弹性介质的Low-rank一步法逆时偏移。在中国国内,该类方法应用较少。黄金强等[28-29]分别使用Low-rank两步法及Low-rank有限差分法,进行了TI介质纯qP波波场的高效正演模拟;袁雨欣等[30]则使用Low-rank分解及Low-rank有限差分法求解二阶解耦的弹性波方程,有效提高了计算精度。
本文基于上述研究成果,引入一步法波场延拓方法,推导了黏声介质方程在空间—波数域的表达形式,并结合空间—波数域各向异性介质延拓算子,构建了一种适用于黏声各向异性介质的空间—波数域纯qP波波场延拓算子,该算子消除了伪横波干扰,不受模型参数限制,且地震波场能稳定传播;为兼顾计算精度与计算效率,引入Low-rank分解算法进行求解,实现了基于Low-rank一步法波场延拓的黏声各向异性介质纯qP波正演模拟。通过简单和复杂模型测试,验证了本文方法的正确性及对复杂介质的适用性,为基于Q补偿的各向异性介质逆时偏移提供了理论依据。
1 方法原理 1.1 一步法波场延拓根据一步法波场延拓理论[31],下一时刻的波场延拓可由空间—波数混合域算子近似表示[32],即
| $ p(\mathit{\boldsymbol{x}},t + \Delta t) = \int {\tilde p} (\mathit{\boldsymbol{k}},t){{\rm{e}}^{{\rm{i}}\Phi (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}})\Delta t}}{{\rm{e}}^{{\rm{i}}\mathit{\boldsymbol{kx}}}}{\rm{d}}\mathit{\boldsymbol{k}} $ | (1) |
式中:t为时间坐标;x为空间坐标;k为波数坐标;Φ为角频率函数;Δt为时间步长;(k, t)为p(x,t)的傅里叶变换,即
| $ \tilde p(\mathit{\boldsymbol{k}},t) = \int p (\mathit{\boldsymbol{x}},t){{\rm{e}}^{ - {\rm{i}}\mathit{\boldsymbol{kx}}}}{\rm{d}}\mathit{\boldsymbol{x}} $ | (2) |
将式(1)中的Δt替换成-Δt,可得
| $ p(\mathit{\boldsymbol{x}},t - \Delta t) = \int {\tilde p(\mathit{\boldsymbol{k}},t)} {{\rm{e}}^{ - {\rm{i}}\varPhi (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}})\Delta t}}{{\rm{e}}^{{\rm{i}}\mathit{\boldsymbol{kx}}}}{\rm{d}}\mathit{\boldsymbol{k}} $ | (3) |
结合式(1)与式(3),显然有
| $ \begin{array}{l} p(\mathit{\boldsymbol{x}},t + \Delta t) + p(\mathit{\boldsymbol{x}},t - \Delta t)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \int 2 {\rm{cos}}[\varPhi (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}})\Delta t]\tilde p(\mathit{\boldsymbol{k}},t){{\rm{e}}^{{\rm{i}}\mathit{\boldsymbol{kx}}}}{\rm{d}}\mathit{\boldsymbol{k}} \end{array} $ | (4) |
在上述推导中,式(1)称为一步法波场延拓,式(4)称为两步法波场延拓。通常,一步法延拓比两步法延拓更稳定,但一步法实现较复杂,涉及复数运算;两步法延拓仅为实数运算,其实现过程则相对简捷。
对Φ做如下高频近似[33],即
| $ \varPhi (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}}) = v(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}})|\mathit{\boldsymbol{k}}| + \frac{1}{2}v(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}})(\nabla v)\mathit{\boldsymbol{k}}\Delta t + \cdots $ | (5) |
式中v为地震波场中的相速度。在各向同性介质中,v仅为空间坐标的函数。而在各向异性介质中,地震波的传播速度随传播方向变化,故此时相速度不仅为空间坐标的函数,还是波数矢量k的函数。
进一步地,忽略式(5)中的高阶项,有
| $ \varPhi (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}}) \approx v(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}})|\mathit{\boldsymbol{k}}| $ | (6) |
将式(6)代入式(1)或式(4),对应可得
| $ p(\mathit{\boldsymbol{x}},t + \Delta t) = \int {\tilde p(\mathit{\boldsymbol{k}},t)} {{\rm{e}}^{{\rm{i}}v(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}})|\mathit{\boldsymbol{k}}|\Delta t}}{{\rm{e}}^{{\rm{i}}\mathit{\boldsymbol{kx}}}}{\rm{d}}\mathit{\boldsymbol{k}} $ | (7) |
或者
| $ \begin{array}{*{20}{l}} {p(\mathit{\boldsymbol{x}},t + \Delta t) + p(\mathit{\boldsymbol{x}},t - \Delta t)}\\ {\;\: = \int 2 {\rm{cos}}[v(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}})|\mathit{\boldsymbol{k}}|\Delta t]\tilde p(\mathit{\boldsymbol{k}},t){{\rm{e}}^{{\rm{i}}\mathit{\boldsymbol{kx}}}}{\rm{d}}\mathit{\boldsymbol{k}}} \end{array} $ | (8) |
从式(1)可知,角频率函数Φ控制着波的传播,因此可通过构建不同的Φ得到不同介质中的波的传播。因此,为了构建本文的黏声各向异性介质纯qP波波场延拓算子Φ,引入如下VTI介质纯qP波声学近似下的频散方程[4],即
| $ \begin{array}{*{20}{l}} {{\omega _{{\rm{qP}}}} = \left[ {\frac{1}{2}(v_{\rm{h}}^2k_x^2 + v_{\rm{v}}^2k_z^2) + } \right.}\\ {{{\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}\sqrt {{{(v_{\rm{h}}^2k_x^2 + v_{\rm{v}}^2k_z^2)}^2} - \frac{{8\eta }}{{1 + 2\eta }}v_{\rm{h}}^2v_{\rm{v}}^2k_x^2k_z^2} } \right]}^{\frac{1}{2}}}} \end{array} $ | (9) |
式中:vv为沿对称轴方向的qP波相速度;
结合式(6)与式(9),可得
| $ \begin{array}{*{20}{l}} {{\varPhi _{{\rm{qP}}}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}}) \approx v(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}})|\mathit{\boldsymbol{k}}| = \left[ {\frac{1}{2}(v_{\rm{h}}^2k_x^2 + v_{\rm{v}}^2k_z^2) + } \right.}\\ {{{\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}\sqrt {{{(v_{\rm{h}}^2k_x^2 + v_{\rm{v}}^2k_z^2)}^2} - \frac{{8\eta }}{{1 + 2\eta }}v_{\rm{h}}^2v_{\rm{v}}^2k_x^2k_z^2} } \right]}^{\frac{1}{2}}}} \end{array} $ | (10) |
该式即为由角频率函数Φ控制的VTI介质纯qP波波场延拓算子。
另一方面,考察如下二维黏声方程[34]
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {v_x}}}{{\partial t}} = \frac{1}{\rho }\frac{{\partial p}}{{\partial x}}}\\ {\frac{{\partial {v_z}}}{{\partial t}} = \frac{1}{\rho }\frac{{\partial p}}{{\partial z}}}\\ {\frac{{\partial p}}{{\partial t}} = \frac{{{\tau _\varepsilon }}}{{{\tau _\sigma }}}\rho v_{\rm{P}}^2\left( {\frac{{\partial {v_x}}}{{\partial x}} + \frac{{\partial {v_z}}}{{\partial z}}} \right) - \rho v_{\rm{P}}^2e}\\ {\frac{{\partial e}}{{\partial t}} = \frac{1}{{{\tau _\sigma }}}\left[ {\left( {\frac{{{\tau _\varepsilon }}}{{{\tau _\sigma }}} - 1} \right)\left( {\frac{{\partial {v_x}}}{{\partial x}} + \frac{{\partial {v_z}}}{{\partial z}}} \right) - e} \right]} \end{array}} \right. $ | (11) |
式中:vx、vz分别为x、z方向的速度场;p为压力场;e为记忆变量;ρ为密度;vP为纵波速度;τσ、τε分别为应力和应变的松弛时间,其表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {{\tau _\sigma } = \frac{1}{{Q\omega }}(\sqrt {{Q^2} + 1} - 1)}\\ {{\tau _\varepsilon } = \frac{1}{{Q\omega }}(\sqrt {{Q^2} + 1} + 1)} \end{array}} \right. $ | (12) |
式中:Q为品质因子;ω为角频率。
将式(11)变换到频率—波数域,即有
| $ \left\{ \begin{array}{l} \begin{array}{*{20}{l}} {{\rm{i}}\rho \omega {{\tilde v}_x} = {\rm{i}}{k_x}\tilde p}\\ {{\rm{i}}\rho \omega {{\tilde v}_z} = {\rm{i}}{k_z}\tilde p} \end{array}\\ {\rm{i}}\omega \tilde p = \frac{{{\tau _\varepsilon }}}{{{\tau _\sigma }}}\rho v_{\rm{P}}^2({\rm{i}}{k_x}{{\tilde v}_x} + {\rm{i}}{k_z}{{\tilde v}_z}) - \rho v_{\rm{P}}^2\tilde e\\ {\rm{i}}\omega \tilde e = \frac{1}{{{\tau _\sigma }}}\left[ {\left( {\frac{{{\tau _\varepsilon }}}{{{\tau _\sigma }}} - 1} \right)({\rm{i}}{k_x}{{\tilde v}_x} + {\rm{i}}{k_z}{{\tilde v}_z}) - \tilde e} \right] \end{array} \right. $ | (13) |
由式(13)前两项可得
| $ \left\{ {\begin{array}{*{20}{l}} {{{\tilde v}_x} = \frac{{{k_x}\tilde p}}{{\rho \omega }}}\\ {{{\tilde v}_z} = \frac{{{k_z}\tilde p}}{{\rho \omega }}} \end{array}} \right. $ | (14) |
将式(14)代入式(13)后两项,并消去,得到
| $ \frac{{{\omega ^2}}}{{v_{\rm{P}}^2}} = (k_x^2 + k_z^2)\frac{{1 + {\rm{i}}\omega {\tau _\varepsilon }}}{{1 + {\rm{i}}\omega {\tau _\sigma }}} $ | (15) |
令
| $ {\omega ^2} = v_{\rm{P}}^2(k_x^2 + k_z^2)\left( {\frac{{1 + {\omega ^2}{\tau _\varepsilon }{\tau _\sigma }}}{{1 + {\omega ^2}\tau _\sigma ^2}} + {\rm{i}}\frac{{\omega \tau {\tau _\sigma }}}{{1 + {\omega ^2}\tau _\sigma ^2}}} \right) $ | (16) |
当Q不是特别小的情况下,τ≪1,即有
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{1 + {\omega ^2}{\tau _\varepsilon }{\tau _\sigma }}}{{1 + {\omega ^2}\tau _\sigma ^2}} \approx 1}\\ {\frac{{\omega \tau {\tau _\sigma }}}{{1 + {\omega ^2}\tau _\sigma ^2}} \approx \frac{\tau }{2}} \end{array}} \right. $ | (17) |
因此,式(16)可简化为
| $ {\omega ^2} \approx v_{\rm{P}}^2(k_x^2 + k_z^2)\left( {1 + \frac{{{\rm{i}}\tau }}{2}} \right) $ | (18) |
即黏声介质的角频率函数在空间—波数域表达为
| $ {\varPhi _{{\rm{AcQ}}}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}}) \approx {\omega _{{\rm{AcQ}}}} = v(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}})|\mathit{\boldsymbol{k}}|\sqrt {1 + \frac{{{\rm{i}}\tau }}{2}} $ | (19) |
该式即为由Φ控制的黏声介质波场延拓算子。可见,在空间—波数混合域,由非黏弹性转变成黏弹性,只需乘以
结合式(10)与式(19),得到由Φ控制的黏声VTI介质纯qP波波场延拓算子
| $ \begin{array}{*{20}{l}} {\varPhi (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}}) \approx \left[ {\frac{1}{2}(v_{\rm{h}}^2k_x^2 + v_{\rm{v}}^2k_z^2) + } \right.}\\ {{{\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}\sqrt {{{(v_{\rm{h}}^2k_x^2 + v_{\rm{v}}^2k_z^2)}^2} - \frac{{8\eta }}{{1 + 2\eta }}v_{\rm{h}}^2v_{\rm{v}}^2k_x^2k_z^2} } \right]}^{\frac{1}{2}}}\sqrt {1 + \frac{{{\rm{i}}\tau }}{2}} } \end{array} $ | (20) |
更进一步地,对于黏声TTI介质纯qP波波场延拓算子,可做如下坐标变换
| $ \left\{ {\begin{array}{*{20}{l}} {{k_x} = {k_x}{\rm{cos}}\theta - {k_z}{\rm{sin}}\theta }\\ {{{\tilde k}_z} = {k_x}{\rm{sin}}\theta + {k_z}{\rm{cos}}\theta } \end{array}} \right. $ | (21) |
式中θ为极化角,便有
| $ \begin{array}{l} \varPhi (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}}) \approx \left[ {\frac{1}{2}(v_{\rm{h}}^2\tilde k_x^2 + v_{\rm{v}}^2\tilde k_z^2) + } \right.\\ {\kern 1pt} {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{1}{2}\sqrt {{{(v_{\rm{h}}^2\tilde k_x^2 + v_{\rm{v}}^2\tilde k_z^2)}^2} - \frac{{8\eta }}{{1 + 2\eta }}v_{\rm{h}}^2v_{\rm{v}}^2\tilde k_x^2\tilde k_z^2} } \right]^{\frac{1}{2}}}\sqrt {1 + \frac{{{\rm{i}}\tau }}{2}} \end{array} $ | (22) |
因此,通过式(1)和式(20)或式(22),可实现声各向异性介质纯qP波波场的稳定延拓。
为了便于后文模型测试对比,此处给出常规二维黏声TTI介质拟声波方程[12],即
| $ \left\{ \begin{array}{l} \frac{{{\partial ^2}{p_{\rm{h}}}}}{{\partial {t^2}}} = \rho v_{\rm{P}}^2[(1 + 2\varepsilon ){H_x}{p_{\rm{h}}} + \sqrt {1 + 2\delta } {H_z}{p_{\rm{v}}}] - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\rho \tau {v_{\rm{P}}}\sqrt {1 + 2\varepsilon } }}{2}\sqrt { - {H_x}} \frac{{\partial {p_{\rm{h}}}}}{{\partial t}}\\ \frac{{{\partial ^2}{p_{\rm{v}}}}}{{\partial {t^2}}} = \rho v_{\rm{P}}^2(\sqrt {1 + 2\delta } {H_x}{p_{\rm{h}}} + {H_z}{p_{\rm{v}}}) - \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \frac{{\rho \tau {v_{\rm{P}}}}}{2}\sqrt { - {H_z}} \frac{{\partial {p_{\rm{v}}}}}{{\partial t}} \end{array} \right. $ | (23) |
式中:ph、pv分别为压力场水平分量和垂直分量;Hx、Hz为坐标变换算子,其表达式为
| $ \left\{ {\begin{array}{*{20}{l}} {{H_x} = \frac{{{\partial ^2}}}{{\partial {x^2}}}{\rm{co}}{{\rm{s}}^2}\theta + \frac{{{\partial ^2}}}{{\partial {z^2}}}{\rm{si}}{{\rm{n}}^2}\theta - \frac{{{\partial ^2}}}{{\partial x\partial z}}{\rm{sin}}2\theta }\\ {{H_z} = \frac{{{\partial ^2}}}{{\partial {x^2}}}{\rm{si}}{{\rm{n}}^2}\theta + \frac{{{\partial ^2}}}{{\partial {z^2}}}{\rm{co}}{{\rm{s}}^2}\theta + \frac{{{\partial ^2}}}{{\partial x\partial z}}{\rm{sin}}2\theta } \end{array}} \right. $ | (24) |
式(23)即为常规二维黏声TTI介质拟声波波动方程。因该式令对称轴方向的横波速度为零,会产生菱形伪横波干扰,其本质原因在于对qP波相速度公式中的根式项做了平方处理,进而引入了增根,并在倾角变化剧烈的强各向异性区域极易出现数值模拟不稳定现象,从而限制了其广泛应用。
1.3 Low-rank分解算法由式(1)可知,在时间方向每延拓一步,需做一次傅里叶变换和Nxz次傅里叶反变换(Nxz=NxNz,Nx、Nz分别为模型x、z方向上的网格点数),其计算复杂度为O(Nxz2),这对于大规模复杂模型地震波波场延拓来说,计算成本极其昂贵。为了降低计算成本,本文引入Low-rank分解算法[35],只需几次(通常为2或3次)傅里叶反变换,计算复杂度为mNxzO(lgNxz) (m为很小的实数),从而显著降低了计算成本。
Low-rank基本思想是对空间—波数域的传播矩阵W进行分解,即
| $ {\mathit{\boldsymbol{W}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}}) = 2{\rm{cos}}[\varPhi (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}})\Delta t]} $ | (25a) |
或
| $ {\mathit{\boldsymbol{W}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}}) = {{\rm{e}}^{{\rm{i}}\varPhi (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}})\Delta t}}} $ | (25b) |
式中W(x, k)刻画了波的所有传播特征,包括了动力学与运动学特征,且式(25a)为两步法延拓波场矩阵,只涉及实数运算,式(25b)为一步法波场延拓矩阵,还涉及到复数运算。
当Δt固定时,有如下分解
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{W}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}}) \approx {\mathit{\boldsymbol{W}}_1}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{W}}_2}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \sum\limits_{m = 1}^M {\sum\limits_{n = 1}^N {{\mathit{\boldsymbol{W}}_1}} } (x,{k_m}){a_m}{\mathit{\boldsymbol{W}}_2}({\mathit{\boldsymbol{x}}_n},\mathit{\boldsymbol{k}})} \end{array} $ | (26) |
式中:W1、W2为矩阵W分解后的矩阵,且W1表示矩阵W中M个线性无关的列向量组成的最大空间体积,表征空间位置x,W2表示矩阵W中N个线性无关的行向量组成的最大空间体积,表征波数位置k;A={amn}为连接矩阵W1和W2的权重系数。特别地,当模型给定时,通过设定容许误差和Δt,即可求取上述子矩阵和权系数及对应子矩阵的秩M和N,且在整个波场延拓过程中,上式分解过程只需做一次分解即可,适用于并行计算。
Low-rank分解具体实施步骤如下。
(1) 求取子矩阵W1:
1) 从全矩阵W中随机选取βR行(通常β取3或4,R为全矩阵W的秩)组成一个新矩阵S1;
2) 对S1进行旋转QR分解,即
| $ {\mathit{\boldsymbol{S}}_1}{\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_1} = {\mathit{\boldsymbol{Q}}_1}{\mathit{\boldsymbol{R}}_1} $ | (27) |
式中Π1为包含矩阵S1各列置换信息的置换矩阵;
3) 取Π1中前R个置换序号组成序列Λ1={k1, k2, …, kR};
4) 取全矩阵W中对应序列Λ1的列向量,组成的矩阵W1即为所求
| $ {\mathit{\boldsymbol{W}}_1} = \mathit{\boldsymbol{W}}(:,{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_1}) = [{W_{{k_1}}},{W_{{k_2}}}, \cdots ,{W_{{k_R}}}] $ | (28) |
(2) 求取子矩阵W2:
1) 从全矩阵W中随机选取βR列组成一个新矩阵S2,其转置为S2T;
2)对S2T进行旋转QR分解,即
| $ \mathit{\boldsymbol{S}}_2^{\rm{T}}{\mathit{\boldsymbol{ \boldsymbol{\varPi} }}_2} = {\mathit{\boldsymbol{Q}}_2}{\mathit{\boldsymbol{R}}_2} $ | (29) |
式中Π2为包含矩阵S2T各列置换信息的置换矩阵。
3) 取Π2中前R个置换序号组成序列Λ2={x1, x2, …, xR};
4)取全矩阵W中对应序列Λ2的行向量,组成的矩阵W2即为所求
| $ {\mathit{\boldsymbol{W}}_2} = \mathit{\boldsymbol{W}}({\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_2},:) = {[{W_{{x_1}}},{W_{{x_2}}}, \cdots ,{W_{{x_R}}}]^{\rm{T}}} $ | (30) |
(3) 求取最佳近似分离权系数A:
选取子矩阵W1和子矩阵W2相互交叉的部分求伪逆,即
| $ \mathit{\boldsymbol{A}} = {\mathit{\boldsymbol{W}}^ + }({\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_2},{\mathit{\boldsymbol{ \boldsymbol{\varLambda} }}_1}) $ | (31) |
(4) 结合以上步骤就可得矩阵的Low-rank分解
| $ \mathit{\boldsymbol{W}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}}) \approx {\mathit{\boldsymbol{W}}_1}\mathit{\boldsymbol{A}}{\mathit{\boldsymbol{W}}_2} $ |
经过上述步骤Low-rank分解后,可将式(26)分别代入式(8)和式(7)中,就有
| $ \begin{array}{l} p(\mathit{\boldsymbol{x}},t + \Delta t) + p(\mathit{\boldsymbol{x}},t - \Delta t)\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \int 2 {\rm{cos}}[\varPhi (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}})\Delta t]\tilde p(\mathit{\boldsymbol{k}},t){{\rm{e}}^{{\rm{i}}\mathit{\boldsymbol{kx}}}}{\rm{d}}\mathit{\boldsymbol{k}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \approx \sum\limits_{m = 1}^M {{\mathit{\boldsymbol{W}}_1}} (\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{k}}_m})\left\{ {\sum\limits_{n = 1}^N {{a_{mn}}} \left[ {\int {{\mathit{\boldsymbol{W}}_2}} ({\mathit{\boldsymbol{x}}_n},\mathit{\boldsymbol{k}}) \times } \right.} \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tilde p(\mathit{\boldsymbol{k}},t){{\rm{e}}^{{\rm{i}}\mathit{\boldsymbol{kx}}}}{\rm{d}}\mathit{\boldsymbol{k}}]\} \end{array} $ | (32) |
| $ \begin{array}{l} p(\mathit{\boldsymbol{x}},t + \Delta t) = \int {\tilde p(\mathit{\boldsymbol{k}},t)} {{\rm{e}}^{{\rm{i}}\varPhi (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{k}})\Delta t}}{{\rm{e}}^{{\rm{i}}\mathit{\boldsymbol{kx}}}}{\rm{d}}\mathit{\boldsymbol{k}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \approx \sum\limits_{m = 1}^M {{\mathit{\boldsymbol{W}}_1}} (\mathit{\boldsymbol{x}},{\mathit{\boldsymbol{k}}_m})\left\{ {\sum\limits_{n = 1}^N {{a_{mn}}} \left[ {\int {{\mathit{\boldsymbol{W}}_2}} ({\mathit{\boldsymbol{x}}_n},\mathit{\boldsymbol{k}}) \times } \right.} \right.\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tilde p(\mathit{\boldsymbol{k}},t){{\rm{e}}^{{\rm{i}}\mathit{\boldsymbol{kx}}}}{\rm{d}}\mathit{\boldsymbol{k}}]\} \end{array} $ | (33) |
式(32)为基于Low-rank分解的两步法波场延拓公式,式(33)为基于Low-rank分解的一步法波场延拓公式。
2 模型试算 2.1 均匀模型为了验证本文构建的纯qP波算子不受模型参数的限制,且无伪横波干扰,设计了尺寸为2000m×2000m的均匀介质模型。其空间网格单元为5m×5m,时间步长为1ms,总时间采样点数为1000;纵波震源位于模型中心,采用主频为25Hz的Ricker子波震源;边界条件为海绵边界条件;接收排列范围是0~2000m,排列深度为750m,道间距为10m,共201道接收。均匀黏声各向异性纯qP波介质弹性参数见表 1。
|
|
表 1 均匀黏声各向异性介质纯qP波弹性参数 |
图 1上部为黏声TTI介质常规拟声波方程分别在介质类型Ⅲ(图 1a)、Ⅳ(图 1b)、Ⅴ(图 1c)时400ms时刻波场快照,图 1下部为黏声TTI介质纯qP波方程分别在介质类型Ⅲ(图 1d)、Ⅳ(图 1e)、Ⅴ(图 1f)时400ms时刻波场快照。从图中可见常规拟声波方程(即直接将横波速度设为0)在ε>δ时虽能稳定传播,但会出现菱形假象,严重干扰了有效波;在ε < δ时会出现不稳定现象;只有在ε=δ时才能稳定传播且无假象。这样就极大地限制了其应用。而本文构建纯qP波方程(图 1下部),无论是ε < δ、ε>δ还是ε=δ时,都能稳定地传播且不受横波干扰,表明本文方法突破了该限制,具有更强适用性。
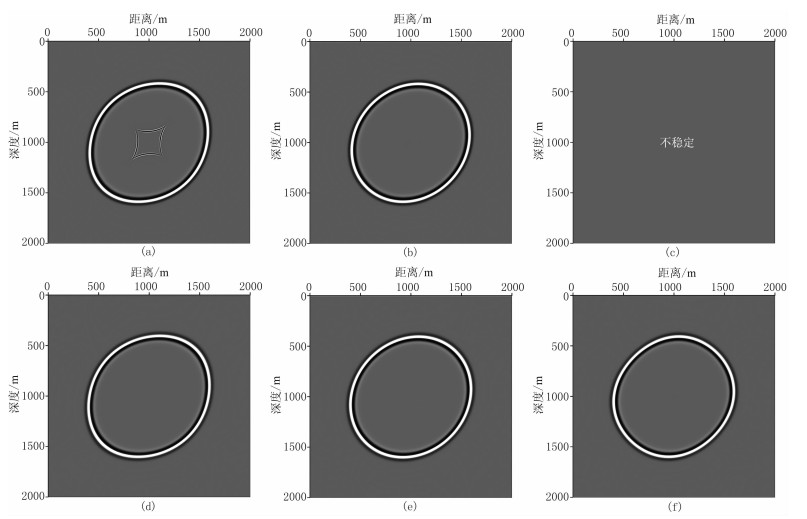
|
图 1 均匀黏声各向异性介质拟声波方程(上)和纯qP波方程(下)400ms时刻波场快照 (a)、(d)对应类型Ⅲ介质;(b)、(e)对应类型Ⅳ介质;(c)、(f)对应类型Ⅴ介质 |
图 2为纯qP波方程分别在介质类型Ⅰ、Ⅱ、Ⅲ时400ms时刻波场快照。对比对应为黏声VTI(图 2a)、HTI(图 2b)和TTI(图 2c)三种介质发现,通过引入坐标旋转,使得TTI介质具有更强适用性,更能反映实际地下真实介质的情况。
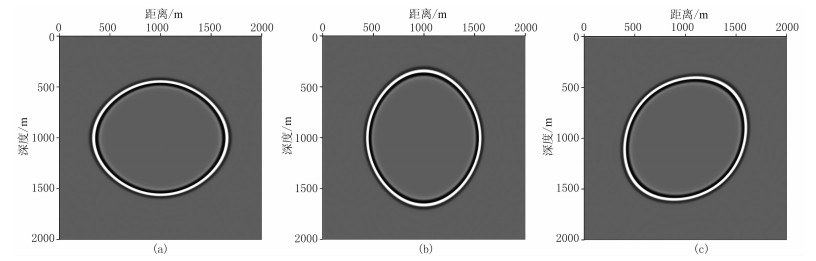
|
图 2 纯qP波方程在均匀黏声各向异性介质中400ms时刻波场快照 (a)介质类型Ⅰ;(b)介质类型Ⅱ;(c)介质类型Ⅲ |
采用表 2所示介质参数做正演模拟,研判本文构建的纯qP波算子是否同时具有各向异性特征及黏滞性特征,并分别取四种介质的四分之一波场拼成一张波场快照以突显对比效果(图 3)。从图中对比发现,横向对比可体现出各向异性特征,即声波波前为一个圆,在VTI介质中波前为椭圆;纵向对比可体现出黏滞性特征,即波前走时差异及能量差异。为了更直观地分析,采用表 1介质类型Ⅲ中的参数,并设定不同的Q值(无穷大、200、50和20),得到不同Q值时的地震记录。
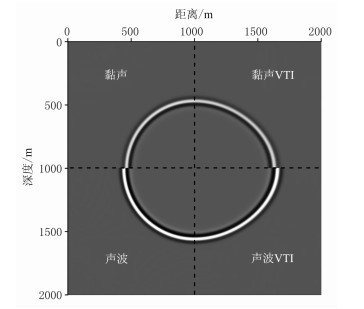
|
图 3 不同介质类型在400ms时刻的波场快照对比 |
|
|
表 2 不同介质类型弹性参数 |
从不同Q值下的单道波形记录及频谱(图 4)对比可知,由于地下介质的黏滞性,使得地震波的振幅得到明显的衰减,品质因子Q越低,其振幅衰减的越多,波形记录的相位延迟越严重,波形变宽,则畸变也越严重。从频谱图看到,品质因子Q越低,其能量越低,子波主频也越低,符合真实实际地下介质中地震波由于地层的吸收衰减能量逐渐减弱,高频衰减快,主频降低的特征,说明了本文构建的纯qP波算子的正确性,即能同时体现出各向异性特征及黏滞性特征。
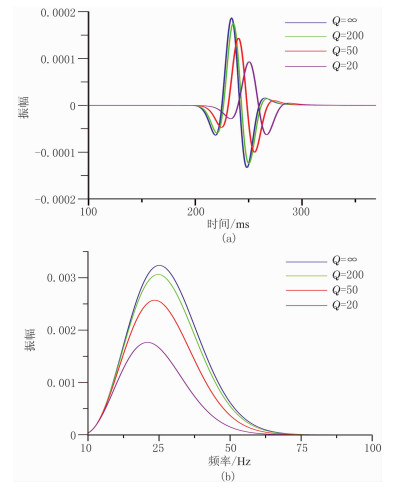
|
图 4 不同Q值下的单道波形记录(a)及频谱(b)对比 |
选用Overthrust模型测试Low-rank分解算法的稳定性。该模型构造较简单,有利于观测波的传播规律,特别是运动学特性;此外,模型中部区域各向异性特征明显,且倾角变化剧烈,是测试分析算法稳定性的标准模型(图 5)。该模型尺寸为7000m×2000m,空间网格单元为10m×10m,时间步长为2ms,总时间采样点数为1250,记录长度为2.5s,纵波震源位置为(3500m,10m),震源是主频为30Hz的Ricker子波,选取海绵边界条件,接收排列范围为0~7000m,排列深度为0,道间距为20m,共351道接收。模型参数如图 5所示,其中品质因子由经验公式[36]Q=14v2.2得到。
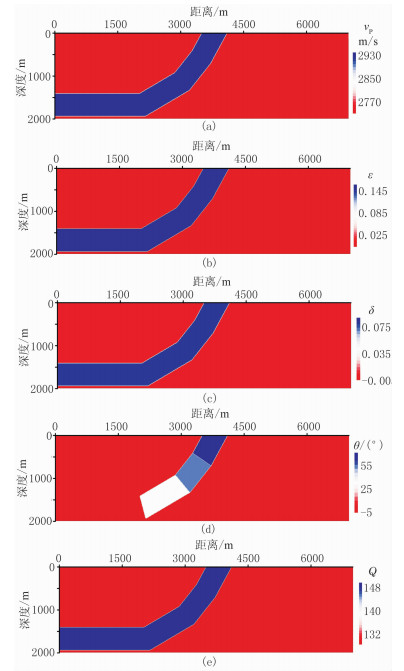
|
图 5 二维黏声TTI Overthrust模型参数 (a)vP模型;(b)ε模型;(c)δ模型;(d)θ模型;(e)Q模型 |
首先验证Low-rank分解算法重构矩阵的有效性及正确性。选取图 5模型中心处(vP=3000m/s,θ=50°,ε=0.15,δ=0.08)的真实矩阵,即得到该真实矩阵的实部(图 6a)、虚部(图 6d)和模(图 6g),Low-rank近似矩阵的实部(图 6b)、虚部(图 6e)和模(图 6h),以及真实矩阵与Low-rank近似矩阵的实部(图 6c)、虚部(图 6f)和模(图 6i)的误差。对比可知Low-rank近似矩阵接近于真实矩阵;此外,其误差的数量级仅为10-7,充分表明Low-rank分解能精确地重构真实矩阵。
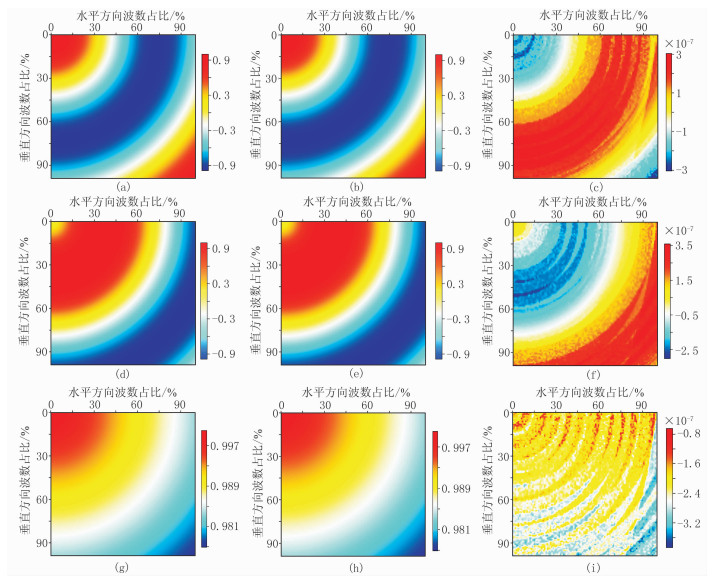
|
图 6 Overthrust模型中心处的传播矩阵W(x, k)=eiΦ(x, k)Δt (a)、(d)、(g)对应真实矩阵的实部、虚部及其模;(b)、(e)、(h)对应Low-rank近似矩阵的实部、虚部及其模;(c)、(f)、(i)分别为真实矩阵与Low-rank近似矩阵的实部、虚部及其模的误差 |
然后探讨基于Low-rank分解算法的波场延拓的稳定性。应用一步法波场延拓得到不同子波主频、不同时间步长的600ms时刻波场快照(图 7)。对比子波主频为30Hz、时间步长为2ms(图 7a)与子波主频为60Hz、相同时间步长(图 7b)的波场可知,提高地震子波主频使子波波长变短,空间子波的分辨率明显提高,其地震波场特征更清晰,也说明了子波主频与波长呈反比关系;若使用有限差分正演,一个波长内约有两个采样点,必然会严重干扰有效波,并形成显著的频散,而Low-rank分解算法能在不减小网格单元尺寸的情况下适应高频正演且不损失精度,证明Low-rank分解算法是高精度波场延拓算法。同样地,将子波主频为60Hz、时间步长为4ms(图 7c)的波场与图 7b对比,可知在相同高频子波主频下,Low-rank算法能通过提高时间步长提升计算效率且不损失计算精度。据稳定性条件,有限差分法时间步长不大于1.5ms,说明Low- rank分解算法比有限差分算法能更有效地通过提高地震子波主频和时间步长改善地震记录分辨率和计算效率,且不损失计算精度,表明Low-rank分解算法能同时兼顾计算精度和计算效率。

|
图 7 不同参数下的Low-rank一步法600ms时刻波场快照 (a)f=30Hz,Δt=2ms;(b)f=60Hz,Δt=2ms;(c)f=60Hz,Δt=4ms |
一般而言,Low-rank分解算法的计算效率与秩R有很大关系。R值大小决定正反傅里叶变换的次数,即R越大,正、反傅里叶变换次数越多,计算量越大,导致计算效率降低。
表 3为不同时间步长和不同容许误差下的秩R。从表中可知,当容许误差一定时,随时间步长增大,R逐渐增加。值得注意的是,虽然随着时间步长的增大,R也增大,其计算效率会降低,但增大时间步长所提高的计算效率足以弥补R增加导致的计算效率降低,即增大时间步长还是会在总体上提高计算效率;当时间步长一定时,R随着容许误差的降低而增大。特别地,时间步长的选取一般通过试验得到,即在满足精度及稳定性要求的前提下,试验选取最大时间步长。通常,在设定容许误差并满足计算精度要求的前提下,以R不超过12时的时间步长为宜。
|
|
表 3 不同时间步长和容许误差下的秩R |
再次设计尺寸为2000m×2000m的两层均匀介质模型,空间网格单元为5m×5m,纵波震源置于(1000m,900m)处,震源选取主频为30Hz的Ricker子波。为了便于对比,采用常密度声学介质,上、下层厚度均为1000m,上、下层纵波速度分别为1700、2300m/s。
图 8为有限差分法、Low-rank两步法及Low- rank一步法在不同时间步长下得到的400ms时刻波场快照。对比可知:当时间步长为1ms时,三种方法的波场都能稳定地传播;当步长为2ms时,有限差分法出现不稳定,难以进行波场延拓;当步长增至5ms时,Low-rank两步法出现频散,达到能正演的极限,而此时Low-rank一步法所得波场仍能稳定地传播,并保持很高计算精度;当步长高达15ms时,Low-rank一步法出现频散,计算精度开始下降,而其他两种方法根本无法进行波场延拓。该对比结果表明:Low-rank一步法的稳定性最高,其次是Low-rank两步法,有限差分法则是最低。再次证实Low-rank算法是一种能兼顾计算精度和计算效率的较新颖算法。

|
图 8 三种方法在不同时间步长下得到的400ms时刻波场快照 (a)、(d)、(g)、(j)对应有限差分法(FDM);(b)、(e)、(h)、(k)对应Low-rank两步法;(c)、(f)、(i)、(l)对应Low-rank一步法 (a)~(c)Δt=1ms;(d)~(f)Δt=2ms;(g)~(i)Δt=5ms;(j)~(l)Δt=15ms |
若针对上述双层均匀介质模型进行计算效率分析,会因模型网格点数较少,单炮计算时间很短,而不便于比较,故取10炮CPU耗时进行计算效率分析、对比,其中单炮记录时长为2s。
从上述三种正演模拟法在不同时间步长时的CPU耗时(表 4)可见:当时间步长为1ms时,有限差分法计算效率最高,其次为Low-rank两步法,而Low-rank一步法因要做复数运算,使得其计算效率最低。另一方面,由于Low-rank两步法和一步法的稳定性比有限差分法高较多,因此可使用较大时间步长。结合图 8及表 4可知,在同等计算精度条件下,Low-rank两步法和一步法因可使用较大时间步长,使其计算效率高于有限差分法,且随着时间步长的增加,无论是Low-rank两步法还是一步法,其计算效率均降低,即说明在满足计算精度前提下,增加时间步长,能提高计算效率。
|
|
表 4 不同方法在不同时间步长时的CPU耗时 |
采用二维Hess黏声TTI介质模型(图 9)测试Low-rank一步法纯qP波波场延拓对复杂介质的适应性。该模型尺寸为3000m×2500m,空间网格单元为5m×5m,时间步长为5ms,总时间采样点为500,纵波震源置于(2000m,10m)处,仍采用前述震源子波和边界条件,接收排列范围是0~3000m,排列深度为0,接收点间距为10m,共301道接收。模型参数见图 9,品质因子同样可由经验公式[36]Q=14v2.2得到,极化角θ为45°。
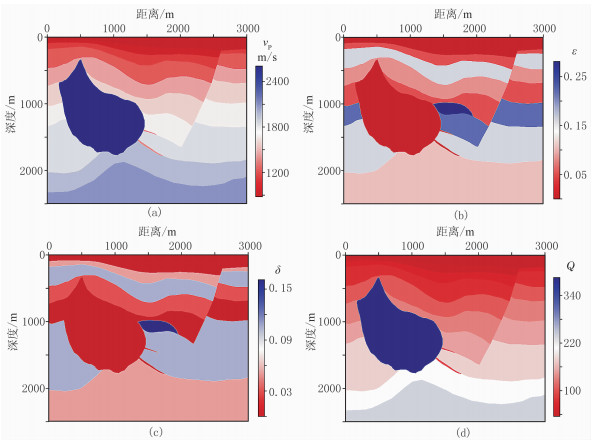
|
图 9 二维Hess黏声TTI介质模型参数 (a)纵波速度vP;(b)纵波各向异性参数ε;(c)变异系数δ;(d)品质因子Q |
从黏声TTI介质纯qP波800ms时刻波场快照(图 10a)可见,波场中只含有纯P波,无横波干扰,且波场特征复杂;同时,地震记录(图 10b)上表现出浅部能量强、深部能量弱的特征,与实际采集的地震记录特征相同。这为地下波场特征研究及该类介质的逆时偏移提供了更多理论依据,也表明本文构建的纯qP波方程能适应复杂介质和复杂构造,能够稳定地对其进行波场延拓。
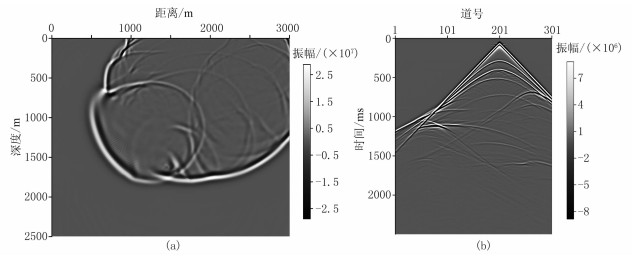
|
图 10 二维Hess黏声TTI介质800ms时刻波场快照(a)及地震记录(b) |
对比不同时间步长时所得地震记录及其差值(图 11),可见10ms步长地震记录(图 11a)的浅部反射同相轴不连续,出现轻微频散,说明5ms步长地震记录的精度高于10ms步长,即随着时间步长的增加,计算精度降低。因此,在可接受计算精度前提下,采用较大时间步长,可显著提高计算效率。
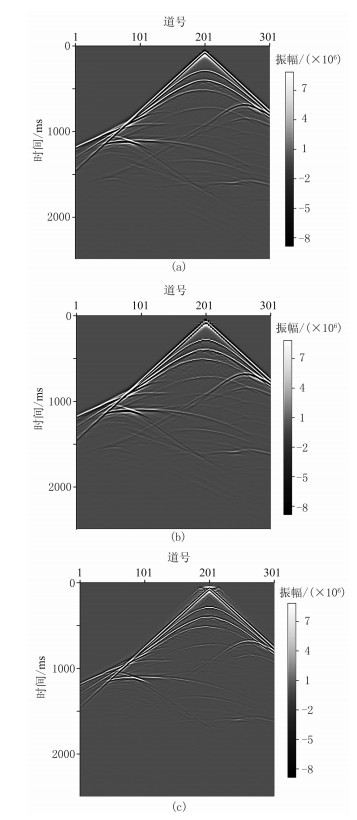
|
图 11 时间步长为5ms(a)和10ms(b)时的地震记录及其差值(c) |
为检验所提方法对倾角剧变复杂介质的稳定性,截取一段倾角变化范围是-55°~55°的二维BP2007黏声TTI介质模型(图 12)进行测试。该模型规模为17km×11.25km,空间网格单元为6.25m×6.25m,时间步长为5ms,总时间采样点为1600,记录长度为8s,纵波震源位于(68.5km,0),采用主频为20Hz的Ricker子波震源,仍为上述边界条件,接收排列范围是0~17km,排列深度为0,接收点间距为25m,共681道接收。模型参数见图 12,品质因子仍沿用上述方式得到。
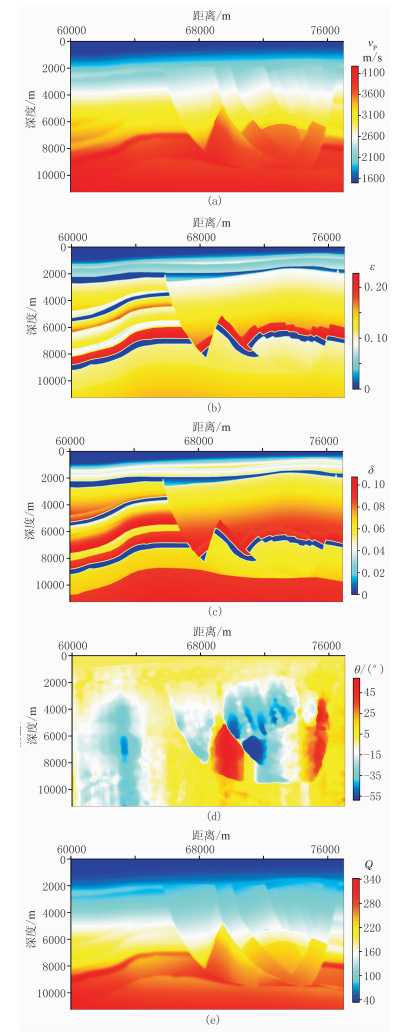
|
图 12 二维BP2007黏声TTI介质模型参数 (a)纵波速度vP;(b)纵波各向异性参数ε;(c)变异系数δ;(d)极化角θ;(e)品质因子Q |
图 13为采用二维BP2007模型得到的黏声TTI介质纯qP波4s时刻波场快照及其地震记录。从波场快照(图 13a)可见,地震波场能稳定地传播,说明所提方法能适应倾角剧烈变化的情形,具有较高稳定性;同时,在地震记录(图 13b)中,地震波能量表现出浅部强、深部弱的特征,体现了地下介质的黏滞性特征,即说明本文方法能在兼顾计算精度的同时,使用较大时间步长,以提高计算效率,并能够适用于复杂介质、复杂构造,包括倾角剧变情形,是一种稳定高效的正演模拟方法。
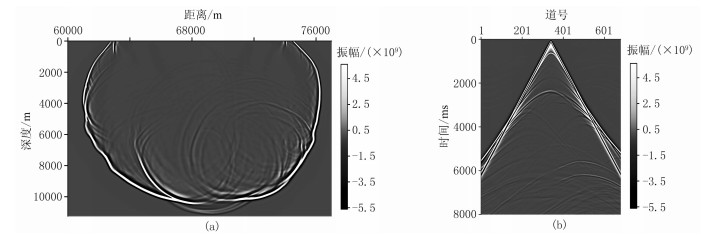
|
图 13 二维BP2007黏声TTI介质4s时刻波场快照(a)及地震记录(b) |
本文在前人研究基础上,引入一步法波场延拓方法,构建了一种适用于黏声各向异性介质的空间—波数域纯qP波波场延拓算子,该算子消除了伪横波干扰,不受模型参数限制,且地震波场能稳定传播;为兼顾计算精度与计算效率,引入Low-rank分解算法进行求解,实现了基于Low-rank一步法波场延拓的黏声各向异性介质纯qP波正演模拟。通过多种模型的测试,得出以下认识和结论:
(1) 通过本文构建的纯qP波算子计算得到的波场,能同时表现出各向异性特征和黏滞性特征,更符合实际地下介质情况,也证明所构建纯qP波算子的正确性;
(2)本文方法克服了拟声波方程的局限性,消除了伪横波干扰,不受模型参数限制且地震波场能稳定地传播,具有较为广泛的应用前景;
(3)本文方法可适应较大时间步长,无数值频散,能同时兼顾计算效率和计算精度,是一种稳定、高效的正演模拟方法。
| [1] |
Chichinina T, Obolentseva I, Gik L, et al. Attenuation anisotropy in the linear-slip model:Interpretation of physical modeling data[J]. Geophysics, 2009, 74(5): WB165-WB176. |
| [2] |
丁亮, 刘洋. 逆时偏移成像技术研究进展[J]. 地球物理学进展, 2011, 26(3): 1085-1100. DING Liang, LIU Yang. Progress in reverse time migration imaging[J]. Progress in Geophysics, 2011, 26(3): 1085-1100. DOI:10.3969/j.issn.1004-2903.2011.03.039 |
| [3] |
Alkhalifah T. Acoustic approximations for processing in transversely isotropic media[J]. Geophysics, 1998, 63(2): 623-631. |
| [4] |
Alkhalifah T. An acoustic wave equation for anisotropic media[J]. Geophysics, 2000, 65(4): 1239-1250. |
| [5] |
Du X, Bancroft J C, Lines L R.Reverse-time migration for tilted TI media[C].SEG Technical Program Expanded Abstracts, 2005, 24: 1930-1933.
|
| [6] |
Zhou H B, Zhang G Q, Bloor R.An anisotropic acoustic wave qeuation for modeling and migration in 2D TTI media[C].SEG Technical Program Expanded Abstracts, 2006, 25: 194-198.
|
| [7] |
Duveneck E, Milcik P, Bakker P M, et al. Acoustic VTI wave equations and their application for anisotrpic reverse-time migration[J]. SEG Technical Program Expanded Abstracts, 2008, 27: 2186-2190. |
| [8] |
程玖兵, 陈茂根, 王腾飞, 等. 各向异性介质qP波传播描述Ⅱ:分离纯模式标量波[J]. 地球物理学报, 2014, 57(10): 3389-3401. CHENG Jiubing, CHEN Maogen, WANG Tengfei, et al. Description of qP-wave propagation in anisotropic media, Part Ⅱ:Separation of pure-mode scalar waves[J]. Chinese Journal of Geophysics, 2014, 57(10): 3389-3410. DOI:10.6038/cjg20141025 |
| [9] |
程玖兵, 康玮, 王腾飞. 各向异性介质qP波传播描述Ⅰ:伪纯模式波动方程[J]. 地球物理学报, 2013, 56(10): 3474-3486. CHENG Jiubing, KANG Wei, WANG Tengfei. Description of qP-wave propagation in anisotropic media, Part Ⅰ:Pseudo-pure-mode scalar wave equa-tions[J]. Chinese Journal of Geophysics, 2013, 56(10): 3474-3486. DOI:10.6038/cjg20131022 |
| [10] |
Zhang Y, Zhang P, Zhang H Z.Compensating for visco-acoustic effects in reverse-time migration[C].SEG Technical Program Expanded Abstracts, 2010, 29: 3160-3164.
|
| [11] |
Suh S, Yoon K, Cai J, et al.Compensating visco-acoustic effects in anisotropic resverse-time migration[C].SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [12] |
Xu W C, Li Z C, Deng W Z, et al.Anisotropic visco-acoustic wave RTM based on second-order quasi-differential equation[C].SEG Technical Program Expanded Abstracts, 2015, 34: 4013-4017.
|
| [13] |
李金丽, 刘建勋, 姜春香, 等. 黏声VTI介质正演模拟与照明分析[J]. 石油地球物理勘探, 2017, 52(5): 906-914. LI Jinli, LIU Jianxun, JIANG Chunxiang, et al. Forward modeling and illumination analysis in visco-acoustic VTI media[J]. Oil Geophysical Prospecting, 2017, 52(5): 906-914. |
| [14] |
Duveneck E, Bakker P M. Stable P-wave modeling for reverse-time migration in tilted TI media[J]. Geophysics, 2011, 76(2): S65-S75. |
| [15] |
Grechka V, Zhang L B, Rector J W. Shear waves in a-coustic anisotropic media[J]. Geophysics, 2004, 69(2): 576-582. |
| [16] |
郭成锋, 杜启振, 张明强, 等. 改进的TTI介质纯P波方程正演模拟与逆时偏移[J]. 地球物理学报, 2017, 60(1): 258-270. GUO Chengfeng, DU Qizhen, ZHANG Mingqiang, et al. Numerical simulation and reverse time migration using an improved pure P wave equation in tilted transversely isotropic media[J]. Chinese Journal of Geophysics, 2017, 60(1): 258-270. |
| [17] |
Zhang Y, Zhang H Z, Zhang G Q. A stable TTI re-verse time migration and its implementation[J]. Geophysics, 2011, 76(3): WA3-WA11. |
| [18] |
Zhan G, Pestana R C, Stiffa P L. Decoupled equations for reverse time migration in tilted transversely isotropic media[J]. Geophysics, 2012, 77(2): T37-T45. |
| [19] |
Xu S, Tang B, Mu J, et al.Quasi-P wave propagation with an elliptic differential operator[C].SEG Technical Program Expanded Abstracts, 2015, 34: 4380-4384.
|
| [20] |
杨鹏, 李振春, 谷丙洛. 一种TI介质纯qP波正演方法及其在逆时偏移中的应用[J]. 地球物理学报, 2017, 60(11): 4447-4467. YANG Peng, LI Zhenchun, GU Bingluo. Pure quasi-P wave forward modeling method in TI media and its application to RTM[J]. Chinese Journal of Geophy-sics, 2017, 60(11): 4447-4467. DOI:10.6038/cjg20171130 |
| [21] |
胡书华, 王宇超, 刘文卿, 等. 复杂TTI介质稳定的纯qP波波场模拟方法[J]. 石油地球物理勘探, 2018, 53(2): 280-287. HU Shuhua, WANG Yuchao, LIU Wenqing, et al. Pure quasi-P wave stable simulation in complex TTI medium[J]. Oil Geophysical Prospecting, 2018, 53(2): 280-287. |
| [22] |
张庆朝, 朱国维, 周俊杰, 等. TTI介质qP波伪谱法正演模拟[J]. 石油地球物理勘探, 2019, 54(2): 302-311. ZHANG Qingchao, ZHU Guowei, ZHOU Junjie, et al. qP-wave numerical simulation in TTI media with pseudo-spectral method[J]. Oil Geophysical Prospecting, 2019, 54(2): 302-311. |
| [23] |
Du X, Fowler P J, Fletcher R P. Recursive integral time extrapolation methods for waves:A comparative review[J]. Geophysics, 2014, 79(1): T9-T26. |
| [24] |
Fomel S, Ying L X, Song X L. Seismic wave extrapolation using lowrank symbol approximation[J]. Geophysical Prospecting, 2012, 61(3): 526-536. |
| [25] |
Song X L, Alkhalifah T. Modeling of pseudoacoustic P-waves in orthorhombic media with a low-rank approximation[J]. Geophysics, 2013, 78(4): C33-C40. |
| [26] |
Fang G, Fomel S, Du Q Z, et al. Lowrank seismic-wave extrapolation on a staggered grid[J]. Geophy-sics, 2014, 79(3): T157-T168. |
| [27] |
Sun J Z, Fomel S, Ying L X. Low-rank one-step wave extrapolation for reverse time migration[J]. Geophy-sics, 2015, 81(1): S39-S54. |
| [28] |
黄金强, 李振春, 江文. TTI介质Low-rank有限差分法高效正演模拟及逆时偏移[J]. 石油地球物理勘探, 2018, 52(6): 1198-1209. HUANG Jinqiang, LI Zhenchun, JIANG Wen. An efficient forward modeling with the Low-rank finite-difference algorithm for complex TTI media and its application in inverse time migration[J]. Oil Geophy-sical Prospecting, 2018, 52(5): 915-927. |
| [29] |
黄金强, 李振春. 基于Low-rank分解的复杂TI介质纯qP波正演模拟与逆时偏移[J]. 地球物理学报, 2017, 60(2): 704-721. HUANG Jinqiang, LI Zhenchun. Modeling and reverse time migration of pure quasi-P-waves in complex TI media with a Low-rank decomposition[J]. Chinese Journal of Geophysics, 2017, 60(2): 704-721. |
| [30] |
袁雨欣, 胡婷, 王之洋, 等. 求解二阶解耦弹性波方程的低秩分解法和低秩有限差分法[J]. 地球物理学报, 2018, 61(8): 3324-3333. YUAN Yuxin, HU Ting, WANG Zhiyang, et al. Solving second-order decoupled elastic wave equations using low-rank decomposition method and low-rank finite differences[J]. Chinese Journal of Geophysics, 2018, 61(8): 3324-3333. |
| [31] |
Zhang Y, Zhang G Q. One-step extrapolation method for reverse time migration[J]. Geophysics, 2009, 74(4): A29-A33. |
| [32] |
Wards B D, Margrave G F, Lamoureux M P.Phase-shift time-stepping for reverse-time migration[C].SEG Technical Program Expanded Abstracts, 2008, 27: 2262-2266.
|
| [33] |
Fomel S. On anelliptic approximations for qP velocities in VTI media[J]. Geophysical Prospecting, 2004, 52(3): 247-259. DOI:10.1111/j.1365-2478.2004.00413.x |
| [34] |
李振春, 郭振波, 田坤. 黏声介质最小平方逆时偏移[J]. 地球物理学报, 2014, 57(1): 214-228. LI Zhenchun, GUO Zhenbo, TIAN Kun. Least-squares inverse time migration in visco-acoustic media[J]. Chinese Journal of Geophysics, 2014, 57(1): 214-228. |
| [35] |
Engquist B, Ying L. A fast directional algorithm for high frequency acoustic scattering in two dimensions[J]. Communications in Mathematical Sciences, 2009, 7(2): 327-345. |
| [36] |
李庆忠.走向精确勘探的道路[M].北京: 石油工业出版社, 1993. LI Qingzhong.Road to Precise Exploration[M].Petroleum Industry Press, Beijing, 1993. |



 顾汉明, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院, 430074。Email:
顾汉明, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院, 430074。Email: