② 中海油研究总院有限责任公司, 北京 100027;
③ 油气藏地质及开发工程国家重点实验室(成都理工大学), 四川成都 610059
② CNOOC Research Institute Co. Ltd., Beijing 100027, China;
③ State Key Laboratory of Oil and Gas Reservoir Geology and Exploitation(Chengdu University of Technology), Chengdu, Sichuan 610059, China
三维地震勘探是油气勘探的主要技术,包括地震资料采集、处理及解释流程。由于受经济成本、地质条件等因素限制,地震采集数据一般为欠采样数据且含有噪声[1-2],将对数据处理和地质解释产生严重影响。因此,三维地震数据去噪与重建是一个有重要意义的课题。
地震数据去噪方法很多,主要分为滤波法和数学变换法两类。地震数据重建方法主要分为五类:预测滤波法、波动方程法、相干倾角插值法、矩阵降秩法和数学变换法。其中数学变换法是基于压缩感知理论的一类稀疏变换算法,是目前较为主流的地震数据重建和去噪算法,如傅里叶变换[3-4]、Radon变换[5-6]、小波变换[7-8]、曲波变换[9-10]等稀疏变换算法。
上述传统的基于变换域的去噪和数据重建算法都是对原始数据进行某种变换,然后在变换域对系数进行阈值处理,从而恢复高精度数据。传统算法中稀疏变换的基函数一般是固定不变的,不同的稀疏变换局限于处理特定结构的数据,使这些算法无法适应结构复杂的地震数据。块匹配三维协同滤波(BM3D)和块匹配四维协同滤波(BM4D)是一类利用数据局部相似性的算法[11-12],近年来被用于地震信号恢复,这类算法可用于结构复杂的地震数据重建与去噪。为了获得一种自适应的稀疏变换基函数,人们提出了多种通过字典学习估计基函数的自适应稀疏变换算法,这类算法能够自适应地从数据本身派生出模型,从而处理结构复杂的数据。常用的具有代表性的字典学习算法有:①最优方向法[13],是一种较早提出的字典学习算法,用L0范数计算数据的稀疏性、用交替优化方式求解学习模型;②K奇异值分解(K-singular value decomposition, K-SVD)算法[14-15],是对K均值算法的拓展,通过字典更新和稀疏编码两个步骤的不断迭代处理数据;③在线字典学习算法[16-17],通过一次只处理一个样本并结合最小角回归算法进行系数编码获得更快的字典学习收敛速度,实现大规模样本的字典学习。此外,还有广义主成分分析、组结构字典学习等具有代表性的字典学习算法。
上述字典学习算法都对字典的自由度进行一定控制,从而使算法稳定。数据驱动紧框架(data-driven tight frame,DDTF)理论[18]限定学习字典为一组平移不变的冗余小波紧框架,通过进一步控制字典的自由度,使DDTF算法拥有良好的鲁棒性,并且利用小波紧框架完美的重构特性,可更好地保留数据的精细特征。
DDTF算法已广泛用于图像处理领域,近年来也尝试处理二维地震数据[19]。本文将DDTF理论扩展到处理三维地震数据,并通过仿真实验和实际数据处理,对比曲波变换、BM4D和DDTF的三维地震数据去噪与重建效果。数值试算结果表明,DDTF算法在地震数据去噪和重建方面更具优势。
1 基本原理应用DDTF算法实现三维地震数据去噪和重建包含两个主要阶段:第一阶段是DDTF字典学习阶段,以数据驱动的方式获取地震数据的稀疏表示;第二阶段是去噪和插值阶段,通过对稀疏系数进行阈值处理实现数据去噪、重建。
1.1 DDTF定义1 设{fi}i∈N∈H,其中{fi}i∈N是一个序列,N为自然数集或是自然数集的某一子集,H为希尔伯特(Hilbert)空间,如果存在两个正常数A、B,且A≤B,有
| $ A\left\| f \right\|_2^2 \le \sum\limits_{i \in \mathit{\boldsymbol{N}}} | \langle {f_i},f\rangle {|^2} \le B\left\| f \right\|_2^2{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \forall f \in \mathit{\boldsymbol{H}} $ | (1) |
则称{fi}i∈N是H中的框架,其中A、B为框架的上、下界。当A=B时,{fi}i∈N称为紧框架。对于紧框架,框架界的值称为冗余比,若衡量冗余比的界值A=B=1,则紧框架是一组正交基,此时{fi}i∈N称为正规化紧框架[20],即
| $ \left\| f \right\|_2^2 = \sum\limits_{i \in \mathit{\boldsymbol{N}}} | \langle {f_i},f\rangle {|^2}\;\:\forall f \in \mathit{\boldsymbol{H}} $ |
在紧框架上可以定义滤波器组(字典)矩阵W及其转置WT
| $ {\mathit{\boldsymbol{W}}:f \in \mathit{\boldsymbol{H}} \to \{ \langle {f_i},f\rangle \} \in {{\rm{L}}_2}(\mathit{\boldsymbol{N}})} $ | (2) |
| $ {{\mathit{\boldsymbol{W}}^{\rm{T}}}:\{ {\mathit{\boldsymbol{a}}_i}\} \in {{\rm{L}}_2}(\mathit{\boldsymbol{N}}) \to \sum\limits_i {{\mathit{\boldsymbol{a}}_i}} {f_i} \in \mathit{\boldsymbol{H}}} $ | (3) |
式中:L2(N)表示可测集为N的L2空间;ai为WT中的第i个列向量,{ai}为ai的向量集。利用W可以将原始数据变换为系数,利用WT又能把处理过的系数重构为数据。
定义2 小波紧框架是将小波理论和框架理论相结合的产物,小波紧框架是正交小波基的一般变换,即在小波系统中引入冗余性。可测集为R的L2空间L2(R)中的小波框架是由有限母小波Ψ={ψ1, …, ψm}∈L2(R)集合的平移和放大产生的[21],即
| $ \mathit{\boldsymbol{X}}(\mathit{\boldsymbol{ \boldsymbol{\varPsi} }}) = \{ {2^{j/2}}{\psi _l}({2^j} \cdot - k)\;\:1 \le l \le m,j、k \in \mathit{\boldsymbol{Z}}\} $ | (4) |
当X(Ψ)是紧框架时,称之为小波紧框架。本文使用小波紧框架初始化字典对字典进行限定。
利用DDTF算法的去噪和重建问题可以看作最优化问题,目标函数为
| $ \mathop {{\rm{arg}}{\kern 1pt} {\kern 1pt} {\rm{min}}}\limits_{\mathit{\boldsymbol{v}},\mathit{\boldsymbol{W}}} \left\| {\mathit{\boldsymbol{v}} - \mathit{\boldsymbol{Wg}}} \right\|_2^2 + \lambda {\left\| \mathit{\boldsymbol{v}} \right\|_0}\;\:{\rm{ s}}{\rm{. t}}{\rm{.}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{W}} = \mathit{\boldsymbol{I}} $ | (5) |
式中:v为系数向量;g为数据向量;λ为拉格朗日常数,用于平衡重构误差‖v-Wg‖22和稀疏性‖v‖0的权重参数;I为单位矩阵。
通过以下迭代过程得到目标函数。
(1) 稀疏编码阶段。固定W,通过经典的稀疏近似问题求解系数向量v
| $ {\mathit{\boldsymbol{v}}^{(k)}}: = \mathop {{\rm{arg}}{\kern 1pt} {\kern 1pt} {\rm{min}}}\limits_\mathit{\boldsymbol{v}} \left\| {\mathit{\boldsymbol{v}} - {\mathit{\boldsymbol{W}}^{(k)}}\mathit{\boldsymbol{g}}} \right\|_2^2 + {\lambda ^2}{\left\| \mathit{\boldsymbol{v}} \right\|_0} $ | (6) |
通过硬阈值方法解决上述优化问题[18]。
(2) 字典更新阶段。固定v,求解W
| $ {\mathit{\boldsymbol{W}}^{(k + 1)}}: = \mathop {{\rm{arg}}{\kern 1pt} {\kern 1pt} {\rm{min}}}\limits_\mathit{\boldsymbol{W}} \left\| {{\mathit{\boldsymbol{v}}^{(k)}} - \mathit{\boldsymbol{Wg}}} \right\|_2^2\;\:{\rm{ s}}{\rm{. t}}{\rm{. }}\;\:{\mathit{\boldsymbol{W}}^T}\mathit{\boldsymbol{W}} = \mathit{\boldsymbol{I}} $ | (7) |
Cai等[18]推出了上述问题的显式解,本文省略了推导过程
| $ {{\mathit{\boldsymbol{W}}^{(k + 1)}} = \mathit{\boldsymbol{S}}{\mathit{\boldsymbol{U}}^{\rm{T}}}} $ | (8) |
可以通过SVD法得出S和U
| $ {\mathit{\boldsymbol{V}}{\mathit{\boldsymbol{G}}^{\rm{T}}} = \mathit{\boldsymbol{UD}}{\mathit{\boldsymbol{S}}^{\rm{T}}}} $ | (9) |
式中:U、S和D分别为将VGT通过SVD算法分解所得的两个相互正交的矩阵和一个对角矩阵;V=[v1, v2, …, vN]为gN在W下变换所得系数向量组合而成的矩阵;G=[g1, g2, …, gN]为矢量形式的样本组合矩阵。
图 1为DDTF初始字典与训练字典。由图可见,对应于初始字典(图 1a),在训练字典中可以看到明显的结构性特征(图 1b),故训练字典能更稀疏地表示原始数据。

|
图 1 DDTF初始字典(a)与训练字典(b) |
字典训练的样本由数据分块策略获取,且为了获取更多的样本,在分块时保证块之间具有一定的重叠度。由数据分块策略得到的样本不但可以获取数据本身的先验信息,且基于数据块之间的相似性,在保留数据有效信息的同时去除无用信息。本文将数据分块后,然后将块向量化,作为一个列向量得到样本矩阵(图 2)。数据分块时使用分块算子B,块聚合时使用合成算子BT。若将块转换为数据时,把每一个像素除以其重叠度,即可得到原始数据。
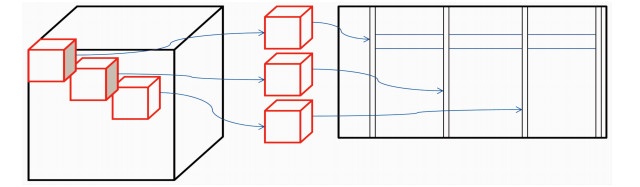
|
图 2 数据分块 |
从迭代中得到训练字典W后,采用稀疏促进方法去噪和重建。优化以下目标函数
| $ \mathit{\boldsymbol{g}} = \mathop {{\rm{arg}}{\kern 1pt} {\kern 1pt} {\rm{min}}}\limits_\mathit{\boldsymbol{g}} \left\| {{\mathit{\boldsymbol{g}}_0} - \mathit{\boldsymbol{Ag}}} \right\|_2^2 + {\left\| {\mathit{\boldsymbol{Wg}}} \right\|_1} $ | (10) |
式中:g0为采样数据;A为采样矩阵。如果A=I,上述目标函数表示去噪问题。如果A是一个稀疏采样矩阵,则上述目标函数表示插值问题。
对于去噪问题,使用单步阈值算法求解
| $ {{D_\theta }(\mathit{\boldsymbol{g}}) = \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{T}}_\theta }({\mathit{\boldsymbol{W}}^{\rm{T}}}\mathit{\boldsymbol{g}})} $ | (11) |
| $ {\left\{ {\begin{array}{*{20}{l}} {{{\{ {T_\theta }(\mathit{\boldsymbol{v}})\} }_i} = {T_\theta }({\mathit{\boldsymbol{v}}_i})}\\ {{T_\theta }({\mathit{\boldsymbol{v}}_i}) = {\rm{max}}(|{\mathit{\boldsymbol{v}}_i}| - \theta ,0)} \end{array}} \right.} $ | (12) |
式中Tθ为软阈值算子,其中θ为阈值参数。
对于插值问题,使用迭代收缩阈值(IST)算法求解
| $ \left\{ {\begin{array}{*{20}{l}} {{\mathit{\boldsymbol{g}}^\prime } = {D_\theta }[{\mathit{\boldsymbol{g}}^{(k)}}]}\\ {{\mathit{\boldsymbol{g}}^{(k + 1)}} = {\alpha _k}{W^{\rm{T}}}({\mathit{\boldsymbol{g}}^0} - \mathit{\boldsymbol{W}}{\mathit{\boldsymbol{g}}^\prime }) + {\mathit{\boldsymbol{g}}^\prime }} \end{array}} \right. $ | (13) |
式中参数αk控制算法的稳定性,迭代过程中αk从1减小到0。
1.4 算法实现流程算法主要包含两个阶段(图 3)。
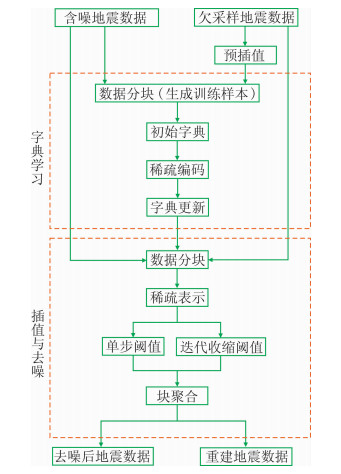
|
图 3 本文算法流程 |
(1) 字典学习,在此阶段利用小波紧框架初始化字典,再通过稀疏编码和字典更新得到训练后的字典。
(2) 去噪或插值,由训练后的字典得到数据的稀疏表示。若输入含噪地震数据,则使用单步阈值法处理稀疏系数,得到去噪后数据;若输入预插值后的欠采样地震数据,则使用迭代收缩阈值法处理稀疏系数,得到重建数据。
2 仿真实验和实际应用对于三维地震数据去噪和重建,应用DDTF算法进行仿真实验,作为算法对比,选用固定基函数的典型稀疏变换方法(曲波变换)和基于块匹配策略的协同滤波算法(BM4D)处理地震数据。利用三维合成地震数据和三维实际地震数据作为原始数据,原始数据尺寸为128×128×128,字典尺寸和样本尺寸为8×8×8,并尽量选择能达到最高信噪比(SNR)的其他参数,利用
| $ {\rm{SNR}} = 10 \times {\rm{lg}}\frac{{\left\| {{\mathit{\boldsymbol{X}}^*}} \right\|_2^2}}{{\left\| {{\mathit{\boldsymbol{X}}^*} - \mathit{\boldsymbol{X}}} \right\|_2^2}} $ | (14) |
初步判断不同方法的数据处理效果。式中X*和X分别表示原始地震数据及去噪或重建后的地震数据。
2.1 仿真实验为了验证本文算法的可行性和优势,合成了一个三维地震数据作为仿真实验模型并验证处理结果(图 4)。
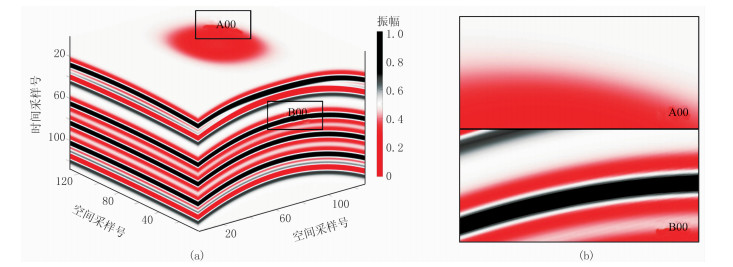
|
图 4 三维合成地震数据(a)及其局部放大(b) |
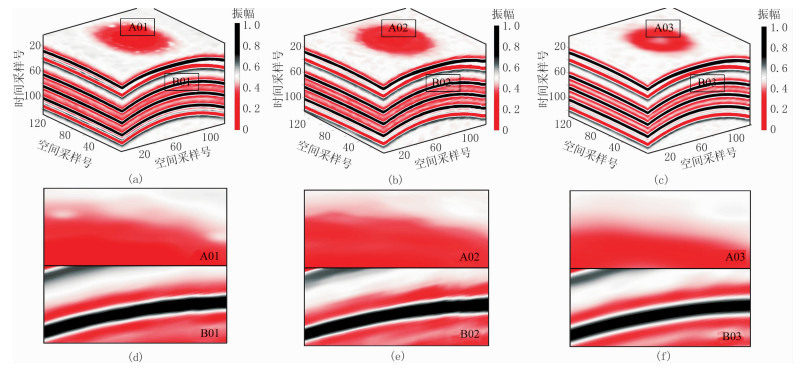
对纯净的三维合成地震数据添加强随机噪声后,致使部分有效信号被强噪声覆盖,同相轴连续性变差、细节变模糊(图 5)。曲波变换具有多尺度、多方向性质,适用于处理同相轴完整、连续的地震数据。BM4D通过相似匹配获取数据先验信息,DDTF通过字典学习获取数据先验信息。上述三种算法对含噪数据(图 5)的去噪结果(图 6)中均残留少量噪声,整体去噪效果较好,但DDTF的去噪效果更好(图 6c、图 6f),同相轴更完整。
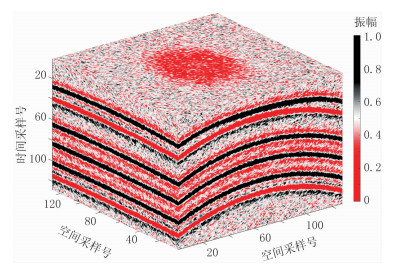
|
图 5 对图 4a数据添加20%随机噪声(SNR=14.44dB) |
|
图 6 合成数据去噪结果及其局部特征 (a)曲波变换(SNR=21.22dB);(b)BM4D(SNR=23.83dB);(c)DDTF(SNR=25.15dB);(d)~(f)分别为图a~图c的局部放大 |
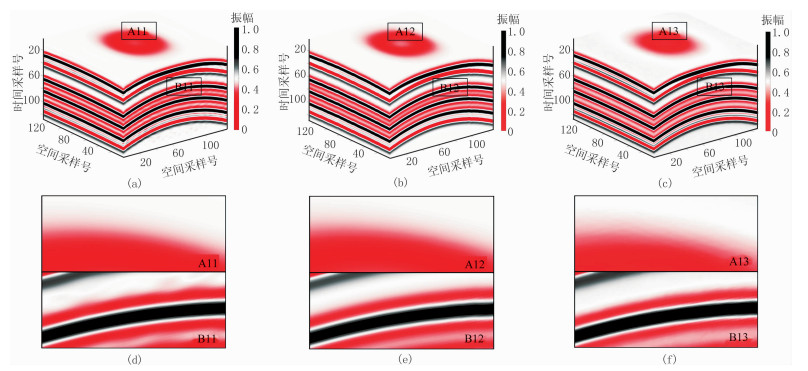
对图 4a数据随机剔除50%的地震道得到欠采样三维合成地震数据(图 7),其同相轴不连续、有效信号缺失严重。同样使用曲波变换、BM4D、DDTF算法对图 7数据的重建结果表明:①整体上三种算法的重建效果较好,较完整地恢复了同相轴。②曲波变换重建效果较好,但是同相轴外的区域产生了少量噪声,造成同相轴局部扭曲(图 8a、图 8d);BM4D重建结果中存在同相轴局部轻微错动(图 8b、图 8e);DDTF重建结果中同相轴更完整且连续,重建数据的信噪比最高(图 8c、图 8f)。

|
图 7 欠采样合成三维地震数据(SNR=3.29dB) |
|
图 8 合成数据重建结果及其局部特征 (a)曲波变换(SNR=21.81dB);(b)BM4D(SNR=24.77dB);(c)DDTF(SNR=27.42dB);(d)~(f)分别为图a~图c的局部放大 |
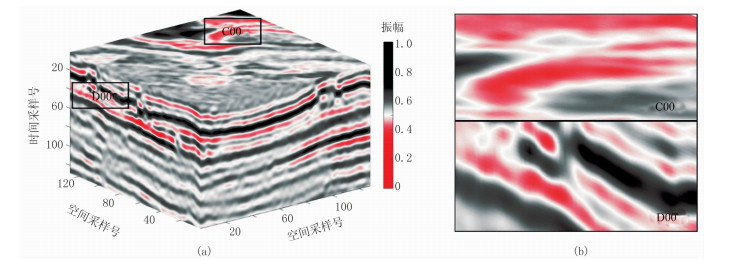
为了验证DDTF算法的实际应用效果,从新疆A区的三维实际地震数据中截取了尺寸为128×128×128的数据(图 9a)作为含噪数据或欠采样数据的原始数据,并验证处理结果。
|
图 9 三维实际地震数据(a)及其局部放大(b) |
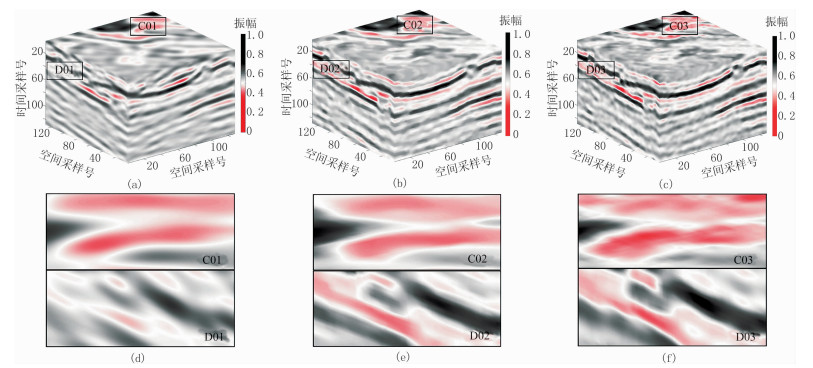
对实际三维地震数据添加20%的随机噪声,能量较强的噪声几乎将能量较弱的有效信号全部覆盖,同相轴连续性很差、细节特征丢失严重(图 10)。应用曲波变换、BM4D和DDTF三种算法对图 10数据的去噪结果表明:①由于实际地震数据结构更复杂,传统的固定基函数的曲波变换算法的去噪效果较差,同相轴连续性差(图 11a、图 11d)。因此由固定的模型套用结构复杂的数据是勉强的,须利用数据的先验信息自适应构建稀疏变换的基函数。②BM4D和DDTF能够较好地利用数据的先验信息,去噪效果较好,但是BM4D的去噪结果过于平滑,缺失了数据本身的一些细节特征(图 11b、图 11e);DDTF的去噪结果更多地保留了原始数据的精细特征,且信噪比更高(图 11c、图 11f)。

|
图 10 对图 9a数据添加20%的随机噪声(SNR=14.56dB) |
|
图 11 实际数据去噪结果及其局部特征 (a)曲波变换(SNR=27.91dB);(b)BM4D(SNR=28.88dB);(c)DDTF(SNR=30.48dB);(d)~(f)分别为图a~图c的局部放大 |
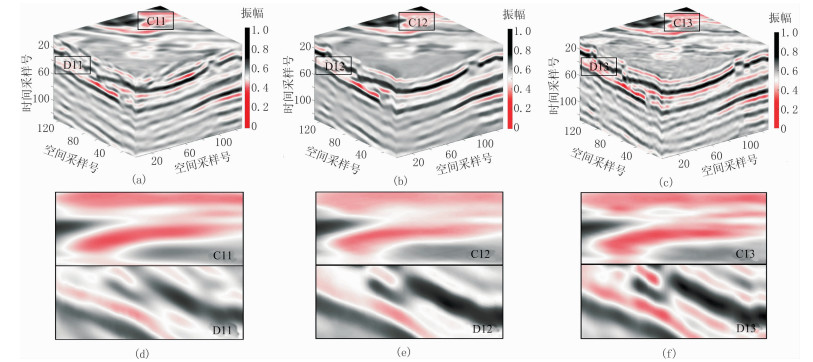
对实际三维地震数据随机剔除50%的地震道得到欠采样数据(图 12),使用曲波变换、BM4D、DDTF算法对欠采样数据的重建结果表明:①由于曲波变换固定基函数的局限性,重建结果不理想(图 13a、图 13d);BM4D的重建结果过于平滑,细节特征缺失严重(图 13b、图 13e);DDTF的重建结果信噪比更高,且尽量保留了原始数据的精细特征,从而验证了DDTF算法的实用性(图 13c、图 13f)。②曲波变换和BM4D在处理结构更复杂的实际地震数据时,去噪和重建效果较仿真实验差,但是DDTF去噪和重建效果仍然较好。

|
图 12 欠采样实际三维地震数据(SNR=3.01dB) |
|
图 13 实际数据重建结果及其局部特征 (a)曲波变换(SNR=29.12dB);(b)BM4D(SNR=29.81dB);(c)DDTF(SNR=31.66dB);(d)~(f)分别为图a~图c的局部放大 |
表 1为不同方法的计算时间对比。由表可见,DDTF算法的计算时间是另外两种算法的几倍至几十倍,原因为:一是计算机自身属性;二是DDTF方法采用字典学习算法,大量的字典训练量会消耗较多的时间;三是DDTF算法进行数据重建时进行了多重迭代过程,同样会消耗较多的时间。在实际工作中如果遇到数据量更大的三维地震数据,可以采用并行化算法,或在数据分块时减少块之间的重叠,减少训练样本数量,从而提高DDTF算法的计算效率。
|
|
表 1 不同方法的计算时间对比 |
本文基于DDTF理论,研究了三维地震数据去噪和重建问题。DDTF算法通过字典学习,能从数据本身得到最优的稀疏表示,从而适用于结构复杂的地震数据,并且利用小波紧框架完美的重构特性,可以很好地恢复原始数据的精细特征。仿真实验和实际数据应用结果表明:DDTF算法对结构简单的三维合成地震数据及结构复杂的实际三维地震数据都具有良好的去噪和重建效果,但计算效率较低,还需进一步改进;曲波变换对实际数据的去噪和重建效果较差;BM4D的去噪和重建结果过于光滑,会丢失一些结构特征。
| [1] |
霍志周, 熊登, 张剑锋. 地震数据重建方法综述[J]. 地球物理学进展, 2013, 28(4): 1749-1756. HUO Zhizhou, XIONG Deng, ZHANG Jianfeng. The overview of seismic data reconstruction methods[J]. Progress in Geophysics, 2013, 28(4): 1749-1756. |
| [2] |
唐刚.基于压缩感知和稀疏表示的地震数据重建与去噪[D].北京: 清华大学, 2010. TANG Gang.Seismic Data Reconstruction and Denoising Based on Compressed Sensing and Sparse Representation[D].Tsinghua University, Beijing, 2010. http://cdmd.cnki.com.cn/Article/CDMD-10003-1011280421.htm |
| [3] |
Duijndam A J W, Schonewille M A, Hindriks C O H. Reconstruction of band-limited signals, irregularly sampled along one spatial direction[J]. Geophysics, 1999, 64(2): 524-538. |
| [4] |
Naghizadeh M, Innanen K A. Seismic data interpolation using a fast generalized Fourier Transform[J]. Geophysics, 2011, 76(1): V1-V10. |
| [5] |
Trad D, Ulrych T, Sacchi M. Latest views of the sparse Radon transform[J]. Geophysics, 2003, 68(1): 386-399. |
| [6] |
Wang J, Ng M, and Perz M. Seismic data interpolation by greedy local Radon transform[J]. Geophysics, 2010, 75(6): WB225-WB234. |
| [7] |
Zhang R, Ulrych T. Physical wavelet frame denoising[J]. Geophysics, 2003, 68(1): 225-231. |
| [8] |
陈祖斌, 王丽芝, 宋杨, 等. 基于压缩感知的小波域地震数据实时压缩与高精度重构[J]. 石油地球物理勘探, 2018, 53(4): 674-681, 693. CHEN Zubin, WANG Lizhi, SONG Yang, et al. Seismic data real-time compression and high-precision reconstruction in the wavelet domain based on the compressed sensing[J]. Oil Geophysical Prospecting, 2018, 53(4): 674-681, 693. |
| [9] |
Herrmann F J, Hennenfent G. Non-parametric seismic data recovery with curvelet frames[J]. Geophysical Journal International, 2008, 173(1): 233-248. |
| [10] |
张华, 刁塑, 温建亮, 等. 应用二维非均匀曲波变换压制地震随机噪声[J]. 石油地球物理勘探, 2019, 54(1): 16-23. ZHANG Hua, DIAO Su, WEN Jianliang, et al. A random noise suppression with 2D non-uniform curvelet transform[J]. Oil Geophysical Prospecting, 2019, 54(1): 16-23. |
| [11] |
孙成禹, 刁俊才, 李文静. 基于曲波噪声估计的三维块匹配地震资料去噪[J]. 石油地球物理勘探, 2019, 54(6): 1188-1194. SUN Chengyu, DIAO Juncai, LI Wenjing. 3D block matching seismic data denoising based on Curvelet noise estimation[J]. Oil Geophysical Prospecting, 2019, 54(6): 1188-1194. |
| [12] |
Maggioni M, Katkovnik V, Egiazarian K, et al. Nonlocal transform-domain filter for volumetric data denoising and reconstruction[J]. IEEE Transactions on Image Processing, 2013, 22(1): 119-133. |
| [13] |
Engan K, Aase S O, Husoy J H.Method of optimal directions for frame design[C].IEEE International Conference on Acoustics, 2002, doi: 10.1109/ICASSP.1999.760624.
|
| [14] |
Aharon M, Elad M, Bruckstein A. K-SVD:An algorithm for designing overcomplete dictionaries for sparse representation[J]. IEEE Transactions on Signal Processing, 2006, 54(11): 4311-4322. |
| [15] |
张岩, 任伟建, 唐国维. 应用结构聚类字典学习压制地震数据随机噪声[J]. 石油地球物理勘探, 2018, 53(6): 1119-1127. ZHANG Yan, REN Weijian, TANG Guowei. Random noise suppression on seismic data based on structured-clustering dictionary learning[J]. Oil Geophysical Prospecting, 2018, 53(6): 1119-1127. |
| [16] |
Mairal J, Bach F, Ponce J, et al. Online learning for matrix factorization and sparse coding[J]. Journal of Machine Learning Research, 2009, 11(1): 19-60. |
| [17] |
李勇, 张益明, 雷钦, 等. 模型约束下的在线字典学习地震弱信号去噪方法[J]. 地球物理学报, 2019, 62(1): 417-426. LI Yong, ZHANG Yiming, LEI Qin, et al. Online dictionary learning seismic weak signal denoising method under model constraints[J]. Chinese Journal of Geophysics, 2019, 62(1): 417-426. |
| [18] |
Cai J F, Ji H, Shen Z, et al. Data-driven tight frame construction and image denoising[J]. Applied and Computational Harmonic Analysis, 2014, 37(1): 89-105. |
| [19] |
Liang J, Ma J, Zhang X. Seismic data restoration via data driven-tight frame[J]. Geophysics, 2014, 79(3): V65-V74. |
| [20] |
Christensen O.An Introduction to Frames and Riesz Bases[M].Birkhäuser, Boston, 2003.
|
| [21] |
Lawton W M. Necessary and sufficient conditions for constructing orthonormal wavelet bases[J]. Journal of Mathematical Physics, 1991, 32(1): 57-61. |



 李勇, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院, 610059。Email:
李勇, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院, 610059。Email: