在地震数据现场采集中,由于需要考虑客观存在的障碍物、禁采区、海洋拖缆羽状漂移和采集经济成本等因素,地震数据沿空间方向通常呈现不规则分布或规则缺失分布;在地震数据预处理中,必要的剔除废炮、废道等操作也会导致地震道缺失。而后续的常规数据处理,如速度分析、叠加、偏移等,应建立在完整的地震数据基础上。因此,亟待探寻可行的重建完整数据的方法。
现行的地震数据重建算法可分为四大类:①基于滤波器方法[1],主要是依据建立卷积插值滤波器实现数据重建;②基于波场延拓算子重建方法[2-3],如常见的利用Kirchhoff积分算子;③基于快速降秩插值方法[4-6],即是将插值问题转化为图像填充问题;④基于数学变换方法,如常用的傅里叶变换、拉东变换、小波变换、曲波变换等,先变换到数字域进行处理,再反变换回时空域[7-14]。本文方法属第四类,即通过改进算法,在重建的同时消除伴生假频。
空间均匀网格下缺失的地震数据分为规则缺失和非均匀缺失。一般非均匀缺失数据转换到频域,它引起的假频信息转化为低幅值不相干随机噪声,可设置其阈值门限,通过稀疏迭代去噪法进行消除。而规则缺失数据在频域中产生的假频与真实频谱相近,基于传统的迭代稀疏促进求解方法很难取得高分辨率、高保真、高信噪比的重建结果。为此,人们提出了较多数据重建方法以压制假频干扰,如倾角扫描法,此类方法需先扫描同相轴倾角[15],然后沿倾角方向加权、内插地震道;Sinc地震道插值方法[16]是对满足采样定理的数据做加密采样点处理,不需获取同相轴倾角,运算速度快,但无法正确内插含有空间假频的地震道;小波变换地震道插值方法是利用小波变换的时频分析特性[17],多级重构实现地震道插值,但该插值算法较复杂,且精度较低。
对于不规则空间带限二维地震数据,结合非均匀快速傅里叶变换和最小二乘反演算法,都取得了较好的重建效果[18-23];此方法也可应用于规则欠采样数据中,但其抗假频效果欠佳,且不能有效区分真实频谱与假频信息。凸集投影(Projection onto convex sets,POCS)算法对于随机的和规则的欠采样数据都能重建出完整数据[24-25],但对规则缺失较严重数据,此方法去假频效果不甚理想。在f-k域由规则采样引起的假频幅值与真实频谱相近,为了进行区分,需对整个频域范围内所有频率进行搜寻。在信号分离和插值方面,与τ-p域相比,f-k域简捷有效,主要是因为τ-p重建方法计算量大,且重建效果不如f-k域方法,尤其对低信噪比数据[26]。同时,f-k域方法可利用所有期望频率的信息对缺失数据施行稳定的插值和去噪。
本文采用傅里叶变换,在传统POCS方法中引入Naghizade[27]提出的选择函数,以去除规则欠采样引起的假频信息。将此方法应用于理论数据和实际资料处理,均取得了较理想效果。
1 方法原理 1.1 建立选择函数首先对所有频率或在任意频率范围内进行扫描搜索,以确定主要能量的斜率或路径。
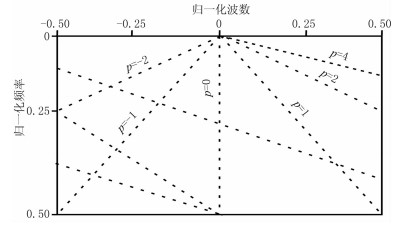
设d(t,x)为原始地震数据,D(f,k)为其相应的f-k域振幅谱。为了简化,将频率和波数做归一化处理,令时间轴和距离轴上采样间隔都为1,且f-k频谱关于频率轴对称,只需考虑正频率的频谱,得到归一化频率范围f∈(0,0.5)、归一化波数范围k∈(-0.5,0.5)(图 1)。设定每条角度射线起始位置为频域原点(f,k)∈(0,0),从图 1看出,可沿着角度射线方向求取射线上振幅能量之和。
|
图 1 f-k域角度射线扫描示意图 |
则每条射线所扫描的能量值为
| $ \begin{array}{l} \mathit{\boldsymbol{M}}(p) = \sum\limits_{n = 1}^{{N_f}} \mathit{\boldsymbol{D}} \left( {{f_n},k = p{f_n} - \left\lfloor {p{f_n} + 0.5} \right\rfloor } \right)\\ \;\;\;\;\;\;\;\;\;\;n \in \left( {1,2, \cdots ,{N_f}} \right) \end{array} $ | (1) |
式中:p为角度射线扫描斜率,其取值范围依据不同数据的频谱分布而定;n为归一化频率f的索引;算子
第二步,依据函数M(p)的峰值和扫描斜率范围,初始化一个零矩阵H,其维度与数据频谱维度相同,目的是把p1,p2,…,pL射线上反射波能量准确分配到矩阵H中(令L个角度射线上的值为1,其余各处为0)。则有
| $ \begin{array}{*{20}{c}} {\mathit{\boldsymbol{H}}\left( {{f_n},k = {p_j}{f_n} - \left\lfloor {{p_j}{f_n} + 0.5} \right\rfloor } \right) = 1}\\ {j = 1,2, \cdots ,L} \end{array} $ | (2) |
式中:j为角度射线p的索引;n、f、k同式(1)。
最后,考虑到邻近各角度射线两侧的能量应为同相轴能量,为拾取更完整同相轴信息,将所得H与一维方脉冲函数B(1,Lb)做卷积,沿波数轴方向拓宽每个角度射线,最终得出选择函数
| $ \mathit{\boldsymbol{W}}(f,k) = \mathit{\boldsymbol{H}}(f,k) \otimes \mathit{\boldsymbol{B}}\left( {1,{L_{\rm{b}}}} \right) $ | (3) |
式中:Lb是函数B沿波数轴方向上的长度,代表各个角度射线扫描的宽度,且函数B沿频率轴方向无值。从式(2)和式(3)可知,在选择函数W中,任何大于1的值都设定为1,小于1的值都设为0。
1.2 POCS算法传统POCS重建方法的迭代表达式为
| $ \begin{array}{l} {\mathit{\boldsymbol{d}}_i}(t,x) = {\mathit{\boldsymbol{y}}_{{\rm{obs}}}}(t,x) + [\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{S}}(t,x)]*\\ \;\;\;\;\;\;\;\;\;\;\;\;\;\;{\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{T}}_i}\mathit{\boldsymbol{F}}{\mathit{\boldsymbol{d}}_{i - 1}}(t,x)\quad i = 1,2, \cdots ,N \end{array} $ | (4) |
式中:di(t, x)为第i次迭代所得重建数据;I为单位矩阵;yobs为原始数据,即d0(t,x);F和FT分别为傅里叶正、反变换算子;N为满足精度要求时最小迭代次数;S(t,x)为采样矩阵;Ti为硬阈值算子,满足
| $ {T_i} = \left\{ {\begin{array}{*{20}{l}} 1&{\left| {{c_i}} \right| \ge {\lambda _i}}\\ 0&{\left| {{c_i}} \right| \le {\lambda _i}} \end{array}} \right. $ | (5) |
式中:ci表示第i次迭代得到的傅里叶系数,满足ci=Fdi(t, x);λi表示第i迭代的阈值,本文选用的阈值[28]为
| $ {\lambda _i} = {C_{\max }}{{\rm{e}}^{\left( {\ln \varepsilon - \ln {C_{\max }}} \right)\sqrt {\frac{{i - 1}}{{N - 1}}} }} $ | (6) |
式中:Cmax为傅里叶系数最大值;ε为靠近零的正值,不同数据ε值有所差别,与数据中噪声能量有关,计算中通过多次测试人工选取。
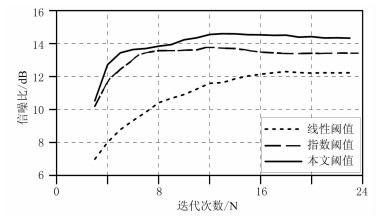
为体现本文阈值参数的优势,将其与文献[28]中的线性阈值与指数阈值做重建对比,其重建后的信噪比公式采用
|
图 2 不同阈值函数重建结果的信噪比曲线 |
将选择函数W代入到传统的POCS迭代重建过程中,即把式(3)代入式(4)中,最终的抗假频POCS重建算法为
| $ \begin{array}{*{20}{c}} {{\mathit{\boldsymbol{d}}_i}(t,x) = {\mathit{\boldsymbol{y}}_{{\rm{obs}}}}(t,x) + [\mathit{\boldsymbol{I}} - \mathit{\boldsymbol{S}}(t,x)]*}\\ {{\mathit{\boldsymbol{F}}^{\rm{T}}}{\mathit{\boldsymbol{T}}_i}\mathit{\boldsymbol{WF}}{\mathit{\boldsymbol{d}}_{i - 1}}(t,x)} \end{array} $ | (7) |
选择函数W能消除规则欠采样产生的假频干扰,使每次迭代过程中有效波能量聚焦,因此修改后的POCS算法能成功地重建规则缺失道。
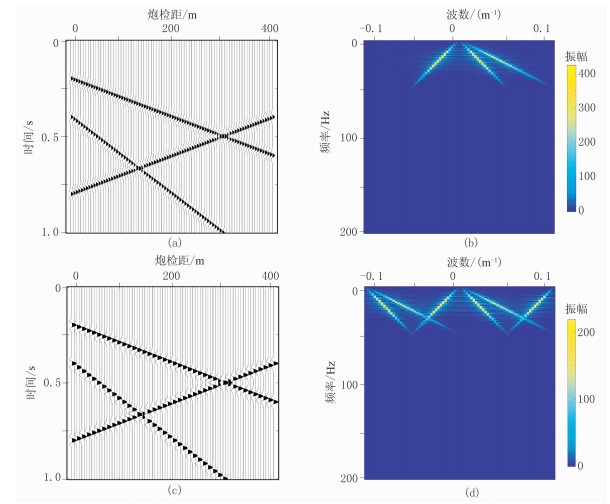
2 数值模拟采用主频为40Hz雷克子波合成81道地震记录(图 3a),每道501个采样点,该记录总共有3个地震反射同相轴,采样间隔为2ms,道距为5m。
|
图 3 原始模型采样及其f-k谱 (a)模型数据;(b)模型数据f-k谱;(c)50%缺失数据;(d)50%缺失数据f-k谱 |
为了更清晰地验证本文抗假频重建方法的可行性,本文通过对比重建后的振幅谱观察假频是否消除,并对比重建后的信噪比。首先,对模型数据(图 3a)进行50%规则欠采样,即去除偶数道数据,只保留奇数道数据,得到欠采样数据(图 3c)及其频率谱(图 3d)。可明显看到,在对应f-k域中(图 3d)因规则欠采样导致的假频与真实频谱(图 3b)较接近。因此,在之后的重建过程中,需消除假频的影响,这样最终才可得到完整而规则的地震数据。
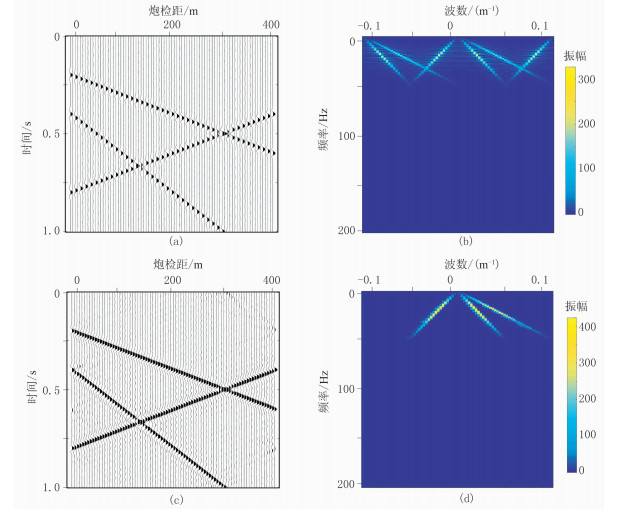
为验证本文方法的有效性,首先采用传统傅里叶变换和POCS算法进行重建,选择迭代次数N=20,阈值函数中的ε值为0.001。观察重建的结果(图 4a)及其对应的振幅谱(图 4b),可见图 4a中偶数道上有效波能量并未得到任何恢复、在图 4b中假频仍然存在,且重建结果的信噪比为2.7dB,说明传统方法无法重建缺失地震道。
|
图 4 两种重建方法对比结果及其f-k频谱 (a)传统方法重建结果;(b)传统方法重建结果f-k频谱;(c)本文方法重建结果;(d)本文方法重建结果f-k频谱 |
再采用本文抗假频的POCS算法进行重建,选定与传统重建相同的参数和迭代次数。依据方法原理,选择函数以图 3d中的原点为起点,对频域中的能量进行扫描,保留3个能量峰值对应的倾角,并在波数方向拓宽扫描范围,利用式(7)得到无假频的重建数据。观察此时所得重建地震数据(图 4c),其偶数道得到很好的重建,同相轴连续完整;且对应振幅谱(图 4d)上也完全看不到假频信息。对比图 4d与图 3b,表明本文所提抗假频POCS算法能有效地重建出规则缺失的地震道数据,且消除了规则欠采样所导致的假频,重建结果的信噪比增至14.5dB。
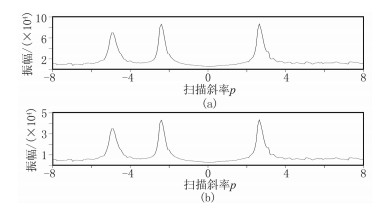
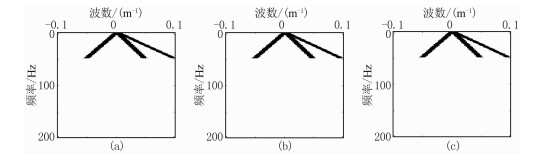
详细展示本文方法如何得到图 4c重建结果。首先,利用式(1)分别求取原始数据和规则缺失50%数据对应的M(p)峰值(图 5),扫描斜率p的范围设为-8~8,对比图 5a与图 5b,其主要能量峰值对应的p值一致。依据峰值范围,设定合适阈值,保留对应同相轴频谱的3个峰值,并分配到矩阵H中,再利用式(3)建立选择函数,结果如图 6。其中大于阈值区域的值为1,小于阈值区域的值为0。可知图 6b中选择函数与图 6a选择函数能量分布一致,说明选择函数识别出了真实频谱。然后将该选择函数引入到POCS方法中,使得在每次POCS算法迭代过程中,该选择函数可很精确地拾取真实频谱,再参与下一次迭代计算,使得原始信号频谱能很快聚焦。
|
图 5 M(p)范围内能量分布图 (a)模型数据;(b)规则缺失50%数据 |
|
图 6 f-k域选择函数值 (a)模型数据f-k域选择函数;(b)规则缺失50%数据f-k域选择函数;(c)规则缺失75%数据f-k域选择函数 |
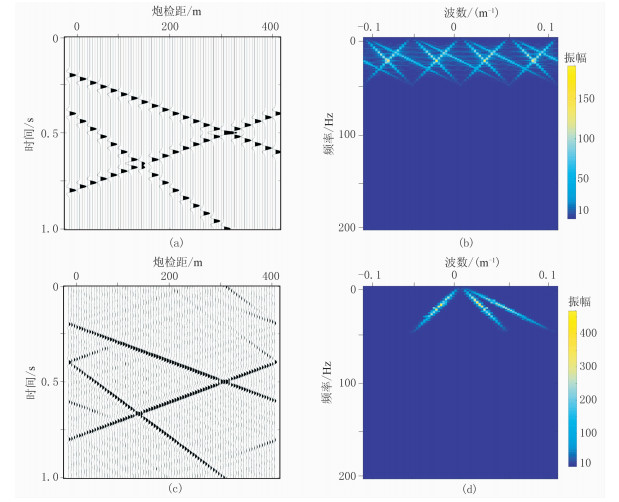
为更进一步验证本文方法的可行性,针对原始模型数据进行25%规则采样,即得到规则缺失75%数据(图 7a)及其对应的频谱(图 7b),可见真实频谱与假频信息相互交错缠绕,且能量非常相似,传统方法很难去除假频信息。采用本文方法,选定合适的迭代次数和阈值参数ε值,得到重建结果(图 7c)及对应f-k谱(图 7d)。该重建结果的信噪比为8.7dB。
|
图 7 25%规则采样重建结果及其f-k谱 (a)75%规则缺失数据;(b)75%规则缺失数据f-k谱;(c)本文方法重建结果;(d)本文方法重建结果f-k谱 |
分析重建结果的f-k谱(图 7d),本文引入的选择函数在重建过程中有效地压制了假频干扰,保留有效波能量。同时从建立的选择函数(图 6c)中可见,同相轴能量对应的峰值与图 6a一致。但相比之下,其75%规则缺失数据重建效果较差,说明当缺失较为严重时,重建结果则难以达到理想效果,周边已知的地震道不足以恢复大范围连续缺失的地震道,因此需发展高维的重建方法,从另一维度进行重建。同时需说明的是,因基于傅立叶变换的二维重建方法只能处理近似线性同相轴,而对于非线性同相轴则需做分窗口重建,使其满足近似线性同相轴的要求。
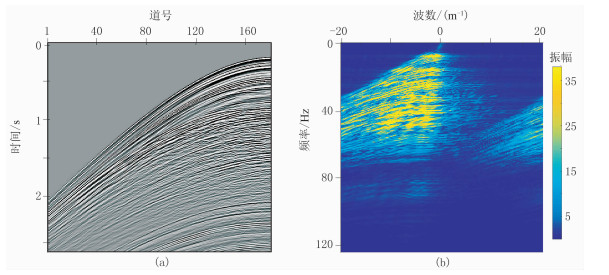
3 实际数据算例选取实际采集地震数据验证本文方法的适用性。图 8为M区海上二维原始地震数据及其振幅谱,道间距为25m,采样率为4ms,180道接收。本文方法基于傅里叶变换,只适应线性或近似线性同相轴地震数据重建,而对于非线性同相轴,通常采用分窗口重建。
|
图 8 现场实测数据(a)及其f-k谱(b) |
为满足处理要求,从原始数据中截取第100~第140道数据,时间轴方向截取0.8~1.6s(图 9a、图 9b)。对该窗口数据进行50%的规则欠采样(图 9c),可见规则采样引起的假频信息(图 9d)与真实频谱(图 9b)非常相似。

|
图 9 截取数据和规则缺失数据及其f-k谱 (a)截取的窗口数据;(b)截取的窗口数据f-k谱;(c)50%规则缺失数据;(d)50%规则缺失数据f-k谱 |
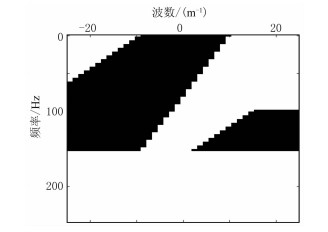
针对该实际数据体,本次选取选择函数中计算倾角p值的范围是-12~12。选择函数以图 9d中原点为起点,对频域中的能量进行扫描,扫描的同相轴能量分布如图 10所示,此扫描范围可最大程度地保留反射波同相轴能量、去除规则采样产生的假频信息。同时,迭代次数和阈值函数ε值的选取也影响重建效果。
|
图 10 实测数据的规则缺失50%数据f-k域选择函数 |
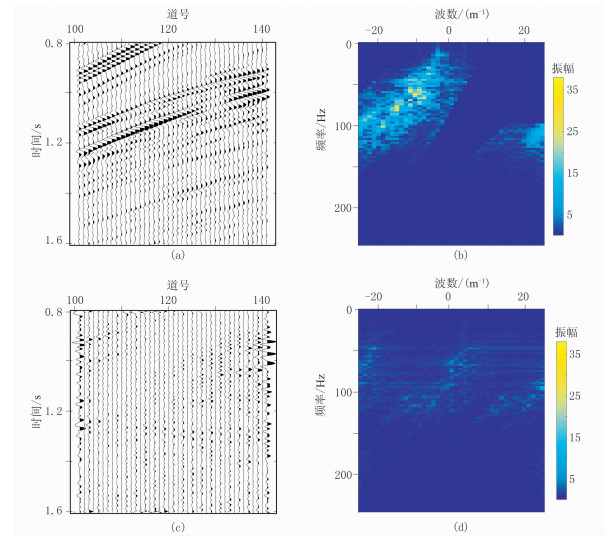
由最终重建结果(图 11a)及对应f-k谱(图 11b)得到重建结果误差(图 11c)及其频谱(图 11d),可见规则采样导致的假频信息得到较彻底压制,并保留了主要反射波同相轴能量,重建结果的信噪比为12.78dB。
|
图 11 重建结果及其f-k谱 (a)本文方法重建结果;(b)图a的f-k谱;(c)重建误差;(d)图c的f-k谱 |
本文结合傅里叶变换与POCS重建算法,研究了倾角扫描选择函数,该函数对全频段的能量轴进行扫描,确定出主要倾角;并把该函数引入传统的重建算法,重建线性或近似线性的同相轴数据;在此基础上,将该方法应用于理论和实际数据,重建出规则缺失的地震数据并压制了假频干扰。
根据对倾角扫描选择函数的分析,在传统傅里叶变换和POCS重建算法的应用中,只可重建线性或近似线性的地震数据。然而,实际数据中缺失的反射波同相轴往往是非线性的,此时需对非线性地震数据做分窗口重建,使得每个窗口内地震数据满足近似线性同相轴。
还可尝试选取另一种数学变换替代傅里叶变换,并结合倾角扫描选择函数,重建非线性同相轴缺失数据。这将是后续研究课题。
| [1] |
张军华, 仝兆岐, 何潮观, 等. 在f-k域实现三维波场道内插[J]. 石油地球物理勘探, 2003, 38(1): 27-30. ZHANG Junhua, TONG Zhaoqi, HE Chaoguan, et al. 3-D seismic trace interpolation in f-k domain[J]. Oil Geophysical Prospecting, 2003, 38(1): 27-30. |
| [2] |
Naghizadeh M, Sacchi M D. Beyond alias hierarchical scale curvelet interpolation of regularly and irregularly sampled seismic data[J]. Geophysics, 2010, 75(6): WB189-WB202. |
| [3] |
罗大清, 宋炜, 吴律, 等. 加权方向校正及插值预测吸收边界条件的三维波动方程叠前数值模拟[J]. 石油地球物理勘探, 1999, 34(3): 275-284. LUO Daqing, SONG Wei, WU Lü, et al. 3-D wave equation prestack numerical simulation using the absorbing boundary condition that needs weighting-directional correction and interpolation prediction[J]. Oil Geophysical Prospecting, 1999, 34(3): 275-284. |
| [4] |
Ma J W. Three-dimensional irregular seismic data reconstruction via low-rank matrix completion[J]. Geophysics, 2013, 78(5): V181-V192. |
| [5] |
Gao J, Sacchi M D, Chen X. A fast reduced-rank interpolation method for prestack seismic volumes that depend on four spatial dimensions[J]. Geophysics, 2013, 78(1): V21-V30. |
| [6] |
Gao J J, Stanton A, Sacchi M D. Parallel matrix factorization algorithm and its application to 5D seismic reconstruction and denoising[J]. Geophysics, 2015, 80(6): V173-V187. |
| [7] |
张胤彬, 张华, 刘松. 二维小波变换与中值滤波联合去噪方法研究[J]. 中国煤炭地质, 2011, 23(5): 38-41. ZHANG Yinbin, ZHANG Hua, LIU Song. A study on 2D wavelet transform and median filtering jointed denoising method[J]. Coal Geology of China, 2011, 23(5): 38-41. |
| [8] |
Chen Y, Ma J, Fomel S. Double sparsity dictionary for seismic noise attenuation[J]. Geophysics, 2016, 81(2): V17-V30. |
| [9] |
宋维琪, 刘太伟. 地面微地震资料τ-p变换噪声压制[J]. 石油地球物理勘探, 2015, 50(1): 48-53. SONG Weiqi, LIU Taiwei. Surface micro seismic noise suppression with τ-p transform[J]. Oil Geophysical Prospecting, 2015, 50(1): 48-53. |
| [10] |
王清振, 张金淼, 姜秀娣, 等. 基于高维小波变换的高抗噪性边缘检测技术[J]. 石油地球物理勘探, 2016, 51(5): 889-893. WANG Qingzhen, ZHANG Jinmiao, JIANG Xiudi, et al. A robust denoise edge detection method based on high-dimensional wavelet transform[J]. Oil Geophysical Prospecting, 2016, 51(5): 889-893. |
| [11] |
徐彦凯, 曹思远, 何元. 双曲Radon-ASVD方法压制叠前地震数据随机噪声[J]. 石油地球物理勘探, 2017, 52(3): 451-457. XU Yankai, CAO Siyuan, HE Yuan. Prestack seismic random noise attenuation with a hyperbolic Radon-ASVD[J]. Oil Geophysical Prospecting, 2017, 52(3): 451-457. |
| [12] |
Liu W, Cao S, Chen Y, et al. An effective approach to attenuate random noise based on compressive sensing and curvelet transform[J]. Journal of Geophysics & Engineering, 2016, 13(2): 135-145. |
| [13] |
赵子越, 李振春, 张敏. 利用压缩感知技术的离散正交S变换地震数据重建[J]. 石油地球物理勘探, 2020, 55(1): 29-35. ZHAO Ziyue, LI Zhenchun, ZHANG Min. Seismic data reconstruction using discrete orthonormal S-transform based on compressive sensing[J]. Oil Geophysical Prospecting, 2020, 55(1): 29-35. |
| [14] |
张华, 刁塑, 温建亮, 等. 应用二维非均匀曲波变换压制地震随机噪声[J]. 石油地球物理勘探, 2019, 54(1): 16-23. ZHANG Hua, DIAO Su, WEN Jianliang, et al. A random noise suppression with 2D non-uniform curvelet transform[J]. Oil Geophysical Prospecting, 2019, 54(1): 16-23. |
| [15] |
Lu L.Application of local slant stack to trace interpolation[C].SEG Technical Program Expanded Abstracts, 1985, 4: 560-562.
|
| [16] |
李国发. f-k域与f-x域联合实现道内插[J]. 石油地球物理勘探, 1995, 30(5): 693-701. LI Guofa. Joint trace interpolation in f-k and f-x domains[J]. Oil Geophysical Prospecting, 1995, 30(5): 693-701. |
| [17] |
崔兴福, 刘东奇, 张关泉. 小波变换实现地震道内插[J]. 石油地球物理勘探, 2003, 38(1): 93-97. CUI Xingfu, LIU Dongqi, ZHANG Guanquan. Seismic trace interpolation based on wavelet transform[J]. Oil Geophysical Prospecting, 2003, 38(1): 93-97. |
| [18] |
孟小红, 郭良辉, 张致付, 等. 基于非均匀快速傅里叶变换的最小二乘反演地震数据重建[J]. 地球物理学报, 2008, 51(1): 235-241. MENG Xiaohong, GUO Lianghui, ZHANG Zhifu, et al. Reconstruction of seismic data with least squares inversion based on nonuniform fast Fourier transform[J]. Chinese Journal of Geophysics, 2008, 51(1): 235-241. |
| [19] |
刘财, 李鹏, 刘洋, 等. 基于seislet变换的反假频迭代数据插值方法[J]. 地球物理学报, 2013, 56(5): 1619-1627. LIU Cai, LI Peng, LIU Yang, et al. Iterative data interpolation beyond aliasing using seislet transform[J]. Chinese Journal of Geophysics, 2013, 56(5): 1619-1627. |
| [20] |
石颖, 张振, 王建民. 地震数据反假频规则化方法研究[J]. 地球物理学进展, 2013, 28(1): 250-256. SHI Ying, ZHANG Zhen, WANG Jianmin, et al. Investigation on anti-aliasing regularization approach for seismic data[J]. Progress in Geophysics, 2013, 28(1): 250-256. |
| [21] |
高建军, 陈小宏, 李景叶. 不规则地震数据的抗假频重建方法[J]. 石油地球物理勘探, 2010, 45(3): 326-331. GAO Jianjun, CHEN Xiaohong, LI Jingye. Studies on anti-aliasing reconstruction method for irregular seismic data[J]. Oil Geophysical Prospecting, 2010, 45(3): 326-331. |
| [22] |
刘喜武, 刘洪, 刘彬. 反假频非均匀地震数据重建方法研究[J]. 地球物理学报, 2004, 47(2): 299-305. LIU Xiwu, LIU Hong, LIU Bin. A study on algorithm for reconstruction of de-alias uneven seismic data[J]. Chinese Journal of Geophysics, 2004, 47(2): 299-305. |
| [23] |
黄小刚, 王一博, 刘伊克, 等. 半径-斜率域加权反假频地震数据重建[J]. 地球物理学报, 2014, 57(7): 2278-2290. HUANG Xiaogang, WANG Yibo, LIU Yike, et al. Weighted anti-alias seismic data reconstruction in R-P domain[J]. Chinese Journal of Geophysics, 2014, 57(7): 2278-2290. |
| [24] |
Zhang H, Diao S, Yang H Y, et al. Reconstruction of 3D non-uniformly sampled seismic data along two spatial coordinates using non-equispaced curvelet transform[J]. Exploration Geophysics, 2018, 49(6): 906-921. |
| [25] |
Abma R, Kabir N. 3D interpolation of irregular data with a POCS algorithm[J]. Geophysics, 2016, 71(6): E91-E97. |
| [26] |
张红梅, 刘洪. 基于稀疏离散τ-p变换的非均匀地震道重建[J]. 石油物探, 2006, 45(2): 141-145. ZHANG Hongmei, LIU Hong. Non-uniform seismic trace reconstruction based on discrete and sparse τ-p transform[J]. Geophysical Prospecting for Petroleum, 2006, 45(2): 141-145. |
| [27] |
Naghizadeh M. Seismic data interpolation and denoising in the frequency-wavenumber domain[J]. Geophysics, 2012, 77(2): V71-V80. |
| [28] |
张华, 陈小宏. 基于jitter采样和曲波变换的三维地震数据重建[J]. 地球物理学报, 2013, 56(5): 1637-1649. ZHANG Hua, CHEN Xiaohong. Seismic data reconstruction based on jittered sampling and curvelet transform[J]. Chinese Journal of Geophysics, 2013, 56(5): 1637-1649. |



 张华, 江西省南昌市青山湖区广兰大道418号东华理工大学地球物理与测控技术学院, 330013。Email:
张华, 江西省南昌市青山湖区广兰大道418号东华理工大学地球物理与测控技术学院, 330013。Email: