随着油气勘探领域转向更深、更复杂的目标,以地震为代表的单一地球物理勘探技术遇到了极大的挑战,低信噪比、频带限制、复杂地表、复杂构造、埋深大等问题影响了地震成像的分辨率和可靠性,构造解释与建模多解性强,制约了油气勘探进程。为了更准确地获取复杂目标的信息,不同地球物理资料的联合反演方法已成为近年来研究的热点[1-4]。
联合反演从联合方式上可以分为两大类:一类是相对较早的顺序联合反演[5-9],它将一种地球物理资料(如重力)反演的模型(密度模型)通过物性关系转换成另一种反演方法(如地震反演)的初始模型(速度模型),然后进行反演,如此迭代直至获得满意的最终模型,虽然在很多领域已经取得了较好的应用效果[10-13],但其本质仍是单一方法反演。另一类是同步联合反演,因为其理论的完备性,受到越来越多学者的重视。多种数据在反演过程中相互补充、相互制约,可进一步缩小稳定可靠解的范围,达到同时拟合多种观测数据,降低反演多解性。
同步联合反演可以分为基于物性关系和基于几何形状相似性的同步联合反演。基于物性关系的同步联合反演[14-17]是利用Gardener公式[18]和Archie公式[19]或者二者的近似多项式分别建立速度与密度、速度与电阻率之间的关系。基于几何形状相似性的同步联合反演则是假设地下目标的物性边界相同,不同物性模型(速度、密度、电阻率、磁化率等)具有相似的几何形状,其中Gallardo等[20-21]提出的交叉梯度约束的电磁法与地震同步联合反演,已经成为目前同步联合反演方法的主流。上述两类同步反演方法各有优缺点,基于几何形状相似性约束的同步联合反演方法避免了建立物性关系的复杂过程,适合物性资料不足的研究区域,但是其几何相似性的假设过于生硬,尤其是对两种以上地球物理资料进行联合反演时,如MT、重力和地震,反演得到的电阻率、密度和速度模型具有相似的几何形状,不一定符合研究区真实情况。基于物性关系的同步联合反演方法具有较为严谨的岩石物理基础,若研究区的物性资料丰富,能够充分利用已知物性资料获得符合已有认识的反演结果。然而目前大部分反演方法中物性关系是固定不变的,若物性关系不准确则会导致反演结果出现较大偏差,因而限制了此类反演方法的适用范围。
针对现有同步联合反演方法的不足,本文提出一种变密度—速度关系的重力与地震同步联合反演方法。初始物性关系在反演迭代过程中根据当前及上轮迭代的密度和速度模型得到更新,可降低不准确的初始物性关系对反演结果的不利影响,从而提高了重震同步联合反演在低勘探程度区的应用潜力。
1 方法原理假设速度与密度之间存在未知的线性关系,这个线性关系在模型的不同区域可以是不同的,并且在反演过程中可以根据每次迭代的结果自动修正。这种方法对存在由于物性、埋深、温度等原因引起密度—速度关系变化的研究区具有实际意义。本节给出目标函数并推导出反问题的解估计公式,然后给出物性关系更新算法。
1.1 同步联合反演目标函数及解估计重力与地震同步联合反演的目标函数定义为
| $ \begin{array}{*{20}{c}} {\varphi (\mathit{\boldsymbol{m}}) = {w_1}\frac{{{\rm{||}}{\mathit{\boldsymbol{g}}_{{\rm{obs}}}} - {\mathit{\boldsymbol{g}}_{{\rm{cal}}}}{\rm{|}}{{\rm{|}}^2}}}{{2\sigma _{\rm{g}}^2}} + {w_2}\frac{{{\rm{||}}{\mathit{\boldsymbol{S}}_{{\rm{obs}}}} - {\mathit{\boldsymbol{S}}_{{\rm{cal}}}}{\rm{|}}{{\rm{|}}^2}}}{{2\sigma _{\rm{S}}^2}} + }\\ {\frac{1}{2}{w_3}{\rm{||}}\mathit{\boldsymbol{V}} - \mathit{\boldsymbol{B\rho }}{\rm{|}}{{\rm{|}}^2}} \end{array} $ | (1) |
式中:m表示模型参数, 包括速度参数向量V和密度参数向量ρ;gobs是实测重力异常;gcal是正演重力异常;σg是重力数据方差;Sobs是实测地震数据;Scal是正演地震数据;σS是地震数据方差;B是密度—速度关系矩阵;w1、w2、w3是权重。分别对ρ、V求偏导数,得到
| $ \begin{array}{*{20}{c}} {\frac{{\partial \varphi }}{{\partial \mathit{\boldsymbol{\rho }}}} = ({w_1}\frac{{\mathit{\boldsymbol{A}}_{\rm{g}}^{\rm{T}}{\mathit{\boldsymbol{A}}_{\rm{g}}}}}{{\sigma _{\rm{g}}^2}} + {w_3}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}})\mathit{\boldsymbol{\rho }} - }\\ {({w_1}\frac{{\mathit{\boldsymbol{A}}_{\rm{g}}^{\rm{T}}{\mathit{\boldsymbol{g}}_{{\rm{obs}}}}}}{{\sigma _{\rm{g}}^2}} + {w_3}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{V}})} \end{array} $ | (2) |
| $ \frac{{\partial \varphi }}{{\partial \mathit{\boldsymbol{V}}}} = ({w_2}\frac{{\mathit{\boldsymbol{A}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{A}}_{\rm{S}}}}}{{\sigma _{\rm{S}}^2}})\mathit{\boldsymbol{V}} - ({w_3}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{\rho }} + {w_2}\frac{{\mathit{\boldsymbol{A}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{S}}_{{\rm{obs}}}}}}{{\sigma _{\rm{S}}^2}}) $ | (3) |
式中:Ag和AS分别是重力和地震的灵敏度矩阵。
令式(2)和式(3)等于0,可得
| $ \begin{array}{l} \mathit{\boldsymbol{\rho }} = {({w_1}\frac{{\mathit{\boldsymbol{A}}_{\rm{g}}^{\rm{T}}{\mathit{\boldsymbol{A}}_{\rm{g}}}}}{{\sigma _g^2}} + {w_3}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}})^{ - 1}} \times \\ \;\;\;\;\;({w_1}\frac{{\mathit{\boldsymbol{A}}_{\rm{g}}^{\rm{T}}{\mathit{\boldsymbol{g}}_{{\rm{obs}}}}}}{{\sigma _{\rm{g}}^2}} + {w_3}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{V}}) \end{array} $ | (4) |
| $ \mathit{\boldsymbol{V}} = {({w_2}\frac{{\mathit{\boldsymbol{A}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{A}}_{\rm{S}}}}}{{\sigma _{\rm{S}}^{\rm{2}}}})^{ - 1}}({w_3}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{\rho }} + {w_2}\frac{{\mathit{\boldsymbol{A}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{S}}_{{\rm{obs}}}}}}{{\sigma _{\rm{S}}^{\rm{2}}}}) $ | (5) |
联立式(4)和式(5),可得
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{\rho }} = {{(\mathit{\boldsymbol{P}} - \mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{R}}^{ - 1}}\mathit{\boldsymbol{Q}})}^{ - 1}} \times }\\ {\;\;\;\;({w_1}\frac{{\mathit{\boldsymbol{A}}_{\rm{g}}^{\rm{T}}{\mathit{\boldsymbol{g}}_{{\rm{obs}}}}}}{{\sigma _{\rm{g}}^{\rm{2}}}} - {w_2}\mathit{\boldsymbol{Q}}{\mathit{\boldsymbol{R}}^{ - 1}}\frac{{\mathit{\boldsymbol{A}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{S}}_{{\rm{obs}}}}}}{{\sigma _{\rm{S}}^2}})} \end{array} $ | (6) |
| $ \mathit{\boldsymbol{V}} = {\mathit{\boldsymbol{R}}^{ - 1}}({w_2}\frac{{\mathit{\boldsymbol{A}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{S}}_{{\rm{obs}}}}}}{{\sigma _{\rm{S}}^2}} - {\mathit{\boldsymbol{Q}}^{\rm{T}}}\mathit{\boldsymbol{\rho }}) $ | (7) |
式中
| $ \mathit{\boldsymbol{P}} = {w_1}\frac{{\mathit{\boldsymbol{A}}_{\rm{g}}^{\rm{T}}{\mathit{\boldsymbol{A}}_{\rm{g}}}}}{{\sigma _{\rm{g}}^2}} + {w_3}{\mathit{\boldsymbol{B}}^{\rm{T}}}\mathit{\boldsymbol{B}} $ | (8) |
| $ \mathit{\boldsymbol{Q}} = {w_3}{\mathit{\boldsymbol{B}}^{\rm{T}}} $ | (9) |
| $ \mathit{\boldsymbol{R}} = {w_2}\frac{{\mathit{\boldsymbol{A}}_{\rm{S}}^{\rm{T}}{\mathit{\boldsymbol{S}}_{{\rm{obs}}}}}}{{\sigma _S^2}} $ | (10) |
求解上述方程组可采用非线性共轭梯度法[22],在保证反演精度的前提下,提高计算速度,降低内存需求。
1.2 物性关系更新算法Delyon等[23]提出的EM随机近似算法,简称SAEM(Stochastic Approximation of EM)算法,主要包括三步:
(1) 求不完全数据样本x的第k次迭代样本值x(k);
(2)根据下式更新充分统计量T(k)的近似值
| $ {\mathit{\boldsymbol{T}}^{(k)}} = {\mathit{\boldsymbol{T}}^{(k - 1)}} + {\gamma ^{(k)}}[\mathit{\boldsymbol{T}}({\mathit{\boldsymbol{x}}^{(k)}},\mathit{\boldsymbol{y}}) - {\mathit{\boldsymbol{T}}^{(k - 1)}}] $ | (11) |
式中:y是观测数据;{γ(k)}k≥0是正值单调递减步长序列,取γ(k)=1/k;
(3)最大化目标函数,求取统计参数集θ(k+1)。
已经证明该算法在绝大多数情况下是收敛的,参见文献[23]。
本文按照SAEM算法的步骤(2)计算每次迭代密度模型和速度模型的充分统计量,进而更新密度—速度关系。在重震联合反演中,密度模型ρ和速度模型V对应SAEM算法中的样本x,物性关系B为对角阵,若将所有地层分隔成J个具有不同速度—密度线性关系的区域,那么B的对角线上有J个不同的值,则SAEM算法的统计参数集θ=B=[b(1), b(2), …, b(J)],其中b(j)(j=1, 2, …, J)表示第j个区域内的物性关系。物性关系更新算法步骤如下:
(1) 根据式(6)~式(10)求得当前迭代ρ(k)和V(k);
(2) 更新充分统计量T(k)=[u1(k)(j), u2(k)(j)]1≤j≤J,设Cj是第j个区域非观测数据的集合,则
| $ \mathit{\boldsymbol{u}}_1^{(k)} = \mathit{\boldsymbol{u}}_1^{(k - 1)} + {\gamma ^{(k)}}[\sum_{i \in {\mathit{\boldsymbol{C}}_i}} {\mathit{\boldsymbol{\rho }}_{\rm{i}}^{(k)}} \mathit{\boldsymbol{V}}_{\rm{i}}^{(k)} - \mathit{\boldsymbol{u}}_1^{(k - 1)}] $ | (12) |
| $ \mathit{\boldsymbol{u}}_2^{(k)} = \mathit{\boldsymbol{u}}_2^{(k - 1)} + {\gamma ^{(k)}}[\sum_{i \in {\mathit{\boldsymbol{C}}_i}} {{{(\mathit{\boldsymbol{\rho }}_{\rm{i}}^{{\rm{(k)}}})}^2}} - \mathit{\boldsymbol{u}}_2^{(k - 1)}] $ | (13) |
(3)计算θ=B=[b(1),b(2),…,b(J)]
| $ {b^{(k - 1)}}(j) = \frac{{\mathit{\boldsymbol{u}}_1^{(k)}(j)}}{{\mathit{\boldsymbol{u}}_2^{(k)}(j)}} $ | (14) |
采用SEG/EAGE常用的Overthrust模型对本文方法进行测试。速度网格横向剖分数目为801,垂向剖分数目为187,纵、横向间距均为25m。水平坐标范围0~20000m。图 1a为Overthrust速度模型,速度范围为2360~6000m/s。将速度模型通过关系式ρ=v/2000转换成密度模型,进行重力正演。

|
图 1 Overthrust模型 (a)速度模型; (b)1000m处正演单炮记录; (c)重力异常曲线 |
设地震炮点埋深为25m,共放199炮,炮间距为100m,第一炮位置在100m处。利用主频为10Hz的零相位雷克子波激发,地表全孔径接收,道间距为100m,第一道位置在50m处,共200道。时间采样率为4ms,采样点数为8192。图 1b是炮点位于1000m处的单炮记录,是在频率域利用有限差分算法正演获得的。重力观测点位于地表,第一个观测点位于50m处,共100个观测点,间距为200m,正演重力曲线见图 1c。可以看出,重力异常对模型中部的叠瓦状冲断构造以及中深部的背斜(图 1c中方框区域)均有明显的响应。
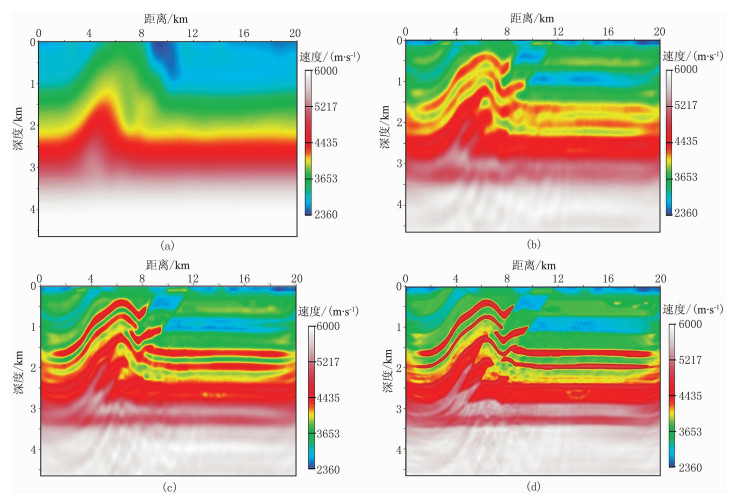
2.1 重/震单独反演从正演频率域地震数据中选取3.5~20.6Hz的7个频率用于全波形反演,保留真实模型浅层100m深度范围内的速度值,深层(≥100m)经平滑处理后作为初始模型(图 2a)。设置最大迭代次数为80,3.5、9.6、20.6Hz三个频点的反演结果分别见图 2b~图 2d。对比图 2a, 可见反演结果边界清晰,取得了很好的效果。
|
图 2 理想速度初始模型的地震全波形反演结果(速度模型) (a)初始速度模型; (b)3.5Hz反演结果; (c)9.6Hz反演结果; (d)20.6Hz反演结果 |
全波形反演(FWI)方法具有局部收敛性,严重依赖于初始速度。若初始模型较完整地保留了低频信息时,FWI经初步迭代后应当就能够收敛在真实解附近。图 3为初始模型为常速度3500m/s时的反演结果。可见,在初始模型不理想的情况下,地震数据单独反演的结果误差很大,出现了更多的高频扰动,没有反映出从浅部到深部速度逐渐增大的趋势。

|
图 3 常速度(3500m/s)初始模型的不同频率地震全波形反演结果(速度模型) (a)3.5Hz;(b)9.6Hz;(c)20.6Hz |
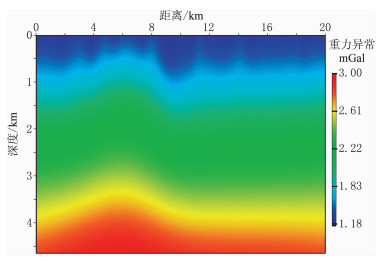
采用重加权共轭梯度法[24]对重力异常数据单独进行反演,得到密度模型。初始模型的密度值设为常数2.0g/cm3。在不加任何约束的情况下,反演结果如图 4所示。可以看出,分辨率较低,不能刻画出叠瓦状冲断构造的基本形态,但其反映的趋势背景是正确的,基本上能反映出了密度从上到下逐渐增大的趋势,模型中部的背斜轮廓亦可大致看出,左右两边的水平沉积地层反映得较为清晰。
|
图 4 常密度(2.0g/cm3)初始模型重力反演剖面 |
采用本文方法对该模型进行重力和地震数据联合反演。
速度初始模型设为常值3000m/s,密度模型设为常值2.0g/cm3,则初始速度—密度关系为v=1500ρ。
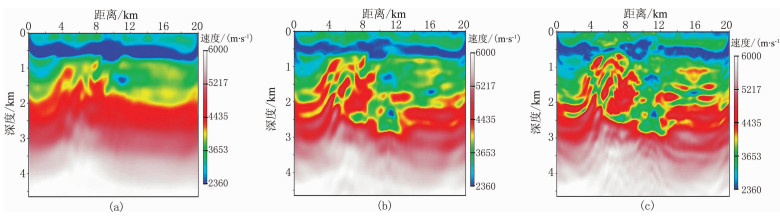
首先开展固定物性关系的同步联合反演试验,以分析在物性关系变化的情况下,采用固定速度—密度关系反演的结果。展示3个频点的反演结果,见图 5。可见反演效果较图 3地震单独反演结果有所提高,反映出从浅部到深部速度逐渐增大的趋势,但是高频部分失真严重,难以准确解释逆断层。说明不准确的密度—速度关系会降低联合反演的精度和可靠性。
|
图 5 基于固定密度—速度关系的不同频率下重震同步联合反演结果(速度模型) (a)3.5Hz;(b)9.6Hz;(c)20.6Hz |
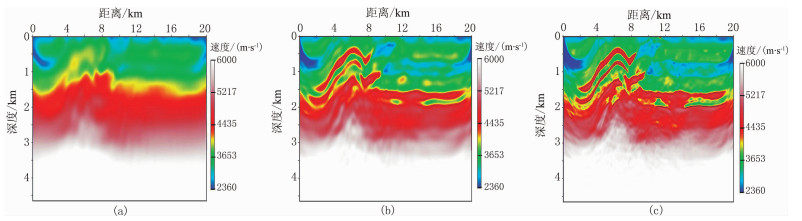
用本文算法开展联合反演试验,检验在反演过程中修正物性关系对结果产生的影响。图 6为采用变物性关系进行同步联合反演结果。可见浅部地层除两侧边界受到边界效应的影响,其他部分都得到了较好的恢复;深部逆掩构造不很清晰,但是基本能够分辨出构造形态,整体效果优于固定物性关系的联合反演结果(图 5)。根据反演剖面,速度—密度的关系为Binv=1985.7,较准确地描述了模型准确的物性关系B=2000。
|
图 6 基于变密度—速度关系的不同频率重震同步联合反演结果(速度模型) (a)3.5Hz;(b)9.6Hz;(c)20.6Hz |
取得理想效果的主要原因是,反演过程中通过重力信息建立了低频背景模型,从而将地震信息的反射分量与透射分量分离。反射分量可集中恢复速度模型中的高频成分。而且在反演过程中不断根据每次迭代模型的更新量调整不准确的初始密度—速度关系,使重、震之间的相互约束关系更合理。
这个实验证明,重震同步联合反演在初始模型和初始密度—速度关系都不理想的情况下,仍能取得较满意的反演效果。
2.3 实际资料试算为验证本文方法的实际应用效果,选取中国西部M区数据进行实验。图 7所示为该区1:50000区域重力异常图,其中有四条重力—地震联合攻关线(图中测线1~测线4)。由图可见,研究区重力异常整体表现出北东向重力高值异常带,但沿测线2异常发生扭曲、错动,测线两侧异常形态、规模存在较大差异,以测线2为界,东西两侧地质构造特征差异较大。

|
图 7 M区区域重力异常图 |
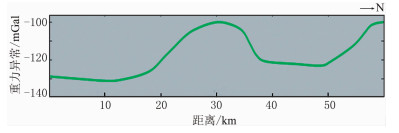
选择测线2开展联合反演实验。图 8为该线重力—地震联合攻关所得重力异常,测线两端对应沉积凹陷,在剖面中间构造带部位是较单一的高异常,形态、幅值均低于测线1的对应位置。
|
图 8 测线2重力异常剖面 |
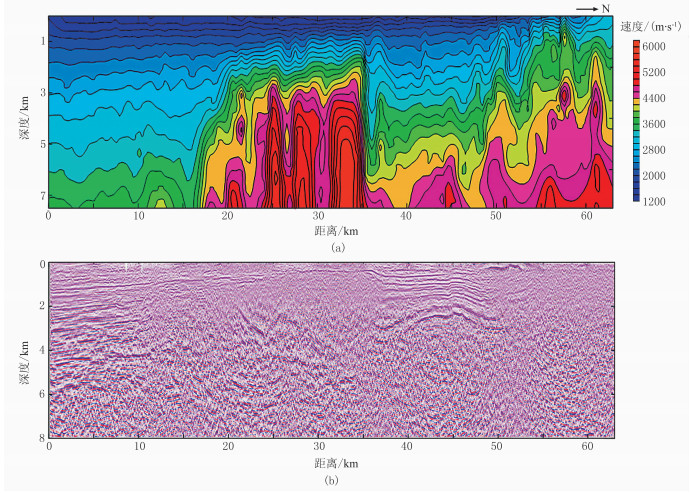
首先按照常规速度分析流程生成初始层速度模型(图 9a)。可以看出该剖面从浅到深、从南向北速度逐渐增大,剖面中部为高速区,整体上速度场畸变比较严重,深层构造刻画不清。从偏移剖面(图 9b)上看,沉积地层反映清晰,但其中深层成像模糊,构造解释存在一定困难。
|
图 9 初始速度模型(a)和深度偏移剖面(b) |
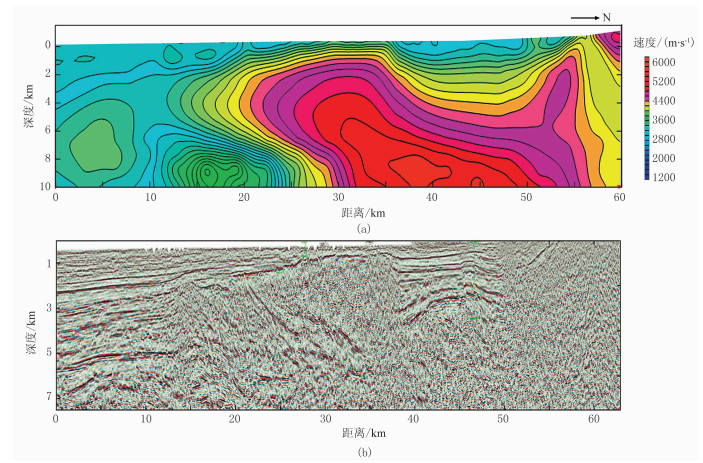
应用本文变密度—速度关系的重磁联合反演得到的速度剖面见图 10a。可以看出,该速度剖面对高速地层的形态刻画清晰,较好地展现了深层逆掩构造。图 10b是基于图 10a的叠前深度偏移剖面。可见剖面波组特征清楚,中深层信噪比和连续性也得到增强,断点、断面清楚,能够较准确、清楚地反映构造面貌。
|
图 10 基于变密度—速度关系的联合反演速度剖面(a)及深度偏移剖面(b) |
本文提出了一种变密度—速度关系的重力与地震同步联合反演方法,给出包含密度—速度关系项的重震同步联合反演目标函数,详细推导了求解密度模型与速度模型的解估计公式。该方法利用重力资料补充地震资料中缺少的低频信息,建立低频背景模型,使地震高频信息能够更准确地恢复模型中的高频成分。
方法的创新之处在于在反演迭代过程中不断更新密度—速度关系,针对不确定的物性关系对反演产生不利影响的问题,提出了一种基于密度模型和速度模型的高阶统计量的物性关系更新算法。模型试算证明,该方法可以有效提高初始模型和初始密度—速度关系都不确定情况下联合反演的效果,较固定密度—速度关系的同步联合反演方法,反演效果有显著提高。实际资料试算检验了方法的实际应用效果,证明方法具有较好的实用性。
本文仅对重震同步联合反演的方法原理做了详细的阐述,但文中所述的反演思路与公式可经简单修改后推广应用于电震、重电震同步联合反演,有待后续深入研究。
| [1] |
徐桂芬, 何展翔, 石艳玲, 等. 电磁-地震联合研究深层火山岩储层——以辽东凹陷火山岩勘探为例[J]. 石油地球物理勘探, 2019, 54(4): 937-946. XU Guifen, HE Zhanxiang, SHI Yanling, et al. Deep volcanic reservoir exploration with jointed electromagnetic and seismic data:an example of volcanic investigation in Liaodong Sag[J]. Oil Geophysical Prospecting, 2019, 54(4): 937-946. |
| [2] |
潘豪杰, 张研, 李红兵. 基于贝叶斯理论的天然气水合物储层弹性-电性数据联合反演[J]. 石油地球物理勘探, 2018, 53(3): 568-577. PAN Haojie, ZHANG Yan, LI Hongbing. Joint inversion of elastic-electrical data for gas hydrate reservoirs based on Bayesian theory[J]. Oil Geophysical Prospecting, 2018, 53(3): 568-577. |
| [3] |
李华东, 于鹏, 刘振友, 等. 基于随机分布共网格模型的重磁电震联合反演技术及应用[J]. 石油地球物理勘探, 2015, 50(4): 742-748. LI Huadong, YU Peng, LIU Zhenyou, et al. Joint inversion of gravity, magnetotelluric and seismic data based on common gridded model with random distri-butions[J]. Oil Geophysical Prospecting, 2015, 50(4): 742-748. |
| [4] |
李德春, 杨书江, 胡祖志, 等. 三维重磁电震资料的联合解释——以库车大北地区山前砾石层为例[J]. 石油地球物理勘探, 2012, 47(2): 353-359. LI Dechun, YANG Shujiang, HU Zuzhi, et al. Integrated interpretation of 3D gravity, magnetic, electromagnetic and seismic data:a case study of conglome-rate mass investigation in piedmont area of Kuche Depression[J]. Oil Geophysical Prospecting, 2012, 47(2): 353-359. |
| [5] |
Vozoff K, Jupp D L B. Joint inversion of geophysical data[J]. Geophysical Journal of the Royal Astronomical Society, 1975, 42(3): 977-991. |
| [6] |
Gomez-Trevino E, Edwards R N. Electromagnetic sounding in the sedimentary basin of southern Ontario:a case history[J]. Geophysics, 1983, 48(3): 311-330. |
| [7] |
Raiche A P, Jupp D L B, Rutter H, et al. The joint use of coincident loop transient electromagnetic and Schlumberger sounding to resolve layered structures[J]. Geophysics, 1985, 50(10): 1618-1627. DOI:10.1190/1.1441851 |
| [8] |
Lines L, Schultz A K, Treitel S. Cooperative inversion of geophysical data[J]. Geophysics, 1988, 53(1): 8-2. |
| [9] |
Dobroka, Gyulai A, Ormos T, et al. Joint inversion of seismic and geo-electric data recorded in an underground coal mine[J]. Geophysical Prospecting, 1991, 39(5): 643-665. DOI:10.1111/j.1365-2478.1991.tb00334.x |
| [10] |
Hering A, Misiek R. A joint inversion algorithm to process geoelectric and surface wave seismic data, Part 1:basis idea[J]. Geophysical Prospecting, 1995, 43(2): 135-156. DOI:10.1111/j.1365-2478.1995.tb00128.x |
| [11] |
Abubakar A, van den Berg P M.Joint inversion of electrode and induction logging data[C].SEG Technical Program Expanded Abstracts, 2000: 2166-2168.
|
| [12] |
Bosch M, McGaughey J. Joint inversion of gravity and magnetic data under lithologic constraints[J]. The Leading Edge, 2001, 20(8): 877-881. DOI:10.1190/1.1487299 |
| [13] |
阎汉杰, 阎红, 李云平. 重磁震统计推断联合建模反演技术研究与应用[J]. 石油大学学报(自然科学版), 2003, 27(3): 36-39. YAN Hanjie, YAN Hong, LI Yunping. Application of gravity-magnetic-seismic combination inversion mode-ling technology based on statistical inference[J]. Journal of University of Petroleum (Edition of Natural Science), 2003, 27(3): 36-39. |
| [14] |
Colombo D, de Stefano M. Geophysical modeling via simultaneous joint inversion of seismic, gravity, and electromagnetic data:Application to prestack depth imaging[J]. The Leading Edge, 2007, 26(3): 326-331. DOI:10.1190/1.2715057 |
| [15] |
Meju M A. Joint inversion of TEM and distorted MT soundings:some effective practical considerations[J]. Geophysics, 1996, 61(1): 56-65. |
| [16] |
Meju M A, Fontes S L, Oliveira M F B. Regional aquifer mapping using combined VES-TEM-AMT/EMAP methods in the semiarid eastern margin of Parnaiba Basin, Brazil[J]. Geophysics, 1999, 64(2): 337-356. |
| [17] |
Zhang G L, Xiang P, Wang J D, et al. Geologic mode-ling study of foothill area of the Junggar Basin rim[J]. Interpretation, 2018, 6(4): SM19-SM26. DOI:10.1190/INT-2018-0003.1 |
| [18] |
Birch F. The velocity of compressional waves in rocks to 10 Kilobars[J]. Journal of Geophysical Research Atmospheres, 1961, 66(7): 2199-2224. DOI:10.1029/JZ066i007p02199 |
| [19] |
Archie G E. The electrical resistivity log as an aid in determining some reservoir characteristics[J]. Tran-sactions of AIME, 1942, 146(1): 54-62. DOI:10.2118/942054-G |
| [20] |
Gallardo L A, Meju M A. Characterization of heterogeneous near-surface materials by joint 2D inversion of DC resistivity and seismic data[J]. Geophysical Research Letters, 2003, 30(13): 1658-1661. |
| [21] |
Gallardo L A, Meju M A. Joint two-dimensional DC resistivity and seismic travel time inversion with cross-gradients constraints[J]. Journal of Geophysical Research Atmospheres, 2004, 109(B3): B03311. |
| [22] |
相鹏. 一种改进的二维MT预条件非线性共轭梯度反演方法[J]. 中国石油大学学报(自然科学版), 2014, 38(4): 42-49. XIANG Peng. Two-dimensional MT inversion method based on an improved preconditioned nonlinear conjugate gradient algorithm[J]. Journal of China University of Petroleum(Edition of Natural Science), 2014, 38(4): 42-49. DOI:10.3969/j.issn.1673-5005.2014.04.006 |
| [23] |
Delyon B, Lavielle M, Moulines E. Convergence of a stochastic approximation version of the EM algorithm[J]. Annals of Statistics, 1999, 27(1): 94-128. DOI:10.1214/aos/1018031103 |
| [24] |
Zhdanov M S.Geophysical Inverse Theory and Regularization Problem[M].Elsevier, Amsterdam, Netherlands, 2002.
|



 相鹏, 山东省东营市东营区聊城路2号胜利油田勘探开发研究院, 266071。Email:
相鹏, 山东省东营市东营区聊城路2号胜利油田勘探开发研究院, 266071。Email: