2 成都理工大学信息科学与技术学院, 四川成都 610059
2 College of Information Science and Technology, Chengdu University of Technology, Chengdu, Sichuan 610059, China
地震数值正演模拟广泛应用于基于模型的射线追踪、覆盖次数统计和观测系统照明等方面[1]。然而三维复杂地质模型的建立是正演的关键步骤,复杂模型的块体构建难度大、耗时长,特别是在采集设计领域,由于工期短、时间紧,设计人员迫切希望在短时间内构建符合设计区域实际地质情况的三维模型。
目前采集设计领域中正演模拟经常使用的射线和射线束方法[2],需要设计三维块状模型,三维块状模型的构建是以具有近似地质属性的层块作为块体构建的基本单元。首先利用曲面构建方法建立地质层位和断层曲面,再利用块体追踪技术提取由层位和断层曲面片所形成的封闭地质块体[3]。块体构建所得到的块状地质模型通常可以用于射线、射线束类正演模拟[4],也可以通过离散化算法转换为规则或者非规则网格模型,支持有限差分或有限元类方法[5]。
三维块体构建算法的历史可以追溯到20世纪80年代,Warburton[6]提出一种基于无限大非连续面识别块体的算法;Lin等[7]提出将拓扑概念引入块体构建中;Lu[8]将方向边和方向环的概念引入块体构建过程;蒋先艺等[9]提出一种封闭模型描述方法,将具有相同属性的地质层面联系在一起,并且给出了一种基于三角形的块体追踪算法,从而得出以地质属性为基础的块体;侯卫生等[10]通过对Lu等[7-8]提出的方法进行改进,可以在曲面上进行搜索得出块体模型;杨洋等[11]简化并改进了传统的线框架模型,提出了线框架拓扑模型,加速并简化了拓扑搜索过程。
目前三维地质块体构建算法已经相当成熟,在块体追踪方面从简单的逐三角形追踪发展为基于线框拓扑的追踪,执行效率和容错性都有很大提高[12]。但本质上,这些方法都是基于模型交线拓扑结构进行块体追踪,对准确的地质数据拓扑结构依赖性较强[13]。因而,在进行块体构建之前需进行多次曲面求交或裁剪等操作,以保证地质模型拓扑关系的正确性。较复杂地质模型存在三角网的尺寸差异过大、密度不均匀、浮点误差等现象,会导致曲面间的拓扑关系存在少量错误,使传统的拓扑一致性块体构建方法失效。然而少量的拓扑错误并不会影响模型整体的正确性,如果能构建出结构正确的块体模型,则少量的拓扑错误和块体局部漏缝并不会对射线或模型离散化造成明显的影响,可以继续用于正演数值模拟[14]。
本文提出一种非拓扑一致的三维地质块体构建技术。该方法模拟人眼视觉观察,完全不依赖交线拓扑信息,仅依靠曲面自身形态提取块体三角网,在不对原曲面进行求交或裁剪等操作的情况下构建三维地质块体。
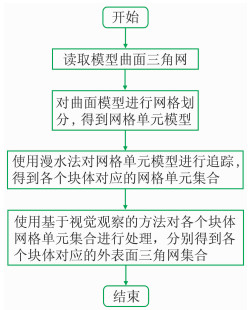
1 非拓扑一致性块体构建算法原理以交线拓扑结构为基础的传统块体构建算法根据三角网邻接关系建立模型的拓扑关系图,并在此基础上进行广度或深度遍历算法进行块体外边界三角网的追踪[15]。因此拓扑关系的正确性决定着此方法的成功率。然而在面对有少量拓扑问题的模型时,通常会从整体把握理解模型结构,忽略局部拓扑错误。基于此思路,本文提出非拓扑一致性块体构建算法,模拟人类观察和处理模型的方式,即首先从整体上确定块体的大致范围,再利用局部观察的方式确定块体的边界三角网(图 1)。
|
图 1 非拓扑一致块体构建算法流程 |
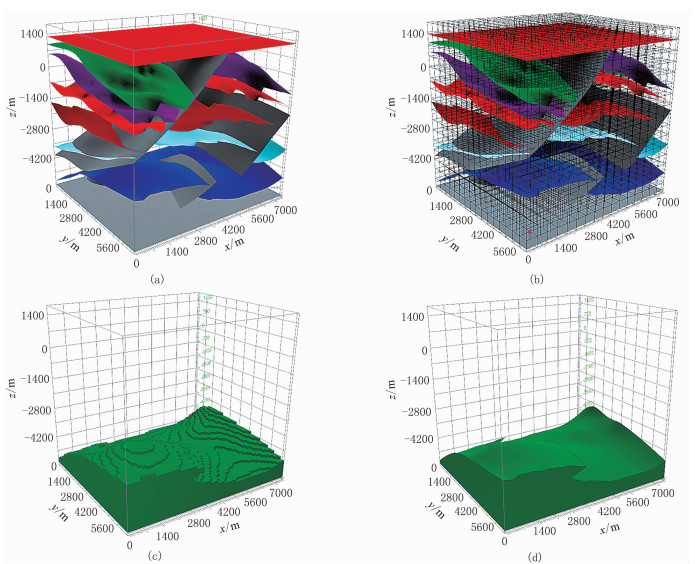
算法首先读取模型的曲面三角网,确定模型空间范围。如图 2a所示,假如模型尺寸为7500m(x)×6400m(y)×7400m(z),包含3条断层、15个层位曲面。
|
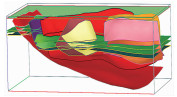
图 2 非拓扑一致块体构建示意图 (a)输入曲面模型;(b)对模型空间进行网格划分;(c)漫水法追踪块体外边界网格单元集合;(d)视觉观察得到的三角网块体模型 |
然后对当前的地质模型进行网格划分。如图 2b所示,以任一不包含三角形的网格单元作为起始种子(图 2b中红点所标明的网格单元),使用漫水填充法[16]对网格单元模型进行边界网格单元追踪,得到近似表示当前地质块体的网格块体——包含块体界面三角形的网格单元集合(图 2c)。
最后以基于视觉观察方式的三角形选取算法逐个对求得的网格块体选取对应外表面的三角形,如图 2d所示。
非拓扑一致性块体构建算法首先要确定块体的基本形态。为此本文利用漫水填充法追踪块体所包含的网格单元集合。漫水法是图形学中常用的一种区域填充法,实质上是一种广度优先遍历的种子填充法,适用于对内定义区域的填充。图形学中的内定义区域,是指区域内部的像素具有类似或相同的属性,而区域外的所有像素具有不同或差别较大的属性。该算法从内区域中的某个像素出发(通常称起始像素为种子),利用广度优先搜索完成内区域填充。本文对该方法进行改造,用于三维空间中地质块体网格单元集合的追踪,具体步骤如下:
(1) 从内存中取得起始种子网格单元,加入到遍历队列;
(2)若遍历队列为空,则返回步骤(1),否则从遍历队列中取出一个网格单元进行步骤(3);
(3)若步骤(2)得到的网格单元已被访问过,则重新进行步骤(2),否则进行步骤(4);
(4)找到所述网格单元周围的六个邻接网格单元,对每一个邻接网格单元,更新所述邻接网格体的投影方向;
(5)对所述邻接网格单元,若其中不含三角形,则将其加入到遍历列表中,并将其标记为“已访问”,并返回步骤(2);否则,将其加入到当前块体的边界区域网格块体队列中,并进行步骤(2),直至遍历所有网格单元。
通过漫水追踪算法获取了地质块体的网格单元集合,为精确提取地质块体外表面三角形做好了准备。非拓扑一致的块体构建算法的最终目标是提取地质块体的外边界三角形,构造地质块体表面三角网。为此需要遍历块体的网格单元,从含有三角形的边界网格单元中找出属于地质块体的三角形,并将它们组合起来,构造块体外表面三角网。在具体实现上,为达到“筛选出被观察到的三角形”这一目的,算法使用了图形库OpenGL对各个网格体进行渲染绘制,选取三角形单元,并采用平行投影的方式绘制渲染网格体相关三角形[17]。将渲染绘制的结果输出到OpenGL的帧缓存对象(FBO)中。FBO是OpenGL内置的对象之一,利用该机制,编码人员可以直接将绘制结果输出到内存中而不是屏幕上[18]。在本文算法中,这一机制恰好符合从绘制结果直接筛选三角形的需求。
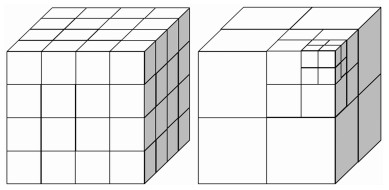
2 非拓扑一致块体构建算法优化在上述非拓扑一致块体构建算法中,网格划分是重要步骤。基本的网格划分方式是均匀型网格划分,其划分方式为无区别地将整个地质模型均匀划分为规模统一、精度一致的网格单元。这种划分方式简单,便于实现,且索引效率较高。其缺陷是既耗费资源又耗费时间。为此,本文提出一种高效方法,即非规则八叉树网格划分方式。该方法将地质模型划分为大小不一的网格单元,即对含有曲面三角网的区域划分为规模更小、精度更高的网格单元,对不含有三角网的区域不再继续划分。由于使用了精度可变的网格体,所需求的内存空间较灵活,可根据场景需求调整[19]。图 3对比了均匀网格体划分与不规则八叉树网格体划分。
|
图 3 均匀网格体划分(左)与不规则八叉树网格体划分(右)对比 |
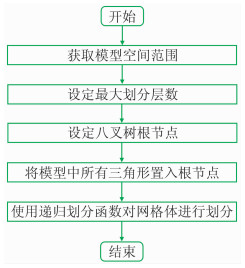
八叉树网格剖分将立体空间从三个维度上同时进行二分,即将原空间划分为8个几何相似的子空间,之后再根据实际情况决定是否需要对某个或某几个子空间进一步划分。同时,任何一个被划分出的子空间都将作为一个节点被保存到八叉树数据结构中,表示整个原始地质空间的数据结构对象将作为八叉树的根节点,而没有被继续划分子空间的数据结构对象将作为八叉树的叶子节点。为了实现上下级节点的索引,表示节点的数据结构应该保留指向上下级数据结构的指针以及相对的位置关系。图 4为八叉树网格剖分算法流程图。
|
图 4 八叉树网格划分算法流程 |
通过递归方式建立不规则八叉树结构,首先从输入的根节点开始,检查当节点的划分层数是否小于最大划分层数,并判断节点包含的三角形数目是否大于1。如果满足条件则从x、y、z三个维度上同时进行二分,将节点划分成8个子节点,为每个子节点设定空间范围,并根据空间范围置入所包含的三角形。然后依次对8个子节点进行前述的检查和递归划分。最终递归调用结束后,不规则八叉树即建立完成。
由于使用八叉树网格剖分将地质空间划分为大小不同、精度不一的网格体,相比均匀型网格块体,其搜索遍历方法更复杂。因此本文使用一种基于局部坐标系机制的溢出方向搜索算法[20]解决寻找指定方向上的邻接网格体问题,完善了对邻接网格体搜索算法。改进后的算法分为三个阶段。第一阶段:搜索目标网格体可能存在的上级网格体,记录由上级网格体到目标网格体的搜索路径;第二阶段:通过第一阶段所给出的搜索路径进行目标网格体的搜索;第三阶段:对目标网格体进行尝试性的细分,以保证作为算法结果的网格体一定是地质空间网格体八叉树的叶子节点。
为了对比八叉树与非八叉树方式的存储效率,对图 2a所示的曲面模型进行实验,结果如表 1所示。若模型包含薄层或透镜体等地质构造,为了精细体现这些构造的细节特征,不规则八叉树应具有较深的划分层数。当划分层数不大于5时,不规则八叉树与规则网格划分规模一致。由表 1中网格规模和划分时间可以看出,随着划分层数的增加,规则网格划分方式的网格单元数目以8倍的速率增长,而八叉树划分方式的网格单元数目和划分耗时增长幅度远小于8,并且呈递减趋势趋于2。因此,使用不规则八叉树方式对地质空间进行网格划分极大地节省了存储空间,提高了块体追踪效率。
|
|
表 1 不规则八叉树划分与规则网格划分的网格单元数量对比 |
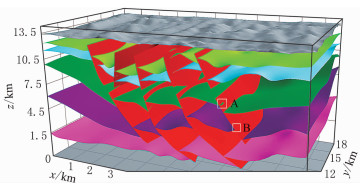
为了验证非拓扑一致性算法的有效性,选择了一个大小为32km(x)×18km(y)×15km(z)的较复杂地质模型(图 5)进行算法测试。模型含有44个层位/断层曲面,存在断裂、尖灭、透镜体等多种地质现象。为了验证算法处理非拓扑一致性模型的能力,在图中A、B两处人为地制造了一些曲面漏缝(图 6左)和交越(图 6右),可以看到模型存在比较明显的拓扑问题。
|
图 5 非拓扑一致模型 |

|
图 6 图 5模型中细节A(左)和B(右) |
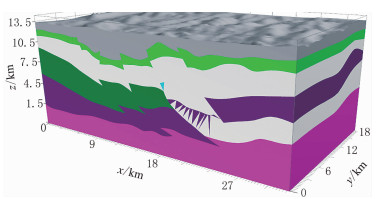
图 7是利用传统曲面缝合性方法建立的块状模型。可以看出,当模型存在拓扑问题时,曲面缝合性方法得到的块体模型结构存在明显问题,即局部存在拓扑错误的块体粘连在一起,得到的块体与原始模型追踪得到块体的结构和数目存在差异。
|
图 7 传统曲面缝合性算法对图 5模型的追踪结果 |
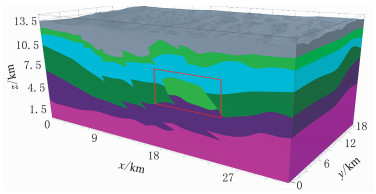
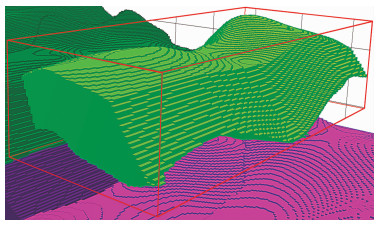
图 8是用网格块体构建方法建立的块状模型,图 9是网格块体构建算法细节。可以看出,网格块体构建算法的整体构建效果较好,但对存在拓扑问题的模型,块体模型没有保留这些细节。
|
图 8 网格块体构建算法对图 5模型的追踪结果 |
|
图 9 网格块体构建算法对图 5模型的追踪结果细节 |
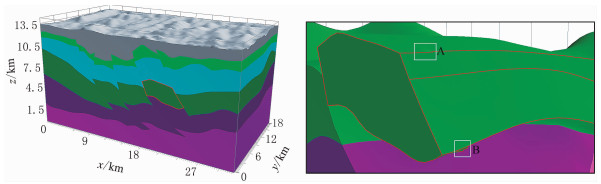
图 10是利用本文非拓扑一致性算法建立的块状模型。块体构建采用Intel i7 4790K、主频为4.0GHz的电脑,耗时23s。
|
图 10 本文算法对图 5模型的追踪结果(左)及细节(右) |
对比图 10与图 8可以看出,当模型存在一定拓扑问题时,本文非拓扑一致块体构建算法得到的块状模型整体结构正确,块体结构和数目与图 8一致。图 10右给出了非拓扑一致性算法在图中A、B两处得到的块体模型细节。可见在原始模型在交线处的漏缝,在本文非拓扑一致性算法建立的块状模型中也呈现出一定的缺漏现象。
实验结果说明非拓扑一致性算法具有很好的容错能力,可以较好地处理存在一定拓扑问题的模型。
为更好地测试基于视觉观察的非拓扑一致块体构建算法的适用性,利用不同形状和复杂程度的曲面模型模拟真实的地层,如表 2所示。与基于三角形追踪的封闭模型描述方法,即曲面缝合型块体构建算法[6]与线框块体构建法[8]作对比。块体构建数据和效果对比情况见表 3和表 4。实验使用的计算机操作系统为Windows10专业版x64、处理器为Intel(R) Core(TM) i7-6800K@3.4GHz(C6T12)、内存为DDR416GB3000MHz。
|
|
表 2 块体构建测试模型 |
|
|
表 3 五个模型块体构建算法效果对比 |
|
|
表 4 五个模型不同算法时间空间资源消耗对比 |
若某次块体构建的结果中出现本应被分离的两个块体黏合到一起,则本次块体构建结果是失败的,此时不记录时间和空间资源的消耗情况。
由表 4可见,本文基于视觉观察效果的块体构建算法虽然在时间资源和空间资源消耗上都数倍于曲面缝合型块体构建算法和线框块体构建算法,但就算法本身而言,对于表 2中最复杂的地质模型b62,块体构建的空间占用不超过2GB,算法执行时间不超过25s,因此一般配置的计算机都可满足其时间和空间需求。该实验证明,即使在地质模型存在交线等拓扑结构的情况下,亦可得到较客观的地质情况。换言之,文中算法具有较强的鲁棒性,且资源消耗在可接受范围内,是一种实用且可靠的地质块体构建算法。
4 结论三维块体构建技术是构造块状地质模型的核心技术,在此过程中,要保证复杂模型的拓扑一致性非常困难。传统的逐三角形追踪和线框追踪方法在模型存在极少量局部拓扑错误时能够建立比较正确的块状模型,但对交线拓扑结构依赖性强,容错性和块体构建成功率较低。本文提出的非拓扑一致性块体构建算法,完全不依赖模型交线拓扑结构,根据曲面模型自身形态即可构建,极大地提升了块体构建成功率。然而相比于传统追踪算法,该算法效率相对较低,为此应用基于八叉树结构提高了算法效率。通过数个典型三维模型的块体构建实验,可以得出以下结论:
(1) 本文基于视觉观察方式的三角形选取算法提出的非拓扑一致性块体构建算法,不依赖于交线拓扑结构,算法容错性较高,能够在很大程度上解决复杂模型拓扑不一致的问题。
(2) 非拓扑一致块体构建算法以网格块体追踪为基础,追踪效率较低,且消耗资源较大,使用八叉树结构对算法进行优化,可以极大地降低内存消耗,一定程度上提高了追踪效率。
(3) 本文提出基于八叉树优化的非拓扑一致性块体构建算法,能够有效解决拓扑不一致模型的块体构建问题,具有较高的容错性和块体构建成功率,并且算法资源消耗在目前主流硬件平台上即可实现。由于该算法降低了对曲面模型的要求,因而也降低了三维复杂地质模型构建的整体难度,提高了块体构建的效率,比传统方法更具实用性。
| [1] |
胡建林, 宋维琪, 张建坤, 等. 交错网格有限差分正演模拟的联合吸收边界[J]. 石油地球物理勘探, 2018, 53(5): 914-920. HU Jianlin, SONG Weiqi, ZHANG Jiankun, et al. Joint absorbing boundary in the staggered-grid finite difference forward modeling simulation[J]. Oil Geophysical Prospecting, 2018, 53(5): 914-920. |
| [2] |
邓飞, 刘超颖. 三维射线快速追踪及高斯射线束正演[J]. 石油地球物理勘探, 2009, 44(2): 158-165. DENG Fei, LIU Chaoying. 3D rapid ray-tracing and Gaussian ray-beam forward simulation[J]. Oil Geophysical Prospecting, 2009, 44(2): 158-165. DOI:10.3321/j.issn:1000-7210.2009.02.007 |
| [3] |
孟宪海, 杨钦, 李吉刚. 基于层面结构的三维闭合地质区块构造算法[J]. 北京航空航天大学学报, 2005, 31(2): 182-186. MENG Xianhai, YANG Qin, LI Jigang. Construction of coherent 3D geological blocks from stratified geological structure[J]. Journal of Beijing University of Aeronautics and Astronautics, 2005, 31(2): 182-186. DOI:10.3969/j.issn.1001-5965.2005.02.016 |
| [4] |
梁文全, 王彦飞, 杨长春. 声波方程数值模拟矩形网格有限差分系数确定法[J]. 石油地球物理勘探, 2017, 52(1): 56-62. LIANG Wenquan, WANG Yanfei, YANG Changchun. Acoustic wave equation modeling with rectangle grid finite difference operator and its linear time space domain solution[J]. Oil Geophysical Prospecting, 2017, 52(1): 56-62. |
| [5] |
王政.非块状模型的三维重力反演[C].中国地球物理学会第六届学术年会论文集, 1990, 138.
|
| [6] |
Warburton P M. Applications of a new computer model for reconstructing blocky rock geometry, analysing single block stability and identifying keystones[J]. International Journal of Rock Mechanics and Mining Sciences & Geomechanics Abstracts, 1984, 21(5): A180. |
| [7] |
Lin D, Fairhurst C, Starfield A M. Geometrical identification of three-dimensional rock block systems using topological techniques[J]. International Journal of Rock Mechanics and Mining Science, 1987, 24(6): 331-338. DOI:10.1016/0148-9062(87)92254-6 |
| [8] |
Lu J. Systematic identification of polyhedral rock blocks with arbitrary joints and faults[J]. Computers and Geotechnics, 2002, 29(1): 49-72. DOI:10.1016/S0266-352X(01)00018-0 |
| [9] |
蒋先艺, 贺振华, 黄德济. 封闭结构模型建立方法[J]. 石油地球物理勘探, 2002, 37(4): 339-342. JIANG Xianyi, HE Zhenhua, HUANG Deji. A method for building a model in closed structure[J]. Oil Geophysical Prospecting, 2002, 37(4): 339-342. DOI:10.3321/j.issn:1000-7210.2002.04.007 |
| [10] |
侯卫生, 吴信才, 刘修国, 等. 一种基于平面地质图的复杂断层三维构建方法[J]. 岩土力学, 2007, 28(1): 169-172. HOU Weisheng, WU Xincai, LIU Xiuguo, et al. A complex fault modeling method based on geological plane map[J]. Rock and Soil Mechanics, 2007, 28(1): 169-172. DOI:10.3969/j.issn.1000-7598.2007.01.031 |
| [11] |
杨洋, 潘懋, 吴耕宇, 等. 三维地质结构模型中闭合地质块体的构建[J]. 计算机辅助设计与图形学学报, 2015, 27(10): 1929-1935. YANG Yang, PAN Mao, WU Gengyu, et al. Sealed geological block modeling in 3D geological structural model[J]. Journal of Computer-Aided Design & Computer Graphics, 2015, 27(10): 1929-1935. DOI:10.3969/j.issn.1003-9775.2015.10.015 |
| [12] |
吴军, 贾雨. 复杂介质的三维块状模型快速射线追踪[J]. 物探化探计算技术, 2008, 30(6): 465-470. WU Jun, JIA Yu. The rapid ray tracing of complex three-dimensional media[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2008, 30(6): 465-470. DOI:10.3969/j.issn.1001-1749.2008.06.005 |
| [13] |
Zene M T A M, Hasan N, Rui Z J, et al. Geological modeling and upscaling of the Ronier 4 block in Bongor Basin, Chad[J]. Journal of Petroleum Exploration and Production Technology, 2019, 9(5): 2461-2476. |
| [14] |
蒋先艺.基于二维与三维复杂结构模型正演的地震数据采集设计方法研究[D].四川成都: 成都理工大学, 2004.
|
| [15] |
杨洋, 李兆亮, 潘懋. 基于拓扑追踪的不规则三角网裁剪算法[J]. 地理与地理信息科学, 2014, 30(3): 21-24. YANG Yang, LI Zhaoliang, PAN Mao. Clipping algorithm for triangulation irregular network based on topology[J]. Geography and Geo-information Science, 2014, 30(3): 21-24. |
| [16] |
Khudeev R.A new flood-fill algorithm for closed contour[C].IEEE International Siberian Conference on Control & Communications, 2005.
|
| [17] |
Woo M, Neider J, Davis T, et al.OpenGL Programming Guide: the Official Guide to Learning OpenGL, Version 1.2[M].Addison-Wesley Longman Publishing, Boston, USA, 1999.
|
| [18] |
Green S.The OpenGL framebuffer object extension[C].Game Developers Conference, 2005.
|
| [19] |
Meagher D. Geometric modeling using octree encoding[J]. Computer Graphics and Image Processing, 1982, 19(2): 129-147. |
| [20] |
Samet H.Applications of Spatial Data Structures: Computer Graphics, Image Processing and GIS[M].Addison-Wesley Longman Publishing, Boston, USA, 1990.
|



 房鹏, 四川省成都市二仙桥东三路1号成都理工大学信息科学与技术学院, 610059。Email:
房鹏, 四川省成都市二仙桥东三路1号成都理工大学信息科学与技术学院, 610059。Email: