2 成都理工大学地球勘探与信息技术教育部重点实验室, 四川成都 610059
2 Key Lab of Earth Exploration & Information Techniques of Ministry of Education, Chengdu University of Technology, Chengdu, Sichuan 610059, China
精确识别地震剖面上具有不连续特征的断层、裂缝等边界和走向信息在地震解释中非常重要,学者们提出了许多突出储层结构及地质构造特征的方法。Bahoric等[1]提出了地震相干分析技术;Roberts[2]提出了曲率属性技术;郑静静等[3-4]将Curvelet变换用于相干方法,使相干算法具有多尺度特征,并将其应用于裂缝识别。边缘检测技术被广泛应用于地震裂缝检测中,该技术是基于图形图像处理和计算机视觉领域技术发展起来的,能够有效提取图像的边缘特征,与油气藏的裂缝检测技术有着诸多相似之处。如基于Prewitt算子、Robert算子、Canny算子、Sobel算子、高斯偏导滤波器(LOG)等微分算子的二维小波分析多尺度边缘检测方法[5]。此外,贺振华等[6]提出的基于地下介质横向变化的地震多尺度边缘检测技术以及陈学华等[7]提出的基于广义S变换的分频裂缝边缘检测方法都在实际应用中取得了很好的效果。
希尔伯特变换也是一种有效的图像边缘检测方法。近年来,传统的希尔伯特变换的应用在多个方面得以不断拓展,如陈学华等[8-9]将一维高阶伪希尔伯特变换应用于地震资料边缘检测;Luo等[10]提出了广义希尔伯特变换(GHT)并应用于地震资料河道成像;熊晓军等[11]将GHT应用于地震资料边缘检测;党志敏等[12]分析了GHT在含噪信号边缘检测中应用效果;李斌等[13]提出了基于多尺度加窗希尔伯特变换的地震资料体边缘检测方法。上述方法均主要基于一维希尔伯特变换。在二维希尔伯特变换[14]被提出后,Kohlmann[15]将其应用于角点检测;王珂等[16]改进其方向性缺陷后,将新方法应用于图像边缘检测;Liu等[17]利用二维希尔伯特变换估计地震倾角、压制随机噪声。但二维希尔伯特变换还未被广泛应用于地震资料的边缘检测。
为此,本文将空间域加窗二维希尔伯特变换应用于三维地震资料边缘检测,并通过引入二维高斯函数压制噪声。该方法考虑到裂缝带、河道以及断层等不连续信息在三维空间上的延续性,利用二维希尔伯特算子同时在水平和深度方向上采用不同孔径计算地质异常体边缘信息,突出不同尺度下不连续性信息的完整异常特征。实际地震资料处理结果表明,本文方法可以清晰地刻画不同尺度的三维地质异常体的完整特征,突出裂缝发育带的边缘位置及断层走向。
1 方法原理 1.1 二维离散希尔伯特变换Read等[14]和Bose等[18]分别给出了二维希尔伯特变换在频域和空间域中的相关定义。
对于一个N1×N2的二维信号,在频域中,假设Po(i, j)和Pe(i, j)分别为两个正交滤波器的频域表达式,则Po(i, j)可以用Pe(i, j)的二维希尔伯特变换表示为
| $\begin{aligned} P_{{\rm{o}}}(i, j) &=[\operatorname{sgn}(i, j)+\mathrm{bdy}(i, j)] P_{\mathrm{e}}(i, j) \\ &=H(i, j) P_{\mathrm{e}}(i, j) \end{aligned} $ | (1) |
式中sgn(i, j)、bdy(i, j)分别为符号函数和边界函数,用于校正边界,其表达式分别为
| $\operatorname{sgn}(i, j)=\left\{\begin{array}{cl}1 & 0<i<\frac{N_{1}}{2}, 0<j<\frac{N_{2}}{2} \\ -1 & \frac{N_{1}}{2}<i<N_{1}, \frac{N_{2}}{2}<j<N_{2} \\ 0 & \text { 其他 }\end{array}\right. $ |
| $\operatorname{bdy}(i, j)=\left\{\begin{array}{rl}1 & j=0, 0<i<\frac{N_{1}}{2} \\ -1 & j=0, \frac{N_{1}}{2}<i<N_{1} \\ 1 & i=0, 0<j<\frac{N_{2}}{2} \\ -1 & i=0, \frac{N_{2}}{2}<j<N_{2} \\ 0 & \text { 其他 }\end{array}\right. $ |
在空间域,二维希尔伯特变换可以表示为二维卷积的形式。给定一个N1×N2的地震沿层切片x(i, j), i=0,1, 2, …, N1-1,j=0, 1, 2, …,N2-1, 其二维希尔伯特变换在空域中表达为
| $\begin{aligned} \hat{x}(i, j) &=h(i, j) * x(i, j) \\ &=\sum\limits_{k_{1}=0}^{N_{1}-1} \sum\limits_{k_{2}=0}^{N_{2}-1} x\left(k_{1}, k_{2}\right) h\left(i-k_{1}, j-k_{2}\right) \end{aligned} $ | (2) |
式中h(i, j)是二维希尔伯特变换算子余切空域表达式
| $h(i, j)=\left(i \cot \frac{\pi}{N_{1}}+j \cot \frac{\pi}{N_{2}}\right) \frac{2}{N_{1} N_{2}} $ | (3) |
假设x(i, j)经二维离散傅里叶变换后的频谱为X(i, j),有
| $\hat{X}(i, j)=H(i, j) X(i, j) $ | (4) |
式中$\hat{X}(i, j)=\operatorname{DFT}[\hat{x}(i, j)]$,其中DFT(·)表示离散傅里叶变换。
1.2 二维加窗希尔伯特变换地震数据中往往存在大量的噪声,对有噪数据直接进行二维希尔伯特变换,无法对噪声进行有效抑制,会对边缘检测结果产生影响。为此,Luo等[10]在传统希尔伯特变换的基础上提出了广义希尔伯特变换(GHT),以此改变传统希尔伯特变换对噪声过于敏感的问题;谢静等[19]提出了基于时间域加窗的希尔伯特变换边缘检测方法。这些方法都是在一维希尔伯特变换基础上进行改进。
在式(2)和式(4)的基础上,笔者加入与人类视觉系统非常接近的高斯函数,用于抑制噪声和优化边缘检测结果。高斯滤波器是根据高斯函数的形状选择权值的线性平滑滤波器,对于抑制服从正态分布的噪声十分有效。二维零均值离散高斯滤波器函数(图 1)的表达式为
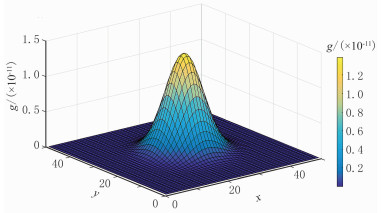
|
图 1 二维离散高斯滤波器(x=y=50, σ=3) |
| $g(x, y ; \sigma)=\frac{1}{2 \pi \sigma^{2}} \mathrm{e}^{-\frac{x^{2}+y^{2}}{2 \sigma^{2}}} $ | (5) |
式中σ为标准差,决定了高斯核宽度。对式(5)进行二维傅里叶变换得到二维高斯函数的频域响应
| $G(u, v ; \sigma)=\mathrm{e}^{-2 \pi^{2} \sigma^{2}\left(u^{2}+v^{2}\right)} $ | (6) |
式中u、v分别表示水平和垂直方向的频率。将式(5)和式(6)分别引入式(2)和式(4),则加入高斯滤波函数的二维希尔伯特变换为
| $\hat{x}(i, j)=h(i, j) * x(i, j) * g(i, j) $ | (7) |
| $\hat{X}(i, j)=H(i, j) X(i, j) G(i, j) $ | (8) |
根据卷积的性质,式(7)和式(8)可写为
| $\hat{x}(i, j)=x(i, j) * h^{\prime}(i, j) $ | (9) |
| $\hat{X}(i, j)=X(i, j) H^{\prime}(i, j) $ | (10) |
式中
| $h^{\prime}(i, j)=h(i, j) * g(i, j) $ | (11) |
| $H^{\prime}(i, j)=H(i, j) G(i, j) $ | (12) |
h′和H′分别为改进后空间域和频率域二维希尔伯特变换算子。改进前、后二维希尔伯特变换算子的空间域和频率域形态如图 2所示。
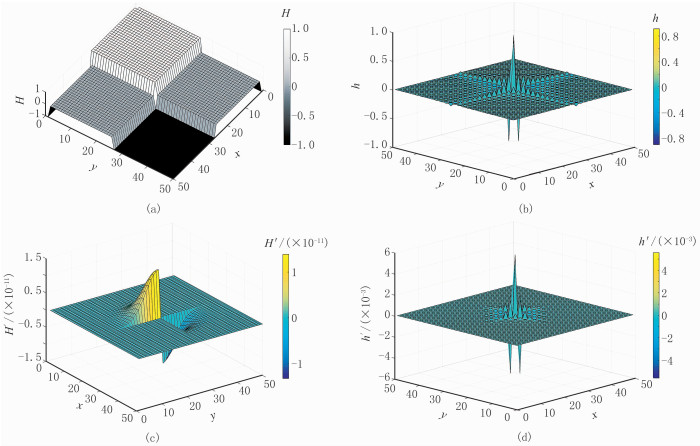
|
图 2 二维希尔伯特算子空间形态 (a)频域算子;(b)空域算子;(c)改进后频域算子;(d)改进后空域算子 |
利用式(9)和式(10)式能够直接对二维数据进行计算,得到平面上的边缘检测结果。但由于不连续性地质异常体在深度方向上存在一定延续度,平面上的检测结果不能很好地反映地下不连续性信息的完整特征,因此,提出了基于二维希尔伯特变换的地震体边缘检测计算方法,从而在三维地震资料中实现地质异常信息的体边缘检测。空间域中二维希尔伯特算子随不同尺度高斯窗同时变化,能够得到边缘检测结果在水平方向上的多尺度特性,结合在时间深度方向上选择不同深度窗,可得到不同尺度的地质异常信息。在地震资料深度方向上进行体边缘检测可通过下式实现
| $E(t, k, \Delta t)=\sum\limits_{\tau=-k}^{k} x(t+\tau \Delta t, i, j) * h^{\prime}(i, j) $ | (13) |
式中:E(t, k, Δt)表示体边缘检测结果,t表示目的层位置,k表示三维地震资料在时间深度方向以目的层t为基准上下采样长度,即三维深度方向上面深度计算时窗长度为2k+1,Δt表示在深度时窗上相邻样点之间的采样间隔;x(t+τΔt, i, j)表示沿层地震数据。
2 模型试算与分析根据式(2)直接对Lena图像(图 3a)进行边缘检测,采用尺寸为3×3的算子计算得到检测结果如图 3b所示。可以看出,直接使用二维希尔伯特变换边缘检测方法可以正确提取图像的边缘特征。
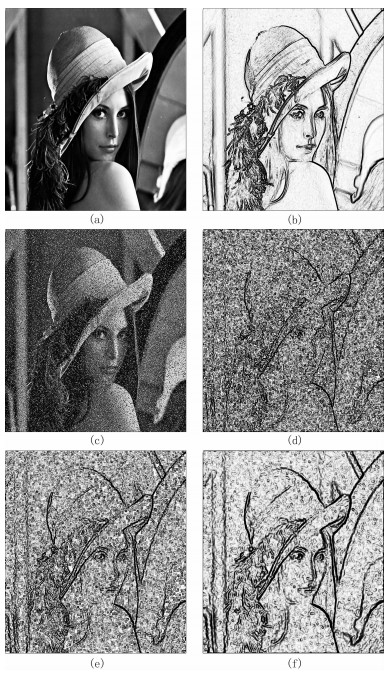
|
图 3 Lena图像边缘检测结果 (a)原始图像;(b)二维希尔伯特变换边缘检测结果;(c)加噪Lena图像;(d)加噪Lena图像未加窗边缘检测结果(σ=0);(e)加噪Lena图像本文方法边缘检测结果(σ=0.09);(f)加噪Lena图像本文方法边缘检测结果(σ=2.00) |
为了验证加入高斯函数后二维希尔伯特变换算子的抗噪效果,在图 3a基础上加入随机噪声,如图 3c所示。二维希尔伯特算子尺寸为3×3,改变σ值得到不同的边缘检测结果,如图 3d~图 3f所示。
图 3d是直接使用二维希尔伯特算子计算得到的边缘检测结果,由图可知,虽然该方法能够检测出图像的部分边缘特征,但受噪声影响严重,导致边缘信息大部分隐藏在噪声中。
从图 3e和3f可以看出,引入高斯函数后,噪声得到了很好的压制,边缘检测结果明显改善。随着滤波因子σ的增大,图像中噪声明显减少,边缘更加清晰突出。
图 3的模型检测结果表明,引入高斯函数后的二维希尔伯特算子具有较强的抗噪能力,能够准确地提取加噪信号中的有效边缘信息,为处理实际地震资料提供了可靠的手段。
3 实际地震资料处理为了说明本文方法在实际地震资料中的应用效果,分别以中国LH地区海上三维地震资料和TH地区陆上三维地震资料为例,与传统边缘检测方法进行对比分析。图 4为LH地区三维地震资料目的层沿层振幅切片,可以看出该地区断裂带较发育。首先对原始地震资料进行保边去噪预处理,再进行边缘检测计算。图 5a和图 5b分别为利用传统GHT边缘检测方法和本文方法的计算结果。传统GHT算子长度为9,本文方法二维希尔伯特算子尺寸为3×3,二维高斯函数参数σ=0.09。对比结果表明,本文方法能够有效检测出裂缝等不连续性特征,提取的边缘信息也更加丰富,相对于传统GHT方法的分辨率更高,说明了本文方法对于复杂构造具有更好的边缘检测能力,有效检测出地震资料中不连续性信息的边缘分布特征。
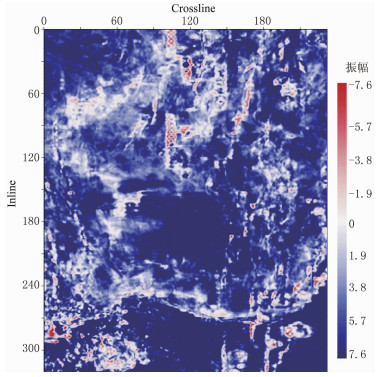
|
图 4 LH地区三维地震资料目标层位沿层振幅切片 |

|
图 5 传统GHT方法和本文方法不同参数边缘检测结果对比 (a)GHT:算子长度为9;(b)本文方法:深度时窗取2ms,算子尺寸为3×3;(c)本文方法:深度时窗取14ms,算子尺寸为3×3;(d)本文方法:深度时窗取26ms,算子尺寸为3×3;(e)本文方法:深度时窗取26ms,算子尺寸为5×5 |
为了进一步对比分析本文方法在不同深度时窗时的边缘检测结果,分别设定深度时窗为14ms和26ms进行地震资料体边缘检测,结果如图 5c和图 5d所示。与图 5b对比可看出,当深度时窗逐渐增大时,由于深度方向上异常信息的增加,不同深度窗下同一位置的不连续信息显示有所差异。当窗口较小时,能够检测出更多细小的异常边缘信息,但对于不连续信息的整体分布特征难以清晰地展现;当深度窗口增大时,在检测出异常信息的同时,可以更加清晰地看到裂缝、断层等的整体分布特征,连续性和方向性也更加完整,可使解释人员更好地掌握目的层段的地质构造信息,利于地震资料的精细解释。
为研究算子尺寸对检测结果的影响,将二维希尔伯特算子尺寸设置为5×5,深度时窗为26ms,结果如图 5e所示。与图 5d对比可知,深度方向上时窗大小不变时,小尺寸算子的检测结果可使断层和裂缝显示清晰、分辨率高并且易于主要异常的定位;算子尺寸增大后,检测结果的信噪比更高,能够更好地反映不连续性地质异常的完整特征。
综上所述,改变深度时窗大小及二维希尔伯特算子的尺寸可使实际边缘检测结果呈现多尺度的特征。
为了进一步分析本文方法的应用效果及优势,对TH某工区陆上三维地震资料进行分析。该区以奥陶系缝洞型油藏为主,岩溶作用较强。受地质构造作用的影响,形成了不同尺度的断裂和溶洞,大大增加了断层和裂缝的识别难度。图 6为该工区原始地震数据目的层沿层切片及使用本文方法与其他方法的对比分析结果。图 6a为原始地震数据目的层沿层切片,从图中能够发现,该地区有着大型断裂及不同尺度溶洞的分布;图 6b为使用本文方法得到的体边缘检测结果;图 6c为对经过构造方向滤波的方差体进行蚂蚁追踪后得到的结果;图 6d为体曲率[20]、蚂蚁体技术及最大似然法的组合检测结果。
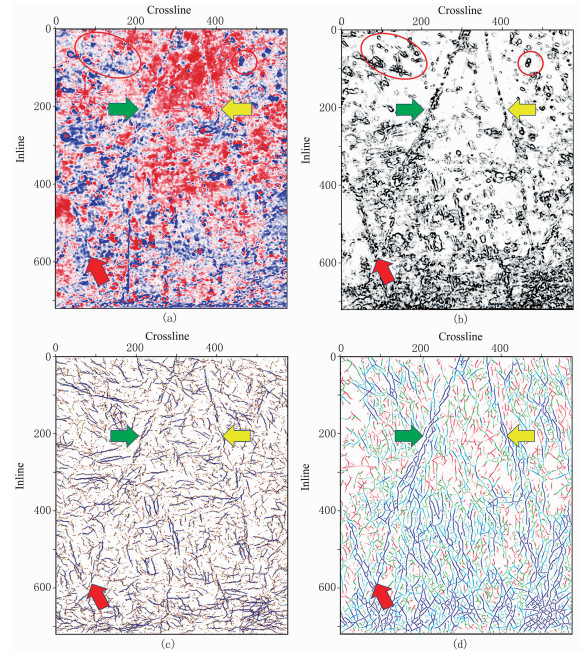
|
图 6 陆上实际地震数据不同方法的边缘检测结果(深度时窗14ms,算子尺寸3×3,σ=0.09) (a)原始数据沿层切片;(b)本文方法;(c)蚂蚁追踪算法;(d)体曲率、蚂蚁追踪及最大似然算法组合法。椭圆标注区域为典型溶洞,图 7同 |
对比分析上述结果可以看出,本文方法清楚地刻画了目的层段的溶洞分布,且能够非常清晰地识别出一个呈反“N”字形断裂系统(箭头所指),此结果利于精确地震解释,具有很好的实用性。
与图 6c的方法结果对比可知,本文方法得到的沿层切片背景更干净,检测出的大断层连续性和延展性更好,边缘的刻画更清晰,而蚂蚁体技术难以很好刻画溶洞及其边界特征。由图 6d多属性处理结果可以看出,其展示的断裂带以及断层信息(反“N”字形分布的断裂)与图 6b检测出的断裂分布特征相吻合,验证了本文方法计算结果的正确性。
为了能够在一个层面上同时清晰地展示出断层、断裂带和溶洞等更多信息,将本文方法的裂缝检测结果(图 6b)与图 6d中的结果进行叠加,结果如图 7所示。由图可知,叠加结果不仅能够更加清楚地展示裂缝系统的分布特征,也能清晰地刻画裂缝及溶洞的边界信息,展示的地质构造信息更加丰富,利于地震资料的精细解释。
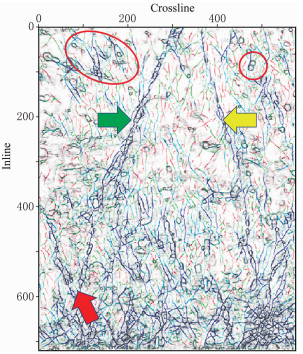
|
图 7 本文方法+曲率+蚂蚁追踪+最大似然体属性叠加结果 |
本文在二维希尔伯特变换理论基础上,将二维高斯函数和二维希尔伯特算子结合提出了一种新的地震资料边缘检测方法,并通过地震资料目的层段计算方法,实现了三维地震资料的体边缘检测。主要得出以下结论:
(1) 引入二维高斯函数后,利用基于改进的二维希尔伯特算子不但能够检测出边缘信息,还能减少噪声干扰,有效增强边缘信息。
(2) 本文空间域加窗二维希尔伯特变换的三维地震资料体边缘检测方法,能够有效检测复杂地质构造异常的边缘信息,刻画地震异常信息的空间分布和走向特征,能够很好地应用于断层、裂缝等地质异常特征的检测。
(3) 将本文方法与多种属性处理结果融合显示后,不仅能够清晰地展示较大断裂系统的分布特征,也能清晰地刻画更多裂缝及溶洞的边界信息,展示的地质构造信息更加丰富,利于地震资料的精细解释。
(4) 在本文方法的基础上,根据裂缝系统在三维空间上的多尺度特性,实现所有不同尺度裂缝系统的三维体边缘检测,并利用数据融合方法将这些结果进行优化融合,则可充分挖掘多尺度裂缝系统的异常信息,实现裂缝储层内部结构的高精度描述。
| [1] |
Bahorich M S, Farmer S L. 3D seismic discontinuity for faults and stratigraphic features:The coherence cube[J]. The Leading Edge, 1995, 14(10): 1053-1058. DOI:10.1190/1.1437077 |
| [2] |
Roberts A. Curvature attributes and their application to 3D interpreted horizons[J]. First Break, 2001, 19(2): 85-100. DOI:10.1046/j.0263-5046.2001.00142.x |
| [3] |
郑静静, 印兴耀, 张广智. 基于Curvelet变换的多尺度分析技术[J]. 石油地球物理勘探, 2009, 44(5): 543-547. ZHENG Jingjing, YIN Xingyao, ZHANG Guangzhi. Mult-scale analysis technique based on Curvelet transform[J]. Oil Geophysical Prospecting, 2009, 44(5): 543-547. DOI:10.3321/j.issn:1000-7210.2009.05.004 |
| [4] |
张广智, 郑静静, 印兴耀. 基于Curvelet变换的多尺度性识别裂缝发育带[J]. 石油地球物理勘探, 2011, 46(5): 757-762. ZHANG Guangzhi, ZHENG Jingjing, YIN Xingyao. Identification technology of fracture zone and its strike based on the Curvelet transform[J]. Oil Geophysical Prospecting, 2011, 46(5): 757-762. |
| [5] |
赵西安, 李德仁. 2维对称小波与多尺度影像边缘特征提取[J]. 测绘学报, 2003, 32(4): 313-319. ZHAO Xi'an, LI Deren. Constructing two dimension symmetric wavelets for extracting edge features of image at multiscales[J]. Acta Geodaetica et Cartographica Sinica, 2003, 32(4): 313-319. DOI:10.3321/j.issn:1001-1595.2003.04.006 |
| [6] |
贺振华, 黄捍东, 胡光岷, 等. 地下介质横向变化的地震多尺度边缘检测技术[J]. 物探化探计算技术, 1999, 24(4): 289-294. HE Zhenhua, HUANG Handong, HU Guangmin, et al. Lateral identification by seismic multi-scale edge detection[J]. Computing Techniques for Geophysical and Geochemical Exploraion, 1999, 24(4): 289-294. DOI:10.3969/j.issn.1001-1749.1999.04.001 |
| [7] |
陈学华, 贺振华, 文晓涛, 等. 基于广义S变换的裂缝分频边缘检测方法[J]. 吉林大学学报(地球科学版), 2011, 41(5): 1605-1609. CHEN Xuehua, HE Zhenhua, WEN Xiaotao, et al. Fracture multi-frequency edge detection based on generalized S transform[J]. Journal of Jilin University (Earth Sciences Edition), 2011, 41(5): 1605-1609. |
| [8] |
陈学华, 贺振华, 黄德济. 高阶伪希尔伯特变换在边缘检测中的应用[J]. 数据采集与处理, 2008, 23(2): 224-227. CHEN Xuehua, HE Zhenhua, HUANG Deji. High-order pseudo Hilbert transform and application in edge detection[J]. Journal of Data Acquisition & Processing, 2008, 23(2): 224-227. DOI:10.3969/j.issn.1004-9037.2008.02.020 |
| [9] |
陈学华, 贺振华, 黄德济. 地震资料的高阶伪希尔伯特变换边缘检测[J]. 地球物理学进展, 2008, 23(4): 1106-1110. CHEN Xuehua, HE Zhenhua, HUANG Deji. Seismic data edge detection based on higher-order pseudo Hilbert transform[J]. Progress in Geophysics, 2008, 23(4): 1106-1110. |
| [10] |
Luo Y, AL-Dossary S, Marhoon M, et al. Generalized Hilbert transform and its applications in geophysics[J]. The Leading Edge, 2003, 22(3): 198-202. DOI:10.1190/1.1564522 |
| [11] |
熊晓军, 贺振华, 赵明金. 一种基于GHT的裂缝检测新方法[J]. 石油地球物理勘探, 2009, 44(4): 442-444. XIONG Xiaojun, HE Zhenhua, ZHAO Mingjin. A new GHT-based fractural detection method[J]. Oil Geophysical Prospecting, 2009, 44(4): 442-444. DOI:10.3321/j.issn:1000-7210.2009.04.011 |
| [12] |
党志敏, 贺振华, 黄德济. GHT在含噪信号边缘检测中的应用效果分析[J]. 石油工业计算机应用, 2008, 16(2): 19-21. DANG Zhimin, HE Zhenhua, HUANG Deji. GHT application results analysis in noisy signal edge detection analysis[J]. Oil Industry Computer Applications, 2008, 16(2): 19-21. |
| [13] |
李斌, 陈学华, 贺振华, 等. 基于多尺度加窗希尔伯特变换的地震资料体边缘检测[J]. 石油物探, 2015, 54(3): 345-349. LI Bin, CHEN Xuehua, HE Zhenhua, et al. Seismic data 3D edge detection based on multi-scale windowed Hilbert transform[J]. Geophysical Prospecting for Petroleum, 2015, 54(3): 345-349. DOI:10.3969/j.issn.1000-1441.2015.03.014 |
| [14] |
Read R R, Treitel S. The stabilization of two-dimensional recursive filters viathe discrete Hilbert transform[J]. IEEE Transactions on Geoscience Electro-nics, 1973, 7(11): 153-160. |
| [15] |
Kohlmann K. Corner detection in natural images based on the 2-D Hilbert transform[J]. Signal Processing, 1996, 48(3): 225-234. DOI:10.1016/0165-1684(95)00138-7 |
| [16] |
王珂, 肖鹏峰, 冯学智, 等. 基于改进二维离散希尔伯特变换的图像边缘检测方法[J]. 测绘学报, 2012, 41(3): 421-427. WANG Ke, XIAO Pengfeng, FENG Xuezhi, et al. The modified algorithm of image edge features detection based on 2-D discrete Hilbert transform[J]. Acta Geodaetica et Cartographica Sinica, 2012, 41(3): 421-427. |
| [17] |
Liu C, Chen C L, Wang D. Seismic dip estimation based on the two-dimensional Hilbert transform and its application in random noise attenuation[J]. Applied Geophysics, 2015, 12(1): 55-63. DOI:10.1007/s11770-014-0474-4 |
| [18] |
Bose N K, Prabhu K A. Two-dimensional discrete Hilbert transform and computational complexity aspects in its implementation[J]. IEEE Transactions on Acoustics Speech and Signal Processing, 1979, 27(4): 356-360. DOI:10.1109/TASSP.1979.1163261 |
| [19] |
谢静, 贺振华, 黄德济. 基于加窗Hilbert变换的高精度边缘检测[J]. 油气地球物理, 2007, 5(1): 27-29. XIE Jing, HE Zhenhua, HUANG Deji. High accuracy edge detection on window-based Hilbert transform[J]. Petroleum Geophysics, 2007, 5(1): 27-29. |
| [20] |
Chen X H, Yang W, He Z H, et al. The algorithm of 3D multi-scale volumetric curvature and its application[J]. Applied Geophysics, 2012, 9(1): 65-72. |



 陈学华, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室, 610059。Email:
陈学华, 四川省成都市成华区二仙桥东三路1号成都理工大学地球物理学院5301室, 610059。Email: