② 中国石油大学(华东)地球科学与技术学院, 山东青岛 266580;
③ 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071
② School of Geosciences, China University of Petroleum(East China), Qingdao, Shandong 266580, China;
③ Laboratory for Marine Mineral Resources, Qing-dao National Laboratory for Marine Science and Technology, Qingdao, Shandong 266071, China
构造应力导致岩层发生形变,形成不同形态的地质构造,控制着裂缝的形成和分布,影响油气的运移。因此,构造应力的预测不仅有助于人们认识和理解地质构造的形成、分布和演化规律,还可以为油气田注水开发过程中井网的布置和调整提供依据[1]。
早期学者采用物理模拟方法对构造应力场分布特征进行研究,以了解构造变形的过程,但该方法存在时空尺度的局限性和实验条件的限制。其后数值模拟技术被引入到构造应力场的研究中,建立的地质模型实现了二维和三维空间的构造应力场数值模拟[2],克服了时空尺度的局限性。谭成轩等[3]利用Super SAP有限元程序探索了含油气盆地三维构造应力场数值模拟方法。陈书平等[4]通过设计的4个地质模型,采用有限元法模拟分析了盆地演化过程中的四期应力场。张帆等[5]针对特定的地震反射层位,利用连续介质弹性有限元模型计算主应力和剪切应力,并预测了研究区内裂缝发育情况。王红才等[6]基于有限元分析方法利用计算机模拟三维构造应力场,并将该方法应用于辽河油田滩海地区。雷景生[7]研究了基于结构优化的有限元网格自动划分方法,并对某油藏的应力场进行数值模拟。王连捷等[8]利用有限元法模拟的三维构造应力场预测油气聚集有利区。付玉华等[9]提出了构造应力场边界载荷的有限元反演方法,用于反演构造应力场的边界力。董培育等[10]利用蒙特卡洛方法,根据库伦─摩尔破裂准则反演巴颜喀拉块体的初始构造应力场。构造应力的数值模拟方法虽克服了时空尺度的局限性,但在模型构建、边界条件和所受载荷类型等方面存在主观性,且模拟的结果存在多解性和可靠性等问题[2]。
曲率属性和构造应力都与裂缝相关,国内外学者研究了曲率属性与构造应力的关系。Price等[11]利用曲率属性估算构造应力,首次建立了应力与曲率、弹性力学参数之间的定量关系。Sheorey[12]在考虑地层曲率和岩层弹性参数、密度与热膨胀系数变化的前提下,利用静弹性热应力模型估算地层应力。Roberts[13]推导了层面曲率的计算公式,并利用弯曲的岩层模型描述曲率与应力的关系。Sigismondi等[14]研究了曲率与构造之间的相关性。刘建伟等[15]基于测井岩石物理参数分析,明确了地应力、破裂压力与岩石弹性参数的关系,实现了非常规油藏应力场及应力甜点的地震预测。孟阳等[16]应用GeoEast系统提取识别断层的敏感分方位地震属性,精细识别了ZJB区块五峰—龙马溪组页岩储层的小断层。王玲玲等[17]基于多裂缝参数地震物理模型,分析叠后属性,优选敏感地震属性进行融合以识别裂缝。何英[18]利用曲率属性估算地层的构造应力,克服了复杂构造应力场模型构建的难点,但是没有给出最大正曲率和最小负曲率与构造应力的直接关系。
利用曲率属性估算构造应力的传统方法是通过提取x、y方向的曲率和xOy面的扭率计算相应的应力分量而求取构造应力,但没有构建曲率属性与构造应力之间的定量关系,且目前的商业软件通常不能直接提取x、y方向的曲率和xOy面的扭率,只能提取最大正曲率、最小负曲率、高斯曲率、平均曲率、极大曲率和极小曲率等属性。为此,本文在薄板弯曲理论的假设条件下,通过研究曲率与构造应力之间的定量关系,推导由最大正曲率、最小负曲率直接表征构造应力的计算公式,即通过提取体曲率属性得到最大正曲率和最小负曲率,进而计算地层构造应力。
1 方法原理 1.1 弹性薄板弯曲理论薄板是指板的厚度远小于其他方向尺度的两个平行平面所围成的板状构件。设薄板的中平面为坐标平面,即z=0。坐标原点O为中平面内一点,x和y轴在中平面内。在x轴正方向上产生的位移为u,y轴正方向上产生的位移为v,z轴正方向上产生的位移为扰度w(x, y)。z轴向上,薄板的时间厚度为z(单位为s)。薄板模型如图 1所示。
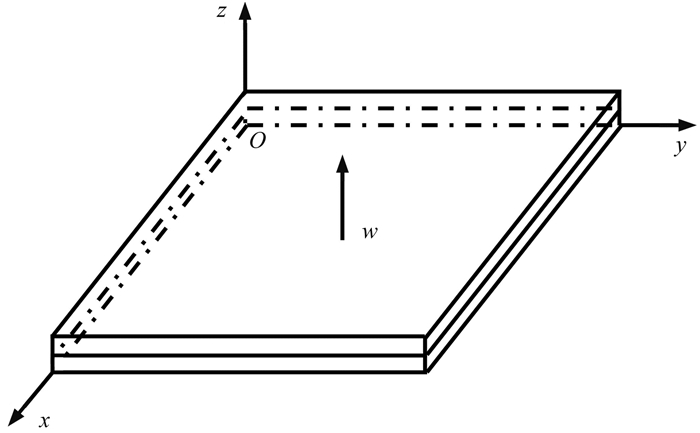
|
图 1 薄板模型 |
一般来说,σx、σy和σz为正应力分量(下标表示受力面的法线方向),对应的应变分量分别为εx、εy和εz;τxy、τxz、τyx、τyz、τzy、τzx为切应力分量(下标中前者表示受力面的法线方向,后者表示应力分量的方向),对应的应变分量分别为γxy、γxz、γyx、γyz、γzy、γzx[19]。
薄板小扰度弯曲的近似理论[20]是以下述三个基本假设条件为基础。
(1) 在平行于中平面的截面上,应力分量τzx和τzy、σz相比于其余应力分量要小得多,因此它们所引起的应变γzx、γzy可忽略不计,即
| $ \left\{ {\begin{array}{*{20}{l}} {{\gamma _{zx}} = 0}\\ {{\gamma _{zy}} = 0} \end{array}} \right. $ | (1) |
由式(1)可得
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial w}}{{\partial x}} + \frac{{\partial u}}{{\partial z}} = 0}\\ {\frac{{\partial w}}{{\partial y}} + \frac{{\partial v}}{{\partial z}} = 0} \end{array}} \right. $ | (2) |
(2) 中平面垂直方向上的正应变εz可以不计,即
| $ \varepsilon_{z}=\frac{\partial w}{\partial z}=0 $ | (3) |
式(3)表明薄板中平面上法线的各点都具有相同的位移w,即为扰度。
(3) 薄板中平面内的各点都没有平行于中平面的位移,表示为
| $ \left\{\begin{array}{l} (u)_{z=0}=0 \\ (v)_{z=0}=0 \end{array}\right. $ | (4) |
由式(4)可得
| $ \left\{\begin{array}{l} \left(\varepsilon_{x}\right)_{z=0}=0 \\ \left(\varepsilon_{y}\right)_{z=0}=0 \\ \left(\gamma_{x y}\right)_{z=0}=0 \end{array}\right. $ | (5) |
薄板的小扰度弯曲问题是对位移进行求解,因此选取扰度w(x, y)作为未知函数,对式(2)中的z变量积分可得扰度w表示的纵向位移u和v[19],即
| $ \left\{ {\begin{array}{*{20}{l}} {u = - z\frac{{\partial w}}{{\partial x}} + {f_1}(x,y)}\\ {v = - z\frac{{\partial w}}{{\partial y}} + {f_2}(x,y)} \end{array}} \right. $ | (6) |
式中f1(x, y)和f2(x, y)为任意函数,进一步由式(4)可得
| $ \left\{\begin{array}{l} u=-z \frac{\partial w}{\partial x} \\ v=-z \frac{\partial w}{\partial y} \end{array}\right. $ | (7) |
弹性力学的基本方程包括平衡方程、物理方程、几何方程和协调方程等。本文选用其中的物理方程和几何方程进行相关推导。根据薄板小扰度弯曲近似理论的假设条件(1)和(2)可知,应变εz、γzx和γzy忽略不计,则由弹性力学的几何方程可得到扰度w表示的主要应变分量,即
| $ \left\{ {\begin{array}{*{20}{l}} {{\varepsilon _x} = \frac{{\partial u}}{{\partial x}} = - z\frac{{{\partial ^2}w}}{{\partial {x^2}}}}\\ {{\varepsilon _y} = \frac{{\partial v}}{{\partial y}} = - z\frac{{{\partial ^2}w}}{{\partial {y^2}}}}\\ {{\gamma _{xy}} = \frac{{\partial v}}{{\partial x}} + \frac{{\partial u}}{{\partial y}} = - 2z\frac{{{\partial ^2}w}}{{\partial x\partial y}}} \end{array}} \right. $ | (8) |
根据薄板弯曲理论的假设条件,弹性力学的广义胡克定律可进一步表示为
| $ \left\{\begin{array}{l} \varepsilon_{x}=\frac{1}{E}\left(\sigma_{x}-\mu \sigma_{y}\right) \\ \varepsilon_{y}=\frac{1}{E}\left(\sigma_{y}-\mu \sigma_{x}\right) \\ \gamma_{x y}=\frac{2(1+\mu)}{E} \tau_{x y} \end{array}\right. $ | (9) |
式中:E表示杨氏模量;μ表示泊松比。将式(9)变形得到
| $ \left\{\begin{array}{l} \sigma_{x}=\frac{E}{1-\mu^{2}}\left(\varepsilon_{x}+\mu \varepsilon_{y}\right) \\ \sigma_{y}=\frac{E}{1-\mu^{2}}\left(\mu \varepsilon_{x}+\varepsilon_{y}\right) \\ \tau_{x y}=\frac{E}{2(1+\mu)} \gamma_{x y} \end{array}\right. $ | (10) |
Roberts[13]提出层面曲率的计算方法,即采用最小二乘法或应用其他的近似法,拟合一个二次曲面,得到地层面的趋势函数,进而估算地层面上某点的曲率分量。其二元二次方程为
| $ w(x, y)=a x^{2}+b y^{2}+c x y+d x+e y+f $ | (11) |
计算曲面某一点曲率的方法有多种,其中分波数的傅氏分析法,利用傅里叶变换的微分性质,将空间域的某变量变换到波数域,乘以-ik因子后再经过傅氏反变换得到该变量在空间域的一阶导数[21-26]。根据地层倾角的定义可知,曲面的一阶导数和二阶导数分别表示地层的视倾角及其一阶导数,利用地层的视倾角及其一阶导数可以计算拟合曲面方程中系数a~e。计算公式[13]为
| $ \left\{\begin{array}{l} a=\frac{1}{2} \frac{\partial^{2} w}{\partial x^{2}}=\frac{1}{2} \frac{\partial p}{\partial x} \\ b=\frac{1}{2} \frac{\partial^{2} w}{\partial y^{2}}=\frac{1}{2} \frac{\partial q}{\partial y} \\ c=\frac{1}{2} \frac{\partial^{2} w}{\partial x \partial y}=\frac{1}{2} \frac{\partial q}{\partial x}+\frac{1}{2} \frac{\partial p}{\partial y} \\ d=\frac{\partial w}{\partial x}=p \\ e=\frac{\partial w}{\partial y}=q \end{array}\right. $ | (12) |
式中p和q为x和y方向地层的视倾角属性。由于各种曲率(如高斯曲率、平均曲率、极大曲率、极小曲率、最大正曲率和最小负曲率等)的计算公式中没有包含系数f,因此无需对f进行计算。在求取拟合曲面方程的系数后,可以计算各种曲率。本文只需要计算最大正曲率和最小负曲率
| $ \left\{\begin{array}{l} K_{\mathrm{pos}}=a+b+\sqrt{(a-b)^{2}+c^{2}} \\ K_{\mathrm{neg}}=a+b-\sqrt{(a-b)^{2}+c^{2}} \end{array}\right. $ | (13) |
式中Kpos、Kneg分别表示最大正曲率、最小负曲率。在薄板小扰度弯曲理论的假设条件下,薄板中平面内各点在不同方向上的曲率与扰度w的关系可以近似表示为[27]
| $ \left\{\begin{array}{l} K_{x}=-\frac{\partial^{2} w}{\partial x^{2}}=-2 a \\ K_{y}=-\frac{\partial^{2} w}{\partial y^{2}}=-2 b \\ K_{x y}=-\frac{\partial^{2} w}{\partial x \partial y}=-c \end{array}\right. $ | (14) |
式中Kx、Ky和Kxy分别为x、y方向的曲率和xOy面的扭率,由式(8)、式(14)可得
| $ \left\{\begin{array}{l} \varepsilon_{x}=-z \frac{\partial^{2} w}{\partial x^{2}}=z K_{x} \\ \varepsilon_{y}=-z \frac{\partial^{2} w}{\partial y^{2}}=z K_{y} \\ \gamma_{x y}=-2 z \frac{\partial^{2} w}{\partial x \partial y}=2 z K_{x y} \end{array}\right. $ | (15) |
由式(10)可得
| $ \left\{\begin{array}{l} \sigma_{x}=\frac{E z}{1-\mu^{2}}\left(K_{x}+\mu K_{y}\right) \\ \sigma_{y}=\frac{E z}{1-\mu^{2}}\left(\mu K_{x}+K_{y}\right) \\ \tau_{x y}=\frac{E z}{1+\mu} K_{x y} \end{array}\right. $ | (16) |
由曲率的性质可知,当地层向上凸起时,曲率为正,地层所受的应力为张应力;当地层向下凹陷时,曲率为负,地层所受的应力为压应力。为了与地质力学体系一致,本文规定张应力为负,压应力为正[28]。
1.4 基于曲率属性的构造应力计算公式| $ \left\{ {\begin{array}{*{20}{l}} {{\sigma _{\max }} = \frac{{{\sigma _x} + {\sigma _y}}}{2} + \sqrt {{{\left( {\frac{{{\sigma _x} - {\sigma _y}}}{2}} \right)}^2} + \tau _{xy}^2} }\\ {\tan \alpha = \frac{{{\sigma _{\max }} - {\sigma _x}}}{{{\tau _{xy}}}}}\\ {{\sigma _{\min }} = \frac{{{\sigma _x} + {\sigma _y}}}{2} - \sqrt {{{\left( {\frac{{{\sigma _x} - {\sigma _y}}}{2}} \right)}^2} + \tau _{xy}^2} }\\ {\tan \beta = \frac{{{\tau _{xy}}}}{{{\sigma _{\min }} - {\sigma _y}}}} \end{array}} \right. $ | (17) |
式中:σmax、σmin分别为最大、最小主应力;α为σmax与x轴的夹角;β为σmin与y轴的夹角。
最大正曲率和最小负曲率是描述裂缝、挠曲、褶皱和断层较有效的曲率属性[29]。为了更好地利用曲率属性表征地层中的主应力,将式(14)代入式(16),得
| $ \left\{\begin{array}{l} \sigma_{x}=-\frac{2 E z}{1-\mu^{2}}(a+\mu b) \\ \sigma_{y}=-\frac{2 E z}{1-\mu^{2}}(\mu a+b) \\ \tau_{x y}=-\frac{E z}{1+\mu} c \end{array}\right. $ | (18) |
由式(13)、式(17)和式(18)经过一系列推导可以得到地层主应力与最大正曲率、最小负曲率之间关系的表达式
| $ \left\{\begin{array}{l} \sigma_{\max }=-\frac{E z}{1-\mu^{2}}\left(K_{\mathrm{neg}}+\mu K_{\mathrm{pos}}\right) \\ \sigma_{\min }=-\frac{E z}{1-\mu^{2}}\left(K_{\mathrm{pos}}+\mu K_{\mathrm{neg}}\right) \end{array}\right. $ | (19) |
由于式(17)、式(19)是在线弹性模型(薄板弯曲理论的假设条件)下推导得到的,而实际地层在构造形变过程中是弹塑性形变,因此在薄板弯曲理论假设条件下估算的构造应力是一种简单的近似简化过程,忽略了地层塑性形变的影响。由式(19)可以得到最大和最小水平主应力变化差与最大水平主应力的比值
| $ T=\frac{\sigma_{\max }-\sigma_{\min }}{\sigma_{\max }}=\frac{(1-\mu)\left(K_{\operatorname{neg}}-K_{\mathrm{pos}}\right)}{K_{\mathrm{neg}}+\mu K_{\mathrm{pos}}} $ | (20) |
最大、最小主应力之间的差异越大,岩石越易于发生破裂而形成裂缝。
1.5 岩石力学参数反演根据式(19)估算构造应力,除了要提取曲率属性,还要利用叠前地震资料反演岩石力学参数。本文采用基于弹性阻抗反演的岩石力学参数叠前地震反演方法获得杨氏模量和泊松比。
宗兆云等[30-31]、印兴耀等[32-33]在Aki-Richards反射系数近似方程的基础上,推导了YPD近似方程,该方程是纵波反射系数与杨氏模量、泊松比及密度等反射系数的线性关系
| $ \begin{aligned} R(\theta)=&\left(\frac{1}{4} \sec ^{2} \theta-2 k \sin ^{2} \theta\right) \frac{\Delta E}{\bar{E}}+\\ &\left[\frac{1}{4} \frac{(2 k-3)(2 k-1)^{2}}{k(4 k-3)} \sec ^{2} \theta+\right.\\ &\left.2 k\left(\frac{2 k-1}{4 k-3}\right) \sin ^{2} \theta\right] \frac{\Delta \mu}{\bar{\mu}}+\left(\frac{1}{2}-\frac{1}{4} \sec ^{2} \theta\right) \frac{\Delta \rho}{\bar{\rho}} \end{aligned} $ | (21) |
式中:θ为入射角;
| $ \begin{array}{*{20}{c}} {\frac{1}{2}\Delta \ln ({\rm{BEI}}) = \left( {\frac{1}{4}{{\sec }^2}\theta - 2k{{\sin }^2}\theta } \right)\frac{{\Delta E}}{{\bar E}} + }\\ {\left[ {\frac{1}{4}\frac{{(2k - 3){{(2k - 1)}^2}}}{{k(4k - 3)}}{{\sec }^2}\theta + } \right.}\\ {\left. {2k\left( {\frac{{2k - 1}}{{4k - 3}}} \right){{\sin }^2}\theta } \right]\frac{{\Delta \mu }}{{\bar \mu }} + \left( {\frac{1}{2} - \frac{1}{4}{{\sec }^2}\theta } \right)\frac{{\Delta \rho }}{{\bar \rho }}} \end{array} $ | (22) |
式中BEI表示脆性弹性阻抗。在界面两侧介质的参数差异较小时,可用微分转换关系表示,即
| $ \frac{\Delta x}{\bar{x}}=\Delta \ln x $ | (23) |
式中:x代指E、μ、ρ等参数;Δx为界面上下介质某个参数之差;x为界面上下介质对应参数的均值。变换式(22),再积分并做指数化和标准化处理,可得到以杨氏模量、泊松比及密度表征的弹性阻抗标准化方程
| $ \operatorname{BEI}(\theta)=\operatorname{BEI}_{0}\left(\frac{E}{E_{0}}\right)^{a(\theta)}\left(\frac{\mu}{\mu_{0}}\right)^{b(\theta)}\left(\frac{\rho}{\rho_{0}}\right)^{c(\theta)} $ | (24) |
其中
| $ \left\{\begin{aligned} a(\theta)=& \frac{1}{4} \sec ^{2} \theta-2 k \sin ^{2} \theta \\ b(\theta)=& \frac{1}{4} \frac{(2 k-3)(2 k-1)^{2}}{k(4 k-3)} \sec ^{2} \theta+\\ & 2 k\left(\frac{2 k-1}{4 k-3}\right) \sin ^{2} \theta \\ c(\theta)=& \frac{1}{2}-\frac{1}{4} \sec ^{2} \theta \end{aligned}\right. $ |
式中BEI0、E0、μ0和ρ0分别是入射角为0°时BEI、E、μ和ρ的平均值。
对式(24)两边取对数,得到易于求解的线性化形式为[30-31]
| $ \ln \frac{\operatorname{BEI}(\theta)}{\operatorname{BEI}_{0}}=a(\theta) \ln \frac{E}{E_{0}}+b(\theta) \ln \frac{\mu}{\mu_{0}}+c(\theta) \ln \frac{\rho}{\rho_{0}} $ | (25) |
基于式(25)构建的方程组,利用叠前弹性阻抗反演得到的弹性阻抗数据体及测井数据等资料,可以得到任意采样点的杨氏模量和泊松比。将得到的杨氏模量和泊松比代入到构造应力计算公式(式(19))中,结合基于局部τ-p变换的曲率属性提取方法[22]得到的曲率及地层厚度z,就可以估算地层的构造应力。
与传统的构造应力求取公式(式(16)和式(17))相比较,本文方法不需要计算Kx、Ky和Kxy参数。目前Kx、Ky和Kxy参数通常不能由商业软件直接提取,需编写相关程序计算拟合曲面方程(式(11))的系数进而得到。而最大正曲率和最小负曲率属性可通过主流商业软件直接获得。因此,本文方法实用、简单易行。
2 应用实例将本文方法应用于中国东部某页岩段(S层)裂缝型油气藏区。研究区内发育一系列北东向、北西向及近东西向的断裂,断裂附近的裂缝较为发育。裂缝呈“X”型或树状,裂缝密度西部较东部大。
为了验证本文方法,对比两种方法求取构造应力的效果。
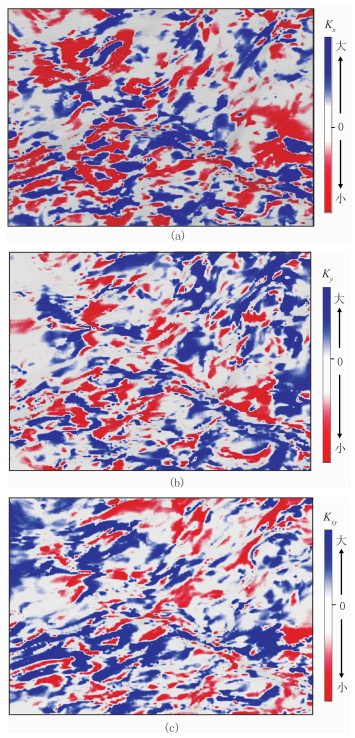
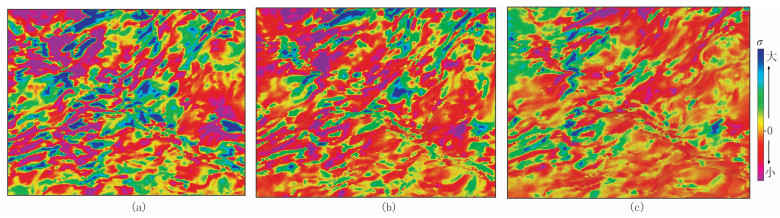
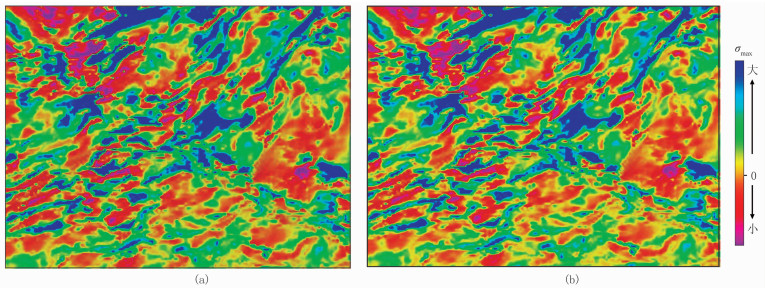
按照前人传统方法,提取Kx、Ky和Kxy(图 2);结合叠前地震反演得到的杨氏模量和泊松比,通过式(16)求得σx、σy和σxy(图 3);最后基于式(17)求取S层最大主应力(图 4a)。
|
图 2 S层Kx(a)、Ky(b)和Kxy(c)沿层切片 |
|
图 3 S层σx(a)、σy(b)和σxy(c)沿层切片 |
|
图 4 不同方法得到的S层最大主应力沿层切片对比 (a)传统方法;(b)本文方法 |
利用本文地层曲率属性的提取方法求得最大正曲率、最小负曲率属性(图 5)。应用叠前地震反演的岩石力学参数获取储层的杨氏模量和泊松比,根据式(19)求取S层最大主应力(图 4b)。
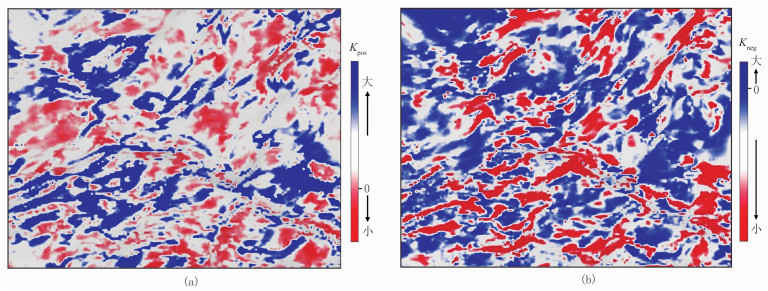
|
图 5 S层最大正曲率(a)和最小负曲率(b)沿层切片 |
从图 4可以看出,两种方法计算得到的构造应力沿层切片结果基本一致。
由于本文方法所用的式(19)是基于前人方法的式(17)推导得到的,在推导过程中没有采用近似简化的过程,直接表达了曲率属性与构造应力之间的关系,因此本文方法所得到的构造应力沿层切片与前人方法得到的构造应力切片基本一致,从而证明了本文方法的正确性。
3 结束语在薄板弯曲理论的假设条件下,研究了曲率属性与构造应力之间的定量关系,推导了利用最大正曲率和最小负曲率属性表征构造应力的计算公式,提出了直接利用提取的最大正曲率和最小负曲率属性估算地层构造主应力的方法。
该方法利用相关商业软件就可以得到所需的最大正曲率和最小负曲率属性,不需要通过提取x、y方向的曲率和xOy面的扭率计算相应的应力分量进而求取构造应力,更加实用、简单易行。
| [1] |
李志明, 张金珠. 地应力与油气勘探开发[M]. 北京: 石油工业出版社, 1997. LI Zhiming, ZHANG Jinzhu. In-situ Stress and Petroleum Exploration and Development[M]. Beijing: Petroleum Industry Press, 1997. |
| [2] |
张胜利. 构造应力场模拟——有限元理论、方法和研究进展[J]. 西北地震学报, 2010, 32(4): 405-410. ZHANG Shengli. Modeling of tectonic stress field:the theory, method and related research progress of the finite element method[J]. Northwestern Seismological Journal, 2010, 32(4): 405-410. |
| [3] |
谭成轩, 王连捷, 孙宝珊, 等. 含油气盆地三维构造应力场数值模拟方法[J]. 地质力学学报, 1997, 3(1): 71-80. TAN Chengxuan, WANG Lianjie, SUN Baoshan, et al. An approach to numerical simulation of 3-D tectonic stress field of the oil-gas-bearing basin[J]. Journal of Geomechanics, 1997, 3(1): 71-80. |
| [4] |
陈书平, 戴俊生, 宋全友, 等. 胶莱盆地构造应力场特征及数学模拟[J]. 石油大学学报(自然科学版), 1998, 22(3): 19-25. CHEN Shuping, DAI Junsheng, SONG Quanyou, et al. Features of tectonic stress fields in Jiaolai basin[J]. Journal of the University of Petroleum, China (Edition of Natural Science), 1998, 22(3): 19-25. |
| [5] |
张帆, 贺振华, 黄德济, 等. 预测裂隙发育带的构造应力场数值模拟技术[J]. 石油地球物理勘探, 2000, 35(2): 154-163. ZHANG Fan, HE Zhenhua, HUANG Deji, et al. Structural stress field numerical simulation technique for fracture zone prediction[J]. Oil Geophysical Prospecting, 2000, 35(2): 154-163. DOI:10.3321/j.issn:1000-7210.2000.02.003 |
| [6] |
王红才, 王薇, 王连捷, 等. 油田三维构造应力场数值模拟与油气运移[J]. 地球学报, 2002, 23(2): 175-178. WANG Hongcai, WANG Wei, WANG Lianjie, et al. Three dimensional tectonic stress field and migration of oil and gas in Tanhai[J]. Acta Geoscientica Sinica, 2002, 23(2): 175-178. DOI:10.3321/j.issn:1006-3021.2002.02.014 |
| [7] |
雷景生. 油藏构造应力场的数值模拟技术研究[J]. 海南大学学报自然科学版, 2004, 22(1): 28-32. LEI Jingsheng. The study of numerical value simulation for oil store tectonic stress field[J]. Natural Science Journal of Hainan University, 2004, 22(1): 28-32. |
| [8] |
王连捷, 王红才, 王薇, 等. 油田三维构造应力场、裂缝与油气运移[J]. 岩石力学与工程学报, 2004, 23(23): 4052-4057. WANG Lianjie, WANG Hongcai, WANG Wei, et al. Relation among three dimensional tectonic stress field, fracture and migration of oil and gas in oil field[J]. Chinese Journal of Rock Mechanics and Engineering, 2004, 23(23): 4052-4057. DOI:10.3321/j.issn:1000-6915.2004.23.024 |
| [9] |
付玉华, 王兴明, 袁海平. 构造应力场边界载荷反演的有限元逆逼近法[J]. 岩土力学, 2009, 30(6): 1850-1855. FU Yuhua, WANG Xingming, YUAN Haiping. Finite element inverse analysis of boundary load for tectonic stress field[J]. Rock and Soil Mechanics, 2009, 30(6): 1850-1855. DOI:10.3969/j.issn.1000-7598.2009.06.056 |
| [10] |
董培育, 程惠红, 石耀霖, 等. 基于Monte Carlo方法数值反演区域初始构造应力场——以巴颜喀拉块体为例[J]. 地球物理学报, 2019, 62(8): 2858-2870. DONG Peiyu, CHENG Huihong, SHI Yaolin, et al. Numerical inversion of regional initial tectonic stress based on Monte Carlo method:A case study of BayanHar block[J]. Chinese Journal of Geophysics, 2019, 62(8): 2858-2870. |
| [11] |
Price N J, Cosgrove J W. Analysis of Geological Structures[M]. Cambridge: Cambridge University Press, 1990.
|
| [12] |
Sheorey P R. A theory for in situ, stresses in isotropic and transverseley isotropic rock[J]. International Journal of Rock Mechanics and Mining Sciences, 1994, 31(1): 23-34. DOI:10.1016/0148-9062(94)92312-4 |
| [13] |
Roberts A. Curvature attributes and their application to 3D interpreted horizons[J]. First Break, 2001, 19(2): 85-100. DOI:10.1046/j.0263-5046.2001.00142.x |
| [14] |
Sigismondi E A, Soldo C J. Curvature attributes and seismic interpretation:Case studies from Argentina basins[J]. The Leading Edge, 2003, 22(1): 1122-1126. |
| [15] |
刘建伟, 张云银, 曾联波, 等. 非常规油藏地应力和应力甜点地球物理预测——渤南地区沙三下亚段页岩油藏勘探实例[J]. 石油地球物理勘探, 2016, 51(4): 792-800. LIU Jianwei, ZHANG Yunyin, ZENG Lianbo, et al. Geophysical prediction of stress and stress desserts in unconventional reservoirs:an example in Bonan area[J]. Oil Geophysical Prospecting, 2016, 51(4): 792-800. |
| [16] |
孟阳, 许颖玉, 李静叶, 等. OVT域地震资料属性分析技术在断裂精细识别中的应用[J]. 石油地球物理勘探, 2018, 53(增刊2): 289-294. MENG Yang, XU Yingyu, LI Jingye, et al. Fault identification with OVT-domain seismic attribute analysis[J]. Oil Geophysical Prospecting, 2018, 53(S2): 289-294. |
| [17] |
王玲玲, 魏建新, 黄平, 等. 依托物理模型的叠后裂缝敏感地震属性优选与应用[J]. 石油地球物理勘探, 2019, 54(1): 127-136. WANG Lingling, WEI Jianxin, HUANG Ping, et al. Fracture-sensitive poststack seismic attribute optimization based on the physical model[J]. Oil Geophysical Prospecting, 2019, 54(1): 127-136. |
| [18] |
何英.高精度曲率分析方法及其在构造识别中的应用[D].四川成都: 成都理工大学, 2011. HE Ying.High Precision Curvature Analysis and its Application of Structural Identification[D].Chengdu University of Technology, Chengdu, Sichuan, 2011. |
| [19] |
陆基孟, 王永刚. 地震勘探原理[M]. 山东东营: 中国石油大学出版社, 2009. LU Jimeng, WANG Yonggang. The Principle of Seismic Exploration[M]. Dongying, Shandong: China University of Petroleum Press, 2009. |
| [20] |
徐芝纶. 弹性力学(第4版)[M]. 北京: 高等教育出版社, 2006. XU Zhilun. Elasticity[M]. Beijing: Higher Education Press, 2006. |
| [21] |
Al-Dossary S, Marfurt K J. 3D volumetric multispectral estimates of reflector curvature and rotation[J]. Geophysics, 2006, 71(5): P41-P51. DOI:10.1190/1.2242449 |
| [22] |
王欣.基于局部tau-p变换的地震几何属性提取及融合方法研究[D].山东青岛: 中国石油大学(华东), 2016. WANG Xin.The Study of Seismic Geometry Attribute and Image Fusion Methods Based on Local Tau-p Transformation[D].China University of Petroleum(East China), Qingdao, Shandong, 2016. |
| [23] |
印兴耀, 高京华, 宗兆云. 基于离心窗倾角扫描的曲率属性提取[J]. 地球物理学报, 2014, 57(10): 3411-3421. YIN Xingyao, GAO Jinghua, ZONG Zhaoyun. Curvature attribute based on dip scan with eccentric window[J]. Chinese Journal of Geophysics, 2014, 57(10): 3411-3421. DOI:10.6038/cjg20141027 |
| [24] |
印兴耀, 周静毅. 地震属性优化方法综述[J]. 石油地球物理勘探, 2005, 40(4): 482-489. YIN Xingyao, ZHOU Jingyi. Summary of optimum methods of seismic attributes[J]. Oil Geophysical Prospecting, 2005, 40(4): 482-489. DOI:10.3321/j.issn:1000-7210.2005.04.027 |
| [25] |
张广智, 陈娇娇, 陈怀震. 基于页岩岩石物理等效模型的地应力预测方法研究[J]. 地球物理学报, 2015, 58(6): 2112-2122. ZHANG Guangzhi, CHEN Jiaojiao, CHEN Huaizhen, et al. Prediction for in-situ formation stress of shale based on rock physics equivalent model[J]. Chinese Journal of Geophysics, 2015, 58(6): 2112-2122. |
| [26] |
葛洪魁, 林英松, 王顺昌. 地应力测试及其在勘探开发中的应用[J]. 石油大学学报(自然科学版), 1998, 22(1): 94-99. GE Hongkui, LIN Yingsong, WANG Shunchang. In-situ stresses determination technique and its applications in petroleum exploration and development[J]. Journal of the University of Petroleum, China (Edition of Natural Science), 1998, 22(1): 94-99. |
| [27] |
曾锦光, 罗元华, 陈太源. 应用构造面主曲率研究油气藏裂缝问题[J]. 力学学报, 1982, 2(2): 202-206. ZENG Jinguang, LUO Yuanhua, CHEN Taiyuan. A method for the study of reservoir fracturing based on structural principal curvatures[J]. Chinese Journal of Theoretical and Applied Mechanics, 1982, 2(2): 202-206. |
| [28] |
许艳秋.基于应力场分析的叠前裂缝检测[D].四川成都: 成都理工大学, 2015. XU Yanqiu.Prestack Fracture Prediction Based on Tectonic Stress Field[D].Chengdu University of Technology, Chengdu, Sichuan, 2015. |
| [29] |
肖普拉S, 马弗特K J著; 李建雄, 夏义平, 柯宗强, 等译.地震属性在有利圈闭识别和油藏表征中的应用[M].北京: 石油工业出版社, 2012.
|
| [30] |
宗兆云, 印兴耀, 张峰, 等. 杨氏模量和泊松比反射系数近似公式及叠前地震反演[J]. 地球物理学报, 2012, 55(11): 3786-3794. ZONG Zhaoyun, YIN Xingyao, ZHANG Feng, et al. Reflection coefficient equation and pre-stack seismic inversion with Young's modulus and Poisson ratio[J]. Chinese Journal of Geophysics, 2012, 55(11): 3786-3794. DOI:10.6038/j.issn.0001-5733.2012.11.025 |
| [31] |
宗兆云, 印兴耀, 吴国忱. 基于叠前地震纵横波模量直接反演的流体检测方法[J]. 地球物理学报, 2012, 55(1): 284-292. ZONG Zhaoyun, YIN Xingyao, WU Guochen. Fluid identification method based on compressional and shear modulus direct inversion[J]. Chinese Journal of Geophysics, 2012, 55(1): 284-292. DOI:10.6038/j.issn.0001-5733.2012.01.028 |
| [32] |
印兴耀, 宗兆云, 吴国忱. 岩石物理驱动下地震流体识别研究[J]. 中国科学:地球科学, 2015, 45(1): 8-21. ZONG Zhaoyun, YIN Xingyao, WU Guochen. Research on seismic fluid identification driven by rock physics[J]. Science China:Earth Sciences, 2015, 45(1): 8-21. |
| [33] |
印兴耀, 曹丹平, 王保丽, 等. 基于叠前地震反演的流体识别方法研究进展[J]. 石油地球物理勘探, 2014, 49(1): 22-34, 46. YIN Xingyao, CAO Danping, WANG Baoli, et al. Research progress of fluid discrimination with pre-stack seismic inversion[J]. Oil Geophysical Prospecting, 2014, 49(1): 22-34, 46. |



 印兴耀, 山东省青岛市经济开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
印兴耀, 山东省青岛市经济开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: