② 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071
② Evaluation and Detection Technology Laboratory for Marine Mineral Resources, Qingdao, Shandong 266071, China
各向异性是沉积岩中普遍存在的现象[1]。在地震数据处理中,尤其在面对复杂构造时,常常假设地球介质为各向同性,但是地球介质多呈各向异性,因此需要研究各向异性介质的物理性质。沉积岩的地震各向异性多呈速度各向异性[2],人们广泛研究了与此有关的正、反演问题[3-11]。
Delay[12]推导了TI介质中精确的速度与波传播方程。Thomsen[1]提出了3个各向异性参数ε、δ和γ,大大简化了上述方程,由于适用条件的限制,称为弱各向异性方程。Alkalifah等[13]提出了表征椭圆各向异性的参数η。类比于VTI介质的Thomsen参数,Rüger等[14]引入了一套表征HTI介质的各向异性参数。Tsvankin[15]进一步将Thomsen参数推广到正交各向异性(OA)介质。牛滨华等[16]认为在一般情况下,ε和γ的单调性是一致的,即同时增减或为0。Sarout等[17]通过实验研究了Callovo-Oxfordian页岩弹性波速度各向异性。李磊等[18]提出了常见的TI介质的Thomsen参数约束条件,避免了无物理意义的研究结果。苏云等[19]讨论了弱各向异性介质地震波传播特征。姚振岸等[20]分析了对称轴呈任意空间取向的TI(ATI)介质弹性波速度特征。梁锴等[21]阐述了倾斜椭球各向异性介质弹性波传播特征。李勤等[22]论述了垂向裂隙各向异性煤层地震响应特征。
在各向异性近似的研究方面,梁锴等[23]利用弱各向异性近似和介质分解理论,推导了TTI介质qP波入射的近似反射、透射系数。吴国忱等[24]利用介质分解理论和地震波扰动理论,在保留各向异性一阶扰动量的基础上,建立了地震各向异性参数和岩石力学参数间的近似方程,可预测各向异性岩石的力学参数。梁锴等[25]从TTI介质弹性波相速度精确公式出发,推导了TTI介质qP波和qSV波相速度的一般性近似表达式。
本文提出VTI介质弹性波相速度的扩展各向异性线性近似,即在相速度精确表达式函数曲线与扩展各向异性线性近似函数曲线切点处(下称切点,附录A)进行一阶Taylor展开,构造雅可比矩阵,得到扩展各向异性线性近似公式。该方法通过改变线性近似的切点,使扩展各向异性线性近似适用于各向异性较强的情况。同时给出了相应数值示例,分析了介质各向异性程度不同时扩展各向异性线性近似的适用性。
1 方法与原理 1.1 VTI介质精确弹性波相速度VTI介质有5个独立的弹性常数,分别为C11、C33、C44、C66、C13。Delay[12]推导的弹性波相速度公式为
| $ \left\{\begin{array}{l} V_{\mathrm{P}}(\theta)=\sqrt{\frac{1}{2 \rho}\left[C_{33}+C_{44}+\left(C_{11}-C_{33}\right) \sin ^{2} \theta+D(\theta)\right]} \\ V_{\mathrm{SV}}(\theta)=\sqrt{\frac{1}{2 \rho}\left[C_{33}+C_{44}+\left(C_{11}-C_{33}\right) \sin ^{2} \theta-D(\theta)\right]} \\ V_{\mathrm{SH}}(\theta)=\sqrt{\frac{1}{\rho}\left(C_{66} \sin ^{2} \theta+C_{44} \cos ^{2} \theta\right)} \end{array}\right. $ | (1) |
式中:θ为传播角;ρ为介质密度;而
| $ \begin{array}{*{20}{c}} {D(\theta ) = \left\{ {{{\left[ {\left( {{C_{11}} - {C_{44}}} \right){{\sin }^2}\theta - \left( {{C_{33}} - {C_{44}}} \right){{\cos }^2}\theta } \right]}^2} + } \right.}\\ {{{\left. {{{\left( {{C_{13}} + {C_{44}}} \right)}^2}{{\sin }^2}2\theta } \right\}}^{\frac{1}{2}}}} \end{array} $ | (2) |
Thomsen[1]提出了以下各向异性参数
| $ \left\{\begin{array}{l} \alpha_{0}=\sqrt{\frac{C_{33}}{\rho}} \\ \beta_{0}=\sqrt{\frac{C_{44}}{\rho}} \\ \varepsilon=\frac{C_{11}-C_{33}}{2 C_{33}} \\ \gamma=\frac{C_{66}-C_{44}}{2 C_{44}} \\ \delta=\frac{\left(C_{13}+C_{44}\right)^{2}-\left(C_{33}-C_{44}\right)^{2}}{2 C_{33}\left(C_{33}-C_{44}\right)} \end{array}\right. $ | (3) |
式中:α0、β0分别为qP波和qS波垂直TI介质各向同性面的相速度;ε、δ和γ为表征TI介质各向异性强度的三个无量纲因子,其中ε是度量qP波各向异性强度的参数,δ是影响TI介质对称轴方向附近的qP波速度的参数,γ是度量qS波各向异性强度或横波分裂强度的参数。使用Thomsen参数改写式(1),得
| $ \left\{\begin{array}{l} V_{\mathrm{P}}(\theta)=\alpha_{0} \sqrt{1+\varepsilon \sin ^{2} \theta+D^{*}(\theta)} \\ V_{\mathrm{SV}}(\theta)=\beta_{0} \sqrt{1+\frac{\alpha_{0}^{2}}{\beta_{0}^{2}} \varepsilon \sin ^{2} \theta-\frac{\alpha_{0}^{2}}{\beta_{0}^{2}} D^{*}(\theta)} \\ V_{\mathrm{SH}}(\theta)=\beta_{0} \sqrt{1+2 \gamma \sin ^{2} \theta} \end{array}\right. $ | (4) |
式中
| $ {D^*}(\theta ) = \frac{f}{2}\left\{ {{{\left[ {1 + \frac{{2\delta - \varepsilon }}{f}{{\sin }^2}2\theta + \frac{{4(f + \varepsilon )\varepsilon }}{{{f^2}}}{{\sin }^4}\theta } \right]}^{\frac{1}{2}}} - 1} \right\} $ | (5) |
而
| $ f=1-\frac{\beta_{0}^{2}}{\alpha_{0}^{2}} $ | (6) |
通过观察发现,尽管矿物成分可能是高度各向异性的,但是大多数岩石只呈微弱的各向异性[1]。式(4)虽然用各向异性参数表征相速度,但难以看出该式的物理意义。在各向异性参数的绝对值远小于1的情况下,Thomsen[1]在各向异性参数等于0时,将式(4)Taylor展开,并保留一阶项,得到VTI介质弱各向异性弹性波相速度近似方程
| $ \left\{\begin{array}{l} V_{\mathrm{P}}(\theta)=\alpha_{0}\left(1+\delta \sin ^{2} \theta \cos ^{2} \theta+\varepsilon \sin ^{4} \theta\right) \\ V_{\mathrm{SV}}(\theta)=\beta_{0}\left[1+\frac{\alpha_{0}^{2}}{\beta_{0}^{2}}(\varepsilon-\delta) \sin ^{2} \theta \cos ^{2} \theta\right] \\ V_{\mathrm{SH}}(\theta)=\beta_{0}\left(1+\gamma \sin ^{2} \theta\right) \end{array}\right. $ | (7) |
式(7)形式简洁,相速度为ε、δ和γ的线性函数,且
| $ \left\{\begin{array}{l} \varepsilon=\frac{V_{\mathrm{P}}\left(90^{\circ}\right)-\alpha_{0}}{\alpha_{0}} \\ \delta=4\left[\frac{V_{\mathrm{P}}\left(45^{\circ}\right)}{V_{\mathrm{P}}\left(0^{\circ}\right)}-1\right]-\left[\frac{V_{\mathrm{P}}\left(90^{\circ}\right)}{V_{\mathrm{P}}\left(0^{\circ}\right)}-1\right] \\ \gamma=\frac{V_{\mathrm{SH}}\left(90^{\circ}\right)-\beta_{0}}{\beta_{0}} \end{array}\right. $ | (8) |
由式(8)可见:ε反映了纵波速度各向异性强度,ε越大,纵波速度的各向异性越强,ε等于0时,纵波速度呈各向同性;γ反映了横波速度各向异性强度;δ只与VP(0°)、VP(45°)和VP(90°)有关。
1.3 扩展各向异性线性近似本文提出了扩展各向异性线性近似,即在切点(ε0, δ0, γ0)处进行一阶Taylor展开,构造雅可比矩阵,得到扩展各向异性线性近似公式。首先根据式(4)对各向异性参数求一阶偏导数,得
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{{\partial {V_{\rm{P}}}}}{{\partial \varepsilon }} = \frac{{\alpha _0^2{{\sin }^2}\theta \left[ {1 + \left( {\frac{{2\varepsilon }}{f}{{\sin }^2}\theta - \cos 2\theta } \right)m(\theta )} \right]}}{{2{V_{\rm{P}}}(\theta )}}}\\ {\frac{{\partial {V_{\rm{P}}}}}{{\partial \delta }} = \frac{{m(\theta )\alpha _0^2{{\sin }^2}\theta {{\cos }^2}\theta }}{{{V_{\rm{P}}}(\theta )}}}\\ {\frac{{\partial {V_{{\rm{SV}}}}}}{{\partial \varepsilon }} = \frac{{\alpha _0^2{{\sin }^2}\theta \left[ {1 - \left( {\frac{{2\varepsilon }}{f}{{\sin }^2}\theta - \cos 2\theta } \right)m(\theta )} \right]}}{{2{V_{{\rm{SV}}}}(\theta )}}}\\ {\frac{{\partial {V_{{\rm{SV}}}}}}{{\partial \delta }} = - \frac{{m(\theta )\alpha _0^2{{\sin }^2}\theta {{\cos }^2}\theta }}{{{V_{{\rm{SV}}}}(\theta )}}}\\ {\frac{{\partial {V_{{\rm{SH}}}}}}{{\partial \gamma }} = \frac{{\beta _0^2{{\sin }^2}\theta }}{{{V_{{\rm{SH}}}}(\theta )}}} \end{array}} \right. $ | (9) |
式中
| $ m(\theta)=\left[1+\frac{(2 \delta-\varepsilon) \sin ^{2} 2 \theta}{f}+\frac{4 \varepsilon \sin ^{4} \theta(f+\varepsilon)}{f^{2}}\right]^{-\frac{1}{2}} $ | (10) |
使用在切点(ε0, δ0, γ0)处的一阶偏导数构成雅可比矩阵
| $ \mathit{\boldsymbol{J}}(\theta ) = \left[ {\begin{array}{*{20}{c}} {\frac{{\partial {V_{\rm{P}}}}}{{\partial {\varepsilon _0}}}}&{\frac{{\partial {V_{\rm{p}}}}}{{\partial {\delta _0}}}}&0\\ {\frac{{\partial {V_{{\rm{sv}}}}}}{{\partial {\varepsilon _0}}}}&{\frac{{\partial {V_{{\rm{sv}}}}}}{{\partial {\delta _0}}}}&0\\ 0&0&{\frac{{\partial {V_{{\rm{sH}}}}}}{{\partial {\gamma _0}}}} \end{array}} \right] $ | (11) |
因此,式(4)变为
| $ \left[\begin{array}{c} V_{\mathrm{P}}(\theta) \\ V_{\mathrm{sv}}(\theta) \\ V_{\mathrm{SH}}(\theta) \end{array}\right] \approx \boldsymbol{J}(\theta)\left[\begin{array}{c} \varepsilon-\varepsilon_{0} \\ \delta-\delta_{0} \\ \gamma-\gamma_{0} \end{array}\right]+\left[\begin{array}{c} V_{\mathrm{P} 0}(\theta) \\ V_{\mathrm{SV} 0}(\theta) \\ V_{\mathrm{SH} 0}(\theta) \end{array}\right] $ | (12) |
式中VP0(θ)、VSV0(θ)和VSH0(θ)为式(4)在切点(ε0, δ0, γ0)处的值。式(12)为VTI介质扩展各向异性线性近似弹性波相速度公式。
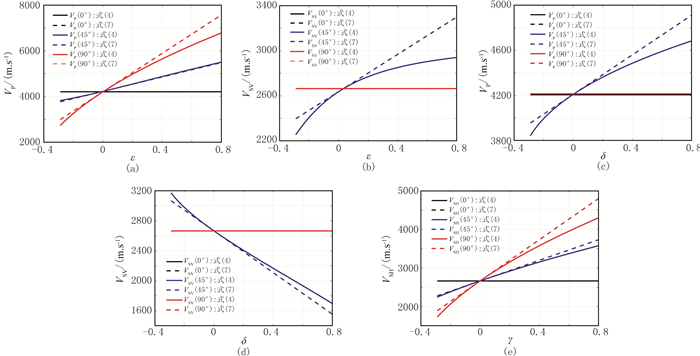
2 数值示例 2.1 弱各向异性线性近似适用性分析本文分析了各向异性参数变化对理论相速度和弱各向异性线性近似相速度的影响。以Berea砂岩[1]为例(表 1),在ε、δ和γ中只有一个发生变化时,绘制弹性波精确相速度(式(4))和弱各向异性线性近似相速度(式(7))随各向异性参数的变化曲线(图 1),其中θ分别为0°、45°和90°。分析图 1可知:
|
|
表 1 Berea砂岩的各向异性参数表[1] |
|
图 1 Berea砂岩速度随各向异性参数变化曲线 (a)VP-ε;(b)VSV-ε;(c)VP-δ;(d)VSV-δ;(e)VSH-γ |
(1) 式(7)是式(4)在切点(0, 0, 0)的线性近似,无论各向异性参数小于0还是大于0,在一般情况下如果各向异性参数的绝对值增大,式(4)与式(7)计算结果的差异变大。
(2) δ对θ为0°和45°时的qP波和qSV波的速度无影响(图 1c、图 1d)。
(3) 式(7)在各向异性参数的绝对值小于0.2时拟合精度很高,由式(7)与式(4)计算的相速度曲线几乎重合。
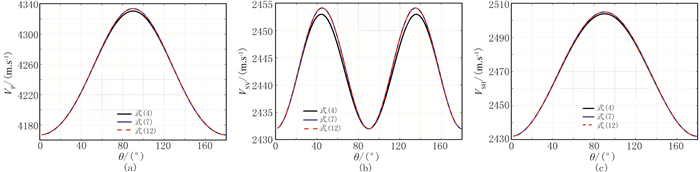
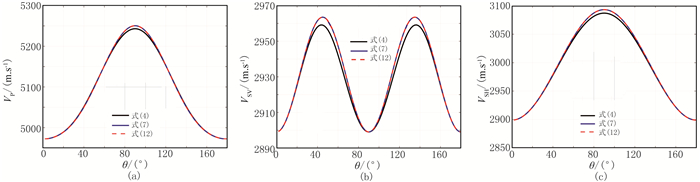
2.2 各向异性参数绝对值较小时情况Thomsen[1]给出的弱各向异性线性近似的条件为各向异性参数的绝对值小于0.2,故本文也将其定义为弱各向异性线性近似适用条件。选取三种各向异性参数绝对值较小的岩石模型(表 2),分别利用式(4)、式(7)和扩展各向异性线性近似弹性波相速度公式(式(12))计算弹性波相速度(图 2~图 4)。
|
|
表 2 各向异性参数绝对值较小的岩石模型参数[1] |

|
图 2 由不同方法计算的Berea砂岩弹性波相速度曲线 (a)VP(θ);(b)VSV(θ);(c)VSH(θ) |
|
图 3 由不同方法计算的Green River页岩弹性波相速度曲线 (a)VP(θ);(b)VSV(θ);(c)VSH(θ) |
|
图 4 由不同方法计算的Silty灰岩弹性波相速度曲线 (a)VP(θ);(b)VSV(θ);(c)VSH(θ) |
由图 2~图 4可见:在Thomsen[1]弱各向异性近似适用条件下,式(7)、式(12)均与式(4)的拟合度很高,并且由式(7)和式(12)得到弹性波相速度曲线基本重合,说明当切点为(0, 0, 0)时两者的计算结果基本相同。
2.3 各向异性参数绝对值较大时情况选取二种各向异性参数绝对值较大(绝对值大于0.2)的岩石模型(表 3),利用式(4)、式(7)和式(12)计算弹性波相速度及其相对误差(图 5~图 8)。
|
|
表 3 各向异性参数绝对值较大的岩石模型参数[1] |

|
图 5 由不同方法计算的Calcareous砂岩弹性波相速度曲线
(a)VP(θ);(b)VSV(θ);(c)VSH(θ) 式(12)在切点处的各向异性参数分别为ε0=0、δ0=-0.3, γ0=0 |

|
图 6 由不同方法计算的Calcareous砂岩弹性波相速度曲线相对误差 (a)VP(θ);(b)VSV(θ);(c)VSH(θ) |
|
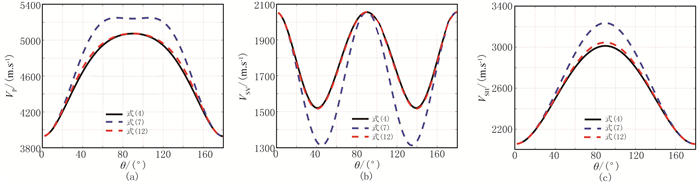
图 7 由不同方法计算的Mesaverde泥页岩弹性波相速度曲线
(a)VP(θ);(b)VSV(θ);(c)VSH(θ) 式(12)在切点处的各向异性参数分别为ε0=0.3、δ0=0.3和γ0=0.3 |

|
图 8 由不同方法计算的Mesaverde泥页岩弹性波相速度曲线相对误差 (a)VP(θ);(b)VSV(θ);(c)VSH(θ) |
图 5、图 6分别为由不同方法计算的Calcareous砂岩弹性波相速度曲线及其相对误差。由图可见:①由式(12)得到的VP和VSV的精度明显高于式(7)(图 5a、图 5b、图 6a、图 6b),如由式(12)得到的VP和VSV的最大相对误差分别为0.10%、-0.13%,由式(7)得到的VP和VSV的最大相对误差分别为1.51%、-1.78%;②由式(7)和式(12)得到的VSH的精度相同,最大相对误差均为0.0025%(图 5c、图 6c),这是由于VSH的各向异性只与γ有关,且Calcareous砂岩的γ在弱各向异性适用范围内所致。
图 7、图 8分别为由不同方法计算的Mesaverde泥页岩弹性波相速度曲线及其相对误差。由图可见:在Mesaverde泥页岩的各向异性参数绝对值大于0.2的情况下(表 3),由式(12)得到的VP、VSV和VSH的精度明显高于式(7),如由式(12)得到的VP、VSV和VSH的最大相对误差分别为0.46%、-0.35%、0.89%,由式(7)得到的VP、VSV和VSH的最大相对误差分别为4.83%、-12.49%、6.87%。
3 讨论弱各向异性线性近似是在切点(0, 0, 0)处对弹性波精确相速度方程的一种线性近似,所以当各向异性参数的绝对值增大时,弱各向异性线性近似所得结果的误差也会相应地变大。当各向异性参数的绝对值很小时,弱各向异性线性近似所得结果的精确度很高,此时认为介质的各向异性较弱。
针对某些各向异性较强的岩石,如Mesaverde泥页岩,因为部分各向异性参数绝对值很大,所以由弱各向异性线性近似计算的相速度有较大误差。在该情况下,弱各向异性线性近似的误差大,可以使用扩展各向异性线性近似。
至于切点的选取问题,笔者认为,在各向异性较强的情况下可以选取各向异性参数的绝对值在0.2~0.8范围的点作为切点,因为Thomsen[1]的强各向异性岩石的各向异性参数大多位于该范围,本文选择的切点处的各向异性参数的绝对值均为0.3。如果选择的切点处的各向异性参数的绝对值太小,由扩展各向异性线性近似与弱各向异性线性近似得到的结果几乎完全一致;如果选择的切点处的各向异性参数的绝对值太大,会失去物理意义。某些矿物的各向异性极强,如部分水晶的各向异性参数的绝对值甚至超过1,对这种矿物可以适当地在各向异性参数绝对值较大处做切线。
在岩石物理实验中由测得的声波速度估算岩石样本各向异性参数时,可根据扩展各向异性线性近似公式快速估算各向异性参数近似值,且速度快,稳定性较好。另一方面,可以以扩展各向异性线性近似公式为理论基础,探讨中强各向异性介质分界面处的反射、透射特征及其近似公式,期望为后续AVO分析、AVO反演、阻抗反演等提供基础。
4 结论本文从VTI介质弹性波精确相速度公式出发,在切点处进行一阶Taylor展开,构造雅可比矩阵,推导了VTI介质弹性波相速度的扩展各向异性线性近似公式。该方法通过调节线性近似的切点,可以适用于各向异性较强的情况。理论分析和数值示例表明:当各向异性参数绝对值较小时,弱各向异性线性近似和扩展各向异性线性近似所得结果均与理论值吻合较好;当各向异性参数绝对值较大时,弱各向异性线性近似所得结果与理论值偏差较大,扩展各向异性线性近似所得结果与理论值吻合较好。说明扩展各向异性线性近似不但适用于各向异性参数较小的情况,而且也适用于各向异性参数较大的情况。
附录A VTI介质弹性波相速度扩展各向异性线性近似误差分析
在点(ε0,δ0,γ0)处,VP的一个切向向量为
VTI介质弹性波相速度扩展各向异性线性近似的绝对误差为
| $ \left\{\begin{aligned} \Delta V_{\mathrm{P}}(\theta)=& | \alpha_{0} \sqrt{1+\varepsilon \sin ^{2} \theta+D^{*}(\theta)}-\\ & \frac{\partial V_{\mathrm{P}}}{\partial \varepsilon_{0}}\left(\varepsilon-\varepsilon_{0}\right)-\frac{\partial V_{\mathrm{P}}}{\partial \delta_{0}}\left(\delta-\delta_{0}\right)-V_{\mathrm{P} 0}(\theta) | \\ \Delta V_{\mathrm{sv}}(\theta)=& | \beta_{0} \sqrt{1+\frac{\alpha_{0}^{2}}{\beta_{0}^{2}} \varepsilon \sin ^{2} \theta-\frac{\alpha_{0}^{2}}{\beta_{0}^{2}} D^{*}(\theta)}-\\ & \frac{\partial V_{\mathrm{SV}}}{\partial_{\varepsilon_{0}}}\left(\varepsilon-\varepsilon_{0}\right)-\frac{\partial V_{\mathrm{SV}}}{\partial \delta_{0}}\left(\delta-\delta_{0}\right)-V_{\mathrm{SV} 0}(\theta) | \\ \Delta V_{\mathrm{SH}}(\theta)=& | \beta_{0} \sqrt{1+2 \gamma \sin ^{2} \theta}-\\ & \frac{\partial V_{\mathrm{SH}}}{\partial \gamma_{0}}\left(\gamma-\gamma_{0}\right)-V_{\mathrm{SH} 0}(\theta) | \end{aligned}\right. $ | (A-1) |
弱各向异性线性近似是在点(0, 0, 0)处对弹性波精确相速度方程的一种线性近似,所以当各向异性参数的绝对值增大时,弱各向异性线性近似所得结果的误差也会相应地变大。由式(A-1)可以看出:扩展各向异性线性近似是在切点(ε0,δ0,γ0)处对弹性波精确相速度方程的一种线性近似;一定存在一个包含切点(ε0,δ0,γ0)的邻域,在该邻域内绝对误差最小(相较于其他切点的线性近似而言)。因为扩展各向异性线性近似可以选取各向异性参数的绝对值较大处作为切点,所以在各向异性参数绝对值较大的情况下,一定存在一个包含切点(ε0,δ0,γ0)的区间,使扩展各向异性线性近似的绝对误差(或相对误差)小于弱各向异性近似。
| [1] |
Thomsen L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. DOI:10.1190/1.1442051 |
| [2] |
吴国忱. 各向异性介质地震波传播与成像[M]. 山东青岛: 中国石油大学出版社, 2006. WU Guochen. Seismic Wave Propagation and Imaging in Anisotropic Media[M]. Qingdao, Shandong: China University of Petroleum Press, 2006. |
| [3] |
Crampin S. A review of wave motion in anisotropic and cracked elastic media[J]. Wave Motion, 1981, 3(4): 343-391. DOI:10.1016/0165-2125(81)90026-3 |
| [4] |
Crampin S. Suggestions for a consistent terminology for seismic anisotropy[J]. Geophysical Prospecting, 1989, 37(7): 753-770. DOI:10.1111/j.1365-2478.1989.tb02232.x |
| [5] |
Hall S A, Kendall J M, Maddock J, et al. Crack density tensor inversion for analysis of changes in rock frame architecture[J]. Geophysical Journal International, 2008, 173(2): 577-592. DOI:10.1111/j.1365-246X.2008.03748.x |
| [6] |
Sarout J, Esteban L, Delle P C, et al. Elastic anisotropy of Opalinus clay under variable saturation and triaxial stress[J]. Geophysical Journal International, 2014, 198(3): 1662-1682. DOI:10.1093/gji/ggu231 |
| [7] |
张繁昌, 桑凯恒, 路亚威. 硬币型裂缝介质的频散与衰减[J]. 石油地球物理勘探, 2019, 54(4): 836-843. ZHANG Fanchang, SANG Kaiheng, LU Yawei. Frequency dispersion and attenuation of porous rocks with penny shaped fractures[J]. Oil Geophysical Prospecting, 2019, 54(4): 836-843. |
| [8] |
王琦, 李庆春, 王芷琪. VTI介质起伏界面混合网格旅行时线性插值计算方法[J]. 石油地球物理勘探, 2018, 53(6): 1175-1187. WANG Qi, LI Qingchun, WANG Zhiqi. A linear traveitime interpolation method with hybrid meshes for VTI medium under rugged interface conditions[J]. Oil Geophysical Prospecting, 2018, 53(6): 1175-1187. |
| [9] |
吴建鲁, 吴国忱, 王伟, 等. 基于等效交错网格的流固耦合介质地震波模拟[J]. 石油地球物理勘探, 2018, 53(2): 272-279. WU Jianlu, WU Guochen, WANG Wei, et al. Seismic forward modeling in fluid-solid media based on equi-valent staggered grid scheme[J]. Oil Geophysical Prospecting, 2018, 53(2): 272-279. |
| [10] |
潘新朋, 张广智, 印兴耀. 非均质HTI介质裂缝弱度参数地震散射反演[J]. 石油地球物理勘探, 2017, 52(6): 1226-1235. PAN Xinpeng, ZHANG Guangzhi, YIN Xingyao. Seismic scattering inversion for fracture weakness in heterogeneous HTI media[J]. Oil Geophysical Prospecting, 2017, 52(6): 1226-1235. |
| [11] |
崔宁城, 黄光南, 李红星, 等. 求解椭圆各向异性介质程函方程的源点快速扫描算法[J]. 石油地球物理勘探, 2019, 54(4): 796-804. CUI Ningcheng, HUANG Guangnan, LI Hongxing, et al. A source fast sweeping method for solving elliptically anisotropic eikonal equation[J]. Oil Geophysical Prospecting, 2019, 54(4): 796-804. |
| [12] |
Daley P F. Reflection and transmission coefficients at the interface between two transversely isotropic media (Matlab software)[J]. Bulletin of the Seismological Society of America, 1977, 67(3): 661-675. |
| [13] |
Alkalifah T, Tsvankin I. Velocity analysis for trans-versely isotropic media[J]. Geophysics, 1995, 60(5): 1550-1566. DOI:10.1190/1.1443888 |
| [14] |
Rüger A, Tsvankin I. Using AVO for fracture detection:Analytic basis and practical solutions[J]. The Leading Edge, 1997, 16(10): 1429-1434. DOI:10.1190/1.1437466 |
| [15] |
Tsvankin I. Anisotropic parameters and P-wave velo-city for orthorhombic media[J]. Geophysics, 1997, 62(4): 1292-1309. DOI:10.1190/1.1444231 |
| [16] |
牛滨华, 孙春岩. 地震波理论研究进展——介质模型与地震波传播[J]. 地球物理学进展, 2004, 19(2): 255-263. NIU Binhua, SUN Chunyan. Developing theory of propagation of seismic waves:medium model and propagation of seismic waves[J]. Progress in Geophysics, 2004, 19(2): 255-263. DOI:10.3969/j.issn.1004-2903.2004.02.008 |
| [17] |
Sarout J, Guéguen Y. Anisotropy of elastic wave velocities in deformed shales:Part 1-Experimental results[J]. Geophysics, 2008, 73(5): D75-D89. DOI:10.1190/1.2952744 |
| [18] |
李磊, 郝重涛. 横向各向同性介质和斜方介质各向异性参数的约束条件[J]. 地球物理学报, 2011, 54(11): 2819-2830. LI Lei, HAO Chongtao. Constraints on anisotropic parameters in transversely isotropic media and the extensions to orthorhombic media[J]. Chinese Journal of Geophysics, 2011, 54(11): 2819-2830. DOI:10.3969/j.issn.0001-5733.2011.11.012 |
| [19] |
苏云, 李军, 唐娟, 等. 弱各向异性介质地震波传播特征分析[J]. 物探化探计算技术, 2010, 32(2): 144-148. SU Yun, LI Jun, TANG Juan, et al. Analysis of seismic wave propagation characteristics in weak anisotropic media[J]. Computing Techniques for Geophysical and Geochemical Exploration, 2010, 32(2): 144-148. DOI:10.3969/j.issn.1001-1749.2010.02.006 |
| [20] |
姚振岸, 孙成禹, 邓小凡, 等. 任意空间取向TI介质弹性波速度特征分析[J]. 石油地球物理勘探, 2017, 52(4): 715-733. YAO Zhenan, SUN Chengyu, DENG Xiaofan, et al. Velocity characteristic analysis of elastic wave for TI media with arbitrary spatial orientation[J]. Oil Geophysical Prospecting, 2017, 52(4): 715-733. |
| [21] |
梁锴, 曹丹平, 印兴耀, 等. 倾斜椭球各向异性介质弹性波传播特征[J]. 石油地球物理勘探, 2018, 53(6): 1142-1151. LIANG Kai, CAO Danping, YIN Xingyao, et al. Elastic wave propagation characteristics of anisotropic media with oblique ellipsoid[J]. Oil Geophysical Prospecting, 2018, 53(6): 1142-1151. |
| [22] |
李勤, 李永博, 李庆春. 垂向裂隙各向异性煤层地震波响应[J]. 地球物理学报, 2019, 62(1): 306-315. LI Qin, LI Yongbo, LI Qingchun. Seismic wave response of anisotropic coal seam in vertical fracture[J]. Chinese Journal of Geophysics, 2019, 62(1): 306-315. |
| [23] |
梁锴, 印兴耀, 吴国忱. TTI介质qP波入射精确和近似反射透射系数[J]. 地球物理学报, 2011, 54(1): 208-217. LIANG Kai, YIN Xingyao, WU Guochen. Exact and approximate reflection and transmission coefficient for incident qP wave in TTI media[J]. Chinese Journal of Geophysics, 2011, 54(1): 208-217. DOI:10.3969/j.issn.0001-5733.2011.01.022 |
| [24] |
吴国忱, 赵小龙, 唐杰, 等. 横观各向同性(TI)岩石弹性模量一阶扰动近似[J]. 中国科学:地球科学, 2017, 47(8): 916-926. WU Guochen, ZHAO Xiaolong, TANG Jie, et al. First-order perturbation approximation for rock elastic moduli in transversely isotropic media[J]. Scientia Sinica Terrae, 2017, 47(8): 916-926. |
| [25] |
梁锴, 金世勋, 印兴耀. TTI介质弹性波相速度的一般性近似[J]. 石油物探, 2018, 57(6): 813-822. LIANG Kai, Kim Sehun, YIN Xingyao. General appro-ximation of phase velocity for elastic waves in TTI media[J]. Geophysical Prospecting for Petroleum, 2018, 57(6): 813-822. DOI:10.3969/j.issn.1000-1441.2018.06.003 |



 梁锴, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
梁锴, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: