② 海洋国家实验室海洋矿产资源评价与探测技术功能实验室, 山东青岛 266071
② Evaluation and Detection Technology Laboratory for Marine Mineral Resources, Qingdao, Shandong 266071, China
自Knott[1]、Zoeppritz等[2]提出振幅随入射角变化的理论以来,因其理论公式结构复杂且物理意义不够明确,人们根据不同研究目的进行了简化与近似。Koefoed[3]给出了精确Zoeppritz方程关于泊松比的反射系数。基于界面上、下弹性参数变化较小的假设,Aki等[4]由散射矩阵推导出P波、SV波反射/透射系数近似表达式。
裂缝型油气藏为非常规油气勘探的重要领域,因储层中存在高角度或近似垂直的裂缝被等效为HTI介质,其地震响应呈方位各向异性特征。Rüger[5]基于Thomsen[6]理论建立了HTI介质纵、横波反射/透射系数近似公式;梁锴等[7]结合TTI介质相速度与偏振方向的关系,推导了TTI介质的弹性波反射/透射近似方程;宗兆云等[8]提出由杨氏模量与泊松比表征的纵波反射系数方程;司芗等[9]推导了TTI介质的准纵波反射系数方程;李春鹏[10]基于HTI介质刚度矩阵得到HTI介质反射/透射系数精确方程;基于介质分解理论与扰动理论,Wu等[11]对TI介质岩石弹性模量进行了一阶扰动近似;单俊臻等[12]推导了方位观测系统纵波入射情况下HTI介质纵波反射系数一阶扰动近似公式。
AVO技术依靠反射系数构建弹性参数与实际数据间的关系。朱兆林等[13]通过模型分析,对比了不同近似方程的精度。毛宁波等[14]基于Rüger近似方程分析了四类裂缝型砂岩储层模型在含油气时的方位AVO特性。
相较于纵波AVO分析,对特征相对复杂的转换波AVO的相关研究较少,实际上横波较纵波对各向异性更敏感。随AVO技术的发展与多波、多分量地震勘探技术的应用,纵、横波资料相结合的重要性逐渐凸显。常规地震勘探中通常利用PP波近似公式获取地层弹性参数,但精度不高。联合转换波与纵波反射系数一阶近似公式进行AVO分析,通过振幅变化信息可获得更精确的储层信息。业界从入射角与反射系数关系出发,分析转换波AVO特征。Bortfeld[15]基于界面参数差异微弱假设,率先推导了PSV波反射系数近似式。Donati等[16]基于Aki近似,得到了体现速度与密度相对变化的转换波近似公式。郑晓东[17-18]、杨绍国等[19]提出由入射角的正弦函数组成的幂级数表示的转换波近似式。李正文等[20]利用PSV波AVO分析方法,获得了横波速度信息与密度信息。Ramos等[21]基于Aki近似方程,给出了幂级数形式的反射系数公式。孙鹏远[22]结合截距梯度理论,提出新的转换波AVO理论体系。唐旭东等[23]讨论了不同转换波近似公式的推导方法及精度。各类近似方程在大入射角情况下,大都无法准确描述转换波振幅变化规律,且由于地震数据随方位变化,对于PSV波方位反射系数的研究也相对薄弱。
本文基于HTI介质反射/透射系数精确表达式,根据介质分解理论与扰动思想,在弱各向异性假设条件下,推导了PSV波反射系数近似表达式,通过正演模拟分析振幅随方位的变化特征,并讨论方位转换波反射系数对各向异性参数的敏感性。在保证与Aki近似方程精度相近的条件下,补充了方位维度,为转换波的方位特征分析及相关弹性参数反演提供了理论基础,可进一步联合纵波方位地震资料准确地预测储层。
1 HTI介质PSV波反射系数一阶近似中深部层系受构造运动与压实作用等影响,多发育有高角度或近垂直排列的裂缝,在弱各向异性假设下,将描述VTI介质的Thomsen各向异性参数进行角度变换(对称轴旋转90°),转化为描述HTI介质的各向异性参数。对比Rüger[5]与Thomsen[6]的各向异性参数表达式可知,两者的横向各向异性介质表达式一致,但刚度矩阵不同。
HTI介质刚度矩阵元素在各向异性参数较小时可由弱各向异性参数δ(V)、ε(V)、γ(V)表述
| $ \left\{\begin{array}{l} c_{11}=\rho \alpha^{2}\left[1+2 \varepsilon^{(\mathrm{V})}\right] \\ c_{13} \approx \rho \alpha^{2}\left[1+2 \delta^{(\mathrm{V})}\right]-2 \rho \beta^{2}\left[1+2 \gamma^{(\mathrm{V})}\right] \\ c_{23}=c_{33}-2 c_{44}=\rho\left(\alpha^{2}-2 \beta^{2}\right) \\ c_{33}=\rho \alpha^{2} \\ c_{44}=\rho \beta^{2} \\ c_{66}=\rho \beta^{2}\left[1+\gamma^{(\mathrm{V})}\right] \end{array}\right. $ | (1) |
式中:δ(V)与准纵波在垂直方向传播和沿45°入射角传播时的各向异性有关;ρ为介质密度参数;α为垂直入射P波速度;β为垂直入射SH波速度。
由HTI介质反射/透射系数精确方程[10]可得P波入射时散射矩阵R与相关系数矩阵M、N关系的精确方程
| $ \mathit{\boldsymbol{MR}} = \mathit{\boldsymbol{N}} $ | (2) |
即
| $ \left[ {\begin{array}{*{20}{l}} {{M_{11}}}&{{M_{12}}}&{{M_{13}}}&{{M_{14}}}&{{M_{15}}}&{{M_{16}}}\\ {{M_{21}}}&{{M_{22}}}&{{M_{23}}}&{{M_{24}}}&{{M_{25}}}&{{M_{26}}}\\ {{M_{31}}}&{{M_{32}}}&{{M_{33}}}&{{M_{34}}}&{{M_{35}}}&{{M_{36}}}\\ {{M_{41}}}&{{M_{42}}}&{{M_{43}}}&{{M_{44}}}&{{M_{45}}}&{{M_{46}}}\\ {{M_{51}}}&{{M_{52}}}&{{M_{53}}}&{{M_{54}}}&{{M_{55}}}&{{M_{56}}}\\ {{M_{61}}}&{{M_{62}}}&{{M_{63}}}&{{M_{64}}}&{{M_{65}}}&{{M_{66}}} \end{array}} \right]\left[ {\begin{array}{*{20}{c}} {{R_{{\rm{PP}}}}}\\ {{R_{{\rm{PSV}}}}}\\ {{R_{{\rm{PSH}}}}}\\ {{T_{{\rm{PP}}}}}\\ {{T_{{\rm{PSV}}}}}\\ {{T_{{\rm{PSH}}}}} \end{array}} \right] = \left[ {\begin{array}{*{20}{c}} {{N_1}}\\ {{N_2}}\\ {{N_3}}\\ {{N_4}}\\ {{N_5}}\\ {{N_6}} \end{array}} \right] $ | (3) |
M、N的矩阵元素与入射波、散射波相关,由弹性矩阵元素、纵横波速度及三角函数构成;R的矩阵元素为各波型的反射(RPP、RPSV、RPSH) /透射(TPP、TPSV、TPSH)系数。
基于扰动理论对式(2)线性化处理,将弹性参数与各向异性参数进行扰动近似,使式(2)线性化。假设两套地层弹性界面处储层参数差异较小,将各向异性程度较低的围岩介质视为均匀各向同性背景项,把弹性参数以及各向异性参数的变化视为扰动项,则R、M、N可分解为背景项与扰动项之和
| $ \left\{ {\begin{array}{*{20}{l}} {\mathit{\boldsymbol{M}} = {\mathit{\boldsymbol{M}}^{\rm{u}}} + \Delta \mathit{\boldsymbol{M}}}\\ {\mathit{\boldsymbol{R}} = {\mathit{\boldsymbol{R}}^{\rm{u}}} + \Delta \mathit{\boldsymbol{R}}}\\ {\mathit{\boldsymbol{N}} = {\mathit{\boldsymbol{N}}^{\rm{u}}} + \Delta {\bf{N}}} \end{array}} \right. $ | (4) |
式中:Mu、Ru、Nu为背景项,描述不受方位影响的弹性参数;ΔM、ΔR、ΔN为扰动项,描述弹性参数扰动变化与各向异性参数变化。
当qP波非垂直入射到HTI介质地层弹性界面时,产生反射qP波、反射qSV波、反射qSH波、透射qP波、透射qSV波、透射qSH波(图 1)。设入射角为θ、方位角为φ,将地震波相速度与偏振方向分解为背景项与一阶扰动项,在弱各向异性条件下,忽略各向异性参数高阶项,则qP波、qSV波、qSH波相速度分别为
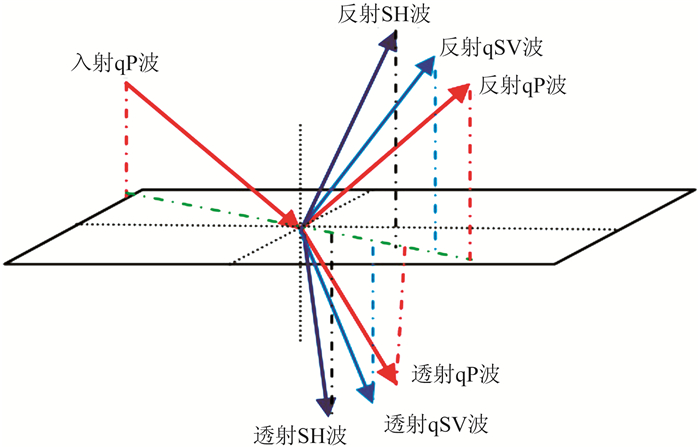
|
图 1 qP波入射到单界面时的反射、透射示意图 |
| $ \left\{\begin{aligned} \alpha_{\mathrm{P}}(\theta, \varphi) \approx & \alpha\left\{1+\delta^{(\mathrm{V})} \sin ^{2} \theta \cos ^{2} \varphi+\right.\\ &\left.\left[\varepsilon^{(\mathrm{V})}-\delta^{(\mathrm{V})}\right] \sin ^{4} \theta \cos ^{4} \varphi\right\} \\ \beta_{\mathrm{SV}}(\theta, \varphi) \approx & \beta\left\{1+\gamma^{(\mathrm{V})}+\frac{\alpha^{2}}{\beta^{2}}\left[\varepsilon^{(\mathrm{V})}-\delta^{(\mathrm{V})}\right] \times\right.\\ &\left.\sin ^{2} \theta \cos ^{2} \varphi+\sin ^{4} \theta \cos ^{4} \varphi\right\} \end{aligned}\right. $ | (5a) |
| $ \beta_{\mathrm{SH}}(\theta, \varphi) \approx \beta\left[1+\gamma^{(\mathrm{V})} \sin ^{2} \theta \cos ^{2} \varphi\right] $ | (5b) |
将式(5)代入Christoffel方程得到HTI介质精确偏振方向表达式,将梁锴等[7]推导的TI介质地震波近似偏振方向进行角度变换,得到HTI介质偏振方向
| $ \left\{ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{P}}_{{\rm{qP}}}} = c\left( {\begin{array}{*{20}{l}} {\sin \theta \cos \varphi + \left( {G\cos \theta + \sin \theta {{\sin }^2}\varphi } \right)Ef[\delta + 2(\varepsilon - \delta )F]}\\ {\sin \theta \sin \varphi + {E^2}f[\delta + 2(\varepsilon - \delta )F]\sin \theta \sin \varphi }\\ {\cos \theta - Ef[\delta + 2(\varepsilon - \delta )F]G\sin \theta \cos \varphi } \end{array}} \right)}\\ {{\mathit{\boldsymbol{P}}_{{\rm{qSV}}}} = c\left( {\begin{array}{*{20}{l}} {G\cos \theta + {{\sin }^2}\theta {{\sin }^2}\varphi - EFf[\delta + 2(\varepsilon - \delta )F]\sin \theta \cos \varphi }\\ {E\sin \theta \sin \varphi + EFf[\delta + 2(\varepsilon - \delta )F]\sin \theta \sin \varphi }\\ { - G\sin \theta \cos \varphi - EFf[\delta + 2(\varepsilon - \delta )F]\cos \theta } \end{array}} \right)}\\ {{\mathit{\boldsymbol{P}}_{{\rm{SH}}}} = c\left( {\begin{array}{*{20}{c}} 0\\ { - \cos \theta }\\ {\sin \theta \sin \varphi } \end{array}} \right)} \end{array}} \right. $ | (6) |
式中ε、γ、δ为Thomsen[6]各向异性参数,与Rüger[5]各向异性参数存在以下关系
| $ \left\{\begin{array}{l} \delta^{(\mathrm{V})}=\delta-2 \varepsilon \\ \varepsilon^{(\mathrm{V})}=-\varepsilon \\ \gamma^{(\mathrm{V})}=-\gamma \end{array}\right. $ |
通过调整常数c以保证地震波偏振方向x分量为正。式(6)中
| $ \left\{\begin{array}{l} E=-\sin \theta \cos \varphi \\ F=\cos ^{2} \theta+\sin ^{2} \theta \sin ^{2} \varphi \\ G=\cos \theta \\ f=\frac{\alpha^{2}}{\alpha^{2}-\beta^{2}}=\left(1-\frac{\beta^{2}}{\alpha^{2}}\right)^{-1}=\frac{1}{f^{\prime}} \end{array}\right. $ | (7) |
同理,各弹性参数及角度在弱各向异性条件下,可表征为背景项与扰动项
| $ \left\{ {\begin{array}{*{20}{c}} {{\alpha _1} = \alpha - \frac{{\Delta \alpha }}{2}}\\ {{\alpha _2} = \alpha + \frac{{\Delta \alpha }}{2}}\\ {{\beta _1} = \beta - \frac{{\Delta \beta }}{2}}\\ {{\beta _2} = \beta + \frac{{\Delta \beta }}{2}}\\ {{\rho _1} = \rho - \frac{{\Delta \rho }}{2}}\\ {{\rho _2} = \rho + \frac{{\Delta \rho }}{2}}\\ {{\theta _{{\rm{P}}1}} = {\theta _{\rm{p}}} - \frac{{\Delta {\theta _{\rm{P}}}}}{2}}\\ {{\theta _{{\rm{P}}2}} = {\theta _{\rm{P}}} + \frac{{\Delta {\theta _{\rm{P}}}}}{2}}\\ {{\theta _{{\rm{SV}}1}} = {\theta _{{\rm{SV}}}} - \frac{{\Delta {\theta _{{\rm{SV}}}}}}{2}}\\ {{\theta _{{\rm{SV}}2}} = {\theta _{{\rm{SV}}}} + \frac{{\Delta {\theta _{{\rm{SV}}}}}}{2}}\\ {{\theta _{{\rm{SH}}1}} = {\theta _{{\rm{SH}}}} - \frac{{\Delta {\theta _{{\rm{SH}}}}}}{2}}\\ {{\theta _{{\rm{SH}}2}} = {\theta _{{\rm{SH}}}} + \frac{{\Delta {\theta _{{\rm{SH}}}}}}{2}} \end{array}} \right. $ | (8) |
式(7)和式(8)中: α、β、ρ、θP、θSV及θSH分别表示垂直入射时纵波速度、横波速度、密度及P波、SV波、SH波的入射/反射角均值;下标1、2分别代表界面上、下介质;Δ表示取界面上、下参数差值。
保留弹性参数一阶项,则
| $ \mathit{\boldsymbol{R}} = {\mathit{\boldsymbol{R}}^{\rm{u}}} + {\left( {{\mathit{\boldsymbol{M}}^{\rm{u}}}} \right)^{ - 1}}\left( {\Delta \mathit{\boldsymbol{N}} - \Delta \mathit{\boldsymbol{M}}{\mathit{\boldsymbol{R}}^{\rm{u}}}} \right) $ | (9) |
由于围岩呈各向同性,不存在反射波,故入射纵波产生透射纵波的透射系数为1,各向同性介质的反射/透射系数矩阵为
| $ {\mathit{\boldsymbol{R}}^{\rm{u}}} = {\left( {{\mathit{\boldsymbol{M}}^{\rm{u}}}} \right)^{ - 1}} \cdot {\mathit{\boldsymbol{N}}^{\rm{u}}} = {\left[ {\begin{array}{*{20}{l}} 0&0&0&1&0&0 \end{array}} \right]^{\rm{T}}} $ | (10) |
将式(10)代入式(9),得反射系数为
| $ \mathit{\boldsymbol{R}} = {\left[ {\begin{array}{*{20}{l}} {\Delta {R_1}}&{\Delta {R_2}}&{\Delta {R_3}}&{1 + \Delta {R_4}}&{\Delta {R_5}}&{\Delta {R_6}} \end{array}} \right]^{\rm{T}}} $ | (11) |
式中的矩阵元素依次表示P、PSV、PSH波反射/透射系数的一阶近似扰动量。
忽略各向异性高阶项并化简,得
| $ R_{\mathrm{PSV}}=\Delta R_{2} $ | (12) |
结合小入射角近似条件,得到P波入射情况下PSV波反射系数公式
| $ \begin{array}{l} R_{\mathrm{PSV}}(\theta, \varphi)=-\frac{\Delta \rho}{\rho} \frac{\sin \theta_{\mathrm{P}}}{2 \cos \theta_{\mathrm{SV}}}\left[2 k \cos \theta_{\mathrm{P}}+\right. \\ \left.\left(1-2 k^{2} \sin ^{2} \theta_{\mathrm{P}}\right) \frac{1}{\cos \theta_{\mathrm{SV}}}\right]-\frac{\Delta \beta}{\beta} \frac{\sin \theta_{\mathrm{P}}}{\cos \theta_{\mathrm{SV}}} \times \\ \left(-2 k \cos \theta_{\mathrm{P}}+2 k^{2} \sin ^{2} \theta_{\mathrm{P}} \frac{1}{\cos \theta_{\mathrm{SV}}}\right)- \\ \Delta \gamma \cdot 2 \cos \varphi\left[\tan \theta_{\mathrm{SV}} \cos \theta_{\mathrm{P}}+\right. \\ \left.k^{2} \sin ^{3} \theta_{\mathrm{P}} \cos ^{2} \varphi\left(1+k^{2} \sin ^{2} \theta_{\mathrm{P}} \cos ^{2} \varphi\right)\right]+ \\ \Delta \delta\left\{\sin \theta_{\mathrm{P}} \frac{\cos \varphi}{2 k+2}-\sin ^{3} \theta_{\mathrm{P}} \frac{(k+3) \cos ^{3} \varphi}{2 k+2}+\right. \\ \left.\sin ^{5} \theta_{\mathrm{P}} \frac{\cos ^{3} \varphi\left[\left(2 k^{2}-1\right) \cos ^{3} \varphi+k^{3}-k^{2}+1\right]}{2 k^{2}-2}\right\}+ \\ \Delta \varepsilon\left(\sin ^{3} \theta_{\mathrm{P}} \frac{\cos ^{3} \varphi}{k+1}-\sin ^{5} \theta_{\mathrm{P}} \frac{\cos ^{5} \varphi}{2}\right) \end{array} $ | (13) |
式中k为横纵波速度之比。当入射角较小时,忽略三角函数3次方以上高阶项,则式(13)简化为
| $ \begin{array}{l} R_{\mathrm{PSV}}(\theta, \varphi)=-\frac{\Delta \rho}{\rho} \frac{\sin \theta_{\mathrm{P}}}{2 \cos \theta_{\mathrm{SV}}}\left[2 k \cos \theta_{\mathrm{P}}+\right. \\ \left.\left(1-2 k^{2} \sin ^{2} \theta_{\mathrm{P}}\right) \frac{1}{\cos \theta_{\mathrm{SV}}}\right]- \\ \frac{\Delta \beta}{\beta} \frac{\sin \theta_{\mathrm{P}}}{\cos \theta_{\mathrm{SV}}}\left(-2 k \cos \theta_{\mathrm{P}}+2 k^{2} \sin ^{2} \theta_{\mathrm{P}} \frac{1}{\cos \theta_{\mathrm{SV}}}\right)- \\ \Delta \gamma\left[2 \cos \varphi\left(\tan \theta_{\mathrm{SV}} \cos \theta_{\mathrm{P}}+k^{2} \sin ^{3} \theta_{\mathrm{P}} \cos ^{2} \varphi\right)\right]+ \\ \Delta \delta\left[\sin \theta_{\mathrm{P}} \cos \varphi\left(\frac{1}{2 k+2}-\sin ^{2} \theta_{\mathrm{P}} \frac{(k+3) \cos ^{2} \varphi}{2 k+2}\right)\right]+ \\ \Delta \varepsilon\left(\sin ^{3} \theta_{\mathrm{P}} \frac{\cos ^{3} \varphi}{k+1}\right) \end{array} $ | (14) |
考虑各向同性介质,式(13)退化为平面PS波反射系数
| $ \begin{array}{l} {R_{{\rm{PSV}}}}\left( \theta \right) = - \frac{{\Delta \rho }}{\rho } \times \\ \frac{{\sin {\theta _{\rm{P}}}}}{{2\cos {\theta _{{\rm{SV}}}}}}\left[ {2k\cos {\theta _{\rm{P}}} + \left( {1 - 2{k^2}{{\sin }^2}{\theta _{\rm{P}}}} \right)\frac{1}{{\cos {\theta _{{\rm{SV}}}}}}} \right] - \\ \frac{{\Delta \beta }}{\beta }\left( { - \frac{{k\sin 2{\theta _{\rm{P}}}}}{{\cos {\theta _{{\rm{SV}}}}}} + \frac{{2{k^2}{{\sin }^3}{\theta _{\rm{P}}}}}{{{{\cos }^2}{\theta _{{\rm{SV}}}}}}} \right) \end{array} $ | (15) |
在小入射角的近似条件下,式(13)与Aki等[4]及Rüger[5]的各向同性公式形式相同。由于式(13)~式(15)中不含纵波速度相对变化量,因此PSV波不受上、下界面纵波速度变化的影响。
综上所述,转换波AVO信息较PP波信息更单纯,某些特性优于PP波[20]。
2 HTI介质PSV波反射系数一阶近似正演分析PSV波反射系数方程由各向同性参数项与各向异性参数项组成,两部分对反射系数影响程度不同。在小入射角情况下,反射系数主要受各向同性参数项控制,各向异性参数项因其系数包含三角函数项而影响微弱,随入射角逐渐增大,各向异性参数影响逐渐增大。由于式(13)在小角度入射条件下可与Aki近似式相互转化,故两者的区别在于各向异性参数部分。反射系数曲线特征与精度差异也由方位各向异性参数项引起。式(13)与Aki近似式、Rüger近似式的各向同性参数项相近,但各向异性参数项的表述形式不同。随方位角逐渐增大至90°,PSV波反射系数仅由横波速度与介质密度控制,各向异性参数对反射系数影响逐渐减弱,各反射曲线间的差异逐渐减小。
为验证式(13)的精度,设计方位观测HTI介质三层模型(图 2)进行正演分析,将式(13)、精确方程、Aki近似公式、Rüger近似公式得到反射系数曲线进行对比。
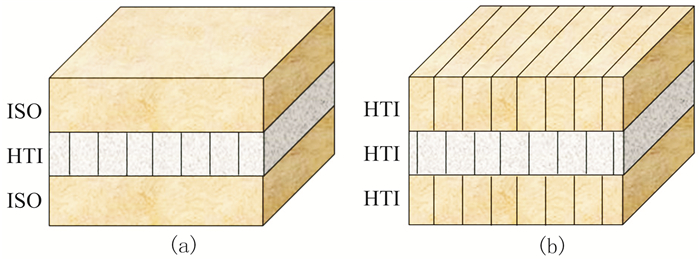
|
图 2 方位观测HTI介质三层模型 (a)模型Ⅰ;(b)模型Ⅱ假设上、下HTI介质对称轴同向,且与测线方向平行 |
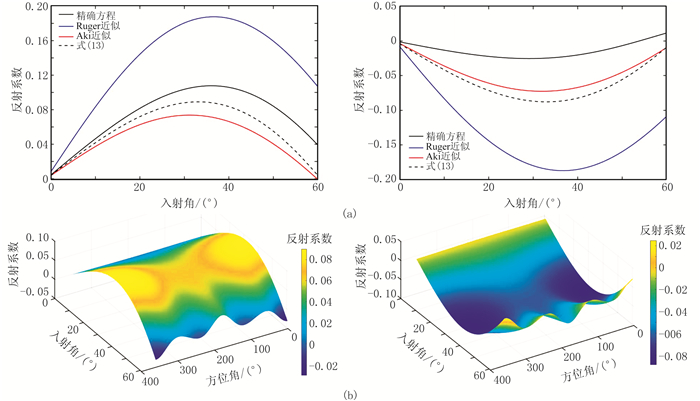
表 1为模型Ⅰ的介质弹性参数。图 3为方位角为0°、30°、60°时模型Ⅰ的PSV波反射系数曲线。由图可见,不同反射系数近似式在小入射角时精度较高,随入射角增大,各近似式的反射系数与精确方程产生不同程度的差异,表现为:①对于上界面,式(13)的精度高于Rüger近似式、低于Aki近似式;由于式(13)忽略了各向异性参数正弦函数高阶项,在入射角较小时与Aki近似式的反射系数曲线趋势不同,随方位角增大,两者的反射系数曲线趋势趋于一致(图 3a)。②对于下界面,在小入射角时式(13)与Aki近似式精度相近,在大入射时式(13)的精度略低于Aki近似式、高于Ruger近似式;随着方位角的增大,式(13)与Aki近似式的反射系数曲线趋势趋于一致(图 3b)。
|
|
表 1 模型Ⅰ的介质弹性参数 |
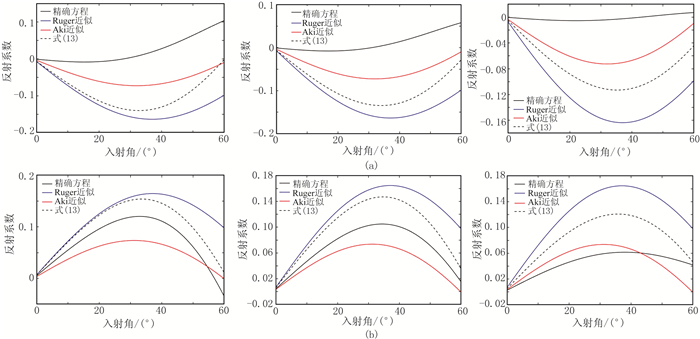
|
图 3 方位角为0°(左)、30°(中)、60°(右)时模型Ⅰ的PSV波反射系数曲线 (a)上界面;(b)下界面 |
图 4为模型Ⅰ的PSV波反射系数曲面。由图可见:在小入射角情况下,上、下界面反射系数曲面波动不大,即反射系数随方位角变化特征不明显;随入射角逐渐增大,方位变化特征愈加明显。由于地层等效为HTI介质,假设测线方向与水平对称轴同向,则平行对称轴方向(方位角为0°)时反射系数随入射角变化幅度最大,垂直对称轴方向(方位角为90°)时反射系数随入射角变化幅度最小。可根据这种方位差异分析PSV波方位AVO特征并进行相关地震资料解释。
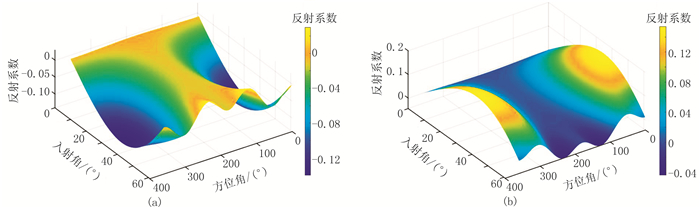
|
图 4 模型Ⅰ的PSV波反射系数曲面 (a)上界面;(b)下界面 |
表 2为模型Ⅱ的介质弹性参数。图 5为模型Ⅱ上、下界面PSV波反射系数曲线、反射系数曲面。由图可见,当界面两侧均为HTI介质时,式(13)仍然适用,在小入射角时式(13)的精度高于中、大入射角;与模型Ⅰ类似,反射系数随方位角的变化特征不明显,随入射角增大,方位特征愈加明显。表现为:①对于上界面,式(13)精度高于Rüger近似式、与Aki近似式相近;式(13)、Rüger近似式与精确方程反射系数曲线拟合程度更高,原因在于Aki近似式仅含各向同性参数项,故在界面上、下均为HTI介质情况下,Aki近似式与精确方程差异更大(图 5a左)。②对于下界面,式(13)与Aki近似式间的差异随方位角增大而减小,即各向异性参数对反射系数影响减小;当方位角增大至90°时,各向异性参数对反射系数无影响,反射系数完全由横波速度与密度的相对变化项控制(图 5a右)。③上、下界面都出现在小入射角时反射系数曲面方位特征不明显现象,随入射角增大,反射系数随方位角变化特征愈加明显;当界面上、下介质各向异性参数差越大时,反射系数随方位变化越明显(图 5b)。
|
|
表 2 模型Ⅱ的介质弹性参数 |
|
图 5 模型Ⅱ上(左)、下(右)界面PSV波反射系数曲线(a)、反射系数曲面(b) |
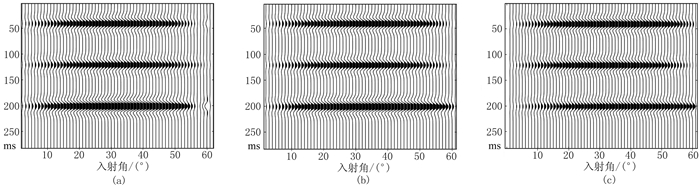
构建HTI介质单界面模型(弹性参数与模型Ⅱ下界面相同),利用主频为30Hz的雷克子波与式(13)、Aki近似式及精确方程模拟平面波共中心点道集,得到不同方位角PSV波共中心点道集(图 6)。可见:式(13)与精确方程模拟结果的振幅方位变化特征基本一致且较明显,Aki近似式模拟结果无法体现方位变化特征;当方位角为0°时,在大入射角范围内精确方程与式(13)的模拟结果均呈极性反转(图 6a),更精确地体现了转换波在弹性界面处的反射特征。因此,式(13)更适用于方位地震资料,可更好地认识方位AVO变化规律。
|
图 6 不同方位角PSV波共中心点道集 (a)φ=0°; (b)φ=30°; (c)φ=60°自上至下的同相轴依次由式(13)、Aki近似式、精确方程所得 |
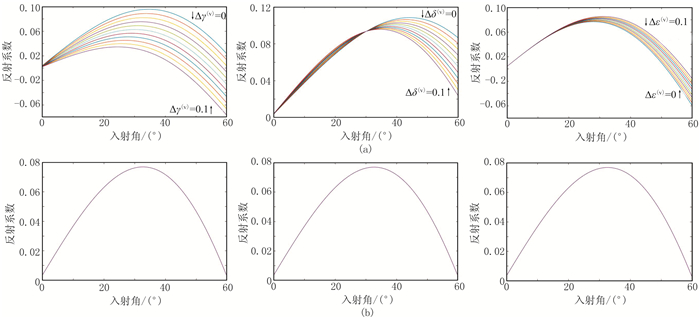
由于不同近似式对各向异性参数表述不同,为进一步了解各向异性参数与方位角的变化对反射系数的影响,观察各向异性参数变化时对反射系数的影响程度。图 7展示了模型Ⅱ中ε(V)、δ(V)、γ(V)变化对反射系数的影响。由图可见:①当方位角为0°时,各向异性参数变化对反射系数影响较大(图 7a),当方位角为90°时,反射系数不受各向异性参数变化的影响(图 7b)。这是由于当方位角为90°时,测线方向与HTI介质对称轴垂直,介质不体现各向异性特征所致。②在小入射角时,各向异性参数变化几乎不影响反射系数,在大入射角时反射系数受各向异性参数变化影响。③γ(V)变化对反射系数影响最大(图 7a左、图 7b左),ε(V)变化对反射系数影响最小(图 7a右、图 7b右),且各向异性参数变化对反射系数的影响与方位角有关。
|
图 7 模型Ⅱ中γ(V)(左)、δ(V)(中)、ε(V)(右)变化对反射系数的影响 (a)φ=0°; (b)φ=90°横波速度与密度相对变化量不变,各向异性参数相对变化量在0~0.1的范围内以0.01为步长变化 |
综上所述,式(13)适用于模拟各向同性/HTI界面反射系数,且精度高于Rüger近似式,通过正演模拟反射系数及共中心点道集验证了其可行性。不同反射系数近似式在小入射角时精度较高,随入射角增大,误差逐渐增大。入射角范围不同,反射系数主控因素不同,文中涉及的反射系数公式的主要区别在于各向异性参数项,故在小入射角时各公式间的差异不大。
3 结束语本文基于介质分解理论与扰动理论,由HTI介质反射/透射系数精确方程出发,推导了PSV波方位反射系数一阶近似公式,并选取方位观测HTI介质三层模型验证其可行性,分析了不同方位转换波振幅变化特征,讨论了各向异性参数变化对反射系数的影响。经模型验证分析,本文所推导的PSV波反射系数一阶近似方程与反射系数精确方程曲线趋势一致,更适用于模拟各向同性/HTI界面反射系数,提高了PSV波AVO分析精度,可结合PP波方位反射系数方程进行叠前地震储层预测。
| [1] |
Knott C G. Reflection and refraction of elastic waves, with seismological applications[J]. Philosophical Magazine Series 5, 1899, 48(290): 64-97. |
| [2] |
Zoeppritz K, Erdbebnenwellen V. On the reflection and penetration of seismic waves through unstable layers[J]. Göettinger Nachrichten, 1919, 1(7B): 66-84. |
| [3] |
Koefoed O. On the effect of Poisson's ratios of rock strata on the reflection coefficients of plane waves[J]. Geophysical Prospecting, 2010, 3(4): 381-387. |
| [4] |
Aki K, Richards P G. Quantitative Seismology:Theory and Methods[M]. W H Freeman, 1980.
|
| [5] |
Rüger A. Variation of P-wave reflectivity with offset and azimuth in anisotropic media[J]. Geophysics, 1998, 63(3): 935-947. |
| [6] |
Thomsen L. Weak elastic anisotropy[J]. Geophysics, 1986, 51(10): 1954-1966. |
| [7] |
梁锴.TI介质地震波传播特征与正演方法研究[D].山东青岛, 中国石油大学(华东), 2009.
|
| [8] |
宗兆云, 印兴耀, 张峰, 等. 杨氏模量和泊松比反射系数近似方程及叠前地震反演[J]. 地球物理学报, 2012, 55(11): 3786-3794. ZONG Zhaoyun, YIN Xingyao, ZHANG Feng, et al. Reflection coefficient equation and pre-stack seismic inversion with Young's modulus and Poisson ratio[J]. Chinese Journal of Geophysics, 2012, 55(11): 3786-3794. |
| [9] |
司芗, 吴国忱. 裂隙等效TTI介质qP波反射特征研究[J]. 地球物理学进展, 2012, 27(5): 2091-2099. SI Xiang, WU Guochen. Study on qP-wave reflectivity in fracture equivalent TTI media[J]. Progress in Geophysics, 2012, 27(5): 2091-2099. |
| [10] |
李春鹏.基于方位地震道集的裂缝型储层预测方法研究[D].山东青岛: 中国石油大学(华东), 2013. LI Chunpeng.Research on Fractured Reservoir Prediction with Azimuthal Seismic data[D].China University of Petroleum(East China), Qingdao, Shandong, 2013. |
| [11] |
Wu G C, Zhao X L, Tang J, et al. First-order perturbation approximation for rock elastic moduli in transversely isotropic media[J]. Science China(Earth Sciences), 2017, 60(9): 1645-1654. |
| [12] |
单俊臻, 吴国忱, 龚诚诚. HTI介质方位观测PP波反射系数一阶扰动近似[J]. 石油地球物理勘探, 2019, 54(2): 371-379. SHAN Junzhen, WU Guochen, GONG Chengcheng. First-order perturbation approximation of PP wave reflection coefficient for HTI medium based on azimuthal geometry[J]. Oil Geophysical Prospecting, 2019, 54(2): 371-379. |
| [13] |
朱兆林, 赵爱国. 裂缝介质的纵波方位AVO反演研究[J]. 石油物探, 2005, 44(5): 499-503. ZHU Zhaolin, ZHAO Aiguo. Azimuthal AVO inversion of P-wave in fractured medium[J]. Geophysical Prospecting for Petroleum, 2005, 44(5): 499-503. |
| [14] |
毛宁波, 谢涛, 杨凯, 等. 裂缝储层地震方位AVO正演模拟研究及应用[J]. 石油天然气学报, 2008, 30(5): 59-63. MAO Ningbo, XIE Tao, YANG Kai, et al. Study and application on AVO forward modeling of seismic orientation for fractured reservoirs[J]. Journal of Oil and Gas Technology, 2008, 30(5): 59-63. |
| [15] |
Bortfeld R. Approximations to the reflection and transmission coefficients of plane longitudinal and transverse waves[J]. Geophysical Prospecting, 1961, 9(4): 485-502. |
| [16] |
Donati M, Martin N W.A Comparison of Approximations for the Converted-Wave Reflection[R].Crewes Research Reports, Calfary, 1998, 159-179.
|
| [17] |
郑晓东. Zoeppritz方程的近似及其应用[J]. 石油地球物理勘探, 1991, 26(2): 129-144. ZHENG Xiaodong. Approximation of Zoeppritz equation and its application[J]. Oil Geophysical Prospecting, 1991, 26(2): 129-144. |
| [18] |
郑晓东. AVO理论和方法的一些新进展[J]. 石油地球物理勘探, 1992, 27(3): 305-317. ZHENG Xiaodong. Some new developments of AVO technique[J]. Oil Geophysical Prospecting, 1992, 27(3): 305-317. |
| [19] |
杨绍国, 周熙襄. Zoeppritz方程的级数表达式及近似[J]. 石油地球物理勘探, 1994, 29(4): 399-412. YANG Shaoguo, ZHOU Xixiang. Series expression and approximation of Zoeppritz's equation[J]. Oil Geophysical Prospecting, 1994, 29(4): 399-412. |
| [20] |
李正文, 胡光岷. P-SV波AVO分析[J]. 成都理工学院学报(自然科学版), 1996, 23(4): 73-79. LI Zhengwen, HU Guangmin. P-SV wave AVO analysis[J]. Journal of Chengdu Institute of Technology(Science & Technology Edition), 1996, 23(4): 73-79. |
| [21] |
Ramos A C B, Castagna J P. Useful approximations for converted-wave AVO[J]. Geophysics, 2001, 66(6): 1721-1734. |
| [22] |
孙鹏远. P-SV波反射系数近似及其AVO属性特征[J]. 地球学报, 2006, 27(1): 85-89. SUN Pengyuan. P-SV wave reflection coefficient approximations and characteristics of AVO attributes[J]. Acta Geoscientica Sinica, 2006, 27(1): 85-89. |
| [23] |
唐旭东, 甘利灯, 李凌高. 转换波反射系数近似公式及精度分析[J]. 石油物探, 2008, 47(2): 150-155. TANG Xudong, GAN Lideng, LI Linggao. Approximate formula of PS-wave reflection coefficient and its precision analysis[J]. Geophysical Prospecting for Petroleum, 2008, 47(2): 150-155. |



 吴国忱, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
吴国忱, 山东省青岛市黄岛区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: