② CNPC物探重点实验室, 北京 102249;
③ 中国石油大学(北京)地球物理学院, 北京 102249;
④ 中国地质调查局油气资源调查中心, 北京 100083
② CNPC Key Lab of Geophysical Prospecting, Beijing 102249, China;
③ College of Geophysics, China University of Petroleum(Beijing), Beijing 102249, China;
④ Oil & Gas Survey, CGS, Beijing 100083, China
地震偏移利用波场传播算子将地表观测的地震数据转换为地下空间分布的像,是整个地震数据处理流程的重要一环。在众多偏移方法中,逆时偏移方法因无成像倾角限制、保幅性能好及易于向复杂介质扩展等优点,已成为重要的地震成像方法。然而,受制于几何扩散、有限的观测孔径和子波带宽等因素影响,逆时偏移的成像结果仍存在振幅分布不均衡、噪声干扰及分辨率低等问题。最小二乘逆时偏移方法是逆时偏移技术的进一步发展,它将地震偏移视为反演问题,通过匹配反射波数据反演地下的反射系数模型,利用多次迭代压制成像噪声,同时能在一定程度上消除子波频带不足的负面影响,提高成像分辨率。
近年来,随着计算机性能的大幅提升,特别是GPU并行计算技术的推广,具有诸多优点的最小二乘逆时偏移方法已成为研究热点之一。最小二乘逆时偏移方法最早由Dai等[1]基于声波方程提出。针对该方法应用中存在的问题,现阶段许多学者从不同的角度对其做了进一步的完善。如Yao等[2-3]和Dai等[4]对最小二乘逆时偏移的成像精度进行了研究。Yao等[5]将最小二乘逆时偏移表述为矩阵—向量形式,讨论了非线性的最小二乘逆时偏移方法。根据反射系数具有稀疏特性,Wu等[6]研究了L1范数约束的最小二乘逆时偏移方法。方修政等[7]使用逆散射成像条件替代传统的成像条件,压制了最小二乘逆时偏移中的成像噪声。针对复杂介质的影响,诸多学者研究了基于弹性波动方程的最小二乘逆时偏移方法[8-10]。Fang等[11]利用卷积型目标函数提出了不依赖于震源的弹性波最小二乘逆时偏移方法。李振春等[12]和郭旭等[13]进一步研究了基于VTI介质的最小二乘逆时偏移方法。最小二乘逆时偏移需对波动方程进行Born近似,为提高近似精度,陈生昌等[14]提出反射波动方程,并讨论了基于反射波动方程的最小二乘逆时偏移方法。在提高计算效率方面,正则化约束下的多震源最小二乘逆时偏移方法在近年得到了较广泛的关注[15-18]。
此外,吸收衰减补偿的逆时偏移方法近年来也是研究热点之一。根据互相关成像条件[19],为了补偿地震数据在传播路径上的振幅衰减和相位畸变,震源波场和伴随波场都是随时间呈指数增长的,该过程可通过求解振幅衰减和相位畸变解耦的黏滞波动方程实现[20-22]。然而,数值求解振幅增长的黏滞波动方程存在数值不稳定问题,通常采用低通滤波器滤掉高频成分[23-25];同时又因截止频率不易选取,会导致高频丢失,进而降低了分辨率。Wang等[26]和Zhao等[27]分别提出了不同的稳定化策略,但都无法从根本上避免数值不稳定问题。
最小二乘逆时偏移方法采用迭代思路反演反射率。若考虑介质的衰减性质,其正演和伴随算子都是能量衰减型的,因此不存在数值不稳定问题。Dutta等[28]最早提出利用最小二乘逆时偏移方法补偿介质黏滞性对成像结果的影响,避免了衰减补偿逆时偏移的不稳定问题;李振春等[29]也讨论了基于黏滞声学介质的最小二乘逆时偏移方法;Guo等[30]进一步研究了基于广义标准线性体黏弹性波动方程的最小二乘逆时偏移方法;曲英铭等[31]在最小二乘逆时偏移中同时考虑了介质的黏滞性和各向异性。
目前大多数衰减补偿最小二乘逆时偏移方法均采用线性体黏滞波动方程作为正演方程[32-33],该方程难以准确描述常Q(地震品质因子)模型[34],由其模拟的地震波衰减和频散与实际测量结果有一定差距[35]。基于此,本文利用一种新颖的分数阶拉普拉斯算子黏滞声波方程作为正演方程,推导其Born正演模拟算子,由此提出了一种新的衰减补偿型最小二乘逆时偏移方法,用于补偿介质的黏滞性对逆时偏移成像结果的影响。
1 黏滞声波最小二乘逆时偏移 1.1 分数阶拉普拉斯算子黏滞声波方程Born正演模拟算子是通过线性化全波方程得到的,本文采用Chen等[36]提出的常分数阶拉普拉斯算子黏滞声波方程描述地震波在黏滞声学介质中衰减和频散。该方程可表述为
| $ \mathscr{A}{u_0} = s(t)\mathscr{l}(\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_{\rm{s}}}) $ | (1) |
式中:u0为波场变量;s(t)为震源子波;l为单位脉冲函数;x表示二维空间坐标;xs为震源位置;且有
| $ \begin{array}{l} \mathscr{A} = \frac{1}{{\lambda c_0^2}}\frac{{{\partial ^2}}}{{\partial {t^2}}} - {\eta _1}( - {\nabla ^2}) + {\eta _2}{( - {\nabla ^2})^{\frac{{33}}{{32}}}} + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \tau \frac{\partial }{{\partial t}}{( - {\nabla ^2})^{0.505}} \end{array} $ | (2) |
其中▽2为拉普拉斯算子,并且
| $ \left\{ {\begin{array}{*{20}{l}} {{\eta _1} = \frac{{32}}{{\pi Q}} - 1}\\ {{\eta _2} = \frac{{32}}{{\pi Q}}{{(\frac{{{c_0}}}{{{\omega _{\rm{d}}}}})}^{\frac{1}{{16}}}}}\\ {\tau = \frac{1}{{Q{c_0}}}}\\ {\lambda = {{(\frac{{{\omega _{\rm{d}}}}}{{{\omega _0}}})}^{\frac{2}{{\pi Q}}}} {\rm{cos}}{ ^2}\frac{2}{Q} {\rm{cos}}{ ^2}\frac{1}{Q}} \end{array}} \right. $ | (3) |
式中:Q为地震品质因子;c0为定义在参考角频率ω0上的地震波速度;ωd为震源的主频。
Chen等[36]证实,在Q≥15的情况下,黏滞声波方程式(1)的精度能很好地匹配Zhu等[20]所提出的变分数阶拉普拉斯算子常Q黏滞声波方程的精度。与后者相比,式(1)中拉普拉斯算子的阶数不随空间变化,因此数值求解该波动方程更容易。
目前求解分数阶拉普拉斯算子黏滞声波方程的数值方法包括伪谱法[37]、矩阵转换法[38]、矩阵低秩分解法[39]等。为简单起见,采用伪谱法对式(1)进行离散,分别使用二阶中心差分和一阶向后差分算子近似式(1)中的二阶和一阶时间偏导数,同时利用快速傅里叶变换(FFT)计算分数阶拉普拉斯算子,例如
| $ {( - {\nabla ^2})^{\frac{{33}}{{32}}}}{u_0} = {\mathscr{F}^{ - 1}}(|k{|^{\frac{{33}}{{16}}}}\mathscr{F}({u_0})) $ | (4) |
式中:
为了推导全波方程(式(1))对应的Born正演模拟算子,对背景速度模型c0施加微小扰动c=c0+δc,相应地,波场也产生微小扰动u0→u=u0+δu。将扰动后的速度模型c和波场u代入式(1),并利用以下泰勒近似
| $ \left\{ {\begin{array}{*{20}{l}} {\frac{1}{{{{({c_0} + \delta c)}^2}}} \approx \frac{1}{{c_0^2}} - \frac{{2\delta c}}{{c_0^3}}}\\ {{{({c_0} + \delta c)}^{\frac{1}{{16}}}} \approx c_0^{\frac{1}{{16}}}(1 + \frac{1}{{16}}\frac{{\delta c}}{{{c_0}}})}\\ {\frac{1}{{{c_0} + \delta c}} \approx \frac{1}{{{c_0}}}(1 - \frac{{\delta c}}{{{c_0}}})} \end{array}} \right. $ | (5) |
可得到
| $ \begin{array}{*{20}{c}} {\frac{1}{\lambda }(\frac{1}{{c_0^2}} - \frac{{2\delta c}}{{c_0^3}})\frac{{{\partial ^2}u}}{{\partial {t^2}}} - {\eta _1}( - {\nabla ^2})u + }\\ {{\eta _2}(1 + \frac{1}{{16}}\frac{{\delta c}}{{{c_0}}}){{( - {\nabla ^2})}^{\frac{{33}}{{32}}}}u + }\\ {\tau (1 - \frac{{\delta c}}{{{c_0}}})\frac{\partial }{{\partial t}}{{( - {\nabla ^2})}^{0.505}}u}\\ { = s(t)\mathscr{l}(\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_{\rm{s}}})} \end{array} $ | (6) |
将式(6)减去式(1),并经简单整理得到
| $ \mathscr{A}\delta u = m\mathscr{D}u $ | (7) |
其中
| $ \mathscr{D} = \frac{1}{\lambda }\left[ {\frac{2}{{c_0^2}}\frac{{{\partial ^2}}}{{\partial {t^2}}} - \frac{{{\eta _2}}}{{16}}{{( - {\nabla ^2})}^{\frac{{33}}{{32}}}} + \tau \frac{\partial }{{\partial t}}{{( - {\nabla ^2})}^{0.505}}} \right] $ | (8) |
将
| $ \left\{ {\begin{array}{*{20}{l}} {\mathscr{A}{u_0} = s(t)\mathscr{l}(\mathit{\boldsymbol{x}} - {\mathit{\boldsymbol{x}}_{\rm{s}}})}\\ {\mathscr{A}\delta u = m\mathscr{D}{u_0}} \end{array}} \right. $ | (9) |
显然,Born正演模拟包含两次黏滞声波方程正演模拟:一次是利用背景速度模型c0计算背景波场u0;另一次是将背景波场作为震源,计算反射波场δu,且反射波场与反射率m之间是线性关系。因此,Born近似下的最小二乘逆时偏移是线性反演问题。
1.3 伴随算子和梯度利用拉格朗日乘子法定义扩展的目标函数[41]
| $ \begin{array}{*{20}{l}} {E(\mathit{\boldsymbol{m}},\delta u) = \frac{1}{2}\left\| {{\mathit{\boldsymbol{u}}^{{\rm{ cal }}}} - {\mathit{\boldsymbol{u}}^{{\rm{ obs }}}}} \right\|_2^2 + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \int {\int \mu } (\mathscr{A}\delta u - m\mathscr{D}{u_0}){\rm{d}}t{\rm{d}}\mathit{\boldsymbol{x}}} \end{array} $ | (10) |
式中:m={mi, j|0≤i<N1, 0≤j<N2},其中N1和N2分别为x和z方向的网格数,下标i和j对应网格索引;ucal={
推导伴随波场可令
| $ {\mathscr{A}^*}\mu = \mathscr{R}(\delta {u^{{\rm{obs}}}} - \delta {u^{{\rm{cal}}}}) $ | (11) |
其中
| $ {\eta _2}{( - {\nabla ^2})^{\frac{{33}}{{32}}}} - \tau \frac{\partial }{{\partial t}}{( - {\nabla ^2})^{0.505}} $ | (12) |
注意
进一步计算目标函数对反射率模型的偏导数,即目标函数的梯度可由背景波场和伴随波场的零延迟互相关求取
| $ \mathit{\boldsymbol{g}} = - \int \mu \mathscr{D}{u_0}{\rm{d}}t $ | (13) |
式(11)和式(13)的具体推导过程见附录A。
本文采用L-BFGS局部寻优算法更新模型
| $ {\mathit{\boldsymbol{m}}^{n + 1}} = {\mathit{\boldsymbol{m}}^n} + \alpha {\mathit{\boldsymbol{z}}^n} $ | (14) |
式中:m0为初始模型;α为采用线搜索确定的最优步长[42];zn为模型下降方向,可表示为zn=-Ha-1gn,其中Ha-1为海塞矩阵的近似逆矩阵,gn为第n次迭代的梯度,且n为迭代次数。
L-BFGS算法通过保存前l步(本文l=5)的模型变化量和梯度变化量,利用双向递归算法[43]直接计算Ha-1gn,而不需显式地计算矩阵Ha-1。
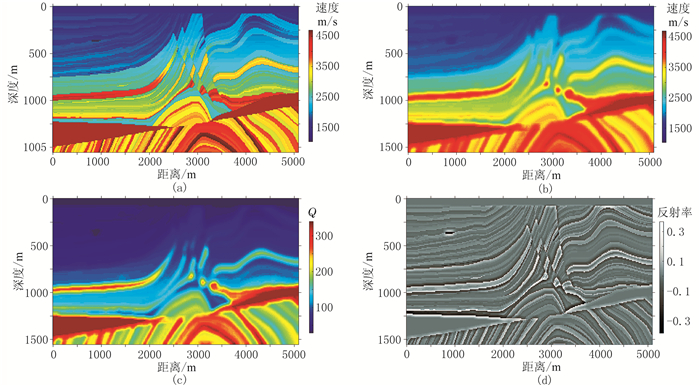
2 数值例子 2.1 合成数据反演首先使用Marmousi模型检验本文所提最小二乘逆时偏移方法效果。模型尺寸为340(x)×156(z),网格单元为15m×10m,最大和最小速度分别为4700、1028m/s。基于真实速度模型(图 1a)得到光滑后速度模型(图 1b);再利用经验公式Q=12(c0/1000)2.2由光滑速度模型生成Q模型(图 1c),最小Q值为28;进而得到真实的反射率模型(图 1d)。假设速度模型(图 1a和图 1b)定义在参考频率200Hz上。基于真实的速度模型求解黏滞声波方程式(1),生成60炮观测记录,检波点位于地表,炮点位于深度20m处,炮间距75m,第1炮距离模型左边界水平距离为300m,采用中间放炮两边接收的排列,最大炮检距为1800m,道间距15m。使用主频为20Hz雷克子波作为震源,记录时长为2.5s,时间采样间隔为1ms。
|
图 1 Marmousi模型的真实速度(a)、背景速度(b)、Q值(c)和反射率(d)模型显示 |
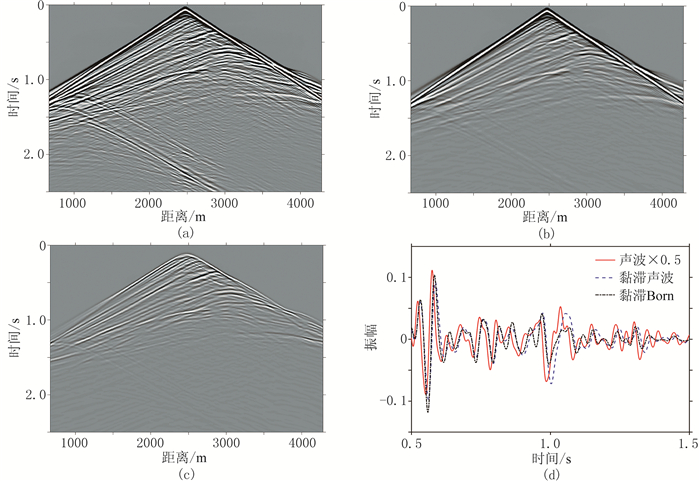
图 2为模拟的第30炮共炮点记录,炮点位于x=2475m。对比黏滞声波记录(图 2b)与声波记录(图 2a),可见存在明显振幅衰减。基于真实反射率模型计算的黏滞Born模拟记录(图 2c)中主要包含一次反射波形,说明Born模拟不同于全波模拟。观察该炮第100道(x=2160m)记录的波形(图 2d),可见黏滞声波数据相较于声波数据存在明显的振幅衰减和相位滞后,同时黏滞Born模拟数据与黏滞全波数据也有较明显差异,这缘于线性化波动方程误差。
|
图 2 三种共炮点记录及其单道对比 (a)声波;(b)黏滞声波;(c)黏滞声波Born模拟;(d)第100道地震记录对比 |
不同反演方法获得的反射率模型如图 3所示,所使用的初始模型为零,其中黏滞声波数据声波最小二乘逆时偏移的第1次迭代结果(图 3a),相当于传统声波逆时偏移的结果,可见虽然浅层结构较清晰,但深层能量弱,振幅沿深度分布不均衡,且与真实反射率模型(图 1d)有明显差异。黏滞声波数据黏滞声波最小二乘逆时偏移的第1次迭代结果(图 3c),整体上与图 3a相似,但位于500m<x<1000m、z≈300m处的小异常体的顶底界面在整个剖面中更突出,说明黏滞声波最小二乘逆时偏移在一定程度上补偿了介质的黏滞性。

|
图 3 针对黏滞全波和黏滞Born数据采用两种偏移方法反演得到的反射率模型 (a)、(b)对应黏滞全波数据声波最小二乘逆时偏移第1和第60次迭代;(c)、(d)对应黏滞全波数据黏滞声波最小二乘逆时偏移第1和第60次迭代;(e)黏滞Born数据声波最小二乘逆时偏移第60次迭代;(f)黏滞Born数据黏滞声波最小二乘逆时偏移第60次迭代 |
当迭代次数增至60时,声波最小二乘逆时偏移反演黏滞声波数据的结果分辨率较低,存在明显的低频干扰(图 3b)。相对而言,黏滞声波最小二乘逆时偏移方法很好地补偿了介质的黏滞性,其反演结果(图 3d)在z<800m范围内与真实反射率模型吻合很好,在该深度以下的背斜和不整合面的成像也较清晰,但也存在一些噪声,这是由于正演与反演算子欠匹配造成的。实际上,观测数据是由全波方程式(1)生成的,反射波与反射率之间是非线性关系,但反演时利用Born算子进行线性反演,因此反演结果与真实结果存在差异。
作为对比,使用黏滞Born数据作为观测数据进行最小二乘逆时偏移,同样迭代60次。从偏移结果可知:当正演和反演算子同为线性时,反演结果有明显改善;声波最小二乘逆时偏移反演结果(图 3e)对构造成像较清晰,但振幅仍未恢复,尚存在低频噪声;而黏滞声波最小二乘逆时偏移反演结果(图 3f)与真实反射率模型(图 1d)十分接近。
图 4进一步比较了三种最小二乘逆时偏移方法所对应的目标函数的收敛速度。从该图易知,三者中黏滞Born数据的黏滞声波最小二乘逆时偏移的收敛速度最快,其次是黏滞全波数据的黏滞声波最小二乘逆时偏移,而黏滞全波数据的传统声波最小二乘逆时偏移的收敛速度相对最慢。

|
图 4 三种最小二乘逆时偏移目标函数的收敛速度对比 |
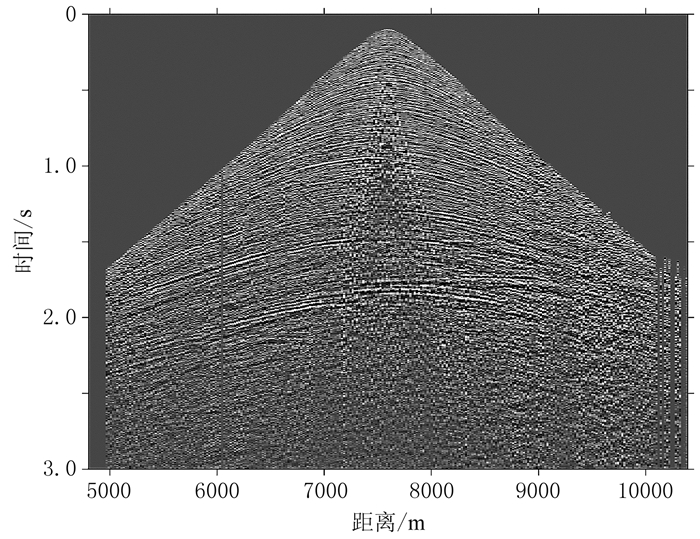
进一步使用一条二维实际测线证实本文所提黏滞声波最小二乘逆时偏移方法的可行性。该测线共80炮,炮间距为200m,炮点深度为20m,记录时长为3s,时间采样间隔为1ms,道间距为20m,从频谱分析知该数据主频约为20Hz。速度(图 5a)和Q(图 5b)模型的网格数为680(x)×320(z),网格间距为20m,假设速度模型定义在参考频率20Hz上。从第40炮共炮点记录(图 6)可见若干反射波同相轴、未消除彻底的面波及其他干扰噪声。最小二乘逆时偏移中使用主频为20Hz雷克子波作为震源,并假设初始的反射率模型为零。

|
图 5 实际地震资料的速度模型(a)和Q模型(b) |
|
图 6 实际共炮点记录 |
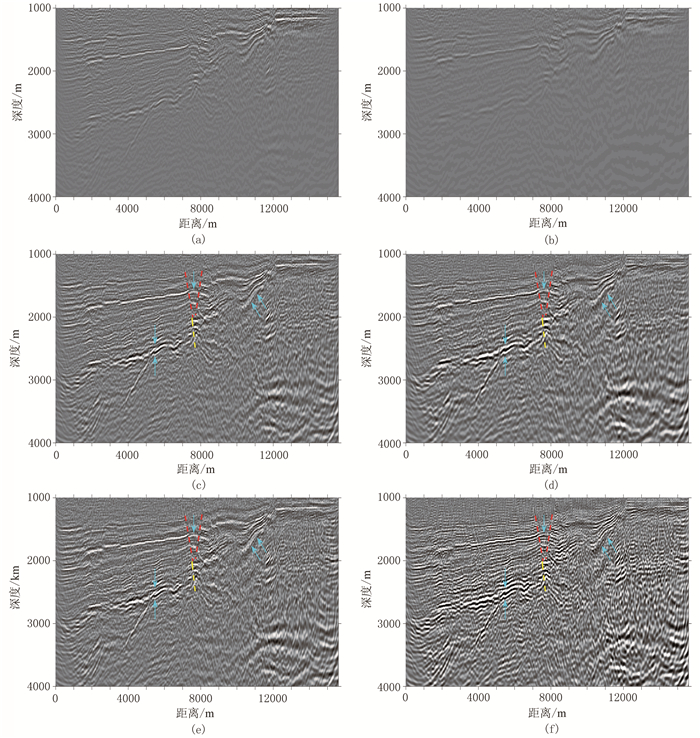
图 7显示了由最小二乘逆时偏移得到的反射率剖面,其中包括声波最小二乘逆时偏移第1(图 7a)、第20(图 7c)、第40(图 7e)次和黏滞声波最小二乘逆时偏移第1(图 7b)、第20(图 7d)和第40(图 7f)次的迭代结果,且第1次迭代相当于逆时偏移。由第1次迭代的结果(图 7a和图 7b)可知,声波和黏滞声波逆时偏移均未能补偿介质的黏滞性,其偏移剖面深层的能量明显弱于浅层,特别是黏滞声波逆时偏移中因为震源和伴随波场的能量都是衰减的,导致其偏移剖面(图 7b)的分辨率低于声波偏移剖面(图 7a)。当迭代次数增至20时,黏滞声波最小二乘逆时偏移逐渐补偿了介质的黏滞性,成像结果(图 7d)优于传统声波最小二乘逆时偏移(图 7c)。对比图 7c与图 7d中解释的3条断层及若干同相轴可知,补偿吸收衰减后的断层面变得较突出,位于两条断层之间的小断块也能清晰可辨。
|
图 7 实际数据的最小二乘逆时偏移剖面 (a)、(c)、(e)对应声波最小二乘逆时偏移迭代1、20、40次;(b)、(d)、(f)对应黏滞声波最小二乘逆时偏移迭代1、20、40次 |
当迭代次数进一步增至40时,黏滞声波最小二乘逆时偏移结果进一步凸显了高频细节,其成像剖面(图 7f)呈现更多具有一定连续性的细轴。可对比图 7d与图 7f中位于5000m<x<6000m、z≈2500m处箭头标记的同相轴,该同相轴在图 7d中横向连续性差,但在图 7f中变得更连续。此外,位于x=11000m、z≈2000m处箭头标记的同相轴在图 7d中偏“胖”,而在图 7f中较“瘦”,也证实黏滞声波最小二乘逆时偏移提升了成像分辨率。相比之下,当迭代次数由20增至40时,传统声波最小二乘逆时偏移成像结果(图 7c与图 7e)的差别不大,表明声波最小二乘逆时偏移陷入局部极小值。
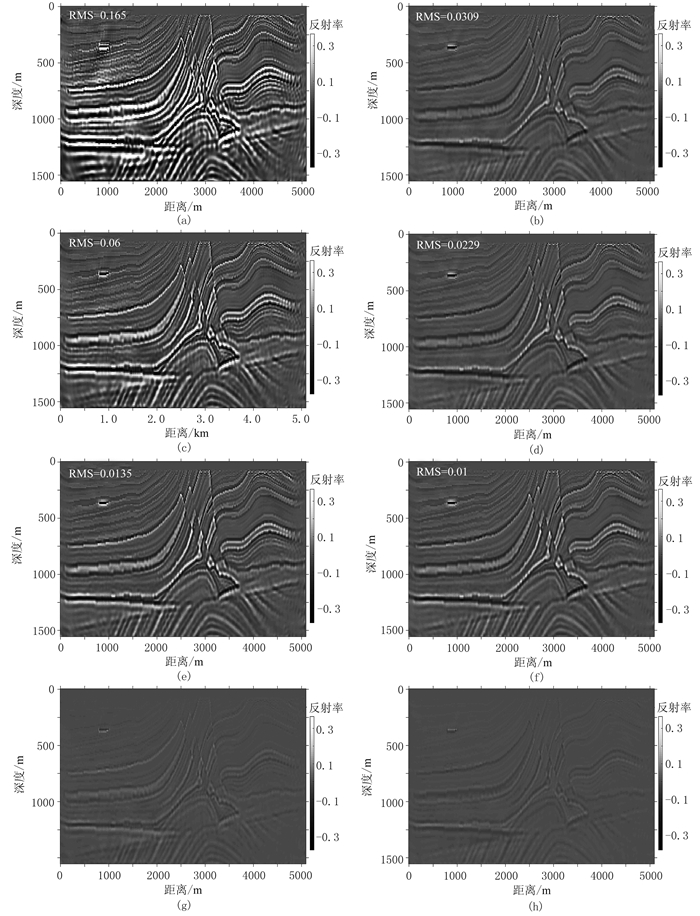
3 讨论为了考察Q模型不准确对最小二乘逆时偏移结果的影响,这里重复图 3f中合成数据测试,即利用黏滞声波最小二乘逆时偏移方法反演黏滞Born数据。所使用的Q模型与图 1c中真实Q模型分别存在-50%、-30%、-10%、50%、30%和10%的相对误差,最大迭代次数为60次。其反演结果如图 8所示,其中标注的RMS值是与参考解(图 3f)之间的均方根误差。从该反演结果可知:当Q偏小时,黏滞声波最小二乘逆时偏移剖面的振幅存在正向异常,表明补偿过度;当Q偏大时,偏移剖面的振幅偏弱,表明补偿不够。当Q模型的相对误差为-10%和10%时,其反演结果(图 8e和图 8f)与参考剖面(图 3f)较为接近,其误差剖面(图 8g和图 8h)的幅度较弱,说明黏滞声波最小二乘逆时偏移方法对于10%的Q模型误差具有一定的稳健性。
|
图 8 不同相对误差Q模型的黏滞Born数据使用黏滞声波最小二乘逆时偏移迭代60次的结果 (a)-50%;(b)50%;(c)-30%;(d)30%;(e)-10%;(f)10%;(g)图e与参考解(图 3f)的差异;(h)图f与参考解的差异RMS表示偏移结果与参考解之间的均方根误差 |
本文基于一种新颖的分数阶拉普拉斯算子常Q黏滞声波方程,提出了一种具有补偿介质吸收衰减功能的最小二乘逆时偏移方法。该方法从常分数阶拉普拉斯算子黏滞声波方程出发,定义了相应的Born正演模拟算子,在拉格朗日乘子法框架下推导出伴随算子和梯度表达式,并利用L-BFGS局部寻优算法迭代更新反射率模型。因正演和伴随算子都是能量衰减型的,故本文的黏滞声波最小二乘逆时偏移方法能避免常规Q补偿逆时偏移方法数值不稳定的弊端。合成和实际数据的反演算例都证实了本文所提方法能较好地补偿介质的黏滞性,提高成像分辨率。
附录A 黏滞声波最小二乘逆时偏移伴随算子和梯度表达式
二维情况下目标函数(式(10))的具体形式为
| $ \begin{array}{*{20}{l}} {E(\mathit{\boldsymbol{m}},\delta u) = \frac{1}{2}\left\| {{\mathit{\boldsymbol{u}}^{{\rm{cal}}}} - {\mathit{\boldsymbol{u}}^{{\rm{obs}}}}} \right\|_2^2 + }\\ {\qquad \int {\int {\int {\mu \left[ {\frac{1}{{\lambda c_0^2}}\frac{{{\partial ^2}\delta u}}{{\partial {t^2}}} - {\eta _1}( - {\nabla ^2})\delta u + {\eta _2}{\nabla ^2}{)^{\frac{{33}}{{32}}}}\delta u + } \right.} } } }\\ {\left. {{\kern 1pt} \qquad \tau \frac{\partial }{{\partial t}}{{( - {\nabla ^2})}^{0.505}}\delta u - m\mathscr{D}{u_0}} \right]{\rm{d}}t{\rm{d}}x{\rm{d}}z} \end{array} $ | (A-1) |
根据拉格朗日乘子法[41],令
| $ \frac{\partial }{{\partial \delta u}}\{ \frac{1}{2}\left\| {{\mathit{\boldsymbol{u}}^{{\rm{cal}}}} - {\mathit{\boldsymbol{u}}^{{\rm{obs}}}}} \right\|_2^2\} = \int {\int {\int \mathscr{R} } } (\delta {u^{{\rm{cal}}}} - \delta {u^{{\rm{obs}}}}){\rm{d}}t{\rm{d}}x{\rm{d}}z $ | (A-2) |
对式(A-1)右端第二项先利用分部积分公式化简,再求其导数,例如
| $ \begin{array}{*{20}{l}} {\int {\int {\int {\frac{\partial }{{\partial \delta u}}(\mu \frac{1}{{\lambda c_0^2}}\frac{{{\partial ^2}\delta u}}{{\partial {t^2}}}){\rm{d}}t{\rm{d}}x{\rm{d}}z} } } }\\ {\quad = \int {\int {\frac{\partial }{{\partial \delta u}}} } \left\{ {\frac{1}{{\lambda c_0^2}}\left[ {\mu \left. {\frac{{\partial \delta u}}{{\partial t}}} \right|_0^T - \int {\frac{{\partial \delta u}}{{\partial t}}} \frac{{\partial \mu }}{{\partial t}}{\rm{d}}t} \right]} \right\}{\rm{d}}x{\rm{d}}z}\\ {\begin{array}{*{20}{l}} {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \int {\int {\frac{\partial }{{\partial \delta u}}} } \left\{ {\frac{1}{{\lambda c_0^2}}\left[ {\mu \left. {\frac{{\partial \delta u}}{{\partial t}}} \right|_0^T - } \right.} \right.}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left. {\left. {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {{\kern 1pt} \delta u\frac{{\partial \mu }}{{\partial t}}|_0^T - \int \delta u\frac{{{\partial ^2}\mu }}{{\partial {t^2}}}{\rm{d}}t} \right)} \right]} \right\}{\rm{d}}x{\rm{d}}z} \end{array}\quad } \end{array} $ | (A-3) |
假设零值边界条件δu(t=0, T)=0,μ(t=0, T)=0,则式(A-3)可进一步化简为
| $ \int {\int {\int {\frac{\partial }{{\partial \delta u}}} } } (\mu \frac{1}{{\lambda c_0^2}}\frac{{{\partial ^2}\delta u}}{{\partial {t^2}}}){\rm{d}}t{\rm{d}}x{\rm{d}}z = \int {\int {\int {\frac{1}{{\lambda c_0^2}}} } } \frac{{{\partial ^2}\mu }}{{\partial {t^2}}}{\rm{d}}t{\rm{d}}x{\rm{d}}z $ | (A-4) |
同理,假设空间无穷远处满足零值边界条件,则有
| $ \begin{array}{*{20}{l}} {\int {\int {\int {\frac{\partial }{{\partial \delta u}}} } } [\mu {\eta _1}( - {\nabla ^2})\delta u]{\rm{d}}t{\rm{d}}x{\rm{d}}z}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \int {\int {\int {{\eta _1}} } } ( - {\nabla ^2})\mu {\rm{d}}t{\rm{d}}x{\rm{d}}z} \end{array} $ | (A-5) |
由式(A-4)和(A-5)的推导可知,当微分算子
| $ \int {\int {\int {\frac{\partial }{{\partial \delta u}}} } } (\mu \iota \delta u){\rm{d}}t{\rm{d}}x{\rm{d}}z = \int {\int {\int \iota } } \mu {\rm{d}}t{\rm{d}}x{\rm{d}}z $ | (A-6) |
从式(A-6)可得
| $ \begin{array}{l} \int {\int {\int {\frac{\partial }{{\partial \delta u}}} } } \left[ {\mu {\eta _2}{{( - {\nabla ^2})}^{\frac{{33}}{{32}}}}\delta u} \right]{\rm{d}}t{\rm{d}}x{\rm{d}}z\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \int {\int {\int {{\eta _2}} } } {( - {\nabla ^2})^{\frac{{33}}{{32}}}}\mu {\rm{d}}t{\rm{d}}x{\rm{d}}z \end{array} $ | (A-7) |
| $ \begin{array}{*{20}{l}} {\int {\int {\int {\frac{\partial }{{\partial \delta u}}} } } [\tau \frac{\partial }{{\partial t}}{{( - {\nabla ^2})}^{0.505}}\delta u]{\rm{d}}t{\rm{d}}x{\rm{d}}z}\\ {\quad {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = - \int {\int {\int \tau } } \frac{\partial }{{\partial t}}{{( - {\nabla ^2})}^{0.505}}\mu {\rm{d}}t{\rm{d}}x{\rm{d}}z} \end{array} $ | (A-8) |
将式(A-2)、式(A-5)、式(A-7)和式(A-8)代入
梯度计算公式可由
| $ \begin{array}{*{20}{l}} {{{(\frac{{\partial E}}{{\partial m}})}_{i,j}} = - {{\left[ {\frac{{\partial E}}{{\partial m}}\int {\int {\int \mu } } (m\mathscr{D}{u_0}){\rm{d}}t{\rm{d}}x{\rm{d}}z} \right]}_{i,j}}}\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = - {{[\int \mu (\mathscr{D}{u_0}){\rm{d}}t]}_{i,j}}} \end{array} $ | (A-9) |
式中下标i和j为二维模型的网格索引。将其写成向量形式即为梯度表达式
| $ \mathit{\boldsymbol{g}} = - \int \mu \mathscr{D}{u_0}{\rm{d}}t $ | (A-10) |
| [1] |
Dai W, Wang X, Schuster G T. Least-squares migration of multisource data with a deblurring filter[J]. Geophysics, 2011, 76(5): R135-R146. |
| [2] |
Yao G, Jakubowicz H. Least-squares reverse-time migration[C]. SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [3] |
Yao G, Jakubowicz H.Non-linear least-squares reverse-time migration[C]. SEG Technical Program Expanded Abstracts, 2012, 31: 1-5.
|
| [4] |
Dai W, Fowler P, Schuster G T. Multi-source plane-wave least-squares reverse-time migration[J]. Geophysical Prospecting, 2012, 60(4): 681-695. DOI:10.1190/GEO2012-0377.1 |
| [5] |
Yao G, Jakubowicz H. Least-squares reverse-time migration in a matrix-based formulation[J]. Geophysical Prospecting, 2016, 64(3): 611-621. |
| [6] |
Wu D, Yao G, Cao J, et al. Least-squares RTM with L1 norm regularization[J]. Journal of Geophysics and Engineering, 2016, 13(5): 666-673. DOI:10.1190/segam2016-13948030.1 |
| [7] |
方修政, 钮凤林, 吴迪. 基于逆散射成像条件的最小二乘逆时偏移[J]. 地球物理学报, 2018, 61(9): 3770-3782. FANG Xiuzheng, NIU Fenglin, WU Di. Least-squares reverse-time migration enhanced with the inverse scattering imaging condition[J]. Chinese Journal of Geophysics, 2018, 61(9): 3770-3782. |
| [8] |
Feng Z, Schuster G T. Elastic least-squares reverse-time migration[J]. Geophysics, 2017, 82(2): S143-S157. |
| [9] |
Duan Y, Guitton A, Sava P. Elastic least-squares reverse time migration[J]. Geophysics, 2017, 82(4): S315-S325. |
| [10] |
Ren Z, Liu Y, Sen M K. Least-squares reverse-time migration in elastic media[J]. Geophysical Journal International, 2017, 208(2): 1103-1125. |
| [11] |
Fang J, Zhou H, Chen H, et al. Source-independent elastic least-squares reverse time migration[J]. Geophysics, 2019, 84(1): S1-S16. |
| [12] |
李振春, 黄金强, 黄建平, 等. 基于平面波加速的VTI介质最小二乘逆时偏移[J]. 地球物理学报, 2017, 60(1): 240-257. LI Zhenchun, HUANG Jinqiang, HUANG Jianping, et al. Fast least-squares reverse time migration based on plane-wave encoding for VTI media[J]. Chinese Journal of Geophysics, 2017, 60(1): 240-257. |
| [13] |
郭旭, 黄建平, 李振春, 等. 基于一阶速度-应力方程的VTI介质最小二乘逆时偏移[J]. 地球物理学报, 2019, 62(6): 2188-2202. GUO Xu, HUANG Jianping, LI Zhenchun, et al. Least-squares reverse time migration based on first-order velocity-stress wave equation in VTI media[J]. Chinese Journal of Geophysics, 2019, 62(6): 2188-2202. |
| [14] |
陈生昌, 周华敏. 地震数据的反射波动方程最小二乘偏移[J]. 地球物理学报, 2018, 61(4): 1413-1420. CHEN Shengchang, ZHOU Huamin. Least squares migration of seismic data with reflection wave equation[J]. Chinese Journal of Geophysics, 2018, 61(4): 1413-1420. |
| [15] |
Dai W, Schuster G T. Plane-wave least-squares re-verse-time migration[J]. Geophysics, 2013, 78(4): S165-S177. DOI:10.1190/geo2012-0377.1 |
| [16] |
Xue Z, Chen Y, Fomel S, et al. Seismic imaging of incomplete data and simultaneous-source data using least-squares reverse time migration with shaping re-gularization[J]. Geophysics, 2016, 81(1): S11-S20. |
| [17] |
Chen Y, Chen H, Xiang K, et al. Preserving the discontinuities in least-squares reverse time migration of simultaneous-source data[J]. Geophysics, 2017, 82(3): S185-S196. |
| [18] |
Zhang Q, Mao W, Chen Y. Attenuating crosstalk noise of simultaneous-source least-squares reverse time migration with GPU-based excitation amplitude imaging condition[J]. IEEE Transactions on Geoscience and Remote Sensing, 2019, 57(1): 587-597. |
| [19] |
Claerbout J F. Toward a unified theory of reflector mapping[J]. Geophysics, 1971, 36(3): 467-481. |
| [20] |
Zhu T, Harris J M. Modeling acoustic wave propagation in heterogeneous attenuating media using decoupled fractional Laplacians[J]. Geophysics, 2014, 79(3): T105-T116. |
| [21] |
吴玉, 符力耘, 陈高祥. 基于分数阶拉普拉斯算子解耦的黏声介质地震正演模拟与逆时偏移[J]. 地球物理学报, 2017, 60(4): 1527-1537. WU Yu, FU Liyun, CHEN Gaoxiang. Forward mode-ling and reverse time migration of viscoacoustic media using decoupled fractional Laplacians[J]. Chinese Journal of Geophysics, 2017, 60(4): 1527-1537. |
| [22] |
罗文山, 陈汉明, 王成祥, 等. 时间域黏滞波动方程及其数值模拟新方法[J]. 石油地球物理勘探, 2016, 51(4): 707-713. LUO Wenshan, CHEN Hanming, WANG Cheng-xiang, et al. A novel time-domain viscoacoustic wave equation and its numerical simulation[J]. Oil Geophysical Prospecting, 2016, 51(4): 707-713. |
| [23] |
Zhu T, Harris J M, Biondi B. Q-compensated reverse time migration[J]. Geophysics, 2014, 79(3): S77-S87. |
| [24] |
Sun J, Zhu T, Fomel S. Viscoacoustic modeling and imaging using low-rank approximation[J]. Geophy-sics, 2015, 80(5): A103-A108. |
| [25] |
Li Q, Zhou H, Zhang Q, et al. Efficient reverse time migration based on fractional Laplacian viscoacoustic wave equation[J]. Geophysical Journal International, 2016, 204(1): 488-504. |
| [26] |
Wang Y, Zhou H, Chen H, et al. Adaptive stabilization for Q-compensated reverse time migration[J]. Geophysics, 2018, 83(1): S15-S32. |
| [27] |
Zhao X, Zhou H, Chen H, et al. A stable approach for Q-compensated viscoelastic reverse time migration using excitation amplitude imaging condition[J]. Geophysics, 2018, 83(5): S459-S476. |
| [28] |
Dutta G, Schuster G T. Attenuation compensation for least-squares reverse time migration using the visco-acoustic-wave equation[J]. Geophysics, 2014, 79(6): S251-S262. |
| [29] |
李振春, 郭振波, 田坤. 黏声介质最小平方逆时偏移[J]. 地球物理学报, 2014, 57(1): 214-228. LI Zhenchun, GUO Zhenbo, TIAN Kun. Least-squares reverse time migration in visco-acoustic me-dium[J]. Chinese Journal of Geophysics, 2014, 57(1): 214-228. |
| [30] |
Guo P, McMechan G A. Compensating Q effects in viscoelastic media by adjoint-based least-squares reverse time migration[J]. Geophysics, 2018, 83(2): S151-S172. |
| [31] |
曲英铭, 李金丽, 王云超, 等. 最小二乘逆时偏移中黏弹性和各向异性的校正:以渤海湾地区地震数据为例[J]. 地球物理学报, 2019, 62(6): 2203-2216. QU Yingming, LI Jinli, WANG Yunchao, et al. Correction of viscoelasticity and anisotropy in least-squares reverse time migration:a Bohai Bay seismic case study[J]. Chinese Journal of Geophysics, 2019, 62(6): 2203-2216. |
| [32] |
姚振岸, 孙成禹, 喻志超, 等. 融合点扩散函数的预条件黏声最小二乘逆时偏移[J]. 石油地球物理勘探, 2019, 54(1): 73-83. YAO Zhen'an, SUN Chengyu, YU Zhichao, et al. Preconditioned visco-acoustic least-squares reverse time migration integrated with point spread function[J]. Oil Geophysical Prospecting, 2019, 54(1): 73-83. |
| [33] |
吴吉忠, 左虎. 叠前衰减补偿时间偏移及GPU实现[J]. 石油地球物理勘探, 2019, 54(1): 84-92. WU Jizhong, ZUO Hu. Attenuation compensation in prestack time migration and its GPU implementation[J]. Oil Geophysical Prospecting, 2019, 54(1): 84-92. |
| [34] |
Kjartansson E. Constant Q-wave propagation and attenuation[J]. Journal of Geophysical Research, 1979, 84(B9): 4737-4748. |
| [35] |
蔡瑞乾, 孙成禹, 伍敦仕, 等. 黏声波动方程变机制数有限差分正演[J]. 石油地球物理勘探, 2019, 54(3): 529-538. CAI Ruiqian, SUN Chengyu, WU Dunshi, et al. Finite-difference numerical modeling with variable mechanisms for viscoacoustic wave equation[J]. Oil Geophysical Prospecting, 2019, 54(3): 529-538. |
| [36] |
Chen H, Zhou H, Li Q, et al. Two efficient modeling schemes for fractional Laplacian viscoacoustic wave equation[J]. Geophysics, 2016, 81(5): T233-T249. |
| [37] |
Carcione J M. A generalization of the Fourier pseudospectral method[J]. Geophysics, 2010, 75(6): A53-A56. |
| [38] |
Chen H, Zhou H, Rao R, et al. A matrix-transform numerical solver for fractional Laplacians viscoacoustic wave equation[J]. Geophysics, 2019, 84(4): T283-T297. DOI:10.1190/geo2018-0271.1 |
| [39] |
Chen H, Zhou H, Rao R, et al. Fractional Laplacian viscoacoustic wave equation low-rank temporal extrapolation[J]. IEEE Access, 2019, 7(1): 93187-93197. |
| [40] |
Chen H, Zhou H, Lin H, et al. Application of perfectly matched layer for scalar arbitrarily wide-angle wave equations[J]. Geophysics, 2013, 78(1): T29-T39. |
| [41] |
Plessix R E. A review of the adjoint-state method for computing the gradient of a functional with geophysical applications[J]. Geophysical Journal International, 2006, 167(2): 495-503. |
| [42] |
Métivier L, Brossier R. The SEISCOPE optimization toolbox:a large-scale nonlinear optimization library based on reverse communication[J]. Geophysics, 2016, 81(2): F1-F15. |
| [43] |
Nocedal J. Updating quasi-Newton matrices with limited storage[J]. Mathematics of Computation, 1980, 35(151): 773-773. |



 周辉, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院, 102249。Email:
周辉, 北京市昌平区府学路18号中国石油大学(北京)地球物理学院, 102249。Email: