② 山东省煤田地质局物测队, 山东济南, 山东 250104
② Geophysical Prospecting Team of Shandong Bureau of Geology, Jinan, Shandong 250104, China
勘探地震数据的成像方法包含Kirchhoff法和波动方程法(单程波、逆时偏移等)两大类。Kirchhoff方法以单地震道为计算输入,成像结果可根据输入数据的炮检距值进行排列以获得炮检距域共成像点道集,该道集中各道的炮检距值来自于输入道的炮检点间距。为区别于其他局部炮检距方法,也被称为“地表炮检距道集”。该道集是偏移迭代中速度更新的纽带,可为地震数据AVO分析、属性提取等深度信息发掘提供基础数据[1]。
波动方程方法考虑了多值射线路径等复杂传播,具有更高的成像精度[2-6]。但炮域计算的波动方法偏移只能输出零炮检距剖面,无法应用地表炮检距道集实施类似Kirchhoff偏移的后续计算,带来应用上的局限性。如针对山地资料起伏地表进行波动方程偏移时,无法应用Kirchhoff偏移,只能用波动方程偏移输出的地表炮检距道集进行速度更新[7-9]。部分波动方程偏移计算中,将炮点和检波点位置的间距作为偏移输出的标签,在最终偏移结果输出中重排以获得一个炮检距道集。该炮检距并非地表炮检距,不能进行速度更新等迭代。另外,波动方程偏移输出的角度道集深层角度窄小[10-11],且已有的研究[12]表明,不同方法计算的角度道集中,相同速度误差导致的成像结果中同一成像点同相轴的曲率不同,表现出应用于速度更新的不稳定性。因此,如何在目前应用的炮域波动方程偏移计算中高效输出地表炮检距道集,是具有实际应用意义的研究方向。
炮域波动方程偏移输出地表炮检距道集最直接的方法是, 将检波点数据按炮检距大小分成若干份后分别偏移,用炮检距均值标识不同结果,得到地表炮检距道集。该方法需对每炮数据多次执行偏移计算,计算强度大,难以大规模实施[13]。Zhao等[14]改进了上述算法,只计算少数炮检距段,再通过插值补齐所需炮检距位置数据。另一类波动方程地表炮检距输出方法被称为波动方程Kirchhoff偏移,因其所用Born方程与Kirchhoff积分公式相似,故而得名。差异之处在于:计算中炮点和检波点传播格林函数是用波动方程而非射线追踪法[15-17]。
属性偏移是通过两次偏移计算,将地震数据中的几何、物理属性,如走时、反射角、入射角、炮检距等,从地震数据映射到偏移结果中,从这两次成像结果的比值提取属性。该方法由Bleistein[18]提出,在立体层析等计算中获得应用[19]。Giboli等[20]和Lemaistre等[21]讨论了应用此方法输出炮检距属性的可能。本文以属性偏移为基础,研究了应用该方法进行地表炮检距域成像点道集计算;并以逆时偏移为例,分析了其计算强度(Computing intensity);分别以2D和3D模型对算法进行了数值验证,并将其应用于实际金属矿地震数据的真地表成像计算,获得了其地表炮检距道集。
1 属性偏移辅助波动方程炮域偏移输出炮检距道集的理论与实现 1.1 基于属性偏移的炮域地表炮检距道集理论| $ \begin{array}{l} I(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}}) = \int {\int G } (\mathit{\boldsymbol{x}},t|\mathit{\boldsymbol{s}},0)G(\mathit{\boldsymbol{x}}, - t|\mathit{\boldsymbol{r}},0) \times \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \ddot d(\mathit{\boldsymbol{r}},t|\mathit{\boldsymbol{s}},0){\rm{d}}\mathit{\boldsymbol{r}}{\rm{d}}t \end{array} $ | (1) |
式中:x为成像点位置;s为炮点位置;r为检波点位置;I(x,s)为炮点s在x点成像结果;G(x, t|s, 0)为炮点数据正传格林函数;G(x, -t|r, 0)为检波点数据反传格林函数;
Bleistein[18]指出,通过两次偏移计算,可估算出加权于数据上的定量参数,即描述成如下过程
| $ \begin{array}{*{20}{l}} {{I_{\rm{w}}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}}) = \int {\int G } (\mathit{\boldsymbol{x}},t|\mathit{\boldsymbol{s}},0)G(\mathit{\boldsymbol{x}}, - t|\mathit{\boldsymbol{r}},0) \times }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} [\ddot d(\mathit{\boldsymbol{r}},t|\mathit{\boldsymbol{s}},0)w(\mathit{\boldsymbol{x}}|\mathit{\boldsymbol{s}},\mathit{\boldsymbol{r}})]{\rm{d}}\mathit{\boldsymbol{r}}{\rm{d}}t} \end{array} $ | (2) |
式中w(x|s, r)是与成像点处炮点、检波点位置等有关的加权参数,它直接作用于偏移前数据,可以是入射角、反射角、炮点坐标或检波点坐标等。该加权参数可通过式(1)与式(2)两次偏移结果的比值估算得到
| $ w(\mathit{\boldsymbol{x}}|\mathit{\boldsymbol{s}},\mathit{\boldsymbol{r}}) \approx \frac{{{I_{\rm{w}}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}})}}{{I(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}})}} $ | (3) |
若加权系数w(x|s, r)为地表炮检距,则可计算出成像点位置的地表炮检距值,进而输出地表炮检距道集。
将式(1)~式(3)简化至波动方程偏移的互相关成像条件中[16],具体表示为
| $ I(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}}) = \int u (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}},t)\int v (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}},\mathit{\boldsymbol{r}},t){\rm{d}}\mathit{\boldsymbol{r}}{\rm{d}}t $ | (4) |
式中:u(x, s, t)是t时刻的炮点波场;v(x, s, r, t)是t时刻s处激发的检波点波场。
将炮检距h=s-r与炮域检波点数据相乘,再对乘积做偏移,结果为
| $ {I_{\rm{h}}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}}) = \int u (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}},t)\int \mathit{\boldsymbol{h}} v(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}},\mathit{\boldsymbol{r}},t){\rm{d}}\mathit{\boldsymbol{r}}{\rm{d}}t $ | (5) |
通过求式(5)与式(4)比值,获得单炮s在成像点x处的炮检距为
| $ {h_A}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}}) = \frac{{{I_{\rm{h}}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}})}}{{I(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}})}} $ | (6) |
根据获取的成像区各点炮检距值,将单炮成像结果排放到相应的炮检距中。依次计算所有炮点记录并叠加,便可获得最终的地表炮检距道集
| $ I(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{h}}) = \int I (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}})\delta [\mathit{\boldsymbol{h}} - {h_A}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}})]{\rm{d}}\mathit{\boldsymbol{s}} $ | (7) |
式中δ(·)为脉冲函数。
针对三维情形,依据式(4)~式(6)分别计算横向和纵向炮检距,继而获得总的炮检距值。
据式(5)推知横向炮检距加权数据偏移结果为
| $ {I_{{\rm{h}}x}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}}) = \int u (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}},t)\int {({\mathit{\boldsymbol{r}}_x} - {\mathit{\boldsymbol{s}}_x})} v(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}},\mathit{\boldsymbol{r}},t){\rm{d}}\mathit{\boldsymbol{r}}{\rm{d}}t $ | (8) |
同理,纵向炮检距加权数据偏移结果为
| $ {I_{{\rm{h}}y}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}}) = \int u (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}},t)\int {({\mathit{\boldsymbol{r}}_y} - {\mathit{\boldsymbol{s}}_y})} v(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}},\mathit{\boldsymbol{r}},t){\rm{d}}\mathit{\boldsymbol{r}}{\rm{d}}t $ | (9) |
据式(6)可得两个方向的炮检距分别为
| $ \left\{ {\begin{array}{*{20}{l}} {{h_{Ax}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}}) = \frac{{{I_{{\rm{h}}x}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}})}}{{I(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}})}}}\\ {{h_{Ay}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}}) = \frac{{{I_{{\rm{h}}y}}(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}})}}{{I(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}})}}} \end{array}} \right. $ | (10) |
根据求取的两个方向炮检距属性,重复计算各炮,即可获得最终的成像结果
| $ I(\mathit{\boldsymbol{x}},\mathit{\boldsymbol{h}}) = \int I (\mathit{\boldsymbol{x}},\mathit{\boldsymbol{s}})\delta (\mathit{\boldsymbol{h}} - \sqrt {h_{Ax}^2 + h_{Ay}^2} ){\rm{d}}\mathit{\boldsymbol{s}} $ | (11) |
波动方程偏移中,尤以逆时偏移计算强度最大。随着计算技术的发展,特别是图形处理器(GPU)的出现,通过众核并行加速,大幅度提高了逆时偏移的有限差分计算效率[24],推动了其工业计算应用。在GPU上进行逆时偏移计算时,为了突破CPU和GPU间带宽瓶颈的限制,采用随机边界处理条件[25],两次计算炮点波场传播,以计算换存储,节省了数据传输耗时。逆时偏移在GPU上的计算过程为:炮点波场正传到边界处被随机化,进行反传;检波点波场反传;二者在相同时刻相关成像;逐炮偏移叠加,获得整体的成像叠加剖面。
炮域波动方程偏移输出的是零炮检距剖面,即叠加剖面。根据上述属性偏移理论,需通过调制后数据的偏移结果与原始数据的偏移结果的比值计算成像点处的炮检距值,进而抽取获得成像后的地表炮检距道集。通过分析可知,两种偏移结果除输入的检波点数据不同外,其他成像要素均一致,因此可将整个计算过程整合到一起。
总结成像过程为:炮点波场正传到边界处并被随机化,然后反传;检波点波场和调制后的检波点波场分别反传,炮点波场和两个检波点波场分别在相同时刻相关成像,输出两种偏移单炮结果;应用两个波场比值抽取炮检距道集,逐炮计算叠加,获得最终成像的地表炮检距道集结果。
图 1是逆时偏移输出地表炮检距道集计算流程。显然,去掉调制波场成像部分即为普通逆时偏移。因炮点波场正、反两次传播未变,只是检波点正传部分增加了调制波场,故其总计算量仅增加约三分之一。

|
图 1 逆时偏移中两次偏移输出地表炮检距道集的计算流程 |
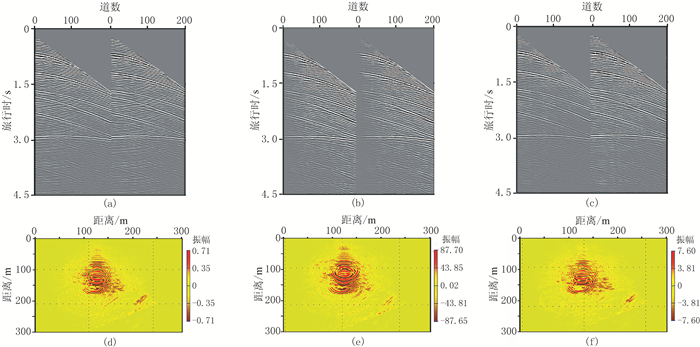
选用Marmousi模型进行方法流程试算,并与Kirchhoff计算的地表炮检距道集进行对比分析。
首先对所有240炮记录进行炮检距调制计算;然后分别对原数据和调制数据应用处理流程(图 1)进行深度偏移,每个单炮记录偏移结果根据式(6)所求炮检距值进行炮检距映射计算,叠加所有炮即可获得最终地表炮检距道集。
图 2是原始单炮记录和地表炮检距调制后的单炮记录,从图 2b可见调制后单炮中地震道能量随着炮检距的增加而增大。
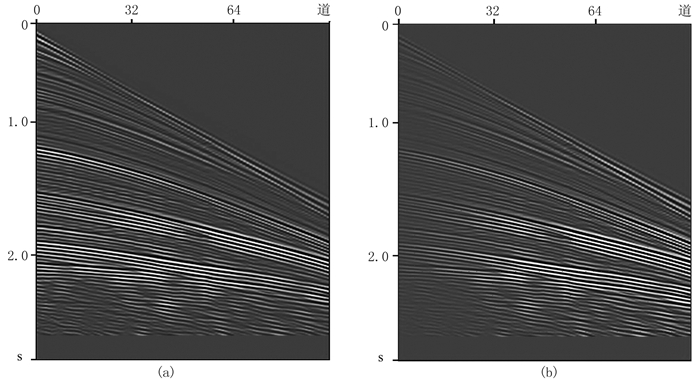
|
图 2 Marmousi模型单炮记录(a)及用地表炮检距调制结果(b) |
对原始数据和调制后的数据分别采用相同的成像参数进行偏移。针对原始单炮偏移结果(图 3a),求取两次偏移结果的比值,获得成像点对应的地表炮检距值(图 3b)。
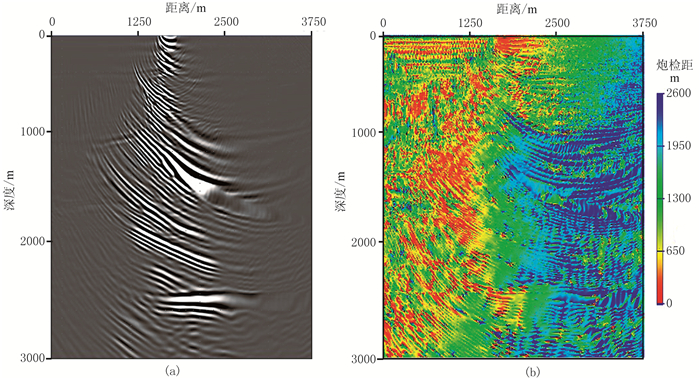
|
图 3 原始单炮偏移结果(a)及求取的成像点对应炮检距值(b) |
将成像结果按炮检距值分选到不同的炮检距,并将所有炮集记录依据上述流程计算、叠加、输出,获得最终的地表炮检距成像道集。应用Kirchhoff深度偏移对Marmousi模型进行成像计算,将其地表炮检距道集与本文方法进行对比。道集中最小炮检距为200m,最大炮检距为2600m,炮检距步长为100m。图 4和图 5分别是CMP150和CMP350处两种方法的道集对比。从中可见两种道集的总体振幅特征相似,但因波动方程偏移成像质量更好,浅层无动校拉伸问题,故储层更能聚焦成像,道集整体更为平直和光滑。
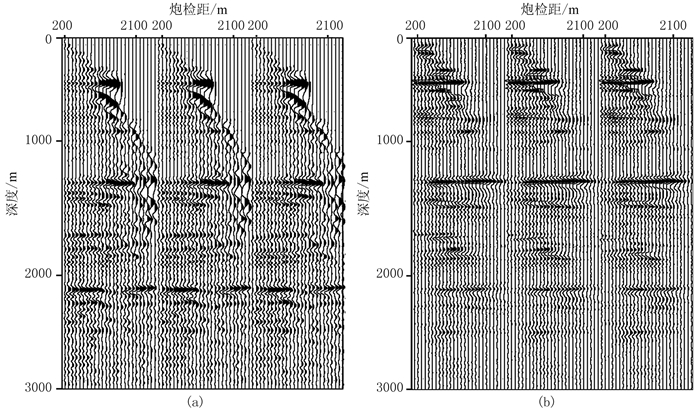
|
图 4 CMP150处Kirchhoff偏移(a)与逆时偏移(b)输出的地表炮检距道集对比 |
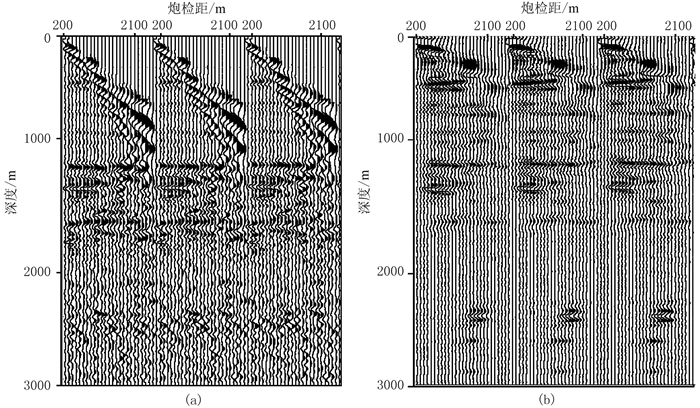
|
图 5 CMP350处Kirchhoff偏移(a)与逆时偏移(b)输出的地表炮检距道集对比 |
当速度模型准确时,偏移获得的共成像点道集呈平直状态;当速度模型存在误差,道集会不同程度地向下弯曲和向上翘起,这也是速度更新的基础。将Marmousi模型速度值分别提高和降低5%,进行输出地表炮检距道集计算。图 6显示提速5%时,同相轴呈欠偏移而向下弯曲;图 7是降速5%时,同相轴呈过偏移而向上弯曲。

|
图 6 提速5%欠偏移时成像道集剖面(a)及局部放大结果(b) |
|
图 7 降速5%过偏移时成像道集剖面(a)及局部放大结果(b) |
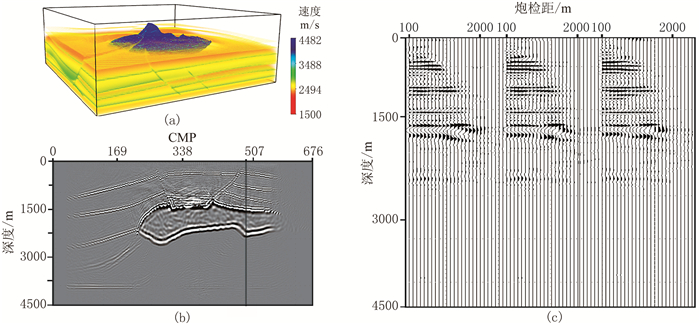
采用窄方位角SEG/EAGE模型作为3D测试模型,共计4800炮。三维地表炮检距计算时,需分别针对两个方向进行单炮数据调制并偏移计算,获取两个方向的炮检距分量后,采用式(12)抽取炮检距道集,最终将多炮叠加而获得最终道集剖面。
图 8是单炮记录中部分排列原始记录和两个方向调制后的结果及其偏移结果的深度切片。图 9是从计算结果中抽取的单条叠加剖面和单个炮检距道集。道集中,最小炮检距为100m,最大炮检距为2600m,炮检距步长为100m。
|
图 8 三维地表炮检距道集计算中部分单炮记录、调制结果及最终成像的深度切片 (a)部分原始单炮记录;(b)横向炮检距调制后的部分单炮记录;(c)纵向炮检距调制后的部分单炮记录;(d)原始单炮偏移结果深度切片;(e)图b偏移结果深度切片;(f)图c偏移结果深度切片 |
|
图 9 3D盐丘模型(a)、对应偏移剖面(b)及其中黑线处炮检距道集(c) |
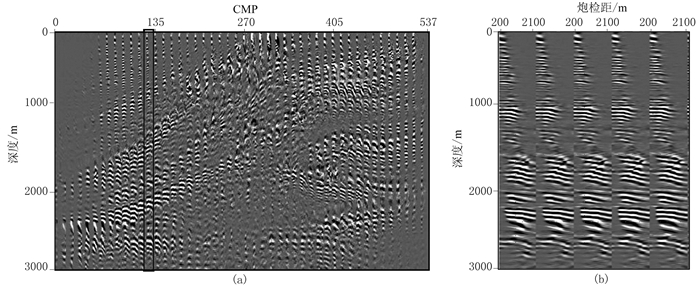
闽西南是中国重要的多金属矿集区,推覆体是其中一种重要的控矿构造。寻找深部推覆体赋存状态是深部矿产勘探的重要内容。地震勘探因其勘探深度和分辨率优势被寄予厚望。2017年,在该区采集了一条长约18000m二维地震测试剖面,炮间距为60m,道间距为20m,满覆盖次数约为60。该测线也是该区首条应用于金属矿勘探的地震测线。
区内地表结构复杂,高差大,基岩出露且地表不均匀性强,单炮记录信噪比低,成像计算难度大。通过系列研究和对比,波动方程真地表偏移获得最优成像结果[26-27],其中偏移速度模型来自地表层析反演速度与深层均方根速度转换的层速度的叠合。深度偏移对速度模型反应敏感,往往需几轮偏移和速度迭代计算。目前,迭代计算及速度准确性判断需要地表炮检距道集,而本文研究使这种真地表波动方程偏移速度更新及判断成为可能。
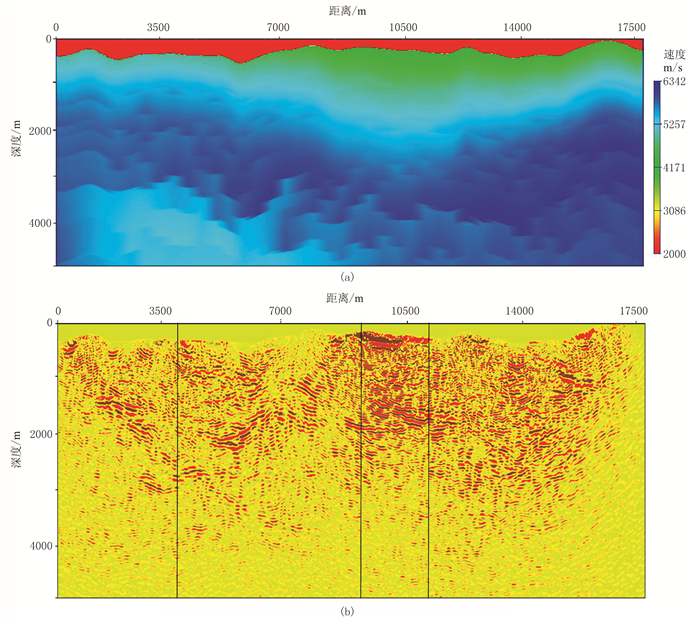
图 10a为地表与深层拼接的深度域速度模型;图 10b为应用该模型进行起伏地表偏移的剖面,从该剖面中选择三处(图 10b竖线)分别输出炮检距道,其最小炮检距为100m,最大炮检距为3600m,炮检距步长为100m。
|
图 10 波动方程真地表偏移速度模型(a)和偏移剖面(b) 黑竖线标示炮检距道集的三个位置 |
从图 11所示的地表炮检距道集可看出,不同成像位置处的道集初至时间不同,代表了不同地表高程变化。道集上不同程度存在速度优化的空间,同时道集上进一步的滤波等处理对提高最终成像质量有潜在可能,这些问题有待后续研究。

|
图 11 用本文方法输出的图 10标识位置的地表炮检距道集 |
本文介绍了一种基于属性偏移的两次偏移计算输出地表炮检距道集策略,它具有算法简便、运算效率高的特点,适合于大规模数据应用。但该方法计算的稳定性要求所计算成像点仅有一个稳相点,因此在复杂模型的炮检距映射中需引入光滑或正则化计算等。波动方程地表炮检距道集的高效计算,为单独应用波动方程偏移结果进行速度迭代和成像提供了基础,为类似波动方程真地表偏移等特殊计算的速度迭代提供了保障。
| [1] |
YilmazÖZ.SeismicDataAnalysis, Processing, Inver-sion and Interpretation[M].Society of Exploration Geophysicists, 2001, https://doi.org/10.1190/1.9781560801580.
|
| [2] |
Bednar J. A brief history of seismic migration[J]. Geophysics, 2005, 70(3): 3MJ-20MJ. |
| [3] |
吴帮玉, 杨辉, 孙文博, 等. 三维共偏移叠前地震数据反假频射线束形成偏移成像[J]. 地球物理学报, 2018, 61(8): 3297-3309. WU Bangyu, YANG Hui, SUN Wenbo, et al. Common offset 3D prestack seismic data anti-aliasing beamforming migration and imaging[J]. Chinese Journal of Geophysics, 2018, 61(8): 3297-3309. |
| [4] |
柯璇, 石颖. 基于一步法波场延拓的正演模拟和逆时偏移成像[J]. 地球物理学报, 2017, 60(11): 4468-4479. KE Xuan, SHI Ying. Forward simulation and reverse time migration imaging based on one step wavefield extrapolation[J]. Chinese Journal of Geophysics, 2017, 60(11): 4468-4479. DOI:10.6038/cjg20171131 |
| [5] |
陈生昌. 基于反射波动方程的地震反射数据波形成像[J]. 石油地球物理勘探, 2018, 53(3): 487-501. CHEN Shengchang. Seismic reflection data waveform imaging based on reflection wave equation[J]. Oil Geophysical Prospecting, 2018, 53(3): 487-501. |
| [6] |
李庆洋. T分布起伏地表最小二乘逆时偏移[J]. 石油地球物理勘探, 2019, 54(5): 1075-1083. LI Qingyang. Least-squares reverse time migration on undulated surface based on T-distribution[J]. Oil Geophysical Prospecting, 2019, 54(5): 1075-1083. |
| [7] |
程玉坤, 刘建红, 周振晓, 等. 速度建模特色技术的实际应用[J]. 石油地球物理勘探, 2017, 52(增刊2): 110-115. CHENG Yukun, LIU Jianhong, ZHOU Zhenxiao, et al. Depth-domain velocity model building for prestack depth imaging[J]. Oil Geophysical Prospecting, 2017, 52(S2): 110-115. |
| [8] |
刘定进, 胡光辉, 蔡杰雄, 等. 高斯束层析与全波形反演联合速度建模[J]. 石油地球物理勘探, 2019, 54(5): 1046-1056. LIU Dingjin, HU Guanghui, CAI Jiexiong, et al. A joint velocity model building method with Gaussian beam tomography and full waveform inversion for land seismicdata[J]. Oil Geophysical Prospecting, 2019, 54(5): 1046-1056. |
| [9] |
Sava P, Fomel S. Angle-domain common gathers by wavefield continuation methods[J]. Geophysics, 2003, 68(3): 1065-1074. |
| [10] |
Sirgue J, Jousselin P and Audebert F.Understanding wave-equation images gathers: A prerequisite for advanced post-processing and velocity model building[C].Extended Abstracts of 72nd EAGE Conference & Exhibition, 2010, 437-441.
|
| [11] |
Xu S, Zhang Y, Tang B. 3D angle gathers from reverse-time migration[J]. Geophysics, 2011, 76(2): S77-S92. |
| [12] |
Montel J and Lambare G.RTM and Kirchhoff angle domain common-image gathers for migration velocity analysis[C].SEG Technical Program Expanded Abstracts, 2011, 30: 3120-3124.
|
| [13] |
Yang Z, Huang S, Yan R.Improved subsalt tomography using RTM surface offset gathers[C]. SEG Technical Program Expanded Abstracts, 2015, 34: 5254-5258.
|
| [14] |
Zhao Y and Zhang H.Cost reduction of RTM surface offset gathers by local coherent events based interpolation[C].SEG Technical Program Expanded Abstracts, 2015, 34: 4587-4590.
|
| [15] |
Ehinger A, Lailly P, Marfurt K. Green's function implementation of common-offset, wave-equation migration[J]. Geophysics, 1996, 61(6): 1813-1821. DOI:10.1190/1.1444097 |
| [16] |
Etgen J.3D wave equation Kirchhoff migration[C].SEG Technical Program Expanded Abstracts, 2012, 31, http://dx.doi.org/10.1190/segam2012-0755.1.
|
| [17] |
Zhang G, Zhang M. Common-image gathers in the offset domain from reverse-time migration[J]. Journal of Applied Geophysics, 2014, 103: 99-103. DOI:10.1016/j.jappgeo.2014.01.005 |
| [18] |
Bleistein N. On the imaging of reflectors in the earth[J]. Geophysics, 1987, 52(7): 931-942. DOI:10.1190/1.1442363 |
| [19] |
Nguyen S, Baina R, Alerini M, et al. Stereo tomo-graphy assisted by migration of attributes[J]. Geophysical Prospecting, 2008, 56(5): 613-625. DOI:10.1111/j.1365-2478.2008.00699.x |
| [20] |
Giboli M, Baina R, Opera L, et al. Reverse time migration surface offset gathers: Part 1-A new method to produce "classical" common image gathers[C]. SEG Technical Program Expanded Abstracts, 2012, 31, http://dx.doi.org/10.1190/segam2012-1007.1.
|
| [21] |
Lemaistre L, Lencrerot R, Jousselin P, et al. Reverse time migration surface offset gathers part 2: using the full power of wide azimuth information[C]. SEG Technical Program Expanded Abstracts, 2012, 31: http://dx.doi.org/10.1190/segam2012-0421.1.
|
| [22] |
Schuster G. Reverse-time migration=generalized diffraction stack migration[C]. SEG Technical Program Expanded Abstracts, 2002, 21: 1280-1283.
|
| [23] |
Stolt R H, Benson A K. Seismic migration:theory and practice//Handbook of Geophysical Exploration[M]. Geophysical Press, 1986.
|
| [24] |
Liu H, Li B, Liu H, et al. The issue of prestack reverse time migration and solutions with graphic processing unit implementation[J]. Geophysical Prospecting, 2012, 60(5): 906-918. DOI:10.1111/j.1365-2478.2011.01032.x |
| [25] |
Clapp R. Reverse time migration with random boun-daries[C]. SEG Technical Program Expanded Abstracts, 2009, 28: 2343-2347.
|
| [26] |
Liu G, Meng X, Ni J, et al. Evaluation of the 2D reflection seismic method toward the exploration of thrust-controlled mineral deposits in southwestern Fujian Province, China[J]. Geophysics, 2018, 83(4): B209-B220. DOI:10.1190/geo2017-0289.1 |
| [27] |
Liu G, Meng X, Liu Y. Depth migration with the near surface:A case study for mineral exploration in China[J]. Interpretation, 2019, 7(4): T809-T817. DOI:10.1190/INT-2018-0125.1 |



 刘国峰, 北京市海淀区学院路29号中国地质大学(北京)地球物理与信息技术学院, 100083。Email:
刘国峰, 北京市海淀区学院路29号中国地质大学(北京)地球物理与信息技术学院, 100083。Email: