② 山东科技大学山东省沉积成矿作用与沉积矿产重点实验室, 山东青岛 266580;
③ 中国石油大庆榆树林油田有限责任公司地质研究所, 黑龙江大庆 163000
② Key Laboratory of Sedimentary Mineralization and Sedimentary Minerals, Shandong University of Science and Technology, Qingdao, Shandong 266580, China;
③ Geological Research Institute of Daqing Yushulin Oilfield Co., Ltd. Daqing, Helongjiang 163000, China
由于已充分考虑射线偏折影响,叠前深度偏移技术在速度横向变化剧烈及高倾角构造区可获得较好成像效果。然而,深度偏移对初始速度模型较为敏感,速度的准确性制约最终的成像精度[1-2],因此获取高精度速度模型对于提高成像质量具有重要意义。在速度反演过程中,速度场分为低波数段(速度值)和高波数段(速度分界面)[3-5]。目前,通常使用层析反演和偏移速度估计低波数成分,将反射界面解释数据及其他先验信息(井数据、VSP数据等)作为约束加入速度反演中,获得高波数成分。然而,任何一种速度分析或反演方法都不可能一次性完成高精度速度建模,需反复迭代从而尽可能地接近真实速度场。为进一步提高速度场精度,估计出更多的波数段速度场成分,通常采用多种技术方法结合使速度建模结果更为精细,包含更多细节、更多尺度速度变化情况。
全波形反演(FWI)作为一种高精度速度建模和油藏描述方法,具有反映地下地质构造细节及岩性类别等特征[6],成为物探行业研究热点。该方法利用叠前地震波场中的动力学、运动学信息估计地层介质弹性参数,在低频速度模型建立和中高频地震成像之间建立联系。经过多年的发展研究,已被证实是反演高精度地球物理参数的有效手段[7-8]。
然而,从数学角度来看,FWI是一个高度病态的非线性问题,需要解决收敛性和多解性问题[9]。从地球物理角度来看,该方法涉及模型的误差泛函建立、波场数值模拟、数据预处理等多方面内容[10-11],因此该技术的研发依旧任重道远。FWI作为一种地球物理反演方法,目前大多采用迭代的局部优化技术来实现,其寻优过程是尽量减少观测数据与模拟数据之间差异的不断尝试,但这一线性问题是不适定的,求解模型存在多解性。
为克服这一缺陷,先验信息约束必不可少,排除一些可能的错误模型,力促反演结果收敛到先验模型附近的最优解。秦宁等[12]采用井数据对反演过程进行约束,反演结果同真实速度吻合度较高。王咸彬等[5]利用散乱数据插值方法和网格剖分将测井速度和偏移速度进行融合,在断层、尖灭等特殊岩性体部位获得较好速度场建模。Rüger等[13]应用局部解释数据约束反演过程,所得结果与理论模型较好吻合。Peters等[14]在反演的目标函数正则化项中附加上倾角约束,并在Marmousi模型和BP模型中取得较好应用效果。
本文将地层解释数据构成预条件矩阵,应用预条件正则化约束反演过程,给出反演的误差泛函及梯度计算公式,构建一种基于地质模型约束的误差泛函表达式。与常规全波形反演方法相比,它具有较高的速度反演精度。采用Marmousi模型测试并比较不同速度反演方法的处理结果,证明改进方法具有较高反演精度;最后利用M工区实际地震数据叠前深度偏移结果验证了该方法的有效性。
1 方法原理FWI利用波动方程数值解代替反演过程中的半解析解,精确模拟地震波在地层介质中的传播规律,同时提供完整的波形信息,有效提高反演精度[15-16],增强其实用性。
1.1 常规FWI方法原理大部分反演问题都采用最小二乘估算反演误差。全波形反演作为一种最优化问题,其实质就是一种不断测试并调整的自动循环优化过程[17]。通过使用地震数据的所有信息,包括振幅、相位、走时等,作为输入参数进行反演,最终目的是使观测的实际地震数据与给定模型模拟得到的地震数据之间误差最小化[18]。常规FWI目标函数式为
| $ \Delta d = {\left\| {{\mathit{\boldsymbol{W}}_{\rm{d}}}({\mathit{\boldsymbol{s}}_{{\rm{obs}}}} - \mathit{\boldsymbol{s}})} \right\|^2} + {\alpha ^2}{\left\| {{\mathit{\boldsymbol{W}}_{\rm{n}}}(\mathit{\boldsymbol{V}} - {\mathit{\boldsymbol{V}}_{{\rm{input}}}})} \right\|^2} $ | (1) |
式中:V为反演速度场;Vinput为输入速度场矢量;sobs为记录的波场矢量;s为模拟地震波场矢量;α为正则化参数;Wd为m道原始记录的标准方差δdj(j=1, 2, …, m)的对角矩阵,Wn为m道模拟地震波场标准方差δnj(j=1, 2, …, m)的对角矩阵,且有
| $ \left\{ \begin{array}{l} {\mathit{\boldsymbol{W}}_{\rm{d}}} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{\delta _{{{\rm{d}}_1}}}}}}&0& \cdots &0\\ 0&{\frac{1}{{{\delta _{{{\rm{d}}_2}}}}}}&0& \cdots \\ {}&{}& \vdots &{}\\ 0& \cdots &0&{\frac{1}{{{\delta _{{{\rm{d}}_m}}}}}} \end{array}} \right]\\ {\mathit{\boldsymbol{W}}_{\rm{n}}} = \left[ {\begin{array}{*{20}{c}} {\frac{1}{{{\delta _{{{\rm{n}}_1}}}}}}&0& \cdots &0\\ 0&{\frac{1}{{{\delta _{{{\rm{n}}_2}}}}}}&0& \cdots \\ {}&{}& \vdots &{}\\ 0& \cdots &0&{\frac{1}{{{\delta _{{{\rm{n}}_m}}}}}} \end{array}} \right] \end{array} \right. $ | (2) |
求式(1)对反演速度模型V的一阶导数
| $ \mathit{\boldsymbol{V}} = {\mathit{\boldsymbol{A}}^{ - 1}}\mathit{\boldsymbol{b}} $ | (3) |
其中
| $ \begin{array}{*{20}{l}} {\mathit{\boldsymbol{A}} = {\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{W}}_{\rm{d}}^{\rm{T}}{\mathit{\boldsymbol{W}}_{\rm{d}}}\mathit{\boldsymbol{G}} + {\alpha ^2}\mathit{\boldsymbol{W}}_{\rm{n}}^{\rm{T}}{\mathit{\boldsymbol{W}}_{\rm{n}}}}\\ {\mathit{\boldsymbol{b}} = {\mathit{\boldsymbol{G}}^{\rm{T}}}\mathit{\boldsymbol{W}}_{\rm{d}}^{\rm{T}}{\mathit{\boldsymbol{W}}_{\rm{d}}}\mathit{\boldsymbol{s}}_j^{{\rm{obs}}} + {\alpha ^2}\mathit{\boldsymbol{W}}_{\rm{n}}^{\rm{T}}{\mathit{\boldsymbol{W}}_{\rm{n}}}{\mathit{\boldsymbol{V}}_{{\rm{input}}}}} \end{array} $ |
式中G表示正演算子。
1.2 地质构造约束全波形反演基本原理常规FWI方法反演未考虑地质构造因素的影响,其反演精度有待进一步提高。因此,本文将地质构造因素引入目标函数,作为约束条件参与速度场的迭代更新,则目标函数式(1)变为
| $ \begin{array}{*{20}{l}} {\Delta d = {{\left\| {{\mathit{\boldsymbol{W}}_{\rm{d}}}({\mathit{\boldsymbol{s}}_{{\rm{obs}}}} - \mathit{\boldsymbol{s}})} \right\|}^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \xi [\alpha {{\left\| {{\mathit{\boldsymbol{W}}_{\rm{n}}}(\mathit{\boldsymbol{V}} - {\mathit{\boldsymbol{V}}_{{\rm{input}}}})} \right\|}^2} + }\\ {{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \beta {{\left\| {\mathit{\boldsymbol{ \boldsymbol{\varGamma} V}}} \right\|}^2} + \gamma {{\left\| {\mathit{\boldsymbol{ \boldsymbol{\varLambda} V}}} \right\|}^2}]} \end{array} $ | (4) |
式中:Γ和Λ分别表示平行和垂直地层倾角的正则项(见式(8));α、β、γ、ξ分别为正则化参数。
求解式(4)对V的一阶导数
| $ \mathit{\boldsymbol{V}} = \frac{1}{6}{\mathit{\boldsymbol{A}}^{ - 1}}\mathit{\boldsymbol{B}} $ | (5) |
其中
| $ \begin{array}{l} \mathit{\boldsymbol{A}} = {{\mathit{\boldsymbol{\bar G}}}^{\rm{T}}}\mathit{\boldsymbol{\bar W}}_{\rm{d}}^{\rm{T}}{{\mathit{\boldsymbol{\bar W}}}_{\rm{d}}}\mathit{\boldsymbol{\bar G}} + \xi (\alpha \mathit{\boldsymbol{\bar W}}_{\rm{n}}^{\rm{T}}{{\mathit{\boldsymbol{\bar W}}}_{\rm{n}}} + \beta {{\mathit{\boldsymbol{ \boldsymbol{\bar \varGamma} }}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\bar \varGamma} }} + \gamma {{\mathit{\boldsymbol{ \boldsymbol{\bar \varLambda} }}}^{\rm{T}}}\mathit{\boldsymbol{ \boldsymbol{\bar \varLambda} }})\\ \mathit{\boldsymbol{B}} = {{\mathit{\boldsymbol{\bar G}}}^{\rm{T}}}\mathit{\boldsymbol{\bar W}}_{\rm{d}}^{\rm{T}}{\mathit{\boldsymbol{W}}_{\rm{d}}}\mathit{\boldsymbol{s}}_j^{{\rm{obs}}} + \xi \alpha \mathit{\boldsymbol{\bar W}}_{\rm{n}}^{\rm{T}}{{\mathit{\boldsymbol{\bar W}}}_{\rm{n}}}{\mathit{\boldsymbol{V}}_{{\rm{input}}}} \end{array} $ |
且有
| $ \left\{ \begin{array}{l} {{\mathit{\boldsymbol{\bar W}}}_d} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{W}}_{{{\rm{d}}_1}}}}&0& \cdots &0\\ 0&{{\mathit{\boldsymbol{W}}_{{{\rm{d}}_2}}}}&0& \cdots \\ {}&{}& \ddots &{}\\ 0& \cdots &0&{{\mathit{\boldsymbol{W}}_{{{\rm{d}}_m}}}} \end{array}} \right]\\ {{\mathit{\boldsymbol{\bar W}}}_n} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{W}}_{{{\rm{n}}_1}}}}&0& \cdots &0\\ 0&{{\mathit{\boldsymbol{W}}_{{{\rm{n}}_2}}}}&0& \cdots \\ {}&{}& \ddots &{}\\ 0& \cdots &0&{{\mathit{\boldsymbol{W}}_{{{\rm{n}}_m}}}} \end{array}} \right]\\ \mathit{\boldsymbol{\bar G}} = \left[ {\begin{array}{*{20}{c}} {{\mathit{\boldsymbol{G}}_1}}&0& \cdots &0\\ 0&{{\mathit{\boldsymbol{G}}_2}}&0& \cdots \\ {}&{}& \ddots &{}\\ 0& \cdots &0&{{\mathit{\boldsymbol{G}}_m}} \end{array}} \right] \end{array} \right. $ | (6) |
式中:Wd1表示矩阵Wd的列向量;Wn1表示Wn的列向量。对于改进的目标函数表达式(4),其重点是引入地质构造算子。
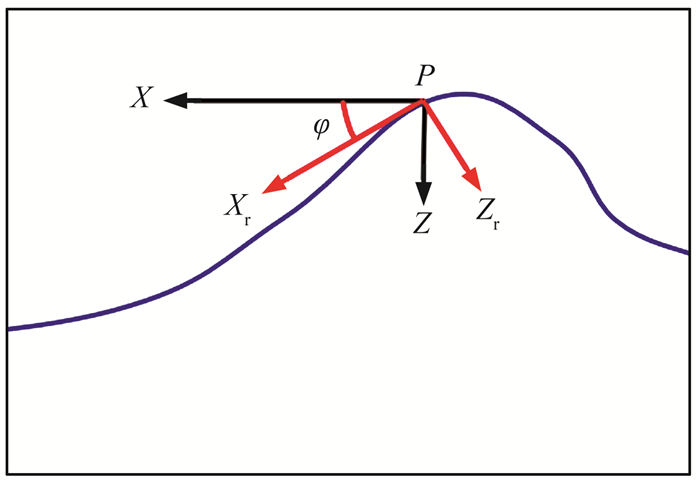
很多方法将目标点位置处的地层倾角或周围某一特定的角度作为构造算子[19-20]。在本算法中,工区的所有地质倾角都作为构造算子参与反演。从解释数据中读取相关信息后,计算地震振幅在垂直方向rz(x, z)和水平方向rx(x, z)的一阶深度域导数、一阶空间导数,则倾角为水平坐标轴X与数据最小梯度方向矢量之间的夹角(图 1)[21]。基于上述定义,倾角公式为
| $ \varphi (x,z) = {\rm{tan}}{ ^{ - 1}}\frac{{{\mathit{\boldsymbol{r}}_x}(x,z)}}{{{\mathit{\boldsymbol{r}}_z}(x,z)}} $ | (7) |
|
图 1 倾角示意图 蓝线表示地震反射同相轴;φ表示反射点所在位置倾角;X-Z表示正常坐标系;Xr-Zr表示旋转后的坐标系 |
计算出构造角度之后,需沿局部倾角构建地质构造反演算子Γ和Λ,构建结果如图 1所示。利用该算子计算反演公式(4)的两个正则项,对振幅在垂直方向和水平方向的一阶时间、空间导数Rx(x, z)、Rz(x, z)进行一阶Tikhonov正则化,地质构造反演算子表达式为
| $ \left\{ \begin{array}{l} \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} = {\mathit{\boldsymbol{Q}}_{ {\rm{cos}} }}{\mathit{\boldsymbol{R}}_x} + {\mathit{\boldsymbol{Q}}_{ {\rm{sin}} }}{\mathit{\boldsymbol{R}}_z}\\ \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} = - {\mathit{\boldsymbol{Q}}_{{\rm{sin}} }}{\mathit{\boldsymbol{R}}_x} + {\mathit{\boldsymbol{Q}}_{ {\rm{cos}} }}{\mathit{\boldsymbol{R}}_z}\\ {\mathit{\boldsymbol{Q}}_{{\rm{cos}}}} = \left[ {\begin{array}{*{20}{c}} { {\rm{cos}} {\varphi _1}}&0& \cdots &0\\ 0&{ {\rm{cos}} {\varphi _2}}&0& \cdots \\ \ddots &{}&{}&{}\\ 0& \cdots &0&{ {\rm{cos}} {\varphi _m}} \end{array}} \right]\\ {\mathit{\boldsymbol{Q}}_{{\rm{sin}}}} = \left[ {\begin{array}{*{20}{c}} { {\rm{sin}} {\varphi _1}}&0& \cdots &0\\ 0&{ {\rm{sin}} {\varphi _2}}&0& \cdots \\ {}& \ddots &{}&{}\\ 0& \cdots &0&{ {\rm{sin}} {\varphi _m}} \end{array}} \right] \end{array} \right. $ | (8) |
式中φj(j=1, 2, …, m)表示m道记录中的第j道所在位置处的倾角。
速度梯度可表示为目标函数对速度V的导数
| $ \mathit{\boldsymbol{T}}(\mathit{\boldsymbol{V}}) = \frac{{\partial \Delta d(\mathit{\boldsymbol{V}})}}{{\partial \mathit{\boldsymbol{V}}}} $ | (9) |
将式(4)代入式(9),可得
| $ \begin{array}{l} \mathit{\boldsymbol{T}}(\mathit{\boldsymbol{V}}) = \frac{{\partial \Delta d(\mathit{\boldsymbol{V}})}}{{\partial \mathit{\boldsymbol{V}}}} = \langle 2{\mathit{\boldsymbol{W}}_{\rm{d}}}(\mathit{\boldsymbol{s}} - {\mathit{\boldsymbol{s}}_{{\rm{obs}}}}) + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} 2\xi [\alpha {\mathit{\boldsymbol{W}}_{\rm{m}}}(\mathit{\boldsymbol{V}} - {\mathit{\boldsymbol{V}}_{{\rm{input}}}}) + \beta \mathit{\boldsymbol{ \boldsymbol{\varGamma} \boldsymbol{\varLambda} }} + \gamma \mathit{\boldsymbol{ \boldsymbol{\varLambda} V}}]\frac{{\partial \mathit{\boldsymbol{s}}}}{{\partial \mathit{\boldsymbol{V}}}}\rangle \end{array} $ | (10) |
式中〈·〉表示向量或矩阵的内积运算。
关于速度V的导数表示为
| $ \frac{{\partial s}}{{\partial \mathit{\boldsymbol{V}}}} = \mathop {{\rm{lim}}}\limits_{_{\varepsilon \to 0}} \frac{{\mathit{\boldsymbol{s}}(\mathit{\boldsymbol{V}} + \varepsilon \Delta \mathit{\boldsymbol{V}}) - \mathit{\boldsymbol{s}}(\mathit{\boldsymbol{V}})}}{{\varepsilon \Delta \mathit{\boldsymbol{V}}}} $ | (11) |
式中ΔV表示速度扰动。将式(11)中的s(V+εΔV)、s(V)分别代入常密度声波方程,即表示为
| $ \left\{ \begin{array}{l} \frac{1}{{{\mathit{\boldsymbol{V}}^2}}}\frac{{{\partial ^2}\mathit{\boldsymbol{s}}(\mathit{\boldsymbol{V}})}}{{\partial {t^2}}} = \frac{{{\partial ^2}\mathit{\boldsymbol{s}}(\mathit{\boldsymbol{V}})}}{{\partial {x^2}}} + \frac{{{\partial ^2}\mathit{\boldsymbol{s}}(\mathit{\boldsymbol{V}})}}{{\partial {z^2}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {12{\rm{a}}} \right)\\ \frac{1}{{{{(\mathit{\boldsymbol{V}} + \varepsilon \Delta \mathit{\boldsymbol{V}})}^2}}}\frac{{{\partial ^2}\mathit{\boldsymbol{s}}(\mathit{\boldsymbol{V}} + \varepsilon \Delta \mathit{\boldsymbol{V}})}}{{\partial {t^2}}}\\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} = \frac{{{\partial ^2}\mathit{\boldsymbol{s}}(\mathit{\boldsymbol{V}} + \varepsilon \Delta \mathit{\boldsymbol{V}})}}{{\partial {x^2}}} + \frac{{{\partial ^2}\mathit{\boldsymbol{s}}(\mathit{\boldsymbol{V}} + \varepsilon \Delta \mathit{\boldsymbol{V}})}}{{\partial {z^2}}}{\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \left( {12{\rm{b}}} \right){\kern 1pt} {\kern 1pt} \end{array} \right. $ |
将式(12b)对V进行泰勒展开,舍弃高阶项后得
| $ \begin{array}{*{20}{l}} {\frac{{1 - \frac{{2\varepsilon \Delta \mathit{\boldsymbol{V}}}}{\mathit{\boldsymbol{V}}}}}{{{V^2}}}\frac{{{\partial ^2}\mathit{\boldsymbol{s}}(\mathit{\boldsymbol{V}} + \varepsilon \Delta \mathit{\boldsymbol{V}})}}{{\partial {t^2}}}}\\ {\quad = \frac{{{\partial ^2}\mathit{\boldsymbol{s}}(\mathit{\boldsymbol{V}} + \varepsilon \Delta \mathit{\boldsymbol{V}})}}{{\partial {x^2}}} + \frac{{{\partial ^2}\mathit{\boldsymbol{s}}(\mathit{\boldsymbol{V}} + \varepsilon \Delta \mathit{\boldsymbol{V}})}}{{\partial {z^2}}}} \end{array} $ | (13) |
将式(12a)与式(13)合并,可得
| $ (\frac{1}{{{\mathit{\boldsymbol{V}}^2}}}\frac{{{\partial ^2}}}{{\partial {t^2}}} - \frac{{{\partial ^2}}}{{\partial {x^2}}} - \frac{{{\partial ^2}}}{{\partial {z^2}}})\frac{{\partial \mathit{\boldsymbol{s}}}}{{\partial \mathit{\boldsymbol{V}}}}\varepsilon \Delta \mathit{\boldsymbol{V}} = \frac{{2\varepsilon \Delta \mathit{\boldsymbol{V}}}}{{{V^3}}}\frac{{\mathit{\boldsymbol{s}}(\mathit{\boldsymbol{V}} + \varepsilon \Delta \mathit{\boldsymbol{V}})}}{{\partial {t^2}}} $ | (14) |
对式(14)采用波场扰动的局部近似,可表示为
| $ (\frac{1}{{{\mathit{\boldsymbol{V}}^2}}}\frac{{{\partial ^2}}}{{\partial {t^2}}} - {\nabla ^2})\frac{{\partial \mathit{\boldsymbol{s}}}}{{\partial \mathit{\boldsymbol{V}}}} = \frac{2}{{{\mathit{\boldsymbol{V}}^3}}}\frac{{{\partial ^2}\mathit{\boldsymbol{s}}(\mathit{\boldsymbol{V}})}}{{\partial {t^2}}} $ | (15) |
式中右端项
| $ \frac{{\partial \mathit{\boldsymbol{s}}}}{{\partial \mathit{\boldsymbol{V}}}} = f\left[ {\frac{2}{{{\mathit{\boldsymbol{V}}^3}}}\frac{{{\partial ^2}\mathit{\boldsymbol{s}}(\mathit{\boldsymbol{V}})}}{{\partial {t^2}}}} \right] $ | (16) |
再将式(16)代入式(10),则对应的速度更新梯度表示为
| $ \begin{array}{l} \mathit{\boldsymbol{T}}(\mathit{\boldsymbol{V}}) = \frac{4}{{{\mathit{\boldsymbol{V}}^3}}}\sum {_\tau \frac{{{\partial ^2}s(\mathit{\boldsymbol{V}})}}{{\partial {\tau ^2}}}} f[{\mathit{\boldsymbol{W}}_{\rm{d}}}(\mathit{\boldsymbol{s}}(\mathit{\boldsymbol{V}}) - {\mathit{\boldsymbol{s}}_{{\rm{obs}}}})] + \\ {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} {\kern 1pt} \xi [\alpha \sum {_\tau {\mathit{\boldsymbol{W}}_{\rm{n}}}} \mathit{\boldsymbol{s}}(\mathit{\boldsymbol{V}} - {\mathit{\boldsymbol{V}}_{{\rm{input}}}}) + \beta \sum \mathit{\boldsymbol{ \boldsymbol{\varGamma} }} \mathit{\boldsymbol{V}} + \gamma \sum \mathit{\boldsymbol{ \boldsymbol{\varLambda} }} \mathit{\boldsymbol{V}}] \end{array} $ | (17) |
对于本文使用的反演方法,需要指定式(4)中的正则化参数,地质构造算子的相对权重(α、β、γ)和全局权重(ξ)控制调节方程中模拟波场与记录波场的误差泛函项与地质构造约束项的权重关系。相关参数可由解释人员确定相对权重以调整地质解释构造,采用一般交叉验证方法,找到ξ的最优值[22],从而提高反演结果的质量。
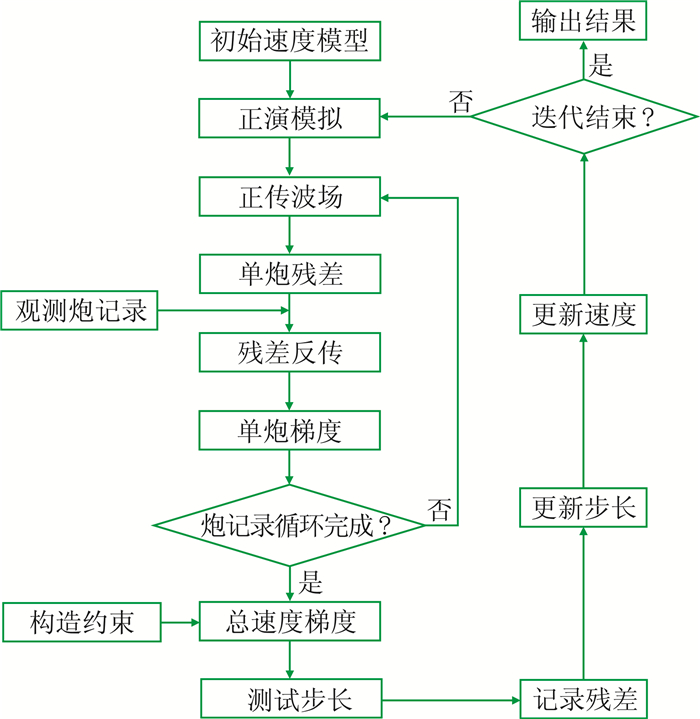
本文提出的基于构造模型约束的FWI反演流程如图 2所示。其实现过程可概括为:①采用层析速度作为初始速度模型输入;②做正演模拟,对模拟记录与实际观测记录求取残差,并将所有时刻的炮记录残差反传,计算单炮梯度;③炮模拟循环完毕后,计算整个速度场梯度值;④将构造解释数据引入式(4)对正则化项进行约束,给定一个初始测试步长进行迭代更新;并根据反射界面和断层位置的变化更新解释数据,通过迭代结果判断并优化当前的步长,从而使最终结果满足终止条件,输出反演结果;否则继续迭代计算。
|
图 2 构造模型约束全波形反演流程图 |
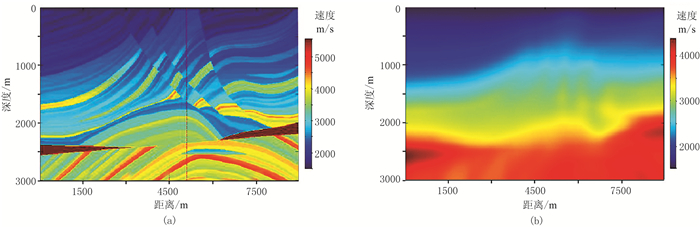
为了验证本文方法的有效性,本次选用Mar-mousi模型进行测试。模型中地层倾角变化剧烈,存在高速异常体,记录的地震波场中以复杂反射波场为主。对原始纵波速度场(图 3a)做平滑处理后作为初始速度场(图 3b)。
|
图 3 用于测试的原始纵波速度场(a)和平滑后初始速度场(b) |
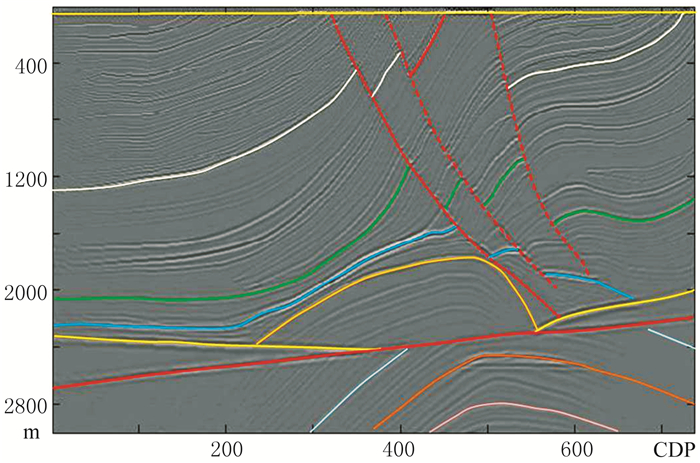
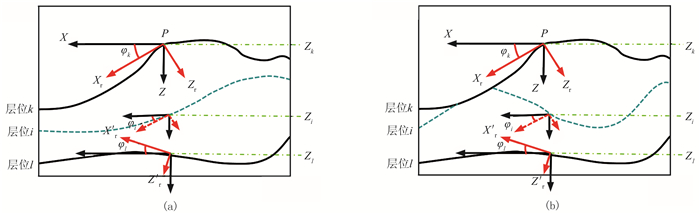
在成像剖面中,解释几个强反射地层和断层,解释数据分布如图 4所示。地层解释数据进行约束时,设置解释数据中地层与地层、地层与断层间接触关系。通常情况下,两套地层为整合接触,可设置两套地层之间地层为等比例分布,顶底地层之间的同一个X坐标位置P的地层倾角计算公式为
| $ {\varphi _i} = {\varphi _k} + ({\varphi _k} - {\varphi _l})*\frac{{{z_i} - {z_k}}}{{{z_l} - {z_k}}} $ | (18) |
|
图 4 Marmousi模型解释数据 |
式中zk、zi、zl和φk、φi、φl分别表示当前X坐标位置处不同地层的深度坐标和地层倾角(图 5a)。两套地层为不整合接触(剥蚀),可设置层间趋势与底层相同(图 5b),顶底地层之间的同一个X坐标位置P地层倾角计算公式为
| $ {\varphi _i}{\rm{ = }}{\varphi _k} $ | (19) |
|
图 5 整合(a)与不整合(b)地层之间地层倾角及坐标计算示意图 |
对于断层,主要是控制地层速度反演不能跨越断层进行,维持断层两侧的速度差异性[23]。基于上述方法原理,建立整个工区的构造约束算子并参与反演过程。
采用时间2阶、空间8阶的有限差分波动方程进行正演,选用主频为15Hz、采样率为1.5ms的雷克子波作为震源。检波点位于表面,采样间隔为20m,炮间距为100m。一共进行93个炮点正演。
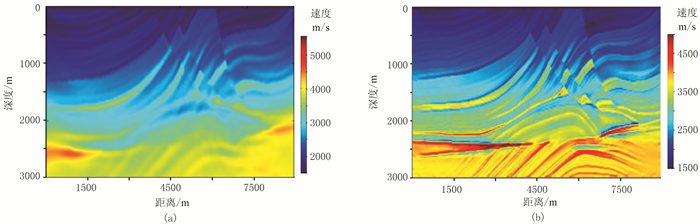
将图 3b的初始速度作为输入,分别采用式(8)和式(11)进行600次迭代,得到常规FWI(图 6a)和本文改进方法(图 6b)的反演结果。
|
图 6 常规FWI方法(a)与改进方法(b)反演速度结果对比 |
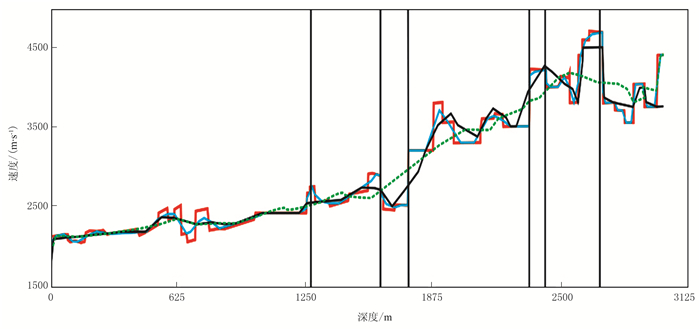
抽取图 3a中红线所在位置的原始速度、输入速度和反演速度值进行对比,结果如图 7所示。
|
图 7 速度对比结果 红线为真实速度,绿线为输入速度;黑线为常规反演结果,蓝线为改进方法反演结果;竖线表示解释地层所在位置 |
对比两种反演方法的反演速度结果可见,在输入速度模型较为精确的情况下,常规FWI方法可较好反演出与真实速度相匹配的速度场,但对于细节的反映与真实速度相差较大。在地层因素的约束下,本文改进方法反演结果能显示速度细节,反演速度与真实速度匹配较高。
3 实际数据应用采用M工区地震数据进行测试,深度偏移层速度作为初始输入速度场,提取子波作为震源子波进行
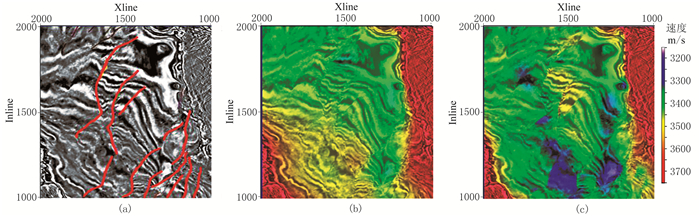
正演[6]。解释数据的水平切片如图 8a所示,设置强反射界面之间的地层接触关系,将解释数据引入反演公式,常规FWI反演和地质模型约束FWI反演的速度结果如图 8b和图 8c所示。可以看到,将地质模型约束引入到速度反演当中,提高了速度反演精度,改善复杂结构的成像质量。本文改进方法在速度反演时,速度的更新以地质模型为约束条件,在不同的模型位置处根据约束条件获取不同的速度变化值,地质构造分界面速度值发生变化,速度精度得以提高。
|
图 8 解释数据和反演速度结果 (a)解释数据水平切片;(b)常规FWI反演速度切片;(c)地质模型约束的FWI反演速度切片 |
选取某位置的成像剖面进行对比,结果如图 9所示。可见常规FWI速度反演的偏移剖面(图 9a)与基于地质模型约束的FWI反演的偏移剖面(图 9b)整体构造形态大致相同,但后者断面成像清晰,构造形态更加符合地质认识,断面下部反射特征明显,波阻特征清楚,成像质量好于前者。

|
图 9 常规FWI(a)与地质模型约束FWI(b)反演速度的成像剖面 |
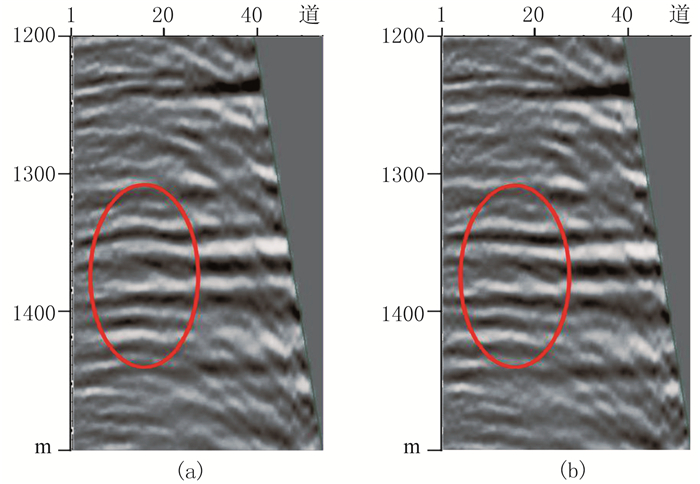
抽取剖面中蓝线位置处的道集(图 10)进行对比,可见常规FWI反演速度的成像道集同相轴未完全校平,依然表现为扭曲。而基于地质模型约束的FWI反演速度,其成像道集同相轴已被明显拉平,且能量聚焦,说明该位置处速度准确。
|
图 10 常规FWI(a)与模型约束FWI(b)反演速度的偏移(NMO)道集 |
基于地质模型约束的FWI反演方法,能够有效反演精度较高、与真实速度误差较小的速度场,该方法受到地震解释数据建立的地质模型约束,改进了常规FWI的误差泛函建立方式;模型测试结果表明,本文所提方法具有较好的反演效果;在实际数据应用中,采用本文方法反演的速度进行叠前深度偏移,能够得到较好的成像结果。
| [1] |
慕鑫茹, 黄建平, 李振春, 等. 基于最佳平方逼近的TTI介质解耦qP波与qSV波逆时偏移[J]. 石油地球物理勘探, 2019, 54(6): 1280-1292. MU Xinru, HUANG Jianping, LI Zhenchun, et al. Reverse time migration of decoupled qP- and qSV-waves in TTI media with the optimal quadratic approximation[J]. Oil Geophysical Prospecting, 2019, 54(6): 1280-1292. |
| [2] |
马俊彦, 张龙, 罗昭洋, 等. 黏滞介质Q偏移技术在准噶尔盆地南缘低信噪比地区的应用[J]. 石油地球物理勘探, 2018, 53(增刊1): 94-99. MA Junyan, ZHANG Long, LUO Zhaoyang, et al. Q migration of low-SNR seismic data for viscoelastic media in Southern Junggar Basin[J]. Oil Geophysical Prospecting, 2018, 53(S1): 94-99. |
| [3] |
妥军军, 谭佳, 罗昭洋, 等. 叠前深度偏移技术在齐古复杂构造成像中的应用[J]. 石油地球物理勘探, 2018, 53(增刊1): 100-106. TUO Junjun, TAN Jia, LUO Zhaoyang, et al. Prestack depth migration for Qigu complex structure imaging[J]. Oil Geophysical Prospecting, 2018, 53(S1): 100-106. |
| [4] |
王华忠, 冯波, 王雄文, 等. 地震波反演成像方法与技术核心问题分析[J]. 石油物探, 2015, 54(2): 115-125. WANG Huazhong, FENG Bo, WANG Xiongwen, et al. Analysis of seismic inversion imaging and its technical core issues[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 115-125. DOI:10.3969/j.issn.1000-1441.2015.02.001 |
| [5] |
王咸彬, 吴成梁. 散乱数据插值方法及其在背景速度建模中的应用[J]. 石油物探, 2017, 56(1): 126-140. WANG Xianbin, WU Chengliang. Scattered data interpolation methods and its application in background velocity model building[J]. Geophysical Prospecting for Petroleum, 2017, 56(1): 126-140. DOI:10.3969/j.issn.1000-1441.2017.01.015 |
| [6] |
丁继才, 孙文博, 黄小刚, 等. 海上地震数据全波形反演实际应用[J]. 石油物探, 2017, 56(1): 75-80. DING Jicai, SUN Wenbo, HUANG Xiaogang, et al. The strategies of FWI realization for marine seismic data[J]. Geophysical Prospecting for Petroleum, 2017, 56(1): 75-80. DOI:10.3969/j.issn.1000-1441.2017.01.009 |
| [7] |
Lailly P.The seismic inversion problem as a sequence of before stack migration[C].Conference on Inversion Scattering: Theory and Application, 1983, 206-220.
|
| [8] |
Tarantola A. Inversion of seismic reflection data in the acoustic approximation[J]. Geophysics, 1984, 49(8): 1259-1266. DOI:10.1190/1.1441754 |
| [9] |
刘定进, 胡光辉, 蔡杰雄, 等. 高斯束层析与全波形反演联合速度建模[J]. 石油地球物理勘探, 2019, 54(5): 1046-1056. LIU Dingjin, HU Guanghui, CAI Jiexiong, et al. A joint velocity model building method with Gaussian beam tomography and full waveform inversion for land seismic data[J]. Oil Geophysical Prospecting, 2019, 54(5): 1046-1056. |
| [10] |
杨勤勇, 胡光辉, 王立歆. 全波形反演研究现状及发展趋势[J]. 石油物探, 2014, 53(1): 77-83. YANG Qinyong, HU Guanghui, WANG Lixin. Research status and development trend of full waveform inversion[J]. Geophysical Prospecting for Petroleum, 2014, 53(1): 77-83. DOI:10.3969/j.issn.1000-1441.2014.01.011 |
| [11] |
韩如冰, 郎超. 频率域八阶NAD有限差分模拟及全波形反演[J]. 石油地球物理勘探, 2019, 54(6): 1254-1266. HAN Rubing, LANG Chao. The eighth-order frequency-domain NAD method and full-waveform inversion[J]. Oil Geophysical Prospecting, 2019, 54(6): 1254-1266. |
| [12] |
秦宁, 王延光, 杨晓东, 等. 时域全波形反演影响因素分析及井数据约束探索[J]. 地球物理学进展, 2015, 30(1): 210-216. QIN Ning, WANG Yanguang, YANG Xiaodong, et al. Analysis of influencing factors and exploration of well constrained for full waveform inversion in time domain[J]. Progress in Geophysics, 2015, 30(1): 210-216. |
| [13] |
Rüger A, Stork C.Interpretive Full Waveform Inversion using region constraints[C].SEG Technical Program Expanded Abstract, 2012, 31: 1-5.
|
| [14] |
Peters B, Felix J, Felix H. Constraints versus penal-ties for edge-preserving full-waveform inversion[J]. The Leading Edge, 2017, 36(1): 94-100. DOI:10.1190/tle36010094.1 |
| [15] |
Biondi B, Almomin A. Tomographic full-waveform inversion (TFWI) by combining FWI and wave-equation migration velocity analysis[J]. The Leading Edge, 2013, 32(9): 1074-1080. DOI:10.1190/tle32091074.1 |
| [16] |
李海山, 杨午阳, 雍学善. 三维一阶速度-应力声波方程全波形反演[J]. 石油地球物理勘探, 2018, 53(4): 730-736. LI Haishan, YANG Wuyang, YONG Xueshan. Three-dimensional full waveform inversion based on the first-order velocity-stress acoustic wave equation[J]. Oil Geophysical Prospecting, 2018, 53(4): 730-736. |
| [17] |
包乾宗, 陈俊霓, 吴浩. 基于地震数据包络的多尺度全波形反演方法[J]. 石油物探, 2018, 57(4): 584-591. BAO Qianzong, CHEN Junni, WU Hao. Multi-scale full waveform inversion based on logarithmic envelope of seismic data[J]. Geophysical Prospecting for Petroleum, 2018, 57(4): 584-591. DOI:10.3969/j.issn.1000-1441.2018.04.012 |
| [18] |
高福春, Paul W, R Gerhard P. 全波形反演的一个新目标函数:数据域中的微分相似优化[J]. 石油物探, 2017, 56(1): 26-30. GAO Fuchun, Paul W, R Gerhard P. A new objective function for full waveform inversion:differential semblance optimization in data domain[J]. Geophysical Prospecting for Petroleum, 2017, 56(1): 26-30. DOI:10.3969/j.issn.1000-1441.2017.01.003 |
| [19] |
Li Y G, Oldenburg D. W. Incorporating geologic dip information into geophysical inversions[J]. Geophysics, 2000, 65(1): 148-157. |
| [20] |
Lelievre P G, Oldenburg D W. A comprehensive study of including structural orientation information in geophysical inversions[J]. Geophysics Journal International, 2009, 178: 623-637. DOI:10.1111/j.1365-246X.2009.04188.x |
| [21] |
Hamid H, Pidlisecky A. Structurally constrained im-pedance inversion[J]. Interpretation, 2016, 4(4): T577-T589. DOI:10.1190/INT-2016-0049.1 |
| [22] |
Wahba G, Sen M K, Srinivasan S.Splines models for observational data[C].Society for Applied and Industrial Mathematics, 1990, 480.
|
| [23] |
彭海龙, 邓勇, 赫建伟, 等. 基于断层与层位约束的3D速度建模方法在消除断层阴影中的应用研究[J]. 地球物理学进展, 2017, 32(6): 2520-2526. PENG Hailong, DENG Yong, HE Jianwei, et al. Resolving fault shadow problems by pre-stack depth migration based on 3D velocity model building with fault and horizon constrained interpretation[J]. Progress in Geophysics, 2017, 32(6): 2520-2526. |



 李振春, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email:
李振春, 山东省青岛市经济技术开发区长江西路66号中国石油大学(华东)地球科学与技术学院, 266580。Email: