② 地球内部多尺度成像湖北省重点实验室, 湖北武汉 430074
② Hubei Subsurface Multiscale Imaging Key Laboratory, Wuhan, Hubei 430074, China
根据惠更斯原理,震源激发的一次球面波遇到不连续体时,该不连续体会作为二次震源产生绕射波场。绕射波可以照明一次反射波难以照明的缝洞、断层、尖灭点等不规则地质目标体,对该类探区地下储层探测有重要意义[1-2]。然而,绕射波相对于反射波能量往往较低,在溶洞发育的碳酸盐岩地区,若存在较强反射界面,常规成像剖面中绕射波能量往往会被掩盖[3]。因此,在特定的地震地质条件下,开发合适的绕射波成像方法,突出绕射能量有重要的应用价值[4-6]。
通常,实现绕射波成像可以在数据域先进行绕射波和反射波的分离再成像,也可以在全波场数据成像过程中对反射波能量进行压制而实现绕射波成像。
先分离后成像的方法大多基于反射波与绕射波的运动学和动力学特征差异,在数据域进行反射波和绕射波分离,然后分别进行处理。Landa等[7]基于绕射波与反射波在共炮检距域的运动学特征差异提出绕射波剖面法(D-Section),通过描述沿绕射波时距曲线分布的波场值偏离其平均值的估计标准差以增强绕射点处的振幅。Nowak[8]利用绕射波和反射波同相轴轨迹差异,通过Radon变换从地震记录中分离出绕射波数据。刘太臣等[9]利用奇异值谱分析法压制共炮检距域中的反射波强能量线性信号,重构Hankel矩阵,提取绕射波信息。
先分离后成像的方法重点在于数据域的绕射波和反射波分离,而在成像过程中进行反射波压制实现绕射波成像则更多地依赖成像算子本身。Kirchhoff积分偏移方法高效灵活,可以用来实现绕射波成像。Moser等[10]根据第一菲涅耳带反射能量集中、绕射能量分散的特点,修改Kirchhoff积分偏移公式中的加权函数,从而提取绕射能量。Klokov等[11]利用平面波分解和Radon变换的方法实现倾角道集内绕射波和反射波能量的分离。为达到更好的反射能量压制效果,Klokov等[12]又在前期研究基础上提出在倾角域使用相似谱分析,以拾取更准确的反射同相轴顶点。Hou等[13]则将倾角道集按角度重新编码,使拟双曲线形态的反射波同相轴变成了噪点,然后利用混合滤波方法去除反射波能量。随着计算技术的发展,基于波动方程的成像方法也被用于绕射波成像。Nakata等[14]提出几何平均成像条件下的逆时偏移(Reverse Time Migration,RTM)成像,该方法通过修改互相关成像条件,将检波器反传波场的算术平均项更改为几何平均项,从而提取绕射信息。Liu等[15]则根据倾角道集内表现为噪点的反射波和表现为直线的绕射波同相轴之间的形态差异滤除反射信号,实现绕射波的偏移成像。
实际上,倾角道集中反射波和绕射波的运动学特征依赖于偏移算子[16-19]。研究不同偏移算子情况下绕射波在倾角域的特征,然后基于合适的成像算子进行倾角域滤波实现绕射波成像。本文从倾角域中绕射波和反射波共成像点道集的形态差异入手,利用RTM和Kirchhoff积分偏移分别对特定的模型数据进行倾角域角度道集输出,对比两种成像方法在绕射波成像能力方面的差异并分析原因,最后基于RTM倾角道集,利用中值滤波提取绕射波信息以达到对绕射波偏移成像的目的。
1 理论方法 1.1 倾角域RTMRTM成像过程简要概括为:由震源端外推波场记录地下每个成像点不同时刻的波场值;然后对地震记录在时间方向上进行反向外推并存储地下每个成像点不同时刻的波场值[20-21];最后利用成像条件进行成像。经典RTM的互相关成像条件[22]可以表示为
| $ {\mathit{{I}}_{{\rm{RTM}}}}(\mathit{\boldsymbol{x}}) = \sum\limits_{t = 0}^{{t_{ {\rm{max}} }}} {{u_{\rm{s}}}} (\mathit{\boldsymbol{x}},t){u_{\rm{r}}}(\mathit{\boldsymbol{x}},t) $ | (1) |
式中:us(x, t)和ur(x, t)分别为炮点和检波点波场;x为地下成像点的位置;tmax为最大记录时间;IRTM(x)为逆时偏移成像结果。在正传源端波场和反推检波端波场时,通过计算波印廷矢量可以获得波场的传播方向。波印廷矢量可表示为[23-24]
| $ \mathit{\boldsymbol{P}} = - \nabla u\frac{{\partial u}}{{\partial t}}u $ | (2) |
式中:P为波的传播方向矢量;
| $ {\theta _{{\rm{s,r}}}} = \frac{{{\mathit{\boldsymbol{P}}_{\rm{s}}} \cdot {\mathit{\boldsymbol{P}}_{\rm{r}}}}}{{|{\mathit{\boldsymbol{P}}_{\rm{s}}}| \times |{\mathit{\boldsymbol{P}}_{\rm{r}}}|}} $ | (3) |
| $ {\theta _{{\rm{s,}}z}} = \frac{{{\mathit{\boldsymbol{P}}_{\rm{s}}} \cdot \mathit{\boldsymbol{Z}}}}{{|{\mathit{\boldsymbol{P}}_{\rm{s}}}|}} $ | (4) |
| $ {\theta _{\rm{d}}} = \frac{{{\theta _{{\rm{s,r}}}}}}{2} - {\theta _{{\rm{s,}}z}} $ | (5) |
式中:θs, r为入射波与反射波的夹角,即张角;θd为反射界面法向矢量与垂直矢量Z的夹角,即需要计算的界面倾角;θs,z为入射波与Z的夹角。

|
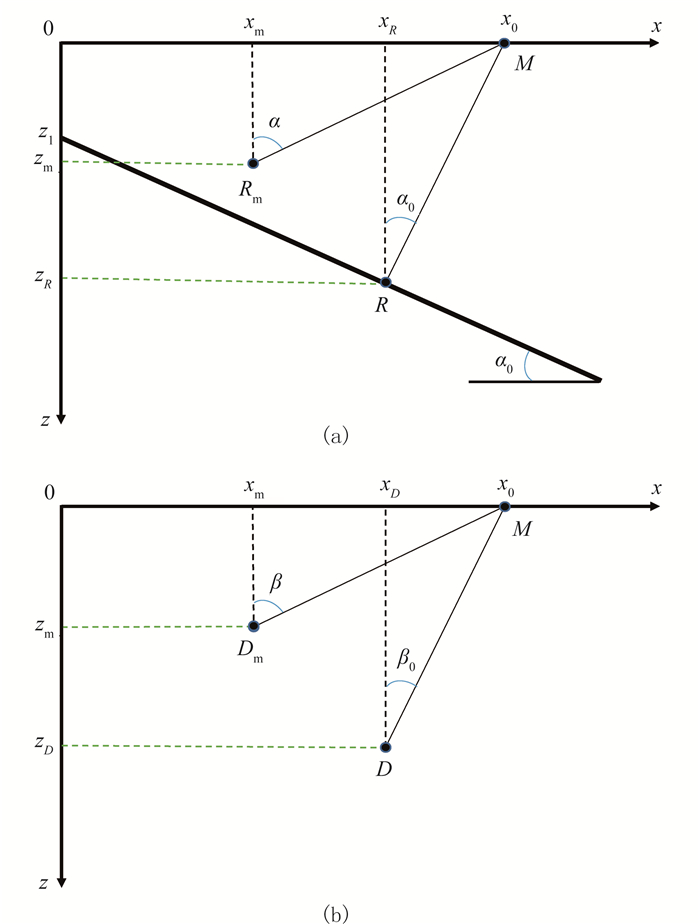
图 1 简单介质情况下地下反射界面(a)和绕射点(b)与炮检点的几何关系示意图 |
远场近似下Kirchhoff偏移公式[25]为
| $ I(\mathit{\boldsymbol{x}}) = \frac{1}{{2\pi }}\int {\rm{d}} \xi \frac{{ {\rm{cos}} \theta }}{{vr}}\frac{{\partial u(\xi ,t)}}{{\partial t}} $ | (6) |
式中:ξ为地面点坐标;θ为成像点处入射射线与法线的夹角;v为成像点处地震波传播速度;r为成像点与检波器之间的距离。
通常,Kirchhoff积分深度偏移需要进行旅行时计算。基于旅行时梯度场,可以方便地得到炮点波场和检波点的波场传播方向矢量Ps和Pr[26-27]
| $ {\mathit{\boldsymbol{P}}_{\rm{s}}} = (\frac{{\partial {T_{\rm{s}}}}}{{\partial x}},\frac{{\partial {T_{\rm{s}}}}}{{\partial z}}) $ | (7) |
| $ {\mathit{\boldsymbol{P}}_{\rm{r}}} = (\frac{{\partial {T_{\rm{r}}}}}{{\partial x}},\frac{{\partial {T_{\rm{r}}}}}{{\partial z}}) $ | (8) |
式中Ts和Tr分别为炮点和检波点旅行时场。进而通过式(3)~式(5)可计算倾角。
1.3 中值滤波对输出倾角道集进行中值滤波,达到分离绕射波的目的[15, 28]
| $ {I_{{\rm{ diff }}}}(\mathit{\boldsymbol{x}}) = \sum\limits_{i = 0}^n {{M_{{\theta _{\rm{d}}} \in [{m_i} - n,{m_i} + n]}}} [I(\mathit{\boldsymbol{x}},{\theta _{\rm{d}}})] $ | (9) |
式中:Idiff为绕射波场成像结果;n为滑动窗口的总数量;mi为滤波窗口的中值;Mθd表示沿倾角θd方向的中值滤波算子,其滑动窗口范围为[mi-n, mi+n],通过调控n值不同程度地抑制反射波能量。将滤波后的倾角道集叠加可得到绕射波成像结果。
2 倾角域波特征分析均匀介质情况下反射和绕射点的自激自收示意图如图 2所示。在几何地震学假设下,针对地下反射界面(图 2a),自激自收记录与地下反射点关系为
| $ {x_0} = {x_R} + {z_R} {\rm{tan}} {\alpha _0} $ | (10) |
| $ t = \frac{{2{z_R}}}{{v {\rm{cos}} {\alpha _0}}} $ | (11) |
|
图 2 自激自收观测下反射(a)和绕射(b)时深关系示意图 |
式中:x0为地表自激自收点M的横坐标;t为M点自激自收的旅行时;α0为地下界面真实倾角;(xR, zR)为地下任意反射点R的坐标。在单反射界面情况下,反射界面深度可以表示为
| $ {z_R}({x_R}) = {z_1} + {x_R} {\rm{tan}} {\alpha _0} $ | (12) |
式中z1为反射界面与z轴交点的深度。由式(10)和式(12)可得
| $ {z_R}({x_0}) = ({z_1} {\rm{cos}} {\alpha _0} + {x_0} {\rm{sin}} {\alpha _0}){\rm{cos}} {\alpha _0} $ | (13) |
将式(13)代入式(11),可得到任意检波点的自激自收时间
| $ t({x_0}) = \frac{{2({z_1} {\rm{cos}} {\alpha _0} + {x_0} {\rm{sin}} {\alpha _0})}}{v} $ | (14) |
偏移过程是将地表数据剖面u(x0, t)转换成地下成像剖面R(xm, zm), 即
| $ {x_{\rm{m}}} = {x_0} - \frac{{{v_{\rm{m}}}t}}{2} {\rm{sin}} \alpha $ | (15) |
| $ {z_{\rm{m}}} = \frac{{{v_{\rm{m}}}t}}{2} {\rm{cos}} \alpha $ | (16) |
式中:α为偏移倾角,也即倾角道集横轴坐标;vm为偏移速度。将式(14)代入式(15)和式(16),可得
| $ {x_{\rm{m}}} = {x_0}(1 - \frac{{{v_{\rm{m}}}}}{v} {\rm{sin}} {\alpha _0} {\rm{sin}} \alpha ) - \frac{{{x_{\rm{m}}}}}{v}{z_1}{\rm{sin}} {\alpha _0} {\rm{sin}} \alpha $ | (17) |
| $ {z_{\rm{m}}} = {x_0}\frac{{{v_{\rm{m}}}}}{v} {\rm{sin}} {\alpha _0} {\rm{cos}} \alpha + \frac{{{v_{\rm{m}}}}}{v}{z_1}{\rm{cos}} {\alpha _0}{\rm{cos}} \alpha $ | (18) |
联立式(17)和式(18)消去x0,并将xm替换为x,zm替换为zα(x, α),可得倾角道集的几何形态曲线
| $ {z_\alpha }(x,\alpha ) = \frac{{{z_1}( {\rm{cos}} {\alpha _0} + x {\rm{sin}} {\alpha _0}){v_{\rm{m}}} {\rm{cos}} \alpha }}{{v - {v_{\rm{m}}} {\rm{sin}} {\alpha _0} {\rm{sin}} \alpha }} $ | (19) |
对式(19)求关于α的偏导数,有
| $ \frac{{\partial {z_\alpha }(x,\alpha )}}{{\partial \alpha }} = \frac{{({z_1} {\rm{cos}} {\alpha _0} + x {\rm{sin}} {\alpha _0})({v_{\rm{m}}} {\rm{sin}} {\alpha _0} - v {\rm{sin}} \alpha )}}{{{{(v - {v_{\rm{m}}} {\rm{sin}} {\alpha _0} {\rm{sin}} \alpha )}^2}}} $ | (20) |
令式(20)等于0,可得
| $ {\rm{sin}} \alpha = \frac{{{v_{\rm{m}}}}}{v} {\rm{sin}} {\alpha _0} $ | (21) |
由式(21)可知,在偏移速度正确,即vm=v的情况下,α=α0为式(19)的一个极小值点。因此,对于当偏移速度正确时,倾角道集中反射波是一个有极小值点的拟双曲线,且该曲线极小值点对应着反射界面真实的界面深度和真实的界面倾角。
均匀介质中,在几何地震学假设下,针对地下绕射点(图 2b),其自激自收记录与地下绕射点关系为
| $ {x_0} = {x_D} + {z_D} {\rm{tan}} {\beta _0} $ | (22) |
| $ t({x_0}) = \frac{{2\sqrt {{{({x_0} - {x_D})}^2} + z_D^2} }}{v} $ | (23) |
式中:β0为地表自激自收点M和绕射点D(xD, zD)连线与Z的夹角。同样将地表数据剖面u(x0, t)转换成地下成像剖面D(xm, zm),即
| $ {x_{\rm{m}}} = {x_D} + {z_D}\frac{{v {\rm{sin}} {\beta _0} - {v_{\rm{m}}} {\rm{sin}} \beta }}{{v {\rm{cos}} {\beta _0}}} $ | (24) |
| $ {z_{\rm{m}}} = {z_D}\frac{{{v_{\rm{m}}} {\rm{cos}} \beta }}{{v {\rm{cos}} {\beta _0}}} $ | (25) |
式中:β为M点和Dm点连线关于Z的夹角。联立式(24)和式(25),消去β0,并将xm替换为x,zm替换为zβ(x, β),可得
| $ \begin{array}{*{20}{c}} {{z_\beta }(x,\beta ) = \frac{1}{{{v^2} - v_{\rm{m}}^2 {\rm{sin}}{ ^2}\beta }}\{ {v_{\rm{m}}} {\rm{cos}} \beta [(x - {x_D}){v_{\rm{m}}} {\rm{sin}} \beta + }\\ {\sqrt {z_D^2({v^2} - v_{\rm{m}}^2 {\rm{sin}}{ ^2}\beta ) + {{(x - {x_D})}^2}{v^2}} ]\} } \end{array} $ | (26) |
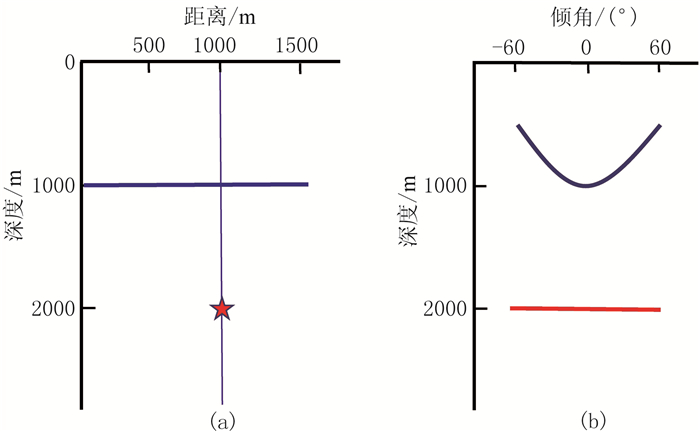
由式(26)可见,在偏移速度正确且记录点位于绕射点正上方的情况下,即vm=v、x=xD时,该式可简写为zβ(x, β)=zD,此时关于绕射点的倾角道集是一条水平的直线。在x≠xD情况下,绕射波倾角道集表现为一条没有极值点的曲线[29]。图 3展示了一个绕射点和一个水平反射界面在倾角道集的几何形态,其中蓝线表示水平反射界面,星号表示绕射点。在图 3b展示的地表1000m处的倾角道集中,绕射波被拉平,位于真实深度处,反射波深度—倾角关系表现为拟双曲线形态,曲线顶点对应反射界面真实的倾角和深度。
|
图 3 典型的反射和绕射模型(a)及其对应的倾角道集形态(b)示意图 |
为验证以上理论分析的正确性,选取一个两层模型,网格数为400×400,网格间距为10m×10m。模型速度如图 4所示,在下层介质中包含一高速绕射点。利用有限差分法进行模拟,正演参数包括:子波为主频20Hz的雷克子波,炮间距为50m,共81炮,最大炮检距为1500m,采用双边接收,检波器间距为10m。Kirchhoff积分偏移和RTM的成像结果如图 5所示,其输出的倾角道集如图 6所示。

|
图 4 两层介质速度模型 |

|
图 5 两层模型Kirchhoff积分偏移(a)和RTM(b)的成像结果对比 |
|
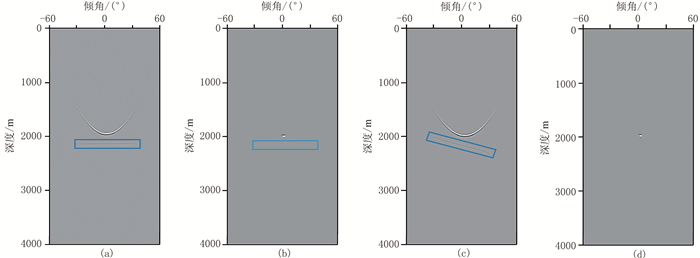
图 6 两层模型Kirchhoff积分偏移和RTM在不同CDP处倾角道集对比 (a)CDP200,Kirchhoff积分偏移;(b)CDP200,RTM;(c)CDP250,Kirchhoff积分偏移;(d)CDP250,RTM |
在图 6a和图 6b中,在绕射点正上方(CDP200)绕射点倾角道集响应均为直线。对于反射波同相轴,Kirchhoff方法为一条拟双曲线且能量聚焦在拟双曲线的顶点,而RTM法则聚焦为一个点,两者反射波能量主要聚集在真实的界面深度和倾角处。图 6c和图 6d展示了绕射点右侧(CDP250)的倾角道集,其中Kirchhoff方法得到绕射波的响应为一条没有驻点的曲线,RTM方法则看不到绕射波的响应。造成图 6c与图 6d存在差异原因可以归结为二者成像的实现方式不同。经典Kirchhoff积分法偏移的实现方式是利用输出道的观点,依照旅行时关系在成像域进行数据到成像结果的投影;而RTM则基于全波波动方程,采用有限差分进行波场外推,在成像点进行相关成像。相比而言,后者对反射波场有更好的聚焦能力。
3 数值实验由于RTM偏移算子对反射波聚焦能力更好,本文采用RTM进行倾角道集输出,并在倾角域进行中值滤波处理,以便能有效滤除倾角道集中位于真实倾角和深度位置处的反射波能量,保留绕射波能量,实现绕射波成像。
首先,基于上文两层模型CDP200和CDP250处倾角道集,进行中值滤波处理,结果如图 7所示。对比图 7与图 6b和图 6d可以看出,两处倾角道集中反射波的点状响应被视作“噪点”滤除而绕射波同相轴得到有效的保留,其最后叠加成像结果如图 8所示。对比图 5和图 8,可以看出图 5中反射界面能量被滤除而绕射点能量得到保留。

|
图 7 中值滤波后CDP200(a)和CDP250(b)处倾角道集 |

|
图 8 RTM绕射波成像结果 |
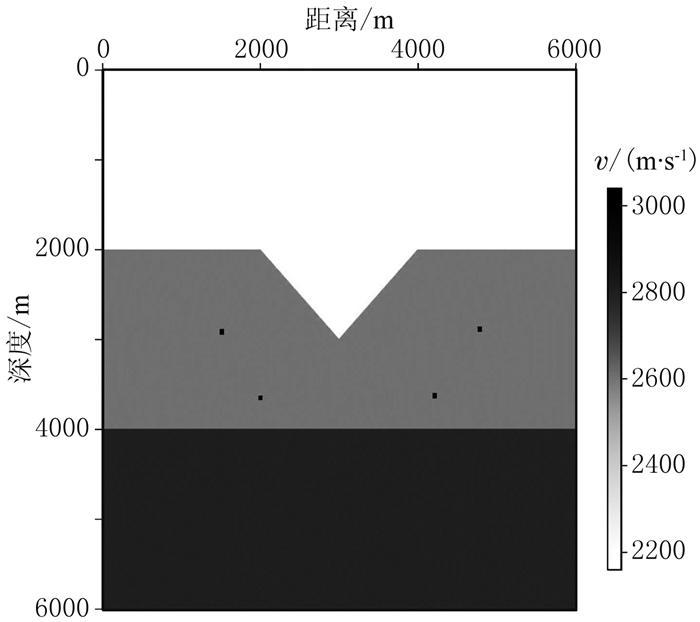
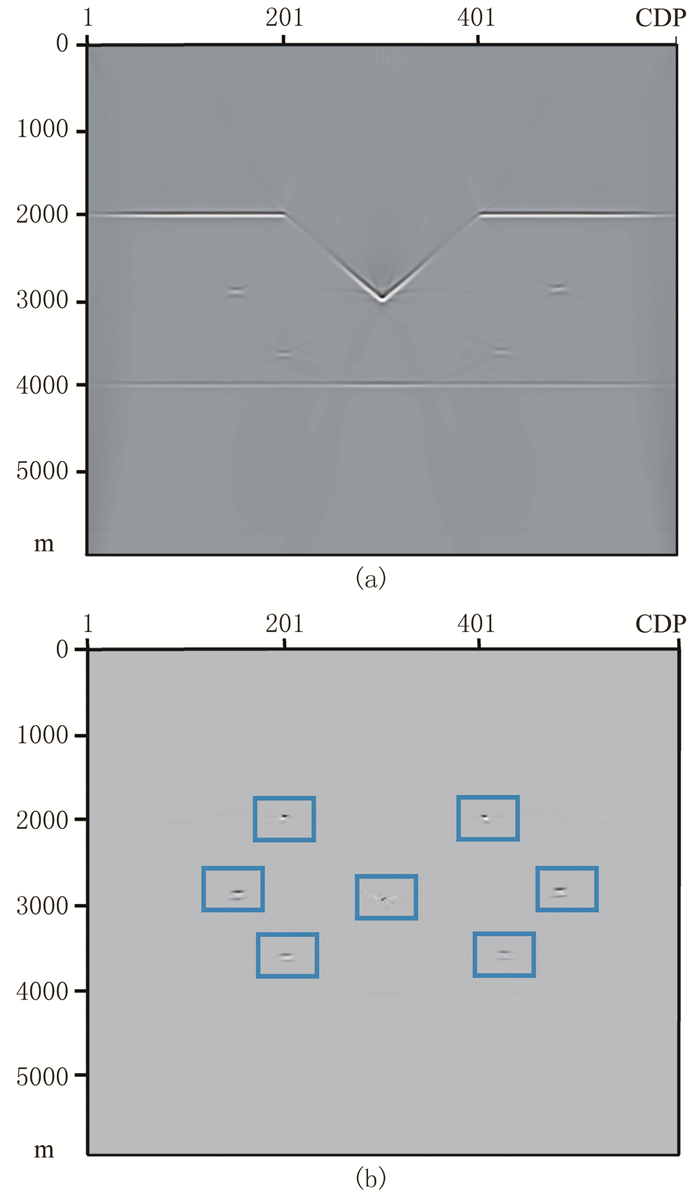
然后,采用稍复杂的绕射体模型(图 9)进一步测试本文方法效果。如图 9所示,该模型四个绕射体位于第二层介质中,界面角点也可产生绕射波。模型网格数为600×600,网格间距为10m×10m。采用主频为20Hz的雷克子波用有限差分法进行波场模拟,双边接收,共121炮,炮间距为50m,最大炮检距为1500m,检波器间距为10m。传统RTM成像和绕射波RTM成像结果如图 10所示,可以看出,在绕射波RTM成像剖面中,反射界面能量被充分压制,蓝色方框所示的绕射点的能量则得到了有效的保留。
|
图 9 绕射体模型 |
|
图 10 绕射体模型常规RTM(a)和绕射波RTM(b)成像结果对比 蓝色方框所示为绕射点位置 |
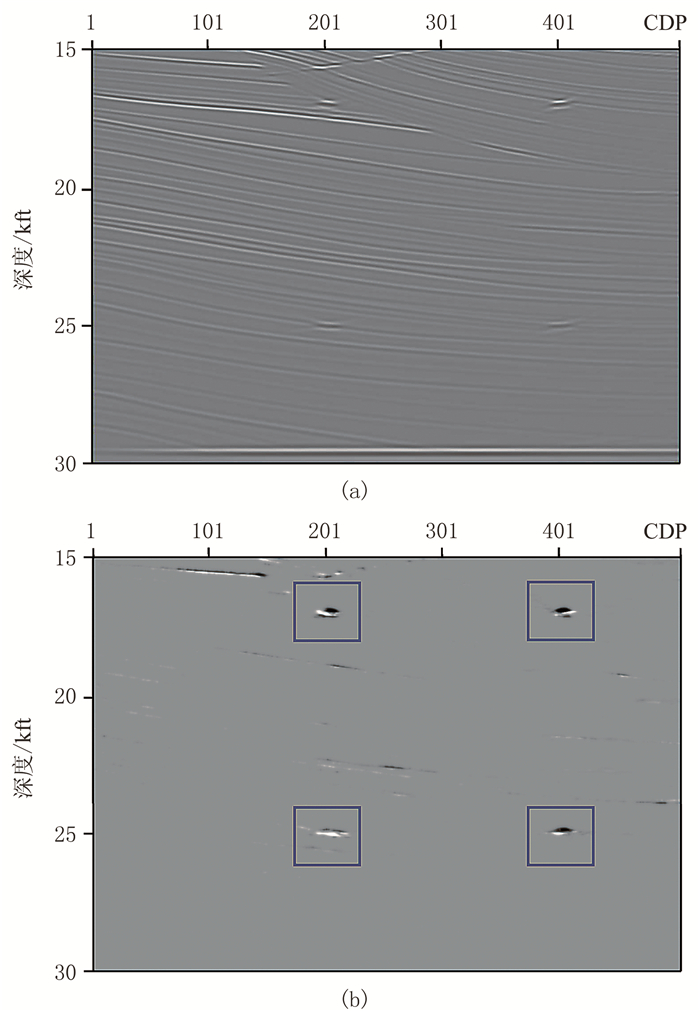
最后,采用含绕射点的部分Sigbee2A模型验证本文方法的有效性,其速度模型如图 11所示。该模型网格数为500×700,采样间隔为25ft×25ft。对该模型模拟数据采用经典RTM成像和RTM绕射波成像,结果如图 12所示,中值滤波前、后CDP200处倾角道集如图 13所示。由图 12可以看出,常规RTM成像绕射波波能量淹没在反射同相轴中,在成像剖面中不够明显。RTM绕射波成像则使绕射波的能量得到保留,反射波的能量得到极大的削弱, 突出了绕射点所在的位置。由于该模型较为复杂,在该情况下采用波印廷矢量,存在严重的波场交叉,可能得到不准确的波场传播方向,使得计算出来的倾角不够准确,反射波的响应很难聚焦为“点”,而是表现为“短线”(图 13a),但在该情况下反射波还是被较彻底地去除了(图 13b)。

|
图 11 部分Sigbee2A速度模型 |
|
图 12 部分Sigbee2A模型常规RTM(a)和绕射波RTM(b)成像结果对比 蓝色方框所示为绕射点位置 |
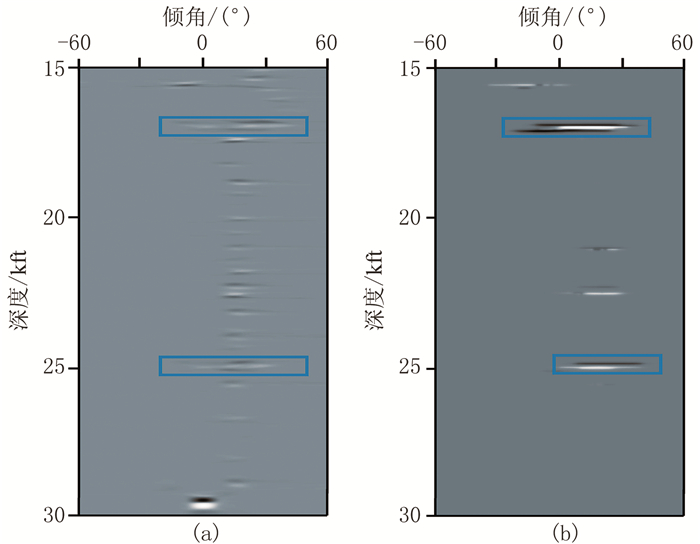
|
图 13 部分Sigbee 2A模型CDP200处中值滤波处理前(a)、后(b)倾角道集对比 蓝色方框内为绕射波在倾角道集的响应 |
当绕射点位于模型深部,RTM低频噪声对绕射波成像影响有限。但对于某些构造模型,在低频噪声与绕射点重叠的部分时,为消除低频噪声对成像剖面质量的影响,可以根据低频噪声的角度特性,在互相关成像条件中添加角度加权因子[30-34]。
4 结论本文对倾角域反射波和绕射波的几何形态进行了理论分析,利用Kirchhoff积分偏移和RTM算子分别进行倾角道集输出,研究了不同成像算子在倾角域对绕射波的成像能力。Kirchhoff积分偏移计算的倾角道集中,反射波同相轴形态表现为下凹的拟双曲线形,驻点位于实际倾角位置,绕射波同相轴则为一条拉平的直线;RTM得到的倾角道集中反射波同相轴表现为孤立的“噪点”,绕射波同相轴为一条直线。数值实验结果表明,在倾角域,RTM算子对反射波有着更好的聚焦能力。在RTM输出的倾角道集中,利用中值滤波可将反射波能量滤除而保留绕射波能量,进而实现绕射波的成像。
| [1] |
Sun Z, Hou X Y, Zhang D, et al.Complex carbonate reservoir characterization using diffraction-imaging dataset[C].SEG Technical Program Expanded Abstracts, 2017, 36: 986-990.
|
| [2] |
Protasov M, Tcheverda V, Lisitsa V, et al.Detection of highly cavernous subseismic zones in carbonate re-servoirs by scattered waves[C].SEG Technical Program Expanded Abstracts, 2017, 36: 1001-1005.
|
| [3] |
Reynolds S, Beshry B, Hunt L, et al.Reason, diffraction imaging, and interpretive confidence: Case histories[C].SEG Technical Program Expanded Abstracts, 2017, 36: 996-1000.
|
| [4] |
曲寿利, 朱生旺, 赵群, 等. 碳酸盐岩孔洞型储集体地震反射特征分析[J]. 地球物理学报, 2012, 55(6): 2053-2061. QU Shouli, ZHU Shengwang, ZHAO Qun, et al. Analysis of seismic reflection characters for carbonate Karst reservoir[J]. Chinese Journal of Geophysics, 2012, 55(6): 2053-2061. |
| [5] |
朱生旺, 李佩, 宁俊瑞. 局部倾角滤波和预测反演联合分离绕射波[J]. 地球物理学报, 2013, 56(1): 280-288. ZHU Shengwang, LI Pei, NING Junrui. Reflection/diffraction separation with a hybrid method of local dip filter and prediction inversion[J]. Chinese Journal of Geophysics, 2013, 56(1): 280-288. |
| [6] |
刘培君, 黄建平, 李振春, 等. 一种基于反稳相的深度域绕射波分离成像方法[J]. 石油地球物理勘探, 2017, 52(5): 967-973. LIU Peijun, HUANG Jianping, LI Zhenchun, et al. A diffraction imaging method in the depth domain driven by anti-stationary phase strategy[J]. Oil Geophysical Prospecting, 2017, 52(5): 967-973. |
| [7] |
Landa E, Keydar S. Seismic monitoring of diffraction images for detection of local heterogeneities[J]. Geophysics, 1998, 63(3): 1093-1100. DOI:10.1190/1.1444387 |
| [8] |
Nowak E J.Diffractor localization via weighted Radon transforms[C].SEG Technical Program Expanded Abstracts, 2004, 23: 2108-2111.
|
| [9] |
刘太臣, 胡江涛, 王华忠, 等. 奇异值谱分析在绕射波分离及成像中的应用[J]. 石油物探, 2014, 53(1): 46-53. LIU Taichen, HU Jiangtao, WANG Huazhong, et al. Diffraction wavefield separation and imaging using singular spectrum analysis[J]. Geophysical Prospecting for Petroleum, 2014, 53(1): 46-53. DOI:10.3969/j.issn.1000-1441.2014.01.007 |
| [10] |
Moser T, Howard B C. Diffraction imaging in depth[J]. Geophysical Prospecting, 2008, 56(5): 627-641. DOI:10.1111/j.1365-2478.2007.00718.x |
| [11] |
Klokov A, Fomel S. Separation and imaging of seismic diffractions using migrated dip-angle gathers[J]. Geophysics, 2012, 77(6): S131-S143. DOI:10.1190/geo2012-0017.1 |
| [12] |
Klokov A, Baina R, Landa E.Separation and imaging of seismic diffractions in dip angle domain[C].Extended Abstracts of 72nd EAGE Conference & Exhibition, 2010.
|
| [13] |
Hou X, Sun S Z.A new method for diffraction separation based on trace randomized realignment and denoising in migrated dip-angle domain[C].Extended Abstracts of 80th EAGE Conference & Exhibition, 2018, 1-5.
|
| [14] |
Nakata N, Beroza G C. Reverse time migration for microseismic sources using the geometric mean as an imaging condition[J]. Geophysics, 2016, 81(2): KS51-KS60. |
| [15] |
Liu L, Vincent E, Ji X, et al. Imaging diffractors using wave-equation migration[J]. Geophysics, 2016, 81(6): S459-S468. DOI:10.1190/geo2016-0029.1 |
| [16] |
Klokov A, Fomel S. Selecting an optimal aperture in Kirchhoff migration using dip-angle images[J]. Geophysics, 2013, 78(6): S243-S254. DOI:10.1190/geo2013-0109.1 |
| [17] |
Dafni R, Symes W W. Scattering and dip angle decomposition based on subsurface offset extended wave-equation migration[J]. Geophysics, 2016, 81(3): S119-S138. |
| [18] |
Dafni R, Symes W W. Kinematic artifacts in the subsurface-offset extended image and their elimination by a dip-domain specularity filter[J]. Geophysics, 2016, 81(6): S477-S495. DOI:10.1190/geo2016-0115.1 |
| [19] |
徐辉. 倾角成像道集中反射波和绕射波特征分析及成像质量改善方法研究[J]. 石油物探, 2015, 54(2): 133-141. XU Hui. The analysis of characteristics of reflection and diffraction wave in dip angle gathers and the method for enhancing the imaging quality[J]. Geophysical Prospecting for Petroleum, 2015, 54(2): 133-141. DOI:10.3969/j.issn.1000-1441.2015.02.003 |
| [20] |
Baysal E, Kosloff D D, Sherwood J W C. Reverse-time migration[J]. Geophysics, 1983, 48(11): 1514-1524. DOI:10.1190/1.1441434 |
| [21] |
Baysal E, Kosloff D D, Sherwood J W C. A two-way nonreflecting wave equation[J]. Geophysics, 1984, 49(2): 132-141. |
| [22] |
Claerbout J F. Toward a unified theory of reflector mapping[J]. Geophysics, 1971, 36(3): 467-481. DOI:10.1190/1.1440185 |
| [23] |
Yoon K, Marfurt K J. Reverse-time migration using the Poynting vector[J]. Geophysical Exploration, 2006, 37(1): 102-107. DOI:10.1071/EG06102 |
| [24] |
吴成梁, 周阳, 胡江涛, 等. 高效逆时偏移角度道集生成方法研究[J]. 石油物探, 2018, 57(3): 404-418. WU Chengliang, ZHOU Yang, HU Jiangtao, et al. E-fficient generation of reverse time migration angle gathers[J]. Geophysical Prospecting for Petroleum, 2018, 57(3): 404-418. DOI:10.3969/j.issn.1000-1441.2018.03.010 |
| [25] |
Schneider W A. Integral formulation for migration in two and three dimensions[J]. Geophysics, 1978, 43(1): 49-76. |
| [26] |
Liu S, Wang H, Liu T, et al. Kirchhoff PSDM angle-gather generation based on the traveltime gradient[J]. Applied Geophysics, 2015, 12(1): 64-72. DOI:10.1007/s11770-014-0470-8 |
| [27] |
刘少勇, 蔡杰雄, 王华忠, 等. 山前带地震数据射线(束)叠前成像方法研究与应用[J]. 石油物探, 2012, 51(6): 598-605. LIU Shaoyong, CAI Jiexiong, WANG Huazhong, et al. Technology and application of beam ray prestack imaging method in foothill areas[J]. Geophysical Prospecting for Petroleum, 2012, 51(6): 598-605. DOI:10.3969/j.issn.1000-1441.2012.06.008 |
| [28] |
Jiang W, Liu Z and Zhang J.Diffraction imaging using reverse time migration with Poynting vectors[C].SEG Technical Program Expanded Abstracts, 2017, 36: 1028-1032.
|
| [29] |
Bai Y, Sun Z, Chen L, et al.Seismic diffraction separation in 2D and 3D space[C].Extended Abstracts of 73nd EAGE Conference & Exhibition, 2011.
|
| [30] |
唐永杰, 宋桂桥, 刘少勇, 等. 基于波长平滑算子的逆时偏移回转波假象去除方法[J]. 石油地球物理勘探, 2018, 53(1): 80-86. TANG Yongjie, SONG Guiqiao, LIU Shaoyong, et al. Turning wave false image removal based on wavelength-dependent smoothing operator in reverse time migration[J]. Oil Geophysical Prospecting, 2018, 53(1): 80-86. |
| [31] |
刘梦丽, 黄建平, 李闯, 等. 基于角度滤波成像的最小二乘逆时偏移[J]. 石油地球物理勘探, 2018, 53(3): 469-477. LIU Mengli, HUANG Jianping, LI Chuang, et al. Least-squares reverse time migration based on the angular filtering imaging condition[J]. Oil Geophysical Prospecting, 2018, 53(3): 469-477. |
| [32] |
Yoon K, Marfurt K J and Starr W.Challenges in reverse-time migration[C].SEG Technical Program Expanded Abstracts, 2004, 23: 1057-1060.
|
| [33] |
Zhang Y, Sun J.Practical issues of reverse time migration: true amplitude gathers, noise removal and harmonic-source encoding[C].ASEG Extended Abstracts, 2009, 1-5.
|
| [34] |
秦宁. VTI介质角度叠加逆时偏移[J]. 石油地球物理勘探, 2019, 54(2): 111-117. QIN Ning. Reverse time migration in VTI media based on ADCIGs[J]. Oil Geophysical Prospecting, 2019, 54(2): 111-117. |



 刘少勇, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院, 430074。Email:
刘少勇, 湖北省武汉市洪山区鲁磨路388号中国地质大学(武汉)地球物理与空间信息学院, 430074。Email: